2. 深圳市大族精密传动科技有限公司, 广东 深圳 518057
2. Dazu Laser Technology Industry Group Co., Ltd., Shenzhen, Guangdong 518057, P. R. China
与传统渐开线谐波减速器相比,双圆弧齿形谐波减速器具有承载力大、啮合齿数多、啮合间隙小、啮合精度高等优点,被广泛应用于机器人、航天航空、医疗器械、仪表设备等各个领域[1-2]。由于双圆弧刚轮采用非渐开线齿形,双圆弧齿形插齿刀几何参数的计算方法及变化规律较复杂,其刀具设计及齿廓加工工艺是谐波传动制造环节的重难点之一。同时由于插齿刀本身结构的特点,其切削刃投影与刀具理论齿形之间存在一定误差,使加工出来的刚轮齿形与理论设计齿形不一致[3-4]。因此开展双圆弧谐波传动刚轮插齿刀设计与齿形误差分析具有重要意义。
近年来,国内外学者对刚柔轮加工问题进行了研究。Lai等[5]提出了一种基于CAD/CAM的系统化几何造型技术,在刃形设计上采用分段逼近的方法可缩短设计周期,提高普通直齿插齿刀的加工精度;Kawalec等[6]对螺旋齿插齿加工过程建立数学模型进行有限元分析,提出增强齿根强度的顶圆角的设计方法;Lin等[7]讨论了渐开线插齿刀的设计原理和模型,提出反包络法等刀具设计方法,可提高插削刀具的精度和寿命;日本Youshino等[8]分析了插齿加工工艺,采用单元切除法设计了可加工任意齿廓形状的插齿刀,但刀具制造成本高,难以实现;Tsay等[9]提出了一种插齿刀参数优化方法,对渐开线齿形直齿插齿刀的切削过程进行分析,建立齿形优化数学模型,提高了插齿刀设计的理论齿形精度;辛洪兵[10]在2008年提出双圆弧谐波齿轮插齿刀,并申请专利,该刀具可以保证双圆弧谐波齿轮传动具有良好的综合性能,但未给出插齿刀齿廓具体求解方式;刘熙刚等[11]把滚刀作为基准齿形共轭出柔轮齿廓以及加工刚轮的插齿刀的齿廓,再由插齿刀加工出刚轮,通过控制刚柔轮的啮合侧隙来确定基准齿形刀具,该方法虽为刚柔轮加工刀具的设计提供了新思路,但因刚轮齿形的求解并不直接由柔轮齿形共轭得到,因此并不能完全保证柔轮与刚轮的共轭关系;聂少文等[12]利用插齿刀齿形推导双圆弧刚轮齿形,并对刀具齿形进行了包络验证,但未对插齿刀齿面相关参数进行分析研究;孟漪等[13]针对加工小模数渐开线齿廓刚轮的插齿刀提出采用变模数、变压力角的方法来进行设计,考虑了谐波齿轮变位系数较大时内齿圈刚轮直径大于分度圆直径的情况,该种方法适用于渐开线齿形刚轮刀具的设计;陈鹏等[14]以刚轮齿形为基础,利用齿廓法线法求解插齿刀齿形,采用包络法验证所求插齿刀齿形的正确性,并根据啮合侧隙及齿廓是否干涉研究了插齿刀的通用性;李佳等[15-16]针对插齿刀存在理论齿形误差的问题,提出了一种无理论刃形误差的渐开线齿轮插齿刀设计方法,该方法可在理论上避免刃形误差,可有效提高插齿精度,但插齿刀齿面多为自由曲面,刀具与制造工艺复杂,加工成本较高。
综上所述,渐开线齿形的插齿法加工研究相对较为成熟,目前针对加工双圆弧齿形的插齿刀的研究多为插齿刀理论齿形推导,而双圆弧谐波齿轮插齿刀齿面几何参数的计算方法和变化规律以及前后角对双圆弧插齿刀理论齿形误差的影响研究少有文献涉及;虽有学者提出无理论刃形误差的设计方法,但因制造困难,加工成本高,不能大面积推广。
笔者基于加工双圆弧齿形刚轮的插齿刀齿形,根据啮合原理采用运动学法建立插齿刀齿形及齿面数学模型研究刀具侧刃后角、侧刃前角等重要齿面参数的计算方法及其影响因素,并分析插齿刀几何参数对理论齿形误差的影响。
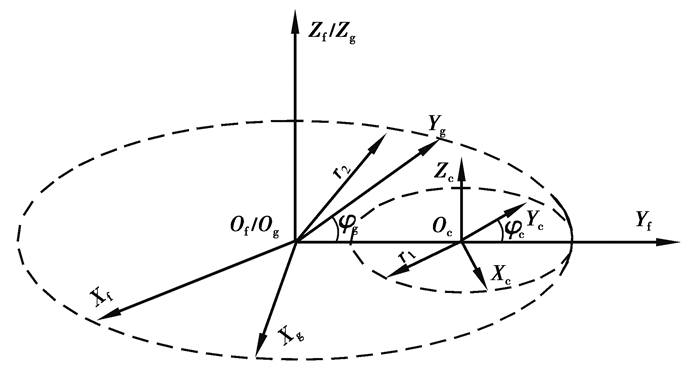
1 基于运动学法的双圆弧刚轮插齿刀齿形数学建模对刚轮运用运动学法求解插齿刀齿形时,需建立齿轮加工刀具的模型,该模型中将刚轮看作刀具,插齿刀看作被加工齿轮,从而利用刚轮齿形求解插齿刀齿形[12]。建立的齿轮加工刀具模型如图 1所示,齿轮加工刀具的过程可视为两个齿轮的内啮合,当插齿刀转角为φc时,刚轮相应转过角度φg,r1为插齿刀分度圆半径,r2为刚轮的分度圆半径。刚轮与插齿刀的啮合方程为
| $ \boldsymbol{n}_{\mathrm{g}} \cdot \boldsymbol{V}_{\mathrm{g}}^{\mathrm{cg}}=0, $ | (1) |
|
图 1 刚轮加工坐标系 Fig. 1 Rigid machining coordinate system |
式中:ng为刚轮齿廓法向量;Vggc为在刚轮坐标系中插齿刀与刚轮的相对速度矢量。
假定坐标系Sc(XcOcYc)、Sg(XgOgYg)和Sf(XfOfYf)分别与插齿刀、刚轮和机床刚性固接,则插齿刀转角φc和刚轮转角φg的关系为
| $ i_{\mathrm{cg}}=\frac{\varphi_{\mathrm{c}}}{\varphi_{\mathrm{g}}}=\frac{z_{\mathrm{g}}}{z_{\mathrm{c}}}, $ | (2) |
式中:icg为刚轮与插齿刀的传动比;zg为刚轮齿数;zc为插齿刀齿数。
在坐标系Sg(XgOgYg)中,刚轮齿面位置向量为
| $ \boldsymbol{r}_{\mathrm{g}}=x_{\mathrm{g}} \boldsymbol{i}_{\mathrm{g}}+y_{\mathrm{g}} \boldsymbol{j}_{\mathrm{g}}+z_{\mathrm{g}} \boldsymbol{k}_{\mathrm{g}}, $ | (3) |
式中:ig、jg、kg分别为X、Y、Z轴方向的单位向量。若刚轮上任一点为啮合点,在该处的啮合方程ng· Vggc=0一定成立;反之当齿廓上一个点的参数满足啮合方程时,则该点一定为啮合点。将齿廓方程与啮合方程联立得
| $ \left\{\begin{array}{c} \boldsymbol{r}_{\mathrm{g}}=x_{\mathrm{g}} \boldsymbol{i}_{\mathrm{g}}+y_{\mathrm{g}} \boldsymbol{j}_{\mathrm{g}}+z_{\mathrm{g}} \boldsymbol{k}_{\mathrm{g}}, \\ \boldsymbol{n}_{\mathrm{g}} \cdot \boldsymbol{V}_{\mathrm{g}}^{\mathrm{gc}}=0。\end{array}\right. $ | (4) |
方程的解即为啮合点[14-16]。利用坐标变换,把啮合点从刚轮坐标系Sg(XgOgYg)变换到插齿刀坐标系Sc(XcOcYc)中,即可得到插齿刀齿廓
| $ \boldsymbol{r}_{\mathrm{c}}=\boldsymbol{M}_{\mathrm{cg}} \cdot \boldsymbol{r}_{\mathrm{g}}, $ | (5) |
式中Mcg为刚轮坐标系到插刀坐标系的变换矩阵,
| $ \boldsymbol{M}_{\mathrm{cg}}=\left[\begin{array}{cccc} \cos \left(\varphi_{\mathrm{c}}-\varphi_{\mathrm{g}}\right) & \sin \left(\varphi_{\mathrm{c}}-\varphi_{\mathrm{g}}\right) & 0 & -E_{\mathrm{c}} \cdot \sin \left(\varphi_{\mathrm{c}}\right) \\ -\sin \left(\varphi_{\mathrm{c}}-\varphi_{\mathrm{g}}\right) & \cos \left(\varphi_{\mathrm{c}}-\varphi_{\mathrm{g}}\right) & 0 & -E_{\mathrm{c}} \cdot \cos \left(\varphi_{\mathrm{c}}\right) \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right], $ | (6) |
式中:φ1为插齿刀旋转角度;φ2为刚轮旋转角度;Ec为加工中心距。
利用坐标变换求得插齿刀在刚轮坐标系下的速度Vgc为
| $ \boldsymbol{V}_{\mathrm{g}}^{\mathrm{c}}=\boldsymbol{M}_{\mathrm{gc}} \cdot \boldsymbol{V}_{\mathrm{c}}^{\mathrm{c}}, $ | (7) |
式中:Mgc为Sc(XcOcYc)到Sg(XgOgYg)的坐标变换矩阵;Vcc为插齿刀在Sc(XcOcYc)坐标系中的线速度。
在坐标系Sg(XgOgYg)中刚轮与插齿刀的相对速度Vggc为
| $ \boldsymbol{V}_{\mathrm{g}}^{\mathrm{gc}}=\boldsymbol{V}_{\mathrm{g}}^{\mathrm{g}}-\boldsymbol{V}_{\mathrm{g}}^{\mathrm{c}}, $ | (8) |
式中Vgg为刚轮在Sg(XgOgYg)坐标系中的线速度。
将ng、Vggc代入式(1),解得φg,将φg带入式(2)求得φc,进而利用式(5)求得插齿刀齿廓rc。
以HD25120型号谐波减速器为例,其刚轮基本设计参数如表 1所示,刚轮齿形包括齿顶过渡段、凸齿廓段、公切线段、凹齿廓段、齿根过渡段。
| 表 1 刚轮基本设计参数 Table 1 Basic design parameters of the wheel |
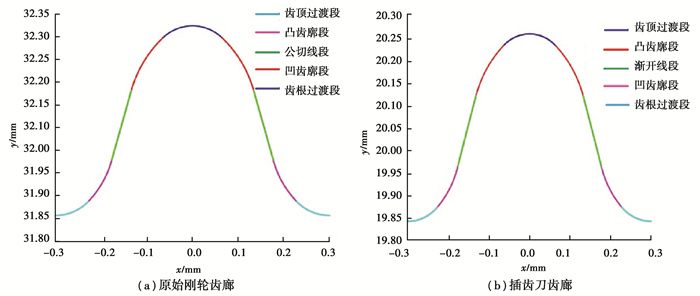
采用MATLAB编写程序,得到原始刚轮齿形如图 2(a)所示。
|
图 2 刚轮齿廓与插齿刀齿廓 Fig. 2 Tooth profile of rigid gear and tooth profile of shaper |
刚轮齿廓所有圆弧段经过共轭计算后,均近似为刀具圆弧齿廓,公切线段经过共轭计算后成为渐开线齿廓。
利用运动学法求解得到双圆弧刚轮插齿刀齿形如图 2(b)所示,插齿刀齿廓对应于刚轮齿廓,包括齿顶过渡段、凸齿廓段、渐开线段、凹齿廓段、齿根过渡段。
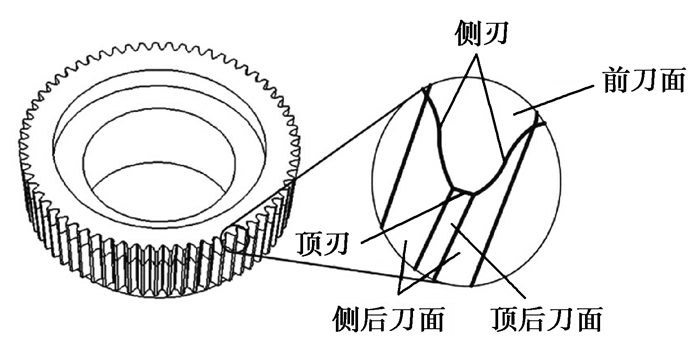
2 双圆弧刚轮插齿刀几何参数计算如图 3所示,插齿刀的刀齿由2条侧刃、1条顶刃、1个前刀面、2个侧后刀面和1个顶后刀面构成。插齿刀的外形和齿轮相似,为保证刀具能正常进行切削工作,插齿刀必须具有切削角度:前角和后角[16-18]。双圆弧插齿刀齿面几何角度选取没有参考标准,因此参照渐开线齿形插齿刀前后角选取原则[17],针对表 1中双圆弧刚轮所对应的插齿刀,初选刀具顶刃前角为5°,顶刃后角为6.5°。
|
图 3 插齿刀几何结构示意图 Fig. 3 Schematic diagram of the geometry of the gear shaper |
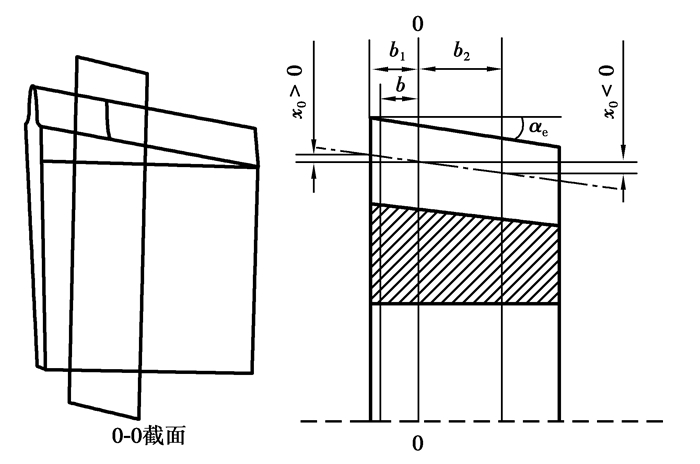
由于插齿刀顶刃和侧刃都有后角,插齿刀自前刀面向后尺寸逐渐缩小,即在插齿刀各端剖面中,直径和齿厚都不相等,如图 4所示。插齿刀不同端剖面中的齿形相当于不同变位系数齿轮的齿形。在0-0截面中,变位系数为0(x0=0,该0-0剖面称为原始截面);在原始截面向左的各端剖面为正变位(x0为正值),原始截面向右的各端剖面为负变位(x0为负值),各截面的变位系数x0与该截面到原始截面的距离b成正比,该截面的变位量X0为
| $ X_{0}=x_{0} m=b \tan \alpha_{\mathrm{e}}, $ | (9) |
|
图 4 插齿刀0-0截面 Fig. 4 0-0 Cross section |
式中:m为插齿刀模数;αe为插齿刀的顶刃后角。
根据式(9),设原始截面前刀具的可刃磨长度为b1,原始截面后刀具的可刃磨长度为b2,则插齿刀的可刃磨长度L为
| $ L=b_{1}+b_{2}=\frac{x_{\max } m}{\tan \alpha_{\mathrm{e}}}-\frac{x_{\min } m}{\tan \alpha_{\mathrm{e}}}, $ | (10) |
式中:xmax为最大变位系数;xmin为最小变位系数。
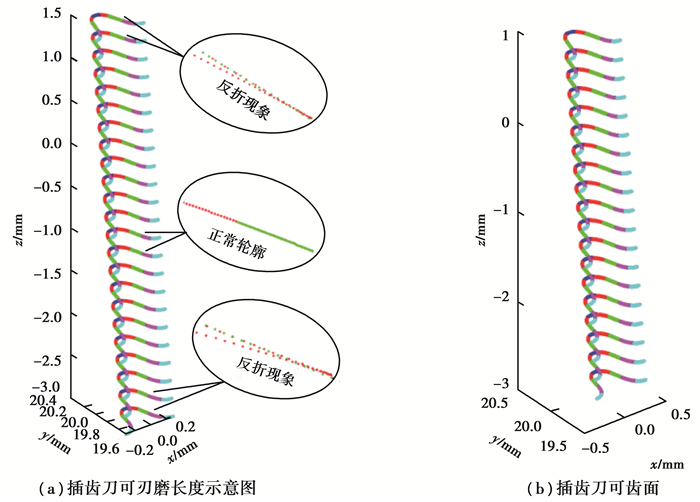
在设计插齿刀时,变位系数取得过大或过小都会使插齿刀齿廓出现反折现象,即齿廓失效。当插齿刀顶刃后角为6.5°时,计算出插齿刀齿面如图 5(a)所示,插齿刀0-0截面前可刃磨长度b1为0.93 mm,由式(9)得最大变位系数xmax为0.401,0-0截面后刀具的可刃磨有效长度b2为2.7 mm,最小变位系数xmin为-1.165,由式(10)得可刃磨长度L为3.63 mm。当变位系数大于xmax或小于xmin时,齿廓出现失效现象。基于上述变位系数得到插齿刀齿面如图 5(b)所示。
|
图 5 插齿刀可刃磨长度及插齿刀齿面 Fig. 5 Grindable length and tooth surface of the gear shaper |
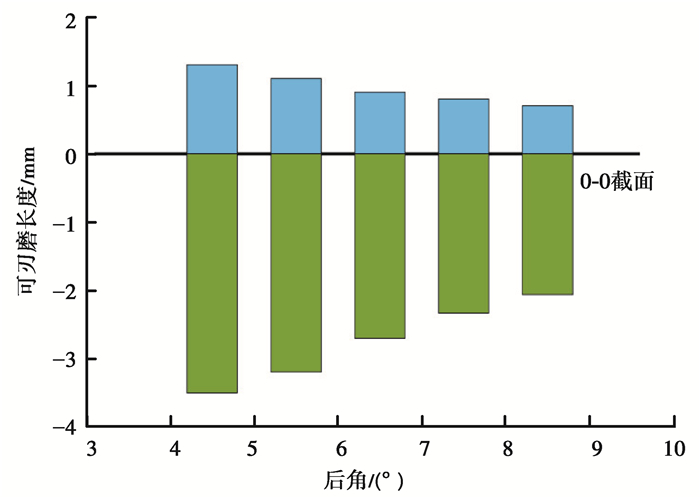
为研究顶刃后角的大小对插齿刀可刃磨长度的影响,分别取设计值6.5°及其前后的4.5°、5.5°、7.5°、8.5°进行计算分析。计算得到插齿刀可刃磨长度变化如图 6所示,可以看出插齿刀0-0截面之前的可刃磨长度逐渐减小,0-0截面之后的可刃磨长度也逐渐减小,即插齿刀的可刃磨长度随插齿刀顶刃后角增大而减小。因此增加插齿刀后角,刀具刃磨长度减小。
|
图 6 后角对插齿刀可刃磨长度的影响 Fig. 6 Influence of back angle on grindable length of gear shaper |
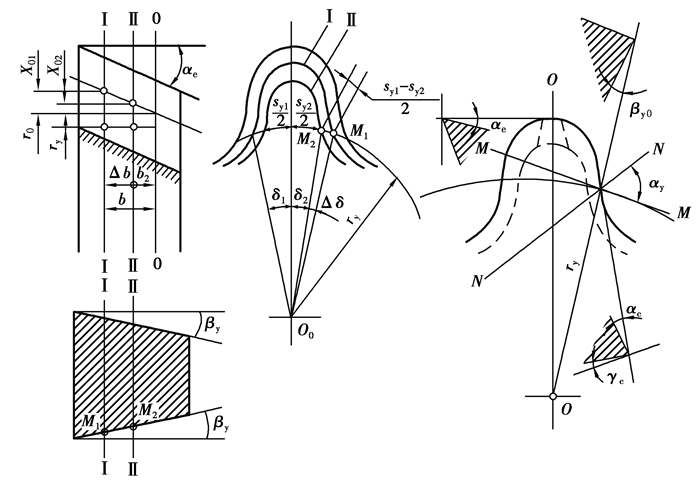
插齿刀顶刃后角为顶后刀面与水平面的夹角;由于顶刃后角的存在,当插齿刀展开时2个侧后刀面实际为角度相同旋向相反的螺旋面,使插齿刀存在侧刃后角。在切削过程中,侧刃后角决定插齿刀齿后面相对于被加工面的摩擦力大小,也决定插齿刀齿后面的磨损量大小,侧刃后角太小,对耐用度不利。如图 7所示,刀齿侧面是螺旋面,齿侧面与节圆柱的交线是螺旋线,图中X01为Ⅰ-Ⅰ截面的变位量,X02为Ⅱ-Ⅱ截面的变位量,sy1为Ⅰ-Ⅰ截面中任意半径齿厚,sy2为Ⅱ-Ⅱ截面中任意半径齿厚。侧刃任意点(半径ry)处的齿面螺旋角βy计算方法如下:
| $ \tan {\beta _{\rm{y}}} = \frac{{\frac{1}{2}\left( {{s_{{\rm{y1}}}} - {s_{{\rm{y2}}}}} \right)}}{{\Delta b}}, $ | (10) |
|
图 7 双圆弧插齿刀齿面示意图 Fig. 7 Schematic diagram of the tooth surface of double-arc gear shaper |
式中Δb为Ⅰ-Ⅰ截面和Ⅱ-Ⅱ截面间的距离。
sy1和sy2的计算方法如下:
| $ {{s_{{\rm{y1}}}} = \frac{{2{r_{\rm{y}}}}}{{{r_0}}}\left( {\frac{{{\rm{ \mathsf{ π} }}m}}{4} + {x_{01}}m\tan {\alpha _0} + {r_0}{\theta _0} - {r_0}{\theta _{\rm{y}}}} \right),} $ | (11) |
| $ {{s_{{\rm{y}}2}} = \frac{{2{r_y}}}{{{r_0}}}\left( {\frac{{{\rm{ \mathsf{ π} }}m}}{4} + {x_{02}}m\tan {\alpha _0} + {r_0}{\theta _0} - {r_0}{\theta _{\rm{y}}}} \right),} $ | (12) |
联立式(10)~(12),化简后得到
| $ \tan \beta_{\mathrm{y}}=\frac{r_{\mathrm{y}}}{r_{0}} \tan \alpha_{\mathrm{e}} \tan \alpha_{0}, $ | (13) |
式中:r0为分度圆半径;m为插齿刀模数;x01为Ⅰ-Ⅰ截面的变位系数;x02为Ⅱ-Ⅱ截面的变位系数;α0为分度圆压力角;θ0为分度圆处的展角;θy为任意半径处的展角。
侧刃上任意点A在M-M截面中的后角即是齿形表面的螺旋角βy,N-N截面和M-M截面的夹角为αy,αy为半径ry处的压力角,插齿刀侧刃后角αyc为
| $ \tan \alpha_{\mathrm{yc}}=\tan \beta_{\mathrm{y}} \cos \alpha_{\mathrm{y}}, $ | (14) |
即
| $ \tan \alpha_{\mathrm{yc}}=\frac{r_{\mathrm{y}}}{r_{0}} \tan \alpha_{\mathrm{e}} \tan \alpha_{0} \cos \alpha_{\mathrm{y}}, $ | (15) |
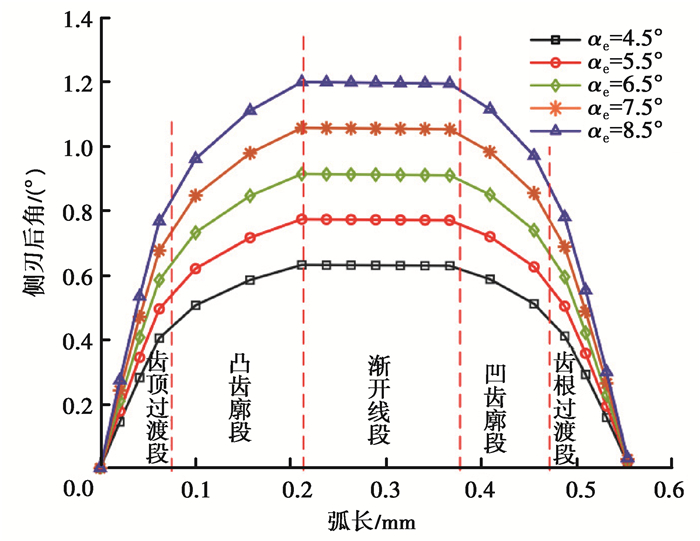
对表 1中的刚轮计算其对应刀具在不同顶刃后角情况下齿顶到齿根各点处的侧刃后角的变化趋势。如图 8所示,双圆弧插齿刀侧刃后角从齿顶到齿根先增大后减小,在渐开线段达到最大;并且随着顶刃后角增大,侧刃后角也增加。可以看出双圆弧形齿形的侧刃后角与渐开线齿形不同,渐开线齿形侧刃后角为一定值,不随半径的变化而变化,而双圆弧齿形插齿刀的侧刃后角与半径及该点的压力角均有关。在顶刃后角一定时,分度圆压力角越大,越有利于切削;顶刃后角越大,插齿刀侧刃后角越大,刀具耐用度越高。
|
图 8 双圆弧插齿刀侧刃后角 Fig. 8 Back angle of side edge of double-arc gear shaper |
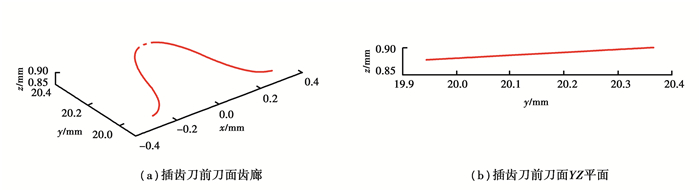
插齿刀存在顶刃前角γ,使插齿刀的前刀面为内凹的圆锥面,当插齿刀顶刃前角γ=5°、后角为6.5°时,计算得插齿刀的前刀面如图 9(a)所示,其YZ平面如图 9(b)所示。
|
图 9 插齿刀前刀面 Fig. 9 Rake face of the gear shaper |
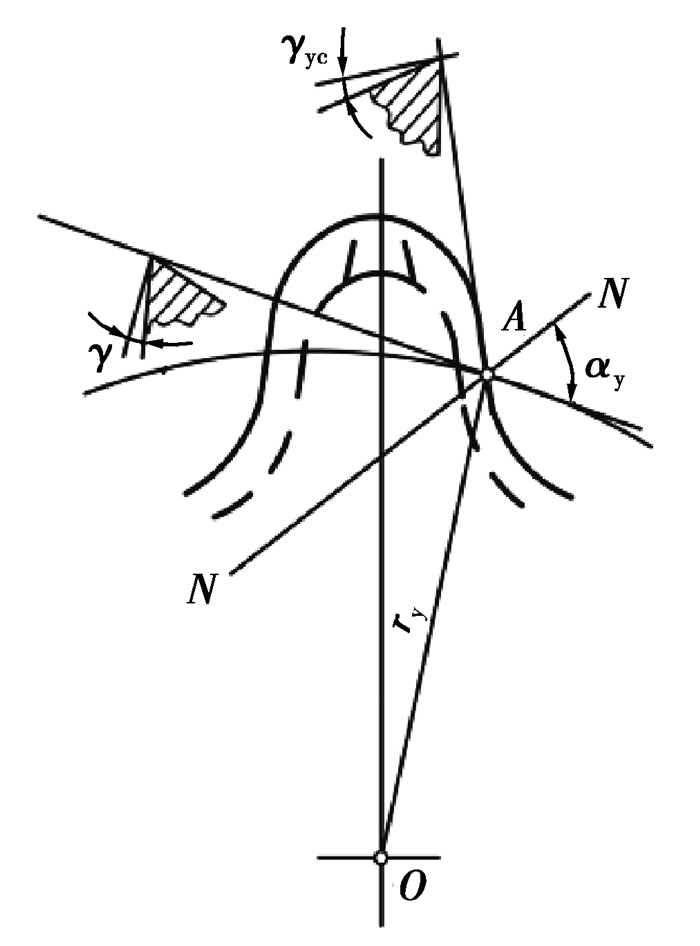
由于插齿刀前刀面是圆锥面,故插齿刀的侧刃也有前角。插齿刀的侧刃前角越大,加工表面质量越佳,越有利于切削[17-19]。插齿刀侧刃前角应在与切削刃在基面中的投影相垂直的截面,即在N-N截面(图 10)中测量。侧刃上任意点A的前角γyc可用式(16)计算[17]:
| $ \tan {\gamma _{{\rm{yc}}}} = \tan \gamma \sin {\alpha _{\rm{y}}}, $ | (16) |
|
图 10 双圆弧插齿刀侧刃前角 Fig. 10 Front angle of side edge of double-arc gear shaper |
式中αy为侧刃上任意点处的压力角。
针对表 1中的刚轮,计算其对应刀具在不同顶刃前角和不同顶刃后角的情况下齿顶到齿根段侧刃前角的变化情况。
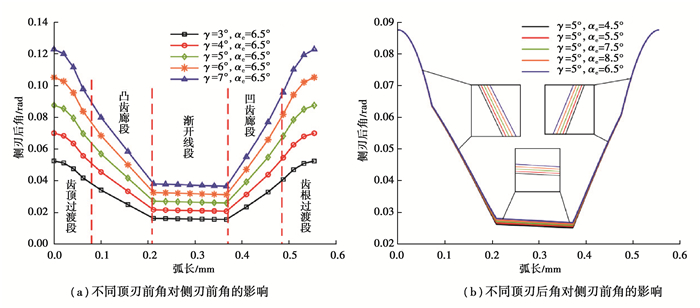
顶刃后角一定时,分别取顶刃前角设计值5°及其前后的3°、4°、6°、7°进行计算分析,如图 11(a)所示,侧刃前角从齿顶到齿根先减小后增加,最大值出现在齿顶与齿根段,最小值出现在渐开线段;并且在同一位置,随着顶刃前角增加,侧刃前角也增加。
|
图 11 插齿刀侧刃前角 Fig. 11 Front edge angle of the shaper |
顶刃前角一定时,分别取顶刃后角设计值6.5°及其前后的4.5°、5.5°、7.5°、8.5°进行计算分析,结果如图 11(b)所示,侧刃前角整体变化趋势为从齿顶到齿根先减小后增加,最大值出现在齿顶与齿根段,最小值出现在渐开线段;随着顶刃后角增加,双圆弧插齿刀齿顶与齿根处的侧刃前角最大值不变,在其余各处,顶刃后角越大,侧刃前角越大。
综合对比图 11(a)与图 11(b)可以看出,侧刃前角随着顶刃前角增大而增大,并且侧刃前角对顶刃前角的敏感性大于顶刃后角。
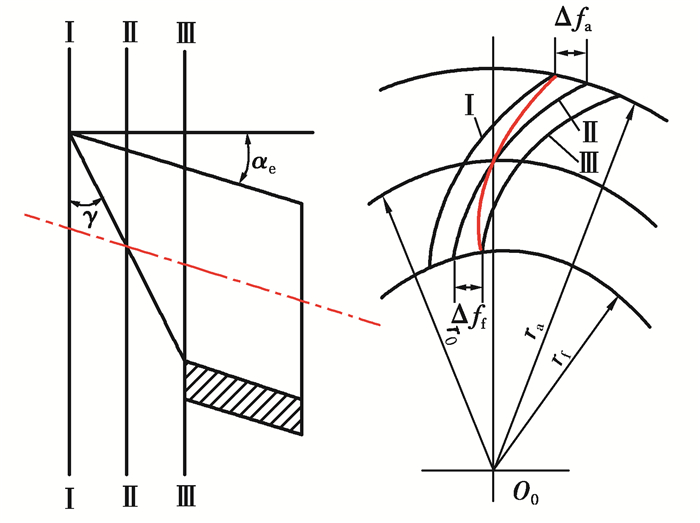
3 双圆弧刚轮插齿刀齿形误差分析插齿刀切削齿轮时,切削刃上下运动的轨迹表面与被加工齿轮啮合,故切削刃在基面上的投影应和理论齿形重合才没有理论上的误差[18-19]。插齿刀有前角和后角才能进行正常的插齿工作。插齿刀有后角时,插齿刀的齿形表面是双圆弧螺旋面;插齿刀顶刃前角γ=0°时,刀具的前刀面为刀具理论齿形,没有误差,当插齿刀的顶刃前角γ>0°时,刀具的前刀面为圆锥面,前刀面和齿形表面(双圆弧螺旋面)的交线(切削刃)在基面中的投影已不是刀具的理论齿形。切削刃投影与插齿刀理论齿形之间的误差称为插齿刀齿形误差。如图 12所示,如以Ⅱ-Ⅱ截面中的理论齿形为基准,则齿顶在Ⅰ-Ⅰ截面中,齿顶厚度增加Δfa(每侧),同理齿根处齿厚将减薄Δff,造成较大的齿形误差[17]。
|
图 12 双圆弧插齿刀齿形误差分析 Fig. 12 Tooth profile error analysis of the double-circular-arc gear shaper |
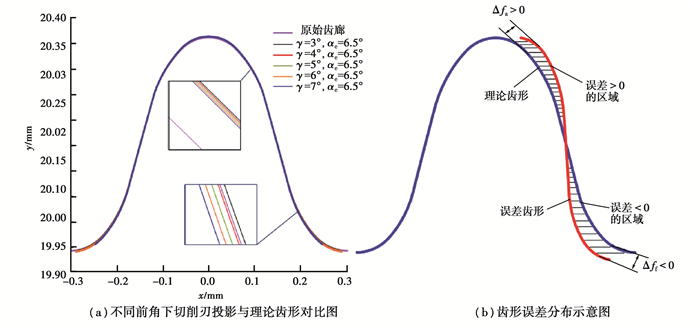
为比较插齿刀齿形误差对顶刃前角的敏感性,取后角为设计值6.5°,分别取顶刃前角设计值5°及设计值前后的3°、4°、6°、7°作为研究对象,相应的切削刃投影与理论齿形的对比如图 13(a)所示。可以看出,在靠近齿顶部分,切削刃投影大于插齿刀理论齿形,在靠近齿根部分,切削刃投影小于插齿刀理论齿形,整体齿形误差如图 13(b)。
|
图 13 齿形对比与齿形误差分布示意图 Fig. 13 Tooth profile comparison and tooth profile error distribution |
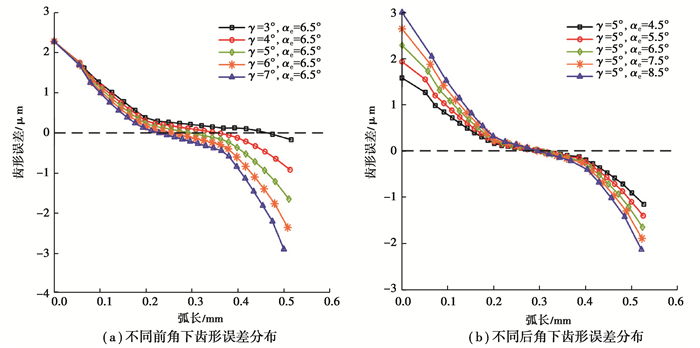
根据所求理论齿形与切削刃投影,取理论齿形与切削刃投影的法向距离作为误差,不同前角的切削刃投影与插齿刀齿形误差分布如图 14(a)。可以看出,插齿刀齿形误差随着弧长增加由正值逐渐过渡为负值;在齿顶部分误差为正,切削刃投影大于刀具理论齿形,并且随着顶刃前角增加,误差逐渐减小,但误差最大值不变;在齿根部分误差为负,切削刃投影小于刀具理论齿形,并且随着顶刃前角增加,误差绝对值逐渐增大;在设计插齿刀的前角时,应尽量减小齿顶误差和齿根误差,并使误差均布在0附近,从而减小插齿刀齿形整体误差。综合可知,插齿刀齿根误差最大值对顶刃前角的敏感性大于插齿刀齿顶误差最大值;在本组数据中,当前角取3°时,插齿刀齿形误差最小,即前角越小,插齿刀齿形误差越小,但减小前角不利于切屑流出[19],因此在设计前角时可在保证切屑正常流出的情况下尽量减小前角。
|
图 14 插齿刀齿形误差 Fig. 14 Tooth shape error of the shaper |
为比较插齿刀齿形误差对顶刃后角的敏感性,取顶刃前角为设计值5°,分别取顶刃后角设计值6.5°及设计值前后的4.5°、5.5°、7.5°、8.5°作为研究对象。顶刃后角为插齿刀前刀面齿形求解的必要参数,顶刃后角不同,插齿刀前刀面的理论齿形也不同,此处不再逐一给出齿形对比图。
根据所求理论齿形与切削刃投影,取理论齿形到切削刃投影的法向距离作为齿形误差,求得齿形误差分布如图 14(b)。由图可知,随着弧长增加,插齿刀齿形误差逐渐由正值过渡为负值,即在齿顶部分,切削刃投影大于理论齿形,在齿根部分,切削刃投影小于理论齿形;随着顶刃后角增大,在靠近齿顶段误差逐渐增大,在靠近齿根段误差绝对值逐渐增大,即顶刃后角越大,插齿刀齿形综合误差越大;齿顶段误差最大值大于齿根段误差最大值,即插齿刀齿顶误差最大值对顶刃后角的敏感性大于插齿刀齿根误差最大值。
4 算例谐波传动为高精密传动,因此对加工谐波齿轮的插齿刀有较高的精度要求,通常为AA级精度,参考行业标准小模数直齿插齿刀JB/T 3095—2006[20],模数在0.1~0.5 mm范围内AA级精度插齿刀的齿形误差应小于等于3 μm,该齿形误差为插齿刀有效齿廓双边误差最大值的总和,即图 14中正负误差绝对值最大值的和,下文统一称为标准齿形误差。
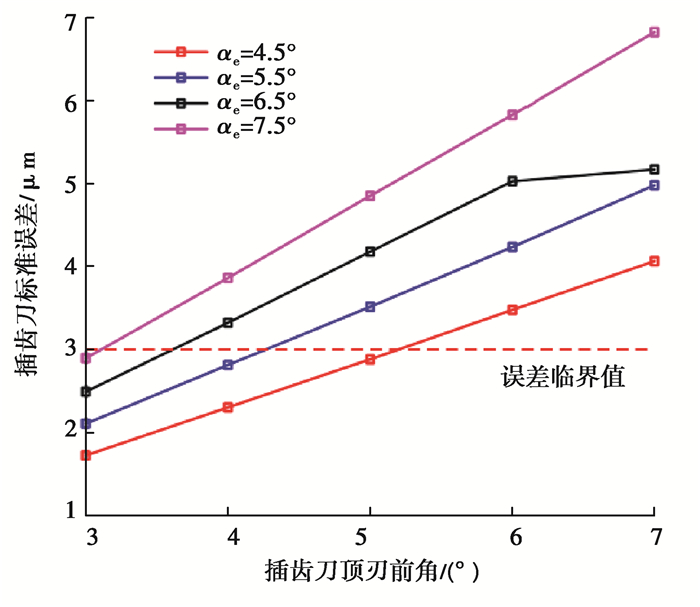
以表 1中刚轮对应的插齿刀为例,由几何关系可知,插齿刀齿顶处误差最大值由顶刃后角决定,由图 14(b)可以看出,当顶刃后角为8.5°时,插齿刀齿顶处误差即插齿刀单边误差最大值已达到3 μm,因此该角度不可选用。下面结合顶刃前角进一步选取合适的前角和后角。当顶刃后角为7.5°时,分别取前角为3°、4°、5°、6°、7°,计算其标准齿形误差;同理可求顶刃后角为6.5°、5.5°、4.5°时的标准齿形误差,如图 15。由图可知,满足精度要求的前后角组合有(3°,4.5°)(3°,5.5°)(3°,6.5°)(3°,7.5°)(4°,4.5°)(4°,5.5°)和(5°,4.5°)。
|
图 15 不同前后角插齿刀标准误差 Fig. 15 Standard errors of gear-shaper cutters with different front angles and different rear angles |
增大插齿刀顶刃前角与顶刃后角有利有弊[17]。增大顶刃前角,可提高加工表面质量,增加刀具的耐用度,但插齿刀齿形误差增大,而谐波传动属于高精密传动,其表面质量要求高,因此刀具在满足精度要求的条件下可选择较大前角;增大插齿刀顶刃后角,可明显提高刀具耐用度,但会降低刀具的可刃磨次数,增加刀具齿形误差,双圆弧谐波传动刚轮插齿刀加工成本高,因此提高其使用寿命十分重要,而小模数插齿刀,其可刃磨长度较短,减小后角可增加其可刃磨长度,因此在满足精度要求的条件下,可选择较小顶刃后角。综合分析可得,对加工表 1中刚轮的插齿刀,顶刃前角可选择5°,顶刃后角可选择4.5°,由图 6可知,此时插齿刀可刃磨长度为4.8 mm;由图 14(b)可以看出,此时插齿刀齿顶处齿形误差为1.574 μm,齿根处齿形误差为-1.1531 μm,标准齿形误差为2.7271 μm,满足AA级插齿刀齿形精度要求。
5 结论1) 基于啮合原理,建立双圆弧刚轮加工坐标系,依据刚轮齿形,采用运动学法求解插齿刀齿形及齿面数学模型。该方法基于柔轮齿形推导出刚轮齿形、刚轮齿形进一步求解插齿刀齿形的技术路线,可保证柔轮与刚轮的共轭关系。
2) 双圆弧插齿刀可刃磨长度随顶刃后角增大而减小;侧刃后角的大小与该点的半径及压力角大小均有关,顶刃后角越大,侧刃后角越大。
3) 侧刃前角在齿顶与齿根段达到最大值,在渐开线段最小,侧刃前角随顶刃前角增加而增加,随顶刃后角增加而增加,并且侧刃前角对顶刃前角的敏感性大于对顶刃后角的敏感性。
4) 顶刃后角一定时,顶刃前角越大,插齿刀标准齿形误差越大;齿根误差最大值对顶刃前角的敏感性大于齿顶误差最大值对顶刃前角的敏感性。顶刃前角一定时,顶刃后角越大,标准齿形误差越大,并且齿顶误差最大值对顶刃后角的敏感性大于齿根误差最大值对顶刃后角的敏感性。在设计插齿刀时,可在保证插齿刀齿形精度要求的条件下,选取较大的顶刃前角和较小的顶刃后角,这样既可保证插齿刀的齿形精度,又可提高插齿刀的可刃磨长度。
| [1] |
辛洪兵. 谐波传动的国内外发展现状与趋势[J]. 现代制造, 2009(35): 8-10. Xin H B. Development status and trend of harmonic drive at home and abroad[J]. Maschinen Markt, 2009(35): 8-10. (in Chinese) |
| [2] |
辛洪兵. 双圆弧谐波齿轮传动基本齿廓设计[J]. 中国机械工程, 2011, 22(6): 656-662. Xin H B. Design for basic rack of harmonic drive with double-circular-arc tooth profile[J]. China Mechanical Engineering, 2011, 22(6): 656-662. (in Chinese) |
| [3] |
Jeong K S, Lee D G, Kwak Y K. Adhesive joining technology for manufacturing of the composite flexspline for a harmonic drive[J]. The Journal of Adhesion, 1996, 55(3/4): 329-350. |
| [4] |
Oh H S, Jeong K S, Lee D G. Design and manufacture of the composite flexspline of a harmonic drive with adhesive joining[J]. Composite Structures, 1994, 28(3): 307-314. DOI:10.1016/0263-8223(94)90017-5 |
| [5] |
Lai H Y, Wu D S. An enhanced DFM model for shaper cutters[J]. The International Journal of Advanced Manufacturing Technology, 2002, 19(7): 482-491. DOI:10.1007/s001700200051 |
| [6] |
Kawalec A, Wiktor J, Ceglarek D. Comparative analysis of tooth-root strength using ISO and AGMA standards in spur and helical gears with FEM-based verification[J]. Journal of Mechanical Design, 2006, 128(5): 1141-1158. DOI:10.1115/1.2214735 |
| [7] |
Lin S W, Han C S, Tan J B, et al. Mathematical models for manufacturing a novel gear shaper cutter[J]. Journal of Mechanical Science and Technology, 2010, 24(1): 383-390. DOI:10.1007/s12206-009-1022-z |
| [8] |
Yoshino H, Shao M, Ishibashi A. Design and manufacture of pinion cutters for finishing gears with an arbitrary profile[J]. JSME International Journal Series 3, Vibration, Control Engineering, Engineering for Industry, 1992, 35(2): 313-319. DOI:10.1299/jsmec1988.35.313 |
| [9] |
Tsay C B, Liu W Y, Chen Y C. Spur gear generation by shaper cutters[J]. Journal of Materials Processing Technology, 2000, 104(3): 271-279. DOI:10.1016/S0924-0136(00)00570-7 |
| [10] |
辛洪兵. 双圆弧谐波齿轮插齿刀: CN101134254A[P]. 2008-03-05. Xin H B. Double circular arc harmonic wave wheel gear shaped cutter: CN101134254A[P]. 2008-03-05. (in Chinese) |
| [11] |
刘熙刚. CTC齿形谐波传动啮合参数的优化研究[D]. 南京: 南京理工大学, 2013. Liu X G. Optimization of engagement parameters of CTC tooth harmonic drive[D]. Nanjing: Nanjing University of Science and Technology, 2013. (in Chinese) |
| [12] |
聂少文, 胡吉全, 吴奋敬, 等. 短齿双圆弧谐波齿轮刀具设计与仿真研究[J]. 起重运输机械, 2016(12): 82-86. Nie S W, Hu J Q, Wu F J, et al. Study on design and simulation of short-gear biarc harmonic gear tool[J]. Hoisting and Conveying Machinery, 2016(12): 82-86. (in Chinese) DOI:10.3969/j.issn.1001-0785.2016.12.031 |
| [13] |
孟漪. 加工小模数渐开线齿廓谐波齿轮用插齿刀设计[J]. 工具技术, 2016, 50(4): 68-71. Meng Y. Design of shaper cutter with making small module involute tooth profile harmonic gear[J]. Tool Engineering, 2016, 50(4): 68-71. (in Chinese) DOI:10.3969/j.issn.1000-7008.2016.04.017 |
| [14] |
陈鹏. 双圆弧齿形谐波齿轮传动的参数设计与性能分析[D]. 南京: 南京理工大学, 2016. Chen P. Parameter design and performance analysis of double arc tooth harmonic gear drive[D]. Nanjing: Nanjing University of Science and Technology, 2016. (in Chinese) |
| [15] |
李佳, 李晓群, 王鹏, 等. 无理论刃形误差直齿插齿刀设计[J]. 中国机械工程, 2015, 26(12): 1563-1568. Li J, Li X Q, Wang P, et al. Design of straight teeth gear shaping cutter without theoretical cutting edge profile errors[J]. China Mechanical Engineering, 2015, 26(12): 1563-1568. (in Chinese) DOI:10.3969/j.issn.1004-132X.2015.12.002 |
| [16] |
李佳, 李清泉, 郑淑贤. 无理论刃形误差插齿刀设计方法[J]. 机械设计, 2018, 35(7): 1-7. Li J, Li Q Q, Zheng S X. Cutting-edge design method for gear shaping cutters free from theoretical errors[J]. Journal of Machine Design, 2018, 35(7): 1-7. (in Chinese) |
| [17] |
袁哲俊. 齿轮刀具设计[M]. 北京: 国防工业出版社, 2014: 119-231. Yuan Z J. Design of gear cutters[M]. Beijing: National Defense Industry Press, 2014: 119-231. (in Chinese) |
| [18] |
Kapelevich A. Geometry and design of involute spur gears with asymmetric teeth[J]. Mechanism and Machine Theory, 2000, 35(1): 117-130. DOI:10.1016/S0094-114X(99)00002-6 |
| [19] |
Radzevich S P. Gear cutting tools[M]. Boca Raton: CRC Press, 2010.
|
| [20] |
中华人民共和国国家发展和改革委员会. 小模数直齿插齿刀: JB/T 3095-2006[S]. 北京: 机械工业出版社, 2007. National Development and Reform Commission of the People's Republic of China. Fine-pith gear shaper cutters for spur gear: JB/T 3095-2006[S]. Beijing: China Machine Press, 2007. (in Chinese) |
 2021, Vol. 44
2021, Vol. 44


