在重载、高速齿轮传动中,常出现较大的冲击载荷、振动和噪声,甚至出现齿根裂纹、断齿等故障,影响传动系统的可靠性和使用寿命。因此研究如何减小系统冲击载荷,提高传动系统的可靠性和使用寿命具有重要意义。
齿轮系统动态性能的优化主要围绕传动系统的动力优化设计展开,国内外专家学者对此进行了大量的研究工作。在齿轮系统减振降噪和传递性能方面,耿智博等[1]和孙伟等[2]通过优化齿轮的基本参数和齿轮箱体的结构参数减小了零部件的振动加速度,降低了齿轮系统的振动幅值和噪声;Tamboli等[3]和Chandrasekaran等[4]采用遗传算法优化了模数、齿数和齿宽等,使得齿轮系统在制造成本、传递效率和紧凑性方面达到最优。而在齿轮系统的动载特性方面,S'witoński等[5]和周迪等[6]建立了机械部件的结构参数与接触应力之间的明确关系;Korta等[7]和Artoni等[8]通过优化齿面修形参数减小了齿面接触应力;林何等[9]研究了传动系统在内外部激励作用下的动载特性,分析了齿侧间隙、时变啮合刚度等因素对系统动载的影响规律;欧阳天成等[10]以单个啮合周期的啮合刚度波动标准差最小为优化目标,减小了单齿载荷和动态啮合力的波动幅值;李启山[11]基于模糊可靠理论分析了采煤机传动系统的可靠性,得出了动态可靠性随工作时间增加而逐渐降低的结论,但是并没有提出提升采煤机牵引机构可靠性的方法。上述研究大多考虑的是如何通过降低振动响应来降低噪声、提高齿轮系统的传递效率及承载能力,并没有考虑如何减小传动系统的冲击载荷,防止传动系统故障的产生。
采煤机的运行工况恶劣、负载较大,传动系统常出现磨损、断齿、胶合等故障。因此,笔者以采煤机的传动系统为例,研究降低传动系统冲击载荷的方法,建立包含电机动态模型、耦合轮系和行星轮系动力学模型的采煤机动力传动系统机电耦合模型。在运行过程中,通过动态优化采煤机的运动参数来降低截割传动系统的冲击载荷,并搭建实验台架,验证通过动态优化参数降低传动系统冲击载荷方法的有效性。
1 动力传动系统机电耦合模型为研究采煤机运动参数动态优化对截割传动系统中冲击载荷的影响,建立了截割传动系统和牵引传动系统的动力学模型。
1.1 截割传动系统建模采煤机截割动力传动系统由3台电动机、耦合轮系和行星轮系构成,如图 1所示。耦合轮系是由3个输入齿轮和1个输出齿轮构成的定轴轮系,汇集3台电机的动力。耦合轮系和行星轮系均有3条传动路线,每条传动路线分担1/3的负载,可提高传动系统的功率密度,减小系统体积。

|
图 1 截割动力传动系统 Fig. 1 Powertrain of the cutting unit |
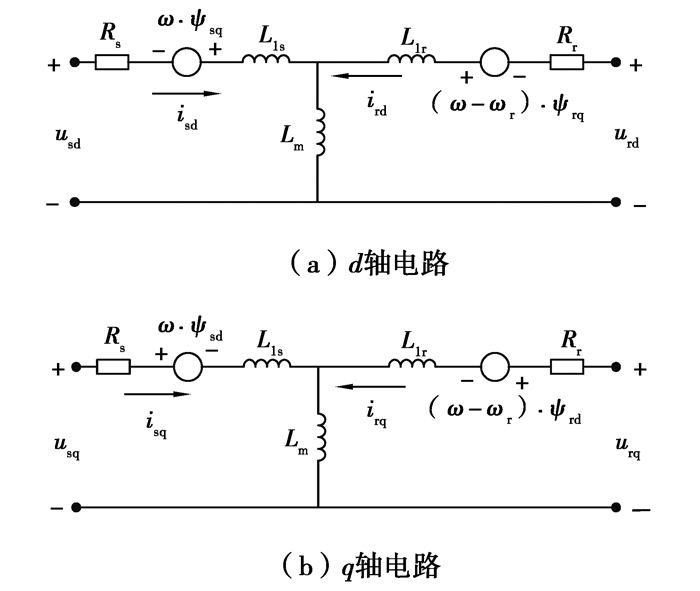
采用旋转正交坐标系(dq坐标系)建立电机动态模型[12-13],dq坐标系等效电路如图 2所示。图中usd和isd为d轴的定子电压和电流; urd和ird为d轴的转子电压和电流; usq和isq为q轴的定子电压和电流; urq和irq为q轴的转子电压和电流;Rs和Rr为定子和转子电阻;ψsd和ψsq为d轴和q轴定子磁链; ψrd和ψrq为d轴和q轴转子磁链;ω为dq坐标系相对于定子的旋转角速度; ωr为电角速度;Lls和Llr为定子和转子漏感; Lm为定子与转子同轴等效绕组间的互感;Ls和Lr为定子和转子等效两相绕组的自感。
|
图 2 电机的动态等效电路 Fig. 2 Dynamic equivalent circuit of the motor |
将电机动态模型转化为矩阵形式:
| $ \left(\begin{array}{l} u_{\mathrm{sd}} \\ u_{\mathrm{sq}} \\ u_{\mathrm{rd}} \\ u_{\mathrm{rq}} \end{array}\right)=\left(\begin{array}{cccc} R_{\mathrm{s}} & 0 & 0 & 0 \\ 0 & R_{\mathrm{s}} & 0 & 0 \\ 0 & 0 & R_{\mathrm{r}} & 0 \\ 0 & 0 & 0 & R_{\mathrm{r}} \end{array}\right)\left(\begin{array}{c} i_{\mathrm{sd}} \\ i_{\mathrm{sq}} \\ i_{\mathrm{rd}} \\ i_{\mathrm{rq}} \end{array}\right)+\frac{\mathrm{d}}{\mathrm{d} t}\left(\begin{array}{c} \psi_{\mathrm{sd}} \\ \psi_{\mathrm{sq}} \\ \psi_{\mathrm{rd}} \\ \psi_{\mathrm{rq}} \end{array}\right)+\left(\begin{array}{c} -\omega_{\mathrm{dq}} \cdot \psi_{\mathrm{sq}} \\ \omega_{\mathrm{dq}} \cdot \psi_{\mathrm{sd}} \\ -\left(\omega_{\mathrm{dq}}-\omega_{\mathrm{r}}\right) \cdot \psi_{\mathrm{rq}} \\ \left(\omega_{\mathrm{dq}}-\omega_{\mathrm{r}}\right) \cdot \psi_{\mathrm{rd}} \end{array}\right), $ | (1) |
| $ \left(\begin{array}{c} \psi_{\mathrm{sd}} \\ \psi_{\mathrm{sq}} \\ \psi_{\mathrm{rd}} \\ \psi_{\mathrm{rq}} \end{array}\right)=\left(\begin{array}{cccc} L_{\mathrm{s}} & 0 & L_{\mathrm{m}} & 0 \\ 0 & L_{\mathrm{s}} & 0 & L_{\mathrm{m}} \\ L_{\mathrm{m}} & 0 & L_{\mathrm{r}} & 0 \\ 0 & L_{\mathrm{m}} & 0 & L_{\mathrm{r}} \end{array}\right)\left(\begin{array}{c} i_{\mathrm{sd}} \\ i_{\mathrm{sq}} \\ i_{\mathrm{rd}} \\ i_{\mathrm{rq}} \end{array}\right)。$ | (2) |
电机的电磁转矩为:
| $ T_{\mathrm{m}}=1.5 n_{\mathrm{p}}\left(\psi_{\mathrm{sd}} i_{\mathrm{sq}}-\psi_{\mathrm{sq}} i_{\mathrm{sd}}\right), $ | (3) |
式中np为电机转速。
耦合轮系的动力学模型如图 3所示。该模型考虑了齿轮的惯量、齿轮的质量、齿轮间啮合刚度、径向支撑刚度、阻尼等因素。图中rcp和rcs分别为主动齿轮和从动齿轮的基圆半径;θcpi和θcs分别为主动齿轮i和从动齿轮的旋转角位移;xcpi和ycpi分别为主动齿轮i(i=1, 2, 3)在x和y向的振动位移; xcs和ycs分别为从动齿轮在x和y向的振动位移;αc为啮合角; ψci为主动齿轮i的位置角; ψci = (i-1)·120°;kcpix和ccpix分别为主动齿轮i在x向的支撑刚度和阻尼; kcpiy和ccpiy分别为主动齿轮i在y向的支撑刚度和阻尼; kcsx和ccsx分别为从动齿轮在x向的支撑刚度和阻尼; kcsy和ccsy分别为从动齿轮在y向的支撑刚度和阻尼;Icpi和Ics分别为主动齿轮i和从动齿轮的转动惯量;mcpi和mcs分别为主动齿轮i和从动齿轮的质量;Fcpis为主动齿轮i和从动齿轮沿着啮合线方向上的动态啮合力;Tcpi为作用在主动齿轮i上的驱动转矩; Tcs为作用在从动齿轮上的负载转矩。

|
图 3 耦合轮系动力学模型 Fig. 3 Coupled gear train dynamics model |
耦合轮系的数学模型为:
| $ \left\{\begin{array}{l} T_{\mathrm{cp}i}-r_{\mathrm{cp}} F_{\mathrm{cpis}}=I_{\mathrm{cp}} \ddot{\theta}_{\mathrm{cp}i}, \\ F_{\mathrm{cp} i \mathrm{~s}} \cos \alpha-k_{\mathrm{cp} x} x_{\mathrm{cp} i}-c_{\mathrm{cp} x} \dot{x}_{\mathrm{cp} i}=m_{\mathrm{cp} i} \ddot{x}_{\mathrm{cp} i}, \\ -F_{\mathrm{cp} i \mathrm{~s}} \sin \alpha-k_{\mathrm{cp}y} y_{\mathrm{cp}i}-c_{\mathrm{cp}y} \dot{y}_{\mathrm{cp} i}=m_{\mathrm{cp} i} \ddot{y}_{\mathrm{cp}i}, \\ r_{\mathrm{cs}} \sum\limits_{i=1}^{3} F_{\mathrm{cp} i \mathrm{~s}}-T_{\mathrm{cs}}=I_{\mathrm{cs}} \ddot{\theta}_{\mathrm{cs}}, \\ -\sum\limits_{i=1}^{3} F_{\mathrm{cp} i \mathrm{~s}} \cos \left(\alpha_{\mathrm{c}}+\psi_{\mathrm{c}i}\right)-k_{\mathrm{cs}x} x_{\mathrm{cs}}-c_{\mathrm{cs} x} \dot{x}_{\mathrm{cs}}=m_{\mathrm{cs}} \ddot{x}_{\mathrm{cs}}, \\ \sum\limits_{i=1}^{3} F_{\mathrm{cp} i \mathrm{~s}} \sin \left(\alpha_{\mathrm{c}}+\psi_{\mathrm{c}i}\right)-k_{\mathrm{cs} y} y_{\mathrm{cs}}-c_{\mathrm{cs} y} \dot{y}_{\mathrm{cs}}=m_{\mathrm{cs}} \ddot{y}_{\mathrm{cs}}。\end{array}\right. $ | (4) |
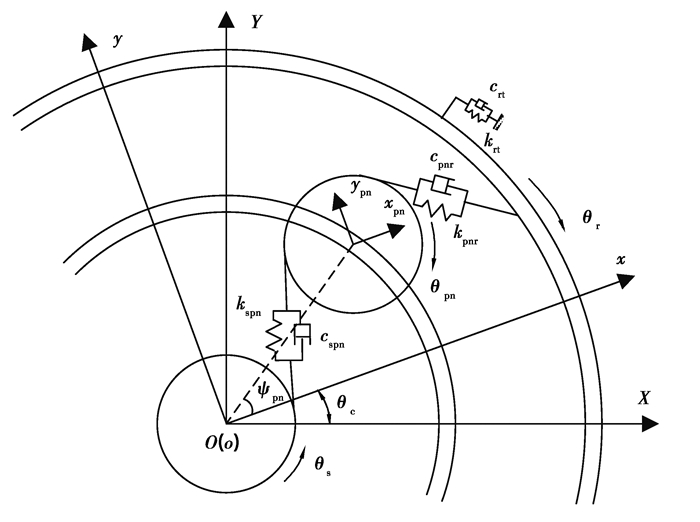
行星轮系的动力学模型如图 4所示。其中XOY为固定坐标系,xoy为固联在行星架上的旋转坐标系。在模型中考虑了齿轮和行星架的惯量、轮齿的弹性、齿轮间的啮合阻尼、齿圈的切向支撑等因素。图中θs、θpn和θr分别为太阳轮、行星轮和齿圈在xoy坐标系中的角位移; θc为行星架在XOY坐标系中的角位移;krt和crt分别为齿圈的切向支撑刚度和阻尼;kspn和cspn分别为太阳轮与行星轮间的时变啮合刚度和啮合阻尼;kpnr和cpnr分别为行星轮与齿圈间的时变啮合刚度和啮合阻尼。
|
图 4 行星轮系动力学模型 Fig. 4 Dynamic model of the planetary gear set |
行星轮系的数学模型为:
| $ \left\{\begin{array}{l} I_{\mathrm{s}}\left(\ddot{\theta_{\mathrm{s}}}+\ddot{\theta}_{\mathrm{c}}\right)=T_{\mathrm{s}}-\sum\limits_{n=1}^{3} r_{\mathrm{sb}} F_{\mathrm{spn}}, \\ I_{\mathrm{p}} \ddot{\theta}_{\mathrm{pn}}=r_{\mathrm{pb}} F_{\mathrm{spn}}-r_{\mathrm{pb}} F_{\mathrm{pnr}}, \\ \left.I_{\mathrm{r}} \ddot{\theta}_{\mathrm{r}}-\ddot{\theta}_{\mathrm{c}}\right)=\sum\limits_{n=1}^{3} r_{\mathrm{rb}} F_{\mathrm{pnr}}-k_{\mathrm{rt}}\left(\theta_{\mathrm{r}}-\theta_{\mathrm{c}}\right)-c_{\mathrm{rt}}\left(\dot{\theta}_{\mathrm{r}}-\dot{\theta}_{\mathrm{c}}\right), \\ I_{\mathrm{c}} \ddot{\theta_{\mathrm{c}}}=\sum\limits_{n=1}^{3} r_{\mathrm{c}} F_{\mathrm{spn}} \cos \alpha_{\mathrm{t1}}+\sum\limits_{n=1}^{3} r_{\mathrm{c}} F_{\mathrm{pnr}} \cos \alpha_{\mathrm{t2}}-T_{\mathrm{c}}。\end{array}\right. $ | (5) |
式中:Is、Ip、Ic和Ir分别为太阳轮、行星轮、行星架和齿圈的转动惯量;rsb、rpb和rrb分别为太阳轮、行星轮和齿圈的基圆半径; rc为行星轮中心分布圆的半径;αt1为太阳轮与行星轮的啮合角; αt2为行星轮与齿圈的啮合角;Ts为作用在太阳轮上的输入转矩; Tc为作用在行星架上的负载转矩;太阳轮与行星轮间的动态啮合力Fspn和行星轮与齿圈间的动态啮合力Fpnr分别为:
| $ F_{\mathrm{spn}}=k_{\mathrm{spn}}\left(r_{\mathrm{sb}} \theta_{\mathrm{s}}-r_{\mathrm{pb}} \theta_{\mathrm{pn}}\right)+c_{\mathrm{spn}}\left(r_{\mathrm{sb}} \dot{\theta}_{\mathrm{s}}-r_{\mathrm{pb}} \dot{\theta}_{\mathrm{pn}}\right), $ | (6) |
| $ F_{\mathrm{pnr}}=k_{\mathrm{pnr}}\left(r_{\mathrm{pb}} \theta_{\mathrm{pb}}-r_{\mathrm{rb}} \theta_{\mathrm{r}}\right)+c_{\mathrm{pnr}}\left(r_{\mathrm{pb}} \dot{\theta}_{\mathrm{pn}}-r_{\mathrm{rb}} \dot{\theta}_{\mathrm{r}}\right) 。$ | (7) |
采煤机牵引传动系统由三级定轴轮系和一级行星轮系构成[14]。调节牵引速度时存在惯性力。因此在牵引模型中考虑了系统的惯性,数学模型为:
| $ m_{\mathrm{h}} \dot{v_{\mathrm{q}}}=2 T_{\mathrm{h}} i_{\mathrm{h}} / r_{\mathrm{hp}}-F_{\mathrm{h}}。$ | (8) |
式中:mh为左右牵引动力传动系统转动惯量等效至机身的等效质量与机身质量之和;vq为牵引速度;Th为牵引电机输出转矩;ih为牵引传动系统的传动比;rhp为销轮的半径;Fh为牵引阻力。
1.3 负载模型作用在截割传动系统上的阻力矩为[15]:
| $ T_{\mathrm{d}}=R_{\mathrm{c}} \sum\limits_{n=1}^{N_{\mathrm{T}}} Z_{n}。$ | (9) |
式中:Rc为滚筒半径;NT为参与截割的截齿数量;Zn可表达为:
| $ Z_{n}=\frac{10 A_{\mathrm{p}} B_{\mathrm{T}} K_{\mathrm{c}}\left(0.3+0.35 b_{\mathrm{p}}\right) h_{\mathrm{c}}}{\left(b_{\mathrm{p}}+K_{\psi} \sqrt{h_{\mathrm{c}}}\right) \cos \beta_{\mathrm{T}}}。$ | (10) |
式中:Ap为煤层平均截割阻抗;BT为截齿切削宽度;Kc和Kψ为经验系数;bp为截齿宽度;βT为截齿相对于机身推进方向的偏转角;hc为截齿平均切削厚度:
| $ h_{\mathrm{c}}=\left(1-\cos \varphi_{\mathrm{T}}\right) v_{\mathrm{q}} /\left(\varphi_{\mathrm{T}} N_{\mathrm{T} 1} n_{\mathrm{d}}\right), $ | (11) |
式中: φT为煤体对滚筒的围包角;NT 1为同一截线上的截齿数;nd为截割传动系统输出转速。
牵引阻力Fh由推进阻力Fhp、摩擦阻力Fhf和机身重力沿坡道的分力FhG构成。其表达式为:
| $ F_{\mathrm{h}}=F_{\mathrm{hp}}+F_{\mathrm{hf}}+F_{\mathrm{hG}} \text { 。} $ | (12) |
作用在滚筒上的推进阻力与截割阻力呈比例关系,可表达为:
| $ F_{\mathrm{hp}}=k_{\mathrm{d} 3} \frac{T_{\mathrm{d}}}{R_{\mathrm{d}}}, $ | (13) |
式中:Rd为截割半径;kd3为与截齿磨损程度有关的系数,kd3= 0.6~0.8。
机体自重所导致的摩擦阻力可表达为:
| $ F_{\mathrm{hf}}=G \cdot \cos \alpha \cdot f , $ | (14) |
式中:α为坡角度;f为摩擦阻力系数,取0.18;G取411 600 N。
机身重力沿坡道的分力,即:
| $ F_{\mathrm{hG}}=G \sin \alpha。$ | (15) |
截割传动系统中的冲击载荷较大时,会加速齿轮传动系统疲劳破坏,甚至导致齿轮出现齿根裂纹、断齿等故障,影响生产。因此,选取截割传动系统动态啮合力均值最小为目标函数,以提高传动系统的可靠性。评价函数为:
| $ \min f(x)=F_{\mathrm{p}},$ | (16) |
式中Fp为行星轮系动态啮合力均值。
2.2 设计变量截割传动系统输出转速和牵引速度均可调节,且二者影响截割传动系统中的冲击载荷。因此,以截割传动系统输出转速nd和牵引速度vq为设计变量:
| $ \boldsymbol{x}=\left[n_{\mathrm{d}}, \quad v_{\mathrm{q}}\right]^{\mathrm{T}}。$ | (17) |
截割线速度是截割传动系统输出转速的函数,当截割线速度较大时,截齿磨损严重。截割传动系统输出转速和牵引速度过大也影响采煤机运行的安全性。考虑截割传动系统输出转速和牵引速度的设计值时,约束设计变量为:
| $ 20 \leqslant n_{\mathrm{d}} \leqslant 35, $ | (18) |
| $ 3 \leqslant v_{\mathrm{q}} \leqslant 7。$ | (19) |
在采煤机运行过程中,参与截割的截齿数量和每个截齿的受力随时间变化,使作用在滚筒上的切向阻力产生波动,切向阻力的波动幅度影响采煤机的稳定性。因此,约束载荷波动系数为:
| $ \frac{1}{\bar{F}} \sqrt{\sum\limits_{k=1}^{36}\left(F_{k}-\bar{F}\right)^{2} / 36} \leqslant 0.05, $ | (20) |
式中:Fk为滚筒在任意位置k时所受切向阻力的合力;F为滚筒旋转一周所受切向阻力的均值。
2.3.3 截割电机转矩和牵引电机转矩为确保采煤机正常运行,截割电机和牵引电机的转矩不大于其额定转矩即可。
| $ T_{\mathrm{mc}} \leqslant T_{\mathrm{mc}{\text {_额 }}}, $ | (21) |
| $ T_{\mathrm{mh}} \leqslant T_{\mathrm{mh}{\text {_额 }}}, $ | (22) |
式中:Tmc为截割电机转矩;Tmh为牵引电机转矩。
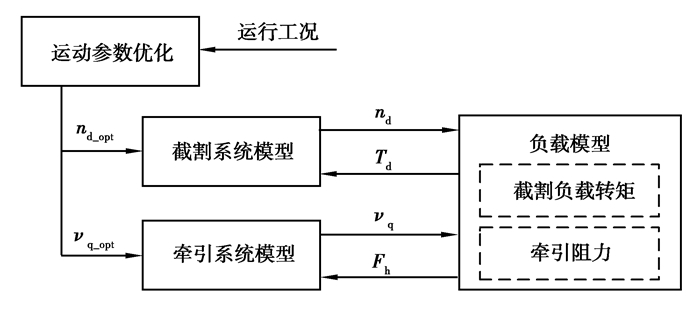
2.4 运动参数动态优化模型遗传算法具有全局优化能力强、优化速度快、优化精度高等优点,利用该算法对2个运动参数进行优化。图 5为运动参数动态优化分析模型的原理图,在第1节所建立的模型基础上,运用了运动参数优化的方法。在采煤机运行过程中,根据当前的工况,采用遗传算法获得设计变量的最优值nd_opt和vq_opt。以截割传动系统输出转速和牵引速度的最优值为目标,以最大的电机加速度进行调速,即调速时间已为最佳,使截割传动系统动态啮合力均值最小。
|
图 5 运动参数动态优化分析模型的原理图 Fig. 5 Diagram of kinematic parameter optimization |
将运动参数动态优化应用于某型采煤机,采煤机的主要参数如表 1所示。
| 表 1 采煤机主要参数 Table 1 Main parameters of the drum shearer |
在采煤机运行过程中,工况复杂多变,在不同工况下,运动参数的最优值不同。在运行过程中,根据工况信息动态优化截割传动系统输出转速和牵引速度。
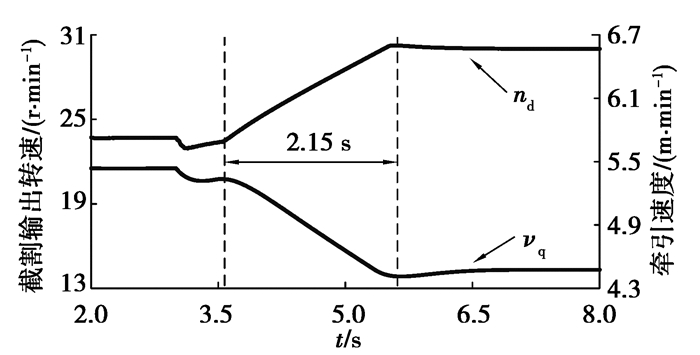
以负载转矩突变工况为例,分析运动参数动态优化对截割传动系统冲击载荷的影响。负载突变前,负载转矩为70 kN·m,经优化计算可得:运动参数的最优值为[nd_opt, vq_opt] = [23.7 r/min, 5.44 m/min]。负载突变后,负载转矩为97 kN·m,经优化计算可得:运动参数的最优值[nd_opt, vq_opt] = [30.2 r/min, 4.47 m/min]。以运动参数最优值为目标,调节截割传动系统输出转速和牵引速度,运动参数动态优化的结果如图 6~9所示。图 6为截割传动系统输出转速和牵引速度的实际值,图 7为作用在截割传动系统上的负载转矩,图 8为牵引阻力的变化曲线,图 9为截割传动系统耦合轮系和行星轮系的动态啮合力。
|
图 6 截割传动系统输出转速和牵引速度 Fig. 6 Cutting system output speed and hauling speed |
|
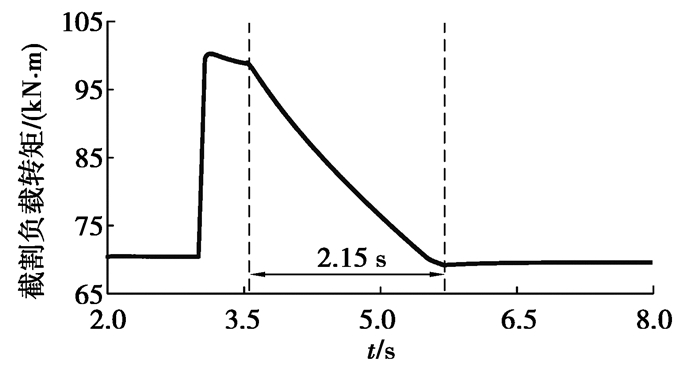
图 7 截割传动系统负载转矩 Fig. 7 Load torque on the cutting system |
|
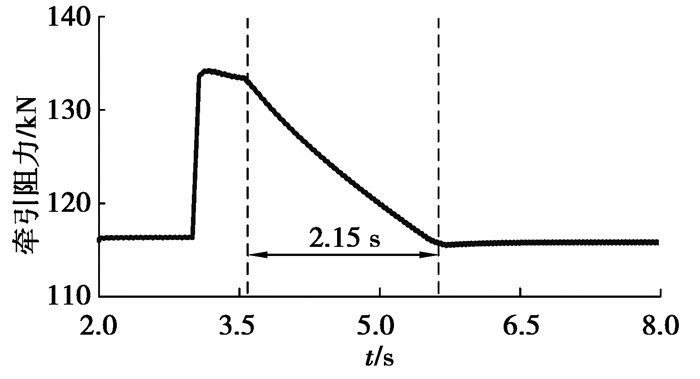
图 8 牵引阻力 Fig. 8 Traction resistance |
|
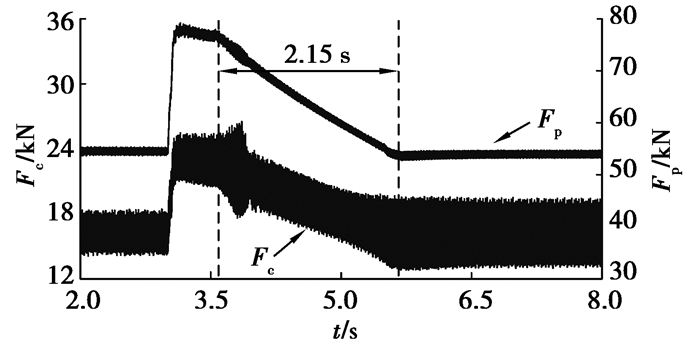
图 9 耦合轮系啮合力Fc和行星轮系动态啮合力Fp Fig. 9 Dynamic mesh forces of the coupling and planetary gear sets |
第3 s时,截割传动系统负载转矩突变增加,伴随着牵引阻力突变增加,截割传动系统中的动态啮合力增加(图 7~9);截割传动系统输出转速和牵引速度略有减小(图 6)。在第3.55 s时,截割电机和牵引电机以运动参数的最优值为目标进行调速,截割传动系统输出转速由23.69 r/min逐渐增加至30.15 r/min,牵引速度由5.441 m/min逐渐减小至4.473 m/min(图 6)。随着截割传动系统输出转速增加和牵引速度减小,截割传动系统负载转矩及牵引阻力逐渐减小,截割传动系统动态啮合力也逐渐减小(图 7~9)。
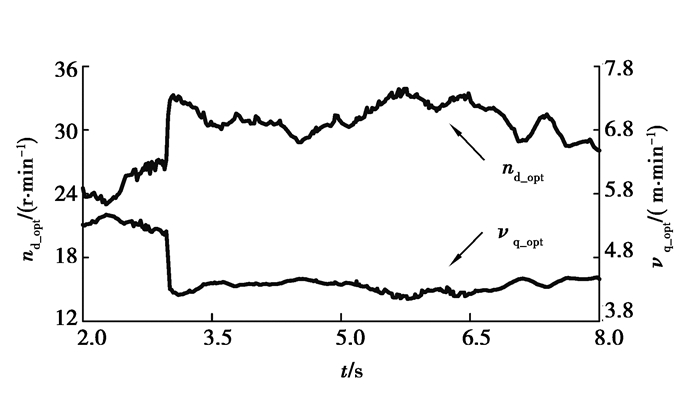
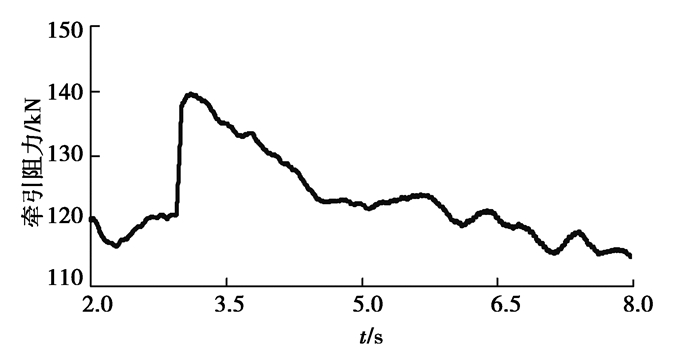
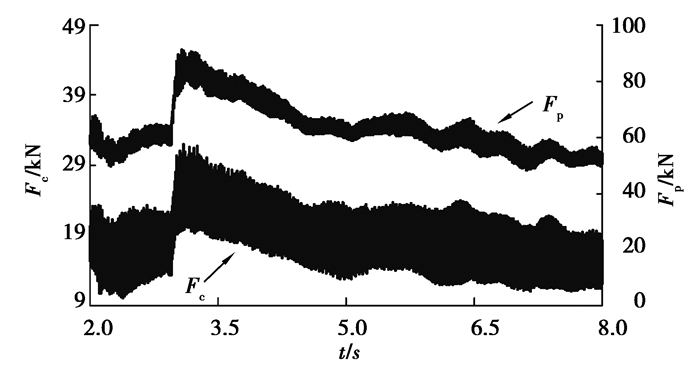
3.3 实际载荷突变工况下运动参数动态优化结果分析实际采煤过程中,载荷突变的情况较为复杂,采煤机截割负载中存在着低频成分和随机成分[16]。将截割阻抗由180 kN/m突变增加至250 kN/m,在此基础上叠加低频成分(0.5 Hz)和随机成分,来模拟实际采煤过程中载荷突变的工况,在此工况下分析运动参数动态优化对实际采煤过程中截割传动系统冲击载荷的影响。图 10为截割传动系统输出转速和牵引速度的优化结果,图 11为截割传动系统输出转速和牵引速度的实际值,图 12为作用在截割传动系统上的负载转矩,图 13为牵引阻力的变化曲线,图 14为截割传动系统耦合轮系和行星轮系的动态啮合力。
|
图 10 截割输出转速nd_opt和牵引速度目标值vq_opt Fig. 10 Cutting system target output speed and target hauling speed |

|
图 11 截割传动系统输出转速nd和牵引速度vq Fig. 11 Cutting system output speed and hauling speed |

|
图 12 截割传动系统负载转矩 Fig. 12 Load torque on the cutting system |
|
图 13 牵引阻力 Fig. 13 Traction resistance |
|
图 14 耦合轮系啮合力Fc和行星轮系动态啮合力Fp Fig. 14 Dynamic mesh forces of the couplimg and planetary gear sets |
在第3 s时,截割阻抗突变增加,随着截割传动系统负载转矩和牵引阻力突变增加,耦合轮系和行星轮系动态啮合力也增加(图 12~14)。此外,截割传动系统输出转速目标值增加,牵引速度目标值减小,由于负载中存在波动成分,运动参数最优值也存在波动(图 10)。随后截割电机和牵引电机按照目标值进行调速,由于电机加速度的限制,截割输出转速和牵引速度逐渐变化至目标值,如图 11所示。随着截割传动系统输出速度和牵引速度变化,截割负载转矩和牵引阻力逐渐减小,耦合轮系和行星轮系的动态啮合力也逐渐减小(图 12~14)。
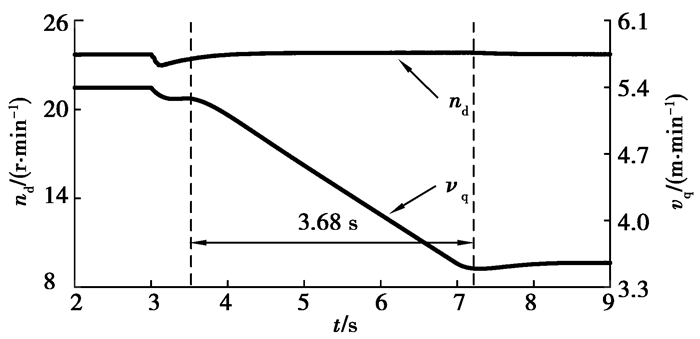
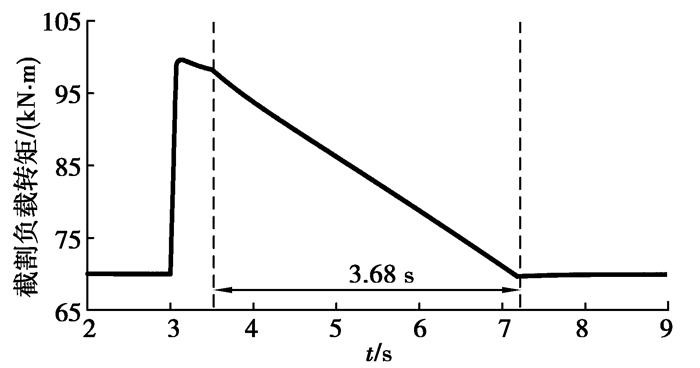
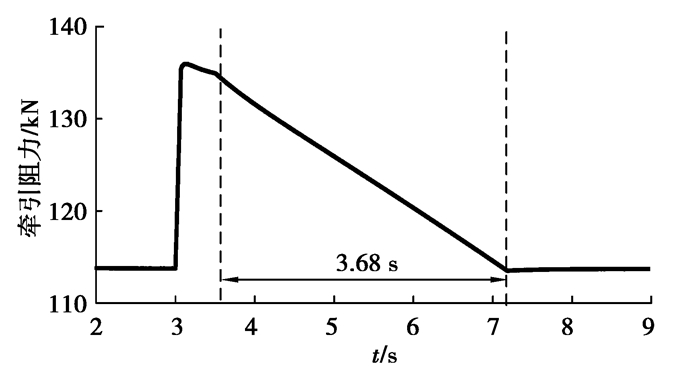
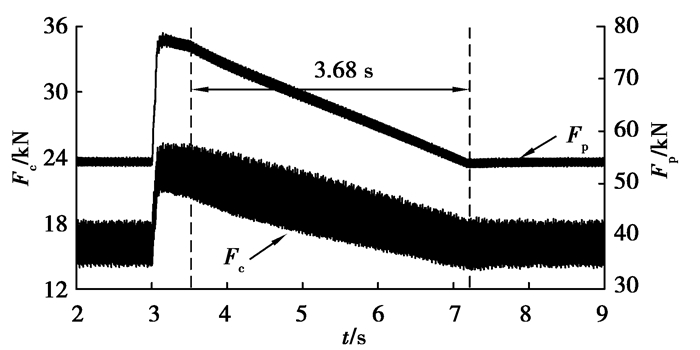
3.4 牵引调速结果分析当负载突变时,工程应用中主要采用牵引调速的方法。对比了运动参数动态优化与牵引调速的结果以分析动态参数优化的效果。图 15~18为牵引调速的结果,其中图 15为截割传动系统输出转速和牵引速度的实际值,图 16为作用在截割传动系统上的负载转矩,图 17为牵引阻力的变化曲线,图 18为截割传动系统耦合轮系和行星轮系的动态啮合力。在第3 s时,截割阻抗由180 kN/m突变增加至250 kN/m,截割传动系统负载转矩、牵引阻力及耦合轮系和行星轮系动态啮合力增加(图 16~18)。在第3.5 s时,牵引部开始调速,牵引速度由5.404 m/min逐渐减小至3.562 m/min,使截割传动系统负载转矩、牵引阻力以及耦合轮系和行星轮系动态啮合力逐渐减小。
|
图 15 截割传动系统输出转速nd和牵引速度vq Fig. 15 Cutting system output speed and hauling speed |
|
图 16 截割传动系统负载转矩 Fig. 16 Load torque on the cutting system |
|
图 17 牵引阻力 Fig. 17 Traction resistance |
|
图 18 耦合轮系啮合力Fc和行星轮系动态啮合力Fp Fig. 18 Dynamic mesh forces of the coupling and planetary gear sets |
通过运动参数动态优化与牵引调速的对比可知,相比于牵引调速,运动参数动态优化的方法使调速持续时间由3.68 s减少至2.15 s,减少41.6%,大幅度地降低了减小冲击载荷所需的调速时间。
4 实验验证建立了采煤机截割动力传动系统的实验台架,如图 19所示。台架由3台驱动电机、耦合轮系、行星轮系、飞轮、升速箱和测功机组成。驱动电机的额定功率为15 kW、额定转速为1 481 r/min,飞轮用于模拟系统的惯量。在测控系统中建立了牵引系统的模型,与截割动力传动系统实验装置相配合,进行运动参数优化对截割传动系统冲击载荷影响的实验。

|
图 19 实验台架 Fig. 19 Test bench |
通过控制器调节测功机施加的负载转矩,模拟负载突变工况,以研究运动参数优化对截割传动系统冲击载荷的影响。通过离线优化获得截割传动系统输出转速和牵引速度的最优值,将截割传动系统输出转速最优值用于调节截割传动系统的转速,将牵引速度最优值用于牵引系统模型的计算,将传感器测得的截割传动系统输出转速和牵引模型输出的牵引速度用于计算负载转矩的目标值。
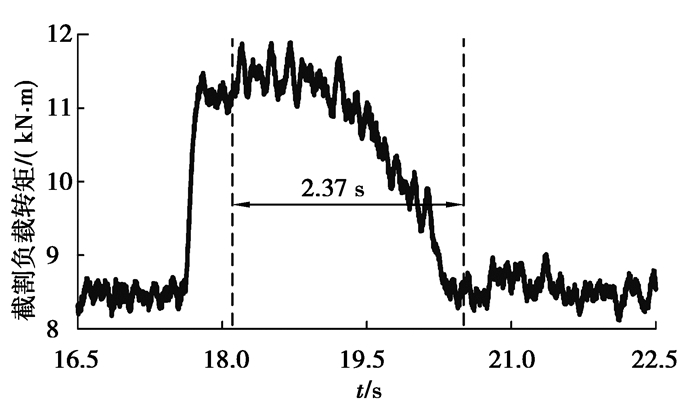
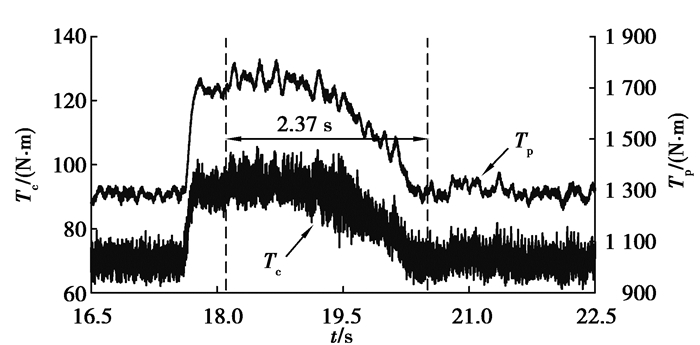
图 20和21分别为实验台架测得的截割传动系统负载转矩、耦合轮系输入转矩和行星轮系输入转矩。由于无法测得齿轮间动态啮合力,因此使用轮系的输入转矩反映传动系统中的冲击载荷。在第17.6 s时,测功机施加突变负载,使截割传动系统负载转矩、耦合轮系和行星轮系输入转矩突变增加。在第18.1 s时,截割电机和牵引电机以运动参数最优值为目标值进行调速,截割传动系统负载转矩、耦合轮系和行星轮系输入转矩略有增大后逐渐减小。升速箱增大了测功机转速,便于加载。但是它使测功机转子等效至飞轮输出端的等效转动惯量非常大,在变速过程中产生非常大的惯性转矩。因此,在调速时,图 20和21中的转矩略有增大后逐渐减小。
|
图 20 实验测得的截割传动系统负载转矩 Fig. 20 Test result of load torque on the cutting system |
|
图 21 实验测得的耦合轮系输入转矩Tc和行星轮系输入转矩Tp Fig. 21 Test result for input torques of coupling and planetary gear sets |
在单一载荷突变工况,实验结果的趋势与仿真结果的趋势相似,即随着负载的突变增大,传动系统中的冲击载荷也增大。随后截割电机和牵引电机以动态参数最优值为目标进行调速,在实验中,调速过程持续约2.37 s,与对应的仿真结果中的2.15 s相近。因此在实验和仿真过程中,负载转矩和轮系间动态啮合力均呈现先增大后减小的趋势,验证了运动参数优化的有效性。
5 结论1) 建立了采煤机动力传动系统的模型,分析了运动参数动态优化对截割传动系统冲击载荷的影响,通过台架实验验证了仿真结果。
2) 以截割传动系统行星轮系动态啮合力均值最小为优化目标,在系统运行过程中,根据当前工况采用遗传算法获取截割传动系统输出转速和牵引速度的最优值。在单一载荷突变工况下,运动参数动态优化使截割传动系统负载转矩、耦合轮系和行星轮系动态啮合力减小,提高了传动系统可靠性。通过将截割阻抗数值由180 kN/m突变增加至250 kN/m,并在此基础上叠加低频成分(0.5 Hz)和随机成分,模拟了采煤机实际工作时载荷突变的运行工况,通过仿真得到了与单一载荷突变工况下相同的结论。此外,对比了牵引调速和动态参数优化两种方法的调速效果,发现动态参数优化可以加快载荷降低的速率,缩短调速时间。
3) 通过台架实验验证了运动参数动态优化对截割传动系统冲击载荷的影响。截割传动系统负载转矩和传动系统冲击载荷的实验与仿真结果的趋势相似,调速持续时间的实验结果约为2.37 s,与仿真结果中的2.15 s相近,验证了运动参数优化的有效性。
| [1] |
耿智博, 肖科, 王家序, 等. 汽车变速器齿轮传动系统动态特性研究及优化[J]. 湖南大学学报(自然科学版), 2018, 45(8): 22-31. Geng Z B, Xiao K, Wang J X, et al. Analysis and optimization design on dynamic characteristic of gear transmission system of automobile transmission[J]. Journal of Hunan University (Natural Sciences), 2018, 45(8): 22-31. (in Chinese) |
| [2] |
孙伟, 李想, 魏静, 等. 大功率风电增速器的多目标优化设计[J]. 重庆大学学报, 2015, 38(1): 110-119, 147. Sun W, Li X, Wei J, et al. Multi-objective dynamic optimization design of high-power wind turbine gearbox[J]. Journal of Chongqing University, 2015, 38(1): 110-119, 147. (in Chinese) |
| [3] |
Tamboli K, Patel S, George P M, et al. Optimal design of a heavy duty helical gear pair using particle swarm optimization technique[J]. Procedia Technology, 2014, 14: 513-519. DOI:10.1016/j.protcy.2014.08.065 |
| [4] |
Chandrasekaran G, Sreebalaji V S, Saravanan R, et al. Multiobjective optimisation of bevel gear pair design using NSGA-Ⅱ[J]. Materials Today: Proceedings, 2019, 16: 351-360. DOI:10.1016/j.matpr.2019.05.101 |
| [5] |
Świtoński E, Mężyk A. Selection of optimum dynamic features for mechatronic drive systems[J]. Automation in Construction, 2008, 17(3): 251-256. DOI:10.1016/j.autcon.2007.05.001 |
| [6] |
周笛, 张旭方, 张义民. 采煤机牵引部可靠性灵敏度分析及优化设计[J]. 东北大学学报(自然科学版), 2017, 38(1): 81-85. Zhou D, Zhang X F, Zhang Y M. Reliability sensitivity analysis and optimization design on tractive drive system of shearer loader[J]. Journal of Northeastern University (Natural Science), 2017, 38(1): 81-85. (in Chinese) DOI:10.3969/j.issn.1005-3026.2017.01.017 |
| [7] |
Korta J A, Mundo D. Multi-objective micro-geometry optimization of gear tooth supported by response surface methodology[J]. Mechanism and Machine Theory, 2017, 109: 278-295. DOI:10.1016/j.mechmachtheory.2016.11.015 |
| [8] |
Artoni A, Gabiccini M, Guiggiani M, et al. Multi-objective ease-off optimization of hypoid gears for their efficiency, noise, and durability performances[J]. Journal of Mechanical Design, 2011, 133(12): 121007. DOI:10.1115/1.4005234 |
| [9] |
林何, 王三民. 参数对分扭-并车齿轮传动系统动载和均载特性的影响[J]. 机械传动, 2019, 43(5): 18-22, 63. Lin H, Wang S M. Influence of parameter on dynamic load and load sharing characteristic of split torque-combine power gear transmission system[J]. Journal of Mechanical Transmission, 2019, 43(5): 18-22, 63. (in Chinese) |
| [10] |
欧阳天成, 黄豪中, 王攀, 等. 胶印机齿轮传动系统动力学建模及优化设计[J]. 东南大学学报(自然科学版), 2016, 46(6): 1172-1178. Ouyang T C, Huang H Z, Wang P, et al. Dynamics modeling and dynamic optimization design for offset press gear transmission system[J]. Journal of Southeast University (Natural Science Edition), 2016, 46(6): 1172-1178. (in Chinese) |
| [11] |
李启山. 基于模糊可靠理论的采煤机牵引机构传动可靠性分析[J]. 机械管理开发, 2019, 34(8): 104-105. Li Q S. Transmission reliability analysis of shearer traction mechanism based on fuzzy reliability theory[J]. Mechanical Management and Development, 2019, 34(8): 104-105. (in Chinese) |
| [12] |
常玉洁. 综合考虑参数时变的异步电机模型研究[D]. 北京: 北京交通大学, 2019. Chang Y J. Research on asynchronous motor model considering synthetically time-varying parameters[D]. Beijing: Beijing Jiaotong University, 2019. (in Chinese) |
| [13] |
Salo M, Tuusa H. A vector controlled current-source PWM rectifier with a novel current damping method[J]. IEEE Transactions on Power Electronics, 2000, 15(3): 464-470. DOI:10.1109/63.844506 |
| [14] |
杨文奇. 采煤机牵引部双电机驱动协调控制研究[D]. 重庆: 重庆大学, 2016. Yang W Q. Research on coordinated control of dual-motor driving system of shearer's haulage unit[D]. Chongqing: Chongqing University, 2016. (in Chinese) |
| [15] |
高红斌, 杨兆建. 滚筒采煤机负载的波动性分析[J]. 机械科学与技术, 2013, 32(7): 1054-1059. Gao H B, Yang Z J. Analysis on the load fluctuation of roller shearer[J]. Mechanical Science and Technology for Aerospace Engineering, 2013, 32(7): 1054-1059. (in Chinese) |
| [16] |
张启志. 采煤机截割振动信号采集系统的研究[D]. 北京: 煤炭科学研究总院, 2017. Zhang Q Z. Research on cutting vibration signal acquisition system of shearer[D]. Beijing: China Coal Research Institute, 2017. (in Chinese) |
 2021, Vol. 44
2021, Vol. 44

