b. 兰州交通大学 铁道车辆热工教育部重点实验室, 兰州 730070
b. Key Laboratory of Railway Vehicle Thermal Engineering, Ministry of Education of China, Lanzhou Jiaotong University, Lanzhou 730070, P. R. China
太阳能热水系统由于其具有“节能效益高、投资和维护成本低”等优点,已被广泛应用于生活热水、地板供暖、工业生产等方面[1-2]。目前已有的研究主要涉及水箱的外形结构[3-7]、进出口水管结构及运行工况[8-12]、内置隔板结构[13-17]等方面,目的是通过对蓄热水箱进行结构优化以获得最佳的蓄热性能。但这些研究都是针对静态运行模式或者动态模式下的单个水箱展开的。而实际情况是太阳辐射强度的瞬时变化以及用户端回水参数的不稳定性等因素常常导致太阳能集热器出水温度(对应蓄热水箱热水入口温度)、蓄热水箱冷水入口温度及流速均呈动态变化,若仅配置单一结构的水箱其蓄热性能往往会偏离系统最佳的设计状态。实际运行中,客观上必然存在一组流体参数能使得某特定结构蓄热水箱的蓄热性能最优。因此,合理调节太阳能热水系统的流体运行参数使得蓄热水箱性能最优并科学管理水箱的运行模式,是适应太阳辐射强度动态变化、提高太阳能蓄热水箱蓄热性能的重要举措。目前,结合当地气象条件寻求能在不同时段充分利用太阳能资源的流体参数与蓄热水箱的最佳组合并探索合理的运行模式的研究,还未见报道。笔者在太阳能相变蓄热地板供暖系统的实验研究基础上,对乌鲁木齐地区太阳能辐射强度不同的3个典型时刻对应的多个工况进行计算,根据对不同结构蓄热水箱在不同流体参数下蓄热性能的评价结果,得出了各时刻最佳的水箱结构以及与之对应的最优运行参数,研究结果对于该地区推广太阳能供暖系统采用多水箱交替运行以提高供暖可靠性具有重要的工程指导意义。
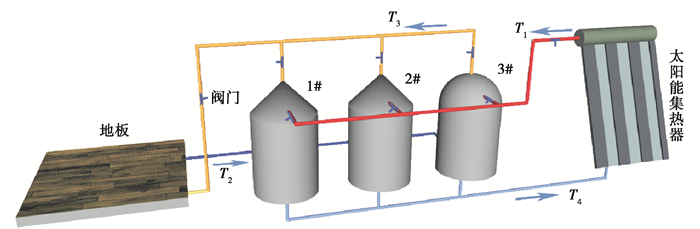
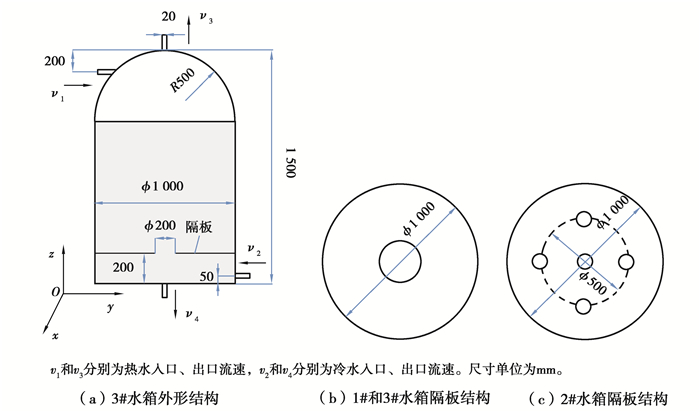
1 模型介绍 1.1 物理模型太阳能地板供暖系统中各水箱并联运行方式如图 1所示,T1和T3分别为热水进、出口温度,T2和T4分别为冷水进、出口温度。1#和2#水箱为锥顶结构[3],锥顶高度为0.15 m,3#水箱为半球形顶结构。3个水箱直径均为1.0 m,水箱总高度均为1.5 m,内置隔板的厚度均为0.003 m,其安装位置距水箱底面的距离均为0.2 m,冷热水进、出口短管直径均为0.02 m,安装位置如图 2(a)所示。各水箱隔板结构如图 2(b)、(c)所示,1#和3#水箱的隔板均为单圆孔结构,开孔面积为0.031 4 m2;2#水箱的隔板为5孔结构,有4个小圆孔均布在直径为0.5 m的定位圆圆周上,面积相等的5个小圆孔的面积之和与1#水箱的隔板开孔面积相等。
|
图 1 水箱并联运行示意图 Fig. 1 Schematic diagram of parallel water tanks |
|
图 2 蓄热水箱、内置隔板物理模型及冷热水流向示意图 Fig. 2 Physical model of hot water storage tank and internal barrier, fluid flow direction of cold and hot water |
考虑系统运行时水箱内流速低、压力变化小、水温变化小等实际情况,计算中假定流体的物理属性不变、为不可压缩流体、忽略黏性耗散效应。求解水箱内流动与换热的控制方程如下[18]:
连续性方程:
| $ \frac{{\partial \rho }}{{\partial t}} + \sum\limits_{i = 1}^3 {\frac{\partial }{{\partial {x_i}}}} \left( {\rho {u_i}} \right) = 0; $ | (1) |
动量方程:
| $ \frac{{\partial \left( {\rho {u_i}} \right)}}{{\partial t}} + \sum\limits_{j = 1}^3 {\frac{\partial }{{\partial {x_j}}}} \left( {\rho {u_j}{u_i}} \right) = - \frac{{\partial P}}{{\partial {x_i}}} + \sum\limits_{j = 1}^3 {\frac{{\partial {\tau _{ij}}}}{{\partial {x_j}}}} + \rho {f_i}; $ | (2) |
能量方程:
| $ \rho {C_{\rm{p}}}\frac{{\partial T}}{{\partial t}} = {\mathop{\rm div}\nolimits} (\lambda \overline {{\mathop{\rm grad}\nolimits} } \;T) + T\beta \frac{{{\rm{d}}P}}{{{\rm{d}}t}} + q + \mathit{\Phi }; $ | (3) |
其中,
湍流动能方程:
| $ \rho \frac{{\partial k}}{{\partial t}} + \rho {u_j}\frac{{\partial k}}{{\partial {x_j}}} = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\eta + \frac{{{\eta _{\rm{t}}}}}{{P{r_{\rm{t}}}}}} \right)\frac{{\partial k}}{{\partial {x_j}}}} \right] + {\eta _{\rm{t}}}\frac{{\partial {u_j}}}{{\partial {x_i}}}\left( {\frac{{\partial {u_j}}}{{\partial {x_i}}} + \frac{{\partial {u_i}}}{{\partial {x_j}}}} \right) - {c_{\rm{D}}}\rho \frac{{{k^{3/2}}}}{{{l_{\rm{m}}}}}; $ | (4) |
湍流动能耗散率方程:
| $ \rho \frac{{\partial \varepsilon }}{{\partial t}} + \rho {u_j}\frac{{\partial \varepsilon }}{{\partial {x_k}}} = \frac{\partial }{{\partial {x_k}}}\left[ {\left( {\eta + \frac{{{\eta _{\rm{t}}}}}{{{\sigma _\varepsilon }}}} \right)\frac{{\partial \varepsilon }}{{\partial {x_k}}}} \right] + {c_1}\frac{\varepsilon }{k}{\eta _{\rm{t}}}\frac{{\partial {u_i}}}{{\partial {x_j}}}\left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right) - {c_2}\rho \frac{{{\varepsilon ^2}}}{k}, $ | (5) |
式中:T为温度,K;η为动力黏度,(N·s)/m2;ρ为密度,kg/m3;β为膨胀系数,1/K;Cp为定压比热,J/(kg·K);Prt为湍流普朗特数,其值在1.0左右;lm为湍流长度标尺,m;c1、c2为经验系数,标准k-ε模型中一般取1.44及1.92。其余符号含义及参数取值见文献[19]。流体为水,密度变化采用Boussinesq假设。
1.3 边界条件和初始条件以文献[20]A1时间段(10月15日—11月15日和3月15日—4月15日)典型日的实验数据为基础,取测试当天3个不同时刻(11:30、15:00、18:00)的热、冷水入口温度与不同的冷水入口流速组合得到的计算工况如表 1所示。水箱中的压力为1个大气压。所有液固交界面均为速度无滑移条件。水箱内壁面和隔板表面均为绝热边界条件,水箱进水口设为速度入口,出水口设为自由出流。
| 表 1 计算工况及流体参数 Table 1 Calculating working conditions and fluid parameters |
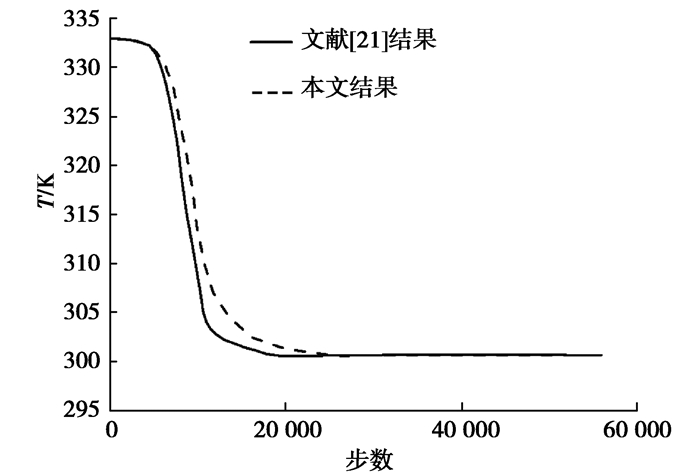
采用1.2节数学模型在文献[21]的条件下对文献[21]的流动与传热过程进行了数值模拟,并将得到的水箱出口温度计算结果与文献[21]的结果进行比对,如图 3所示,其相对偏差的最大值仅为1.39%,则1.2节数学模型可用于后续计算。
|
图 3 本文结果与文献结果对比 Fig. 3 Comparison of the results of this study with the results of literature |
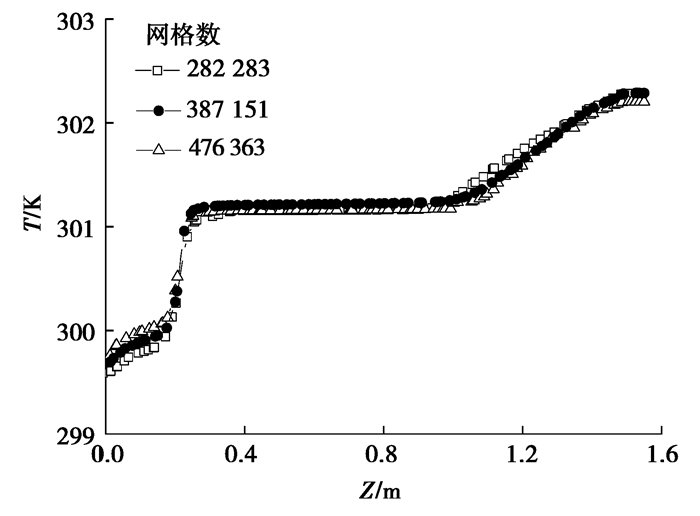
采用非结构化四面体网格对计算区域进行离散[22]。采用3套网格对1#水箱进行计算,所得水箱中轴线上的温度计算结果吻合得很好,如图 4所示。考虑计算的经济性,取1#水箱的计算网格数为387 151。同理,得到2#和3#水箱的计算网格数分别为402 951和394 260。
|
图 4 网格独立性验证 Fig. 4 Grid independence verification |
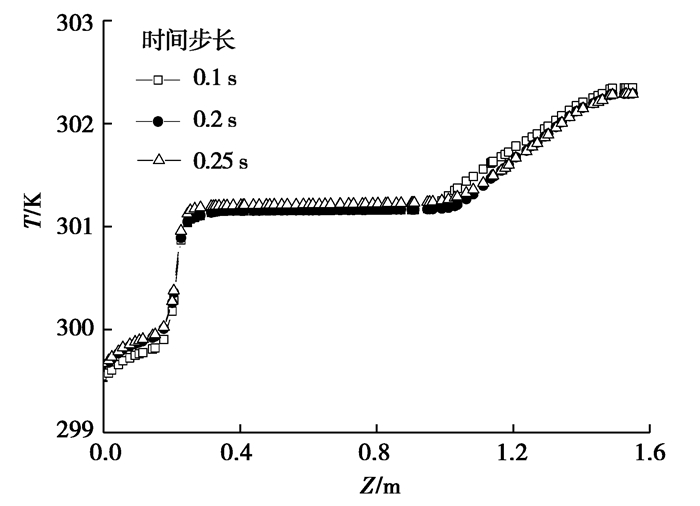
取3个时间步长对1#水箱进行计算,计算时间为30 min。不同时间步长所得结果吻合得很好,如图 5所示。这里以0.25 s作为后续计算的时间步长。
|
图 5 时间步长确定 Fig. 5 Time step determination |
采用非耦合隐式算法求解控制方程。离散格式与文献[18]相同,采用SIMPLE算法求解速度和压力耦合问题[19]。松弛因子设置以及求解控制方程时的收敛条件均与文献[18]相同。
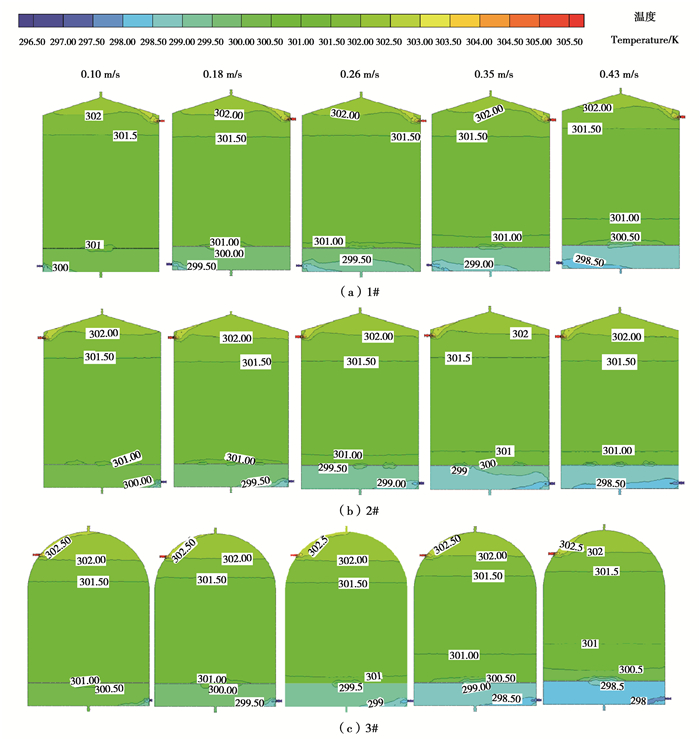
3 计算结果及分析 3.1 水箱温度场比较水箱顶部形状及隔板结构均以边界条件的形式影响温度场分布。图 6为各水箱在11:30时刻不同工况下的温度场结构。可以看出,当冷水入口流速小于0.26 m/s时,隔板上方高温水范围及热分层受冷水入口流速的影响均很微弱;当冷水入口流速超过0.26 m/s时,隔板上方高温水范围及热分层受冷水入口流速的影响显著。其中,3#水箱高温水范围的缩减程度最明显,2#水箱缩减最小。这说明当隔板开孔面积相同、冷水入口流速较大时,锥顶形状与多开孔隔板的组合结构相比于球顶形状与单开孔隔板的组合结构更有利于形成良好的热分层效果和较大的高温水范围。因此,从热分层的稳定性角度考虑,锥顶形状与多开孔隔板的组合(即2#水箱)结构对流动工况的适应性更强。
|
图 6 不同水箱内x=0截面温度场随v2的变化(11:30) Fig. 6 Changes of temperature field in x=0 section with v2 in different water tanks (11:30) |
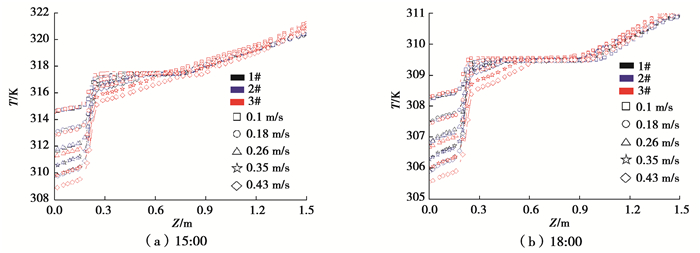
图 7分别为15:00和18:00各水箱温度沿z轴正向分布曲线。可以看出,当冷水入口流速为0.1 m/s时,3#水箱上部区域温度更高,此时,3#水箱斜温层厚度更小(热水与冷水之间的过渡区域称作斜温层,斜温层越薄,温度梯度越大,水箱分层效果越好[23]),具有更好的热分层效果。当冷水入口流速大于0.35 m/s时,在z<0.75 m的范围,3#水箱温度整体上低于其余2个水箱。因此,针对大流量的运行模式,热用户应尽量避免运行3#水箱。
|
图 7 沿z轴正向温度分布曲线 Fig. 7 The distribution of temperature along z direction |
评价蓄热水箱热分层效果最常用的指标为理查森数[24],它是同时考虑浮升力、惯性力、黏滞力对流体质点运动状态的综合作用效果的无量纲数[17]。热分层效果与理查森数Ri大小呈正相关,其定义式为:
| $ R i=g \beta H \Delta T / v_{2}^{2}; $ | (6) |
式中:β为膨胀系数,1/K;H为水箱高度,m;ΔT为热、冷水出口温度之差,K;v2为冷水入口流度,m/s。
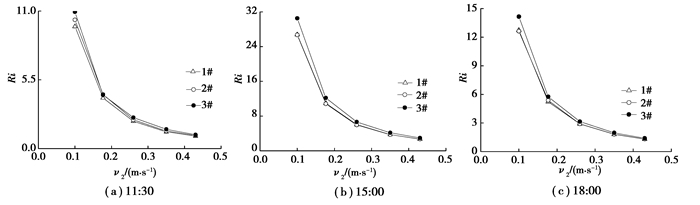
图 8为3个不同时刻Ri值随冷水入口流速的变化曲线。可以看出,同一冷水入口流速下15:00时的Ri值远高于11:30和18:00时的值,这是由于15:00水箱内初始温度较高,使得热分层效果更好,这一结论与文献[25]的研究结论一致。因此,工程实际中蓄热水箱保温措施的好坏直接影响其热分层效果,进而影响水箱的蓄热性能。
|
图 8 Ri数随冷水入口流速的变化 Fig. 8 Variation of Richardson number with inlet velocity of cold water |
对于不同时刻,3个水箱的Ri值均随冷水入口流速的增大呈下降趋势,且下降速率趋于平缓。这是因为一方面,Ri(Ri=Gr/Re2)取决于格拉晓夫数(Gr)和雷诺数(Re)的相对大小,冷水入口流速增大对流场结构的改变(体现为Re)较温差引起的浮升力变化(体现为Gr)更显著,热分层效果因此变差;另一方面,冷水入口流速增大会激励冷热水间的动量与热量交换,水箱内原有的热层结构被破坏,进而导致热分层效果变差。另外,3#水箱Ri值均高于其他2个水箱,3个水箱Ri值之间的差异随冷水入口速的增大而减小。
综上,从热分层效果的角度考虑,11:30,不同冷水入口流速下1#水箱的热分层效果均最差,在这一时刻优先运行3#水箱,其次为2#水箱;15:00和18:00,1#和2#水箱的热分层效果相当,在这2个时刻可以通过调节冷水入口流速来改变运行工况,优先运行3#水箱,1#和2#水箱可以互为备用。
3.3 热、冷水出口温度比较图 9为不同时刻各水箱热、冷水出口温度与v2的变化关系。可以看出,3个典型时刻各水箱冷水出口温度均随冷水入口流速的增大而降低,但就某时刻而言,各水箱热水出口温度取得最大值时的v2并不相同。3个时刻,3#水箱均在冷水入口流速为0.1 m/s时其热水出口温度获得最大值,说明3#水箱更适用于小流量的运行工况。2#水箱在11:30且v2=0.35 m/s时热水出口温度获得最大值,其余时刻均在v2=0.43 m/s时获得最大值,说明2#水箱在冷水入口流速较高的运行工况下热水出口温度更能得到保证;3个时刻1#水箱热水出口温度获得最大值对应的冷水入口流速分别为0.18, 0.35, 0.43 m/s。
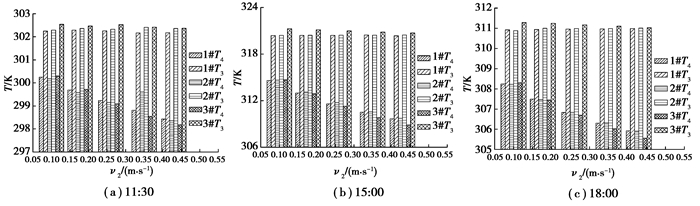
|
图 9 3个不同时刻水箱的热、冷水出口温度 Fig. 9 Temperature values of cold and hot water exit at three different times |
综上,3#水箱更适用于对水温要求较高但用量不大的运行工况,其次为1#水箱。当用户端回水量较大且用户需要较高温度热水时优先启用2#水箱。
图 10为不同时刻各水箱热冷水出口温差与冷水入口流速的变化关系。可以看出,3个典型时刻3#水箱热、冷水出口温差在不同v2下均最高,即在一定范围内调节v2均能使得3#水箱内的热分层效果最佳,这与3.2节依据理查森数指标的分析结果一致。
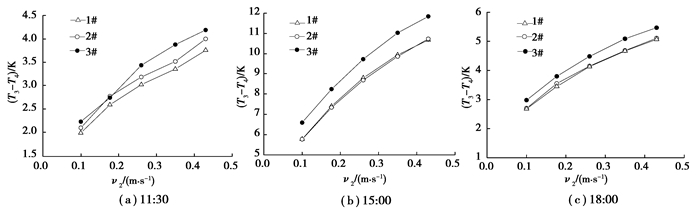
|
图 10 热、冷水出口温差比较 Fig. 10 Comparison of outlet temperature differences of cold and hot water |
对比分析了乌鲁木齐地区外气温度相对稳定的3个典型时刻流体参数对不同结构蓄热水箱蓄热性能的影响,并探讨了在各典型时刻不同结构蓄热水箱对用户需求的适应性,得到的主要结论如下:
1) 针对当地太阳能资源实际情况,在不同外气温度时段对不同结构水箱实行交替运行可有效避免太阳能辐射强度随机性问题。当系统处于太阳能保证率较低的时段,可考虑辅助热源与集热器并联后接入水箱,也可以考虑多个水箱同时开启,以满足不同用户的实际需求。
2) 较低的入口流速能使3种结构的水箱在各时刻均表现出最佳的热分层效果。11:30,优先运行3#水箱,其次为2#水箱;15:00和18:00,可通过调节冷水入口流速来改变运行工况,优先运行3#水箱,但当热用户对水量需求较大时,应尽量避免运行3#水箱。
3) 3#水箱更适用于对水温要求较高但用水量不大的用户需求,其次为1#水箱。当用户端回水量较大且用户需要较高温度热水时优先启用2#水箱。
| [1] |
Çomaklı K, Çakır U, Kaya M, et al. The relation of collector and storage tank size in solar heating systems[J]. Energy Conversion and Management, 2012, 63: 112-117. DOI:10.1016/j.enconman.2012.01.031 |
| [2] |
Taheri Y, Ziapour B M, Alimardani K. Study of an efficient compact solar water heater[J]. Energy Conversion and Management, 2013, 70: 187-193. DOI:10.1016/j.enconman.2013.02.014 |
| [3] |
王烨, 鲍成柯, 付银安, 等. 圆锥形顶太阳能蓄热水箱锥顶结构及运行参数优化[J]. 农业工程学报, 2017, 33(22): 255-261. Wang Y, Bao C K, Fu Y A, et al. Study of structure optimization of solar hot water storage tank with conical top[J]. Transactions of the CSAE, 2017, 33(22): 255-261. (in Chinese) DOI:10.11975/j.issn.1002-6819.2017.22.033 |
| [4] |
Gómez M A, Collazo J, Porteiro J, et al. Numerical study of an external device for the improvement of the thermal stratification in hot water storage tanks[J]. Applied Thermal Engineering, 2018, 144: 996-1009. DOI:10.1016/j.applthermaleng.2018.09.023 |
| [5] |
Chandra Y P, Matuska T. Stratification analysis of domestic hot water storage tanks: a comprehensive review[J]. Energy and Buildings, 2019, 187: 110-131. DOI:10.1016/j.enbuild.2019.01.052 |
| [6] |
Wang Z L, Zhang H, Huang H J, et al. The experimental investigation of the thermal stratification in a solar hot water tank[J]. Renewable Energy, 2019, 134: 862-874. DOI:10.1016/j.renene.2018.11.088 |
| [7] |
Kurşun B, Ökten K. Effect of rectangular hot water tank position and aspect ratio on thermal stratification enhancement[J]. Renewable Energy, 2018, 116: 639-646. DOI:10.1016/j.renene.2017.10.013 |
| [8] |
Majumdar R, Saha S K. Effect of varying extent of PCM capsule filling on thermal stratification performance of a storage tank[J]. Energy, 2019, 178: 1-20. DOI:10.1016/j.energy.2019.04.101 |
| [9] |
Kumar S, Grover R B, Yadav H, et al. Experimental and numerical investigation on suppression of thermal stratification in a water-pool: PIV measurements and CFD simulations[J]. Applied Thermal Engineering, 2018, 138: 686-704. DOI:10.1016/j.applthermaleng.2018.04.070 |
| [10] |
Kang M, Kim J, You H, et al. Experimental investigation of thermal stratification in cryogenic tanks[J]. Experimental Thermal and Fluid Science, 2018, 96: 371-382. DOI:10.1016/j.expthermflusci.2017.12.017 |
| [11] |
Wang Z L, Zhang H, Dou B L, et al. Influence of inlet structure on thermal stratification in a heat storage tank with PCMs: CFD and experimental study[J]. Applied Thermal Engineering, 2019, 162: 114151. DOI:10.1016/j.applthermaleng.2019.114151 |
| [12] |
Bouzaher M T, Bouchahm N, Guerira B, et al. On the thermal stratification inside a spherical water storage tank during dynamic mode[J]. Applied Thermal Engineering, 2019, 159: 113821. DOI:10.1016/j.applthermaleng.2019.113821 |
| [13] |
Dannemand M, Perers B, Furbo S. Performance of a demonstration solar PVT assisted heat pump system with cold buffer storage and domestic hot water storage tanks[J]. Energy and Buildings, 2019, 188/189: 46-57. DOI:10.1016/j.enbuild.2018.12.042 |
| [14] |
Haller M Y, Haberl R, Reber A. Stratification efficiency of thermal energy storage systems: a new KPI based on dynamic hardware in the loop testing - Part Ⅱ: test results[J]. Energy and Buildings, 2019, 202: 109366. DOI:10.1016/j.enbuild.2019.109366 |
| [15] |
王烨, 宋荣飞, 胡悦, 等. 内置隔板开孔方式对太阳能蓄热水箱热分层的影响[J]. 储能科学与技术, 2019, 8(5): 897-903. Wang Y, Song R F, Hu Y, et al. Effect of obstacles with different opening means on thermal stratification in hot water storage tanks[J]. Energy Storage Science and Technology, 2019, 8(5): 897-903. (in Chinese) |
| [16] |
Bai Y K, Yang M, Wang Z F, et al. Thermal stratification in a cylindrical tank due to heat losses while in standby mode[J]. Solar Energy, 2019, 185: 222-234. DOI:10.1016/j.solener.2018.12.063 |
| [17] |
王烨, 王瑞君, 鲁红钰, 等. 太阳能蓄热水箱内置隔板开孔方式对蓄热性能的影响[J]. 农业工程学报, 2019, 35(10): 191-198. Wang Y, Wang R J, Lu H Y, et al. Influence of arrangement of holes on barrier of hot water tank of solar energy on heat storage performance[J]. Transactions of the CSAE, 2019, 35(10): 191-198. (in Chinese) DOI:10.11975/j.issn.1002-6819.2019.10.024 |
| [18] |
王烨, 鲁红钰, 付银安, 等. 具有内置隔板的太阳能蓄热水箱运行参数研究[J]. 应用基础与工程科学学报, 2019, 27(3): 667-676. Wang Y, Lu H Y, Fu Y A, et al. Fluid parameters of solar hot water storage tank with obstacle inside the tank[J]. Journal of Basic Science and Engineering, 2019, 27(3): 667-676. (in Chinese) |
| [19] |
陶文铨. 数值传热学[M]. 第二版. 西安: 西安交通大学出版社, 2001. Tao W Q. Numerical heat transfer[M]. 2nd edition. Xi'an: Xi'an Jiaotong University Press, 2001. (in Chinese) |
| [20] |
张叶, 陈超, 王万江, 等. 太阳能相变蓄热地板辐射供暖系统应用于乌鲁木齐地区办公建筑的实验研究[J]. 暖通空调, 2016, 46(6): 101-109. Zhang Y, Chen C, Wang W J, et al. Experimental study on solar phase change storage floor radiant heating system application to an office building in Urumqi[J]. Heating Ventilating & Air Conditioning, 2016, 46(6): 101-109. (in Chinese) |
| [21] |
Gao W F, Liu T, Lin W X, et al. Numerical study on mixing characteristics of hot water inside the storage tank of a solar system with different inlet velocities of the supply cold water[J]. Procedia Environmental Sciences, 2011, 11: 1153-1163. DOI:10.1016/j.proenv.2011.12.174 |
| [22] |
吕水燕, 张传侠, 叶坤, 等. 高超声速气动热数值模拟的网格模式相关性研究[J]. 兵器装备工程学报, 2019, 40(3): 82-86. Lyu S Y, Zhang C X, Ye K, et al. Study on grid dependency of hypersonic aerothermal simulation[J]. Journal of Ordnance Equipment Engineering, 2019, 40(3): 82-86. (in Chinese) DOI:10.11809/bqzbgcxb2019.03.019 |
| [23] |
Musser A, Bahnfleth W. Evolution of temperature distributions in a full-scale stratified chilled water storage tank[J]. ASHRAE Transactions, 1998, 104(1): 55-67. |
| [24] |
Castell A, Medrano M, Solé C, et al. Dimensionless numbers used to characterize stratification in water tanks for discharging at low flow rates[J]. Renewable Energy, 2010, 35(10): 2192-2199. DOI:10.1016/j.renene.2010.03.020 |
| [25] |
Jordan U, Furbo S. Thermal stratification in small solar domestic storage tanks caused by draw-offs[J]. Solar Energy, 2005, 78(2): 291-300. DOI:10.1016/j.solener.2004.09.011 |
 2021, Vol. 44
2021, Vol. 44

