车辆跟驰理论是利用动力学方法,研究无法超车的单一车道上车辆排队行驶的场景,并以数学模型表达跟驰过程中发生的各种状态的理论[1]。自20世纪50年代以来,国内外学者对车辆跟驰模型进行了大量的研究,Chandler等[2]提出GM模型,该模型清楚地反映车辆跟驰行为中存在的制约性、延迟性以及传递性。Kometani等[3]利用经典牛顿力学提出车辆跟驰期望安全间距,并对期望安全间距进行分析。Kikuchi等[4]利用驾驶员预期逻辑推理,提出基于模糊推理的车辆跟驰模型。Michaels等[5]用驾驶过程中的一系列阈值和期望间距,建立基于生理-心理的车辆跟驰模型。Cremer等[6]利用元胞自动机理论研究道路交通行为,该模型将道路定义为离散的元胞空间,并设置一定的规则对道路跟驰行为进行仿真。Bando等[7]提出优化速度模型,利用车辆间距与优化速度函数描述交通流中的定性特征。目前,由于硬件设备的升级,车辆跟驰行为数据的获取变得更加便捷,基于非参数方法的数据驱动类跟驰模型逐渐发展起来[8-10],这类模型对跟驰数据信息进行挖掘,有助于建立高精度的跟驰模型。
近年来,有学者提出将车辆在道路上的跟驰行为类比为分子之间的相互作用,利用分子动力学原理描述车辆间的跟驰特性与交通流特性。曲大义等[11]利用分子动力学描述了驾驶员对各类刺激反应同向性的状态方程并建立分子跟驰模型,该模型可以更好地描述真实车辆运行状态。郝杰等[12]建立分子动力学车流密集度模型,分析交通流三参数的动态特性。陈文娇等[13]应用分子动力学建立车辆需求安全距离模型并以调查数据对模型进行验证。郭涛等[14]利用李雅普诺夫稳定性判断理论对交通流稳定性进行分子动力学分析并建模,推导出交通流失稳现象产生的机理。曲大义等[15-16]考虑车辆需求安全间距和车道限速,建立分子跟驰模型并对模型进行验证。
1 分子动力学 1.1 分子动力学特性分子动力学是利用牛顿力学分析分子体系的运动,从不同状态构成的系统中抽取分子样本,计算分子体系的构型积分,进而了解分子宏观性质的方法。
分子是由一系列原子结合而形成的整体,由于原子之间的相互作用,使分子之间存在一定的作用力。分子间始终存在引力和斥力,但引力和斥力的大小随分子间距的变化而变化,当分子间距过近时分子间作用力表现为斥力,当分子间距过远时分子间作用力表现为引力,由于这一特性,分子间既不会无限远离也不会无限靠近,而是处于一种动态平衡之中。分子间存在相互作用力为零的状态,既无引力也无斥力,此时分子间的距离称为分子平衡距离。
分子在一维管道中运动时,主要受到分子之间相互作用势以及壁面势的作用,如图 1所示,其中f1为分子之间的引力,f2为分子之间的斥力,f3为壁面对分子的作用力。在分子动力学模拟实验中,壁面对分子的运动也存在相应的影响,即分子所处的环境会对分子造成干扰。

|
图 1 分子受力分析 Fig. 1 Molecular force analysis |
车辆在跟驰状态下和分子动力学存在许多相似之处,宏观表现为“近则远离,远则靠近”。分子在一维管道中的运动与车辆跟驰一致,由于分子间存在引力和斥力,所以分子之间不能无限地靠近和远离。当跟驰车距前车较远时,会进行加速操作以提高自身的通行效率;而跟驰车距前车较近时,会进行减速操作以避免前车突然刹车导致追尾。在跟驰状态下,车辆间距总是在一定的数值下波动。车辆在跟驰过程中也同时存在“分子平衡距离”,此时跟驰车与前车的间距为需求安全间距,驾驶员不进行较大幅度的加减速操作,车辆保持匀速行驶。
2 模型建立 2.1 车辆相互作用势势函数是描述分子间相互作用的数学表达式。Allen和Tildesley提出了2种常用的对势函数模型:间断对势和连续对势,其中Lennard-jones是应用最广泛的连续对势。其一般形式为
| $ \varphi(L)=A\left(\frac{d}{L}\right)^{m}-B\left(\frac{d}{L}\right)^{n}, $ | (1) |
在实际应用中常取
| $ \varphi(L)=4 \varepsilon\left[\left(\frac{\sigma}{L}\right)^{12}-\left(\frac{\sigma}{L}\right)^{6}\right], $ | (2) |
式中:ε为能量;σ为分子平衡距离;L为分子间的实际距离;
基于上述,建立车辆跟驰相互作用势函数:
| $ \varphi(L)=4 \varepsilon\left[\left(\frac{X}{L}\right)^{12}-\left(\frac{X}{L}\right)^{6}\right], $ | (3) |
式中,X为车辆需求安全间距。
将势函数对距离L求导可得跟驰车辆受力及加速度情况为
| $ F=-24 \varepsilon\left[2 \frac{X^{6}}{L^{7}}-\frac{1}{L}\right]\left(\frac{X}{L}\right)^{6}, $ | (4) |
| $ a_{i}=\frac{-24 \varepsilon}{m}\left[2 \frac{X^{6}}{L^{7}}-\frac{1}{L}\right]\left(\frac{X}{L}\right)^{6}, $ | (5) |
简化模型,令
| $ a_{i}=\lambda_{1}\left[2 \frac{X^{6}}{L^{7}}-\frac{1}{L}\right]\left(\frac{X}{L}\right)^{6}。$ | (6) |
与分子动力学一致,环境也会对跟驰车辆的行为产生干扰,从而产生环境加速度aj。
因此,跟驰车辆产生的加速度为
| $ a=a_{i}+a_{j} \text { 。} $ | (7) |
已有研究[16]认为需求安全距离是一个即时状态量,由车辆自身速度决定,具体形式为:
| $ X=\beta V_{n}+\alpha V_{n}{}^{2}, $ | (8) |
式中:β为跟驰车辆驾驶员的反应时间;α为跟驰车辆最大减速度2倍的倒数;Vn为跟驰车辆的即时速度。
同时,参考文献[16]将环境对车辆加速度定义为
| $ a_{j}=\lambda_{2}\left(1-\frac{V_{n}}{V_{e}}\right), $ | (9) |
式中:Ve为车道限速;λ2为待定参数。
由上,得到分子跟驰模型,简称MD模型,为
| $ a=a_{i}+a_{j}=\lambda_{1}\left[2 \frac{X^{6}}{L^{7}}-\frac{1}{L}\right]\left(\frac{X}{L}\right)^{6}+\lambda_{2}\left(1-\frac{V_{n}}{V_{e}}\right) \text { 。} $ | (10) |
由经验可知,车辆需求安全间距不仅与当前车辆速度有关,也与前后两车之间的速度差有关。另外,为避免前后车辆的碰撞,车辆停止时应存在适当间距。因此文中需求安全间距表示为
| $ X_{n}=S_{0}+\beta V_{n}+\frac{V_{n+1}{}^{2}-V_{n}{}^{2}}{2 a_{\max }}, $ | (11) |
式中:S0为两车静止时的间距;Vn+1为前车速度;Vn为跟驰车辆速度;amax为车辆的最大减速度。
则车辆相互作用势产生的加速度为
| $ a_{v}=\lambda_{1}\left[2 \frac{X_{n}{ }^{6}}{L^{7}}-\frac{1}{L}\right]\left(\frac{X_{n}}{L}\right)^{6}。$ | (12) |
Wei等[17]在文章中提到:前车的状态是跟驰车辆的重要的环境刺激因素,因此,文中考虑前后车辆的相对速度,将环境对跟驰车作用而产生的加速度定义为
| $ a_{w}=\lambda_{2}\left(1-\frac{V_{n}}{V_{n+1}}\right), $ | (13) |
建立改进的分子跟驰模型,简称M-MD模型,为:
| $ a=a_{v}+a_{w}=\lambda_{1}\left[2 \frac{X_{n}{ }^{6}}{L^{7}}-\frac{1}{L}\right]\left(\frac{X_{n}}{L}\right)^{6}+\lambda_{2}\left(1-\frac{V_{n}}{V_{n+1}}\right) \text { 。} $ | (14) |
利用高精度车载仪器对车辆跟驰数据进行采集,采集频率为5次/s,采集数据包括车辆速度、车辆车头间距、车辆即时加速度、时间等数据,并利用行车记录仪对试验过程进行记录。为了更精确地获取车辆在不同跟驰状态下的驾驶数据,根据参考文献[18]中的论述,选取交叉口密集地段。交叉口及信号灯的存在有利于采集启动、加速、减速以及停车数据,因此,研究的实验场景为哈尔滨市南岗区嵩山路,采集路段长2.8 km,中途经过6个信号交叉口(试验路段如图 2所示)。由于不同的跟驰状态下的跟驰特性存在差异,因此文中将行车记录仪视频与采集的数据进行匹配,将跟驰数据分为正常跟驰、加速跟驰与减速跟驰3种数据类型。
|
图 2 试验路段 Fig. 2 Test road |
驾驶员在感知到外部信息变化时,需要一定的反应时间才能采取相应操作,由于驾驶员的驾驶行为存在异质性,为确保模型的准确性,需要对跟驰车辆驾驶员的反应时间进行标定。Zhang等[19]通过对车辆轨迹进行研究,提出以±0.15 m·s-2作为前后车加、减速度变化的阈值,根据车辆跟驰行为中加速度阈值变化的时刻确定驾驶员的反应时间。通过对数据的筛选和整理,得到跟驰车驾驶员反应时间分布情况,如图 3所示。通过计算,反应时间的均值为0.396 s,标准差为0.109,文中取0.4 s作为跟驰车辆驾驶员的反应时间。
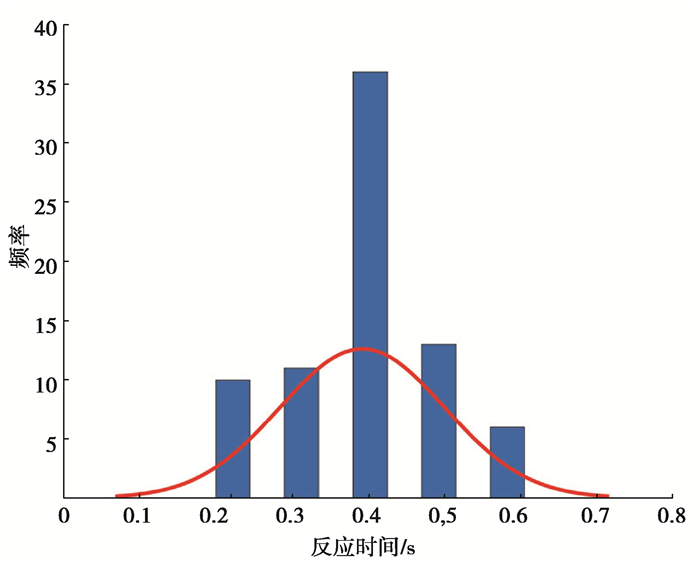
|
图 3 反应时间直方图 Fig. 3 Reaction time histogram |
由于不同跟驰状态下的跟驰特性存在较大差别,因此需要对其数据进行分别标定,从而分析在不同跟驰状态下模型参数的差异以及模型的准确性。选取不同跟驰状态下的跟驰数据各12组,按照参考文献[20]表述的求解非线性方程的遗传算法进行设置,此算法融合了优化和迭代两种机制,能充分发挥遗传算法的全局收敛性和群体搜索能力及经典算法的强局部收敛速度和精度高的特点。具体参数设置如下:方法为轮盘选择法,交叉率为0.85,采用均匀交叉法,变异率为0.01,收敛容许误差为1.0×10-10。参数标定结果如表 1所示。
| 表 1 模型参数标定结果 Table 1 Calibration results of model parameters |
由表 1可知,不同跟驰状态下标定的参数存在较大差异,在正常跟驰状态下,跟驰行为参数变化幅度不大,同时车辆间距较小,驾驶员注意力集中,对前车速度的变化有较大的反应。将速度分为40、50和60 km/h 3组,以车辆进行加减速操作的车辆间距为阈值,在此基础上计算跟驰车辆的加速度变化,结果如图 4所示。
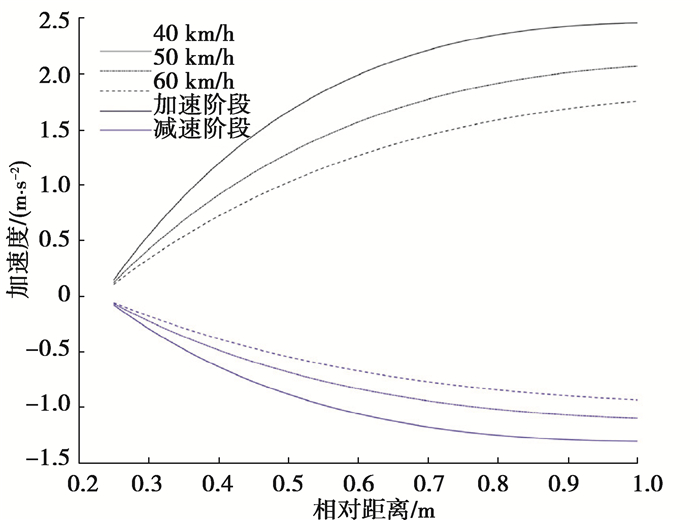
|
图 4 加速度预测值 Fig. 4 Acceleration prediction |
由图 4可知,在同样的速度与相对车辆间距情况下,车辆加、减速度的取值并不是对称的,加速度总是大于减速度,说明该驾驶员倾向于紧跟前车以提高自己的通行效率,这与Wei等[17]的研究结果是一致的,即跟驰车在加速和减速操作时存在不对称性;在同一跟驰状态与跟驰速度下,车辆的相对距离越大,加速度则越大,表明驾驶员在追求通行效率的同时注意保持安全间距。
5 模型评价 5.1 评价指标利用平均绝对误差(MAE,mean absolute error)与均方根误差(RMSE,root mean square error)作为模型的评价指标,其数学表达式为
| $ M_{\mathrm{MAE}}=\frac{1}{N} \sum\limits_{i=1}^{N}\left|y_{i}-\hat{y}_{i}\right| , $ | (15) |
| $ R_{\mathrm{RMSE}}=\sqrt{\frac{1}{N} \sum\limits_{i=1}^{N}\left(y_{i}-\hat{y}_{i}\right)^{2}}, $ | (16) |
式中:yi表示实际得到的真实数据;
将未参与模型标定的跟驰数据代入对应的不同跟驰状态下的跟驰模型中,得到模型预测加速度,经计算得到模型评价结果如表 2所示。
| 表 2 不同模型评价结果 Table 2 Evaluation results of different models |
选取一组未参与模型标定的跟驰数据代入M-MD模型和MD模型中,得到不同模型预测结果对比如图 5所示。
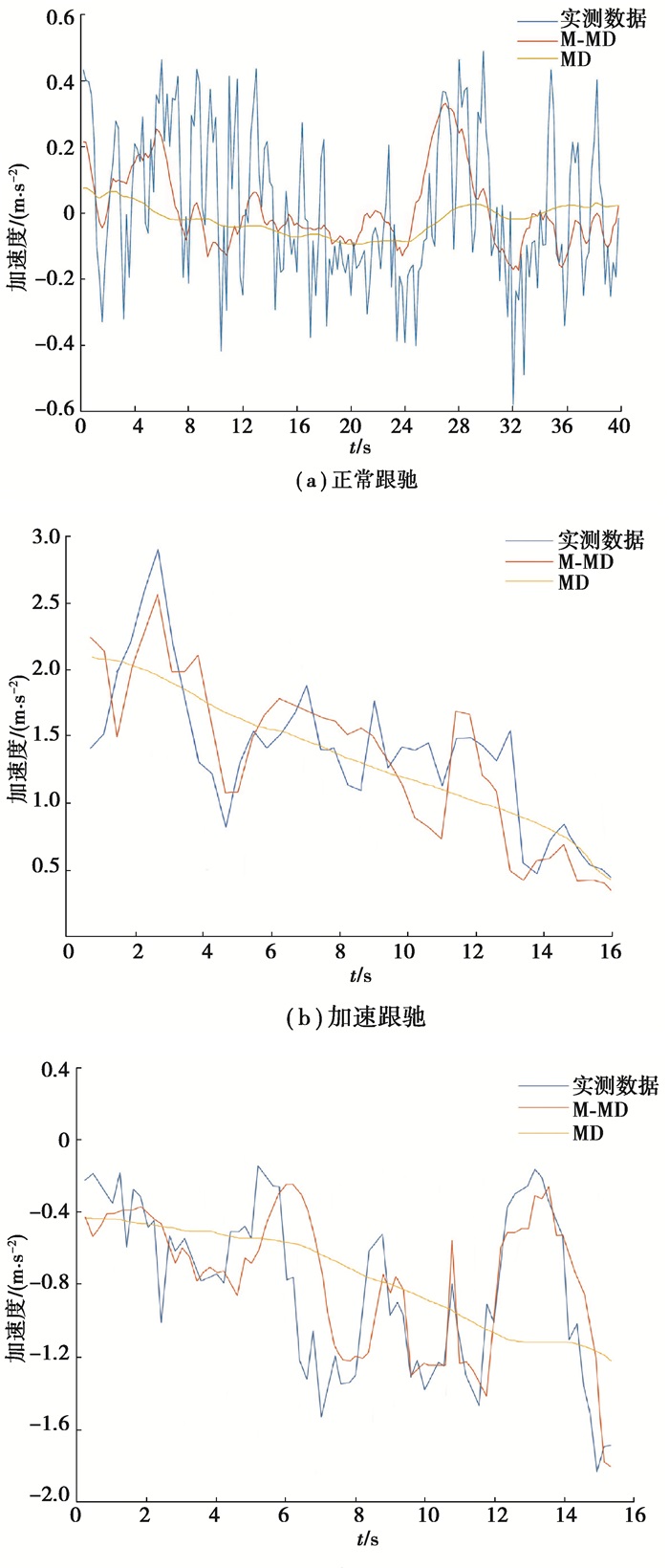
|
图 5 不同模型预测结果对比 Fig. 5 Comparison of prediction results of different models |
由图 5和表 2可以看出,改进的M-MD模型在不同跟驰状态下的预测误差都比MD模型小,MD模型在不同跟驰状态下可以大致预测出加速度的变化趋势,但不能有效地预测跟驰状态下的加速度短时变化,M-MD模型可以根据前导车及跟驰车辆的速度,间距等参数的变化,对跟驰状态下的加速度变化进行更有效的预测。
6 结束语利用车辆安全间距与相对速度对已有的分子跟驰模型进行改进,并对驾驶员反应时间以及模型参数进行标定,最后对不同状态下的跟驰模型进行评价。结果表明:
1) 改进模型可以清楚地反映出跟驰行为中驾驶员加减速操作的不对称性;
2) 改进模型具有更高的精度,可以更有效地模拟真实状况下的车辆跟驰行为;
3) 在同样的相对间距下,不同跟驰速度对应的加减速呈现一定的规律,但原理未知,这将是下一步的研究工作。
| [1] |
王永泉, 陈花玲, 毛文雄. 基于跟驰理论的道路交通噪声预测模型研究[J]. 系统仿真学报, 2004, 16(11): 2413-2416. Wang Y Q, Chen H L, Mao W X. Research on road traffic noise prediction model based on car-following theory[J]. Journal of System Simulation, 2004, 16(11): 2413-2416. (in Chinese) DOI:10.3969/j.issn.1004-731X.2004.11.012 |
| [2] |
Chandler R E, Herman R, Montroll E W. Traffic dynamics: Studies in car following[J]. Operations research, 1958, 6(2): 165-184. DOI:10.1287/opre.6.2.165 |
| [3] |
Kometani E, Sasaki T. On the stability of traffic flow (report-I)[J]. Journal of Operations Research Society of Japan, 1958, 2(1): 11-26. |
| [4] |
Kikuchi S, Chakroborty P. Car-following model based on fuzzy inference system[J]. Transportation Research Record, 1992, 82-82. |
| [5] |
Michaels R M. Perceptual factors in car following[C]//Proceedings of the 2nd International Symposium on Theory of Traffic Flow. 1963: 44-59.
|
| [6] |
Cremer M, Ludwig J. A fast simulation model for traffic flow on the basis of Boolean operations[J]. Mathematics and Computers in Simulation, 1986, 28(4): 297-303. DOI:10.1016/0378-4754(86)90051-0 |
| [7] |
Bando M, Hasebe K, Nakayama A, et al. Dynamical model of traffic congestion and numerical simulation[J]. Physical Review E, 1995, 51(2): 1035. DOI:10.1103/PhysRevE.51.1035 |
| [8] |
Toledo T, Koutsopoulos H N, Ahmed K I. Estimation of vehicle trajectories with locally weighted regression[J]. Transportation Research Record: Journal of the Transportation Research Board, 2007, 1999(1): 161-169. DOI:10.3141/1999-17 |
| [9] |
He Z, Zheng L, Guan W. A simple nonparametric car-following model driven by field data[J]. Transportation Research Part B: Methodological, 2015, 80: 185-201. DOI:10.1016/j.trb.2015.07.010 |
| [10] |
Zhou M F, Qu X B, Li X P. A recurrent neural network based microscopic car following model to predict traffic oscillation[J]. Transportation Research Part C: Emerging Technologies, 2017, 84: 245-264. DOI:10.1016/j.trc.2017.08.027 |
| [11] |
曲大义, 杨建, 陈秀锋, 等. 车辆跟驰的分子动力学特性及其模型[J]. 吉林大学学报(工学版), 2012, 42(5): 1198-1202. Qu D Y, Yang J, Chen X F, et al. Molecular kinetics behavior of car-following and its model[J]. Journal of Jilin University(Engineering and Technology Edition), 2012, 42(5): 1198-1202. (in Chinese) |
| [12] |
郝杰, 曲大义, 张金磊, 等. 基于分子动力学的交通流特性分析方法[J]. 青岛理工大学学报, 2013, 34(6): 87-91, 124. Hao J, Qu D Y, Zhang J L, et al. Analysis method of traffic flow characteristics based on molecular dynamics[J]. Journal of Qingdao Technological University, 2013, 34(6): 87-91, 124. (in Chinese) |
| [13] |
陈文娇, 曲大义, 杨万三, 等. 基于分子动力学的车辆需求安全距离及模型[J]. 青岛理工大学学报, 2014, 35(1): 94-99, 110. Chen W J, Qu D Y, Yang W S, et al. Molecular kinetics behavior of car-following required safe distance and its model[J]. Journal of Qingdao Technological University, 2014, 35(1): 94-99, 110. (in Chinese) DOI:10.3969/j.issn.1673-4602.2014.01.017 |
| [14] |
郭涛, 曲大义, 郝杰, 等. 交通流稳定性的分子动力学分析[J]. 公路交通科技, 2014, 31(5): 129-134. Guo T, Qu D Y, Hao J, et al. Analysis on traffic flow stability by molecular kinetics[J]. Journal of Highway and Transportation Research and Development, 2014, 31(5): 129-134. (in Chinese) DOI:10.3969/j.issn.1002-0268.2014.05.020 |
| [15] |
曲大义, 李娟, 刘聪, 等. 基于分子动力学的车流运行动态特性及其模型[J]. 交通运输系统工程与信息, 2017, 17(4): 188-194. Qu D Y, Li J, Liu C, et al. Dynamic characteristics model of traffic flow based on molecular dynamics[J]. Journal of Transportation Systems Engineering and Information Technology, 2017, 17(4): 188-194. (in Chinese) |
| [16] |
李娟, 曲大义, 刘聪, 等. 基于分子动力学的跟驰特性及其模型[J]. 公路交通科技, 2018, 35(3): 126-131. Li J, Qu D Y, Liu C, et al. Car-following characteristics and its models based on molecular dynamics[J]. Journal of Highway and Transportation Research and Development, 2018, 35(3): 126-131. (in Chinese) |
| [17] |
Wei D L, Liu H C. Analysis of asymmetric driving behavior using a self-learning approach[J]. Transportation Research Part B: Methodological, 2013, 47: 1-14. DOI:10.1016/j.trb.2012.09.003 |
| [18] |
王殿海, 陶鹏飞, 金盛, 等. 跟驰模型参数标定及验证方法[J]. 吉林大学学报(工学版), 2011, 41(S1): 59-65. Wang D H, Tao P F, Jin S, et al. Method of calibrating and validating car-following model[J]. Journal of Jilin University(Engineering and Technology Edition), 2011, 41(S1): 59-65. (in Chinese) |
| [19] |
Zhang X, Bham G H. Estimation of driver reaction time from detailed vehicle trajectory data[J]. Moas, 2007, 7: 574-579. |
| [20] |
罗亚中, 袁端才, 唐国金. 求解非线性方程组的混合遗传算法[J]. 计算力学学报, 2005, 22(1): 109-114. Luo Y Z, Yuan D C, Tang G J. Hybrid genetic algorithm for solving systems of nonlinear equations[J]. Chinese Journal of Computational Mechanics, 2005, 22(1): 109-114. (in Chinese) |
 2021, Vol. 44
2021, Vol. 44


