车载移动自组织网络(简称车载网)是以中、高速运动的车辆为节点的分布式、自组织的移动通信网络,是智能交通系统[1]的基础技术之一。车辆通过信息交互和共享[2]实现碰撞避免、路径规划等目的。鉴于车载网通信协议和应用的实地测试成本较高,危险性较大,因此该类型研究和测试主要通过仿真实验完成。构建实现一个相对真实的车载网仿真环境[3],需要明确模拟车辆节点的移动模式[4],并及时获取模拟车辆的准确位置信息。其中车辆的移动模式直接关系到网络拓扑结构的变化,进而影响到整个车载网的包传递率、吞吐量和传输延迟等性能指标的测量。因此,在仿真实验中,选择性能优异的车辆移动模型是非常有必要的,可以最大程度地模拟路面交通的真实状况,也是通信协议仿真和测试[5]的基础。
根据交通特征的细化程度,可以将移动模型分为宏观移动模型[6]和微观移动模型[7]两类。宏观移动模型主要以车流为研究对象,忽略车辆的个体行为。因此,宏观移动模型无法确切地描述车辆之间的制约关系。微观移动模型主要以单个车辆为研究对象,详细描述车辆的加速、减速、变道和超车等驾驶行为,更加适用于车载网应用的研究。微观移动模型主要包括随机移动模型[8]和车辆跟驰模型[9]。随机移动模型指车辆随机选择速度、方向和目的地信息,但真实环境下车辆的移动并非完全随机,而且受外界环境(如道路方向、周围车辆)的影响,因而随机移动模型无法刻画车辆的真实运动状态。相反,车辆跟驰模型以车辆与前车的行为关系为基础进行建模,可以更加准确地反映真实交通状况下车辆的驾驶行为。
Simulation of Urban Mobility(SUMO)[10]平台是当前车载网交通仿真领域使用最为广泛的模拟平台之一。SUMO平台内嵌多种车辆跟驰模型,并能够对多种类型的道路交通网络进行仿真。此外,SUMO平台含有OpenStreetMap[11]的接口,能够获取世界各地真实的道路交通网数据。当前该平台[12]下主要有CarFollowing-Krauss[13]、SmartSK、CarFollowing-Wiedemann[14]、CarFollowing-PWagner、CarFollowing-BKerner[15]和CarFollowing-IDM[16]6种常用的车辆跟驰模型。然而,到目前为止,笔者并没有发现针对上述车辆跟驰模型所做的对比分析研究。
针对上述问题,文中给出SUMO平台下6种车辆跟驰模型多个性能的详细对比分析。首先,详细描述了SUMO平台下6种车辆跟驰模型;其次,分析并引入影响移动模型性能最明显的3种因素;最终,在多种影响因素的作用下,对比分析了SUMO平台下6种跟驰模型在车辆密度、车辆平均速度、道路占用率等方面的性能。
1 移动模型 1.1 CarFollowing-Krauss模型Krauss模型基于安全距离来进行建模。在该模型中,后车根据上一个时间段前车与后车的距离和速度,来选择当前时间段它应保持的车速。因此,下一时间段的车速应满足:
| $ d_{s} \leqslant d_{p}+g \text { , } $ | (1) |
式中:ds为当前时间段车辆行驶的距离;dp为前车紧急制动的距离;g为车间距。仅当公式等号成立时,所选择的速度被称为安全速度。
因为Krauss是无碰撞模型[17],所以车辆行驶速度不会超过安全车速,并且在每一个仿真步长,都会重新计算安全车速,根据式(1)可以得出安全速度的计算公式为
| $ v_{\text {safe }}=v_{p}+\frac{g-v \tau_{k}}{\left(v_{p}+v\right) / 2 a+\tau_{k}}, $ | (2) |
式中:vp为前车速度;g为车间距;v为当前车速;a为车辆最大减速度;τk为驾驶员反应时间。
由于安全速度并不是下一个仿真步长(通常为1 s)要选择的车速,因此需要一个确定车速的更新策略,Krauss模型更新策略如下:
| $ \begin{gathered} v_{1}=\min \left[v_{t}+b, v_{\max }, v_{\text {safe }}\right], \\ v_{0}=v_{1}-\varepsilon\left\{v_{1}-\left[v_{t}-b\right]\right\}, \\ v_{t+1}=v_{\mathrm{ran}, v_{0}, v_{1}}, \\ x_{t+1}=x_{t}+v_{t+1}, \end{gathered} $ | (3) |
式中:vt是t时刻的车速;b是车辆最大加速度;vmax是道路限制最大车速;vsafe是安全车速;v1是车辆期望速度;v0是由于驾驶员的不完美驾驶,与期望速度所产生最大差值时的速度;vt+1是下一个仿真步长所选择的车速,它在v0-v1中随机选择;xt+1为下一个仿真步长车辆的位置。
由于SamrtSK模型下车辆的运动规则与Krauss模型类似,文中不再详细描述。
1.2 CarFollowing-IDM模型IDM中车辆α加速度
| $ \dot{v}_{\alpha}=a^{(\alpha)}\left[1-\left(\frac{v_{\alpha}}{v_{0}{}^{\alpha}}\right)^{\delta}-\left(\frac{s^{\prime}\left(v_{\alpha}, \Delta v_{\alpha}\right)}{s_{\alpha}}\right)^{2}\right] \text { 。} $ | (4) |
公式(4)是对以下2种计算加速度方法的改进:当路上车辆较少时,车辆用af(vα)=aα[1-(vα/v0α)δ]计算加速度;当车辆α靠近前方车辆时,用-bint(sα, vα, Δvα)=-aα(s′/sα)2计算减速度。其中,期望最小车间距s′可表示为
| $ s^{\prime}(v, \Delta v)=s_{0}{ }^{\alpha}+s_{1}{ }^{\alpha} \sqrt{\frac{v}{v_{0}{ }^{\alpha}}}+\mathrm{T}^{\alpha} v+\frac{v \Delta v}{2 \sqrt{a^{\alpha} b^{\alpha}}} \text { 。} $ | (5) |
拥堵距离s1=0时,IDM加速度包含以下几种模式:
1) 平衡交通:在任意密度的平衡交通(
| $ s_{e}(v)=s^{\prime}(v, 0)\left[1-\left(\frac{v}{v_{0}}\right)^{\delta}\right]-\frac{1}{2}=\left(s_{0}+v T\right)\left[1-\left(\frac{v}{v_{0}}\right)^{\delta}\right]-\frac{1}{2}, $ | (6) |
对于平衡交通中车辆速度计算
| $ \left.V_{e}(s)\right|_{\delta=1, s_0=0}=\frac{s^{2}}{2 v_{0} T^{2}}\left(-1+\sqrt{1+\frac{4 T^{2} v_{0}{}^{2}}{s^{2}}}\right) , $ | (7) |
以及
| $ \left.V_{e}(s)\right|_{\delta \rightarrow \infty}=\min \left\{v_{0},\left(s-s_{0}\right) / T\right\}。$ | (8) |
2) 加速到期望速度:当车辆已达到期望速度,并且车流量密度很低,车辆间的相互影响可忽略,IDM的加速度会减小到af(v)=a(1-v/v0)δ。
3) 对较小车间距的制动:当车间距小于s′没有较大的速度差距,s′的稳定部分s0+vT将影响与Δv成正比的动态因子,此时,加速度减小到
IDM模型参数如表 1所示。
| 表 1 IDM模型参数 Table 1 IDM model parameters |
首先通过一系列阈值来区分不同的车辆驾驶行为,然后使用当前车辆与前车的距离和相对速度来判断车辆属于哪种驾驶状态,最后根据该状态下加速度公式求出加速度。该模型充分考虑了驾驶员的生理、心理因素[18]对驾驶行为的影响和制约,及由此而产生的不同驾驶行为,从建模方法上更接近实际情况,最大限度上仿真实际车辆的驾驶行为。
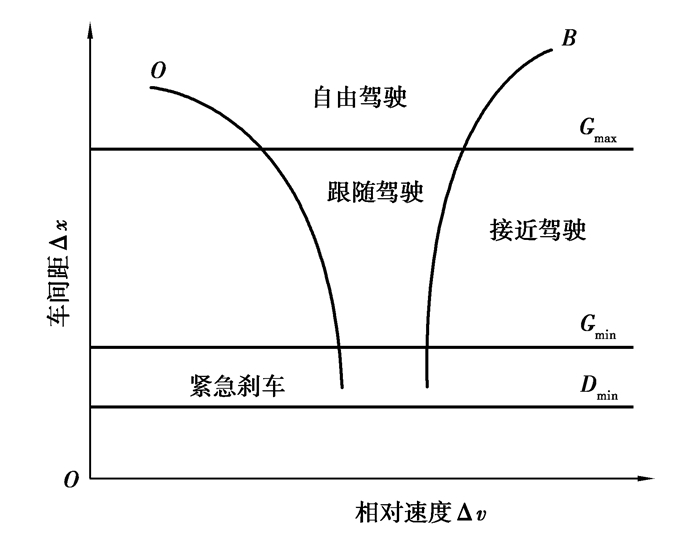
如图 1所示,Wiedemann模型有4种驾驶状态,分别为自由驾驶、接近驾驶,跟随驾驶和紧急刹车,并由阈值Dmin,Gmin,Gmax,O,B来进行划分。以下为这些阈值的含义及计算方法:
| $ D_{\min }=L_{n-1}+D_{\text {add }} \text { , } $ | (9) |
|
图 1 Wiedemann模型的阈值划分 Fig. 1 Threshold division of Wiedemann model |
式中:Dmin表示前车和后车之间的最小距离,若车间距小于Dmin则表示发生碰撞;Ln-1为前车长度;Dadd为校准参数。
| $ \begin{gathered} G_{\min }=D_{\min }+b, \\ b=b_{\text {mult }} * \sqrt{v}, \end{gathered} $ | (10) |
式中:Gmin为车辆跟随过程中的最小车间距;bmult为校准参数;v是前车速度和后车速度中的最小值。
| $ G_{\max }=G_{\text {mult }} * G_{\min } \text { , } $ | (11) |
式中:Gmax为车辆跟随过程中的最大车间距;Gmult为校准参数。
| $ B=\left(\frac{\varDelta x-L_{n-1}-D_{\min }}{C}\right)^{2} $ | (12) |
式中:B是接近边界,用来划分接近驾驶与其他驾驶状态,其中,C为校准参数。
| $ O=B * O_{\text {add }}, $ | (13) |
式中:O是用来划分前车速度比较大时的无反应驾驶和跟随驾驶,其中Oadd为校准参数。
Wiedemann模型下,如果车辆处于自由行驶状态,该车会逐渐加速到期望速度,并以期望速度行驶,直到进入其他行驶状态,其加速度为
| $ b_{\max }=B_{\text {maxmult }} *\left(v_{\max }-v * F_{\text {aktor }}\right) \text { , } $ | (14) |
式中:Bmaxmult和Faktor为校准参数;vmax是车辆最大速度。当车辆从自由驾驶状态下进入接近状态时,加速度为
| $ b_{n}=\frac{1}{2} * \frac{(\varDelta v)^{2}}{G_{\min }-\left(\varDelta x-L_{n-1}\right)}+b_{n-1} \text { , } $ | (15) |
式中,bn-1为前车的加速度。
因为车辆可以从不同的状态进入跟随驾驶状态,所以跟随驾驶状态下的加速度可分为:通过阈值O或Gmax进入跟随驾驶状态,此情况下的加速度为正值;通过阈值B或Gmin进入跟随驾驶状态,此情况下的加速度为负值。
跟随状态下加速度绝对值的计算公式为
| $ a_{\text {null }}=a_{\text {null, mult }} * \mathrm{RND} 3_{\alpha} \text { , } $ | (16) |
式中:anull, mult为校准参数;RND3α是服从正态分布的驾驶因变量。
当车间距小于Gmin时,车辆进入紧急刹车状态,加速度为
| $ b_{\min }=b_{\text {minadd }}+b_{\text {minmult }} * v_{n} \text { , } $ | (17) |
式中:bminadd和bminmult是校准参数;vn是当前车辆的速度。
1.4 CarFollowing-Bkerner模型Bkerner模型基于随机三相交通流建模。车辆更新规则如下:
| $ \left.\begin{array}{l} v_{n+1}=\max \left(0, \min \left(v_{\text {free }}, \tilde{v}_{n+1}+\xi_{n}, v_{n}+a \tau, v_{s, n}\right)\right) \\ x_{n+1}=x_{n}+v_{n+1} \tau \end{array}\right\}, $ | (18) |
式中:
| $ \left.\begin{array}{l} \widetilde{v}_{n+1}=\max \left(0, \min \left(v_{\text {free }}, v_{s, n}, v_{c, n}\right)\right) \\ v_{c, n}= \begin{cases}v_{n}+\varDelta_{n} & \text { for } \quad g_{n} \leqslant G_{n} \\ v_{n}+a_{n \tau} & \text { for } \quad g_{n}>G_{n}\end{cases} \\ \Delta_{n}=\max \left(-b_{n} \tau, \min \left(a_{n} \tau, v_{l, n}-v_{n}\right)\right) \end{array}\right\}, $ | (19) |
式(18)中的参数因子ξn表示:在随机加速或随机减速过程中,车辆是否继续加速或减速;或是维持当前车速
| $ \xi_{n}=\left\{\begin{array}{ccc} -\xi_{b} & \text { if } & S_{n+1}=-1 \\ \xi_{a} & \text { if } & S_{n+1}=1 \\ 0 & \text { if } & S_{n+1}=0 \end{array}\right\}, $ | (20) |
式中:ξa和ξb表示车辆随机减速或是随机加速。
离散时间t=nτ,n=0, 1, 2, 3..;τ是时间步长;vfree是车辆最大速度;
| $ \left.\begin{array}{l} G_{n}=G\left(v_{n}, v_{l, n}\right) \\ G(u, w)=\max \left(0, k \tau u+\psi a^{-1} u(u-w)\right) \end{array}\right\}, $ | (21) |
式中,k>1, ψ是常数。
在式(18)中,vs, n=min(vn(safe), gn/τ+vl(a))是一个安全速度,其中vn(safe)是Gipps方程的解。
| $ v_{n}{}^{(\text {safe})} \tau+X_{d}\left(v_{n}{}^{(\text {safe})}\right)=g_{n}+X_{d}\left(v_{l, n}\right)。$ | (22) |
式中:Xd(u)=bτ2(αβ+α(α-1)/2);b是常数,α是u/bτ的整数部分,β是其小数部分;vl(a)表示期望速度。
车辆在计算加速度或减速度方面,考虑了驾驶员的反应延迟,式(19)中的an和bn采用以下随机函数:
| $ \left.\begin{array}{l} a_{n}=a \theta\left(P_{0}-r_{1}\right) \\ b_{n}=a \theta\left(P_{1}-r_{1}\right) \\ P_{0}=\left\{\begin{array}{ccc} p_{0} & \text { if } & S_{n} \neq 1 \\ 1 & \text { if } & S_{n}=1 \end{array}\right. \\ P_{1}=\left\{\begin{array}{ccc} p_{1} & \text { if } & S_{n} \neq-1 \\ p_{2} & \text { if } & S_{n}=-1 \end{array}\right. \end{array}\right\} \text { , } $ | (23) |
式中:a表示最大加速度;r1是(0,1)之间均匀分布的随机值;当z < 0时,θ(z)=0,当z>=0时,θ(z)=1;概率p0(v),p2(v)给出速度函数,概率p1是模型参数,车辆加速和减速的随机反应延迟分别用1-P0和1-P1表示。Sn描述车辆移动的状态(Sn=-1表示减速,Sn=1表示加速,Sn=0表示恒定速度)。
| $ S_{n}=\left\{\begin{array}{ccc} -1 & \text { if } & \tilde{v}<v_{n-1}-\delta, \\ -1 & \text { if } & \tilde{v}<v_{n-1}+\delta, \\ 0 & & \text { otherwise }, \end{array}\right. $ | (24) |
式中,δ是常数。
1.5 CarFollowing-PWagner模型PWagner模型即人类行为的行动点模型。驾驶员可以在任意的时间步长随机决定是否改变当前的加速度。如果改变,则加速度的值设置为
| $ a(t)=a_{\mathrm{safe}}-\sigma_{a} \xi, $ | (25) |
式中:asafe是车辆安全加速度;σa是加速度影响因子;ξ是[0, 1]之间的随机数。σa的取值范围0.2~0.5 m/s2。如果当前加速度大于asafe,则车辆的加速度会被强制设置为式(25)中所提供的新值。加速度的选择可根据以下不等式确定,如果不等式成立,则加速度是安全的:
| $ d(v+a \tau)+v \tau+1 / 2 a \tau^{2} \leqslant d(V)+\Delta v-l, $ | (26) |
式中:τ表示车辆最小车间距;l表示车辆长度;函数d(v)表示车辆的制动距离;V表示前车的速度。用d(v)=v2/(2b)可求解此方程,得到安全加速度为
| $ a_{\text {safe }}=-\frac{v}{\tau}-\frac{b}{2}+\sqrt{\left(\frac{v}{\tau}-\frac{b}{2}\right)^{2}+\frac{2 b g+V^{2}-v^{2}}{\tau^{2}}} \text { 。} $ | (27) |
SUMO是一个多模态的移动模型仿真器,所涉及的模型不仅包含各种不同的车辆,还包括行人、各种基础设施等,同时可以仿真不同的道路交通网络,如城市道路网络和高速公路网络。目前学术界和工业界主要关注如何解决城市道路交通拥堵问题和安全问题[19],因此常用车辆跟驰模型的仿真环境基本以城市道路网络为仿真实验场景。道路网络结构、交通控制策略和单位车辆行为都会影响车载网移动模型的构建。
2.1 道路网络结构车辆的移动会受到道路网络的限制,包括车的速度、方向。道路网络的交叉口,每条道路上车道的数量、单车道或是多车道等都会影响车辆的行为。当车辆到达路口,或出于转向的考虑,车辆会适当减速。为保障行驶车辆的安全,每条道路也都有相应的最高速度限制,车辆时速必须低于道路的最高限速。
2.2 交通控制策略目前在交通控制方面主要是基于交通灯机制[20]调控交通流。交管部门通过在一定时间段内对某一路口的过往车辆进行统计分析,从而制定相应的交通信号灯转换策略。首先,路口处的交通灯会影响车辆的速度,红灯路口处的车辆密度高;其次,由于交通信号灯策略是固定的,不能实时应对不同方向的不同车辆数,有可能导致车辆很多的路口依然是红灯。不同的移动模型针对车辆在路口处的驾驶行为提出不同的调控策略。
2.3 单个车辆行为每辆车不仅受到道路最高时速的限制,同时也会受到周围车辆行为的影响。一辆车可能会被迫进入加速、减速、变道的状态,道路上车辆较少时,车辆应有较高的平均速度,从而提高到达目的地的效率。
3 实验部分目前,车载网应用背景下对路经规划、交通状况预测以及通信协议的验证大部分是以城市道路网络为实验场景。移动模型在城市道路仿真环境下的性能优劣对路径规划和通信协议的评估和验证[21]至关重要。而且IDM作为车辆跟驰模型,基于速度、车间距以及后车与前车的速度差进行建模,考虑了人为因素(反应时间、估计误差)对模型的影响,对车辆的控制和实际车辆行驶状态更接近,目前在交通仿真领域具有很大优势。并且Li等[22-23]将其作为研究交通动态变化的基础模型。但实际车辆运行状态受到所处环境的影响,如,城市快速道路上车速快,超车频繁;城市中心道路车速慢,超车受限等。Li等没有明确指出具体环境对车辆跟驰模型的影响。文中以IDM为基础,设置不同场景对五种车辆跟驰模型与IDM性能进行对比分析。
实验分为以下3个仿真场景:首先,采用长约5 km的单行道网络拓扑,其目的是在不存在交通灯、变道、控制策略等外界因素的影响下观察不同车辆跟驰模型的性能表现;其次,采用长约8 km的双向双车道且路口处设有交通灯的环形网络拓扑,其目的是模拟真实城市道路网络场景,对比不同车辆跟驰模型的性能差异;最后,由于车辆跟驰行为不受网络拓扑影响,为便于模拟和观察,微观车辆跟驰实验选用单行道网络拓扑环境对不同模型下单个车辆的跟驰行为进行分析。
3.1 单行道场景本实验主要从车辆平均速度、道路占用率和车辆密度3个方面对不同的车辆跟驰模型在单行道环境下所表现的性能进行分析对比。单行道仿真设置为:每隔1.25 s在起点处发一辆车,车辆总数为50,实验中每隔10 s对平均速度、占用率以及车辆密度测试1次。
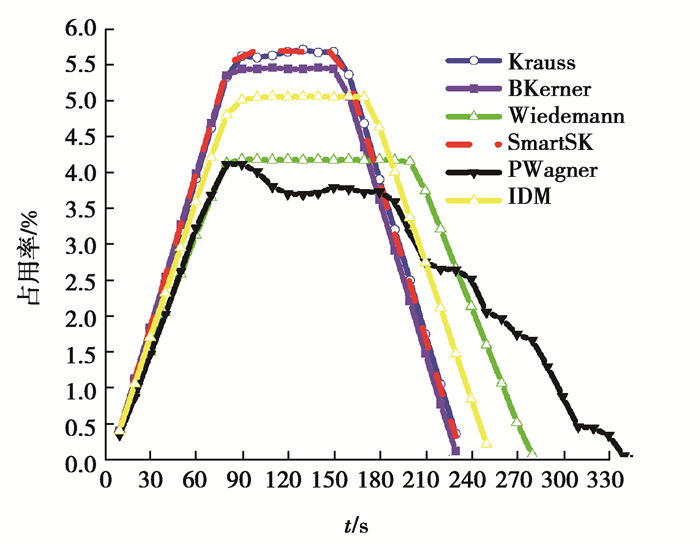
由图 2可以看出,每个移动模型中车辆在经过一段缓冲加速过程后速度趋于稳定。其原因是不同移动模型下道路上的车辆数都达到相对稳定的数值。当有较少的车辆进入道路时,平均速度都有一定程度的升高。根据图 3和图 4描述, Wiedemann和IDM在车辆行驶过程中两车之间要保持相对较大的车间距,因此,Wiedemann和IDM模型在完成整个车辆仿真过程用时大于其他模型。相较于IDM,Wiedemann和PWagner都有相对较低的道路占用率,PWagner的车辆密度和道路占用率最低并且没有稳定阶段,在低密度、低占用率期间(200 s左右)车速波动且速度较低,因此会导致较低的通行效率。SmartSK, Krauss和BKerner模型在车辆密度和道路占用率2个方面高于IDM,并且3个模型的车速比IDM快,相应提高了车辆的通行效率。在单行道网络拓扑中,移动模型有较高的车辆密度、道路占用率和平均速度,才能保证车辆有较高的通行效率。除此之外,实验还考虑车辆初速度,发车间隔对实验结果的影响。当发车间隔太长,会导致车间距过大,车辆跟驰模型不工作;发车间隔太短,则会导致发车延时。经过多次测试实验,选取合适的发车间隔,并且在不同的初速度下,设置多组实验。实验结果与给出的图 2~图 4相同,表明在单行道场景下,相对于IDM,Krauss、SmartSK和BKerner有更好的交通调控效率。

|
图 2 单行道车辆速度变化 Fig. 2 One-way vehicle speed change |

|
图 3 单行道车辆密度变化 Fig. 3 One-way vehicle density change |
|
图 4 车道占用率 Fig. 4 Lane occupancy |
实验设置道路网络拓扑为封闭的环路,左右两条道路长各为1 000 m,上下两条道路长各为3 000 m,路口处设有交通灯。为体现城市道路特点,在上下两条道路的中点各加入一个交通灯,以便更好地调节交通流量。车道设置为双向双车道,可以突显每个模型在控制车辆过程中出现的变道超车行为。实验场景中车辆总数为200,设置node7交通灯(道路网络拓扑左上角)为车辆的发车点,并且车辆绕环路行驶一周在此节点处离开实验场景。仿真过程中车辆分多个批次出发,每个批次内的发车间隔由具体模型决定,每批次之间间隔10~15 s。
宏观上,车辆移动模型主要体现在对车流的控制,包括车流的速度、方向和密度等。为研究每个移动模型在城市道路中对交通流的不同控制性能,实验中对车辆所经过的每条道路上的车辆数据进行统计分析,主要从车辆密度,道路占用率和车辆平均速度3个方面分析Krauss,IDM,Wiedemann,BKerner,PWagner和SmartSK 6个车辆跟驰模型在城市道路中所表现出的性能差异。
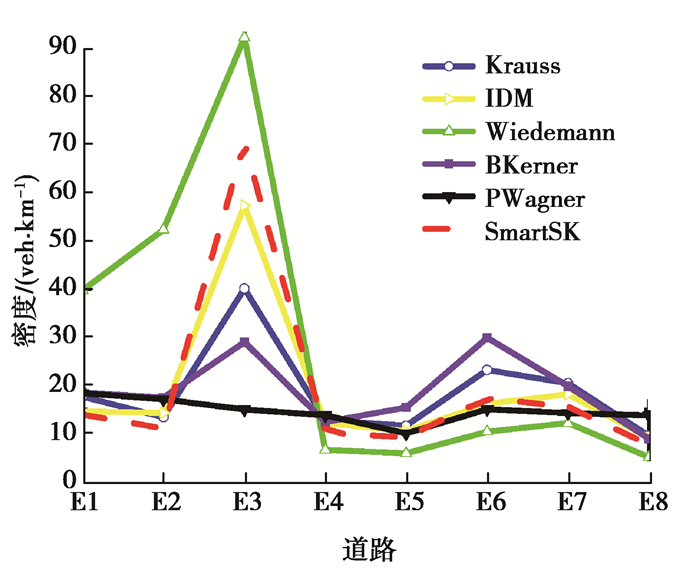
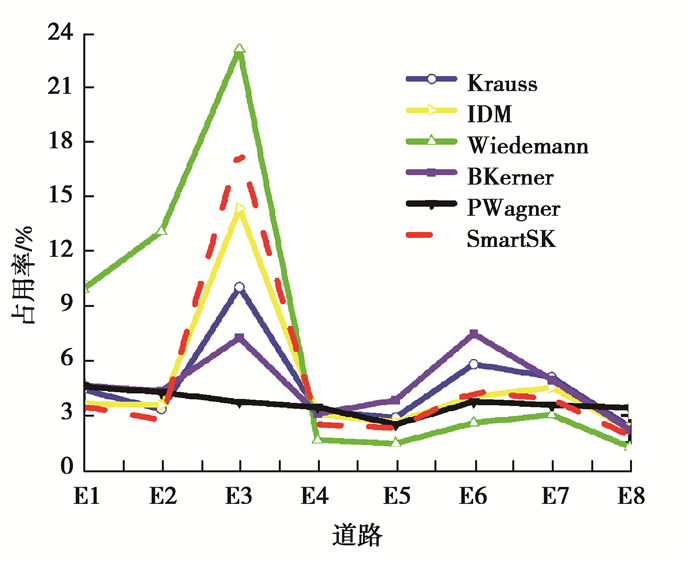
由图 5和图 6可以看出,每条道路上车辆密度和道路占用率在宏观上有大致相同的趋势。车辆出发后经过E1E2的缓冲加速,车速达到平稳状态并进入道路E3。Wiedemann和SmartSK模型在E3边上的车辆密度和道路占用率高于IDM,并且Wiedemann和SmartSK在仿真过程中出现图 7(a),(b)的车辆拥堵现象。由于Wiedemann和SmartSK两个移动模型在E3边上都出现了相应的重度、中度的交通拥堵状态,而且在微观角度分析,2个移动模型中的单个车辆具有相对较低的加速度,这使车辆在通过交通灯路口时花费的时间较长,继而导致后面道路的车辆密度和车道占用率比较高。因此,Wiedemann和SmartSK模型完成200辆车的仿真过程用时大于IDM。如图 7(c),IDM模型对于车辆在交通灯处起步时的控制有一个弊端,经过绿灯时,2车道车辆同时起步后并行向前行驶并在较长的时间内保持同样的行驶状态,与实际车辆驾驶行为不符。实际行驶中两个车道内的车辆应该都有自己的车辆驾驶行为意识[24],例如:超车,变换车道等。
|
图 5 每条道路上的车辆密度 Fig. 5 Vehicle density on each road |
|
图 6 每条道路上的占用率 Fig. 6 Occupancy on each road |

|
图 7 通过交通灯时的车辆状态 Fig. 7 Vehicle status through traffic lights |
E3边上Bkerner模型的密度和占用率与IDM差距过大,由图 8(b)可以看出,Bkerner模型在E3边上没有出现车辆拥堵现象,但低密度低占用率导致道路上车辆数较少。Krauss模型的密度和占用率虽低于IDM,但差距不大并且车辆在通过node2交通灯之后相较于IDM也有较高的车辆密度和道路占用率,这就使Krauss模型完成整个车辆仿真的总时间不会高于IDM模型,车辆能够在较短时间内到达目的地。Krauss模型没有过高的车辆密度和道路占用率,同时也保证了在城市道路环境下交通不会出现拥堵现象。由表 2可以看出,BKerner模型在仿真过程中车间距明显小于阈值(最小车间距),这就说明在仿真过程中出现车辆碰撞现象。微观角度分析,Bkerner模型对单个车辆没有高度有效的控制,当车辆与前车距离接近阈值时不能有效地实施减速。相较于IDM,PWagner模型在车辆密度,道路占用率方面都保持一个较为平缓的趋势,每个车道内的车辆分布比较均匀。但图 8(c)显示,交通灯对PWagner模型没有明显的约束,可以看到红灯亮时车辆并没有减速或是停止。如表 3所示,由于PWagner模型中时间点确定加速度是否改变,从而导致此模型出现较为严重的车辆碰撞现象。移动模型必须确保车辆移动的安全性,频繁出现车辆碰撞的模型不适合完成车辆仿真模拟。

|
图 8 通过交通灯时的车辆状态 Fig. 8 Vehicle status through traffic lights |
| 表 2 BKerner模型车辆碰撞数据 Table 2 BKerner model vehicle collision data |
| 表 3 PWagner模型车辆碰撞数据 Table 3 PWagner model vehicle collision data |
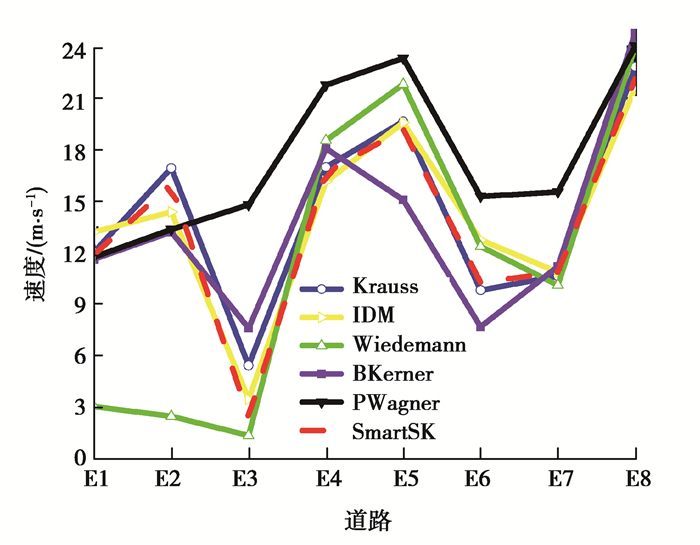
如图 9所示,车辆在缓冲加速阶段,Krauss和SmartSK模型的平均速度优于IDM模型,Wiedemann模型的平均速度和IDM差距较大,导致车辆不能快速进入稳定状态。在SmartSK进入稳定状态后,其速度接近Wiedemann模型,这符合密度图所反映的车流状况。Krauss模型微观上对单个车辆的加速,减速以及变道的控制较好,因此,在车辆达到平稳状态后的速度高于IDM模型。车辆通过E3街道末端的交通灯后进入E4街道,车辆数相对较少,每个移动模型下的车速都会有相应的提升,经过这条道路所花费的时间减少。由于在E5处车辆碰撞导致交通暂时性的拥堵,BKerner的平均速度明显下降,车辆经过E5的时间提高。由于PWagner模型的加速度不依赖于前车数据,并且每批次内的发车间隔较大,因此在仿真过程中始终高于IDM的平均速度。
|
图 9 每条道路上的平均速度 Fig. 9 Average speed on each road |
前车匀速行驶,后车高速接近并实施减速的行为,这种车辆跟驰现象在实际交通中时常发生。以这种跟驰行为为背景设置仿真实验,可以更好地从微观角度分析不同模型下单车的行为状态。选择单行道网络拓扑为实验场景,定义前车以15 m/s的速度匀速行驶,后车以28 m/s的速度接近,并记录后车在不同跟驰模型下速度以及车间距的实时变化。
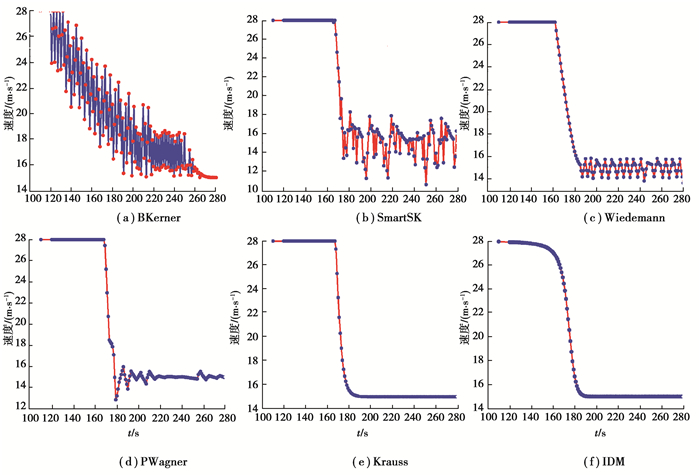
为清晰对比不同模型减速过程中车间距的变化,实验选择162~230 s时间段的数据进行分析。由图 10(a)可知,在BKerner模型下后车接近前车的过程中,车速总体呈波动下降趋势。可以分析出该模型不能稳定控制车辆的速度,当前车减速时,后车可能会处于加速状态,导致出现车辆碰撞,并且BKerner模型车辆开始减速的时间早于其他模型。由图 11减速过程中车间距的变化可以看出,BKerner车间距始终没有达到稳定值。
|
图 10 不同模型下减速过程中车速变化 Fig. 10 Vehicle speed change during deceleration in different models |

|
图 11 不同模型下减速过程中车间距变化 Fig. 11 Change of vehicle spacing during deceleration in different models |
结合图 10和图 11可以看出,Krauss,IDM,Wiedemann,SmartSK和PWagner开始减速的时间较BKerner模型晚。在170~180 s期间,车辆处于减速状态,在减速过程中5个模型对车速均有较好的控制。IDM的车间距大于Krauss和Wiedemann模型,而且减速时间也早于这2个模型。这表明IDM在距前车较远的距离就开始实施减速,如果处在接近路口过程中,宏观上整个车流过早进入减速状态,从而降低了车辆通过路口的效率。Wiedemann,SmartSK和PWagner模型在达到稳定状态时,速度开始频繁波动。Wiedemann模型在180~280 s期间出现明显的波动现象,其原因是车辆在接近模式和跟随模式间不断切换。SmartSK中加速度围绕阈值变化较大,导致车速出现较大波动。PWagner的加速度变化取决于行动点的选择。例如,在220~250 s期间没有选择行动点,车速保持恒定。当车间距较小时,PWagner模型车速出现波动,从微观上看,该模型对单个车辆不能很好的控制,并且存在车辆碰撞的风险。而Krauss模型是在车间距相对较小的情况下开始减速,车辆整个减速过程中具有较高的效率,并且没有出现速度频繁波动的现象。这也表明微观上Krauss模型对单个车辆具有较好的控制性能。
综上所述,在单行道场景下,车辆跟驰模型所处环境简单,道路没有其他限制,因此对模型性能要求较低。实验结果表明,Krauss、SmartSK和BKerner的密度和道路占用率都高于IDM模型,因此,单行道环境下3个模型对交通的调控效率优于IDM。在双向双车道场景下,道路设置交通灯以及多车道,测试不同模型对车辆变道、交通灯前减速及起步的控制性能。在复杂场景下,模型对车辆的控制存在不同问题。Wiedemann和SmartSK由于密度和占用率过高,出现交通拥堵现象;Bkerner不能对车辆进行有效减速并且PWagner模型中没有对交通灯进行相应设置,导致2个模型出现车辆碰撞现象。Krauss和IDM模型对交通的调控性能相近,但Krauss模型在一定程度上避免了交通出现拥堵现象,并且对经过交通灯后的车辆控制符合实际驾驶行为。根据微观角度对模型的分析,Krauss模型对单个车辆高度的控制性能,对在城市道路环境下进行协议的仿真测试极为重要。
4 结束语车辆移动模型的选取对车载网通信协议的分析与验证至关重要。在仿真过程中移动模型能够直接影响协议的吞吐量、包传递率以及传输时延等性能指标。因此,选择尽可能真实反映车辆驾驶行为的移动模型是测试车载网通信协议的关键。
文中详细阐述了SUMO仿真平台下6种车辆跟驰模型的基础理论,并根据车辆跟驰模型的特点设计了3类仿真实验。在车辆平均速度、车辆密度、道路占用率3个指标以及微观角度下对各模型的性能进行对比分析,为车载网仿真研究提供了模型选择的依据和帮助。
| [1] |
Omar H. Intelligent traffic information system based on integration of Internet of Things and agent technology[J]. International Journal of Advanced Computer Science and Applications, 2015, 6(2): 37-43. |
| [2] |
Ghavimi F, Chen H H. M2M communications in 3GPP LTE/LTE-A networks: architectures, service requirements, challenges, and applications[J]. IEEE Communications Surveys & Tutorials, 2015, 17(2): 525-549. |
| [3] |
Ros F J, Martinez J A, Ruiz P M. A survey on modeling and simulation of vehicular networks: Communications, mobility, and tools[J]. Computer Communications, 2014, 43: 1-15. DOI:10.1016/j.comcom.2014.01.010 |
| [4] |
蔡菁, 王腾飞. 基于移动模型的车载自组织网络仿真技术研究[J]. 华中科技大学学报(自然科学版), 2013, 41(S2): 213-217. Cai J, Wang T F. Research on simulation technology of vehicular ad hoc networks based on mobility model[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2013, 41(S2): 213-217. (in Chinese) |
| [5] |
Wang H, Lei S, Wu B, et al. T-START: time, status and region aware taxi mobility model for metropolis[J]. KSⅡ Transactions on Internet & Information Systems, 2018, 12(7): 3018-3040. DOI:10.3837/tiis.2018.07.004 |
| [6] |
Silva F A, Boukerche A, Silva T R M B, et al. A novel macroscopic mobility model for vehicular networks[J]. Computer Networks, 2015, 79: 188-202. DOI:10.1016/j.comnet.2015.01.003 |
| [7] |
Lèbre, M. A, Ménard E. On the importance of real data for microscopic urban vehicular mobility trace[C]//2015 14th International Conference on ITS Telecommunications (ITST). IEEE, 2015: 22-26.
|
| [8] |
张文都, 乔雅. 车载自组织网络下车辆移动模型仿真测试研究[J]. 计算机技术与发展, 2018, 28(11): 188-192, 197. Zhang W D, Qiao Y. Research on vehicular mobility model simulation test in VANETs[J]. Computer Technology and Development, 2018, 28(11): 188-192, 197. (in Chinese) DOI:10.3969/j.issn.1673-629X.2018.11.041 |
| [9] |
魏达, 王沿锡, 王健, 等. 车载自组网移动模型综述[J]. 计算机学报, 2013, 36(4): 677-700. Wei D, Wang Y X, Wang J, et al. A survey on mobility models of vehicular ad hoc networks[J]. Chinese Journal of Computers, 2013, 36(4): 677-700. (in Chinese) |
| [10] |
Behrisch M, Bieker L, Erdmann J, et al. SUMO-simulation of urban mobility: an overview[C]//Proceedings of SIMUL 2011, The Third International Conference on Advances in System Simulation. ThinkMind, 2011: 63-68.
|
| [11] |
Barron C, Neis P, Zipf A. A comprehensive framework for intrinsic OpenStreetMap quality analysis[J]. Transactions in GIS, 2014, 18(6): 877-895. DOI:10.1111/tgis.12073 |
| [12] |
Krajzewicz D, Erdmann J, Behrisch M, et al. Recent development and applications of SUMO-simulation of urban mobility[J]. International Journal on Advances in Systems and Measurements, 2012, 5(3&4): 128-138. |
| [13] |
Krasub S, Wagner P, Gawron C. Metastable states in a microscopic model of traffic flow[J]. Physical Review E, 1997, 55(5): 5597. DOI:10.1103/PhysRevE.55.5597 |
| [14] |
Higgs B, Abbas M, Medina A. Analysis of the wiedemann car following model over different speeds using naturalistic data[C]//3rd International Conference on Road Safety and Simulation. 2011: 1-22.
|
| [15] |
Bifulco, Pariota L, Brackstion M, et al. Driving behavior models enabling the simulation of advanced driving assistance systems: revisiting the action point paradigm[J]. Transportation Research Part C: Emerging Technologies, 2013, 36: 352-366. DOI:10.1016/j.trc.2013.09.009 |
| [16] |
Kerner, B. S, Klenov, et al. Testbed for wireless vehicle communication: a simulation approach based on three-phase traffic theory[C]//2008 IEEE Intelligent Vehicles Symposium. IEEE, 2008: 180-185.
|
| [17] |
Kim K D. Collision free autonomous ground traffic: a model predictive control approach[C]//Proceedings of the ACM/IEEE 4th International Conference on Cyber-Physical Systems. New York: ACM Press, 2013: 51-60.
|
| [18] |
Brackstone M. Driver psychological types and car following: is there a correlation? results of a pilot study[C]//Proceedings of the 2nd International Driving Symposium on Human Factors in Driver Assessment, Training and Vehicle Design: Driving Assessment 2003. Iowa: University of Iowa, 2005: 245-250.
|
| [19] |
Du R, Chen C, Yang B, et al. Effective urban traffic monitoring by vehicular sensor networks[J]. IEEE Transactions on Vehicular Technology, 2014, 64(1): 273-286. |
| [20] |
Liu J, Li J T, Zhang L, et al. Secure intelligent traffic light control using fog computing[J]. Future Generation Computer Systems, 2018, 78: 817-824. DOI:10.1016/j.future.2017.02.017 |
| [21] |
Chen Y S, Hsu C S, Cheng C H. Network mobility protocol for vehicular ad hoc networks[J]. International Journal of Communication Systems, 2014, 27(11): 3042-3063. |
| [22] |
Li Z P, Li W Z, Xu S Z, et al. Stability analysis of an extended intelligent driver model and its simulations under open boundary condition[J]. Physica A: Statistical Mechanics and Its Applications, 2015, 419: 526-536. DOI:10.1016/j.physa.2014.10.063 |
| [23] |
Zhou M F, Qu X B, Jin S. On the impact of cooperative autonomous vehicles in improving freeway merging: a modified intelligent driver model-based approach[J]. IEEE Transactions on Intelligent Transportation Systems, 2017, 18(6): 1422-1428. |
| [24] |
Saifuzzaman M, Zheng Z D. Incorporating human-factors in car-following models: a review of recent developments and research needs[J]. Transportation Research Part C: Emerging Technologies, 2014, 48: 379-403. DOI:10.1016/j.trc.2014.09.008 |
 2021, Vol. 44
2021, Vol. 44


