2. 中国科学院 沈阳计算技术研究所有限公司, 沈阳 110168;
3. 大连理工大学 软件学院, 辽宁 大连 116620
2. Shenyang Institute of Computing Technology Co., Ltd., CAS, Shenyang, Liaoning, 110168, China;
3. School of Software Technology, Dalian University of Technology, Dalian 116620, P. R. China
电力行业中随着化石燃料的不断消耗,其造成的环境污染越来越严重,世界各国的火力发电比例逐渐下降。风能、太阳能、潮汐能等清洁能源受到关注,其中风能具有资源丰富、转换技术相对简单等优点,风力发电被很多国家纳入重点考虑[1]。中国拥有极为丰富的风力资源,绝大多数地区的平均风速都在3 m/s以上,尤其是东北、西北、西南高原和沿海岛屿,平均风速更大,风力发电潜力巨大。但风力发电由于风量不稳定、不可控,存在波动性、随机性,使其发展受到很大程度的制约[2]。风功率的短时预测可以帮助电网进行发电情况的全面监控、并及时做出计划调整,提高电力系统的可靠性。同时,精确的短时风功率预测可以提高风能利用率、解决风储系统的过充或过放问题。
目前,风电场的短时风功率预测已受到研究者们的关注,存在大量相关研究。现存研究采用的方法整体可以分为三类:1)物理方法;2)统计学方法;3)人工智能方法。采用物理方法是指在预测过程中结合天气、气压、障碍物等环境信息对风功率进行预测。数字天气预测[3](NWP, numerical weather prediction)作为物理方法的核心模型已经将所选区域地形等复杂因素考虑进去。一些研究者[4]提出引入风速和风向作为参考变量,结合聚类方法的风功率预测模型。然而,由于复杂的计算因素与环境限制,物理方法的应用受到极大的限制。统计学方法是通过数学函数构造历史数据与输出值之间的映射关系。自回归模型、自回归滑动平均模型、整合滑动平均自回归模型都被用于学习风功率时间序列的统计学规则[5-7]。同时,支持向量机[8](SVMs, support vector machines)、时间序列分析方法[9-10]也应用到风功率预测。统计学方法通过线性化假设,在状态稳定的情况下会给出有竞争力的预测结果。但风功率序列具有随机和间歇特性,使得其数据十分复杂,这些浅层模型不能很好的提取相应的非线性特征[11],因此该类方法仍有提升空间。
由于传统方法难以从风功率数据中提取出深度特征[12], 随着人工智能技术的不断发展,为了充分挖掘风功率历史数据信息,深度学习方法被认为是有效的特征学习方法[13],越来越多的相关人工智能算法被应用到风功率预测领域。其中包括栈式自编码机(SAE, stacked autoencoder)和反向传播方法相结合的预测模型[14],人工神经网络(ANN, artificial neural networks)也被用来预测风功率时间序列中会出现的下一个波动[15]等。而循环神经网络(RNNs, recurrent neural networks),由于它的循环设计能够从序列中学习到高度非线性动态时间信息,在自然处理领域表现突出,并被应用于很多其他时间序列任务中去[16-17]。为了促使RNN在各领域有较好的表现,大量研究被提出,其中包括一个非常流行的RNN变体,即LSTM[18]。但是,若将LSTM直接应用于风功率预测任务,其从整个时间序列中学习复杂的时间和空间模式的能力有限。如沿着时间轴,由于梯度消失模型学习很容易失去长时的依赖关系[19]。提出基于集成多尺度LSTM的短时风功率预测模型,通过不同长度时间序列分别构建预测模型,再融合预测结果,一定程度上缓解由于时间序列过长LSTM失去信息依赖关系的问题,同时保留长时间序列数据中丰富的时序信息和短时间序列中受噪声干扰较少的时序信息,通过LSTM单元构建的深度网络充分挖掘时间序列中数据间隐含的依赖关系,得到更好的短时风功率预测结果。研究以搜集到的中国东北地区风功率数据为实验数据集,验证所提方法有效性。
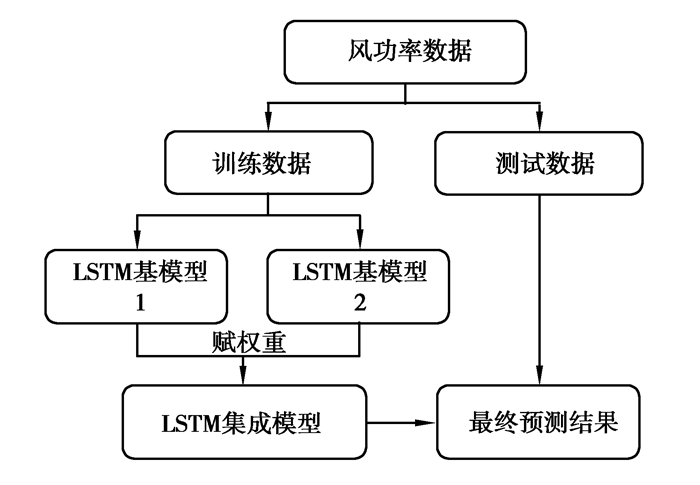
1 集成多尺度LSTM的短时风功率预测模型所提模型采用LSTM从风功率时间序列数据本身进行信息挖掘,构造不同尺度数据集进行同一时间点的数据预测,通过集成学习整合不同预测结果,得到更加接近真实值的最终结果。整体框架如图 1所示。
|
图 1 整体框架图 Fig. 1 Framework of our proposed method |
长短期记忆网络发表于1997年,是循环神经网络的一种,面对长期依赖问题具有很好的解决能力。循环神经网络与其他网络的不同之处在于其隐含层存在自连接,能够通过将输出送到输出端的同时,也送入下一个时间步骤的隐含层。因此它能够持续保存信息,根据之前状态推出之后状态。所有循环神经网络都以一个重复模块链的形式存在,LSTM同样拥有这一重复模块,但其不是一个单一的神经网络层,而是由4部分以一个特殊的方式连接起来的。具体结构如图 2所示。

|
图 2 LSTM网络结构图 Fig. 2 The network structure of LSTM |
在LSTM中,x=[x1, x2, x3, …, xt], T为时间步长,xt为在时刻t的输入,h=[h1, h2, h3, …, hT], ht为在时刻t相应的输出,c=[c1, c2, c3, …, cT], ct为在时刻t记忆细胞相应的状态。细胞状态是LSTM的记忆单元,里边包含了之前网络中的所有信息。
第一步需要决定从之前的网络中忘掉哪些信息,具体通过遗忘门来实现,称之为遗忘阶段。通过读取ht-1和xt,采用sigmoid函数,决定细胞状态上一时刻的信息被遗忘的比例。计算公式如下
| $ f_{t}=\sigma\left(\boldsymbol{W}_{f} \cdot\left[h_{t-1}, x_{t}\right]+\boldsymbol{b}_{f}\right), $ | (1) |
式中:Wf,bf分别为该阶段的权重矩阵、偏置向量,σ为sigmoid函数。
接下来为选择记忆阶段,即将新的输入信息有选择地存储下来,通过输入门实现,并更新细胞状态。首先读取ht-1和xt,通过sigmoid函数来确定需要记录的新信息
| $ i_{t}=\sigma\left(\boldsymbol{W}_{i} \cdot\left[h_{t-1}, x_{t}\right]+\boldsymbol{b}_{i}\right), $ | (2) |
| $ \widetilde{c_{t}}=\tan h\left(\boldsymbol{W}_{c} \cdot\left[h_{t-1}, x_{t}\right]+\boldsymbol{b}_{c}\right), $ | (3) |
| $ c_{t}=f_{t} \cdot c_{t-1}+i_{t} \cdot \widetilde{c_{t}} $ | (4) |
式中:Wi,bi分别为sigmoid层的权重矩阵、偏置向量;Wc,bc分别为tan h层的权重矩阵、偏置向量;tan h为双曲正切函数。
最后为输出阶段,通过输出门实现。通过sigmoid函数计算细胞状态ct输出的信息的比例,然后与经过激活的细胞状态相乘,得到最终输出结果。
| $ o_{t}=\sigma\left(W_{o} \cdot\left[h_{t-1}, x_{t}\right]+b_{o}\right), $ | (5) |
| $ h_{t}=o_{t} * \tan h\left(c_{t}\right) 。$ | (6) |
现有短时风功率预测方法大多关注单个长度下的预测结果,信息有限,通过集成多个尺度时间序列扩充信息容量,是提高预测准确度的一种方法,这一方法可采用装袋算法(Bagging)的思想。
装袋算法是是机器学习领域的一种团体学习算法,它可以通过结合其他分类、回归算法,对准确率、稳定性进行提高的同时,降低结果的方差,避免过拟合的发生,采用这种策略的技术也被称为集成方法(ensemble learning)。其主要思想是分别对几个不同的模型进行训练,所有模型会对测试样本进行相应的输出,再通过取平均值、取多数投票的方法得到最终的结果。同样采用训练多个模型的策略,通过选取不同尺度的时间序列形成不同数据集,通过训练多个LSTM网络对结果进行预测。因不同尺度风功率数据对预测的不同时间长度的风功率结果影响不同,所以针对不同模型赋予不同权重,最终进行模型集成,获得预测结果。具体实现过程如算法描述。
基于多尺度LSTM的集成算法:
Input: 已搜集的东北地区风功率数据。
Step1: 确定具体预测时长,确定预测所需的不同尺度数据,分别从全体数据中进行抽取,形成实验所需训练集和验证集。
Step2: 从训练集中通过抽样构造出大小相同,样本组成尺度不同的训练子集。
Step3: 使用不同训练子集分别训练LSTM模型,形成多个不同模型。
Step4: 不同尺度数据训练模型对验证集进行预测,分别得到预测结果。
Step5: 根据加权投票的法则,从不同尺度训练模型的预测结果得到最终的预测结果P。
Output: 样本预测结果P。
1.3 评价指标由于平均绝对误差(MAE,mean absolute error)和均方根误差(RMSE,root mean squared error) 可以反映预测值与真实值之间的距离。用MAE, RMSE来评估预测性能。公式如下
| $ \mathrm{M} \mathrm{AE}=\frac{1}{n} \sum\limits_{i=1}^{n}\left|\hat{y}_{i}-y_{i}\right| , $ | (7) |
| $ \mathrm{RMSE}=\sqrt{\left(y_{i}-\hat{y}_{i}\right)^{2}} 。$ | (8) |
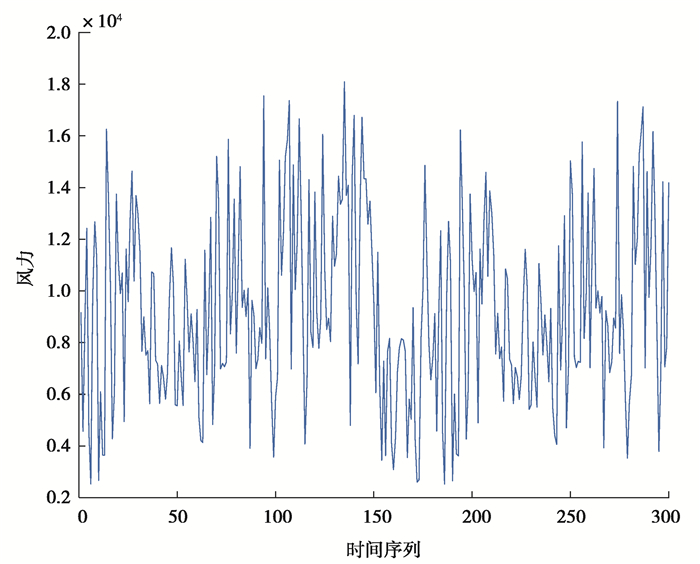
采用搜集到的东北地区2019年上半年的风功率数据作为实验数据对模型性能进行验证。共包含2019年1月1日至2019年6月31日的181 d数据,每15 min进行一次数据采样,每天共有96个数据点。部分数据分布情况如图 3所示。
|
图 3 部分风功率数据分布情况 Fig. 3 Distribution of wind power data |
本模型设计针对短时风功率预测的情况,所以主要进行了2 h风功率预测和4 h风功率预测相关实验。具体实验结果如表 1、表 2所示。
| 表 1 4 h风功率预测MAE和RMSE结果 Table 1 MAEand RMSE results for 4 hours |
| 表 2 2 h风功率预测MAE和RMSE结果 Table 2 2 MAEand RMSE results for 2 hours |
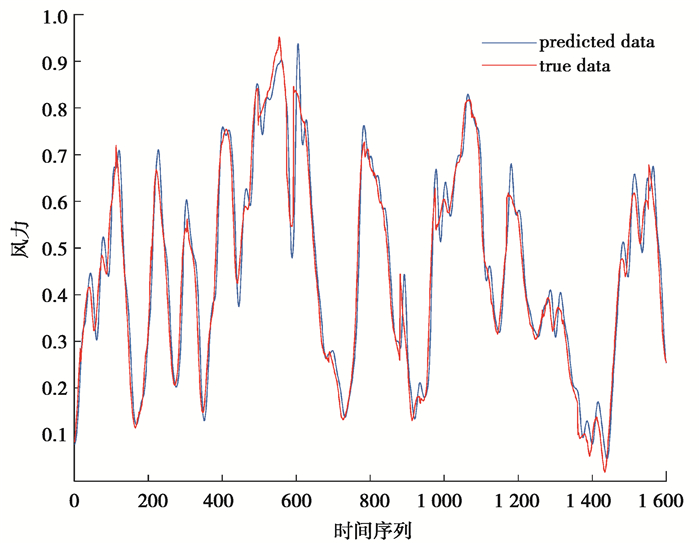
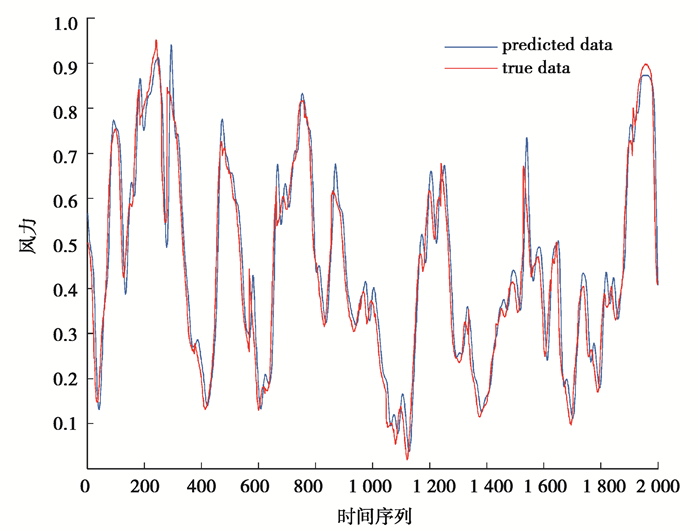
表 1,表 2分别为对4 h风功率情况、2 h风功率情况进行预测得到的实验结果。前4组模型分别为采用需预测数据的前2 h、5 h、10 h和20 h数据进行模型学习,而后进行结果预测。后4组模型分别是集成2 h、5 h;5 h、10 h;5 h、20 h和5 h、10 h、20 h的预测结果,进行最终结果预测。从表中可以看出通过集成前5 h和20 h的风功率预测结果进行预测会得到最小的平均绝对误差和均方根误差,即达到最好的预测效果。图 4、图 5分别为预测2 h和4 h情况下风功率真实值和预测值的分布情况。
|
图 4 预测4 h真实值与预测值分布情况 Fig. 4 Distribution of true data and predicted data for 4 hours forecasting |
|
图 5 预测2 h真实值与预测值分布情况 Fig. 5 Distribution of true data and predicted data for 2 hours forecasting |
实验过程中分别选取预测前的2 h,5 h,10 h和20 h的数据作为不同尺度数据进行预测基模型的建立。再进行不同尺度的模型集成,最后得到效果最好的预测模型。从实验结果中可以看出集成模型和单一基模型相比预测效果更好,但并不是集成的模型越多,得到的实验结果越好。如表 1,表 2所示,不同时长的3个基模型的集成实验结果要低于集成5 h、20 h的2个基模型后得到的实验结果。同时,从实验结果中看预测时长的选取和预测的准确程度并不成正比,即选取被预测时间之前的越长时间的数据进行短时风功率预测并没有得到越好的结果,如选取5 h时长的数据预测效果好于选取10 h时长的数据预测结果,前20 h的数据预测结果表现优异。原因可能是5 h的时长数据具有较少的噪音干扰,而10 h数据包含噪声干扰较多,包含时间序列信息也有限,导致实验结果表现不佳,而20 h时间序列数据包含信息较丰富,弥补了噪音的影响。
实验结果表明,由5 h、20 h的2个基预测模型集成得到最好的预测结果。可以看出预测前的不同尺度数据中包含着对预测结果有影响的不同信息。充分挖掘和利用不同尺度时间数据能有效提高预测结果,对风功率情况有更加精确的把控。从实验结果还可以看出,所提模型对2 h风功率的预测结果要好于对4 h风功率的预测结果。原因可能是时间序列中包含的信息针对较近的风功率情况可以更好地反映出来。
3 结论针对因自然界中风力不稳定、环境变化快等因素导致的风功率存在波动大、难以预测的问题,提出了基于集成多尺度LSTM的短时风功率预测模型,通过挖掘被预测数据前不同尺度数据信息,得到更好的预测结果。主要集成不同尺度数据训练的LSTM基预测模型,对2 h和4 h情况下风功率数据进行预测。实验结果表明集成策略在提高预测精度上起到一定效果,并且在集成被预测数据的前5 h数据和前20 h数据的基预测模型的情况下会得到较好的预测结果。
所提模型融合了不同尺度数据的内在信息,得到较好的实验结果,对电网更好的利用风能提供了一种预测方案。在未来的研究中希望可以通过更多地更复杂的模型结构探索数据内在信息,尽可能提高预测精度。
| [1] |
Zhao J, Wang J Z, Su Z Y. Power generation and renewable potential in China[J]. Renewable and Sustainable Energy Reviews, 2014, 40: 727-740. DOI:10.1016/j.rser.2014.07.211 |
| [2] |
胡青. 大规模风电接入对电网调度运行的影响[J]. 科技风, 2018(14): 168. Hu Q. Influence of large-scale wind power access on power grid dispatching and operation[J]. Science and Technology Wind, 2018(14): 168. (in Chinese) |
| [3] |
Khalid M, Savkin A V. A method for short-term wind power prediction with multiple observation points[J]. IEEE Transactions on Power Systems, 2012, 27(2): 579-586. DOI:10.1109/TPWRS.2011.2160295 |
| [4] |
阎洁, 刘永前, 张浩, 等. 基于风场景识别的动态风电功率概率预测方法[J]. 现代电力, 2016, 33(2): 51-58. Yan J, Liu Y Q, Zhang H, et al. Dynamic wind power probabilistic forecasting based on wind scenario recognition[J]. Modern Electric Power, 2016, 33(2): 51-58. (in Chinese) DOI:10.3969/j.issn.1007-2322.2016.02.009 |
| [5] |
Kavasseri R G, Seetharaman K. Day-ahead wind speed forecasting using f-ARIMA models[J]. Renewable Energy, 2009, 34(5): 1388-1393. DOI:10.1016/j.renene.2008.09.006 |
| [6] |
Chen P Y, Pedersen T, Bak-Jensen B, et al. ARIMA-based time series model of stochastic wind power generation[J]. IEEE Transactions on Power Systems, 2010, 25(2): 667-676. DOI:10.1109/TPWRS.2009.2033277 |
| [7] |
Erdem E, Shi J. ARMA based approaches for forecasting the tuple of wind speed and direction[J]. Applied Energy, 2011, 88(4): 1405-1414. DOI:10.1016/j.apenergy.2010.10.031 |
| [8] |
丁志勇, 杨苹, 杨曦, 等. 基于连续时间段聚类的支持向量机风电功率预测方法[J]. 电力系统自动化, 2012, 36(14): 131-135, 149. Ding Z Y, Yang P, Yang X, et al. Wind power prediction method based on sequential time clustering support vector machine[J]. Automation of Electric Power Systems, 2012, 36(14): 131-135, 149. (in Chinese) |
| [9] |
杨建, 张利, 王明强, 等. 计及出力水平影响与自相关性的风电预测误差模拟方法[J]. 电力自动化设备, 2017, 37(9): 96-102. Yang J, Zhang L, Wang M Q, et al. Wind-power forecasting error simulation considering output level and self-correlation[J]. Electric Power Automation Equipment, 2017, 37(9): 96-102. (in Chinese) |
| [10] |
史坤鹏, 乔颖, 赵伟, 等. 计及历史数据熵关联信息挖掘的短期风电功率预测[J]. 电力系统自动化, 2017, 41(3): 13-18. Shi K P, Qiao Y, Zhao W, et al. Short-term wind power prediction based on entropy association information mining of historical data[J]. Automation of Electric Power Systems, 2017, 41(3): 13-18. (in Chinese) |
| [11] |
Hu Q H, Zhang R J, Zhou Y C. Transfer learning for short-term wind speed prediction with deep neural networks[J]. Renewable Energy, 2016, 85: 83-95. DOI:10.1016/j.renene.2015.06.034 |
| [12] |
Lv Y, Duan Y J, Kang W W, et al. Traffic flow prediction with big data: a deep learning approach[J]. IEEE Transactions on Intelligent Transportation Systems, 2015, 16(2): 865-873. |
| [13] |
Ju Y, Sun G Y, Chen Q H, et al. A model combining convolutional neural network and LightGBM algorithm for ultra-short-term wind power forecasting[J]. IEEE Access, 2019, 7: 28309-28318. |
| [14] |
Jiao R H, Huang X J, Ma X H, et al. A model combining stacked auto encoder and back propagation algorithm for short-term wind power forecasting[J]. IEEE Access, 2018, 6: 17851-17858. |
| [15] |
Cui M J, Ke D P, Sun Y Z, et al. Wind power ramp event forecasting using a stochastic scenario generation method[J]. IEEE Transactions on Sustainable Energy, 2015, 6(2): 422-433. |
| [16] |
Dasgupta S, Osogami T. Nonlinear dynamic Boltzmann machines for time-series prediction[C]//The 31 st AAAI Conference on Artificial Intelligence. San Francisco, USA: AAAI, 2017, 31(1): 1833-1839.
|
| [17] |
Jain A, Kumar A M. Hybrid neural network models for hydrologic time series forecasting[J]. Applied Soft Computing, 2007, 7(2): 585-592. |
| [18] |
Hochreiter S, Schmidhuber J. Long short-term memory[J]. Neural Computation, 1997, 9(8): 1735-1780. |
| [19] |
Lai G K, Chang W C, Yang Y M, et al. Modeling long- and short-term temporal patterns with deep neural networks[C]//The 41st International ACM SIGIR Conference on Research & Development in Information Retrieval. New York, NY, USA: ACM, 2018: 95-104.
|
 2021, Vol. 44
2021, Vol. 44


