b. 重庆理工大学 电气与电子工程学院, 重庆 400054
b. College of Electrical and Electronic Engineering, ChongqingUniversity of Technology, Chongqing 400054, P. R. China
在当前互联网、移动终端和媒体技术飞速发展的时代,以视频为主流媒介的自媒体已迅速普及,并极大地改变了信息的传播生态。在自媒体时代,普通民众可以通过个人摄录、通讯工具(如智能手机等)随时随地拍摄记录目击事件,并在互联网上分享传播。然而,这种拍摄行为具有自由开放性和非正式性,使得自媒体视频普遍存在内容杂乱、失实的现象。因此,自媒体视频内容的有效监管技术是目前媒体内容管理的迫切需求。视频内容的分析和理解往往从对视频对象的特征感知出发,而运动特征是分析视频目标对象行为的关键。但事实上,自媒体视频往往是由业余拍摄者(普通民众)采用手持设备拍摄,视频因此普遍存在较明显的相机运动,而这种运动会掩盖对象的真实运动。例如,若视频拍摄者随着目标对象一起运动,相机的全局运动就会抵消对象的真实运动,造成对象处于静止状态的假象。对视频全局运动进行有效估计,并得到目标对象的真实运动轨迹,对于视频内容描述、对象行为分析、面向对象的视频编码,及自动驾驶场景中的目标测距等应用起着至关重要的作用。
视频序列图像由前景和背景构成,其中背景的运动通常由相机位置变化造成,称为全局运动;而图像中的运动对象代表前景,前景运动是运动对象相对于摄像机的运动,为局部运动。全局运动估计是对视频序列的背景运动进行建模,找到背景运动的规律。但在具有复杂背景的动态视频中,前景和背景中往往存在较多噪声,从而导致全局运动估计存在误差。多年来,对全局运动估计和补偿的研究已积累了一定基础。其中,大多数方法采用基于参数的全局运动估计,例如,基于六参数仿射模型的全局运动估计[1-2]和基于八参数透视模型的估计方法[3-4]。在基于参数的全局运动估计方法中,主要应用运动参数模型预测当前帧运动,并通过最小化与经过运动补偿后参考帧的匹配误差来确定模型参数。一种确定模型参数的实现方案是采用梯度下降方法来最小化残差的L2范数[5-6]。但由于序列图像中存在前景对象的局部运动和噪声,而最小化残差平方和会尽量包含这些局外数据,因此对于背景复杂的全局运动估计,该类方法将会失效。另一种方案是利用随机采样一致性算法(RANSAC, random sample consensus)[7-11]来确定模型参数。这种方法迭代地寻找只有全局运动的内点,而将有局部运动的前景对象和噪声视为外点。Alibay M等人[12]使用抢占式RANSAC算法,并引入了一种运动模型的拉格朗日混合评分方法来计算运动参数。相较于普通的RANSAC算法,抢占式RANSAC算法的速度和精度都有明显提升。但总体来说,基于RANSAC的算法得到可信模型的概率与迭代次数有关,且对内点阈值敏感,因此可能无法得到最优估计。在匹配方面,基于块匹配的两步法是经典的全局运动估计方法[13],近两年也有基于SIFT特征[14]、角点特征[15]、深度卷积神经网络特征[16]等特征匹配的全局运动估计方法,但在全局运动参数估计方面大多采用基于最小二乘或RANSAC的方法。
L1范数是信号的绝对值之和,在L1范数约束下的最优解具有稀疏性,是L0范数的最优凸近似。L1范数最小化是寻求欠定线性系统b=Ax的L1范数解。在压缩感知理论中已被证明,在一定约束条件下,最小化L1范数的解也是最优稀疏解。与L2范数相比,L1范数对噪声和局外点的影响更具有鲁棒性。文献[17]将求解误差(由污损、遮挡等噪声等引起的稀疏误差)的最小化L1范数成功应用于解决人脸对齐问题,并提出一种基于增广拉格朗日方法(ALM, augmented lagrangian methods)的快速凸优化求解方法。文献[18]也将L1范数最小化应用于基于对象的视频编码中。提出一种基于L1范数最小化的全局运动参数估计方法,并实现一套有效的全局补偿方案。假设视频相邻两帧图像包含遵循六参数仿射变换模型的全局运动,通过最小化当前帧经过运动补偿的参考帧与当前帧误差的L1范数进行全局运动模型参数估计;并在此基础上,提出将每帧对象的坐标迭代映射到视频中间帧来揭示对象真实运动轨迹的全局运动补偿方案。通过在大量包含复杂相机运动的视频上进行实验,结果表明方法能够准确地对复杂场景中的全局运动进行估计和补偿,且基于L1范数最小化的运动参数估计方法具有较好鲁棒性。
1 基于L1范数最小化的全局运动参数估计和补偿算法不同内容的视频中包含不同对象的运动轨迹,对象的运动轨迹由水平和垂直方向的坐标表示。基于目标对象原始运动轨迹已知的前提,即目标对象已通过应用现有的目标检测算法[19](Faster RCNN)定位及跟踪算法[20](采用基于稀疏编码的跟踪算法)获得原始运动轨迹。
自然场景视频往往包含由摄像机运动导致的全局运动和被全局运动掩盖的目标对象的局部运动。如图 1所示,(a)中黄色曲线是通过直接应用跟踪算法得到的两目标对象的原始运动轨迹;(b)中黄色曲线是经过全局运动补偿后目标对象的真实轨迹。目标对象是场景中间的2个人,2人的真实运动轨迹是沿着街道有较长距离的位移如图 1(b),但对比2幅轨迹图可以发现,由于摄像机与目标对象的相对运动较小,直接应用跟踪算法得到的原始目标轨迹如图 1(a)与对象的真实运动不符。

|
图 1 示例视频中目标对象的原始轨迹(a)和真实轨迹(b)示意图。 Fig. 1 Illustration of the original(a) and real(b) trajectories of target objects. |
提出基于L1范数最小化的全局运动参数估计算法,并在此基础上对视频的全局运动进行纠正以获得运动对象真实运动轨迹的运动补偿方法。该方法首先对每相邻视频帧进行全局运动参数估计得到相邻之间的运动变换参数,再迭代地将对象在原帧的坐标通过连续相邻帧的变换依次映射到目的帧。具体地,对于任意相邻帧之间的全局运动参数τi,将视频段的中间帧记为fM,则对于fM之前的所有帧,将对象在前一帧的坐标依次应用τi变换映射到后一帧;对于fM之后的所有帧,将对象在后一帧的坐标依次应用τi变换逐步向前映射到前一帧。例如,若帧fi在fM之前,且帧fi中对象的中心坐标是Xi=[u, v]T,则其在全局运动补偿之后相对于中间帧的对象坐标为
| $ X_{i, \text { corr }}=\tau_{M-1}\left(\tau_{M-2}\left(\cdots \tau_{i+1}\left(\tau_{i}\left(\boldsymbol{X}_{i}\right)\right)\right)\right), $ | (1) |
其中
| $ \boldsymbol{\tau}_{i}\left(\boldsymbol{X}_{i}\right)=\tau_{i}\left(\left[\begin{array}{l} u \\ v \end{array}\right]\right)=\left[\begin{array}{l} \alpha_{1}^{i} u+\alpha_{2}^{i} v+\alpha_{3}^{i} \\ \beta_{1}^{i} u+\beta_{2}^{i} v+\beta_{3}^{i} \end{array}\right], $ |
{α1…3i, β1…3i}是帧i到i+1的全局仿射变换参数。图 2中给出了图 1示例视频中连续视频帧的全局运动补偿过程:对于中间帧fM之前的每对相邻视频,前一帧为源帧,后一帧为目的帧;对于中间帧fM之后的每对视频帧,后一帧为源帧,前一帧为目的帧。通过应用基于L1范数最小化的全局运动估计方法求得的每相邻视频帧间的全局运动参数i,将对象在源帧中的坐标映射到目的帧,并依次迭代地映射到中间帧fM。但算法只对每帧进行一次全局运动补偿,且不使用已补偿过的视频帧来计算下一相邻帧的全局运动参数。

|
图 2 基于相邻帧运动参数迭代映射的全局运动补偿方法 Fig. 2 Global motion compensation based on iterative mapping of motion parameters betweenadjacent frames |
以上全局运动补偿方案的关键是找到2帧之间的全局运动参数τ,提出基于当前帧与补偿后参考帧误差的L1范数最小化进行求解。设源帧图像为R(p),目标帧图像为F(p),其中p为像素坐标。全局运动估计的本质是找到一个位移函数Δ(p),使得由源帧经该位移函数重构得到的目标帧F′(p)与真实的目标帧F(p)间的差异最小,即F(p)-R(p+Δ(p))最小。然而,在一帧图像中,不同位置的像素p所对应的位移函数不同,因此需要构建一个几何变换模型来估计图像中每个像素的运动。即全局运动参数估计就是找到一个几何变换模型τ(p),使得F(p)-R(p)·τ最小,
| $ \underset{\tau}{\operatorname{argmin}} F(p)-R(p) \cdot \tau, $ | (2) |
使用公式(1)中6参数仿射模型τ作为全局运动的几何变换模型。于是,基于L1范数最小化的全局运动参数估计问题可定义为
| $ \underset{\tau}{\operatorname{argmin}}\|F(p)-R(p) \cdot \tau\|_{1}, $ | (3) |
式中:p∈Ω,Ω为图像像素空间。对于仿射模型,给定一个像素(px, py),其对应仿射变换位置为(p′x, p′y)
| $ \left[\begin{array}{c} p_{x}^{\prime} \\ p_{y}^{\prime} \end{array}\right]=\left[\begin{array}{c} \alpha_{1} p_{x}+\alpha_{2} p_{y}+\alpha_{3} \\ \beta_{1} p_{x}+\beta_{2} p_{y}+\beta_{3} \end{array}\right] \text { , } $ | (4) |
由于存在非线性warping映射变换,公式(3)仍然是非凸的。根据文献[21],warping算子可由其在当前状态τ0某邻域来线性化逼近,因此,假设Δτ很小,则有R(τ0+Δτ)≈R(p)·τ0+JΔτ,其中J是R(p)·τ0相对于变换参数τ0的Jacobian(雅可比)矩阵,在仿射变换模型中,定义Δτ和Jacobian J如下
| $ \Delta \boldsymbol{\tau}=\left[\varDelta \alpha_{1} \varDelta \alpha_{2} \varDelta \alpha_{3} \varDelta \beta_{1} \varDelta \beta_{2} \varDelta \beta_{3}\right]^{\mathrm{T}}, $ | (5) |
| $ \begin{aligned} \boldsymbol{J} & \triangleq \frac{\partial}{\partial_{\tau}} \operatorname{vec}(R \cdot \tau) \mid \tau=\tau_{0} \in R N \times 6 \\ &=\left[\frac{\partial R}{\partial \alpha_{1}} \frac{\partial R}{\partial \alpha_{2}} \frac{\partial R}{\partial \alpha_{3}} \frac{\partial R}{\partial \beta_{1}} \frac{\partial R}{\partial \beta_{2}} \frac{\partial R}{\partial \beta_{3}}\right], \end{aligned} $ | (6) |
式中:N是R中的像素数。将R沿着X和Y方向的梯度图像分别设为Rx和Ry,则Jacobian矩阵J可变为
| $ \boldsymbol{J}=\left[R_{x} p_{x} R_{x} p_{y} R_{x} R_{y} p_{x} R_{y} p_{y} R_{y}\right], $ | (7) |
根据文献[18],公式(3)可以通过交替迭代求解,即在每次迭代时,外循环更新τ,内循环求解公式(3)的线性逼近
| $ \underset{\varDelta \tau}{\operatorname{argmin}}\left|\boldsymbol{F}-\boldsymbol{R} \cdot \tau_{0}-\boldsymbol{J} \varDelta \tau\right|_{1}, $ | (8) |
式中:F,R是所有p的向量表示。若定义预测残差S=F-R·τ0-JΔτ=ΔF-JΔτ,则公式(8)转化为
| $ \begin{gathered} \underset{\varDelta \tau, S}{\operatorname{argmin}}|S|_{1}, \\ \text { s.t. } \boldsymbol{J}\Delta \tau+S=\boldsymbol{F}-\boldsymbol{R} \cdot \tau_{0} \triangleq \Delta F, \end{gathered} $ | (9) |
从而,公式(9)在无约束的增广拉格朗日函数L中可以写为以下形式
| $ \begin{aligned} \underset{\varDelta \tau, S}{\operatorname{argmin}} L &=|S|_{1}+Y T(\boldsymbol{J} \Delta \tau+S-\Delta \boldsymbol{F})+\\ & \frac{\mu}{2}\|\boldsymbol{J} \Delta \tau+S-\Delta \boldsymbol{F}\|_{2}^{2}, \end{aligned} $ | (10) |
式中:Y和μ代表拉格朗日系数。在非精确交替方向乘子法(ADMM, alternating direction method of multiplier)[22]中,等式10可转化为交替地求解2个分别相对于S和Δτ的子问题以及拉格朗日乘子更新
(子问题w.r.t S)
| $ \underset{S}{\operatorname{argmin}}|S|_{1}+\frac{\mu}{2}\left\|S-\left(\Delta \boldsymbol{F}-\boldsymbol{J} \Delta \tau-\mu^{-1} Y\right)\right\|_{2}^{2}, $ | (11) |
(子问题w.r.t Δτ)
| $ \underset{\varDelta \tau}{\operatorname{argmin}}\left\|\boldsymbol{J} \Delta \tau-\left(\Delta \boldsymbol{F}-S-\mu^{-1} Y\right)\right\|_{2}^{2}, $ | (12) |
(更新拉格朗日乘子)
| $ Y \leftarrow Y+\mu(\boldsymbol{J} \Delta \tau+s-\Delta \boldsymbol{F})。$ | (13) |
求解以上基于L1范数最小化的全局运动参数估计算法过程如表 1所示。对于初始仿射运动参数τ0可以通过块运动估计[13]的方法来得到一个较好的初始值,但通过实验发现将τ0初始化为单位阵对结果没有明显的影响,因此,为减少算法复杂度,默认将τ0初始化为单位阵。
| 表 1 基于最小化L1范数的全局运动估计算法 Table 1 The global motion estimation algorithm based on L1-norm minimization |
相对于全局运动估计,具有全局运动的运动对象是不符合其运动规律的异常点。因此,为减少异常点对全局运动的估计的影响,利用对象检测的矩形区域对每一个对象定义一个二值掩模M,以使运动对象对应像素点不参与全局运动估计的计算。M中运动对象对应位置的元素为0,其余背景像素对应位置的元素为1。
于是上述全局运动参数估计的目标函数转变为
| $ \begin{gathered} \underset{\varDelta \tau . S}{\operatorname{argmin}}|M(S)|_{1}, \\ \text { s.t. } M(\boldsymbol{F})=M\left(R \cdot \tau_{0}\right)+\boldsymbol{J} \Delta \tau+M(S), \end{gathered} $ | (14) |
公式(14)根据表 1算法步骤进行求解。
2 数据集及实验结果分析在多个自媒体用户拍摄的视频上进行了实验,其中包括7个选自哥伦比亚消费者视频(CCV, columbia consumer video)数据集[23],5个选自VOT[24]、OTB[25]、MOT[26]等目标跟踪数据集,以及一些来自媒体网站的自媒体视频样本。整个实验数据集包含了丰富的场景、内容及全局/局部运动模式。每个视频被预处理成约为10 s(帧率30 FPS),且只包含单个场景镜头的视频段。数据集示例视频帧如图 3所示。

|
图 3 全局运动补偿实验数据集示例帧 Fig. 3 Data frame samples for global motion compensation |
在实验数据集上与基于RANSAC的全局运动估计算法进行了对比。基于RANSAC的全局运动估计算法首先提取视频相邻帧的SIFT特征点,并使用最近邻算法(KNN)进行匹配,最后通过对匹配点应用RANSAC算法估计出相邻帧的全局运动仿射变换参数(即公式(1)中τi)。
图 4给出了示例视频段的10帧图像。可以看到,该视频记录了2名女子在公园沿路慢跑的场景。图 5分别给出了由运动跟踪算法得到的对象原始轨迹(如图 5(a)中黄色曲线),利用全局运动补偿后的运动轨迹(如图 5(b)中黄色曲线)和基于RANSAC方法补偿后的运动轨迹(如图 5(c)中黄色曲线)。由于视频拍摄跟随了两名女子的运动,原跟踪轨迹显示2名女子在原地无序地运动,而经过全局运动纠正的轨迹(如图 5(b)、(c)所示)则揭示出2名女子在跑道上长距离运动的真实情况。结合图 4中视频原帧序列,对比图 5(b)、(c)可以看出,虽然基于RANSAC的全局运动估计算法能够在一定程度上反映对象的运动趋势,但与对象的真实运动轨迹仍有一定距离,而本文提出的基于L1范数最小化的全局运动参数估计方法能够更好地对全局运动进行估计,其经过补偿后的轨迹更符合对象的真实运动。

|
图 4 视频段原序列帧(从连续300帧中以均匀间隔抽取10帧) Fig. 4 Original sequence frames of a video segment (10 frames are uniformly drawn from continuous 300 frames) |

|
图 5 对应图 4示例视频段的对象运动轨迹与利用基于不同运动补偿方法纠正后的运动轨迹。 Fig. 5 The object motion trajectory of the sample video segment corresponding to Figure 4 |
图 6分别给出了视频中2个目标对象使用2种全局运动估计算法在X方向和Y方向上轨迹进行纠正的前后对比。可以看出,基于L1范数最小化的全局运动估计算法和运动补偿方法能够很好地揭示运动对象在视频中沿着道路的慢跑运动轨迹,而基于RANSAC的方法则没有很好的找到全局运动规律并将运动对象的真实运动恢复出来。图 7给出了更多基于全局运动补偿的运动对象轨迹与原对象运动轨迹的对比。实验结果表明,提出的基于L1范数最小化进行全局运动参数估计能够准确地反应视频的全局运动规律,并通过全局运动补偿方案恢复出运动对象的真实运动轨迹。
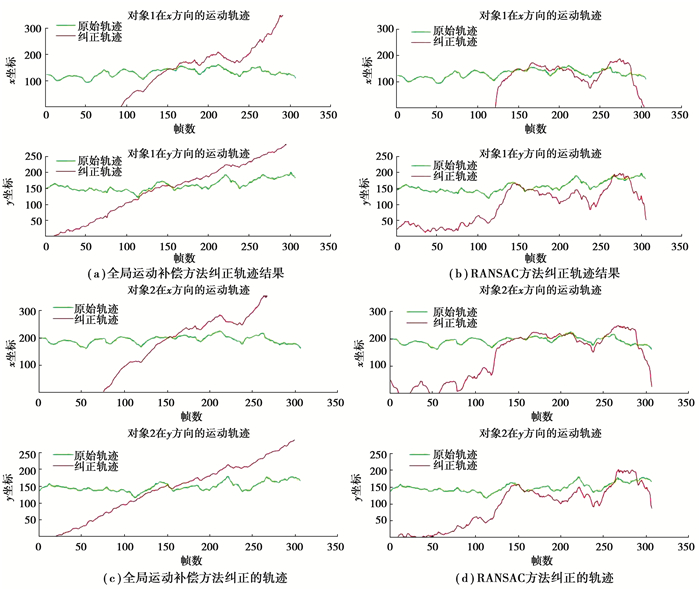
|
图 6 全局运动补偿结果对比 Fig. 6 Comparison of global motion correction results |

|
注: 图中为示例视频段的中间帧, 黄色曲线为对象运动轨 图 7 部分实验数据结果 Fig. 7 Experimental results of some sample videos |
视频序列中通常包含具有不稳定的相机运动,这种图像的全局运动会掩盖目标对象的真实运动轨迹。为了估计出全局运动的规律,从而恢复出目标对象的真实运动,本文提出了基于L1范数最小化的全局运动参数估计算法,和基于相邻帧运动参数迭代映射的全局运动补偿方法从视频的原始轨迹中获得出对象的真实运动轨迹。实验结果表明本文提出的全局运动参数估计和补偿算法能有效地把握全局运动的规律,并从中准确恢复出目标对象的真实运动轨迹。本文提出的方法目前只能离线分析视频的全局运动,如何在线高效地对视频全局运动进行有效估计和补偿将是本文进一步的工作。
| [1] |
He Y W, Qi W, Yang S Q, et al. Feature-based fast and robust global motion estimation technique for sprite coding[EB/OL]. [2000-01-21].
|
| [2] |
Qi B, Ghazal M, Amer A. Robust global motion estimation oriented to video object segmentation[J]. IEEE Transactions on Image Processing, 2008, 17(6): 958-967. DOI:10.1109/TIP.2008.921985 |
| [3] |
MPEG-4 Video Group. ISO/IEC JTC/SC29/WG11/N3908-2001 MPEG-4 Video Verification Model Version 18.0[S]. 2001.
|
| [4] |
Dufaux F, Konrad J. Efficient, robust, and fast global motion estimation for video coding[J]. IEEE Transactions on Image Processing, 2000, 9(3): 497-501. DOI:10.1109/83.826785 |
| [5] |
Keller Y, Averbuch A. Fast gradient methods based on global motion estimation for video compression[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2003, 13(4): 300-309. DOI:10.1109/TCSVT.2003.811360 |
| [6] |
Alzoubi H, Pan W D. Reducing the complexity of MPEG-4 global motion estimation using pixel subsampling[J]. Electronics Letters, 2008, 44(1): 20. DOI:10.1049/el:20082196 |
| [7] |
Fischler M A, Bolles R C. Random sample consensus[J]. Communications of the ACM, 1981, 24(6): 381-395. DOI:10.1145/358669.358692 |
| [8] |
Yang S W, Wang C C. Multiple-model RANSAC for ego-motion estimation in highly dynamic environments[C]//2009 IEEE International Conference on Robotics and Automation. May 12-17, 2009, Kobe, Japan: IEEE, 2009: 3531-3538.
|
| [9] |
Thanh T N, Nagahara H, Sagawa R, et al. An adaptive-scale robust estimator for motion estimation[C]//2009 IEEE International Conference on Robotics and Automation. May 12-17, 2009, Kobe, Japan: IEEE, 2009: 2455-2460.
|
| [10] |
王智慧, 王敬东, 李鹏, 等. 一种基于KLT-RANSAC全局运动估计的电子稳像算法研究[J]. 光电子技术, 2012, 32(1): 46-51, 55. Wang Z H, Wang J D, Li P, et al. Research on electronic image stabilization based on KLT-RANSAC global motion estimation[J]. Optoelectronic Technology, 2012, 32(1): 46-51, 55. (in Chinese) DOI:10.3969/j.issn.1005-488X.2012.01.011 |
| [11] |
Liu Y Q, Gu Y Z, Li J M, et al. Robust stereo visual odometry using improved RANSAC-based methods for mobile robot localization[J]. Sensors(Basel, Switzerland), 2017, 17(10): E2339. DOI:10.3390/s17102339 |
| [12] |
Alibay M, Auberger S, Stanciulescu B, et al. Hybrid visual and inertial RANSAC for real-time motion estimation[C]//2014 IEEE International Conference on Image Processing(ICIP). October 27-30, 2014, Paris, France: IEEE, 2014: 179-183.
|
| [13] |
Rath G B, Makur A. Iterative least squares and compression based estimations for a four-parameter linear global motion model and global motion compensation[J]. IEEE Transactions on Circuits and Systems for Video Technology, 1999, 9(7): 1075-1099. DOI:10.1109/76.795060 |
| [14] |
Guo S X, Qiu C G, Ye X F. A kind of global motion estimation algorithm based on feature matching[C]//2009 International Conference on Mechatronics and Automation. August 9-12, 2009, Changchun, China: IEEE, 2009: 107-111.
|
| [15] |
Kawasaki A, Saito H, Hara K. Motion estimation for non-overlapping cameras by improvement of feature points matching based on urban 3D structure[C]//2015 IEEE International Conference on Image Processing(ICIP). September 27-30, 2015, Quebec City, QC, Canada: IEEE, 2015: 1230-1234.
|
| [16] |
Choi G, Heo P, Oh S R, et al. A new motion estimation method for motion-compensated frame interpolation using a convolutional neural network[C]//2017 IEEE International Conference on Image Processing(ICIP). September 17-20, 2017, Beijing, China: IEEE, 2017: 800-804.
|
| [17] |
Yang A Y, Zhou Z H, Balasubramanian A G, et al. Fast $\ell1$-minimization algorithms for robust face recognition[J]. IEEE Transactions on Image Processing, 2013, 22(8): 3234-3246. DOI:10.1109/TIP.2013.2262292 |
| [18] |
Xue Y. Beyond HEVC: Exploring new frameworks for video coding[D]. Brooklyn: Polytechnic Institute of New York University, 2016.
|
| [19] |
Ren S Q, He K M, Girshick R, et al. Faster R-CNN: towards real-time object detection with region proposal networks[C]//IEEE Transactions on Pattern Analysis and Machine Intelligence. [S. L. ]: IEEE: 1137-1149.
|
| [20] |
Wang D, Lu H C, Yang M H. Online object tracking with sparse prototypes[J]. IEEE Transactions on Image Processing, 2013, 22(1): 314-325. DOI:10.1109/TIP.2012.2202677 |
| [21] |
Szeliski R. Image alignment and stitching: a tutorial[J]. Foundations and Trends © in Computer Graphics and Vision, 2007, 2(1): 1-104. DOI:10.1561/0600000009 |
| [22] |
Boyd S, Parikh N, Chu E, et al. Distributed optimization and statistical learning via the alternating direction method of multipliers[J]. Foundations and Trends in Machine Learning, 2010, 3(1): 1-122. DOI:10.1561/2200000016 |
| [23] |
Jiang Y G, Ye G N, Chang S F, et al. Consumer video understanding: a benchmark database and an evaluation of human and machine performance[C]//ICMR'11: Proceedings of the 1st ACM International Conference on Multimedia Retrieval. [S. L. ]: IEEE, 2011: 1-8.
|
| [24] |
Kristan M, Matas J, Leonardis A, et al. A novel performance evaluation methodology for single-target trackers[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2016, 38(11): 2137-2155. DOI:10.1109/TPAMI.2016.2516982 |
| [25] |
Wu Y, Lim J, Yang M H. Online object tracking: a benchmark[C]//2013 IEEE Conference on Computer Vision and Pattern Recognition. June 23-28, 2013, Portland, OR, USA: IEEE, 2013: 2411-2418.
|
| [26] |
Milan A, Leal-Taixe L, Reid I, et al. MOT16: A benchmark for multi-object tracking[J]. arXiv Preprint: 1603. 00831V2[cs. CV]. 2016, 5.
|
 2021, Vol. 44
2021, Vol. 44

