b. 重庆邮电大学 通信与信息工程学院, 重庆 400065
b. School of Telecommunication and Information Engineering, Chongqing University of Posts and Telecommunications, Chongqing 400065, P. R. China
水是人类社会生产生活必不可少的资源,水资源相关的环境保护与循环利用至关重要。随着社会的进步,水体污染对社会的影响也日益明显,水体被排入大量污染物,对人类的日常生活造成极大的威胁。而水质预测可以为有关部门的干预决策提供重要参考。在许多工业场景中,水质预测也具有重要意义。例如在污水处理工艺中,如果可以通过水质预测提前预知突发的水质超标情况,就能够为工程人员提供预警,预留时间人为干预,保证污水处理出厂水质达标。
水质预测主要有如下几种预测方法:通过构建物理模型的方法[1],灰色系统预测法,神经网络预测法[2],模糊理论预测法[3],以及数理统计预测法等。
颜剑波等人[4]通过分析水质变量之间的规律,建立多元回归模型,对三门峡断面水质进行了预测。刘东君等人[5]结合灰色系统预测法与神经网络,对北京密云水库的溶解氧进行了预测,通过将混合模型分别于2个原型方法作比较,表明混合模型相比2个原型方法,预测结果更为精确和稳定。姜云超等人[6]综合运用BP, SOM与模糊综合评价法对黄河水质进行了评价,取得了较理想的结果。荣洁等人[7]提出指数平滑法-马尔科夫预测模型,将平滑处理后的数据通过马尔科夫预测模型对合肥湖滨与巢湖裕溪口2个断面的CODMn、TP、TN浓度进行了预测。RederK等人[8]使用人工神经网络模型预测水质变化,证实了神经网络模型是被用于水质预测的可行性。Alizadeh M J和Kavianpour M R[9]使用小波神经网络对太平洋希洛湾地区的水质进行了预测,证明了小波神经网络模型相对于其他神经网络模型的优越性。Azimi S等人[10]结合神经网络与改进的模糊聚类技术来预测了水质恶化的概率。
文献中虽然对水质预测方面作了深入的研究,但并未针对原始数据的各项特征对预测任务的影响权重进行评估,而在输入预测模型的数据维度比较多时,对预测任务贡献比较小的特征会干扰预测模型,降低预测模型的性能。因此使用遗传算法来调整各特征维度的权重,使其符合预测模型的特性,提高了预测模型的预测精度,为水质预测提供了一种有价值的解决方案。
1 数据来源与预处理源数据来自重庆市某污水厂2016年1月1日至2018年12月31日之间每日采集的进出水水质数据与活性污泥池监测数据,共有1 096条数据。源数据共有21维,主要包含了进出水的5 d需氧量、化学需氧量、酸碱度、总磷、总氮等水质数据与污水处理总量、耗电量、活性污泥浓度等污水处理设备相关数据。本次水质预测中标签以国家三类水质标准中相关水质的标准为阈值。
在正式使用遗传算法依据数据优化特征权重向量之前,首先要经过一系列数据预处理。处理流程主要分为数据特征初步选择、标签生成、数据标准化处理3个步骤。
为了加快预处理速度,首先依据一般经验剔除一部分较为明显地与问题相关性小的特征,本数据在剔除了若干特征后,剩余17维特征。列出部分数据样例如表 1所示。
| 表 1 数据样例表 Table 1 The data sample |
初步选择特征后,需要为数据生成对应标签。假设使用连续的n d的连续数据来预测下一天的水质情况,则数据将被整合为1 096-n条,17*n维的可用数据。由于本次实验中特征维数基数较大,n值增长会导致数据维数急剧上升,引发维度灾难,从而极大地影响预测模型的性能,所以将此处的n值定为1,使用原数据中的每一条数据预测其后一条(1 d后)的水质情况。
据此依据每条数据的总磷、总氮、BOD5、CODcr 4项出水水质结合国家三类水质标准生成其前一条数据的标签。标签生成步骤完成后,数据共1 095条,17维。
由数据样例可以看出原数据中各特征维度的数据尺度差距非常大,如果直接导入预测模型会导致部分特征维度被模型忽略掉。由于没有关于特征之间权重的可信先验知识的情况下,将数据进行标准化操作,统一所有特征维度的尺度(方差)至相同,然后通过遗传算法进行特征权重调整,达到特征选择的目的。
2 基本原理与预测模型 2.1 SVM基本理论支持向量机是一种基于统计学习理论的一种新类型的广义分类器,由于它使结构风险最小化、有较好的泛化能力,在引入核函数后,还能将在低维输入空间线性不可分的样本通过映射至高位空间使样本变得线性可分,被广泛应用于各种监督学习场景下[11-13]。近年来,不少研究将SVM应用于各类预测分析问题[14],在进行小样本数据预测时,其预测能力甚至优于BP神经网络方法和RBF神经网络。
设样本(x1, y1), (x2, y2), …,(xk, yk)∈RN×R,其中xi为输入数据,yi对应标签,k为数据总数,则其最小化目标函数可表示为
| $ R(\omega)=\min\limits_{\omega, b, \zeta}\left[\frac{1}{2} \omega^{2}+C \sum\limits_{i=1}^{n} \zeta_{i}\right], \\ \text { s.t. }\left\{\begin{array}{l} \boldsymbol{\omega}^{\mathrm{T}} \varphi\left(x_{i}\right)+b \geqslant 1-\zeta_{i} \\ \zeta_{i} \geqslant 0, i=1, \cdots, n, \end{array}\right. $ | (1) |
式中:C为平衡模型经验风险与模型复杂度的惩罚因子;ζ为非负松弛变量;φ() 为受核函数相关的函数;K(xi, xj)=φ(xi)Tφ(xj)。
通过拉格朗日法将上述最优化问题转化为对偶问题。
| $ \min \left[\frac{1}{2} \boldsymbol{\alpha}^{\mathrm{T}} Q \alpha-\boldsymbol{e}^{\mathrm{T}} \alpha\right], \\ \text { s.t. }\left\{\begin{array}{c} \boldsymbol{y}^{\mathrm{T}} \alpha=0 \\ 0 \leqslant \alpha_{i} \leqslant C, i=1, \cdots, n \end{array}\right., $ | (2) |
最后可得决策函数
| $ \operatorname{sgn}\left(\sum\limits_{i=1}^{n} y_{i} \alpha_{i} K\left(x_{i}, x\right)+\rho\right), $ | (3) |
模型在预测时,输入数据x,则可通过上式计算得到对应的预测结果。
2.2 遗传算法优化的SVM模型在数据挖掘机器学习领域中,高维数据通常需要特征选择降维以避免使模型受到维度灾难的影响,这使得特征选择成为机器学习算法数据预处理步骤中的重要一环。
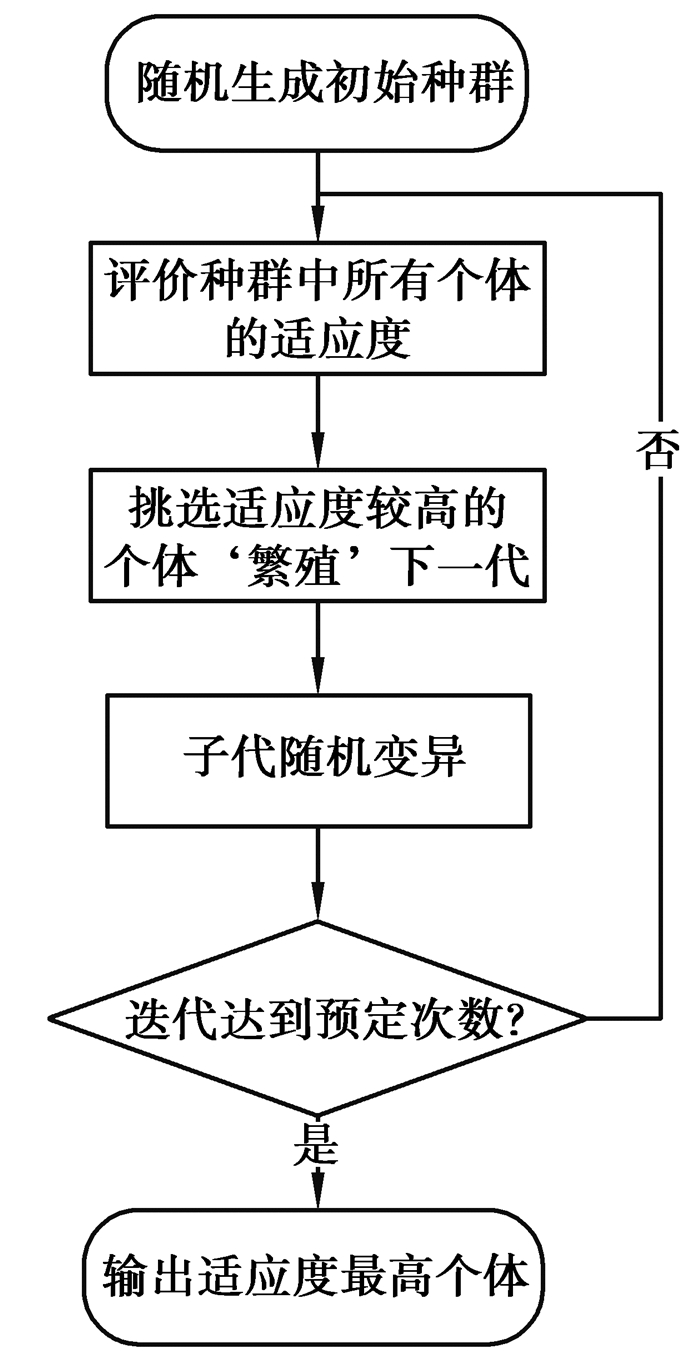
遗传算法是一种模拟物种进化模式而来的迭代优化算法。它通过模拟生物种群的变异、繁衍来优化候选解。由于遗传算法具有全局优化搜索的特点[15],在各个领域都有着广泛的应用[16-20]。遗传算法的流程图如图 1所示。
|
图 1 遗传算法流程图 Fig. 1 The flow chart of Genetic Algorithm |
在使用遗传算法优化SVM模型时,通过选取每个维度的放缩因子组成的向量v=(v1, v2, v3,…,vm) 作为种群个体,将训练集数据以特征权重向量v放缩后数据x′=x×vT供给SVM模型训练,其在验证集上的F1分数作为个体适应度。
遗传算法优化特征权重向量的过程中,是将SVM模型调整得适用于验证集数据分布的特点,在将优化结果放到测试集上进行验证时,由于验证集数据分布不完全与测试集数据分布相同,会因为过拟合而导致模型在测试集上的性能相比于验证集出现退化。这个退化本身是由于过拟合产生的,可以通过调整遗传算法的种群大小、迭代次数、变异程度参数来抑制。
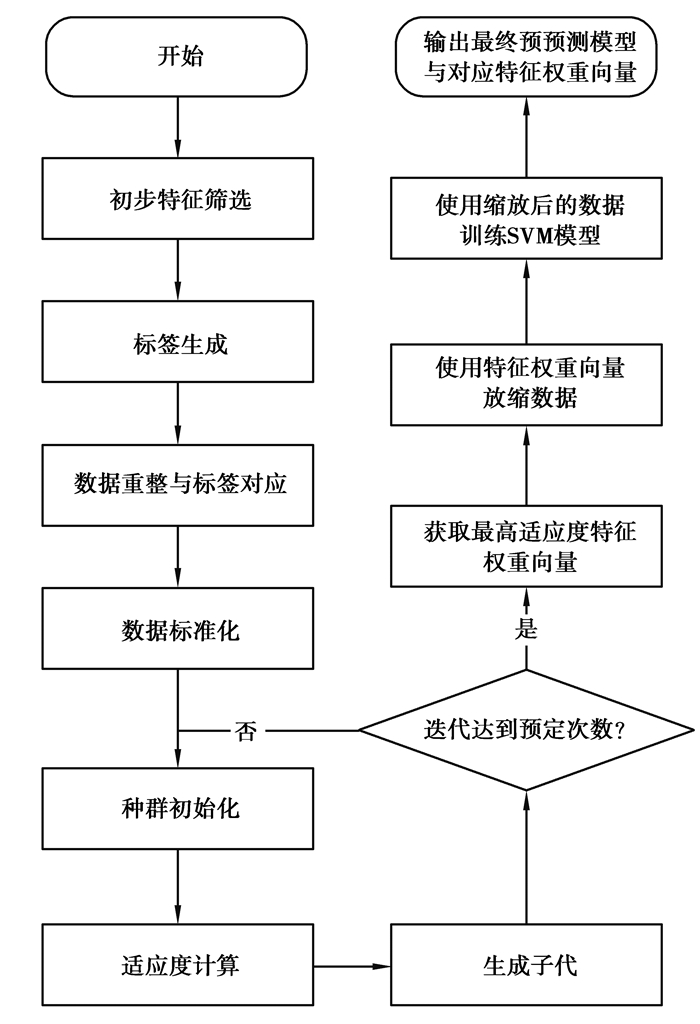
综上所述,采用原始水质数据x、国家三级水质标准训练基于遗传算法与SVM的水质预测模型的完整流程如图 2所示。
|
图 2 预测模型流程图 Fig. 2 The flow chart of model |
本实验所用硬件为联想Y500笔记本一台,CPU型号为I5-3210M,内存8 GB。软件平台为python 3.5.3,主要使用了pandas、numpy、sklearn 3个库。
实验依据污水厂的1 000余条历史数据,对厂方感兴趣的总磷、总氮、氨氮、BOD5、CODcr 5项出水水质分别进行预测,并与传统SVM预测的结果进行对比。
由于模型的过拟合问题可以通过加大验证集数据数量,确保验证集数据分布贴近实际应用时的情形(测试集)来缓和,所以在数据分段时,将数据按3:5:2的比例分为训练集、验证集与测试集。
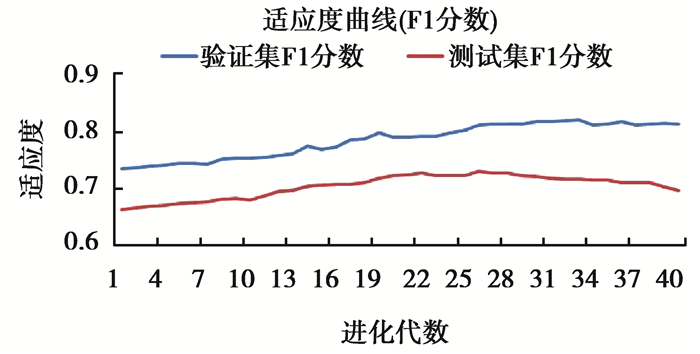
在给定遗传网络中种群大小为10,变异范围为0~0.1的前提下,通过测试观察验证集上的适应度与测试集上的适应度随迭代次数变化情况来确定合适的迭代次数。实验得到的效果图如图 3所示。
|
图 3 遗传算法适应度曲线 Fig. 3 Genetic algorithm fitness curve |
图 3中验证集的适应度随着进化代数小幅震荡提升并在40代左右达到一个稳定值,而对测试集的适应度在第23代左右达到最大值。为了避免实验的随机性影响,保守取最佳迭代次数为20。
由于水质除少数情况外,在大部分的时间中都是合乎国家三类水质标准的,数据表现出不平衡的倾向,本次数据依照4个预测目标的标签平衡情况如表 2所示。
| 表 2 正例样本统计表 Table 2 Positive sample statistics |
类别不平衡的样本容易导致模型过拟合,还容易出现模型正确率较高而召回率、精确率较低,没有实用意义。例如数据中有100个正例与900个反例,模型被训练永远返回新样本预测结果为反例,虽然正确率高达90%,但对于实际问题是没有任何参考价值的。解决类别不平衡问题一般有2大类方法:欠采样与重采样。欠采样通过去除多数类样本使得正例、反例数目接近,但容易导致样本数量过少,也容易产生过拟合;重采样通过重复少数类样本来平衡正反例数目,但简单重复原本就较少的少类样本会使得这部分信息被放大,模型学习到的信息过于‘特殊’。综合考虑下,通过将sklearn库中的SVM模型参数中的class_wight参数设置为‘balanced’,运用加权的方式使得多数类与少数类在加权平衡后,对SVM训练过程中的损失函数起到同样大的作用,缓解数据本身类别不平衡对模型的影响。
在正式实验中,使用基于遗传算法与SVM的水质预测模型与传统线性SVM模型分别对1 000余条水质数据依照国家三类水质进行预测。其中遗传算法参数参考之前的测试,取种群大小为10、变异范围为0~0.1(均匀分布)、迭代次数为20次。两者的SVM模型部分参数为C=1.0,tol=0.000 1,class_wight=balanced。得到预测的正确率、召回率如表 3所示。
| 表 3 预测结果 Table 3 Results of prediction |
从表 3中可以看出,在水质指标方面,总磷与BOD5两项水质指标预测指标较好,较为易于预测,总氮与COD相对难以预测一些。在模型对比方面,改进的SVM在所有水质指标预测上均优于传统SVM,特别在总氮指标预测上,有非常大的提升。说明通过遗传算法优化特征权重向量以达到一定程度上的特征选择的做法的确能够提升分类器的预测性能。
4 结论通过在SVM分类模型的基础上使用遗传算法进行特征选择,提升了模型的性能,使得预测模型能够更加有效地帮助污水厂提前发现问题,保证出厂水质达标。实验结果表明,在对4项主要水质指标的预测上,正确率能达到76%以上,召回率能达到75%,较为可靠地为技术人员提供参考。但模型的召回率与精准率还有提升空间,依然无法完全代替人工检测的功能。这些都还有待进一步研究。
| [1] |
周彦辰, 胡铁松, 陈进, 等. 耦合动态方程的神经网络模型在水质预测中的应用[J]. 长江科学院院报, 2017, 34(9): 1-5. Zhou Y C, Hu T S, Chen J, et al. Application of neural network model coupled with dynamic equation in water quality prediction[J]. Journal of Yangtze River Scientific Research Institute, 2017, 34(9): 1-5. (in Chinese) |
| [2] |
张颖, 高倩倩. 基于灰色模型和模糊神经网络的综合水质预测模型研究[J]. 环境工程学报, 2015, 9(2): 537-545. Zhang Y, Gao Q Q. Comprehensive prediction model of water quality based on grey model and fuzzy neural network[J]. Chinese Journal of Environmental Engineering, 2015, 9(2): 537-545. (in Chinese) |
| [3] |
于慧, 孙宝盛, 李亚楠, 等. 应用灰色模糊马尔科夫链预测海河水质变化趋势[J]. 中国环境科学, 2014, 34(3): 810-816. Yu H, Sun B S, Li Y N, et al. Water quality prediction of haihe river using grey-fuzzy-markov chain model[J]. China Environmental Science, 2014, 34(3): 810-816. (in Chinese) |
| [4] |
刘燕燕, 杨帮华, 丁丽娜, 等. 基于STM32的红外火灾探测系统设计[J]. 计算机测量与控制, 2013, 21(1): 51-53. Liu Y Y, Yang B H, Ding L N, et al. Design of software system in infrared fire detection based on STM32[J]. Computer Measurement & Control, 2013, 21(1): 51-53. (in Chinese) DOI:10.3969/j.issn.1671-4598.2013.01.017 |
| [5] |
刘东君, 邹志红. 灰色和神经网络组合模型在水质预测中的应用[J]. 系统工程, 2011, 29(9): 105-109. Liu D J, Zou Z H. Applications of gray forecast model combined with artificial neural networks model to water quality forecast[J]. Systems Engineering, 2011, 29(9): 105-109. (in Chinese) |
| [6] |
姜云超, 南忠仁. 三种不确定性水质综合评价方法比较研究[J]. 干旱区资源与环境, 2011, 25(3): 177-180. Jiang Y C, Nan Z R. Comparison of three comprehensively uncertain water quality assessment methods[J]. Journal of Arid Land Resources and Environment, 2011, 25(3): 177-180. (in Chinese) |
| [7] |
荣洁, 王腊春. 指数平滑法-马尔科夫模型在巢湖水质预测中的应用[J]. 水资源与水工程学报, 2013, 24(4): 98-102. Rong J, Wang L C. Application of the exponential smoothing law-markov model in prediction of water quality of Chaohu lake[J]. Journal of Water Resources and Water Engineering, 2013, 24(4): 98-102. (in Chinese) |
| [8] |
Reder K, Alcamo J, Fl rke M. A sensitivity and uncertainty analysis of a continental-scale water quality model of pathogen pollution in African rivers[J]. Ecological Modelling, 2017, 351: 129-139. DOI:10.1016/j.ecolmodel.2017.02.008 |
| [9] |
Alizadeh M J, Kavianpour M R. Development of wavelet-ANN models to predict water quality parameters in Hilo Bay, pacific ocean[J]. Marine Pollution Bulletin, 2015, 98(1/2): 171-178. |
| [10] |
Azimi S, Azhdary Moghaddam M, Hashemi Monfared S A. Prediction of annual drinking water quality reduction based on groundwater resource index using the artificial neural network and fuzzy clustering[J]. Journal of Contaminant Hydrology, 2019, 220: 6-17. DOI:10.1016/j.jconhyd.2018.10.010 |
| [11] |
Xu G X, Gao G W, Hu M X. Detecting spammer on micro-blogs base on fuzzy multi-class SVM[C]//2018 International Conference on Cyber-Enabled Distributed Computing and Knowledge Discovery(CyberC). October 18-20, 2018, Zhengzhou, China: IEEE, 2018: 24-247.
|
| [12] |
Babita, Kumari P, Narayan Y, et al. Binary movement classification of sEMG signal using linear SVM and Wavelet Packet Transform[C]//2016 IEEE 1st International Conference on Power Electronics, Intelligent Control and Energy Systems(ICPEICES). July 4-6, 2016, Delhi, India: IEEE, 2016: 1-4.
|
| [13] |
Pomboza-Junez G, Terriza J H. Hand gesture recognition based on sEMG signals using Support Vector Machines[J]. 2016 IEEE 6th International Conference on Consumer Electronics-Berlin(ICCE-Berlin), 2016, 174-178. |
| [14] |
王见, 陈义, 邓帅. 基于改进SVM分类器的动作识别方法[J]. 重庆大学学报, 2016, 39(1): 12-17. Wang J, Chen Y, Deng S. A gesture-recognition algorithm based on improved SVM[J]. Journal of Chongqing University, 2016, 39(1): 12-17. (in Chinese) |
| [15] |
Grefenstette J J. Proceedings of the first international conference on genetic algorithms and their applications[M]. UK: Psychology Press, 2014.
|
| [16] |
Yu F, Xu X Z. A short-term load forecasting model of natural gas based on optimized genetic algorithm and improved BP neural network[J]. Applied Energy, 2014, 134: 102-113. |
| [17] |
Choi K, Kim G, Suh Y, et al. Assignment of collaborators to multiple business problems using genetic algorithm[J]. Information Systems and e-Business Management, 2017, 15(4): 877-895. DOI:10.1007/s10257-016-0328-5 |
| [18] |
Thakur M, Meghwani S S, Jalota H. A modified real coded genetic algorithm for constrained optimization[J]. Applied Mathematics and Computation, 2014, 235: 292-317. |
| [19] |
Changdar C, Mahapatra G S, Kumar Pal R. An efficient genetic algorithm for multi-objective solid travelling salesman problem under fuzziness[J]. Swarm and Evolutionary Computation, 2014, 15: 27-37. |
| [20] |
Ghiduk A S. Automatic generation of basis test paths using variable length genetic algorithm[J]. Information Processing Letters, 2014, 114(6): 304-316. |
 2021, Vol. 44
2021, Vol. 44


