空间适宜性分析是城乡规划的基础环节[1]。这种分析在考虑与土地适宜性相关的各种影响因子后,对土体的适宜性进行综合评价。评价的结果可为后续的城乡规划提供参考,是规划的依据之一。地理信息系统(GIS)的出现,虽然使传统的多因素地图叠合法得以在GIS的支撑下将空间信息按照数学法则运算,进而形成空间决策的多准则决策法,但现有的单目标多准则决策法适用的范围较为有限,难以处理多个决策目标的问题。相比较而言,双目标多准则决策法较单目标多准则决策法适用于更多的空间决策问题,尤其能对2种相互冲突的决策目标进行分析,并最终得出合理的空间决策方案。然而,目前双目标多准则决策也存在目标决策的决策模型复杂性高,空间决策的可操作性差等问题。这不但使目标决策问题未能得到简单有效地解决,也使该决策法的技术较难应用于实践。因此,文中以提升目标决策法的可操作性和简洁性为重点,在深入阐释空间双目标多准则决策原理并系统梳理其操作流程的基础上,建立一种能有效与GIS软件结合的双目标决策平面法的决策流程,并提出一种简易可行的决策平面冲突区的划分方法,以提升双目标多准则决策中目标决策法的可操作性和简洁性。
1 结合GIS的多准则决策方法研究进展多准则决策(MCDM, multi-criteria decision making)是一种将决策目标的相关影响因素作为判定准则进行综合分析,最后得出决策方案的体系化方法。这种方法的优势之一在于它可以同时兼顾存在不可公度性(non-commensurable)准则的分析。此外,该方法将各类准则统一量纲后从宏观整体的角度进行整合分析的体系化决策过程,也减少了决策者的主观判断对决策形成偏见的可能性。
1.1 多准则决策与空间决策的结合点——GIS随着多准则决策法在诸多学术领域的广泛应用,上世纪80年代该方法逐渐开始应用于城乡规划领域的研究中。但是涉及大量空间决策问题的城乡规划研究难以直接与多准则决策方法进行结合。原因在于空间决策所依靠的空间数据是表示位置、分布和距离等方面的几何数据,其特性为具有空间上的无限性,这意味着基于此类数据所展开的空间决策(如用地类型决策和空间选址决策等)都存在着近乎无限的方案(alternatives)。由于多准则决策模型无法直接处理无限选项的问题,故需要将空间上的无限决策可能性转化为有限准则下的空间内涵,而这一转换过程的实现需要依靠具有栅格和矢量数据的处理能力以及空间数据可视化功能的GIS工具的支撑。这使得GIS成为了MCDM与空间决策相融合的关键连接点,同时也是利用MCDM进行空间决策的必要支持工具。
1.2 国内外在多准则决策与GIS领域的研究进展基于GIS的多准则决策方法的相关研究经历了30多年,期间不断有学者将新的标准化方法、权重确定法以及准则聚合方法等融入到该决策体系中,使该方法体系得到了极大的完善。Watson等[2]将GIS-MCDM技术应用于处理南英格兰的太阳能与风力发电厂选址问题。方芳等[3]分析了国内外MCDM与GIS结合的相关研究,并探讨了此方法的现有问题以及今后的发展方向。Greene等[4-5]详细梳理了MCDM与GIS结合的空间决策法的原理和流程,并详尽地分析了各类决策规则、权重算法等优劣性。钮心毅等[6]在Eastman的基础上提出了新的双目标决策平面冲突区划分方法,并以此方法进行了实践应用。Malczewski[7]对1990年到2004年间的300多篇GIS和多准则决策结合方法的研究文献进行了分类总结,并对该方法的发展趋势进行了讨论。Malczewski等[8]将次序加权平均法(OWA)融入到了基于GIS的MCDM决策体系中,使得准则的聚合方式更加动态化。Laaribi等[9]提出了将GIS和MCDM结合的空间决策支持系统(SDSS),并深入阐述了将GIS和多准则分析结合进行空间决策的必要性。Eastman等[10]提出通过栅格结构的数据分析来进行多准则与多目标决策方法,并创建了解决双目标多准则决策的决策平面法。Banai[11]把模糊集合理论和层次分析法融入GIS与MCDM结合的方法中,让决策准则在权重分配方法上得到了优化提升。Carver[12]将GIS的空间信息处理能力作为技术支撑与多准则决策进行结合,构建出一整套系统化的研究方法,并以放射性污染物处理厂的选址问题为例进行了该方法的实践。Voogd[13]提出将MCDM应用于城市与区域规划领域,并构建相关理念与方法。
现阶段学者们对于GIS与多准则决策方法的相关研究成果多集中于单目标多准则决策领域,而有关双目标多准则决策研究文献不但数量较少,且时间也相对较早,主要为Eastman和钮心毅于1995年与2008年的研究。这反映出人们对双目标多准则决策领域的关注度较低。其次,双目标多准则决策技术的核心——决策平面(decision space)的相关方法不够完善,决策平面冲突区的有效划分方法依旧缺失。上述问题的存在,不但使双目标多准则决策中的目标决策问题无法得到有效解决,也限制了基于此方法的有关实践应用研究。
2 双目标多准则决策较单目标多准则决策的方法升级 2.1 决策机制的增设单目标多准则决策在明确某一单一决策目标后,针对该目标建立准则层进行决策分析。这种层次的决策所确定的决策目标不具有和其他决策目标的可比性,故无法完成冲突目标(conflicting objectives)在同一块土地空间上相互竞争的空间决策(如土地利用布局决策)。
文中所介绍的双目标多准则决策法是一种适用于相互冲突的决策目标的多准则决策技术方法。它在单目标层次多准则决策的基础上,增加了可适用于两种相互冲突目标的目标决策机制——决策平面。此决策机制为决策目标之间的比较提供了可能,使决策者能在权衡比较目标空间适宜性的基础上,得出空间目标分配的最优方案。相比较而言,双目标多准则决策不但较单目标多准则决策能适应更多类型的空间决策问题,其决策流程中目标决策程序的潜在目标比较机制也大大削弱了目标选取上的主观性,使空间决策更具准确性和客观性。
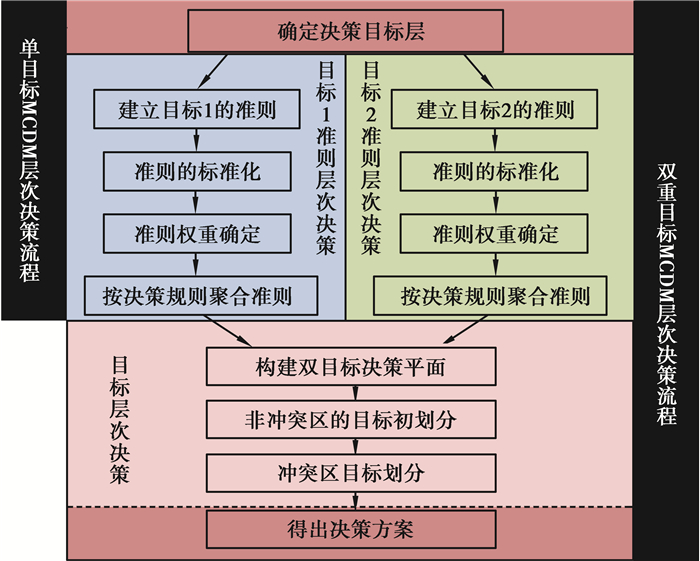
2.2 决策体系结构延伸在决策体系结构上,单目标MCDM是双目标MCDM的决策基础,而双目标MCDM是单目标MCDM的流程延续。单目标层次的MCDM主要为准则层次的决策,该决策的主要步骤分为确定决策目标、准则层的构建、准则的标准化、准则的加权以及准则层的聚合,如图 1所示。而双目标MCDM则在单目标MCDM的基础上进一步延伸出目标层次的决策,该层次的决策依靠双目标决策平面完成目标分配,其主要步骤包括双目标决策平面的构建、决策平面非冲突区的目标初分配和决策平面冲突区的划分。
|
图 1 结合GIS的双目标MCDM流程 Fig. 1 GIS-based dual objectives MCDM process |
决策平面(decision space)是双目标多准则决策的核心,它是以2个目标的适宜性为坐标的平面坐标系统,空间栅格数据的每个像元都可以根据其适宜性数值对应到该平面坐标系统中,使决策者能通过决策平面对复杂的空间系统进行决策。
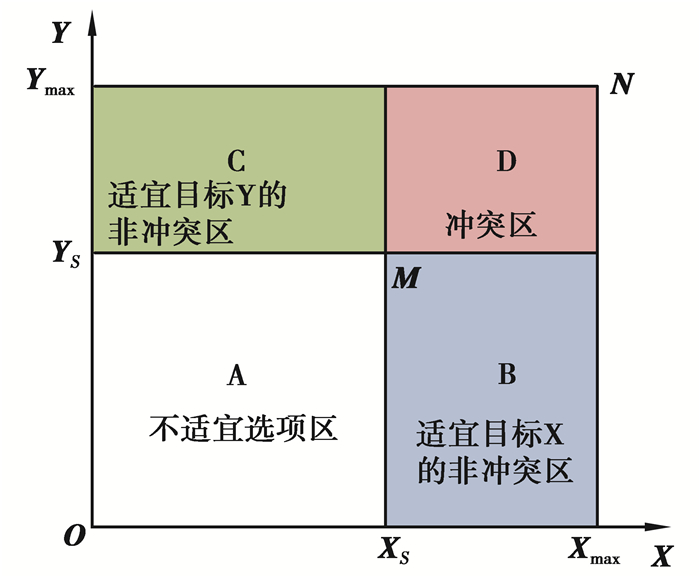
3.1 双目标决策平面的构成决策平面的X轴和Y轴对应2个决策目标的适宜性得分,如图 2所示。Xmax和Ymax为目标X与目标Y适宜性得分的最大值。XmaxN和YmaxN 2条线段与X轴和Y轴围合成的矩形为空间适宜性得分在决策平面上的对应区域,也是需要进行决策的目标区域,故文中称其为决策区。Xs与Ys是分区点,其作用为确定目标X与目标Y得分的适宜与非适宜区间。过Xs、Ys垂直于X轴、Y轴的2条线将决策区分为4个子区域,分别为:A区,对双目标都不适宜的不适宜选项区;B区,对目标X适宜但对目标Y不适宜的非冲突区;C区,对目标Y适宜但对目标X不适宜的非冲突区;D区,对双目标都适宜的冲突区。
|
图 2 双目标MCDM决策平面 Fig. 2 MCDM decision space for dual objectives |
A、B、C 3个区都可以在确定2个目标的适宜性分区点(Xs与Ys)的位置后进行目标分配决策。但冲突区D作为对2个目标都具有高适宜度的区域,却无法通过单目标层面的适宜性分析进行目标分配,而如何解决冲突区的分配正是决策平面法的重点和难点。
目前,对于冲突区的划分方法主要由Eastman提出,主张通过冲突区原点(M点)的划分线与水平坐标夹角的正切值(tangent,即分割线斜率)来确定冲突区划分线的位置,进而对冲突区进行目标划分。而划分线与横坐标夹角θ的正切值由X与Y 2个目标的目标权重(wx、wy)的比值来决定,满足:
文中将建立决策平面法的体系化决策流程框架,并介绍一种新的决策平面冲突区的目标划分法。该方法能与ArcGIS软件结合,使决策平面上的目标分配能在GIS工具上进行操作,完成双目标MCDM的目标决策流程。研究将决策平面法的决策过程分为2个步骤:
步骤一,决策平面非冲突区的目标初划分,如图 2所示。该过程将完成对决策区的适宜与不适宜区间的划分,即确定Xs与Ys在X轴与Y轴上的位置。由于对决策目标适宜区间的划分是在单目标决策层次下完成的,所以此过程只需要根据目标自身的适宜性需求确定其适宜性的数值区间,不需要考虑竞争目标的适宜性数值。在确定适宜与非适宜的区间(Xs、Ys的位置)之后,决策区根据是否适宜与是否冲突而被分成4个子区域(A区、B区、C区、D区)。文中将过点Xs与Ys的X轴与Y轴垂线的相交点M命名为定区点,定区点是确定决策区4个子区位置和形态的关键点,也是新形成的冲突区D的原点。该点位置的确定是冲突区形成的基础,也是决策平面冲突区目标划分的开始。
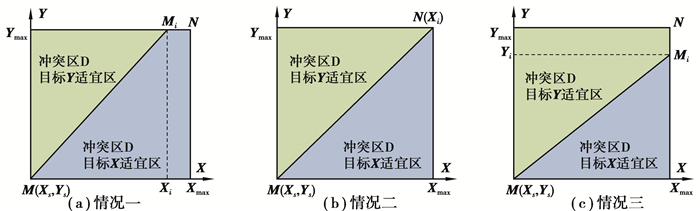
步骤二,决策平面冲突区的划分:前文提到Eastman在划分冲突区时通过双目标权重比来确定过定区点(M)的划分线与横坐标夹角的正切值,进而确定冲突区划分线的位置。但需要注意的是,冲突区划分的本质是对其面积的划分。所以,相对于Eastman的方法,在决策目标的权重比等于目标在冲突区分得的面积比的情况下进行划分能取得更加合理与准确的划分结果。因此,文中提出一种决策平面冲突区划分的改进方法,即针对划分线在冲突区可能出现的3种情况。根据划分线与冲突区边界的交点确定划分线位置,进而完成对冲突区的划分,如图 3所示。
|
图 3 决策平面冲突区划分的3种情况 Fig. 3 Three possible partitions of conflict region on decision space |
1) 情况一,划分线过M点,在冲突区内与线段YmaxN相交于Mi。此时冲突区分配给目标Y的为划分线左侧的三角形区域,分配给目标X的为划分线右侧的梯形区域。
2) 情况二,划分线过M点和N(Mi)点。此时冲突区分配给目标Y的为划分线左侧的三角形区域,分配给目标X的为划分线右侧的三角形区域。
3) 情况三,划分线过M点,在冲突区内与线段XmaxN相交于Mi。此时冲突区分配给目标Y的为划分线左侧的梯形区域,分配给目标X的为划分线右侧的三角形区域。
第1种情况下,目标X的权重大于目标Y的权重,即wy/wx < 1。此时,权重比wy/wx等于目标Y所对应的三角形面积与目标X所对应的梯形面积的比值,通过点Mi(Xi, Ymax)确定冲突区划分线的位置。该点的纵坐标Ymax为目标得分最大值,其横坐标Xi在确定wy/wx后计算得出,计算公式为
| $ X_{i}=X_{\max }-\frac{\left(1-\frac{w_{y}}{w_{x}}\right)\left(X_{\max }-X_{s}\right)}{\left(1+\frac{w_{y}}{w_{x}}\right)}, $ | (1) |
式中:Xmax与Xs分别对应冲突区X坐标的最大值和最小值;wx与wy为目标X和目标Y的目标权重。
第2种情况下,目标Y与目标X的权重相等,即wy/wx=1。该情况下Xi=Xmax,划分线为过原点M和点N(Mi)的冲突区矩形的对角线连线,冲突区的面积被均等地分配给X和Y 2个目标。
第3种情况下,目标Y的权重大于目标X的权重,即wy/wx>1。此时,权重比wy/wx等于目标Y所对应的梯形面积与目标X所对应的三角形面积的比值,通过点Mi(Xmax, Yi)确定冲突区划分线的位置。该点的横坐标Xmax为目标得分最大值,其纵坐标Yi在确定wy/wx后计算得出,计算公式为
| $ Y_{i}=Y_{\max }-\frac{\left(\frac{w_{y}}{w_{x}}-1\right)\left(Y_{\max }-Y_{s}\right)}{\left(1+\frac{w_{y}}{w_{x}}\right)}, $ | (2) |
式中:Ymax与Ys分别对应冲突区Y坐标的最大值和最小值;wx与wy为目标X和目标Y的目标权重。
在Xi或Yi确定之后,冲突区划分线的位置就可以被确定,以实现利用决策平面完成对冲突目标的完全分配。这种基于几何模型的目标决策方法便捷性高、可操作性强,不需要依靠GIS之外的数学模型构建工具,只通过ArcGIS的散点图生成功能即可以完成对决策目标的划分。
4 应用案例——北京市百善镇 4.1 区域介绍百善镇总面积约34.78 km2,辖13个行政村,截止2017年12月总人口约为3.48万人。百善镇南有温榆河景观资源,适于建设依托滨水的湿地公园及配套餐饮、民宿和农家乐设施。加之百善镇临近北京市区,交通上有昌平线和高速公路等较为便捷和廉价的出行选项,故该地为适合北京市区居民节假日消遣旅游地之一,旅游开发潜力巨大。另一方面,百善镇域内包含温榆河河段、沙河水库以及大量基本农田和林地等生态保护价值较高的水域与地文资源,故该镇也具有极高的生态环境保护价值。由于百善镇同时具有较高的开发潜力和保护价值,且开发与保护2种目标又具有相互冲突的特性,故该镇在用地布局决策上难度很大。因此,文中选取百善镇为案例,用双目标多准则决策与GIS结合的方法对2种目标的土地利用空间布局进行决策分析。所使用的主要软件为ArcGIS10.5和TerrSet18.07。由于本案例以OWA算子方法对准则层进行聚合,而ArcGIS上难以进行OWA模型的计算,故需使用TerrSet软件实现OWA聚合。
4.2 决策目标层与准则层的确定本案例的双目标为开发性质的目标和保护性质的目标。经数次实地调研发现,百善镇域内有数量较多且价值较高的旅游资源,旅游开发是最具潜力的开发模式。因此,将开发的形式限定在旅游开发。旅游建设开发目标下的准则选取主要包括:C1土规中的建设适宜性、C2路网可达性、C3距地铁站的距离,以及C4距离滨水资源的距离。C1土规中的建设适宜性反映土地利用规划中不同用地类型所对应的建设开发适宜性的差别。主要依据上位土地利用规划中的用地类型进行评价,评价结果分为不适宜建设、较不适宜建设、中、较适宜建设、适宜建设5个级别。C2路网可达性反映交通的便捷程度对旅游发展的影响,距离交通路网越近的区域旅游开发的适宜性越高。C3距地铁站的距离反映游客出行的交通便捷性。百善镇临近北京市区的地理区位,决定了其所吸引的主要旅游客源为北京市区的居民,而地铁是相当一部分游客前往百善镇的重要交通手段。因此,距地铁站口的距离越近,旅游相关设施建设的适宜性就越高。C4距离滨水资源的距离反映旅游资源的利用程度。旅游设施建设距离旅游景观资源越近,其旅游价值就越高。
生态环境保护目标下的准则选取主要包括:C1距河流水库的距离、C2距基本农田的距离、C3距村庄居民生活区的距离、C4植被现状的保护价值。C1距河流水库的距离反映河流水域的生态保护价值。距离河流越近,其生态保护的适宜性越高。C2距基本农田的距离反映基本农田的生态保护价值。距离基本农田越近,生态保护的适宜性就越高。C3距村庄居民生活区的距离反映生态保护对人的影响。距离村庄居民日常生活区域越近的地方,生态环境保护的价值越高。C4植被现状的保护价值反映不同现状用地类型所对应的生态保护适宜性的差别。根据百善镇用地现状的调研数据,对于现状用地类型的生态保护价值进行评价,评价结果分为保护价值低、保护价值较低、保护价值中、保护价值较高、保护价值高5个等级。
4.3 双目标下各准则的标准化与权重分配在确定决策的目标层和准则层以及各准则的空间属性之后,文中将准则的适宜性进行标准化分级并加权,如表 1所示。适宜性的标准化分为不适宜、较不适宜、中、较适宜、适宜5个级别。各准则的权重通过层次分析法(AHP)进行计算。
| 表 1 目标层、准则层、空间属性、标准化和准则权重 Table 1 Objectives, criteria, spatial attributes, standardization and criteria weights |
在准则的聚合上选用次序加权平均法(OWA)。该方法相对传统的加权线性组合法(WLC)而言,进一步考虑了决策风险的因素,是一种可以根据决策者对决策风险的接受度来改变准则补偿(criteria trade-off)程度的动态准则聚合法。OWA中的次序权重能够在布尔OR运算逻辑(决策风险最大)与AND运算逻辑(决策风险最小)之间动态变化,决策者可通过改变α的取值来调节决策的风险。这个过程的实质是通过对准则之间的补偿程度进行干预来改变准则的聚合结果。
Malczewski在同时考虑了准则权重和次序权重后,对OWA的运算进行了修正,并得出:
| $ \mathrm{O} \mathrm{WA}_{i}=\sum\limits_{j=1}^{n}\left(\frac{w_{j} v_{j}}{\sum _{j=1}^{n} w_{j} v_{j}}\right) z_{i j}, (i, j=1, 2, \cdots, n), $ | (3) |
式中:wj为各项准则的权重; vj为次序权重; zij为准则属性值。次序权重vj的计算公式为
| $ v_{j}=\left(\sum\limits_{k=1}^{j} u_{k}\right)^{\alpha}-\left(\sum\limits_{k=1}^{j-1} u_{k}\right)^{\alpha}, (k=1, 2, \cdots, n), $ | (4) |
式中:uk为准则重要等级可用AHP法进行确定;α为风险系数,其值取决于决策者对决策风险的态度。当α趋近于0时,决策风险最大;当α趋近于正无穷时,决策风险最小。
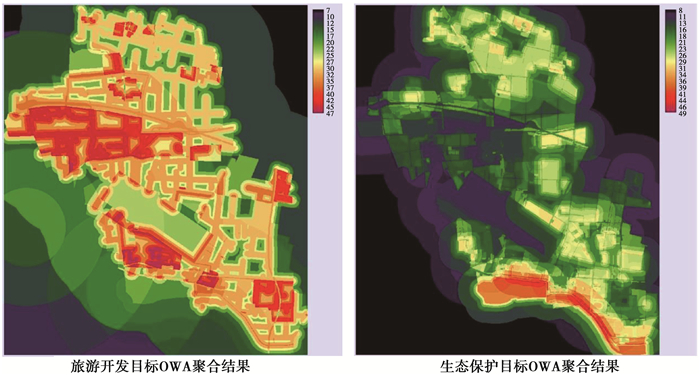
表 2给出了3种决策风险等级,并进行了比较。取α=1时风险中等的情况,通过TerrSet软件的OWA模块对各项准则进行OWA聚合,并生成旅游开发目标和生态保护目标的准则聚合图,如图 4所示。
| 表 2 OWA方法中3种决策风险等级的比较 Table 2 Comparison of the 3 risk levels of decision-making in OWA method |
|
图 4 百善镇旅游开发与生态保护目标OWA聚合后的空间适宜性图 Fig. 4 Spatial suitability maps of tourism development and ecological conservation by OWA aggregation |
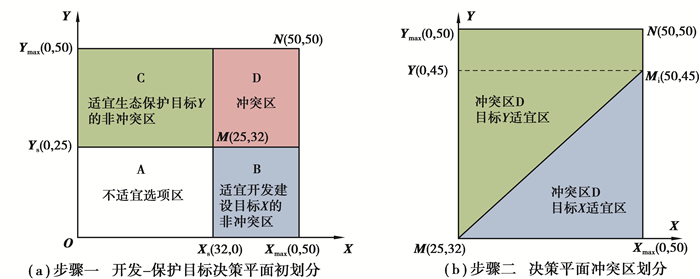
在完成单目标层次的聚合后,建立双目标多准则决策的决策平面(如图 5步骤一所示)。该决策平面的X坐标对应旅游开发目标,Y坐标对应生态保护目标。2个目标的适宜性得分区间为[0, 50],即Xmax和Ymax的值为50。利用决策平面进行空间目标划分的过程按照上文4.2的介绍的2个步骤进行。
|
图 5 决策平面初分配与冲突区划分 Fig. 5 Initial allocation of decision space and partition of conflict region |
步骤一,决策平面的初划分(如图 5(a)所示):根据百善镇的实际发展与保护需要,将旅游建设开发目标的适宜得分区间设定为[32,50],将生态环境保护目标的适宜得分区间设定为[25,50],即定区点M的坐标(Xs, Ys)为(32, 25)。在定区点M确定后,决策平面被初步划分为不适宜选项区A、适宜旅游开发目标的非冲突区B、适宜生态保护目标的非冲突区C以及冲突区D。
步骤二,决策平面冲突区的划分(如图 5(b)所示):根据百善镇的实地发展与保护需要,将旅游开发的目标权重wx和生态保护的目标权重wy分别定值为0.4和0.6。此时, wy/wx>1,目标划分线与冲突区的位置属于图 3(c)所示,故选公式(2)对Mi点位置进行确定。经计算Yi=45,即Mi点坐标为(50, 45),冲突区划分线位置如图 5(b)所示。
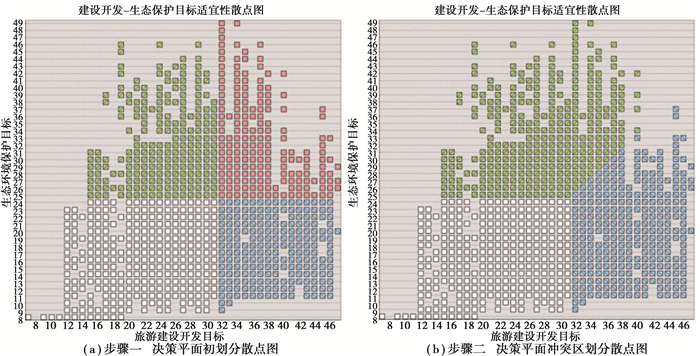
4.6 双目标决策平面与ArcGIS散点图功能的结合在决策平面上将适宜区域完全分配于2个目标之后,通过ArcGIS软件将2个目标的分析图结合(combine)并生成建设开发-生态保护目标的适宜性散点图,如图 6所示,其中步骤一、步骤二所示的散点图分别为决策平面初划分散点图和决策平面冲突区划分散点图。图中的白点、蓝点、绿点和红点区域分别对应决策平面中的不适宜选项区、适宜开发目标的非冲突区、适宜保护目标的非冲突区以及冲突区。决策者可在该散点图模块中对各不同适宜值的点进行按目标归类,该操作使散点对应的空间区域同步地被分配于对应目标,最终实现双目标空间上的用地决策。
|
图 6 百善镇旅游开发和生态保护目标适宜性得分散点图 Fig. 6 Scatters of the suitability score for tourism development and ecological conservation |
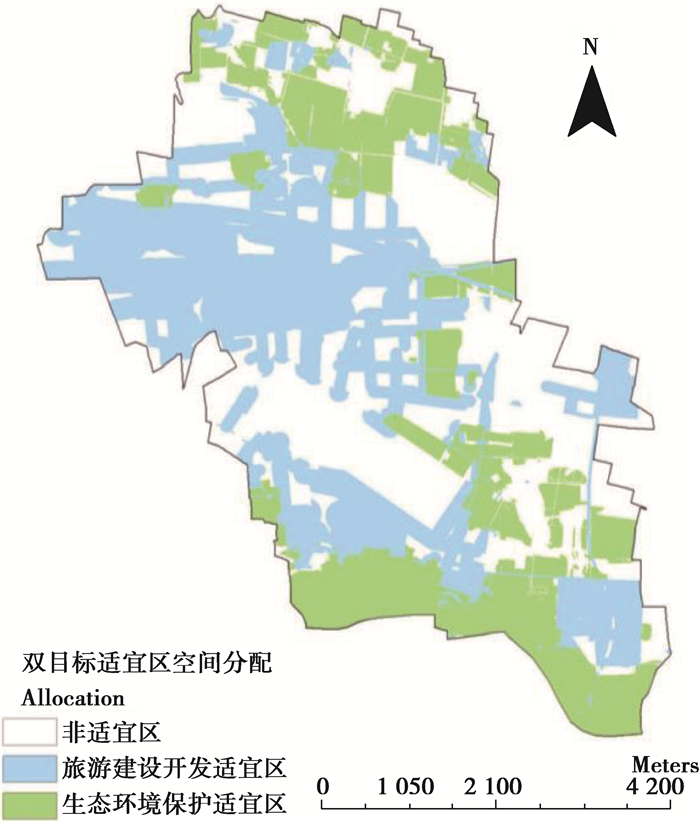
本案例最终的双目标适宜区空间分配如图 7所示。从图中旅游建设开发适宜区与生态环境保护适宜区的分布来看,旅游建设开发适宜区主要分布于交通可达性高、适宜建设的区域,而生态环境保护适宜区主要分布于临近水源、基本农田等生态环境保护价值较高的区域。可见,双目标MCDM决策法使不同的目标用地在空间分布上都具有较为合理的结果,符合经验层面上的决策判断。
|
图 7 百善镇旅游开发与生态保护目标空间分配图 Fig. 7 Spatial allocation of objectives of Tourism development and ecological conservation |
由于现有的多准则决策方法不具备目标决策功能,只能适用于单一目标的多准则决策分析,文中所介绍的基于GIS的双目标多准则决策方法在单目标多准则决策的基础上,增加了决策平面法这一空间目标决策机制,以使多准则决策方法能同时适应2种相互冲突目标的空间决策,一定程度上实现了空间分析决策方法的创新,不但有助于相关理论研究的深入,也体现出一定的实用价值。
1) 在决策流程优化方面,针对现阶段决策平面法存在的决策流程不明确问题,将决策过程划分为决策平面非冲突区初划分和决策平面冲突区划分2个步骤。其中,非冲突区初划分旨在通过确定双目标的适宜与非适宜区间,将决策平面分为4个子区域,并进行相应的目标分配;决策平面冲突区划分则是对初划分中形成的冲突区所进行的划分。这一过程的划分使得决策平面法的决策流程更加明确化和层次化,且易于操作。
2) 在冲突区的划分方面,以冲突区划分的本质——面积划分为切入点,首次提出了通过以目标权重比确定目标在冲突区分得的面积比的方式来确定冲突区划分线的位置,进而完成对冲突区划分的方法,具有一定的方法创新意义。
3) 在实践应用方面,以北京市昌平区百善镇为案例对基于GIS的双目标多准则决策方法进行了应用检验,并演示了通过ArcGIS软件来完成决策平面法的操作过程。经实践操作,该决策方法可有效地与ArcGIS软件结合,完成百善镇域内的旅游开发和生态保护2种目标的空间布局决策,具有一定的实践应用与实际操作价值。目前该方法只适用于双目标多准则决策问题的解决,2种以上的多目标决策问题的解决方法,尚有待进一步研究。
| [1] |
陈晨, 宋小冬, 钮心毅. 土地适宜性评价数据处理方法探讨[J]. 国际城市规划, 2015, 30(1): 70-77. Chen C, Song X D, Niu X Y. Discussion on data processing method of land suitability evaluation[J]. Urban Planning International, 2015, 30(1): 70-77. (in Chinese) |
| [2] |
Watson J J W, Hudson M D. Regional scale wind farm and solar farm suitability assessment using GIS-assisted multi-criteria evaluation[J]. Landscape and Urban Planning, 2015, 138: 20-31. DOI:10.1016/j.landurbplan.2015.02.001 |
| [3] |
方芳, 梁旭, 李灿, 等. 空间多准则决策研究概述[J]. 测绘科学, 2014, 39(7): 9-12, 39. Fang F, Liang X, Li C, et al. Review of spatial multi-criteria decision making[J]. Science of Surveying and Mapping, 2014, 39(7): 9-12, 39. (in Chinese) |
| [4] |
Greene R, Devillers R, Luther J E, et al. GIS-based multiple-criteria decision analysis[J]. Geography Compass, 2011, 5(6): 412-432. DOI:10.1111/j.1749-8198.2011.00431.x |
| [5] |
Nyerges T, Jankowski P. Regional and urban GIS[M]. New York: Guilford Press, 2010.
|
| [6] |
钮心毅. 一种结合GIS的双重目标多准则决策方法及其应用[J]. 地理与地理信息科学, 2008, 24(2): 91-95. Niu X Y. A GIS-based multi-criteria decision making approach for dual objectives and its application[J]. Geography and Geo-Information Science, 2008, 24(2): 91-95. (in Chinese) |
| [7] |
Malczewski J. GIS-based multicriteria decision analysis: a survey of the literature[J]. International Journal of Geographical Information Science, 2006, 20(7): 703-726. DOI:10.1080/13658810600661508 |
| [8] |
Malczewski J, Chapman T, Flegel C, et al. GIS-multicriteria evaluation with ordered weighted averaging(OWA): case study of developing watershed management strategies[J]. Environment and Planning A: Economy and Space, 2003, 35(10): 1769-1784. DOI:10.1068/a35156 |
| [9] |
Laaribi A, Chevallier J J, Martel J M. A spatial decision aid: a multicriterion evaluation approach[J]. Computers, Environment and Urban Systems, 1996, 20(6): 351-366. DOI:10.1016/S0198-9715(97)00002-1 |
| [10] |
Eastman J R, Jin W, Kyem P A K, et al. Raster procedures for multi-criteria/multi-objective decisions[J]. Photogrammetric Engineering & Remote Sensing, 1995, 61(5): 539-547. |
| [11] |
Banai R. Fuzziness in geographical information systems: contributions from the analytic hierarchy process[J]. International Journal of Geographical Information Systems, 1993, 7(4): 315-329. DOI:10.1080/02693799308901964 |
| [12] |
Carver S J. Integrating multi-criteria evaluation with geographical information systems[J]. International Journal of Geographical Information Systems, 1991, 5(3): 321-339. DOI:10.1080/02693799108927858 |
| [13] |
Voogd H. Multicriteria evaluation for urban and regional planning[M]. Delft: Delftsche Uitgevers Maatschappij, 1983.
|
 2021, Vol. 44
2021, Vol. 44


