2. 重庆大学 输配电装备及系统安全与新技术国家重点实验室, 重庆 400044
2. State Key Laboratory of Power Transmission Equipment & System Security and New Technology, Chongqing University, Chongqing 400044, P. R. China
覆冰是一种美丽的自然现象,但对于电网输电线路而言却是一种严重的灾害。对于输电线路导线,覆冰造成的主要问题有:覆冰使得导线负荷增大,导致倒杆、倒塔现象。此外,导线不同期脱冰可导致导线舞动、导线断线、导线相间或对地的短路现象[1-3]。
覆冰形成的首要条件是具有可冻结的气温,即环境温度低于0 ℃。环境温度对覆冰的影响主要体现在覆冰类型和覆冰速率上。不同环境温度下结构物表面形成覆冰种类不同,按照形成条件可以分为:雨凇、硬雾凇、软雾凇、白霜和雪等5类。雨凇发生在低海拔地区,形成气温一般在-2~0 ℃,冰纯粹、透明且坚硬。其密度一般在0.8~0.917 g/cm3,结冰后对结构物的附着力很强。雾凇分为硬雾凇和软雾凇,其形成温度分别在-10~-3 ℃和-13~-8 ℃,硬雾凇密度区间为0.6~0.8 g/cm3,而软雾凇为0.3~0.6 g/cm3,硬雾凇附着力相对软雾凇要强。白霜和雪的形成温度低于-10 ℃,且密度小于0.3 g/cm3,附着力也相对较小。在覆冰速率方面,水滴冻结过程需要向外界释放冻结潜热,潜热释放的效率由对流换热系数决定,对流换热系数越大标志着潜热释放速率越大,即水滴冻结越快,覆冰越快[4-6]。
除温度外,输电线路覆冰还需要满足两个基本条件,第一是空气中有可以冻结为覆冰的过冷却水滴,第二是有风力的作用。风的作用有两点,一方面可以向导线表面运送过冷却水滴,另一方面是带走导线覆冰冻结过程中释放出的潜热,加快覆冰增长[7]。
为能准确掌握输电线路导线覆冰规律,从而可通过监测的环境参数可靠地预测其覆冰增长情况,研究者们提出了相应的统计、理论、数学模型。
Imai[8]于1954年提出导线雨凇覆冰增长模型,模型重点考虑了温度、风速对覆冰增长的影响,但忽略了空气中液态水含量的影响。1955年Lenhard[9]提出的覆冰模型则认为导线覆冰主要由降水形成。
2000年Makkonen[10]对导线覆冰模型涉及的物理过程总结为3个方面,即过冷却水滴和导线表面的碰撞过程;碰撞的过冷却水滴在导线表面被捕获的过程;被捕获的过冷却水滴在导线表面的冻结过程。为计算覆冰速率,Makkonen使用3个系数,即碰撞系数α1、捕获系数α2和冻结系数α3,表征3个物理过程发生的效率。模型要求输入风速、温度、空气中液态水含量及水滴中值体积直径等4项环境参数。但这些参数在实际覆冰条件下实时改变,恶劣的覆冰环境给测量带来极大的困难[11-12]。
现有对导线覆冰的研究主要集中于数值模型的建立和计算,验证手段主要依赖在人工气候室进行的覆冰试验[13-14]。相关的研究发现:自然条件下导线覆冰增长特性和人工试验具有较大的差异[15],包括覆冰速率、形态等。这主要是由于自然环境条件的时变性造成的[16]。为获得自然条件下导线覆冰增长规律,笔者对不同导线进行了自然覆冰试验,积累了大量试验数据,总结了导线自然覆冰增长特性,为改进现有的导线覆冰数值计算模型,建立输电线路覆冰预报、预警机制提供了依据。
1 雪峰山自然覆冰试验 1.1 试验环境条件自然覆冰试验在重庆大学雪峰自然覆冰试验基地进行。如图 1所示,覆冰基地位于湖南省洪江市东部雪峰山脉主峰苏宝顶地域,每年覆冰期内的最低气温达到-15 ℃,风速最大达到35 m/s,年平均降水量为1 500 mm,覆冰厚度最大至500 mm。

|
图 1 重庆大学雪峰山覆冰试验基地 Fig. 1 Xuefeng Mountain icing test base of Chongqing University |
首先采用单短导线进行覆冰试验,单短导线采用相同工艺制作,粗糙度可近似看作相同。不同样品间的差异性主要是导线直径和防冰涂料的有无,具体参数如表 1所示。试验时观测环境条件的变化,覆冰开始后,间隔记录导线迎风侧和背风侧覆冰增长情况,记录数据包括导线覆冰厚度及冰形。
| 表 1 6种短导线基本参数(试验样品) Table 1 The main parameters of 6 different samples |
1号和2号导线覆冰情况如图 2~3所示,导线迎风侧和背风侧的覆冰厚度随着覆冰时间的增加而逐渐增大。覆冰均匀性较差,迎风面覆冰较背风面更为严重,覆冰增长明显。其主要原因是:当气流携带空气中的过冷却水滴绕过导线时,空气的黏滞性导致气流在导线的迎风面被阻滞,从而在导线的背风面形成湍流漩涡;在导线的迎风面,由于过冷却水滴动量大于气流的动量,使得过冷却水滴在惯性作用下与气流分离,在与导线碰撞后形成覆冰。

|
图 2 样品1号线导线表面覆冰厚度 Fig. 2 Icing situation on conductor No. 1 |

|
图 3 样品2号线导线表面覆冰厚度 Fig. 3 Icing situation on conductor No. 2 |
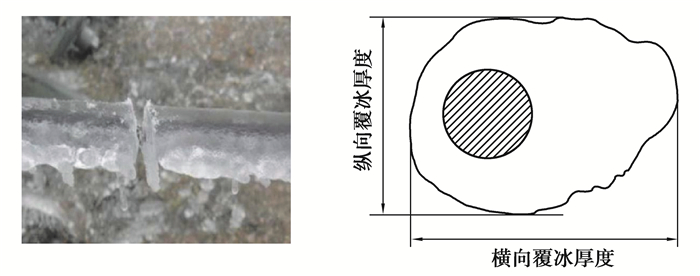
如图 4所示,为了分析雾凇覆冰在导线表面不同方向的增长情况,定义了导线的横轴覆冰增长量和纵轴覆冰增长量。横轴覆冰增长量是导线迎风侧覆冰净增长的长度。纵轴覆冰增长量是与风向垂直的方向覆冰净增长的长度。
|
图 4 导线横向和纵向覆冰厚度 Fig. 4 Horizontal and vertical icing thickness of conductor |
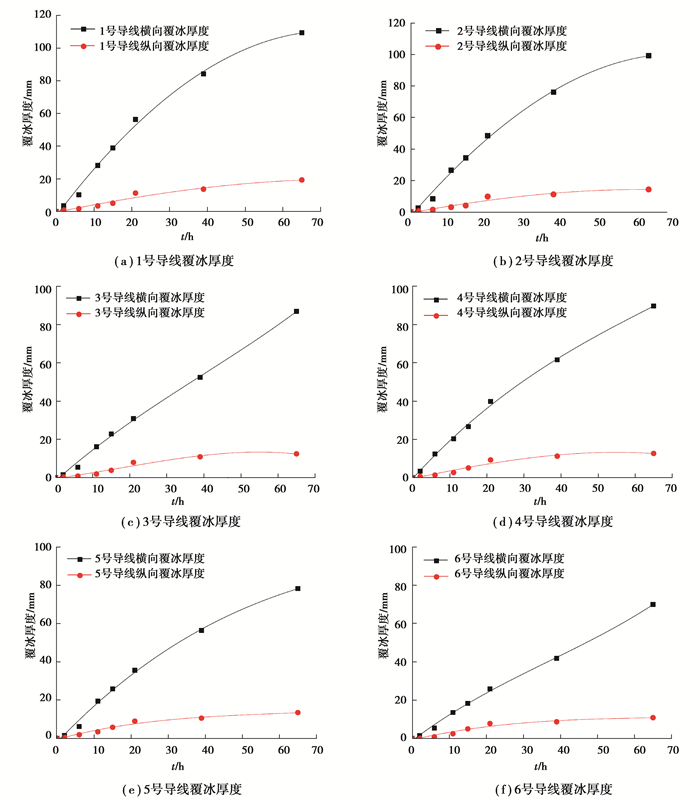
由图 5可知,不同直径的导线横轴、纵轴覆冰增长量均随时间非线性增长。初始时刻增长较快,随着时间增加呈现饱和趋势。由于风速、风向的影响,横轴方向的覆冰增长量明显大于纵轴方向。
|
图 5 6种导线覆冰厚度增长情况(试验值) Fig. 5 Icing thickness of six different conductors (tests) |
1号导线与2号导线直径相同,但是2号导线表面有防冰涂料,对比可发现随着时间的增长,具有防冰涂料的导线其覆冰增长略微慢于无防冰涂料的导线。这表明防冰涂料对导线表面的覆冰增长具有一定的阻碍作用,但效果并不十分明显,这种作用主要体现在覆冰初期,当导线表面有一层覆冰后,涂料的防冰作用基本无体现。
3~6号为无防冰涂料的导线,对比可以发现:不同直径导线的横向覆冰厚度均大于纵向覆冰厚度,直径越小覆冰增长越快,且直径越小的导线,其覆冰增长速率在后期减小的越慢。其原因解释如下:从流体力学角度分析,相对于大直径导线,小直径导线表面的水滴绕流程度小,覆冰增长快。这种绕流程度可通过计算导线表面水滴碰撞系数α1获得[17]。
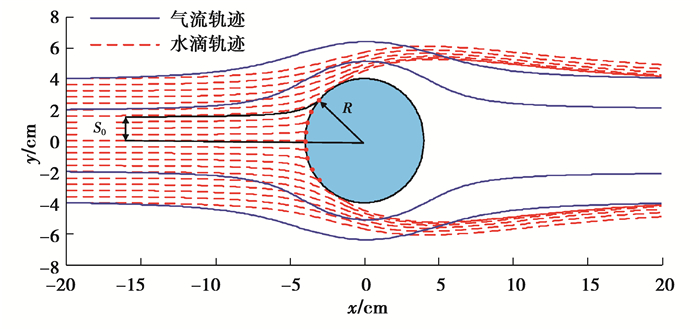
2 导线表面的水滴碰撞系数如图 6所示,若离中心线初始高度为S0的水滴可到达半径为R的导线两端的极限碰撞点,则在该环境条件下导线表面的水滴碰撞系数α1计算式为:
| $ {a_1} = \frac{{{S_0}}}{R}。$ | (1) |
|
图 6 导线表面水滴碰撞系数计算示意图 Fig. 6 Schematic diagram of calculation of water droplet collision coefficient on conductor |
水滴碰撞系数值α1越大,说明水滴在导线表面的绕流程度越低,水滴碰撞导线的效率越高,覆冰增长越快,其计算过程如下。假设水滴以相同运动速度随气流向导线表面运动,忽略水滴自身重量而只考虑气流对水滴的黏性阻力Fd。
| $ {\mathit{\boldsymbol{F}}_{\rm{d}}} = {m_{\rm{w}}}\frac{{{\rm{d}}\mathit{\boldsymbol{v}}}}{{{\rm{d}}t}} = \frac{1}{2}{\rho _{\rm{a}}}{S_{\rm{w}}}{C_{\rm{D}}}\left| {\mathit{\boldsymbol{u}} - \mathit{\boldsymbol{v}}} \right|\left( {\mathit{\boldsymbol{u}} - \mathit{\boldsymbol{v}}} \right), $ | (2) |
式中:mw是水滴质量,kg;Sw是水滴最大横截面积,m2;u、v分别为气流和水滴的二维速度向量,m/s;ρa为空气密度,kg/m3;空气阻尼系数CD。
气流速度可通过求解圆的势函数方程得到,水滴在绕流导线表面的速度及坐标可通过二阶差分算法获得[18]。
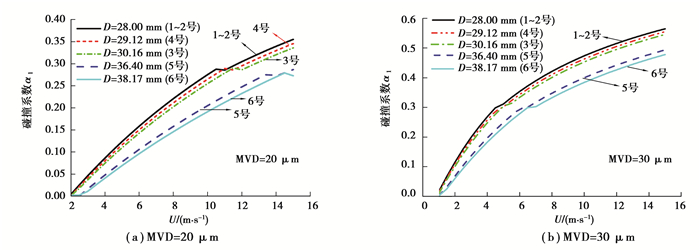
本次覆冰试验为雾凇覆冰,故仿真采用2种典型水滴中值直径(MVD),即20 μm和30 μm[4],计算不同风速条件下6种导线表面的水滴碰撞系数值α1,结果如图 7所示。可以看到,6种导线表面的水滴碰撞系数值均随风速的增大而非线性增长。1~4号导线表面α1值十分相近,且明显高于5号和6号导线,这和前文自然覆冰试验结果相吻合,也再次证明了雾凇覆冰时大直径导线覆冰增长速率小于小直径导线的结论。
|
图 7 不同风速和MVD下6种导线表面水滴碰撞系数 Fig. 7 Collision efficiency of six conductors under different wind velocity and MVD |
与1.2节所述短导线不同,对于输电线路而言,杆塔间的跨度均较大,导线在覆冰过程中并非静止存在,导线在覆冰受力后易发生扭转现象,而导线的扭转又会反作用于其覆冰增长过程。
图 8为1号长导线覆冰增长过程中冰形的变化示意图,随着时间的推移,覆冰越来越严重。在覆冰初期,覆冰主要在迎风侧增长,背风侧覆冰很少。随着覆冰量逐渐增多,导线的扭矩大于刚矩,发生扭转,覆冰出现了分层,导线背风侧逐渐转向迎风侧,导致原来的背风侧的覆冰大量增加,同时使得导线整体覆冰面积增大,进一步提高了覆冰速率。

|
图 8 单长导线(1号)雾凇覆冰冰形变化 Fig. 8 Rime shapes on conductor No. 1 (long) |
导线雨凇覆冰过程和雾凇存在明显差异,观测结果如图 9所示。覆冰初期,导线上覆冰为较薄的雾凇,随着环境条件的改变,导线表面出现水膜,覆冰转为雨凇。

|
图 9 单长导线(1号)雨凇覆冰冰形变化 Fig. 9 Glaze shapes on conductor No. 1 (long) |
从覆冰中期开始,导线上积冰形式变为雨凇。这是由于温度逐渐升高(小于0 ℃),空气中的过冷却水滴直径增大,覆冰条件的改变为雨凇覆冰的形成提供了良好的外部环境。大多数情况下,雨凇是由过冷却水滴或毛毛雨滴发展起来的,即冻雨覆冰。在雨凇覆冰情况下,黏结到导线的水滴完全冻结之前,过冷却水滴的碰撞连续发生,导线表面可以获得过量的过冷却水,过量的水滴在导线表面形成水膜,水膜不断加厚,其影响效应主要有两点:
1) 相对于雾凇覆冰,水膜的存在使得导线覆冰表面光滑,呈现出半透明翼型覆冰冰形。
2) 如图 10所示,当水膜量增大到张力和风力无法维持时,水膜将在重力作用下向导线下表面流动,并在下表面形成滴落的水滴,水滴在滴落过程中又被冻结为冰棱,使得导线雨凇覆冰冰形变得更为复杂。

|
图 10 导线雨凇覆冰时形成的冰棱 Fig. 10 Icicles under conductor during glaze icing |
针对不同型式的导线开展了自然环境覆冰试验,研究了自然条件下导线覆冰增长特性,结果表明:
1) 自然环境条件下,风速对导线雾凇覆冰冰形起决定性作用,覆冰主要在导线迎风面(横向迎风侧)累积,而背风侧和纵向覆冰较少。
2) 导线雾凇覆冰时一般易形成翼型覆冰冰形,覆冰厚度随时间呈现非线性增长。导线直径越小,覆冰厚度增长越快。
3) 导线表面水滴碰撞系数值准确反映了导线直径和覆冰厚度增长特性的关系,导线直径越小,水滴碰撞系数值越大,覆冰效率越高。
4) 长导线覆冰时,覆冰易造成导线扭转,扭转导线背风侧向迎风侧转变,覆冰出现分层,导线覆冰面积增大,增长速率大幅提升。
5) 导线雨凇覆冰时,覆冰表面易形成未冻结的水膜,水膜的存在使得覆冰表面更为光滑,而水膜的流动会在导线下方形成冻结的冰棱,使得导线雨凇覆冰冰形更为复杂。
| [1] |
罗剑波, 郁琛, 谢云云, 等. 关于自然灾害下电力系统安全稳定防御方法的评述[J]. 电力系统保护与控制, 2018, 46(6): 158-170. Luo J B, Yu C, Xie Y Y, et al. A review on risk assessment of power grid security and stability under natural disasters[J]. Power System Protection and Control, 2018, 46(6): 158-170. (in Chinese) |
| [2] |
蒋兴良, 张丽华. 导线覆冰碰冻率及最大覆冰直径分析[J]. 中国电机工程学报, 1999, 19(9): 10-13. Jiang X L, Zhang L H. Collision & freezing efficiency of droplets with conductor and the possible maximum diameter of the iced conductor[J]. Proceedings of the CSEE, 1999, 19(9): 10-13. (in Chinese) DOI:10.3321/j.issn:0258-8013.1999.09.003 |
| [3] |
He Q, Zhang J, Deng M Y, et al. Rime icing on bundled conductors[J]. Cold Regions Science and Technology, 2019, 158: 230-236. DOI:10.1016/j.coldregions.2018.08.027 |
| [4] |
蒋兴良, 舒立春, 孙才新. 电力系统污秽与覆冰绝缘[M]. 北京: 中国电力出版社, 2009. Jiang X L, Shu L C, Sun C X. Insulation of electric power system under pollution and icing conditions[M]. Beijing: China Electric Power Press, 2009. (in Chinese) |
| [5] |
蒋兴良, 易辉. 输电线路覆冰及防护[M]. 北京: 中国电力出版社, 2002. Jiang X L, Yi H. Icing and protection of transmission lines[M]. Beijing: China Electric Power Press, 2002. (in Chinese) |
| [6] |
王守礼, 李家垣. 云南高海拔地区电线覆冰问题研究[M]. 昆明: 云南科技出版社, 1993. Wang S L, Li J Y. Study on the problem of wire icing at high altitude in Yunnan Province[M]. Kun Ming: Yunnan Science and Technology Press, 1993. (in Chinese) |
| [7] |
蒋兴良. 输电线路导线覆冰机理和三峡地区覆冰规律及影响因素研究[D]. 重庆: 重庆大学, 1997. Jiang X L. Study on icing mechanism of overhead transmission line and icing performance in the Three Gorges District[D]. Chongqing: Chongqing University, 1997. (in Chinese) |
| [8] |
Imai I. Studies on ice accretion[J]. Researches on Snow and Ice, 1954, 3(1): 35-44. |
| [9] |
Lenhard R W Jr. An indirect method for estimating the weight of glaze on wires[J]. Bulletin of the American Meteorological Society, 1955, 36(1): 1-5. DOI:10.1175/1520-0477-36.1.1 |
| [10] |
Makkonen L. Models for the growth of rime, glaze, icicles and wet snow on structures[J]. Philosophical Transactions of the Royal Society of London Series A: Mathematical, Physical and Engineering Sciences, 2000, 358(1776): 2913-2939. DOI:10.1098/rsta.2000.0690 |
| [11] |
Fu P, Farzaneh M, Bouchard G. Two-dimensional modelling of the ice accretion process on transmission line wires and conductors[J]. Cold Regions Science and Technology, 2006, 46(2): 132-146. DOI:10.1016/j.coldregions.2006.06.004 |
| [12] |
Fu P, Bouchard G, Farzaneh M. Simulation of ice accumulation on transmission line cables based on time-dependent airflow and water droplet trajectory calculations[C]//Proceedings of OMAE04 23rd International Conference on Offshore Mechanics and Arctic Engineering, June 20-25, 2004, Vancouver, British Columbia, Canada. ASME, 2008: 971-977.
|
| [13] |
刘春城, 刘佼. 输电线路导线覆冰机理及雨凇覆冰模型[J]. 高电压技术, 2011, 37(1): 241-248. Liu C C, Liu J. Ice accretion mechanism and glaze loads model on wires of power transmission lines[J]. High Voltage Engineering, 2011, 37(1): 241-248. (in Chinese) |
| [14] |
郭昊, 刘沛清, 屈秋林, 等. 输电线雾凇覆冰的工程估算方法[J]. 高电压技术, 2011, 37(4): 1041-1049. Guo H, Liu P Q, Qu Q L, et al. Estimation engineering method of rime accretion process on transmission lines[J]. High Voltage Engineering, 2011, 37(4): 1041-1049. (in Chinese) |
| [15] |
蒋兴良, 姜方义, 汪泉霖, 等. 基于最优时间步长模型的输电导线雾凇覆冰预测[J]. 电工技术学报, 2018, 33(18): 4408-4418. Jiang X L, Jiang F Y, Wang Q L, et al. Prediction of rime accretion on transmission line based on optimal time step model[J]. Transactions of China Electrotechnical Society, 2018, 33(18): 4408-4418. (in Chinese) |
| [16] |
蒋兴良, 申强. 环境参数对导线覆冰厚度影响的试验分析[J]. 高电压技术, 2010, 36(5): 1096-1100. Jiang X L, Shen Q. Experimental research on influence of environmental parameters on the conductor icing thickness[J]. High Voltage Engineering, 2010, 36(5): 1096-1100. (in Chinese) |
| [17] |
汪泉霖. 输电线路导线无扭转覆冰过程的仿真实验方法研究[D]. 重庆: 重庆大学, 2018. Wang Q L. Study on the simulation experiment method of ice accretion on transmission line without torsion[D]. Chongqing: Chongqing University, 2018. (in Chinese) |
| [18] |
陈凌. 旋转圆柱体覆冰增长模型与线路覆冰参数预测方法研究[D]. 重庆: 重庆大学, 2011. Chen L. Study on model of ice accretion on rotating cylinder and method for forecasting icing parameters during icing on transmission lines[D]. Chongqing: Chongqing University, 2011. (in Chinese) |
 2021, Vol. 44
2021, Vol. 44


