2. 重庆大学 电气工程学院, 重庆 400044
2. School of Electrical Engineering, Chongqing University, Chongqing 400044, P. R. China
配电网承担着向用户分配电能的重要职责,其可靠性水平决定了电力系统能否满足用户用电需求。据电力公司统计,约80%的用户停电由配电网故障所致[1],因此,配电网可靠性评估在电力系统可靠性中有非常重要的地位。
配电网可靠性评估对配电网的规划和检修等有重要的指导价值。目前,电力公司的配电网可靠性评估方法通常基于某类配电设备的历史平均故障率,经过数学运算获得配电网可靠性指标[2]。该方法的缺陷是未考虑同类设备间的差异性与设备状态的时效性,使配电网可靠性评估脱离实际情况。而基于设备状态监测量评估设备健康状态,可以有效反应配电设备的差异性与时效性,大幅提高配电网可靠性评估的准确度[3-4]。
目前关于配电网可靠性评估的研究可以分为两类:1)配电设备可靠性评估;2)配电网系统可靠性评估[5]。
配电设备可靠性评估是配电网可靠性评估的基础。文献[6-10]中分析了设备的健康指数与设备故障率的关系曲线,以计算设备的故障率。栗然等[11]基于设备的服役年龄和检修记录计算设备的健康指数,该研究反映了设备状态的差异性与时效性,但未考虑设备所处环境及运行状态对设备健康状态的影响。顾佳浩等[12]基于设备在线状态监测量对健康指标进行排序并赋予相应的指标权重,但设定的健康指数权重受主观因素影响。
系统可靠性评估是将设备可靠性指标转化为系统负荷点可靠性指标的方法。顾佳浩等[12]和Billinton等[13]基于FMEA通过串并联分析得到负荷点的故障率与修复率,该方法存在维数灾。为简化运算,韦婷婷[14]和黄辉[15]依据开关划分网络等效区域,减小了计算量。史常凯等[10]和许林成[16]基于最小路法,求系统最小路集,将设备分为最小路设备和非最小路设备,并将非最小路设备等效到最小路上,该方法效率虽高于FMEA,但对非最小路设备的分析较为复杂。
为了合理有效地评估配电系统可靠性,笔者提出了综合考虑检修策略和设备健康指数的配电网可靠性评估方法,其思路如下:首先基于logistic回归模型计算配电设备的健康指标权重与健康指数[4, 17];依据设备健康指数与故障率的函数关系计算设备可用率;最后基于最小路法与故障枚举法[18-19]枚举设备故障状态,计算各故障状态的概率、负荷点的故障率与停电时间,并获得配电网整体的缺电量指标。
1 基于logistic回归模型的健康指数评估方法 1.1 健康指数与设备状态的关系配电网健康指数理论是一种模仿人体健康评价的配电网可靠性评估方法,主要应用于各类配电网规划、检修计划等[1]。健康指数理论将现场设备的实时状态监测数据按照一定数学规则进行组合,得到评价设备状况的实时健康指数。设备健康指数可以有效反应设备实时状态,支持配电系统的可靠性评估,提高电网整体运行管理水平[3]。根据文献[1]和[4],基于健康指数H获得设备的实时故障率,H的取值范围为0~5,健康指数越高,设备健康状态越好。
将设备健康状态划分为5级:1)4≤H≤5,设备各指标合格且处于充裕的状态,可以在符合运行要求的环境下执行全部功能;2)3≤H < 4,设备各指标合格,但部分指标已经逼近极限且不充裕的状态,功能齐全;3)2≤H < 3,设备有轻度缺陷,设备部分指标越限,抗风险能力减小,尚可执行功能,需要小修;4)1≤H < 2,设备有严重缺陷,设备尚能执行功能,但性能严重退化,对应指标大幅度越限,需要大修;5)0 < H < 1,设备有危急缺陷,设备无法正常执行功能,需要大修或更换。
1.2 健康指数的关键特征量选取关键特征量的选取应根据设备主要故障因素,基于科学、可行、全面、简洁原则进行选取[4, 20]。变压器故障的主要原因是设备本体老化、外力因素和运行维护不当。架空线路主要由导线、塔杆、绝缘子部分构成。架空导线故障因素主要有外在条件、运维因素和设备本体等因素;塔杆故障因素主要有外来影响和设备本体因素;绝缘子故障仅有本体因素影响。电缆的主要部件是电缆本体、终端以及接头,其中电缆本体导致的故障占比最高,达64.4%。除以上3类主要设备外还可以根据实际情况考虑断路器、母线、分段开关等设备的故障情况。
1.3 基于Logistic回归的配电设备健康指数计算基于logistic回归改进的健康指数计算模型利用设备实时状态监测量计算设备健康指数,避免了人为设置指标权重的主观性。记第i设备(变压器或线路)的状态监测量实测数据集为Xi=[xi, 1,xi, 2,…,xi, j,…,xi, R],i=1, 2, …, N,N为需评估的设备总数;记第j种状态监测量加权系数集为βj=[β1, j,β2, j,…,βN, j],j=1, 2, …, R,R为设备状态监测量个数;i、j、R和N均为自然数。
综合考虑设备各类状态检测量存在的量纲与数量级的差异性对状态检测量进行标准化处理[12]。将状态监测量分为愈小愈好(ω=-1),愈大愈好(ω=1),中间优型(ω=0)共3种类型,如式(1)所示:
| $ h_{i, j}=\left\{\begin{aligned} &\mathrm{e}^{-\frac{\left(x_{i, j}-x_{i, j}^{\min }\right)^{2}}{2\left(x_{i, j}^{\max }-x_{i, j}^{\min }\right)^{2}}}, \quad x_{i, j} \in\left[x_{i, j}^{\min }, x_{i, j}^{\max }\right], \omega=-1 ; \\ &\mathrm{e}^{-\frac{\left(x_{i, j}^{\max }-x_{i, j}\right)^{2}}{2\left(x_{i, j}^{\max }-x_{i, j}^{\min }\right)^{2}}}, \quad x_{i, j} \in\left[x_{i, j}^{\min }, x_{i, j}^{\max }\right], \omega=1;\\ &\left\{\begin{array}{l} \mathrm{e}^{-\frac{\left(x_{i, j}-x_{i, j}^{\rm{o}}\right)^{2}}{2\left(x_{i, j}^{\max }-x_{i, j}^{\rm{o}}\right)^{2}}}, \quad x_{i, j} \in\left[x_{i, j}^{\rm{o}}, x_{i, j}^{\max }\right], \omega=0 ; \\ \mathrm{e}^{-\frac{\left(x_{i, j}-x_{i, j}^{\rm{o}}\right)^{2}}{2\left(x_{i, j}^{\rm{o}}-x_{i, j}^{\min }\right)^{2}}}, \quad x_{i, j} \in\left[x_{i, j}^{\min }, x_{i, j}^{\rm{o}}\right], \omega=0; \end{array}\right. \\ &0, \quad \text { 其他。} \end{aligned}\right. $ | (1) |
式中:hi, j为设备i的第j个状态检测量的健康指标,xi, jmax、xi, jmin、xi, jo分别为设备i的j状态监测量的最大、最小与最优值。
设备i的健康指数Hi如下式所示:
| $ \left\{\begin{array}{l} H_{i}=5 \sum\limits_{j=1}^{R} \beta_{i, j} h_{i, j}; \\ \sum\limits_{j=1}^{R} \beta_{i, j}=1。\end{array}\right. $ | (2) |
式中:hi, j和βi, j分别表示第i设备的第j状态监测量的健康指标和加权系数。
利用最大似然估计法计算健康指数的logistic回归模型参数。配电设备的健康指数可以视作在第k样本的关键特征量参数的健康指标hi, j, k(k=1,…,Nk, )作用下令yk=1的条件概率(yk=1表示第k样本的设备正常,yk=0表示设备失效)。Nk为设备关键特征量的样本数量;βi, 0决定logistic函数的水平位置。βi(i=1, …, N)的似然函数及其对数形式如下:
| $ L=\prod\limits_{k=1}^{N_{k}}\left[\left(\frac{1}{\left.1+\mathrm{e}^{-\left(\beta_{i}, 0+\sum\limits_{j=1}^{R} \beta_{i, j} h_{i, j, k}\right.}\right)}\right)^{y_{k}}\left(\frac{1}{1+\mathrm{e}^{\left(\beta_{i}, 0+\sum\limits_{j=1}^{R} \beta_{i, j }h_{i, j, k}\right)}}\right)^{\left(1-y_{k}\right)}\right] ; $ | (3) |
| $ \ln L=\sum\limits_{k=1}^{N_{k}}\left[y_{k}\left(\beta_{i, 0}+\sum\limits_{j=1}^{R} \beta_{i, j} h_{i, j, k}\right)-\ln \left(1+\mathrm{e}^{\left(\beta_{i}, 0+\sum\limits_{j=1}^{R} \beta_{i, j }h_{i, j, k}\right)}\right)\right]。$ | (4) |
利用最大似然估计法确定参数βi,即通过求解式(4)中L为最大值时对应的参数βi, j的值。
最后根据式(2)计算设备健康指数集合H=[H1,H2,…,Hi,…,HN]。
2 基于健康指数理论的配电网可靠性评估 2.1 基于健康指数的设备故障概率首先计算设备的故障率λ,设备故障率与健康指数H的关系如下[21]:
| $ \lambda(t)=K(t) \mathrm{e}^{-H(t) C(t)} $ | (5) |
式中:K(t)为t时刻下设备故障曲线的比例系数;C(t)为t时刻下设备故障曲线的曲率系数。
通常情况下比例系数K(t)与曲率系数C(t)无法直接通过故障曲线得到,因此需要通过其他方法对这2类系数进行计算。最常用的方法是依据设备的平均故障率λ及最小故障率λmin进行计算。平均故障率由设备的历史故障数据取得,最小故障率取平均故障率的10%~20% [6, 12]。通常假设λ对应的Hconst=4,λmin对应的Hmin=5,K与C的计算公式如下:
| $ \left\{\begin{array}{l} C=\ln \left(\bar{\lambda} / \lambda_{\min }\right) /\left(H_{\min }-H_{\text {const }}\right) \\ K=\bar{\lambda} \mathrm{e}^{{H} \text { const } C} \end{array}\right. $ | (6) |
计算设备i的可用率Pi(t)及不可用率Qi(t)[11]:
| $ \left\{\begin{array}{l} P_{i}(t)=\frac{\mu_{i}}{\lambda_{i}(t)+\mu_{i}}, \\ Q_{i}(t)=\frac{\lambda_{i}(t)}{\lambda_{i}(t)+\mu_{i}}。\end{array}\right. $ | (7) |
式中:λi(t)表示设备i的故障率;μi=1/ri表示设备i的修复率;ri表示设备i的故障修复时间。
2.2 运行方案在设备故障或检修时,其影响的不仅是本身线路的安全性,还会降低网络整体的可靠性。考虑到配电网多是环网结构辐射状运行,基于图论与最小路法,利用布尔行列式求解负荷点的最小路集,枚举配电网在各种情况下的可行运行方案以及失负荷点[17, 22]。
首先制作包含有向支路的n节点配电网的接线图,将配电网从u节点到v节点的支路记做lu, v,支路的方向是从电源到负载的方向,若不满足该条件则令lu, v=0。然后建立网络图的邻接矩阵C:
| $ \boldsymbol{C}=\left[\begin{array}{cccc} 0 & l_{12} & & l_{1 n} \\ l_{21} & 0 & & l_{2 n} \\ & & \ddots & \\ l_{n 1} & l_{n 2} & & 0 \end{array}\right]。$ | (8) |
建立与C同行列的单位矩阵U,并获得矩阵C+U。选择本次计算的输入节点uin与输出节点uout,去掉有输入节点的列与有输出节点的行,获得布尔行列式S:
| $ |\boldsymbol{S}|=\left|\begin{array}{cccc} 1 & l_{1,2} & & l_{1, n-1} \\ l_{2,1} & 1 & & l_{2, n-1} \\ & & \ddots & \\ l_{n-1,1} & l_{n-1,2} & & 1 \end{array}\right|。$ | (9) |
求解该行列式,即获得从输入节点uin到输出节点uout的最小路集Suin, uout。
已知最小路集,即可利用最小路集及可动作开关集枚举出电网的全部运行方案。设该电网的现行检修计划下系统存在的可能检修状态有Nm种。然后计算正常运行状态以及第m检修状态下,nf个故障设备在发生失效时(nf=0, 1, …, N,m=0, 1, …, Nm,m=0代表正常运行状态,f=0代表非故障状态。)所对应的故障状态和失效故障数量Nm, f为
| $ N_{m, f}=C_{N}^{0}+C_{N}^{1}+\cdots+C_{N}^{n_{f}}。$ | (10) |
式中:CN0、CN1和CNnf表示不同的失效状态组合数。考虑到多个设备同时故障的概率极小,为减小运算量,只计算nf<3的场景。
基于最小路集Suin, uout,列出在第m检修状态,第f故障状态下的可行第y运行方案,并依据TLOC准则[18],列出切掉的负荷点uout。y=1, 2, 3, …, Ny。
2.3 系统可靠性配电网系统可靠性计算分为两个部分,分别为各检修状态下处于故障状态时对应的概率和各状态下的失负荷节点及其失负荷量,下面进行详细介绍。
设备在规划时间段内第m检修状态下处于第f故障状态时对应的概率pm, f及频率Fm, f按下式计算:
| $ \left\{\begin{array}{l} p_{m, f}=\frac{T_{m}}{8\ 760} \prod\limits_{b=1}^{n_{f}} Q_{b} \prod\limits_{d=1}^{n-n_{f}-n_{m}} P_{d} ; \\ F_{m, f}=p_{m, f}\left(\sum\limits_{b=1}^{n_{f}} \mu_{b}+\sum\limits_{d=1}^{n-n_{f}-n_{m}} \lambda_{d}\right)。\end{array}\right. $ | (11) |
式中:nf为第f故障状态所对应的失效设备数量,nm为第m检修状态下正在检修的设备数量,f=1, 2, …, Nm, f,Nm, f为故障状态数;Qb和Pd分别为第b设备和第d设备对应的不可用率与可用率;μb和λd分别为第b设备和第d设备对应的修复率与故障率,b=1, 2, …, nf,d=1, 2, …, n-nf-nm;Tm为第m检修状态在一年中存在的小时数;pm, f的含义是该状态下的失负荷量及失负荷时间在指标中的权重。
计算各状态下的失负荷节点及其失负荷量[23-25]。首先计算在第m检修状态、第f故障状态下运行方案y的系统失负荷量Pm, f, yloss,然后选择其中总失负荷量最小的运行方案作为最优运行方案,记录其失负荷点集合Lm, ffail⊆O与失负荷量Pm, floss、修复时间rm, f及每个负荷节点u∈O的失负荷量Pm, f, uloss; O为负荷点集合。
| $ \left\{\begin{array}{l} P_{m, f}^{\text {loss }}=\min \left\{P_{m, f, y}^{\text {loss }}\right\}, y=1,2, \cdots, N_{y}; \\ P_{m, f}^{\text {loss }}=\sum\limits_{u \in O}^{n} P_{m, f, u}^{\text {loss }} ; \\ r_{m, f}=\sum\limits_{b=1}^{n_{f}} r_{b} / M。\end{array}\right. $ | (12) |
式中:rb为第b设备的修复时间,b=1, 2, …, nf;M为抢修班能同时抢修的设备总数。
最后结合以上两部分内容,计算负荷点u的可用率Au、故障频率Fu、故障时间Du、缺供电量Eu、系统平均供电可用率ASAI、系统平均停电频率SAIFI、系统平均停电时间SAIDI和系统电量不足指标ENSI。
| $ A_{u}=1-\frac{\sum\limits_{m=0}^{N_{m}} \sum\limits_{f=1}^{N f} p_{m, f}}{8\ 760}, \quad u \in L_{m, f}^{\text {fail }} $ | (13) |
| $ F_{u}=\frac{\sum\limits_{m=0}^{N_{m}} \sum\limits_{f=1}^{N f} F_{m, f}}{8\ 760}, \quad u \in L_{m, f}^{\text {fail }}; $ | (14) |
| $ D_{u}=\frac{\sum\limits_{m=0}^{N_{m}} \sum\limits_{f=1}^{N_{f}} f_{m, f} r_{m, f}}{8\ 760}, \quad u \in L_{m, f}^{\mathrm{fail}}; $ | (15) |
| $ E_{u}=\frac{\sum\limits_{m=0}^{N_{m}} \sum\limits_{f=1}^{N{f}} p_{m, f} P_{m, f, u}^{\operatorname{loss}}}{8\ 760}, \quad u \in L_{m, f}^{\operatorname{fail}}; $ | (16) |
| $ \left\{\begin{array}{l} \mathrm{ASAI}=\sum\limits_{u \in O} A_{u} N_{u}^{\mathrm{c}} / \sum\limits_{u \in O} N_{u}^{\mathrm{c}}; \\ \mathrm{SAIFI}=\sum\limits_{u \in O} F_{u} N_{u}^{\mathrm{c}} / \sum\limits_{u \in O} N_{u}^{\mathrm{c}}; \\ \mathrm { SAIDI }=\sum\limits_{u \in O} D_{u} N_{u}^{\mathrm{c}} / \sum\limits_{u \in O} N_{u}^{\mathrm{c}}; \\ \mathrm{ENSI}=\sum\limits_{u \in O} E_{u} 。\end{array}\right. $ | (17) |
式中:Nuc为负荷点u的用户数;u∈Lm, ffail表示式子中仅计算令负荷点u失负荷的第m检修状态和第f故障状态。
2.4 求解过程综合考虑检修策略与设备健康指数的配电网可靠性评估的研究步骤简述如下。
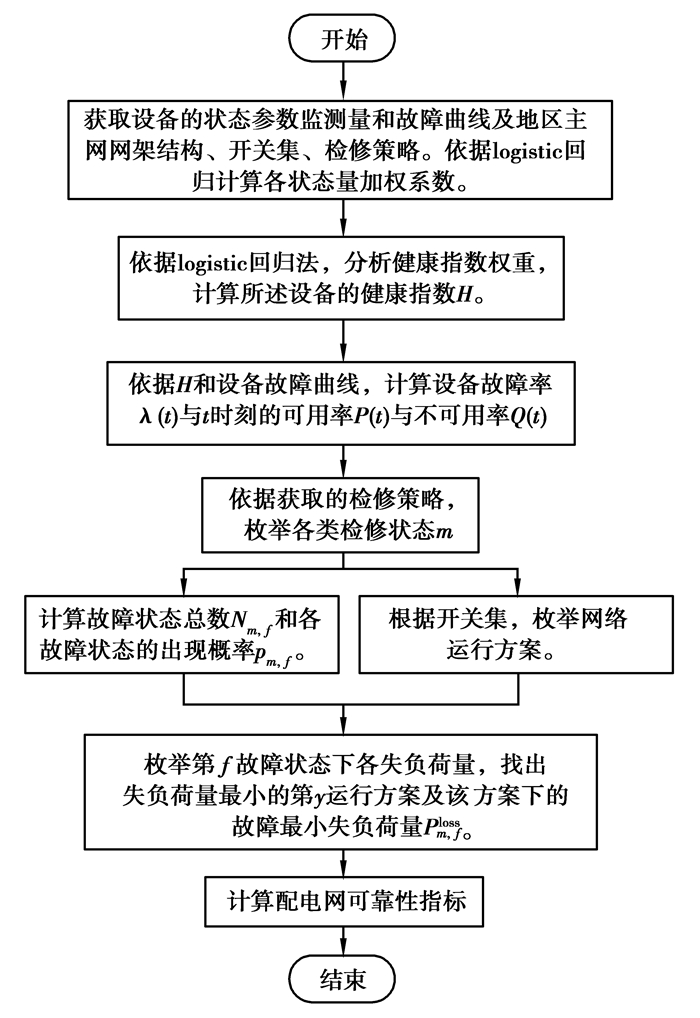
首先根据设备实时状态检测数据按照logistic回归模型求解设备健康指数;然后基于健康指数与设备故障率的函数关系计算设备的故障率、可用率与不可用率;根据现行的检修策略枚举网络各检修状态下的故障状态并计算其出现概率,同时根据图论求解负荷点最小路,枚举网络可用运行方案;最后计算故障状态下可用运行方案的失负荷量,选其中系统失负荷量最小的运行方案,记录其失负荷点与失负荷量,计算列出各状态最小失负荷运行方案下的失负荷点与失负荷量。详细求解过程如图 1所示。
|
图 1 可靠性评估流程 Fig. 1 Reliability assessment process |
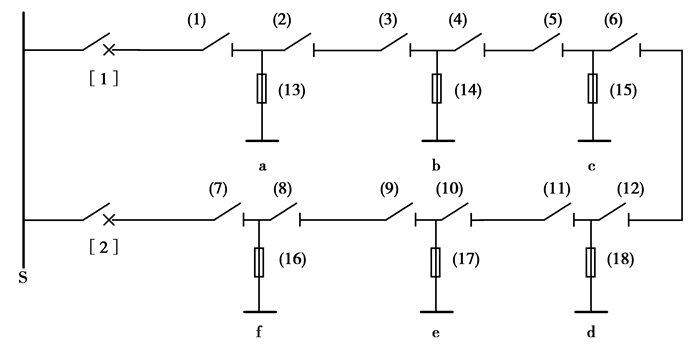
为了验证所提方法的有效性,利用中国南方某地区10 kV电网的负荷数据、设备参数、检修计划和网架结构等信息,评估分析该系统在检修计划影响下的可靠性水平。该配电网共有6个负荷节点和6台10 kV变压器,网架结构如图 2所示。在可靠性评估时只考虑变压器故障,并假设断路器、母线、分段开关动作可靠率为100%。
|
图 2 配电网网架结构 Fig. 2 Distribution network structure |
根据设备状态检测量的历史数据,采用logistic回归模型,根据式(2)~(4)计算设备健康指数及其健康指标权重。设备健康指数的指标权重如表 1所示,设备的实时采样数据与最后算出的健康指数如表 2所示。j=1, 2, 3, 4分别代表油酸值(以滴定1 g油品所需的氢氧化钾质量表示,单位mg/g)、油击穿电压(kV)、油溶解气体含量(μg/g)和油糠醛浓度(mg/kg)。
| 表 1 状态监测量的加权系数βj Table 1 Weighting coefficient βj of condition monitoring quantity |
| 表 2 状态监测量j与设备i的健康指数Hi Table 2 Condition monitoring quantity j and health index Hi of equipment i |
由上表可见,logistic回归模型合理设定了指标权重,准确计算了设备的健康指数,反映了设备的健康状态。然后依据式(5)(6)健康指数与故障率的关系,假设设备最小故障率λmin为设备平均故障率λ的20%,计算设备故障率,根据式(7)计算设备的可用率与不可用率,结果如表 3所示。
| 表 3 设备可用率与不可用率 Table 3 Reliability and unreliability of equipment |
1) 枚举系统运行方案
根据式(8)(9),建立配电网络的邻接矩阵,将其变形为输入节点uin到输出节点uout的布尔行列式,并求解布尔行列式,即得uin到uout的最小路集,并据此枚举该配电网不失负荷的可用开环运行方案,如表 4所示。
| 表 4 系统运行方案 Table 4 System operation scheme |
2) 枚举检修状态下的故障状态
首先枚举各类检修状态下的故障状况,根据式(11)计算相应故障状态概率;然后基于表 4结合故障状态将应该切断的开关置0,获得该故障状态下的运行方案及失负荷节点;最后根据式(12)计算各负荷点的失负荷量。表 5只列出1号变压器停电检修时的故障状态。
| 表 5 检修状态1下的故障状态 Table 5 Fault states in maintenance state 1 |
3) 计算可靠性评价指标
选取系统平均供电可用率ASAI、系统平均停电频率SAIFI、系统平均停电时间SAIDI和系统电量不足指标ENSI作为可靠性评价指标。因为没有取得系统的负荷点用户数数据,故假设Nuc=1(u=a, b, c, d, e, f)。根据式(13)~(16)计算负荷点可靠性指标,结果如下表所示。
| 表 6 负荷点可靠性指标 Table 6 Reliability index of load points |
然后根据式(17)计算系统可靠性指标:系统平均供电可用率ASAI=99.995 4%,系统平均每户停电频率SAIFI=0.002 2 a-1,系统平均每户停电时间SAIDI=0.405 6 h·a-1,系统电量不足指标ENSI=466.079 8 kW·h·a-1。
3.2.3 不考虑健康指数的可靠性评估为了进一步分析健康指数对配电网可靠性评估的作用,在故障率计算中不考虑健康指数,基于历史平均故障率计算设备可用率与不可用率。表 7给出了不考虑健康指数时的负荷点可靠性指标。
| 表 7 不考虑健康指数的负荷点可靠性指标 Table 7 Reliability index of load points without considering health index |
系统平均供电可用率ASAI=99.995 4%,系统平均每户停电频率SAIFI=0.000 055 6 a-1,系统平均每户停电时间SAIDI=0.085 1 h·a-1,系统电量不足指标ENSI=130.406 0 kW·h·a-1。
通过上述评估结果可以看出,当不考虑设备健康指数时,结果明显高估了配电网整体的可靠性水平,且负荷点之间的数据非常接近。这是因为利用历史平均故障率求得的设备可用率忽略了设备的差异性,无法反应设备实际状态,导致配电网可靠性的评估过于乐观。结果表明本文中提出的配电网可靠性评估方法可以有效反应设备的实时健康状态,有效评估网络的负荷点及配电系统的可靠性指标,有利于量化检修计划造成的额外故障风险和查寻系统中的薄弱环节。
4 结论基于健康指数理论和系统可靠性评估准则,提出了一种综合考虑检修策略和设备健康指数的配电网可靠性评估方法,利用中国南方某地区10 kV电网进行了仿真分析。结果表明在评估配电网可靠性时,依据配电网状态监测量评估设备健康状态,可以体现出设备之间的差异性,准确反应设备的状态。本文中提出的方法可以有效评估配电网的整体可靠性,找出配电网络中的薄弱环节,为改善配电网的运行方式、网络结构、检修策略等提供依据,提高了电力系统的运行可靠性。
| [1] |
刘亚民. 供电可靠性指标统计、预测和规划算法的探讨[J]. 现代电力, 2001, 18(1): 20-26. Liu Y M. A study of the reliability indexes statistic, forecasting and planning algorithms for the power supply[J]. Modern Electric Power, 2001, 18(1): 20-26. (in Chinese) DOI:10.3969/j.issn.1007-2322.2001.01.004 |
| [2] |
万东. 配电网可靠性及经济性评估方法研究[D]. 南昌: 南昌大学, 2015. Wan D. Reliability and economy evaluation study on distribution network[D]. Nanchang: Nanchang University, 2015. (in Chinese) |
| [3] |
周莉梅, 马钊, 盛万兴. 现代配电网健康指数理论最新研究进展[J]. 供用电, 2016, 33(1): 3-7, 13. Zhou L M, Ma Z, Sheng W X. Recent development of health index theory for modern distribution network[J]. Distribution & Utilization, 2016, 33(1): 3-7, 13. (in Chinese) |
| [4] |
马钊, 周莉梅, 袁海文, 等. 现代配电网健康指数理论及其应用研究[J]. 中国电机工程学报, 2019, 39(1): 130-140, 328. Ma Z, Zhou L M, Yuan H W, et al. Health index methodology of modern distribution network and its application[J]. Proceedings of the CSEE, 2019, 39(1): 130-140, 328. (in Chinese) |
| [5] |
赵洪山, 赵航宇. 配电网可靠性评估方法研究现状与展望[J]. 现代电力, 2015, 32(5): 15-20. Zhao H S, Zhao H Y. Current status and prospect of reliability evaluation method for distribution network[J]. Modern Electric Power, 2015, 32(5): 15-20. (in Chinese) DOI:10.3969/j.issn.1007-2322.2015.05.003 |
| [6] |
Ma Z, Shang Y W, Yuan H W, et al. Holistic performance evaluation framework: power distribution network health index[J]. IET Generation, Transmission & Distribution, 2017, 11(9): 2184-2193. |
| [7] |
Zuo W J, Yuan H W, Shang Y W, et al. Calculation of a health index of oil-paper transformers insulation with binary logistic regression[J]. Mathematical Problems in Engineering, 2016, 2016: 1-9. |
| [8] |
李二霞, 亢超群, 李玉凌, 等. 基于设备状态评价和电网损失风险的配电网检修计划优化模型[J]. 高电压技术, 2018, 44(11): 3751-3759. Li E X, Kang C Q, Li Y L, et al. Optimization model of distribution network maintenance plan based on equipment condition evaluation and grid loss risk[J]. High Voltage Engineering, 2018, 44(11): 3751-3759. (in Chinese) |
| [9] |
汤雪松, 刘贞, 王洪授, 等. 配电设备故障率分析及检修决策[J]. 绿色科技, 2018(20): 191-192. Tang X S, Liu Z, Wang H S, et al. Failure rate analysis and maintenance decision of distribution equipment[J]. Journal of Green Science and Technology, 2018(20): 191-192. (in Chinese) |
| [10] |
史常凯, 宁昕, 孙智涛, 等. 基于设备实时健康指数的配电网风险量化评估[J]. 高电压技术, 2018, 44(2): 534-540. Shi C K, Ning X, Sun Z T, et al. Quantitative risk assessment of distribution network based on real-time health index of equipment[J]. High Voltage Engineering, 2018, 44(2): 534-540. (in Chinese) |
| [11] |
栗然, 王飞飞, 李增辉. 基于风险评估的配电网检修决策优化[J]. 电力自动化设备, 2013, 33(11): 1-8. Li R, Wang F F, Li Z H. Maintenance decision making optimization based on risk assessment for distribution system[J]. Electric Power Automation Equipment, 2013, 33(11): 1-8. (in Chinese) DOI:10.3969/j.issn.1006-6047.2013.11.001 |
| [12] |
顾佳浩, 淡淑恒. 考虑HI理论和在线监测误差的配电网可靠性评估[J/OL]. 电力系统及其自动化学报: 1-8[2020-09-03]. https://doi.org/10.19635/j.cnki.csu-epsa.000570. Gu J H, Dan S H. Reliability evaluation of distribution network considering HI theory and online monitoring error[J/OL]. Proceedings of the CSU-EPSA: 1-8[2020-09-03]. https://doi.org/10.19635/j.cnki.csu-epsa.000570. (in Chinese) |
| [13] |
Billinton R, Wang P. Reliability-network-equivalent approach to distribution-system-reliability evaluation[J]. IEE Proceedings—Generation, Transmission and Distribution, 1998, 145(2): 149-153. DOI:10.1049/ip-gtd:19981828 |
| [14] |
韦婷婷. 中压配电网可靠性评估若干问题研究[D]. 重庆: 重庆大学, 2016. Wei T T. Research on several problems of reliability assessment of medium voltage distribution networks[D]. Chongqing: Chongqing University, 2016. (in Chinese) |
| [15] |
黄辉. 配电网络可靠性分析与优化研究[D]. 南昌: 南昌大学, 2017. Huang H. Studies on analysis and optimization of distribution network reliability[D]. Nanchang: Nanchang University, 2017. (in Chinese) |
| [16] |
许林成. 10kV配电网供电可靠性研究[D]. 河北秦皇岛: 燕山大学, 2016. Xu L C. Research on power reliability of 10kV distribution network[D]. Qinhuangdao, Hebei: Yanshan University, 2016. (in Chinese) |
| [17] |
郭化诚. 基于健康指数的配电网检修计划及决策优化方法研究[D]. 北京: 华北电力大学, 2018. Guo H C. Research on distribution network maintenance scheduling optimization based on health index[D]. Beijing: North China Electric Power University, 2018. (in Chinese) |
| [18] |
钟文磊. 计及分布式电源配电网可靠性分析研究[D]. 南昌: 南昌大学, 2018. Zhong W L. Research on reliability analysis of distributed power distribution network[D]. Nanchang: Nanchang University, 2018. (in Chinese) |
| [19] |
江归安. 配电网络可靠性评估研究[D]. 南昌: 南昌大学, 2014. Jiang G A. The reliability assessment of the distribution system[D]. Nanchang: Nanchang University, 2014. (in Chinese) |
| [20] |
王荣. 基于设备健康指数的配电网络状态评价方法的研究[D]. 西安: 西安理工大学, 2019. Wang R. Research into power distribution network condition evaluation method based on equipment health index[D]. Xi'an: Xi'an University of Technology, 2019. (in Chinese) |
| [21] |
江归安. 中高压配电网络可靠性评估优化算法[J]. 新余学院学报, 2019, 24(1): 29-32. Jiang G A. Optimization algorithm for medium and high voltage distribution network reliability evaluation[J]. Journal of Xinyu University, 2019, 24(1): 29-32. (in Chinese) DOI:10.3969/j.issn.2095-3054.2019.01.007 |
| [22] |
段青, 赵阅群, 颜磊, 等. 以提高供电可靠性为目标的主动配电网负荷转供优化方法[J]. 电网技术, 2016, 40(10): 3155-3162. Duan Q, Zhao Y Q, Yan L, et al. Load transfer optimization methods for distribution network including distribution generation[J]. Power System Technology, 2016, 40(10): 3155-3162. (in Chinese) |
| [23] |
王步云. 计及储能控制策略的有源配电网可靠性评估[J]. 自动化与仪器仪表, 2018(11): 198-202. Wang B Y. Considering energy storage control strategy for active distribution network reliability evaluation[J]. Automation & Instrumentation, 2018(11): 198-202. (in Chinese) |
| [24] |
李蕊, 李跃, 苏剑, 等. 配电网重要电力用户停电损失及应急策略[J]. 电网技术, 2011, 35(10): 170-176. Li R, Li Y, Su J, et al. Power supply interruption cost of important power consumers in distribution network and its emergency management[J]. Power System Technology, 2011, 35(10): 170-176. (in Chinese) |
| [25] |
陈健. 重要电力用户典型供电模式可靠性与经济性评估及分析方法研究[D]. 武汉: 华中科技大学, 2015. Chen J. Reliability and economic evaluation of important power consumer feeding mode and its assessment[D]. Wuhan: Huazhong University of Science and Technology, 2015. (in Chinese) |
 2021, Vol. 44
2021, Vol. 44


