2. 重庆大学 电气工程学院, 重庆 400044
2. School of Electrical Engineering, Chongqing University, Chongqing 400044, P. R. China
蒙特卡罗仿真(MCS)因其灵活性和易于实现性在大规模电网可靠性评估中受到广泛关注[1]。MCS的收敛性主要取决于系统可靠性水平,对于高可靠性系统,为达到给定仿真精度所需样本容量通常较大,导致仿真时间很长,而方差削减技术则成为加快MCS仿真效率的有效手段。
重要抽样(IS)法是一种广为关注的高效方差削减技术,它通过改变随机变量的概率密度函数(PDF),使得对电网停电风险起重要作用的系统状态更易被抽取,从而实现电网可靠性MCS的速度显著提升[2]。优化求取重要抽样概率密度函数(IS-PDF)的参数是IS取得良好加速性能的关键,如果求取的IS-PDF参数不合适则可能导致相反效果,降低仿真效率。近年来,交叉熵法(CEM)因其在MCS中的高效加速效果而备受关注。CEM首先被用于发电系统充裕性评估[3-5],然后被进一步应用于旋转备用充裕性评估[6-7]、组合系统充裕性评估[8-14]和短期运行风险评估[15-17]。
CEM的核心思路为:由于理论上的最优IS-PDF(即零方差PDF)无法获取,退而求其次,可求取与理论最优IS-PDF之间的交叉熵(衡量两个PDF相似性的指标)最小的PDF作为实际的IS-PDF。将交叉熵概念引入电网可靠性的MCS后,可有效克服原始MCS收敛慢的缺陷。在现有研究中,CEM法采用迭代算法实现对IS-PDF的参数寻优,每次迭代都随机抽取固定数量(即预抽样样本数)的系统状态进行系统性能评估,并将其中不良系统状态用于IS-PDF的参数迭代计算。一方面多次反复迭代导致较大的计算成本;另一方面如果每次迭代所设定的预抽样样本数偏小,则在初始几次迭代中难以保证抽取到数量足够的不良系统状态,导致参数迭代更新效率偏低,迭代次数增加,而设定的预抽样样本数偏大时,计算成本会显著增加。
针对这一问题,提出一种全新的IS-PDF参数求取方法,对实际IS-PDF参数进行直接解析求取,避免传统CEM法中的耗时迭代过程。具体思路包括:首先将每个系统故障状态的理论最优IS-PDF表达成含元件最优无效度和元件原始无效度的非线性等式方程;由于系统故障状态数量庞大,建立的等式方程数量太多,导致难以通过求解非线性方程组获取元件最优无效度,为此进一步引入最小割集概念对系统故障状态进行合并,大大削减方程数量;最后,由于满足理论最优IS-PDF的元件最优无效度并不存在,建立的非线性方程组实际上并无准确解,因此对非线性方程组采用最小二乘估计实现元件最优无效度的有效估计。
1 最优IS-PDF的最小割集等式方程组对于一个包含w个元件的电力系统,以xi表示元件i的状态,xi=0表示正常,xi=1表示故障,则系统状态可表示为x=(x1, x2, …, xw)。若各元件的随机故障相互独立,则系统状态x的原始PDF为:
| $ f(\boldsymbol{x} ; \boldsymbol{u})=\prod\limits_{i=1}^{w}\left[u_{i} x_{i}+\left(1-u_{i}\right)\left(1-x_{i}\right)\right], $ | (1) |
式中:u=(u1, u2, …, uw)表示原始概率密度函数f(x; u)的参数,ui为元件i的原始无效度。电网的故障概率pF(即失负荷概率)可用下式进行无偏估计:
| $ p_{\mathrm{F}}=E_{f}(H(\boldsymbol{x}))=\int_{\boldsymbol{\varOmega}} H(\boldsymbol{x}) f(\boldsymbol{x} ; \boldsymbol{u}) \mathrm{d} \boldsymbol{x} \approx \frac{1}{N} \sum\limits_{i=1}^{N} H\left(x_{i}\right)。$ | (2) |
式中:H(x)为系统性能测度函数,如果x是失负荷状态,则H(x)=1,反之,H(x)=0;Ef(·)表示在概率密度函数f(x; u)下求数学期望;Ω为系统状态空间;N为估计pF所需的样本容量;xi为通过原始f(x; u)随机抽取到的第i个系统状态。
为加快电网可靠性评估的速度,IS法采用重要抽样PDF,即使用g(x; v)来进行系统状态的随机抽取,则pF的估计公式如下:
| $ p_{\mathrm{F}}=E_{\mathrm{g}}(H(\boldsymbol{x}) W(\boldsymbol{x} ; \boldsymbol{u}, \boldsymbol{v})) \approx \frac{1}{N} \sum\limits_{i=1}^{N}\left[H\left(x_{i}\right) W\left(x_{i} ; \boldsymbol{u}, \boldsymbol{v}\right)\right]。$ | (3) |
式中:xi为采用g(x; v)随机抽取的第i个系统状态;W(x; u, v)=f(x; u)/g(x; v)为似然比函数,作用在于保证式(3)的期望值估计具有无偏性,即当N→∞时,pF的估计不会因抽样函数的改变而出现偏离。g(x; v)通常采用与f(x; u)相同的函数形式:
| $ g(\boldsymbol{x} ; \boldsymbol{v})=\prod\limits_{i=1}^{w}\left[v_{i} x_{i}+\left(1-v_{i}\right)\left(1-x_{i}\right)\right]。$ | (4) |
当g(x; v)满足式(5)时,式(3)的统计量具有零方差,此时的g(x; v)即为理论最优IS-PDF,v为理论上的最优IS-PDF参数,即元件最优无效度向量。
| $ g_{\mathrm{op}}(\boldsymbol{x} ; \boldsymbol{v})=\frac{H(\boldsymbol{x}) f(\boldsymbol{x} ; \boldsymbol{u})}{p_{\mathrm{F}}}, \boldsymbol{x} \in \boldsymbol{\varOmega}。$ | (5) |
事实上理论最优IS-PDF只是理论存在,首先pF是未知的待估计量;其次即使pF已知,也不存在一个无效度向量v=(v1, v2, …, vw)恰好满足式(5)。因此寻求一个无效度向量v=(v1, v2, …, vw),使得g(x; v)和H(x)f(x; u)/pF充分接近,则成为可行的技术思路。
CEM以交叉熵(又名Kullback-Leible距离)D(gop, g)来衡量H(x)f(x; u)/pF和g(x; v)的相似性:
| $ D\left(g_{\text {op }}, g\right)=\int_{\boldsymbol{\varOmega}}\left(\frac{H(\boldsymbol{x}) f(\boldsymbol{x} ; \boldsymbol{u})}{p_{\mathrm{F}}}\right) \ln \left(\left(\frac{H(\boldsymbol{x}) f(\boldsymbol{x} ; \boldsymbol{u})}{p_{\mathrm{F}}}\right) / g(\boldsymbol{x} ; \boldsymbol{v})\right) \mathrm{d} \boldsymbol{x}。$ | (6) |
对式(6)最小化以求取参数v,简化后如式(7):
| $ \boldsymbol{v}=\arg \min\limits _{\boldsymbol{v}} \int_{\boldsymbol{\varOmega}}-H(\boldsymbol{x}) f(\boldsymbol{x} ; \boldsymbol{u}) \ln (g(\boldsymbol{x} ; \boldsymbol{v})) \mathrm{d} \boldsymbol{x}。$ | (7) |
上式的等效形式如下:
| $ \boldsymbol{v}=\arg \max\limits _{\boldsymbol{v}} \int_{\boldsymbol{\varOmega}} H(\boldsymbol{x}) f(\boldsymbol{x}, \boldsymbol{u}) \ln g(\boldsymbol{x}, \boldsymbol{v}) \mathrm{d} \boldsymbol{x}。$ | (8) |
将式(8)的积分公式离散化后可得:
| $ \boldsymbol{v} \cong \arg \max\limits _{\boldsymbol{v}} \frac{1}{N_{0}} \sum\limits_{i=1}^{N_{0}} H\left(x_{i}\right) \ln g\left(x_{i}, \boldsymbol{v}\right), $ | (9) |
式中N0为进行参数优化所需的样本容量。要从f(x; u)中抽取足够数量满足H(xi)=1的xi效率极低,尤其所评估的系统可靠性很好时。为此,CEM采用迭代优化求解思路,即对式(9)再次应用重要抽样思想,并在首次迭代时以原始f(x; u)作为重要抽样函数,而在第k次迭代时将第k-1次迭代求得的g(x, vk-1)作为重要抽样函数,如式(10)所示,其中xi从g(x, vk-1)抽取:
| $ v_{k} \cong \arg \max \limits_{v_{k}} \frac{1}{N_{0}} \sum\limits_{i=1}^{N_{0}} H\left(x_{i}\right) W\left(x_{i}, \boldsymbol{u}, v_{k-1}\right) \ln g\left(x_{i}, v_{k}\right)。$ | (10) |
基于式(10)可推导出如下的vk计算公式,其中xi, j为系统状态xi中第j个元件所处的状态(1为故障,0为正常):
| $ v_{k, j}=1-\frac{\sum\limits_{i=1}^{N_{0}} H\left(x_{i}\right) W\left(x_{i}, \boldsymbol{u}, v_{k-1}\right) x_{i, j}}{\sum\limits_{i=1}^{N_{0}} H\left(x_{i}\right) W\left(x_{i}, \boldsymbol{u}, v_{k-1}\right)}, \quad j=1,2, \cdots, w。$ | (11) |
由上述可见,CEM每次迭代都需要随机抽取N0个系统状态,即xi (1≤i≤N0),并对每个xi进行潮流或最优负荷削减计算以判断H(xi)的取值,导致计算成本较高。为避免迭代求解带来的较大计算成本,提出如下参数解析寻优方法。
设Ωf和Ωs分别表示故障和正常系统状态子空间,则理论最优IS-PDF可表示为:
| $ g_{\text {op }}(\boldsymbol{x} ; \boldsymbol{v})=\left\{\begin{array}{l} \frac{f(\boldsymbol{x} ; \boldsymbol{u})}{p_{\mathrm{F}}}, \quad \boldsymbol{x} \in \boldsymbol{\varOmega}_{\mathrm{f}} ;\\ 0, \quad \boldsymbol{x} \in \boldsymbol{\varOmega}_{\mathrm{s}} \end{array}\right. $ | (12) |
可知在理论最优IS-PDF下,正常系统状态的概率变为零,而故障系统状态的概率则按1/pF的比例线性增长。假设式中的pF可用一个预估值来近似,则任意一个故障系统状态x∈ΩF都满足下式:
| $ \prod\limits_{i=1}^{w}\left[v_{i} x_{i}+\left(1-v_{i}\right)\left(1-x_{i}\right)\right]=\frac{\prod\limits_{i=1}^{w}\left[u_{i} x_{i}+\left(1-u_{i}\right)\left(1-x_{i}\right)\right]}{p_{\mathrm{F}}} 。$ | (13) |
对所有x∈ΩF均建立式(13)的非线性等式方程,则可以得到一个含待求参数v的方程组,该方程组所含方程个数等于故障系统状态的数目。由于属于ΩF的故障系统状态数量庞大,一方面不可能也没必要识别出所有属于ΩF的x,另一方面即使能完全识别,庞大的非线性方程数目也将导致无法求解。为此引入最小割集概念解决上述难题。割集是一组元件的集合,当它们失效时会导致系统故障,而引起系统故障的失效元件集中的最小子集称为最小割集。
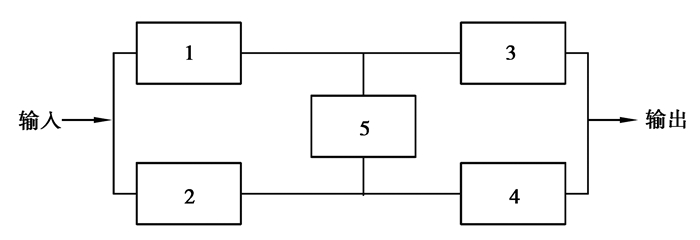
事实上每个最小割集可代表一系列系统故障状态。以图 1的5元件系统为例,Θ={1, 4, 5}为三阶最小割集,即当x1=x4=x5=1时,无论元件2、3处于何种状态组合(注:元件2和3的状态组合共4种),系统都会处于故障状态,可见Θ涵盖了4个引起系统失效的元件状态组合。
|
图 1 用于阐释最小割集概念的5元件系统 Fig. 1 A system with 5 elements for illustrating the concept of the minimum cutset |
推而广之,如果某电网总元件数为w,且元件都为2状态Markov模型,则任意一个k阶最小割集Θ可表征2w-k个引起系统失效的元件状态组合,而对于其中第d个元件状态组合,所有属于Θ的元件其状态必然为1,即有xd, i=1,∀i∈Θ,故参考式(13)可列出如下等式方程:
| $ \prod\limits_{i \in \boldsymbol{\varTheta}} v_{i} \cdot \prod\limits_{j=1 \atop j \notin \boldsymbol{\varTheta}}^{w}\left[v_{j} x_{d, j}+\left(1-v_{j}\right)\left(1-x_{d, j}\right)\right]=\frac{1}{p_{\mathrm{F}}} \prod\limits_{i \in \boldsymbol{\varTheta}} u_{i} \cdot \prod\limits_{j=1 \atop j \notin \boldsymbol{\varTheta}}^{w}\left[u_{j} x_{d, j}+\left(1-u_{j}\right)\left(1-x_{d, j}\right)\right]。$ | (14) |
上述方程可列写出2w-k个,所有方程相加可得:
| $ \prod\limits_{i \in \boldsymbol{\varTheta}} v_{i} \cdot \sum\limits_{d=1}^{2 w-k} \prod\limits_{j=1 \atop j \notin \boldsymbol{\varTheta}}^{w}\left[v_{j} x_{d, j}+\left(1-v_{j}\right)\left(1-x_{d, j}\right)\right]=\frac{1}{p_{\mathrm{F}}} \prod\limits_{i \in \boldsymbol{\varTheta}} u_{i} \cdot \sum\limits_{d=1}^{2 w-k} \prod\limits_{j=1 \atop j \notin \boldsymbol{\varTheta}}^{w}\left[u_{j} x_{d, j}+\left(1-u_{j}\right)\left(1-x_{d, j}\right)\right]。$ | (15) |
考虑到下式成立:
| $ \sum\limits_{d=1}^{2 w-k} \prod\limits_{j=1 \atop j \notin \boldsymbol{\varTheta}}^{w}\left[v_{j} x_{d, j}+\left(1-v_{j}\right)\left(1-x_{d, j}\right)\right]=\sum\limits_{d=1}^{2 w-k} \prod\limits_{j=1 \atop j \notin \boldsymbol{\varTheta}}^{w}\left[u_{j} x_{d, j}+\left(1-u_{j}\right)\left(1-x_{d, j}\right)\right]=1, $ | (16) |
式(15)可简化如下:
| $ \prod\limits_{i \in \boldsymbol{\varTheta}} v_{i}=\frac{1}{p_{\mathrm{F}}} \prod\limits_{i \in \boldsymbol{\varTheta}} u_{i}。$ | (17) |
系统中能够辨识出的n个最小割集Θk (1≤k≤n)都满足式(17),由此得到方程组(18),即最优IS-PDF的最小割集等式方程组,这是求取元件最优无效度v的重要理论公式。采用此方法,可将方程数目由最初等于故障系统状态数降低为最小割集数,从而有效减少了方程数目,降低了方程组求解难度。
| $ \left\{\begin{array}{l} \prod\limits_{i \in \boldsymbol{\varTheta}_{1}} v_{i}=\frac{1}{p_{\mathrm{F}}} \prod\limits_{i \in \boldsymbol{\varTheta}_{1}} u_{i} ; \\ \prod\limits_{i \in \boldsymbol{\varTheta}_{2}} v_{i}=\frac{1}{p_{\mathrm{F}}} \prod\limits_{i \in \boldsymbol{\varTheta}_{2}} u_{i} ;\\ \cdots \\ \prod\limits_{i \in \boldsymbol{\varTheta}_{n}} v_{i}=\frac{1}{p_{\mathrm{F}}} \prod\limits_{i \in \boldsymbol{\varTheta}_{n}} u_{i} \end{array}\right. $ | (18) |
为建立方程组(18),需要事先知道n个最小割集Θk (1≤k≤n),因此首要问题是如何以较小的计算成本搜索和辨识出Θk (1≤k≤n)。对于复杂大电网,采用传统的最小通路法[18]进行最小割集的辨识效率较低。考虑到高阶最小割集事件的识别所需计算成本较高,同时高阶最小割集事件的出现概率远小于低阶最小割集,在元件最优无效度的计算中其影响也远小于低阶最小割集,因此基于最小割集的基本概念,采用解析枚举的方式对最小割集事件进行识别。首先根据计算成本要求事先给定故障元件的最高枚举阶数(即同时故障的最大元件数)R,然后执行以下最小割集辨识算法:
① 初始化:设置最小割集数n1=0,r=1。
②对只有第j (1≤j≤w)个元件故障的1阶事件进行潮流或最优潮流计算,若该事件引起电网失负荷,则该事件是1阶最小割集事件,令n1=n1+1, Θn1={j}。所有1阶事件分析完毕后,令r=r+1。
③ 如果r>R,则最小割集搜索完毕,令n=n1,算法结束,反之转步骤④。
④ 对每个r阶元件故障事件分别进行潮流或最优潮流计算,由故障元件的编号构成集合Ψ。若该r阶事件引起电网失负荷,则判断是否存在某个Θk (1≤k≤n1)使得Θk⊂Ψ,如果存在,则Ψ不是最小割集事件,反之令n1=n1+1, Θn1=Ψ。当所有r阶事件分析完毕后,令r=r+1,转步骤③。
在求取系统的最小割集之后,还需预估系统失负荷概率pF的数值,否则式(18)无法求解。由可靠性评估理论可知,失负荷概率pF可由最小割集事件表示为:
| $ \begin{gathered} p_{\mathrm{F}}=P\left(\boldsymbol{\varTheta}_{1} \cup \boldsymbol{\varTheta}_{2} \cdots \cup \boldsymbol{\varTheta}_{n}\right)=P\left(\boldsymbol{\varTheta}_{1}\right)+P\left(\boldsymbol{\varTheta}_{2}\right)+\cdots+P\left(\boldsymbol{\varTheta}_{n}\right)-\left(P\left(\boldsymbol{\varTheta}_{1} \cap \boldsymbol{\varTheta}_{2}\right)+\cdots+\right. \\ \left.P\left(\boldsymbol{\varTheta}_{n-1} \cap \boldsymbol{\varTheta}_{n}\right)\right) \cdots(-1)^{n-1}\left(P\left(\boldsymbol{\varTheta}_{1} \cap \boldsymbol{\varTheta}_{2} \cdots \cap \boldsymbol{\varTheta}_{n}\right)\right)。\end{gathered} $ | (19) |
式中:P(Θk)为最小割集Θk出现的概率,符号∩表示最小割集事件同时(交叠)出现。上式为pF的理论计算公式,在实际计算时,由于最小割集事件交叠的组合数太多,采用该式计算pF虽然理论可行,但非常烦琐和费时。为克服这一缺陷,应用如下近似计算方法,即分别按(20)和(21)估计失负荷概率pF的上界和下界。
| $ \bar{p}_{\mathrm{F}} \approx \sum\limits_{j=1}^{n} P\left(\boldsymbol{\varTheta}_{j}\right)=\sum\limits_{j=1}^{n} \prod\limits_{i \in \boldsymbol{\varTheta}_{j}} u_{i}; $ | (20) |
| $ \underline{p}{}_{\mathrm{F}} \approx \sum\limits_{j=1}^{n} P\left(\boldsymbol{\varTheta}_{j}\right)-\sum\limits_{j, k=1 \atop j<k}^{n} P\left(\boldsymbol{\varTheta}_{j} \cap \boldsymbol{\varTheta}_{k}\right)。$ | (21) |
如果一个系统中元件的可靠性都较好,则多个Θk交叠出现的可能性很小,即使忽略交叠也不会导致较大误差,此时可直接采用式(20)的上界估计。如果考虑多个(例如2个)Θk同时发生的可能,可采用式(20)和式(21)的平均值来近似估计。
如第1节所述,式(5)的gop(x; v)只是理论存在,并不存在一个参数v=(v1, v2, …, vw)能恰好满足式(5),故由式(5)衍生出的方程组(18)无精确解。为此,采用最小二乘估计,通过式(18)的非线性方程组对v进行近似估计。首先将式(18)按下式转换为线性方程组:
| $ \left\{\begin{array}{l} \sum\limits_{i \in \boldsymbol{\varTheta}_{1}} \ln v_{i}=\sum\limits_{i \in \boldsymbol{\varTheta}_{1}} \ln u_{i}-\ln \left(p_{\mathrm{F}}\right) ; \\ \sum\limits_{i \in \boldsymbol{\varTheta}_{2}} \ln v_{i}=\sum\limits_{i \in \boldsymbol{\varTheta}_{2}} \ln u_{i}-\ln \left(p_{\mathrm{F}}\right) ; \\ \boldsymbol{\cdots} \\ \sum\limits_{i \in \boldsymbol{\varTheta}_{n}} \ln v_{i}=\sum\limits_{i \in \boldsymbol{\varTheta}_{n}} \ln u_{i}-\ln \left(p_{\mathrm{F}}\right) \end{array}\right. $ | (22) |
将方程组(22)的求解转化为最小二乘估计问题:
| $ \min \limits_{\boldsymbol{v}} S=\sum\limits_{k=1}^{n}\left(\sum\limits_{i \in \boldsymbol{\varTheta}_{k}} \ln v_{i}-\left(\sum\limits_{i \in \boldsymbol{\varTheta}_{k}} \ln u_{i}-\ln \left(p_{\mathrm{F}}\right)\right)\right)^{2}。$ | (23) |
式中S为误差平方和。
定义H为“最小割集-元件关联矩阵”,且矩阵阶数为n×w。H中的行对应最小割集,而列对应元件,例如第k行表示最小割集Θk,若某元件i属于Θk,即i∈Θk,则第k行第i列的元素H(k, i)=1,除此外第k行其余元素都为零。
式(22)可用矩阵形式表示为:
| $ \boldsymbol{H} \boldsymbol{y}=\boldsymbol{b}; $ | (24) |
| $ \boldsymbol{y}=\ln \boldsymbol{v}=\left[\ln v_{1}, \ln v_{2}, \cdots, \ln v_{w}\right]^{\mathrm{T}}; $ | (25) |
| $ \boldsymbol{b}=\boldsymbol{H} \cdot \ln \boldsymbol{u}-\boldsymbol{E} \cdot \ln \left(p_{\mathrm{F}}\right)。$ | (26) |
式中E为w阶单位对角阵。
最小二乘估计问题的矩阵表达形式为:
| $ \min \limits_{\boldsymbol{y}} S=(\boldsymbol{H} \boldsymbol{y}-\boldsymbol{b})^{\mathrm{T}}(\boldsymbol{H} \boldsymbol{y}-\boldsymbol{b})。$ | (27) |
在极值点处梯度为零,即$\partial S/\partial \mathit{\boldsymbol{y}} = 0$,则有:
| $ \boldsymbol{H}^{\mathrm{T}} \boldsymbol{H} \boldsymbol{y}-\boldsymbol{H}^{\mathrm{T}} \boldsymbol{b}=0。$ | (28) |
对上式的线性方程组进行求解,可解得y,并进而得到v:
| $ \boldsymbol{y}=\left(\boldsymbol{H}^{\mathrm{T}} \boldsymbol{H}\right)^{-1} \boldsymbol{H}^{\mathrm{T}} \boldsymbol{b}; $ | (29) |
| $ \boldsymbol{v}=\mathrm{e}^{\boldsymbol{y}}。$ | (30) |
利用本节方法可估计属于最小割集中的元件的最优无效度,但某些对系统可靠性指标贡献很小的元件,可能未曾出现在任何一个搜索到的最小割集中,此类元件其最优无效度可取为原始无效度。
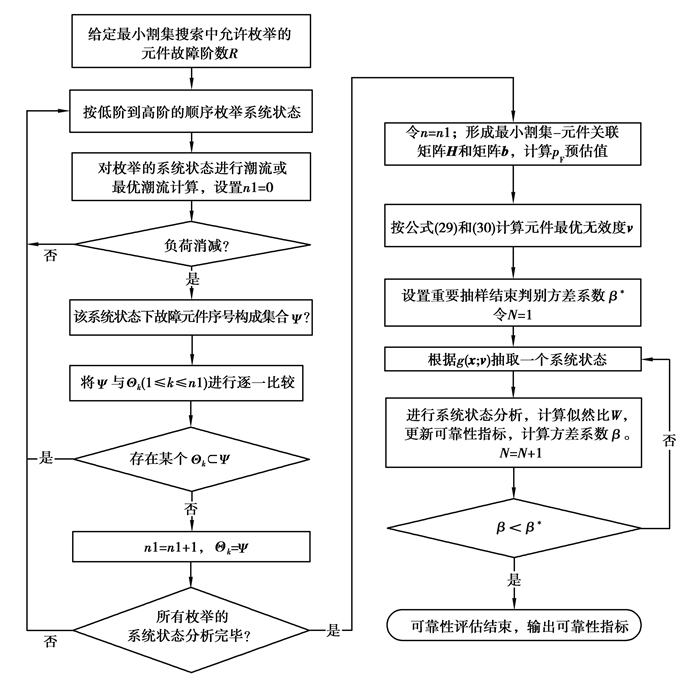
3 基于参数解析寻优的重要抽样算法流程基于参数解析优化,即基于最小割集辨识和最小二乘估计实现v的优化求取,然后采用重要抽样进行电网可靠性的仿真计算,整个过程分为2个环节:1)参数优化环节:搜寻n个Θk (1≤k≤n)并建立式(24)~(26),由式(30)得到IS-PDF的参数v;2)主抽样环节:以g(x; v)为抽样函数,随机抽取N个系统状态,并判断每个系统状态是否失负荷以及负荷削减量,更新可靠性指标统计量。流程图见图 2,详细步骤如下。
|
图 2 基于参数解析寻优的电网可靠性重要抽样算法 Fig. 2 Algorithm description for the proposed IS method |
① 初始化:输入电网元件的电气参数和原始无效度u以及网络拓扑等数据,设置允许阶数R,并令N=i=1。
② 依据上一节的算法搜寻n个Θk (1≤k≤n)。
③ 依据Θk (1≤k≤n)建立式(24)~(26)。
④ 按式(29)(30)计算元件最优无效度v。
⑤ 进入主抽样环节,设置允许的方差系数β*(通常0.01~0.05之间)。
⑥ 采用g(x; v)抽取第i个系统状态xi。
⑦ 对xi进行潮流或最优潮流计算,从而得到失负荷标志H(xi)、负荷削减量C(xi),以及似然比W(xi; u, v)=f(xi; u)/g(xi; v)的数值。
⑧ 按式(31)和(32)更新系统失负荷概率LOLP和期望缺供电量EENS指标。计算方差系数β,判断是否满足β < β*。如果满足,则仿真结束;否则令总的样本容量N=N+1,i=i+1,返回第⑥步。
| $ \mathrm{LOLP}=\frac{1}{N} \sum\limits_{i=1}^{N}\left[H\left(x_{i}\right) W\left(x_{i} ; \boldsymbol{u}, \boldsymbol{v}\right)\right] ; $ | (31) |
| $ \mathrm{EENS}=\frac{1}{N} \sum\limits_{i=1}^{N}\left[H\left(x_{i}\right) W\left(x_{i} ; \boldsymbol{u}, \boldsymbol{v}\right) C\left(x_{i} ; \boldsymbol{u}, \boldsymbol{v}\right)\right]。$ | (32) |
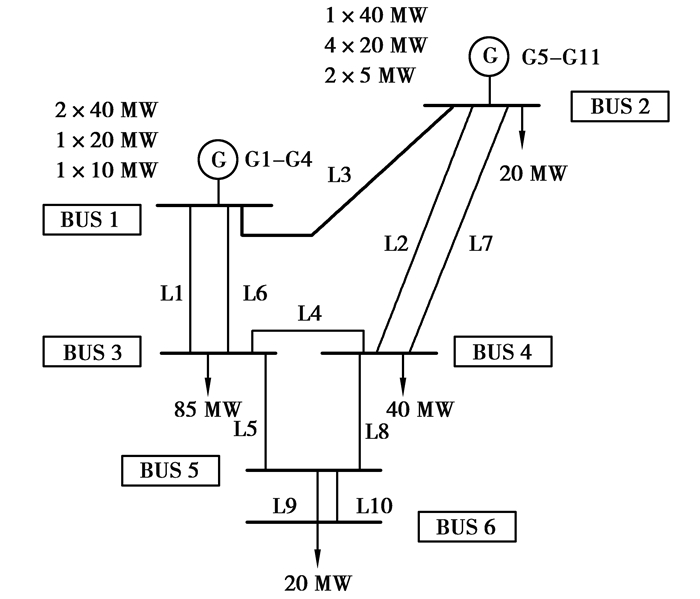
RBTS [19]可靠性测试系统由于所含元件较少,有利于对各种不同方法的应用效果进行直观比较,但该系统不符合N-1确定性可靠性准则,为此在该系统的节点5和6之间增加一条输电线路L10,并将改变后的系统称为MRBTS可靠性测试系统,见图 3。负荷采用年峰荷模型,基于以下4种方法进行电网可靠性评估,其中方法1~3的收敛条件为EENS指标的方差系数β*=0.01。
|
图 3 MRBTS可靠性测试系统的电气接线图 Fig. 3 Single line diagram of MRBTS |
方法1(ISA):采用IS法,但基于解析参数优化,且参数优化环节的枚举阶数R=3;
方法2(ISCE):采用IS法,但基于交叉熵参数优化,在参数优化阶段,每次迭代所需的样本容量为20 000;
方法3(CMCS):原始的非序贯蒙特卡洛仿真,即始终采用原始f(x; u)进行随机抽样;
方法4(ENU):采用状态枚举法,且系统状态枚举到6阶。
将MRBTS系统中部分元件的原始无效度u以及由ISA和ISCE方法在参数优化阶段得到的最优无效度v列于表 1中。从表 1可知,通过ISA和ISCE优化求取的v与原始的u相比都有明显变化,但二者求取的v总体变化规律大致一样。ISCE法所得的v存在一个矛盾,即安装地点、安装容量以及原始参数u都完全一样的2个元件,在参数优化后其v却存在明显差异,例如1#和2#发电机、6#和9#发电机、1#和6#输电线路,但采用本研究中提出的ISA法可以有效避免上述问题。其根本原因在于:ISCE法在参数优化阶段需要进行多次迭代,且每次迭代都需要对元件状态进行大量随机抽样,由于随机抽样的不确定性,即使2个元件完全一模一样,它们在每次随机抽样中也不一定被同时抽取到处于同样状态,因此根据式(11)的参数更新公式计算得到的结果就会存在差异。而ISA法并非采用随机抽样,而是基于解析思路,通过枚举系统状态并寻找其中最小割集,由此建立非线性方程组。由于采用枚举方式,2个相同的元件能保证以同等的概率被枚举,因此相同的元件在参数解析优化后其最优无效度也完全相同。
| 表 1 交叉熵参数和解析参数优化的结果比较 Table 1 Result comparison between CE parameter and analytical parameter optimization |
对MRBTS进行可靠性评估的结果列于表 2,并以ENU法的可靠性指标计算结果作为参照基准进行比较。在可靠性指标的计算准确性上,ISA法得到的LOLP和EENS指标与ENU法相比差异很小,这说明本文方法能保证较好的计算精度。而在所需样本数和计算耗时上,ISA法由于在可靠性评估阶段采用了重要抽样,所需样本比CMCS法大大减少,计算速度也得到显著提升。ISCE法同样在可靠性评估阶段采用了重要抽样,但由于在参数优化阶段采取了迭代寻优方式,并且为了能够在初始迭代中能抽取到足够数量的不良系统状态,每次迭代所需的抽样样本数较大,因此ISCE法在可靠性评估阶段虽然所需样本数比ISA法稍小,但总的样本数和计算耗时却明显高得多。结果表明本文ISA法可在保证计算准确性的情况下大幅度提高评估速度,提高了可靠性评估效率。
| 表 2 MRBTS在不同方法下的准确性和速度比较 Table 2 Comparison of accuracy and speed of MRBTS obtained with various methods |
基于枚举得到的最小割集,用公式(19)解析计算的LOLP指标值为0.007 9,相比于上表结果明显偏小,主要在于枚举阶数R=3不能太高,否则参数优化阶段的计算成本将显著增加。另一方面,从上表也可看出,最小割集的阶数虽然不高,但并不影响本文方法的计算准确性。其原因如下:参数优化阶段的目的在于获取重要抽样概率密度函数的参数,当参数计算完毕,才进入真正的大电网可靠性指标计算阶段,即主抽样阶段。在主抽样阶段抽取的样本数有限的情况下,计算准确性常采用可靠性指标统计量的方差系数来衡量。参数优化阶段采用不同方式得到重要抽样函数参数,将使参数优化阶段的计算成本出现差异,进而影响整个电网可靠性评估(包含参数优化和主抽样阶段)的计算耗时,但并不影响主抽样阶段可靠性指标的计算准确性,因为计算准确性由主抽样阶段所给定的方差系数决定。最小割集阶数越高,得到的重要抽样函数将使主抽样阶段收敛更快,但也带来两个方面的影响:一是参数优化阶段需要枚举和分析的系统状态数呈指数函数急剧增加,计算成本急剧增长,整个电网可靠性评估效率反而下降;二是最小割集阶数过高时,重要抽样函数的参数变化将进入饱和阶段,即参数计算值随最小割集阶数的增加只是微小变动。由此可见,最小割集的阶数并非越高越好,同时考虑到对系统可靠性有重要影响的元件在阶数不高的割集事件中就能体现出来,因此对阶数不高的割集事件中的元件无效度进行优化,突显它们出现的概率,就能在后续主抽样阶段实现可靠性指标计算的显著加速。
4.2 IEEE-RTS79可靠性测试系统将本文方法进一步应用于IEEE-RTS79系统[20],考虑到年峰荷下该系统的可靠性水平较差,采用原始MCS也能较快满足收敛条件,因此在90%负荷水平下采用基于同样的4种方法进行评估分析。
方法1(ISA):采用IS法,但基于解析参数优化,且参数优化环节的枚举阶数R=2;
方法2(ISCE):采用IS法,但基于交叉熵参数优化,在参数优化阶段,每次迭代所需的样本容量为25 000;
方法3(CMCS):原始的非序贯蒙特卡洛仿真,即始终采用原始f(x; u)进行随机抽样;
方法4(ENU):采用状态枚举法,且系统状态枚举到5阶。
对IEEE-RTS79进行可靠性评估后的结果如表 3所示,可见本文ISA法的可靠性指标计算准确性和其他方法大致相当,但可靠性评估效率却明显高于其他方法。虽然ISCE法也采用了重要抽样,但迭代方式的参数寻优效率显著低于解析方式参数寻优,例如ISCE法需要3次迭代共随机抽取75 000个样本用于参数更新,但ISA法只需枚举2485个系统状态,可见参数优化阶段ISCE法所需样本远大于ISA法,导致ISCE法的总体效率不如ISA法。
| 表 3 IEEE-RTS79在不同方法下的准确性和速度比较 Table 3 Comparison of accuracy and speed of IEEE-RTS79 by different methods |
同样基于枚举得到的最小割集直接计算LOLP指标,其数值为0.011 5,与上表结果相比也明显偏小,原因在于枚举阶数R=2不能太高,以避免预抽样阶段出现较大计算成本。同时可见,本文方法得到的可靠性指标计算准确性并未受割集阶数不高的影响。
5 结语基于非序贯蒙特卡罗模拟,从解析法的角度将故障系统状态的最优重要抽样概率密度表达为含元件最优无效度与原始无效度的非线性方程组;利用最小割集能代表一类故障系统状态的特性,基于最小割集实现了方程合并,降低了方程组求解的难度;再引入最小二乘估计,以误差最小为优化目标实现了最优无效度的解析估计。本文方法有效避免了CEM法在迭代参数寻优中随机抽样带来的较大计算负担,提高了蒙特卡罗仿真的效率。
| [1] |
Billinton R, Li W Y. Reliability assessment of electric power systems using Monte Carlo methods[M]. Boston, MA: Springer US, 1994.
|
| [2] |
双滟杰. 电网可靠性蒙特卡罗仿真中最优重要抽样函数求解算法研究[D]. 重庆: 重庆大学, 2017. Shuang Y J. Research on calculation method of importance sampling function in Monte Carlo simulation for power system reliability evaluation[D]. Chongqing: Chongqing University, 2017. (in Chinese) |
| [3] |
Leite da Silva A M, Fernandez R A G, Singh C. Generating capacity reliability evaluation based on Monte Carlo simulation and cross-entropy methods[J]. IEEE Transactions on Power Systems, 2010, 25(1): 129-137. DOI:10.1109/TPWRS.2009.2036710 |
| [4] |
Carvalho L D M, González-Fernández R A, Leite da Silva A M, et al. Simplified cross-entropy based approach for generating capacity reliability assessment[J]. IEEE Transactions on Power Systems, 2013, 28(2): 1609-1616. DOI:10.1109/TPWRS.2012.2213618 |
| [5] |
Tómasson E, Söder L. Generation adequacy analysis of multi-area power systems with a high share of wind power[J]. IEEE Transactions on Power Systems, 2018, 33(4): 3854-3862. DOI:10.1109/TPWRS.2017.2769840 |
| [6] |
Leite da Silva A M, Costa Castro J F D, Billinton R. Probabilistic assessment of spinning reserve via cross-entropy method considering renewable sources and transmission restrictions[J]. IEEE Transactions on Power Systems, 2018, 33(4): 4574-4582. DOI:10.1109/TPWRS.2017.2773561 |
| [7] |
Wang Y. Probabilistic spinning reserve adequacy evaluation for generating systems using an Markov chain Monte Carlo-integrated cross-entropy method[J]. IET Generation, Transmission & Distribution, 2015, 9(8): 719-726. |
| [8] |
赵渊, 王洁, 耿莲, 等. 电网可靠性非序贯蒙特卡洛仿真的扩展交叉熵法[J]. 中国电机工程学报, 2017, 37(7): 1963-1974. Zhao Y, Wang J, Geng L, et al. An extended cross entropy method for non-sequential Monte Carlo simulation of power system reliability assessment[J]. Proceedings of the CSEE, 2017, 37(7): 1963-1974. (in Chinese) |
| [9] |
González-Fernández R A, Leite da Silva A M, Resende L C, et al. Composite systems reliability evaluation based on Monte Carlo simulation and cross-entropy methods[J]. IEEE Transactions on Power Systems, 2013, 28(4): 4598-4606. DOI:10.1109/TPWRS.2013.2267154 |
| [10] |
Leite da Silva A M, González-Fernández R A, Flávio S A, et al. Composite reliability evaluation with renewable sources based on quasi-sequential Monte Carlo and cross entropy methods[C]//2014 International Conference on Probabilistic Methods Applied to Power Systems (PMAPS), July 7-10, 2014, Durham, UK. IEEE, 2014: 1-6.
|
| [11] |
Zhao Y, Tang Y, Li W Y, et al. Composite power system reliability evaluation based on enhanced sequential cross-entropy Monte Carlo simulation[J]. IEEE Transactions on Power Systems, 2019, 34(5): 3891-3901. DOI:10.1109/TPWRS.2019.2909769 |
| [12] |
Tómasson E, Söder L. Improved importance sampling for reliability evaluation of composite power systems[J]. IEEE Transactions on Power Systems, 2017, 32(3): 2426-2434. DOI:10.1109/TPWRS.2016.2614831 |
| [13] |
Geng L, Zhao Y, Li W Y. Enhanced cross entropy method for composite power system reliability evaluation[J]. IEEE Transactions on Power Systems, 2019, 34(4): 3129-3139. DOI:10.1109/TPWRS.2019.2897384 |
| [14] |
Cai J L, Xu Q S, Cao M J, et al. A novel importance sampling method of power system reliability assessment considering multi-state units and correlation between wind speed and load[J]. International Journal of Electrical Power & Energy Systems, 2019, 109: 217-226. |
| [15] |
Wang Y, Guo C X, Wu Q H, et al. Adaptive sequential importance sampling technique for short-term composite power system adequacy evaluation[J]. IET Generation, Transmission & Distribution, 2014, 8(4): 730-741. |
| [16] |
Ansari O A, Chung C Y. A hybrid framework for short-term risk assessment of wind-integrated composite power systems[J]. IEEE Transactions on Power Systems, 2019, 34(3): 2334-2344. DOI:10.1109/TPWRS.2018.2881250 |
| [17] |
Wang Y, Guo C X, Wu Q H. A cross-entropy-based three-stage sequential importance sampling for composite power system short-term reliability evaluation[J]. IEEE Transactions on Power Systems, 2013, 28(4): 4254-4263. DOI:10.1109/TPWRS.2013.2276001 |
| [18] |
Mishra R, Chaturvedi S K. A cutsets-based unified framework to evaluate network reliability measures[J]. IEEE Transactions on Reliability, 2009, 58(4): 658-666. DOI:10.1109/TR.2009.2028090 |
| [19] |
Billinton R, Kumar S, Chowdhury N, et al. A reliability test system for educational purposes-basic data[J]. IEEE Transactions on Power Systems, 1989, 4(3): 1238-1244. DOI:10.1109/59.32623 |
| [20] |
IEEE Probability Methods Subcommittee. IEEE reliability test system[J]. IEEE Transactions on Power Apparatus and Systems, 1979, PAS-98(6): 2047-2054. DOI:10.1109/TPAS.1979.319398 |
 2021, Vol. 44
2021, Vol. 44

