2. 西藏大学 工学院, 拉萨 850000
2. Engineer Institute, Tibet University, Lhasa 850000, P. R. China
在电网容量保持不变的情况下,并网光伏电站(grid-connected photovoltaic power plant,GCPVPP)的增加可能会在发电高峰期(如中午)导致电力基础设施出现过电压问题。为了解决电力系统潜在的此类挑战性难题,各国对电网规范和标准进行了不断的更新,例如,丹麦电网规范要求输出功率大于11 kVA的GCPVPP应能在需要时将输出功率限制在恒定值,通过限制GCPVPP的功率输出,剩余的发电功率可用于提供辅助功能,如频率支持等[1]。功率限制控制(恒定功率控制)[2],功率储备控制[3]和功率爬坡率控制[4]的要求是通过GCPVPPs上的各种电网代码规定的,为了满足这些要求,需要用柔性功率点跟踪(flexible power point tracking,FPPT)算法取代GCPVPPs中现有的最大功率点跟踪(maximum power point tracking,MPPT)算法。
过去,文献中大多数研究的焦点是光伏(photovoltaic,pv)串的最大功率点跟踪,以提高整体功率转换效率和能源利用率。除了传统的MPPT算法如扰动与观测(perturb & observe,P&O)[5]和增量电导算法[6]外,还引入了模型预测[7]、粒子群优化[8]和双Kalman滤波[9]等先进算法从pv串中提取最大功率;文献[10]中还考虑了部分阴影条件下pv串的运行情况分析。随着FPPT需求的引入,针对GCPVPPs的不同配置也引入了几种FPPT算法。实现FPPT操作的方法主要有两类:
1) 在两级GCPVPPs中修改DC-DC换流器控制器或在单级GCPVPPs中修改DC-AC换流器控制器(例如比例积分控制器)。文献[11]中介绍了FPPT的基本原理,重点是稳定性问题;文献[12]介绍了一种基于P&O算法的电压基准计算方法,用于计算与所需有功功率相关的电压基准值。然而,将运行点移动到最大功率点(maximum power point,MPP)的右侧会降低这些算法的鲁棒性,因为在快速降低辐照度的情况下,运行点可能超过光伏板的开路电压。以上算法应用多模运算来调节光伏电池板的输出功率,显然,在运行模式转换期间需要对控制器进行初始化,因此其动态特性较慢。
2) 基于光伏电池板的功率—电压(power-voltage,P-V)特性,根据所需的功率基准调整光伏串的电压基准。这种方法不需要对DC-DC或DC-AC换流器控制器进行任何修改。
由于第二类FPPT算法不需要对控制器进行任何修改,并且能够实现快速的动态特性,因此这里选择第二类算法来从GCPVPPs中产生恒定功率。现有算法在恒定的环境条件(如辐照度和温度)下运行良好,然而,由于环境的变化,光伏阵列的功率和电压特性会有很大的变化,现有解决方案在计算快速辐射变化下的电压基准时可能会遇到一些问题。有文献研究了可用于在快速环境变化期间增强MPPT算法的操作[13],在这种情况下,FPPT算法的性能可能会受到环境条件变化的严重影响,特别是当运行点远离MPP时,原因如下:
1) MPPT的工作范围在MPP附近很窄,而FPPT的工作范围覆盖了P-V曲线的整个区域。因此,根据环境条件调整控制参数具有更大的挑战性;
2) 与MPPT运行相比,FPPT运行期间的电压变化对功率的影响更大,因此环境变化对光伏功率的影响可能更为显著。
此外,不仅环境的变化会影响FPPT的运行,而且由于电网的要求,期望的恒功率基准(pref)也会发生突变。因此,与MPPT相比,FPPT在瞬态下更具挑战性,然而,如何解决这些问题还没有在文献中被提及。
针对上述问题,提出了一种适用于GCPVPPs的自适应FPPT算法。该算法是考虑光伏电池板P-V特性的P&O方法的一种改进,主要贡献如下:1)提出了一种新的FPPT算法的自适应电压阶跃计算策略,可在暂态过程中实现快速动态变化,并满足稳态下低功耗振荡要求。该算法在计算各计算步骤的电压阶跃时,考虑了换流器的工作方式和光伏电池板的电流工作点,此特性可自适应调整电压阶跃,以提高暂态和稳态性能;2)所提算法对于快速的环境变化具有高鲁棒性。在控制器中使用额外的采样区分P & O算法中的特定电压变化与环境变化对pv面板功率的影响。这样,可以避免在快速变化的条件下运行点的错误移动。
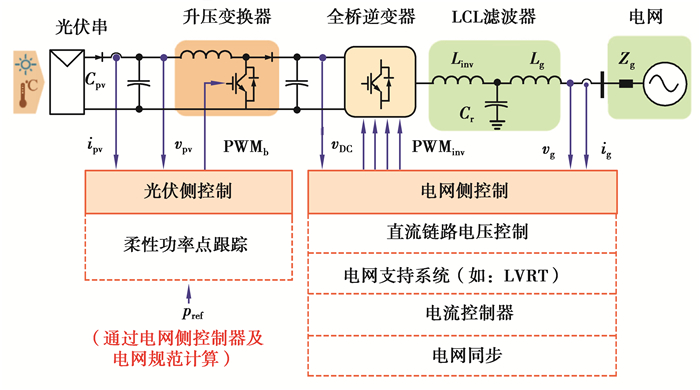
所提出的FPPT算法还可以用于从pv串中提取最大功率,同时能够根据需要将pv功率限制为所需值。该算法在功率限制运行模式期间可以实现快速动态性,且在MPPT模式下操作时可以获得与常规MPPT算法类似的性能,计算时间步长对于所有运行模式都是固定的,从而降低了针对不同运行模式控制器设计的复杂性。另外,所提自适应FPPT算法能够将pv面板的运行点移动到MPP的右侧或左侧,可以在单阶段GCPVPP和两阶段GCPVPP中实现。在3 kVA的两级单相GCPVPP上对所提算法的性能进行了评估,如图 1所示。该两级GCPVPP系统由并网全桥逆变器组成,可满足并网要求,DC-DC升压转换器为系统提供FPPT控制,而所需的功率参考值(pref)由电网侧控制器计算得出。有关此配置的详细说明见文献[3]。PWM为脉冲宽度调制信号,PWMb表示输入升压变压器的PWM信号,PWMinv则表示输入逆变器的PWM信号,vDC为直流电压信号,Cr为滤波器接地电容,Lg为滤波器电网侧等效电感,Zg为电网侧阻抗。
|
图 1 两级GCPVPP的电路结构及总体控制结构 Fig. 1 Circuit configuration and overall control structure of a two-stage GCPVPP |
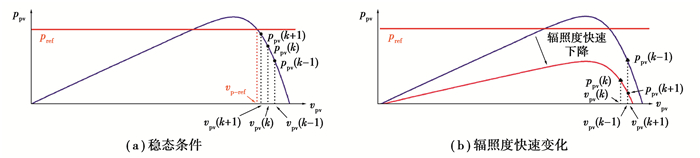
FPPT算法的控制目标是将光伏系统的输出功率调节到一定的设定值。传统方法使用基于P&O的FPPT算法,该算法通过扰动远离MPP的pv电压以降低输出功率,根据电压扰动对光伏输出功率的影响,确定下一个参考电压,如图 2(a)所示。在t=(k-1)T时,pv电压为vpv(k-1),k表示第k次采样,T为采样周期。电压基准在t=(k-1)T时变为vpv(k),控制器在t=kT时将pv电压调节到该值。因此,光伏电池板的瞬时功率从ppv(k-1)变为ppv(k)。在这种情况下,电压呈负变化,即Δvpv=vpv(k)-vpv(k-1) < 0,从而导致正的功率变化,即Δp=ppv(k)-ppv(k-1)>0。基于Δv和Δp的符号,FPPT算法在该计算步骤可降低另一个电压,从而增加光伏功率,使之更接近功率基准(pref),如图 2(a)所示。在恒定或缓慢变化的太阳辐射条件下,光伏功率的变化主要是由CPG算法的扰动引起的,因此,P&O-CPG算法可以根据设定值精确地调节光伏发电功率。
|
图 2 光伏电池板相关参数变化对电压基准值的影响 Fig. 2 The influence of the relative parameter changes of photovoltaic panels on the voltage reference value |
然而,在辐照度快速降低的情况下,上述过程可导致较大的跟踪误差(tracking errors,Et)出现,如图 2(b)所示。FPPT算法在t=(k-1)T时降低相应电压,在t=(k-1)T和t=kT之间的时间间隔内,辐照度快速降低,由辐照度降低引起的功率降低的绝对值大于由光伏电压变化引起的功率增加的绝对值。换言之,扰动过程中光伏功率的变化是由太阳辐射条件的突然变化引起的。因此,将导致Δp的负变化,并且传统的FPPT算法可能对下一个扰动做出错误的决定,如图 2(b)所示。
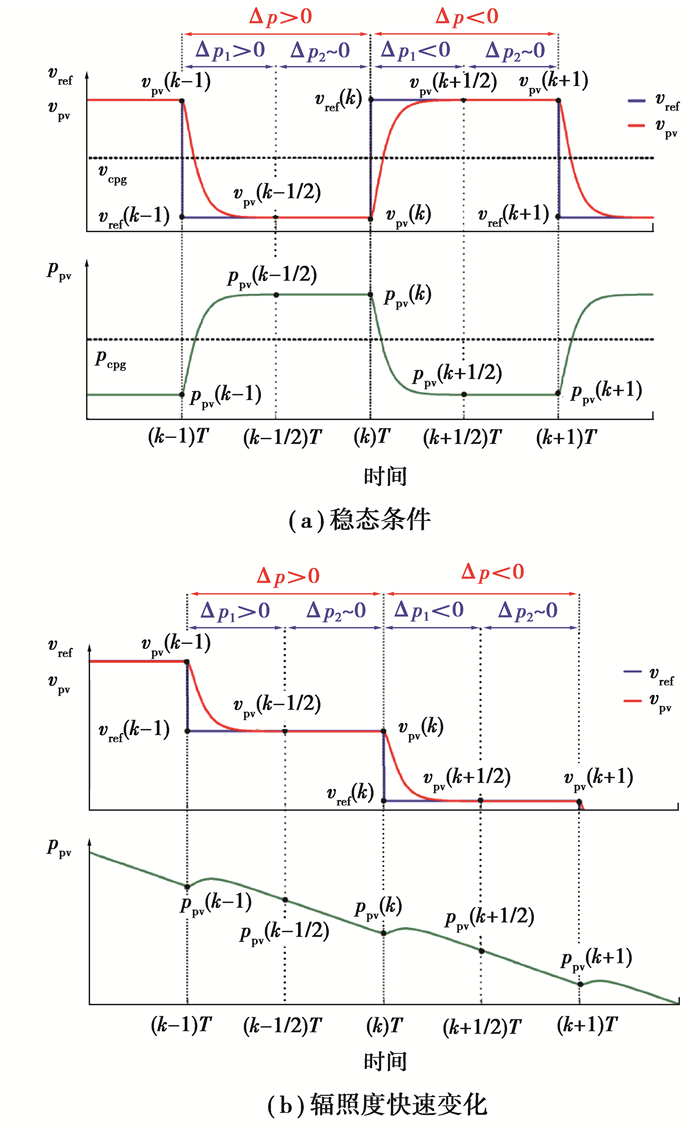
图 3给出了光伏板在FPPT稳态运行期间的电压和功率曲线。从图 3可以看出,工作点在稳态时围绕功率基准pref振荡。pref处的对应电压称为vp-ref,在t=(k-1)T时,电压基准计算算法将新的电压基准设置为vref(k-1),如图 3(a)所示。测量t=(k-1/2)T时的光伏电压和功率,然后设计控制器在半个采样周期T/2内调节光伏电压vpv。因此,在t=(k-1/2)T时,pv电压vpv被调节为其基准值,即vref(k-1)。pv输出功率(ppv)增加到ppv(k-1/2)。在t=(k-1/2)T和t=kT之间,电压基准不随电压基准计算算法改变,因此,在此期间,光伏输出功率ppv保持不变。图 3中vcpg和pcpg为稳态运行期间通过P&O-CPG算法控制的稳态电压和功率。
|
图 3 连续计算步骤间的电压及功率测量 Fig. 3 Extra measurements between consecutive calculation-step |
基于上述讨论,定义2个参数来检测环境变化(辐射和温度)。第一个参数Δp1用于计算(k-1)T和(k-1/2)T之间的光伏功率变化,如图 4所示。
| $ \Delta p_{1}=p_{\mathrm{pv}}(k-1 / 2)-p_{\mathrm{pv}}(k-1)。$ | (1) |
|
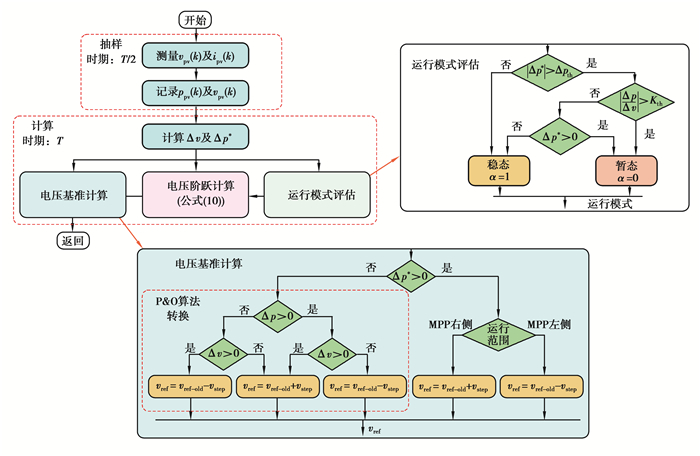
图 4 GCPVPPs自适应恒功率发电算法框图 Fig. 4 Block diagram of the proposed adaptive constant power generation algorithm in GCPVPPs |
在稳态环境条件下,Δp1表明了电压基准扰动引起的功率变化。(k-1/2)T和kT之间的光伏功率变化Δp2定义为:
| $ \Delta p_{2}=p_{\mathrm{pv}}(k)-p_{\mathrm{pv}}(k-1 / 2)。$ | (2) |
显然,在稳定状态恒定太阳辐照度条件Δp2接近于零,因为pv电压基准值在(k-1/2)T和kT之间没有变化。相对较大的Δp2值表明环境条件正在发生变化。
快速辐照度变化对上述参数的影响如图 3(b)所示,光伏板的当前运行点与图 3(a)中的运行点保持相同。然而,考虑辐照度的快速线性降低时,t=(k-1)T处的电压基准被设置为vref(k-1),而由于辐照度的降低,光伏功率ppv在t=(k-1/2)T处降至ppv(k-1/2)。在t=(k-1/2)T和t=kT之间,光伏功率ppv降低。但是,在此期间电压基准值没有改变。因此,在这种情况下,Δp1为负,而在稳态时为正。此外,Δp2也为负值,振幅相对较大,表明环境条件发生变化,在稳态时接近于零。
值得注意的是,Δp1包含了功率变化的信息,这是由于辐照变化的影响和特定的电压基准变化的结合。在电压基准计算中使用参数Δp1,可以在环境变化时将运行点移动到相反的方向。因此,定义以下参数是为了将环境变化的影响与特定电压基准变化的影响分开,如下所示:
| $ \Delta p=\Delta p_{1}-\Delta p_{2}。$ | (3) |
假设环境参数(辐射和温度)的变化在一个计算时间步长内是线性的,任何环境参数的变化都会导致光伏发电量的变化。若环境变化在一个计算时间步长内呈线性变化,则其对Δp1光伏功率的影响等于Δp2,由于Δp是Δp1和Δp2的差值,消除了环境变化对Δp参数的影响。因此,参数Δp仅包括由于控制器的电压基准扰动而引起的光伏功率变化的信息。这样,在快速变化的环境条件下,电压基准计算算法不会跟踪到错误的方向。
2 自适应柔性功率点跟踪算法所提出的自适应FPPT算法框图如图 4所示,在T/2的采样周期内测量vpv和ppv参数。值得注意的是,这种额外的采样不会增加算法的计算复杂度,只需要一个额外的中断来采样输入测量值。该FPPT算法由3部分组成,首先,“运行模式评估”模块将光伏系统的运行模式识别为暂态或稳态,其输出用作“电压阶跃计算”模块的输入数据。随后,实现自适应电压阶跃计算算法,根据前面定义的运行方式和光伏功率变化参数计算电压阶跃。此模块计算出的电压阶跃值用作“电压基准计算”模块的输入,以确定用于将光伏功率调节到其基准值的光伏电压基准。所有这些模块的计算都在一个计算周期T内实现,以下各节将详细介绍这些模块的实现。在所提算法中,当前和先前计算步骤之间的pv电压变化Δv计算如下:
| $ \Delta v=v_{\mathrm{pv}}(k)-v_{\mathrm{pv}}(k-1)。$ | (4) |
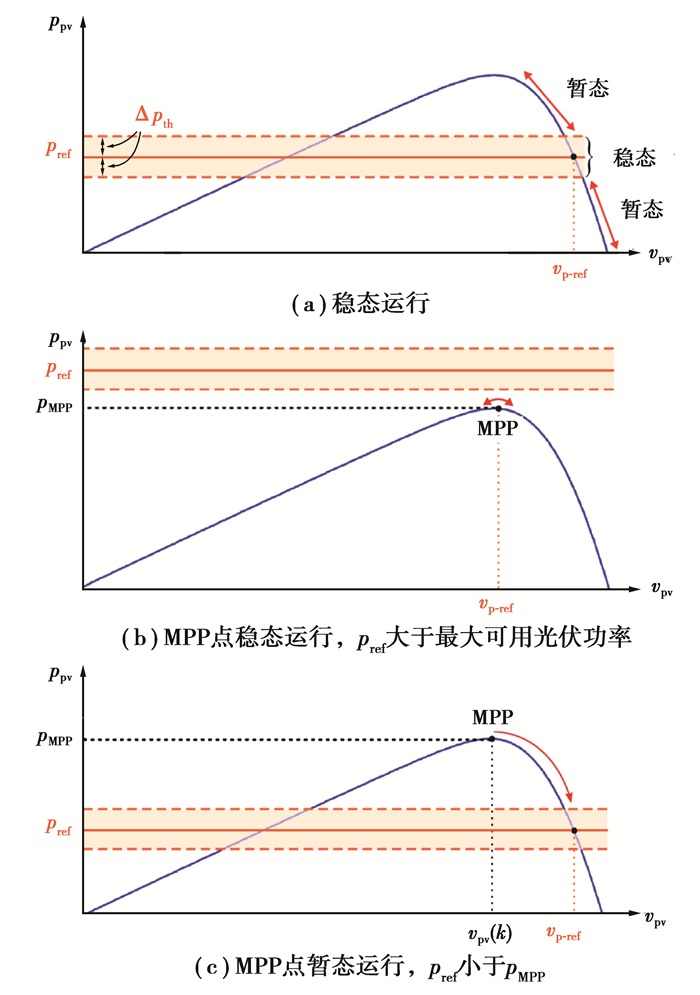
两种主要的运行模式如图 5(a)所示,定义功率阈值Δpth区分这两种工作模式,
| $ \left\{\begin{array}{l} \Delta p^{*} \leqslant \Delta p_{\mathrm{th}} & \text { 稳态 }, \\ \Delta p^{*}>\Delta p_{\mathrm{th}} & \text { 暂态 }, \end{array}\right. $ | (5) |
|
图 5 光伏系统在恒功率发电中的不同运行方式 Fig. 5 Different operation modes of the photovoltaic system in constant power generation |
式中Δp*定义为
| $ \Delta p^{*}=p_{\mathrm{pv}}(k)-p_{\mathrm{ref}}, $ | (6) |
式中ppv(k)是当前计算步骤k下的瞬时光伏功率。在稳态情况下,式(6)中的误差接近于零,而在暂态期间,由于太阳辐照度条件的变化,误差可能相对较大。
在光伏系统在最大功率点运行的情况下,执行式(5)中的比较可能导致运行模式的错误选择。如图 5所示,这种情况可在两种情况下发生:
1) 控制器设置为从光伏系统中提取最大功率,而不是在FPPT下运行。在这种情况下,控制器将功率参考设置为大于标称最大pv功率的值,如图 5(b)所示。
2) 由于部分阴影或其他原因,在FPPT运行期间,最大可用pv功率(pMPP)小于恒定功率基准。在这种情况下,运行模式也类似于图 5(b)。
所提电压基准算法能够计算出上述条件下的MPP电压。为了获得与传统MPPT算法相似或更小的功率振荡,应确保将这些条件归类为稳态情况。光伏电池板在最大功率点处的P-V曲线(Δp/Δv)斜率接近于零,因此,可通过Δp/Δv的绝对值与阈值(Threshold,Kth)相比较,以确定当前运行点是否接近MPP。如果运行点不靠近MPP(|Δp/Δv|>Kth),光伏系统处于暂态模式。需要注意的是,如果当前运行点靠近MPP,可能会出现以下两种不同的情况。
1) 如图 5(b)所示,功率基准大于pMPP。这种运行状态应归类为稳态。在这种运行模式下,由式(6)计算得出的Δp*为正。
2) 在当前计算时间步长内,功率基准可以小于pMPP。然而,由于pref的阶跃减小,运行点仍在MPP处,如图 5(c)所示。这种运行条件导致Δp* < 0,应归类为暂态,以实现快速动态性能。
为了区分这两种情况,在所提出的算法中确定Δp*的符号,如图 4所示。检测到工作模式后,参数α定义为:
| $ \begin{cases}\alpha=0 & \rm { 暂态},\\ \alpha=1 & \rm {稳态}。\end{cases} $ | (7) |
在运行模式评估算法实现时,保证了所有运行条件的正确分类。该算法的主要优点是在MPP上对运行进行适当的分类, 与传统的MPPT算法相比,可以保证MPPT运行被归类为稳态时产生较小的功率振荡。
2.2 自适应电压阶跃计算算法电压阶跃vstep的选择是FPPT算法设计的关键。在暂态过程中,vstep值越大,动态响应越快,但在稳态时会产生较大的功率振荡。另一方面,在较小的vstep值下,可以实现相对较小的稳态功率振荡。然而,这样的选择会导致动态变化缓慢,因此,为了提高系统的动态和稳态性能,提出了一种自适应电压阶跃计算算法。
所提FPPT算法的一个目标是提供与传统MPPT算法相似的MPPT性能。就此而言,可以将固定电压阶跃(对于MPPT而言是最佳电压阶跃)应用于FPPT算法,如式(8)所示,
| $ v_{\text {step }}=v_{\text {step-b }}。$ | (8) |
式中vstep-b是MPPT的最佳电压阶跃,可参照文献[16]进行设计。当FPPT算法采用固定电压阶跃vstep-b时,系统在快速变化的环境下的动力学行为变得缓慢。注意,在FPPT中计算vp-ref时,特定恒定功率基准的电压变化大于在类似环境条件变化下MPP处的电压变化。这是因为MPPT工作范围集中在MPP附近,其P-V曲线的斜率接近于零。因此,在瞬态过程中应施加更大的电压阶跃,改善动态性能。
| $ v_{\text {step }}=\overbrace{\alpha \times v_{\text {step-b }}}^{\text {稳态 }}+\overbrace{(1-\alpha) \times v_{\text {step-tr }}}^{\text {暂态 }},$ | (9) |
式中:vstep-tr是暂态运行的选定电压阶跃,大于最佳电压阶跃vstep-b。在暂态过程中,α=0,vstep=vstep-tr时可产生更快的动力学变化特性,而在α=1的稳态下,可实现相对较低的功率振荡。尽管如此,该算法仍有以下两个缺点:
1) MPP右侧的FPPT操作与相对较小的功率基准会导致大的功率振荡,即使将vstep-b视为电压阶跃,因为P-V曲线(Δp/Δv)斜率较大,对于Δp/Δv值较大的运行点,应采用较小的电压阶跃值,以保持低功率振荡。
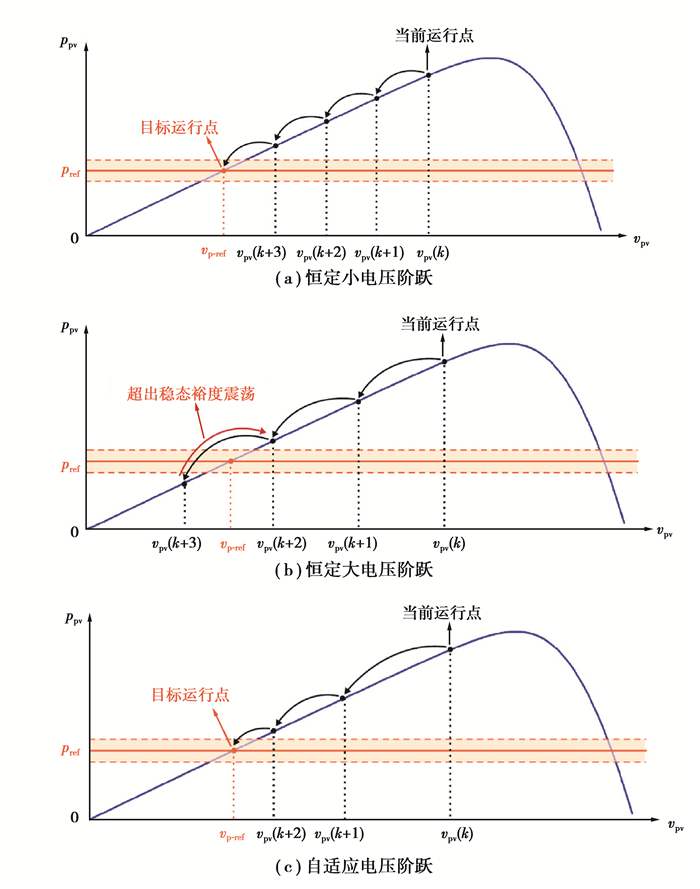
2) 动态瞬变会导致与功率基准的大功率偏差(功率误差)。可通过使用小的电压阶跃值增加响应时间,如图 6(a)所示。另一方面,如图 6(b)所示,通过在瞬态期间应用大的电压阶跃值,运行点超出可以观察到大功率振荡的稳态区域,在这种情况下,运行点振荡超过稳态区域。
|
图 6 暂态电压阶跃算法的原理 Fig. 6 Principles of the proposed voltage-step calculation algorithm during transients |
为了解决以上问题,提出自适应电压步进计算算法:
| $ v_{\text {step }}=\left(\overbrace{\alpha \times\left(1-k_{1} \frac{|\Delta p|}{|\Delta v|}\right)}^{\text {稳态 }}+\overbrace{(1-\alpha) \times k_{2} \times \Delta p^{*}}^{\text {暂态 }}\right) \times v_{\text {step-b }}, $ | (10) |
式中:α由前一节的运行模式评估算法确定,k1和k2为比例因子。
在暂态运行过程中,α=0,即vstep=k2×Δp*×vstep-b。在这种方法中,vstep的值取决于瞬时功率与其参考值之间的误差,在误差较大的暂态过程中,电压阶跃变大,降低了响应时间。当光伏功率接近其参考值时,电压阶跃变小,如图 6(c)所示。
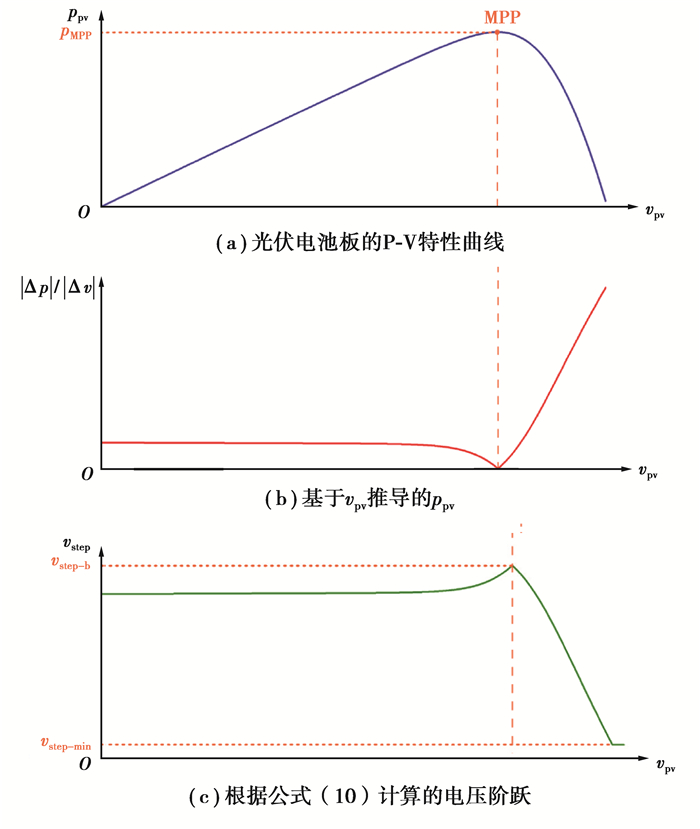
在稳态情况下,α=1,其结果为vstep=(1-k1|Δp|/|Δv|)×vstep-b。图 7(a)和(b)给出了光伏板的P-V特性曲线和|Δp|/|Δv|曲线。|Δp|/|Δv|的值在MPP处接近于零,而在MPP的右侧增加到相对较大的值。图 7(c)绘制了所提算法中的电压阶跃值,由图 7(c)可知,在MPP处,vstep等于vstep-b,而在MPP的右侧,减小为最小值vstep-min。此外,由于P-V特性曲线在该区域呈线性,电压阶跃vstep在MPP的左侧保持接近恒定值。图 7(c)中的进一步观察证实,使用所提出的算法,电压阶跃值可以根据光伏电池板的工作点自适应地修改,因此,在稳定状态下,所有运行点的电压振荡都很小。
|
图 7 稳态电压阶跃算法的原理 Fig. 7 Principles of the proposed voltage-step calculation algorithm in steady state |
所提出的FPPT操作方法的电压基准计算算法如图 4所示。如果光伏系统的瞬时功率小于功率基准(Δp* < 0),则采用传统的P&O将运行点移向MPP以增加功率。如果瞬时功率大于功率基准,则基于预期的工作区域(即MPP的右侧或左侧),电压基准分别增大或减小。关于FPPT电压基准计算算法的详细信息参见文献[14]。
2.4 自适应FTTP设计思路在设计所提出的自适应FPPT算法时,应考虑以下几点:
1) 为光伏系统的最优MPPT运行选择计算时间步长(Tstep)。注意,即使时间步长值相对较大。所提出的自适应FPPT算法也能够实现快速动力学特性。此外,在MPPT算法和FPPT算法中使用相同的计算时间步长,降低算法的计算复杂度。商业系统中MPPT算法的采样频率通常为1~10 Hz[15]。
2) vstep-b是MPPT操作的最佳电压阶跃,可根据文献[16]中的可用算法进行计算。
3) 选择暂态电压阶跃(vstep-tr)比vstep-b大2到3倍,以实现快速动力学。由于MPP右侧P-V特性曲线的斜率大于MPP左侧,因此可以为MPP右侧的vstep-tr选择较小的值。
4) 由于所提出的自适应FPPT算法是基于P&O算法的,在选择新的电压基准时考虑了特定电压变化的影响,因此,该算法要求电压阶跃最小。如图 7(c)所示,在所提算法中应用最小电压阶跃(vstep-min),该最小电压阶跃是根据光伏系统的电压和功率额定值来选择的。
5) 功率阈值(Δpth)选择在系统标称功率的3%~5%。
3 仿真分析使用两级单相光伏并网系统对所提算法的操作和性能进行分析验证,实验装置的系统参数如表 1所示,光伏侧使用Chroma 62150H-1000S光伏模拟器进行仿真,计算步长Tstep选为1 s。为了验证所提自适应FPPT算法在不同条件下的性能,通过4个算例进行仿真分析。
| 表 1 两级光伏并网系统参数 Table 1 Parameters of the two-stage grid connected photovoltaic system |
与传统的电压步进算法进行性能比较时,式(8)固定电压阶跃法称为方法1(m1),而式(9)中条件电压阶跃称为方法2(m2),式(10)中提出的自适应电压步进算法称为方法3(m3)。为了获得这些算法性能之间的数值比较,计算了FPPT操作期间的平均Et(以总能量产额的百分比表示)。跟踪误差根据实际光伏输出功率与其参考功率(即|ppv-pref|)之间的差值计算,然后除以总发电量。
| $ E_{\mathrm{t}}=\frac{\int\left|p_{\mathrm{pv}}-p_{\mathrm{ref}}\right|}{\int\left|p_{\mathrm{pv}}\right|} \times 100。$ | (11) |
跟踪误差是在FPPT期间计算的,其中光伏板的瞬时最大可用功率(pavai)大于或等于所需的功率参考pref。
为了公平比较各种算法的性能,考虑以下几点:1)对于不同算法的所有测试条件,控制系统的其余部分是相同的;2)使用pv仿真器为所有测试条件提供相似的P-V曲线。
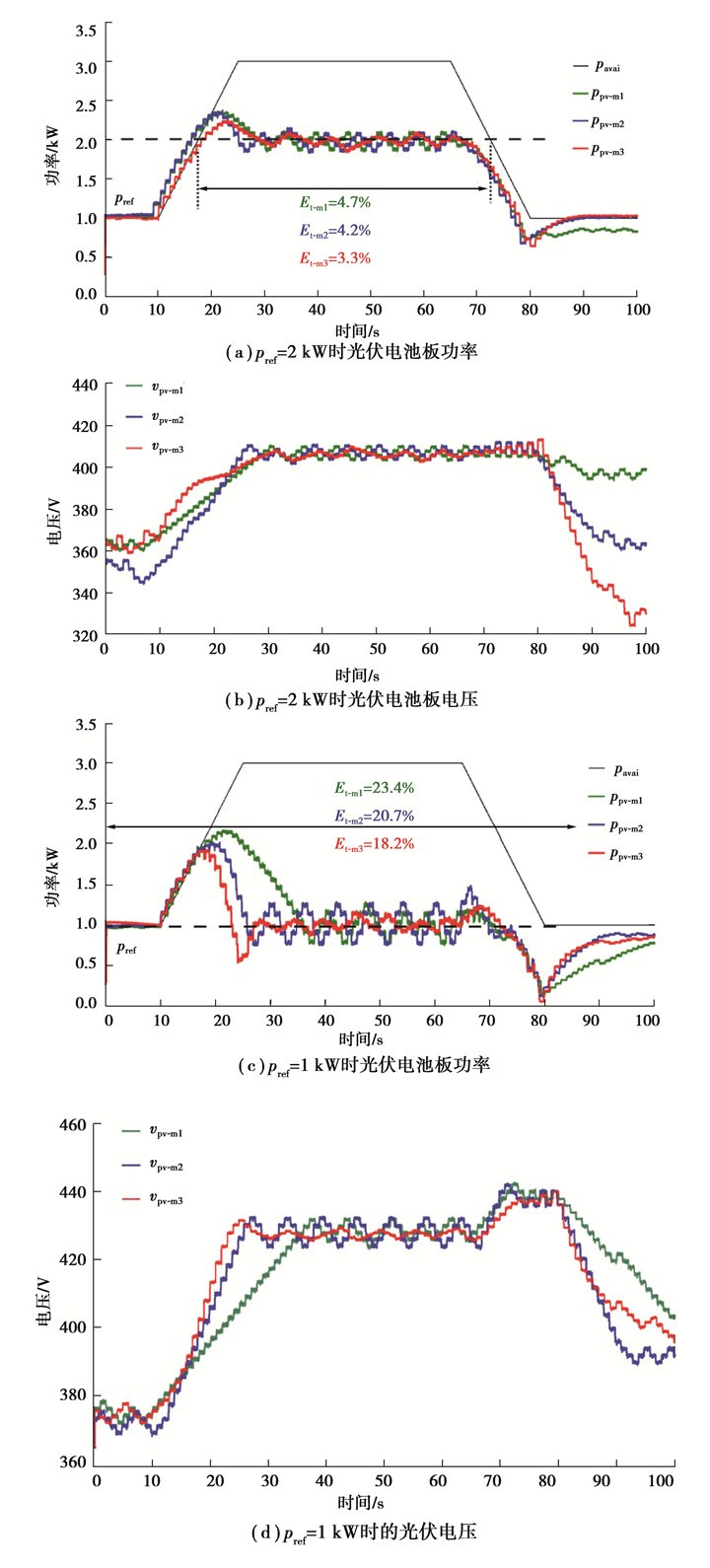
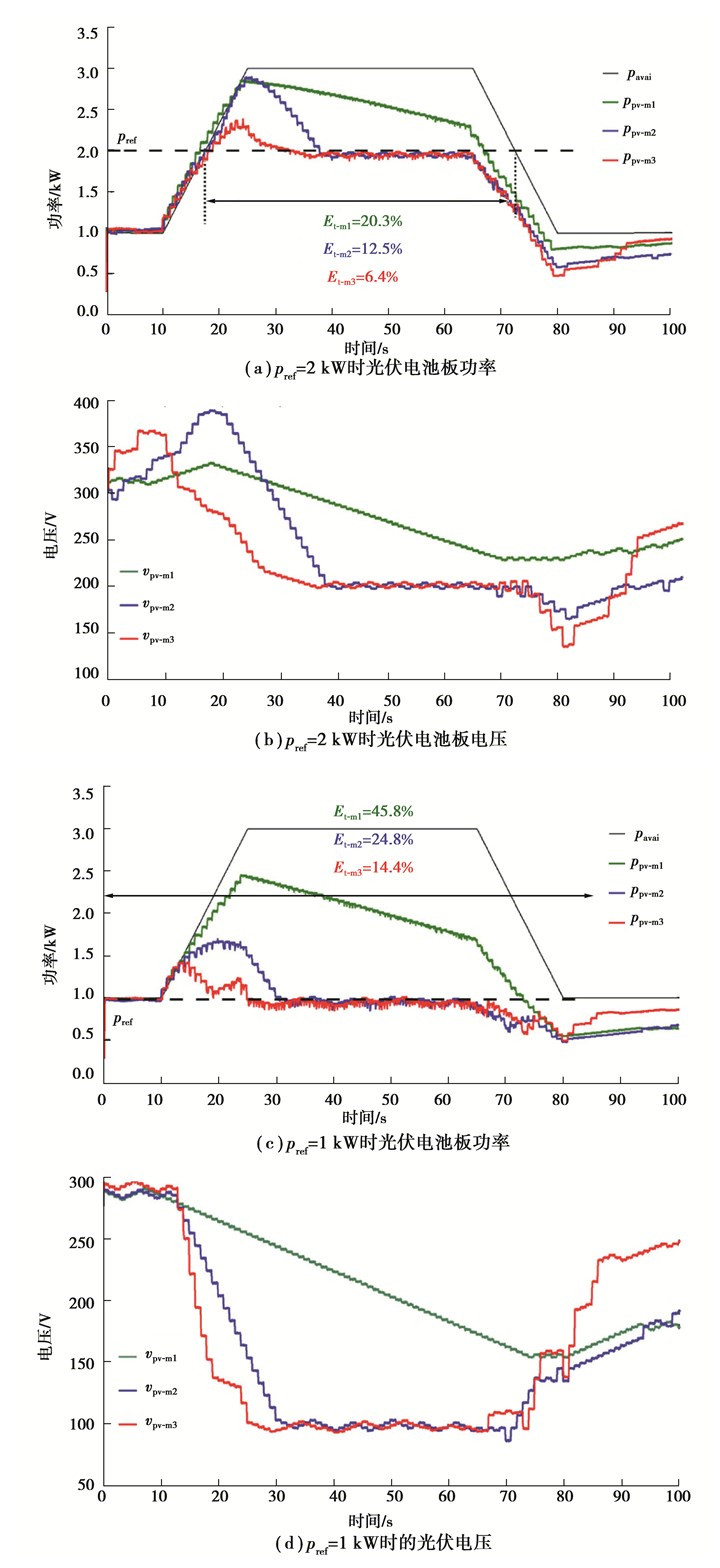
算例一:评估所提出的自适应FPPT算法在辐照度随运行点向MPP右侧移动而快速变化时的性能,结果如图 8所示。选择了两个测试用例,pref=2 kW和pref=1 kW。t=10 s前,辐照度恒定,可用功率为1 kW。辐照度在t=10 s和t=25 s之间迅速增加,其中pavai从1 kW增加到光伏板的标称最大功率,即3 kW。图 8(a)为光伏系统在FPPT运行期间的输出功率,以及在pref=2 kW下实现的电压阶跃计算算法。在结果中,ppv-m1是与方法1相关的PV功率,ppv-m2是与方法2相关的功率,ppv-m3是与方法3相关的功率。与这些算法相关的PV电压如图 8(b)所示。在t=65 s和t=80 s之间,辐照度迅速下降,从而将pavai降低到1 kW,如图所示,方法2的动态性能比方法1快,而所提出的自适应FPPT算法(方法3)的动态性能在三种算法中是最好的。该算法的跟踪误差也小于其他算法(Et-m3=18.2%)。
|
图 8 算例一仿真结果 Fig. 8 Experimental results of case Ⅰ |
图 8(c)和(d)给出了相似环境条件下,在pref=1 kW时各算法的运行性能,由图中结果可知,所提自适应FPPT算法能够在这种快速环境变化下将光伏发电功率调节到参考值。与pref=2 kW的测试条件相比,此测试条件下的跟踪误差更大,因为其功率参考值更小。此外,与其他两种算法相比,本文算法的稳定时间更短。
算例二:在与算例一类似的测试条件下,研究了所提出的FPPT算法对于运行点移动到MPP左侧的性能,结果如图 9所示。MPP左侧的FPPT运行需要在环境变化时进行更大的电压调整。因此,如图 9(a)和(c)所示,具有固定电压阶跃的FPPT算法(方法1)不能在如此快速的环境变化下将功率调节到其参考值。用图 9(b)和(d)中提出的自适应电压阶跃算法计算更大的电压阶跃值,从而可以产生快速的动态响应。此外,如图 9(a)和(c)中所观察到的,稳态中较小的电压阶跃值可以减小功率振荡。对于pref=1 kW,所提自适应FPPT算法的跟踪误差为14.4%,与具有固定电压阶跃的算法相比,该算法的跟踪误差显著减小(Et-m1=45.8%)。值得注意的是,方法1在此期间无法将光伏功率调节至其参考值,而方法2与方法3相比,其稳定时间要更长。
|
图 9 算例二仿真结果 Fig. 9 Experimental results of case Ⅱ |
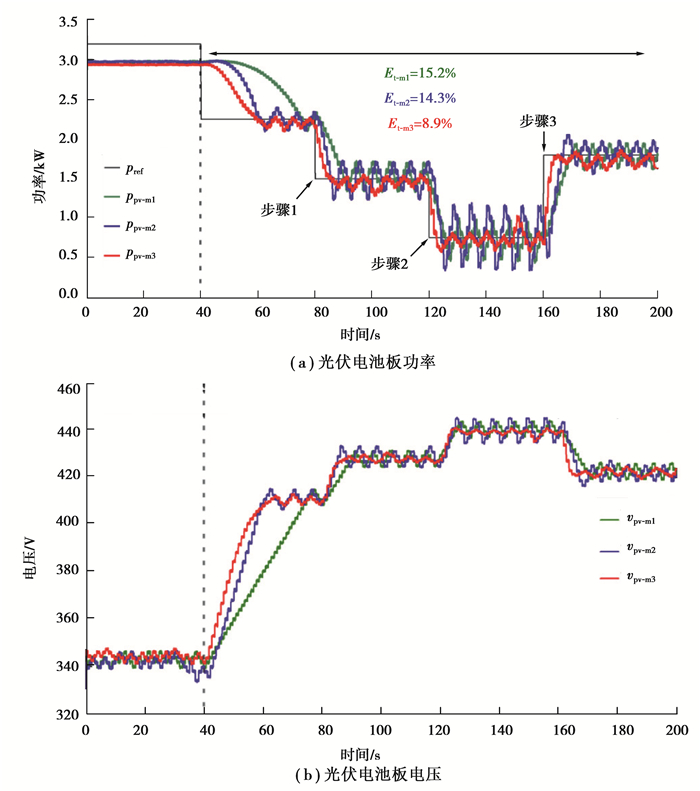
算例三:研究当将运行点移动到MPP的右侧时,所提算法在恒功率基准改变的情况下的性能,结果如图 10所示。在这些试验中,辐照度等于Irr=1 000 W/m2。在t=40 s之前,通过中央控制器对GCPVPP实施MPPT操作,如图 5(b)所示,所提算法通过应用大于光伏系统标称最大功率(即pref=3.5 kW)的功率基准,将光伏电压调节为MPP电压。
|
图 10 算例三仿真结果 Fig. 10 Experimental results of case Ⅲ |
t=40 s时,由外部控制器执行FPPT算法,且pref=2 kW。在t=60 s时,功率基准降低至1.5 kW,而在t=80 s时,功率基准降低至0.5 kW。最后,在t=100 s时,功率基准增加至1.5 kW。图 10(a)中给出了实现上述3种FPPT操作方法的光伏功率,所提自适应FPPT算法(方法3)在跟踪误差较小的情况下,比其他两种传统FPPT算法具有更快的动态响应。在这种情况下的pv电压如图 10(b)所示,在图 10(b)中可以看出,采用所提出的自适应电压阶跃的稳态计算电压阶跃值小于其他算法。
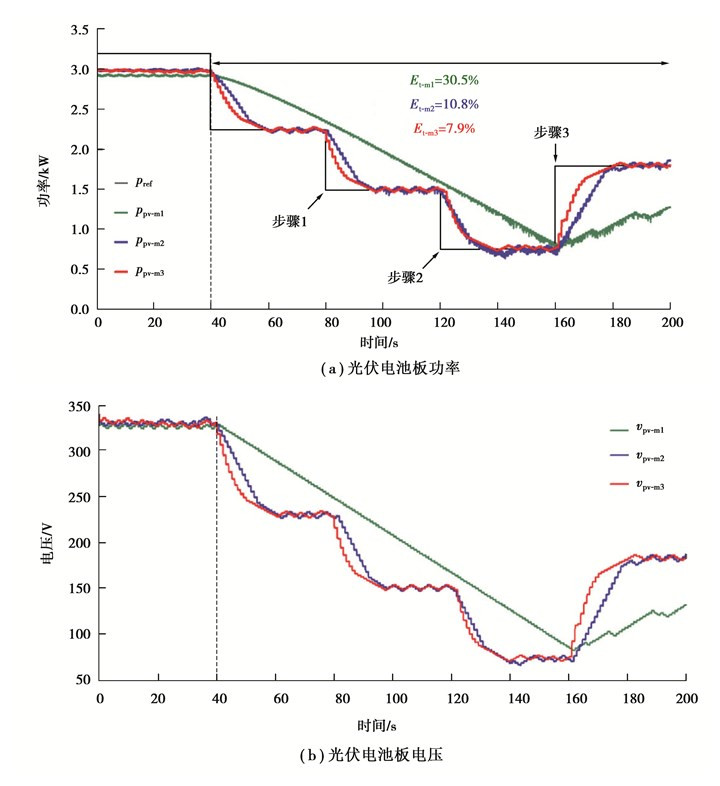
算例四:与算例三类似,研究在功率参考值改变的情况下,当运行点移动到MPP的左侧时,所提出FPPT算法的性能,结果如图 11所示。由此可见,所提出的自适应FPPT算法能够在各种运行条件下,将光伏发电功率调节到所需的参考功率。相比之下,其他两种算法要么无法产生精确的恒定功率,要么动力学特性缓慢。
|
图 11 算例四仿真结果 Fig. 11 Experimental results of case Ⅳ |
表 2和表 3为不同算法跟踪误差和稳定时间的数值比较。与其他两种算法相比,采用自适应电压阶跃FPPT算法的跟踪误差较小。此外,该算法在所有测试条件下的稳定时间都较短,证明了该算法的有效性。也就是说,本文算法可以实现快速、准确、灵活的光伏并网系统有功功率跟踪。
| 表 2 基于跟踪误差的实验结果比较 Table 2 Comparison of experimental results based on the tracking error |
| 表 3 基于设置时间的实验结果比较 Table 3 Comparison of experimental results based on the settling time |
提出了一种适用于光伏电池板电压基准计算的自适应FPPT算法,该算法可将光伏电池板的输出功率调节到一定的功率基准。该算法的主要目标是解决由于GCPVPPs的增长而可能出现的电力系统难题(如过电压),基于瞬时功率误差自适应计算电压阶跃,得到了快速环境变化下的动态响应。通过在控制器中增加额外的测量采样,区分光伏串的特定电压基准变化对光伏功率的影响与环境变化的影响,根据光伏串的工作点计算电压阶跃,减小了稳态时的功率振荡。此外,如果目标功率参考值大于光伏串的最大可用功率,则该算法在MPP下运行,其性能与传统MPPT算法相当。最后通过3 kVA的实验装置仿真证明了所提自适应FPPT算法在不同条件下的灵活性,在所有的仿真测试中,该算法的跟踪误差都有显著的降低。仿真结果证明了所提出的FPPT算法作为现有MPPT算法在GCPVPPs中的附加功能的适用性和有效性。
| [1] |
Gupta A, Chauhan Y K, Pachauri R K. A comparative investigation of maximum power point tracking methods for solar PV system[J]. Solar Energy, 2016, 136: 236-253. DOI:10.1016/j.solener.2016.07.001 |
| [2] |
刘云, 应康, 辛焕海, 等. 基于二次插值法的光伏发电系统控制策略[J]. 电力系统自动化, 2012, 36(21): 29-35. Liu Y, Ying K, Xin H H, et al. A control strategy for photovoltaic generation system based on quadratic interpolation method[J]. Automation of Electric Power Systems, 2012, 36(21): 29-35. (in Chinese) |
| [3] |
Sangwongwanich A, Yang Y H, Blaabjerg F. A sensorless power reserve control strategy for two-stage grid-connected PV systems[J]. IEEE Transactions on Power Electronics, 2017, 32(11): 8559-8569. DOI:10.1109/TPEL.2017.2648890 |
| [4] |
张露江, 张利, 杨要伟, 等. 基于改进贝叶斯网络的风机齿轮箱自动诊断策略研究[J]. 电力系统保护与控制, 2019, 47(19): 145-151. Zhang L J, Zhang L, Yang Y W, et al. Research on automatic diagnosis strategy of wind turbine gearbox based on improved Bayesian network[J]. Power System Protection and Control, 2019, 47(19): 145-151. (in Chinese) |
| [5] |
倪雨, 郝帅翔. 扰动观测法控制MPPT系统运动特性分析[J]. 电子学报, 2015, 43(7): 1388-1394. Ni Y, Hao S X. Motion characteristics analysis of P & Q control MPPT system[J]. Acta Electronica Sinica, 2015, 43(7): 1388-1394. (in Chinese) DOI:10.3969/j.issn.0372-2112.2015.07.021 |
| [6] |
高嵩, 罗浩, 何宁, 等. 基于MPPT的新型变步长增量电导法的研究[J]. 电气传动, 2015, 45(2): 16-19, 49. Gao S, Luo H, He N, et al. Research on a new method for variable step size INC based on maximum power point tracking[J]. Electric Drive, 2015, 45(2): 16-19, 49. (in Chinese) DOI:10.3969/j.issn.1001-2095.2015.02.004 |
| [7] |
赵亮, 刘友波, 余莉娜, 等. 基于深度信念网络的光伏电站短期发电量预测[J]. 电力系统保护与控制, 2019, 47(18): 11-19. Zhao L, Liu Y B, Yu L N, et al. Short-term power generation forecast of PV power station based on deep belief network[J]. Power System Protection and Control, 2019, 47(18): 11-19. (in Chinese) |
| [8] |
朱梓嘉, 肖辉, 赵帅旗, 等. 基于并行组合进化算法的光伏阵列最大功率点追踪[J]. 电力系统保护与控制, 2020, 48(4): 1-10. Zhu Z J, Xiao H, Zhao S Q, et al. Maximum power point tracking of photovoltaic array based on parallel combination evolutionary algorithm[J]. Power System Protection and Control, 2020, 48(4): 1-10. (in Chinese) |
| [9] |
潘明明, 孙晓辉, 于建成. 基于改进Kalman滤波块状态估计方法的分布式光伏发电预测[J]. 供用电, 2019, 36(2): 56-60. Pan M M, Sun X H, Yu J C. A distributed photovoltaic generation prediction based on improved kalman filter block state estimation method[J]. Distribution & Utilization, 2019, 36(2): 56-60. (in Chinese) |
| [10] |
Ghasemi M A, Foroushani H M, Parniani M. Partial shading detection and smooth maximum power point tracking of PV arrays under PSC[J]. IEEE Transactions on Power Electronics, 2016, 31(9): 6281-6292. DOI:10.1109/TPEL.2015.2504515 |
| [11] |
Yang Y H, Blaabjerg F, Wang H. Constant power generation of photovoltaic systems considering the distributed grid capacity[C]//2014 IEEE Applied Power Electronics Conference and Exposition-APEC 2014, March 16-20, 2014, Fort Worth, TX, USA. IEEE, 2014.
|
| [12] |
Urtasun A, Sanchis P, Marroyo L. Limiting the power generated by a photovoltaic system[C]//10th International Multi-Conferences on Systems, Signals & Devices 2013(SSD13), March 18-21, 2013, Hammamet, Tunisia. IEEE, 2013.
|
| [13] |
Escobar G, Pettersson S, Ho C N M, et al. Multi-sampling maximum power point tracker (MS-MPPT) to compensate irradiance and temperature changes[J]. IEEE Transactions on Sustainable Energy, 2017, 8(3): 1096-1105. DOI:10.1109/TSTE.2017.2654965 |
| [14] |
Tafti H D, Maswood A I, Konstantinou G, et al. A general constant power generation algorithm for photovoltaic systems[J]. IEEE Transactions on Power Electronics, 2018, 33(5): 4088-4101. DOI:10.1109/TPEL.2017.2724544 |
| [15] |
Salman, Ai X, Wu Z Y. Design of a P-&-O algorithm based MPPT charge controller for a stand-alone 200W PV system[J]. Protection and Control of Modern Power Systems, 2018, 3: 25. DOI:10.1186/s41601-018-0099-8 |
| [16] |
Kollimalla S K, Mishra M K. A novel adaptive P&O MPPT algorithm considering sudden changes in the irradiance[J]. IEEE Transactions on Energy Conversion, 2014, 29(3): 602-610. DOI:10.1109/TEC.2014.2320930 |
 2021, Vol. 44
2021, Vol. 44

