2. 重庆大学 输配电装备及系统安全与新技术国家重点实验室, 重庆 400044
2. State Key Laboratory of Power Transmission Equipment & System Security and New Technology, Chongqing University, Chongqing 400044, P. R. China
随着海洋资源的不断开发,海岛电力需求增加[1],由于海岛常面临着各种自然灾害,海岛微电网有故障停运的危险。当海岛微电网发生故障全部停电时,需要进行黑启动恢复系统。首先启动具有自启动能力的电源,然后带动没有自启动能力的电源,从而达到恢复整个系统的目的[2]。
现有的文献中主要研究黑启动电源的控制和启动策略。首先对黑启动电源的特点进行研究[3-5],黑启动电源需要直流侧有储能装置且可以建立低压配电网[2],燃气轮机、柴油机和储能等都可以作为黑启动电源。文献[3]对黑启动中柴油机的性能指标进行评估,分析了黑启动柴油机容量选择的两个指标,能够满足负荷容量和过载容量,对电网中的黑启动柴油机配置进行指导。同样,风电场也可以作为黑启动电源,风电场要作为黑启动电源需要储能系统的配合,一种储能容量大小确定方法被提出,以减小储能投资成本和提供足够的黑启动容量[4]。同时,整个微电网也可以作为复杂大电网的黑启动电源,文献[5]以恢复系统的发电量最大和负荷损失量最小为目标构建黑启动微电网网架重构模型,最后构建路径综合评价指标计算节点恢复路径。在黑启动时,对黑启动电源良好的控制可以保证黑启动的稳定,配备储能系统的光伏发电装置可以提高电网的黑启动能力,一种分层优化策略被提出以优化光伏数量和储能充放功率,确保光伏发电功率满足需求,但是没有考虑对电压和频率波动的影响[6]。文献[7]提出的方法有效解决了黑启动过程中电压频率波动的问题,采用多代理系统对全黑微电网进行全自动黑启动,针对黑启动电源控制方式模式切换时候带来的电压和频率波动问题,采用功率锁存器和预同步方法可以有效解决。
黑启动策略通常采用评估的方法进行选择。文献[8]利用综合评价法综合考虑了黑启动的6个指标,采用层次分析法和变异系数法对主客观指标的权重进行计算,然后用逼近理想解排序法对黑启动电源进行排名,最终确定黑启动电源的串行启动顺序。文献[9]在串行恢复的基础上,采用改进熵权法对黑启动电源的指标进行权重评估,考虑节点和线路的重要程度,建立以线路和节点平均重要程度最大为目标的优化模型,优化恢复线路,并采用粒子群算法对模型求解。文献[10]提出了一种基于串行恢复策略的光伏和混合储能系统微电网黑启动策略。首先以储能作为主参考源运行VF控制方式启动建立标准电压和频率,然后评估负载与光伏系统的连接要求,并根据该要求调整PQ控制的微源的处理情况,最终恢复相应的负载和光伏装置。文献[11]采用近邻传播聚类的权重确定法可以有效体现决策矩阵的细微变化,使得黑启动方案的评估有更高的准确性。采用并行的恢复方法可以加快黑启动速度[12-15],首先需要对黑启动电源进行分区分配,针对黑启动电源分配问题,文献[13]提出一种新的建模方法,利用通电和分配二进制量绘制黑启动单元和非黑启动单元的能力曲线,同时优化负荷恢复顺序,能够结合黑启动过程制定分配问题。文献[14]将没有黑启动能力的电源分区分配到黑启动电源中,以形成区域电源,再依据负荷对区域电源的依赖程度对负荷分区,构建以源荷依赖程度最大为目标优化模型,确定负荷恢复范围,并且建立以恢复过程中源荷依赖度积累效率最高为目标的优化模型,计算得到最佳的负荷恢复顺序。文献[15]对黑启动单元和黑启动路径同时进行评估,将Dijkstra算法和潮流计算结合,分析黑启动指标大小,最后得到满足约束的最佳黑启动方案。针对含可再生能源的电网的黑启动策略,文献[16]提出针对风光储作为黑启动电源的评价指标,并基于新能源发电特性设计黑启动电源的预测模型,由预测模型设计控制方法和滚动优化模型,减小了源荷差、储能充放电量和风光储的启停次数。进一步,文献[17]提出一种基于模型预测控制的黑启动电源优化启动方法,将发电动机启动顺序建模为混合整数线性规划模型,然后通过微电网中可再生能源的不确定性概率分布对其进行建模,最后采用MPC技术优化发电动机启动方案,减小了负荷损失量,增大了系统容量。为了降低对可再生能源发电的概率分布和先验数据的依赖性,采用数据驱动的机会约束规划模型解决可再生能源的不确定性,得到可再生能源参与黑启动的最优方案[18]。
以上研究主要是针对电网中电源启动方案的选择,对于负荷恢复和路径恢复的研究还有待深入。此外,现有黑启动在负荷恢复方面全都考虑的是有功负荷,没有考虑异步电动机等在恢复时会极大影响系统电压的感性无功负荷,但是对于海岛微电网,存在大量的基于异步电动机的感性负荷,传统的黑启动策略无法适用,所以笔者提出了一种基于虚拟有功负荷的海岛微电网带大负荷黑启动优化策略。首先,提出黑启动电源启动顺序优化模型,利用熵权法对不同DG的黑启动能力进行评价,并确定其启动顺序;接着,提出虚拟有功负荷构造方法,将大型异步电动机与电容并联,黑启动时由电容向异步电动机提供无功,从而整体表现为有功负荷;其次,提出负荷恢复优化模型,以负荷恢复量最大和负荷恢复重要程度最大作为目标并利用PSO算法求解;最后,提出DG与负荷的路径恢复优化模型并利用最小生成树的Prim算法进行求解。
1 海岛微电网黑启动电源优化策略海岛微电网黑启动过程中,带有黑启动能力的分布式电源(DG)的启动顺序是黑启动能否成功的关键。为了简化黑启动的过程,本文采用离散时间段的方法,将整个黑启动过程分成多个时步,针对每一个时步建立相应模型并求解,并将每个时步的最优方案按时序组合到一起,得到最终的黑启动方案。
参考传统电网的机组恢复顺序[19],结合微电网黑启动的特性以及不同DG对黑启动过程的影响,文献[20]提出黑启动电源启动顺序的一般原则,但是该原则含有较大的主观性,无法以定量的方法确定具体的黑启动电源启动顺序。为了进一步提高黑启动电源启动顺序的合理性,采用熵权法,综合考虑DG的容量、启动时间、带载能力、以及调频调压能力,对不同类型的DG进行黑启动能力评价进而确定DG的启动顺序。
熵权法评价步骤如下:
1) 对评价方案的评价指标建立评价矩阵。假设存在n个评价方案,每个方案包含m个评价指标,则初始评价矩阵D为:
| $ \boldsymbol{D}=\left(d_{i j}\right)_{n \times m}=\left[\begin{array}{cccc} d_{11} & d_{12} & \cdots & d_{1 m} \\ d_{21} & d_{22} & \cdots & d_{2 m} \\ \ldots & \cdots & \cdots & \ldots \\ d_{n 1} & d_{n 2} & \cdots & d_{n m} \end{array}\right]_{n \times m}。$ | (1) |
2) 对初始矩阵进行标准化处理得到标准化矩阵Y。根据效益型指标和成本型指标分为以下2种标准化方法,效益型指标的数值越大性能评价越好,成本型则反之。
效益型指标标准化:
| $ y_{i j}^{+}=\frac{d_{i j}-\min \limits_{i}\left(d_{i j}\right)}{\max \limits_{i}\left(d_{i j}\right)-\min \limits_{i}\left(d_{i j}\right)}, i=1,2, \cdots, n。$ | (2) |
成本型指标标准化:
| $ y_{i j}^{-}=\frac{\max \limits_{i}\left(d_{i j}\right)-d_{i j}}{\max \limits_{i}\left(d_{i j}\right)-\min \limits_{i}\left(d_{i j}\right)}, i=1,2, \cdots, n。$ | (3) |
标准化后矩阵Y为:
| $ \boldsymbol{Y}=\left(y_{i j}\right)_{n \times m}=\left[\begin{array}{cccc} y_{11} & y_{12} & \cdots & y_{1 m} \\ y_{21} & y_{22} & \cdots & y_{2 m} \\ \cdots & \cdots & \cdots & \cdots \\ y_{n 1} & y_{n 2} & \cdots & y_{n m} \end{array}\right]_{n \times m}。$ | (4) |
3) 各评价指标的熵值Pj为:
| $ \boldsymbol{P}_{j}=-k \sum\limits_{i=1}^{n} y_{i j} \ln \left(y_{i j}\right), j=1,2, \cdots, m, $ | (5) |
式中k是一个与样本有关的常数,满足Pj∈[0, 1],规定yij=0时,yijln(yij)=0。
4) 利用熵值计算各评价指标的权重wj为:
| $ \boldsymbol{w}_{j}=\frac{1-\boldsymbol{P}_{j}}{m-\sum\limits_{j=1}^{m} \boldsymbol{P}_{j}}, j=1,2, \cdots, m, $ | (6) |
式中wj越大表示权重越大,该属性越重要;反之属性越不重要。
5) 所有方案的评价值矩阵S为:
| $ \boldsymbol{S}_{n \times 1}=\boldsymbol{Y}_{n \times m} w_{m \times 1}, $ | (7) |
式中S中所代表的数值为各方案的综合评分,数值越大,则该方案越适合。按照以上步骤,取评分最高的1个DG作为微电网的黑启动电源, 其余DG则按照评价值由高到低的顺序进行启动。
2 海岛微电网黑启动负荷恢复优化模型海岛微电网黑启动过程中,为了尽快恢复重要负荷供电,以负荷恢复量最大和负荷恢复重要程度最大作为目标函数并综合考虑负荷恢复约束和组网约束进行黑启动负荷恢复建模。
2.1 黑启动感性负荷处理方法由于海岛特殊的地理环境和经济特点,海岛微电网中电力负荷呈现特殊性。海岛地区基本上以发展岛上旅游业,渔业养殖或者造船业为主,这些产业导致海岛微电网会存在大量的基于大型异步电动机的负荷。在黑启动过程中,由于异步电动机在启动时需要吸收大量的感性无功,导致节点的电压降低,影响黑启动过程。所以在本文中提出虚拟有功负荷构造方法,将异步电动机等感性负荷与并联补偿电容一起等效为有功负荷进而考虑优化问题。并联电容的补偿方式、补偿容量以及具体虚拟有功负荷构造的方法在下文中具体介绍。
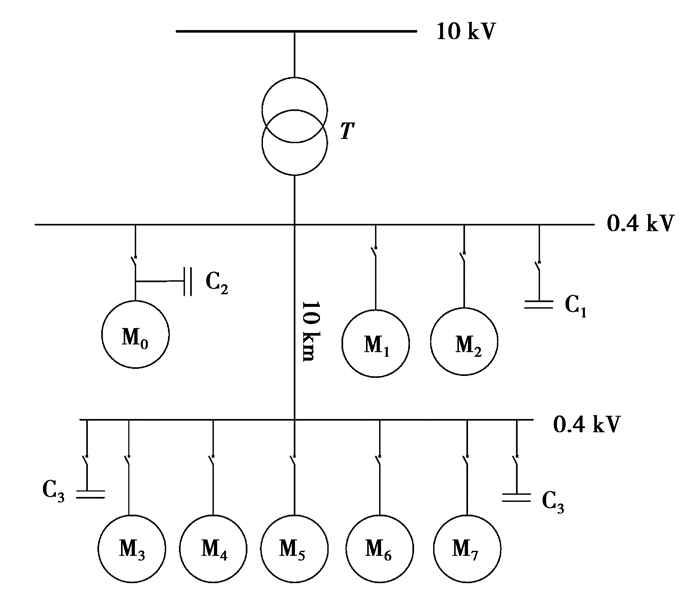
2.1.1 并联电容补偿方式选择并联电容补偿方式的选择通常要兼顾补偿效果和实际网络情况而定。并联电容补偿方式有集中补偿、分散补偿、就地补偿3种[21]。3种补偿方式的示意图如图 1所示。
|
图 1 并联电容补偿方式图 Fig. 1 Parallel capacitance compensation mode |
集中补偿主要将补偿电容安装在变电站的低压母线上,如图 1中C1所示。这种补偿方式利用率高,操作和运行管理方便,适用于线路末端负荷比较稳定、负荷比较集中且容量比较大的情况。
分散补偿是指将补偿电容按照无功负荷的分布情况,分组安装在相应的母线上,如图 1中C3所示。这种补偿方式实现了无功功率不再通过高压主干线路进行输送,减少了主干线路和变压器的有功损耗,具有较好的经济效益且接线简单,运行维护工作量少,适用于线路负荷离主变较远,负荷点较多且互相之间距离较远的情况。
就地补偿是指将补偿电容安装在某个电动机或功率较大的负载旁边,与其用同一台开关控制,同时投运或断开,如图 1中C2所示。这种补偿方式可以根据负荷的运行状态就地补偿无功,补偿效果最好,并且可以避免无功功率在系统中的流动,减少线路有功损耗。
针对海岛微电网中电力负荷特殊性,存在大量的基于大型异步电动机的感性负荷,为了提高补偿效果,这里采用并联电容就地补偿的方式对异步电动机等感性负荷进行补偿。
2.1.2 并联电容补偿容量确定在选择并联电容补偿方式之后,需要进行补偿容量的确定,具体有以下3种确定方式。
1) 功率因数确定法
首先根据所有用电设备的参数计算出负荷总平均功率Pa,以及补偿前的平均功率因数cos φ1,若补偿后需要实现平均功率因数为cos φ2,那么无功补偿容量为
| $ Q_{\mathrm{C}}=\eta P_{\mathrm{a}}\left(\tan \varphi_{1}-\tan \varphi_{2}\right), $ | (8) |
式中:QC为并联电容无功补偿容量; η为日平均负载率,一般取0.7~0.8之间; φ1为补偿前的负载功率因数角; φ2为补偿后的负载功率因数角。
2) 变压器容量确定法
无功补偿容量可以根据变压器容量来确定,其公式为
| $ Q_{\mathrm{C}}=\beta W_{\mathrm{L}} $ | (9) |
式中: QC为并联电容无功补偿容量,β为无功补偿经验系数,一般取值为1/3左右,WL为变压器的容量。
3) 单台电动机补偿法
对单台电动机的无功补偿容量可以根据下式来确定。
| $ Q_{\mathrm{C}} \leqslant \sqrt{3} U I_{0}, $ | (10) |
式中:QC为并联电容无功补偿容量; U为电动机的额定电压; I0为电动机的空载电流。
为了提高电容补偿的效果,采用单台电动机补偿法确定无功补偿容量QC之后,并联补偿电容C的值可以根据式(11)计算。
| $ C=\frac{k Q_{\mathrm{C}}}{2 {\rm{ \mathsf{ π} }} f U^{2}}, $ | (11) |
式中:k为补偿度,表示并联电容实际补偿的无功容量与计算得到无功补偿容量QC的比值,即并联电容实际补偿的无功容量为kQC,k<1为欠补偿、k=1为全补偿、k>1为过补偿。对于不同的网络结构和负荷结构,根据配电网络对于补偿效果的不同要求,并联补偿度的选择有所不同,一般补偿度k可在0~2的范围内,f为系统频率,U为系统电压。
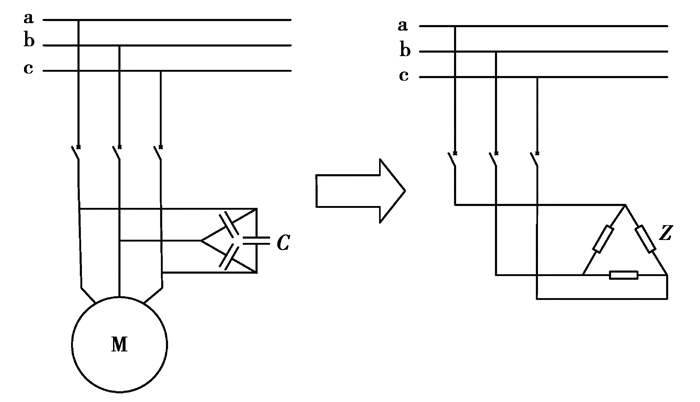
2.1.3 虚拟有功负荷构造方法由于异步电动机等感性负荷在启动瞬间的无功需求是正常情况下的3~5倍,为了解决其恢复时无功需求过大导致系统电压降低的问题,提出一种虚拟有功负荷构造方法,将大型异步电动机与补偿电容并联,在启动过程中由电容向异步电动机提供无功,使得电源向异步电动机提供的感性无功减少,从而使供电线路电流减小,线路电压降减小实现异步电动机负荷侧电压升高。若并联电容补偿方式以及补偿容量选取合适,则整体上表现为在黑启动过程中不再考虑异步电动机恢复时的无功需求,将其等效为有功负荷进行考虑,从而提高黑启动成功率。具体的虚拟有功负荷构造方法如图 2所示。
|
图 2 虚拟有功负荷构造方法图 Fig. 2 Virtual active load construction method |
为了提高并联电容补偿效果,避免无功功率在系统中流动,采用就地补偿的方式,在大型异步电动机旁边并联补偿电容,与其用同一台开关控制,并根据2.1.2节介绍的单台异步电动机补偿法确定其无功补偿需求量QC然后选择具体的补偿度k计算出并联补偿电容C的值。
假设异步电动机启动时有功需求为P,无功需求为QL,按照本文虚拟有功负荷构造的方法确定无功补偿量kQC,那么最终等效的有功负荷PV为:
| $ P_{\mathrm{V}}=P+j Q_{\mathrm{L}}-j k Q_{\mathrm{C}} \approx P。$ | (12) |
为了实现微电网黑启动过程中负荷恢复量最大和负荷恢复重要程度最大,将整体黑启动过程中负荷恢复模型的目标函数设定为:
| $ \left\{\begin{array}{l} F=\max \sum\limits_{k=1}^{K} \gamma F_{1 k}+(1-\gamma) F_{2 k}, \\ F_{1 k}=\max \sum\limits_{i=1}^{n_{L k}} a_{L i} P_{L i} ,\\ F_{2 k}=\max \sum\limits_{i=1}^{n_{L k}} a_{L i} R_{L i}, \\ R_{L i}=\lambda_{L i} P_{L i} 。\end{array}\right. $ | (13) |
式中:总目标函数F表示黑启动过程负荷恢复量最大和负荷恢复重要程度最大,K表示整体黑启动时步总数;目标函数F1k表示第k个时步所恢复的负荷功率最大;目标函数F2k表示第k个时步所恢复的负荷重要程度最大;这里认为负荷恢复量最大和负荷恢复重要程度最大2个目标同等重要,所以在总目标函数F中设定权重γ值为0.5;nLk为第k时步待恢复负荷的数量;aLi为第i个负荷的启动状态,aLi=1表示负荷恢复,aLi=0表示负荷未恢复;PLi表示第i个负荷的功率;RLi为第i个负荷的重要程度;λLi为第i个负荷的等级权值。
通过《供配电系统设计规范》GB 50025—95可知负荷分为一、二、三级,其中一级负荷对供电可靠性的要求最高,若发生供电故障,造成的后果也最严重,此类负荷要求供电不能间断,称之为敏感负荷。二级负荷为可调节负荷,在条件允许的情况下要尽可能地保证供电不间断。三级负荷是非敏感性负荷,对可靠性的要求较低,微网发生故障时对第三种负荷的影响较小。将不同等级的负荷赋予不同权值以区别其重要性,采用文献[9]所述的负荷等级的权值赋权方法,取一级负荷权值为1,二级负荷权值为0.2,三级负荷权值为0.03。
2.3 黑启动负荷恢复约束条件黑启动过程中必须满足如下约束条件,包括负荷恢复约束和组网约束。
1) 负荷恢复约束:
| $ \sum\limits_{i=1}^{n_{L k}} a_{L i} P_{L i} \leqslant \sum\limits_{i=1}^{m} P_{G i}, $ | (14) |
| $ P_{L i} \leqslant P_{\operatorname{eachmax}}=\Delta f \max \sum\limits_{i=1}^{n_{L k}} \frac{P_{L i}}{f_{L i}}。$ | (15) |
式中:PGi表示已接入的第i个DG的功率,m表示已接入DG的个数。Peachmax表示每次接入负荷的最大限度,Δfmax表示系统最大频率下降值,fLi表示系统当前负荷率下的频率响应。负荷的恢复约束主要为两个:一是功率约束,所有恢复负荷的功率之和应小于该时步接入DG的输出功率;另一个是负荷单次接入约束,每次接入负荷的最大功率引起的频率波动应不超过其最大波动限度。
2) 组网约束:
| $ \begin{array}{ll} P_{G i \min } \leqslant P_{G i} \leqslant P_{G i \max } & i=1,2, \cdots, n_{G}, \\ Q_{G i \min } \leqslant Q_{G i} \leqslant Q_{G i \max } & i=1,2, \cdots, n_{G}, \\ U_{i \min } \leqslant U_{i} \leqslant U_{i \max } & i=1,2, \cdots, n_{P}, \\ P_{X i} \leqslant P_{X i}^{\max } & i=1,2, \cdots, n_{L}。\end{array} $ | (16) |
式中:Pimin和Pimax分别为第i个DG有功出力的下限和上限;Qimin和Qimax分别为第i个DG无功出力的下限和上限;Uimin和Uimax分别为节点i的电压下限和上限;nG为系统已启动DG的数量;nP为系统节点总数;nL为系统支路总数;PXi为第i条线路流过的有功功率;PXimax为允许第i条线路流过的最大有功功率。
3 海岛微电网黑启动恢复路径优化模型黑启动恢复路径优化是指在确定DG以及对应负荷的恢复顺序后,求解该时步DG与负荷的最优恢复路径。由于电源和负荷之间的恢复线路有很多选择,主要考虑每条线路的操作时间,目标是选择合适的恢复路径让整个黑启动过程线路操作总时间最短。由于每次路径恢复时包含一个黑启动电源和多个负荷,所以利用最小生成树的概念并采用Prim算法对恢复路径进行寻优从而减少黑启动恢复时间。
3.1 微电网线路赋权方法DG与负荷之间的线路连接像网络一样,可以把整个微电网网络看作“图”,把DG和负荷看作是图中的点,连接线路看作图中的线,而线路操作时间的期望值作为线路的权值。采用文献[22]所述的线路操作时间期望值的计算方法,根据操作人员经验确定乐观操作时间M、悲观操作时间N以及最可能估计时间K,而线路的实际操作时间则在M和N之间呈贝塔分布,操作时间ti的期望E(ti)和方差σi分别为:
| $ \begin{aligned} &E\left(t_{i}\right)=\frac{M+4 K+N}{6} ,\\ &\sigma_{i}=\frac{N-M}{6} 。\end{aligned} $ | (17) |
式中:ti为线路i的操作时间;E(ti)为操作时间ti的期望值;σi为操作时间ti的方差。
3.2 基于最小生成树Prim算法的恢复路径优化最小生成树是指在一个具有N个顶点的带权连通图G中,如果存在某个子图G′,其包含了图G中的所有顶点,只有N-1条边且不形成回路,并且子图G′的各边权值之和最小,则称G′为图G的最小生成树。Prim算法从某一个顶点s开始,每次迭代选择权值最小的边对应的点加入到最小生成树中,逐渐长大覆盖整个连通网的所有顶点,具体算法步骤如下。
1) 图的所有顶点集合为V;初始集合u={s},v=V-u。
2) 在两个集合u,v能够组成的边中,选择一条权值最小的边(u0, v0),加入到最小生成树中,并把v0并入到集合u中。
3) 重复上述步骤,直到最小生成树有N-1条边或者N个顶点为止。
在黑启动恢复过程中,由于每一时步只恢复一个DG,将DG作为路径寻优的起点,在DG和负荷之间寻找一条权值和最小的路径。线路网架恢复分为以下2个步骤:
1) 第一个恢复阶段若负荷只有一个,则求出最短路径、所经过路径、所经过节点;若恢复多个负荷,则把DG和待恢复负荷作为全部顶点,DG作为寻优的起点,利用最小生成树Prim算法选取总权值最小的路径作为恢复的路径。
2) 从第二个启动阶段开始,寻找将要恢复负荷与已恢复路径之间的最短路径,恢复该最短的路径,直到该恢复阶段全部负荷接入。
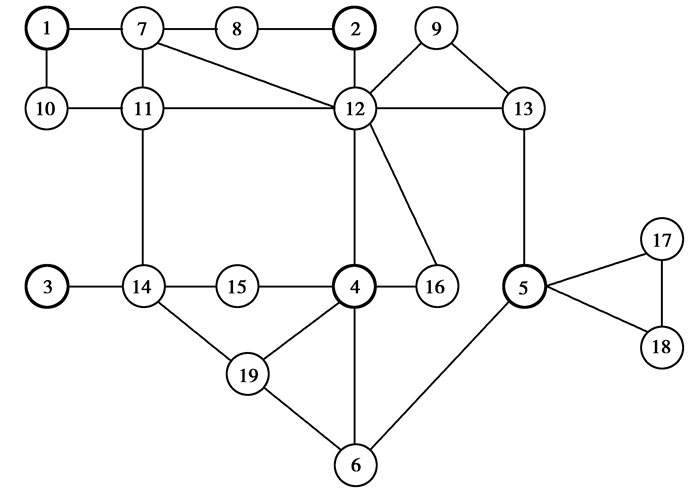
4 算例分析为了验证所提出的基于虚拟有功负荷的海岛微电网黑启动优化策略的可行性,采用IEEE-30节点简化的19节点微电网结构作为测试系统进行仿真实验,如图 3所示,节点1至5为DG,节点6至19为负荷。其中DG的参数如表 1所示,负荷的参数如表 2所示。
|
图 3 19节点微电网结构图 Fig. 3 19-bus microgrid structure diagram |
| 表 1 DG参数评价指标表 Table 1 DG parameter evaluation index |
| 表 2 微电网各负荷数据表 Table 2 Load data of microgrid |
为了验证提出的海岛微电网黑启动优化策略的优势,采用图 3所示的19节点微电网结构进行仿真实验,通过与其他优化方法的黑启动策略进行对比,表明所提策略的优势。
4.1.1 黑启动电源评价影响DG黑启动能力的指标包括DG的容量,启动时间,带载能力和调频调压能力,其中效益型指标包括DG容量、带载能力和调频调压能力,成本型指标包括启动时间。如图 3所示,在微电网中共有5个DG,分别标号为DG1、DG2、DG3、DG4、DG5。
对各个DG进行黑启动能力评价:
1) 初始评价矩阵D
| $ \boldsymbol{D}=\left(d_{i j}\right)_{5 \times 4}=\left[\begin{array}{cccc} 1\ 500 & 4.0 & 5.1 & 95 \\ 500 & 3.2 & 3.7 & 72 \\ 300 & 3.0 & 3.5 & 70 \\ 780 & 3.5 & 3.3 & 85 \\ 600 & 3.4 & 4.0 & 78 \end{array}\right]。$ | (18) |
2) 对初始矩阵标准化处理得到标准阵
| $ \boldsymbol{Y}=\left(y_{i j}\right)_{5 \times 4}=\left[\begin{array}{cccc} 1 & 0 & 1 & 1 \\ 0.167 & 0.8 & 0.222 & 0.08 \\ 0 & 1 & 0.111 & 0 \\ 0.4 & 0.5 & 0 & 0.6 \\ 0.25 & 0.6 & 0.389 & 0.32 \end{array}\right]。$ | (19) |
3) 各评价指标的熵值Pj
取k=(ln n)-1,因为n表示评价方案的个数,在本次仿真中n=5,k=(ln 5)-1。
| $ \boldsymbol{P}_{j}=\left[\begin{array}{llll}0.629 & 0.517 & 0.587 & 0.543\end{array}\right]^{\mathrm{T}}。$ | (20) |
4) 各评价指标的权重wj
| $ \boldsymbol{w}_{j}=\left[\begin{array}{llll}0.215 & 0.280 & 0.240 & 0.265\end{array}\right]^{\mathrm{T}}。$ | (21) |
5) 所有DG的评价值矩阵S
| $ \boldsymbol{S}=\left[\begin{array}{llll}0.720 & 0.334 & 0.307 & 0.399\end{array}\right]^{\mathrm{T}}。$ | (22) |
所以各DG的黑启动能力评价值如表 3所示。
| 表 3 DG的黑启动能力评价表 Table 3 DG black start ability evaluation |
从表 3可以看出,DG1黑启动能力最强,DG3黑启动能力最弱,所以选择DG1作为黑启动主电源,其余DG的启动顺序按照其评价值排序为DG5、DG4、DG2、DG3。
4.1.2 黑启动负荷恢复根据2.1.3节介绍的虚拟有功负荷的构造方法,采用就地补偿的方式,在异步电动机旁边均并联一组电容补偿器。同时为了保证并联电容补偿的有效性和经济性,将补偿度k设定为k=0.9,系统电压等级设为380 V,采用欠补偿方式进行补偿,按照公式(8)求出并联电容值,如表 4所示。
| 表 4 节点电容补偿值 Table 4 Node capacitance compensation value |
在确定补偿电容值之后,在黑启动过程中由电容向异步电动机提供无功,此时异步电动机启动对系统电压的影响很小,相当于在黑启动过程中不再考虑异步电动机的无功需求,整体等效为有功负荷进行考虑,按照2.2节和2.3节建模的方法,并采用PSO算法对该模型进行求解,结果如表 5所示。
| 表 5 黑启动负荷恢复顺序表 Table 5 Black start load recovery sequence |
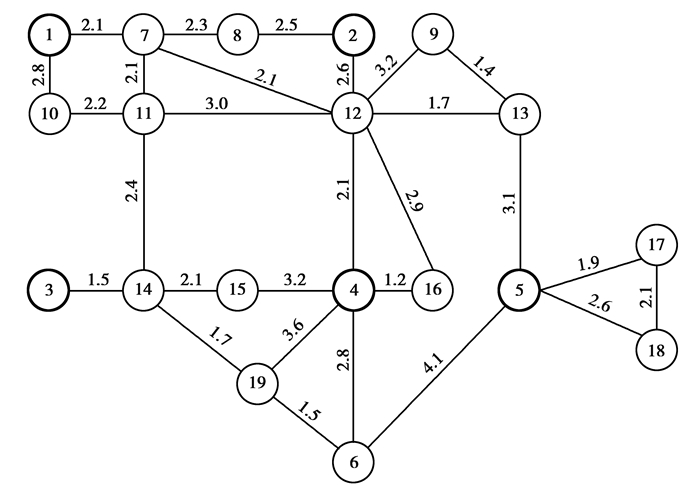
按照3.1节介绍的方法,对微电网中各条线路赋权值,各个节点之间线路权值如图 4所示。
|
图 4 19节点微电网线路权值图 Fig. 4 19-bus microgrid line weight diagram |
根据最小生成树的Prim路径寻优算法,每个恢复时步中,把DG作为路径寻优的起点,在DG和负荷之间寻找一条权值和最小的路径。最终微电网整体黑启动优化策略如表 6所示。
| 表 6 微电网黑启动优化策略 Table 6 Optimization strategy for black start of microgrid |
针对同样的微电网结构以及相应参数,采用其他优化方法制定黑启动策略进行对比,在满足微电网黑启动组网约束的前提下,首先根据文献[23]所述的层次分析法(AHP)对黑启动电源进行评价,并按照其评价值由大到小顺序启动电源,然后优先恢复距离DG近的负荷,接着根据文献[24]所述的Dijkstra算法进行求解电源与负荷之间的恢复路径,并将该对比策略称为A-D优化黑启动策略,其结果如下表所示。
根据表 6和表 7的结果可以看出,所提出的海岛微电网黑启动优化策略,在5个时步内恢复了所有负荷,相比A-D优化策略,负荷恢复量提高了46.8%,并且考虑了恢复负荷的重要程度,实现了每个时步负荷恢复量最大以及负荷重要程度最高的目标;此外,本文的黑启动优化策略路径恢复总时间为37.6 min,A-D优化黑启动策略路径恢复总时间为40.9 min,路径恢复总时间减少了8.8%,提高了微电网黑启动的效率。
| 表 7 A-D优化黑启动策略 Table 7 A-D optimized black start strategy |
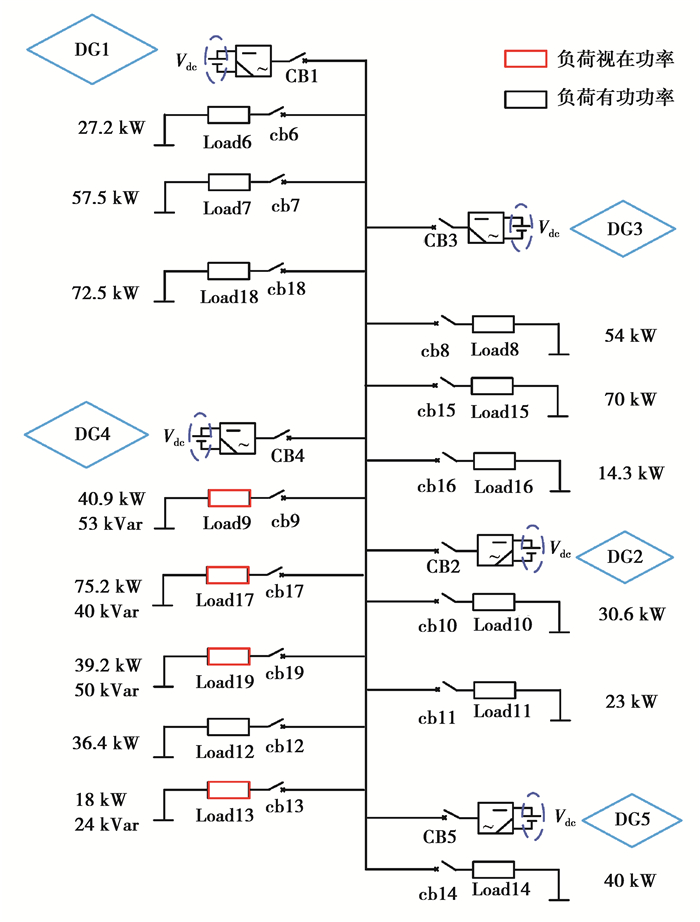
为了验证所提出的在黑启动过程中虚拟有功负荷构造方法的有效性,根据算例1中微电网参数及黑启动优化策略,在Simulink平台搭建相应模型进行黑启动仿真。由于在黑启动路径恢复阶段采用的是最小生成树算法,所以最终恢复的微电网结构是一个辐射型网络,仿真模型如图 5所示。
|
图 5 微电网黑启动仿真模型图 Fig. 5 Microgrid black start simulation model |
黑启动仿真步骤如下:
1) 在0 s时将DG1作为黑启动主电源,采用VF控制方式启动,建立低压配电网。
2) 在1 s时恢复节点15和18的负荷,即Load15和Load18,作为重要负荷启动。
3) 在2 s时采用PQ控制方式启动DG5,并恢复节点8和17的负荷,即Load8和Load17。
4) 在3 s时采用PQ控制方式启动DG4,并恢复节点6、7和14的负荷,即Load6、Load7和Load14。
5) 在4 s时采用PQ控制方式启动DG2,并恢复节点9、11、12和19的负荷,即Load9、Load11、Load12和Load19。
6) 在5 s时采用PQ控制方式启动DG3,并恢复节点10、13和16的负荷,即Load10、Load13和Load16。
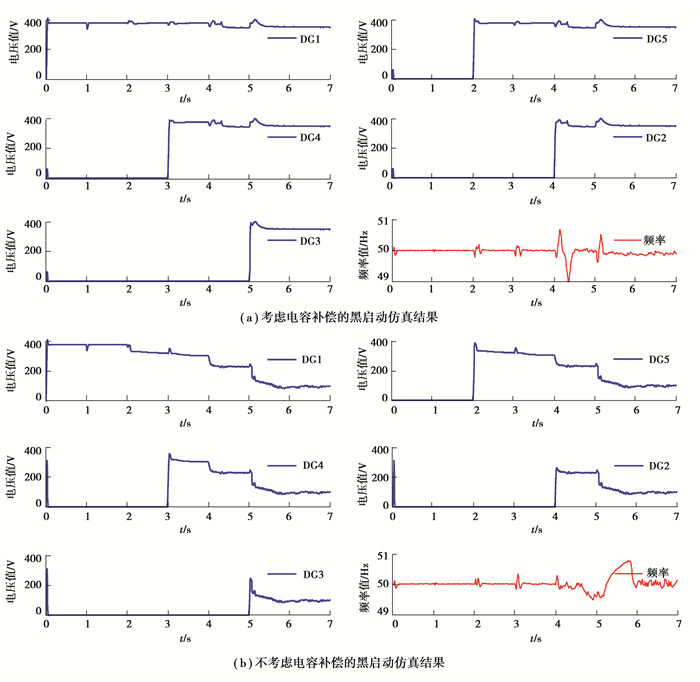
由于节点9、13、17、19的负荷中含有感性无功负荷,所以在恢复这些节点的负荷时,根据2.1节提出的对感性负荷的处理方法,对其进行并联电容补偿进行黑启动仿真;同时为了验证电容补偿的效果,设置一组没有电容补偿的对照组进行黑启动仿真,黑启动仿真结果如图 6所示。
|
图 6 黑启动仿真结果图 Fig. 6 Results of black start simulation |
如图 6(a)所示,整个黑启动仿真过程中电压波动范围在370~380 V,总体较稳定,频率波动范围在49.0~50.5 Hz,且整个过程中低于频率稳定阈值49.5 Hz的时间仅为0.1 s,符合工程应用规范,表明本次黑启动仿真成功。在0~1 s期间由黑启动主电源以VF控制方式启动,建立稳定的电压和频率;在2 s时恢复的负荷中仅包含少量的无功负荷,同时由于并联电容的补偿作用,对系统电压基本没有产生影响;在4 s和5 s恢复的负荷中含有较多的无功负荷,由于并联电容的补偿作用,所以只产生很小幅度的电压降落,不影响整个黑启动过程,同时由于无功负荷以及并联补偿电容的接入,频率在4 s和5 s会有一个瞬时的小幅波动然后恢复到稳定值的过程。如图 6(b)所示,整个黑启动仿真过程中电压大幅下降,表明本次黑启动仿真失败。在2 s、4 s和5 s时恢复的负荷中包含无功负荷,由于没有并联电容的补偿作用,系统电压开始大幅下降导致整个系统电压崩溃,同时由于无功负荷的接入,频率也会有一个小幅度波动。对比图(a)和图(b)结果,表明本文中提出的对黑启动过程中感性负荷的处理方法是有效的,该方法可以实现在黑启动过程中明显减小感性负荷对系统电压造成的影响,保证黑启动过程中电压稳定。
5 结束语针对海岛微电网的特殊性,提出了一种基于虚拟有功负荷的海岛微电网黑启动优化策略。在传统黑启动策略的基础上提出虚拟有功负荷构造方法,在黑启动过程中将大型异步电动机与电容并联,由电容补偿异步电动机的无功需求,从而整体表现为有功负荷,降低异步电机等感性负荷对黑启动的影响,提高黑启动成功率;此外,建立以负荷恢复量最大和负荷恢复重要程度最大作为目标的黑启动优化模型,并且利用最小生成树的Prim算法进行恢复路径优化,提高黑启动负荷恢复效率的同时降低黑启动时间。
为了验证本文方法的有效性,采用IEEE-30节点简化的19节点微电网结构作为测试系统在MATLAB平台进行仿真实验。仿真结果表明,与A-D优化的黑启动策略相比,本文提出的黑启动优化策略提高了负荷的恢复量的同时考虑了恢复负荷的重要程度。并且,本文方法的路径恢复总时间减少8.8%,提高了海岛微电网黑启动的效率。此外,本文还提出了对黑启动过程中感性负荷的处理方法,仿真结果表明该方法可以实现在黑启动过程中明显减小感性负荷对系统电压造成的影响,只需考虑负荷有功功率,简化黑启动过程。
| [1] |
孙湫词, 谭勇华, 李家彪. 新时代我国海岛的生态保护和开发利用[J]. 海洋开发与管理, 2018, 35(8): 22-27. Sun Q C, Tan Y H, Li J B. Ecological protection and exploitation of Islands in China in new era[J]. Ocean Development and Management, 2018, 35(8): 22-27. (in Chinese) DOI:10.3969/j.issn.1005-9857.2018.08.004 |
| [2] |
Asheibi A, Shuaib S. A case study on black start capability assessment[C]//2019 International Conference on Electrical Engineering Research & Practice (ICEERP), November 24-28, 2019, Sydney, NSW, Australia. IEEE, 2019: 1-5.
|
| [3] |
Liu M S, Liu G S, Sun Z Y, et al. Selection and simulation of black-start diesel generating set in regional power grid[C]//2018 China International Conference on Electricity Distribution (CICED), September 17-19, 2018, Tianjin, China. IEEE, 2018: 1774-1777.
|
| [4] |
Liu W P, Liu Y T. Enabling wind farm to be black-start source by energy storage[J]. The Journal of Engineering, 2019, 2019(18): 5138-5141. DOI:10.1049/joe.2018.9302 |
| [5] |
赵昱宣, 孙磊, 林振智, 等. 微网作为黑启动电源的电力系统网架重构优化策略[J]. 电力系统自动化, 2018, 42(17): 9-17, 147. Zhao Y X, Sun L, Lin Z Z, et al. Power network reconfiguration strategy with microgrids as black-start power sources[J]. Automation of Electric Power Systems, 2018, 42(17): 9-17, 147. (in Chinese) DOI:10.7500/AEPS20170824001 |
| [6] |
Li J H, You H F, Qi J, et al. Stratified optimization strategy used for restoration with photovoltaic-battery energy storage systems as black-start resources[J]. IEEE Access, 2019, 7: 127339-127352. DOI:10.1109/ACCESS.2019.2937833 |
| [7] |
孟强, 牟龙华, 许旭锋, 等. 孤立微电网的黑启动策略[J]. 电力自动化设备, 2014, 34(3): 59-64. Meng Q, Mu L H, Xu X F, et al. Black-start strategy of isolated microgrid[J]. Electric Power Automation Equipment, 2014, 34(3): 59-64. (in Chinese) DOI:10.3969/j.issn.1006-6047.2014.03.010 |
| [8] |
方嵩, 彭嵩, 赵晋泉, 等. DG启动及运行特性综合评价指标与方法[J]. 电测与仪表, 2019, 56(14): 5-11. Fang S, Peng S, Zhao J Q, et al. Comprehensive evaluation index and method for startup and operation characteristics of DGs[J]. Electrical Measurement & Instrumentation, 2019, 56(14): 5-11. (in Chinese) |
| [9] |
郑程拓, 丁晓群, 郑能, 等. 考虑负荷恢复效益的微电网黑启动串行恢复策略[J]. 智慧电力, 2017, 45(10): 13-18. Zheng C T, Ding X Q, Zheng N, et al. Serial recovery strategy for microgrid black start considering load recovery benefits[J]. Smart Power, 2017, 45(10): 13-18. (in Chinese) DOI:10.3969/j.issn.1673-7598.2017.10.003 |
| [10] |
Xu Z R, Yang P, Zheng Q R, et al. Study on black start strategy of microgrid with PV and multiple energy storage systems[C]//2015 18th International Conference on Electrical Machines and Systems (ICEMS), October 25-28, 2015, Pattaya, Thailand. IEEE, 2015: 402-408.
|
| [11] |
冷亚军, 吴宗育, 赵文会, 等. 基于近邻传播聚类权重的黑启动方案评估方法[J]. 电力系统自动化, 2020, 44(13): 73-80. Leng Y J, Wu Z Y, Zhao W H, et al. Assessment method of black-start scheme based on affinity propagation clustering weight[J]. Automation of Electric Power Systems, 2020, 44(13): 73-80. (in Chinese) |
| [12] |
汪笃军, 刘天羽. 微电网线路与负荷有序并行恢复的优化方案[J]. 电测与仪表, 2018, 55(13): 67-73. Wang D J, Liu T Y. Optimization scheme of line and load orderly parallel restoration in micro-grid[J]. Electrical Measurement & Instrumentation, 2018, 55(13): 67-73. (in Chinese) |
| [13] |
Patsakis G, Rajan D, Aravena I, et al. Optimal black start allocation for power system restoration[J]. IEEE Transactions on Power Systems, 2018, 33(6): 6766-6776. DOI:10.1109/TPWRS.2018.2839610 |
| [14] |
钟浩, 阮建雄, 王凌云. 考虑源荷依赖度的含分布式电源配电网黑启动策略[J]. 电力系统及其自动化学报, 2020, 32(6): 65-73. Zhong H, Ruan J X, Wang L Y. Black-start strategy for distribution network with distributed generations considering source-load dependence[J]. Proceedings of the CSU-EPSA, 2020, 32(6): 65-73. (in Chinese) |
| [15] |
Birkelbach J, Woiton H, Thiele M, et al. Methodology for the evaluation of existing black start units and optimization for future locations[C]//NEIS 2018 Conference on Sustainable Energy Supply and Energy Storage Systems, September 20-21, 2018, Hamburg, Germany. IEEE: 2018: 99-104.
|
| [16] |
李军徽, 尤宏飞, 李翠萍, 等. 基于模型预测控制的风光储黑启动功率协调策略[J]. 电网技术, 2020, 44(10): 3700-3708. Li J H, You H F, Li C P, et al. Power coordination strategy based on model predictive control for black start with PV-wind-battery system[J]. Power System Technology, 2020, 44(10): 3700-3708. (in Chinese) |
| [17] |
Zhao Y X, Lin Z Z, Ding Y, et al. A model predictive control based generator start-up optimization strategy for restoration with microgrids as black-start resources[J]. IEEE Transactions on Power Systems, 2018, 33(6): 7189-7203. DOI:10.1109/TPWRS.2018.2849265 |
| [18] |
Wu X, Shi S, Wang X L, et al. Optimal black start strategy for microgrids considering the uncertainty using a data-driven chance constrained approach[J]. IET Generation, Transmission & Distribution, 2019, 13(11): 2236-2248. |
| [19] |
谢夏慧, 汪沨, 黎灿兵. 基于模糊AHP的DG启动顺序的优化[J]. 电源技术, 2014, 38(7): 1367-1369. Xie X H, Wang F, Li C B. Optimization of DG start-up sequence based on fuzzy AHP[J]. Chinese Journal of Power Sources, 2014, 38(7): 1367-1369. (in Chinese) DOI:10.3969/j.issn.1002-087X.2014.07.056 |
| [20] |
刘仲, 牟龙华, 许旭锋. 微电网黑启动中考虑负荷恢复优化的分布式电源恢复方案[J]. 电力自动化设备, 2016, 36(3): 46-52. Liu Z, Mu L H, Xu X F. Microgrid black-start considering DG startup sequence and load restoration optimization[J]. Electric Power Automation Equipment, 2016, 36(3): 46-52. (in Chinese) |
| [21] |
曾远方. 串联电容补偿在配电网中的应用研究[D]. 武汉: 华中科技大学, 2016. Zeng Y F. Research on application of series capacitor compensation in distribution network[D]. Wuhan: Huazhong University of Science and Technology, 2016. (in Chinese) |
| [22] |
曾顺奇, 文福拴, 薛禹胜, 等. 计及操作时间不确定性的电力系统网架重构策略优化[J]. 电力系统自动化, 2011, 35(23): 16-21. Zeng S Q, Wen F S, Xue Y S, et al. Optimization of network reconfiguration strategy for power systems considering operating time uncertainty[J]. Automation of Electric Power Systems, 2011, 35(23): 16-21. (in Chinese) |
| [23] |
Xu J Z, Li M Y, Chen Q, et al. Evaluation method of DG black start of distribution network[C]//2020 5th Asia Conference on Power and Electrical Engineering (ACPEE), June 4-7, 2020, Chengdu, China. IEEE, 2020: 2141-2147.
|
| [24] |
Zhang L, Jing Z X, Ji T Y, et al. Optimization of black-start scheme for mitigating overvoltage[C]//2019 IEEE Innovative Smart Grid Technologies-Asia (ISGT Asia), May 21-24, 2019, Chengdu, China. IEEE, 2019: 698-703.
|
 2021, Vol. 44
2021, Vol. 44


