2. 重庆大学 输配电装备及系统安全与新技术国家重点实验室, 重庆 400044;
3. 重庆电力交易中心有限公司, 重庆 400013
2. State Key Laboratory of Power Transmission Equipment & System Security and New Technology, Chongqing University, Chongqing 400044, P. R. China;
3. Chongqing Electric Power Trading Center Co., Ltd., Chongqing 400013, P. R. China
高质量的监测数据对电网数字化发展具有重要现实意义[1],然而量测系统中母线负荷数据存在的各类异常影响了电力系统状态估计[2]、负荷预测[3]等高级数字化应用。如何有效地辨识出母线负荷异常数据,提高数据质量一直是工程界和学术界关注的焦点[4]。
现有母线负荷异常数据辨识方法主要有3类:基于时间序列、基于聚类和基于时频域变换的方法。基于时间序列的方法以负荷数据时序变化规律为基础,通过B样条函数[5]、多项式[6]等基函数将样本中的部分节点拟合成一条光滑曲线;然后在该光滑曲线上下划定时序负荷数据的正常波动范围,将超出该范围的负荷数据辨识为异常数据。该类方法过分依赖序列的平滑特征,只对毛刺类异常较为有效。基于聚类的方法以负荷曲线簇为样本,首先应用k-均值聚类算法[7-8]、模糊C均值聚类算法[9-11]等聚类方法将负荷曲线归为几类;然后各自提取其典型负荷曲线;最后将待辨识的负荷曲线与各典型负荷曲线对比,根据二者差异的大小判断负荷曲线中是否含有异常数据。该类方法以欧氏距离或隶属度作为负荷曲线类别划分依据,忽略了负荷曲线的形状信息,可能导致曲线错误分类,进而影响异常数据辨识准确率。基于时频域变换的方法中,文献[12]通过离散傅里叶变换提取负荷曲线频域日周期分量和周周期分量,将二者叠加并变换回时域生成典型负荷曲线;再通过比较待判定负荷曲线和典型曲线的差异来判定曲线异常与否。该方法仅凭负荷曲线日周期分量和周周期分量复原负荷曲线的特征,存在较大误差。文献[13-14]基于小波变换提取负荷曲线的时频域特征,根据曲线频域模极大值为主要特征辨识时域内的负荷数据突变点,此类方法着重于异常数据的突变特征,仅对于毛刺异常数据的辨识较为有效。
综上所述,现有母线负荷辨识方法存在适应性差、对数据异常特征利用不充分问题。据此,笔者基于母线负荷数据现状剖析了异常数据的基本特征,阐明了因子分析应用于母线负荷异常数据辨识的基本原理,提出了基于因子分析的母线负荷异常数据辨识方法。该方法的核心包括:1)引入因子分析将母线负荷曲线分解为表征曲线正常时序变化规律的基本分量和表征曲线数据异常或随机波动特征的随机分量;2)基于负荷曲线随机分量给出了异常数据辨识的3σ判定准则。
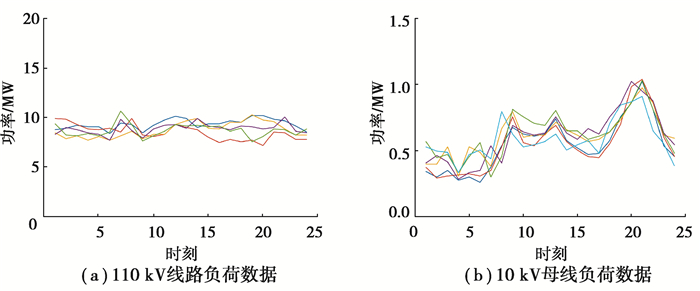
1 母线负荷异常数据基本特征剖析电力系统母线负荷是大量终端负荷的总和,而各类终端负荷一天之内用电模式相对固定,母线负荷自然也会表现出某种相对稳定的日周期性。如图 1所示,110 kV母线的终端负荷为工商、市政、居民等多个类别终端负荷的总和,一天之内负荷平稳波动较小;而10 kV母线终端负荷大多仅包含居民负荷,呈现出显著的双峰特性。
|
图 1 不同电压等级的母线负荷数据 Fig. 1 Bus load data of different voltage levels |
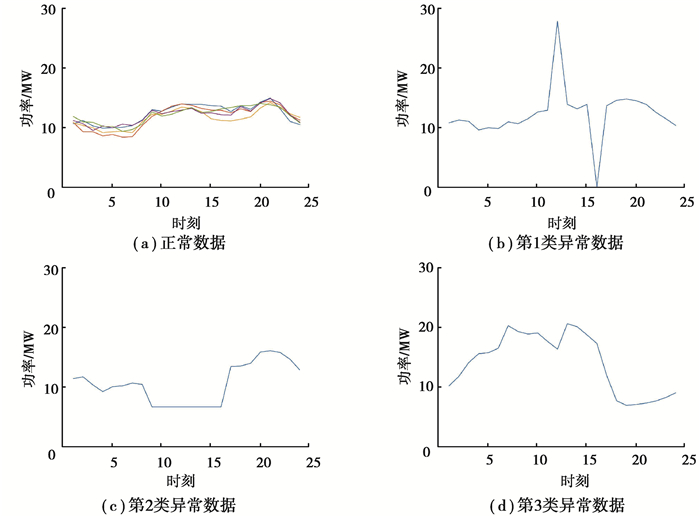
实际量测系统采集到的母线负荷除正常负荷数据外,通常还存在3类异常数据:
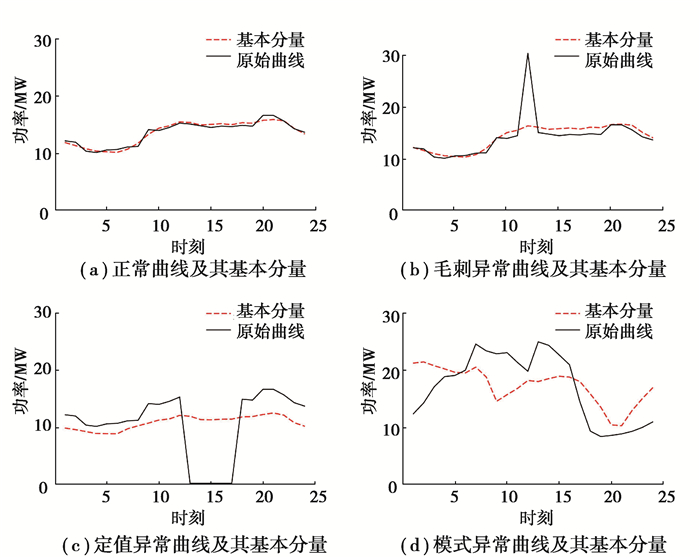
1) 毛刺异常数据。如图 2(b)所示,单个时刻或少数时刻负荷数据出现大幅度突变的异常数据,该类异常数据多来源于数据采集、传输、储存等各环节中的随机干扰。
|
图 2 110 kV母线正常负荷曲线与异常负荷曲线 Fig. 2 Normal and abnormal load curves of 110 kV bus |
2) 定值异常数据。如图 2(c)所示,在某时间段连续不变的异常数据,该类异常数据多来源于量测系统故障。
3) 模式异常数据:如图 2(d)所示,与正常日负荷变化模式相比有显著不同时序变化规律,该类异常数据多来源于电力系统故障。
2 基于因子分析的母线负荷异常数据辨识原理 2.1 因子分析的基本原理因子分析是一种依据变量间相关性将多维变量归结为少数公共因子表示,然后加以分析处理的多维变量统计分析方法[15-16]。其基本思想是将原始变量分解为两部分:一部分是公共因子的线性组合,浓缩表示了原始变量中的绝大部分信息;另一部分是与公共因子无关的特殊因子,反映了公共因子线性组合与原始变量间的差距。因子分析在统计分析中有许多应用,例如对样本变量进行因子分析,提取出反映变量主要特征的公共因子,进而指导样本分类处理[16]。
p维变量x=[x1, …, xi, …, xp]T的因子分析模型为
| $ \boldsymbol{x}=\boldsymbol{A} \boldsymbol{f}+\boldsymbol{\varepsilon}。$ | (1) |
或记为
| $ \left[\begin{array}{c} x_{1} \\ x_{2} \\ \vdots \\ x_{p} \end{array}\right]=\left[\begin{array}{cccc} a_{11} & a_{12} & \cdots & a_{1 m} \\ a_{21} & a_{22} & \cdots & a_{2 m} \\ \vdots & \vdots & & \vdots \\ a_{p 1} & a_{p 2} & \cdots & a_{p m} \end{array}\right]\left[\begin{array}{c} f_{1} \\ f_{2} \\ \vdots \\ f_{m} \end{array}\right]+\left[\begin{array}{c} \varepsilon_{1} \\ \varepsilon_{2} \\ \vdots \\ \varepsilon_{p} \end{array}\right], $ | (2) |
式中:f=[f1, f2, …, fm]T即为提取的公共因子向量,代表了原始变量中不可直接观测但客观存在的m (m < p)个互相独立的共性影响因素;A=(aik)p×m为因子载荷矩阵(i=1, 2, …, p, k=1, 2, …, m),矩阵元素aik为变量xi对公共因子fk的载荷,反映了二者的相关系数,其绝对值越大,相关性越高;ε=[ε1, ε2, …, εp]T为特殊因子向量,反映了公共因子线性组合Af与原始变量x之间的差距。
注意上述因子分析模型对各变量做了如下假设:
1) 公共因子向量f的协方差矩阵满足covf=Em (Em为m阶单位对角矩阵),即公共因子向量各分量间相互独立,且各分量方差为1。
2) 公共因子向量f与特殊因子向量ε的协方差矩阵满足cov(f, ε)=0,即公共因子与特殊因子相互独立。
3) 特殊因子间相互独立,特殊因子向量ε的协方差矩阵满足
| $ \operatorname{cov}(\boldsymbol{\varepsilon})=\left[\begin{array}{cccc} \sigma_{1}^{2} & & & 0 \\ & \sigma_{2}^{2} & & \\ & & \ddots & \\ 0 & & & \sigma_{p}^{2} \end{array}\right] \triangleq \boldsymbol{D}_{\varepsilon}, $ | (3) |
式中σi2为各特殊因子的方差。
2.2 因子分析模型的参数估计对多维变量x建立因子分析模型的关键在于求解因子载荷矩阵A和公共因子向量f。借鉴文献[16]对上述2个参数进行估计。
因子载荷矩阵A的估计采用主成分法,其步骤如下:
1) 为消除变量量纲不同的影响,对含n个p维变量的样本
| $ x_{i j}=\frac{\left(x_{i j}-\frac{1}{n} \sum\limits_{j=1}^{n} x_{i j}\right)}{\sqrt{\frac{1}{n-1} \sum\limits_{j=1}^{n}\left(x_{i j}-\frac{1}{n} \sum\limits_{j=1}^{n} x_{i j}\right)^{2}}}。$ | (4) |
2) 求样本的协方差矩阵S,其各元素为
| $ s_{i j}=\frac{1}{n-1} \sum\limits_{k=1}^{n} x_{i k} x_{j k}。$ | (5) |
3) 对样本协方差矩阵S做特征值分解,得到p个特征值λ1≥λ2≥…≥λp≥0,对应的特征值向量为γ1,γ2,…,γp,可取前m个最大特征值的特征向量估计因子载荷矩阵
| $ \hat{\boldsymbol{A}}=\left[\sqrt{\lambda_{1}} \boldsymbol{\gamma}_{1}, \sqrt{\lambda_{2}} \boldsymbol{\gamma}_{2}, \cdots, \sqrt{\lambda_{m}} \boldsymbol{\gamma}_{m}\right],$ | (6) |
其中参数m由公共因子的累积方差贡献率[16]确定,即
| $ m=\underset{m}{\operatorname{argmin}}\left(\frac{\sum\limits_{i=1}^{m} \lambda_{i}}{\sum\limits_{i=1}^{p} \lambda_{i}} \geqslant r\right)。$ | (7) |
一般认为,当前m个公共因子的累积方差贡献率超过85%时,可认为前m个公共因子的线性组合基本上能够还原原始变量信息。
公共因子向量f,即原始变量在公共因子上的具体得分可通过回归法估计得到
| $ \hat{\boldsymbol{f}}_{j}=\hat{\boldsymbol{A}}^{\mathrm{T}} \boldsymbol{S}^{-1} \boldsymbol{x}_{j}。$ | (8) |
通过以上步骤,得到因子载荷矩阵
| $ \hat{\boldsymbol{\varepsilon}}_{j}=\boldsymbol{x}_{j}-\hat{\boldsymbol{A}} \hat{\boldsymbol{f}}_{j}。$ | (9) |
综上所述即完成多维变量X因子分析模型的参数估计。
2.3 基于因子分析的母线负荷异常数据辨识方法机理终端负荷的用电模式相对固定,母线负荷的时序变化规律具有明显日周期性,因此正常的母线负荷曲线可视作反映日周期性时序变化规律的基本分量和反映负荷随机波动特性的随机分量的叠加,而含有异常数据的负荷曲线在此基础上还叠加了背离正常时序变化规律的异常特征。
考虑到母线负荷曲线各时刻负荷数据间存在明显相关性[17](如深夜至凌晨的用电低谷期负荷水平较低,而上午10时左右和晚上20时左右的用电高峰期负荷水平较高),因此可通过因子分析将母线负荷曲线样本分解为公共因子的线性组合和特殊因子两部分。在可合理假设样本中只含有少量的异常曲线基础上,浓缩表示各负荷曲线绝大多数信息的公共因子线性组合基本上表征了曲线正常时序变化规律,可视作曲线的基本分量;而反映公共因子线性组合和原始曲线差距的特殊因子则表征了曲线数据异常或随机波动特征,可视作曲线的随机分量。
经因子分析得到表征负荷曲线数据异常或随机波动特征的随机分量后,通过检测曲线随机分量中是否含有异常特征,即可实现对异常负荷曲线的判别。
3 基于因子分析的母线负荷异常数据辨识方法 3.1 基于因子分析的负荷曲线基本分量和随机分量的提取通常,母线负荷曲线中的异常数据占比低。但量测、通信设备故障则可能导致负荷数据出现长时段定值异常的情况,且异常占比较高。高占比异常数据将对负荷曲线基本分量提取造成较大干扰。不过此类异常特征明显,可以较为容易地通过预筛选将此类异常的负荷曲线加以排除。而经预筛选后的负荷曲线样本中异常曲线占比很少,样本异常数据含量低,对样本进行因子分析提取基本分量时可忽略异常数据影响。将预筛选后的所有负荷曲线作为样本,设含n条负荷曲线的样本为
| $ \tilde{\boldsymbol{X}}=\left[\begin{array}{cccc} \tilde{x}_{11} & \tilde{x}_{12} & \cdots & \tilde{x}_{1 n} \\ \widetilde{x}_{21} & \tilde{x}_{22} & \cdots & \tilde{x}_{2 n} \\ \vdots & \vdots & & \vdots \\ \tilde{x}_{p 1} & \tilde{x}_{p 2} & \cdots & \tilde{x}_{p n} \end{array}\right], $ | (10) |
式中:xij为样本中第j条负荷曲线第i时刻负荷值;p为负荷曲线的采样频率,取p=24。
基于因子分析的负荷曲线样本基本分量和随机分量的提取步骤如下:
1) 将负荷曲线样本
| $ \boldsymbol{X}=\operatorname{diag}\left(\boldsymbol{\sigma}_{x}\right)^{-1}\left(\tilde{\boldsymbol{X}}-\overline{\boldsymbol{x}} \boldsymbol{e}^{\mathrm{T}}\right), $ | (11) |
式中:
2) 计算标准化负荷曲线样本X的协方差矩阵S为
| $ \boldsymbol{S}=\frac{1}{n-1} \boldsymbol{X} \boldsymbol{X}^{\mathrm{T}}。$ | (12) |
3) 计算负荷曲线样本协方差矩阵S的特征值λ1≥λ2≥…≥λp≥0和对应的单位正交特征向量γ1,γ2,…,γp。
4) 根据式(7)确定公共因子数量m,然后根据式(6)(8)(9)分别估计负荷曲线样本因子分析模型因子载荷矩阵
| $ \begin{gathered} \hat{\boldsymbol{A}}=\left[\sqrt{\lambda_{1}} \boldsymbol{\gamma}_{1}, \sqrt{\lambda_{2}} \boldsymbol{\gamma}_{2}, \cdots, \sqrt{\lambda_{m}} \boldsymbol{\gamma}_{m}\right], \\ \hat{\boldsymbol{F}}=\hat{\boldsymbol{A}}^{\mathrm{T}} \boldsymbol{S}^{-1} \boldsymbol{X} ,\\ \hat{\boldsymbol{\varDelta}}=\boldsymbol{X}-\hat{\boldsymbol{A}} \hat{\boldsymbol{F}}。\end{gathered} $ | (13) |
5) 对负荷曲线进行逆标准化变换后,可得负荷曲线的基本分量Xb和随机分量Xr为
| $ \begin{gathered} \boldsymbol{X}_{\mathrm{b}}=\operatorname{diag}\left(\boldsymbol{\sigma}_{x}\right) \hat{\boldsymbol{A}} \hat{\boldsymbol{F}}+\overline{\boldsymbol{x}} \boldsymbol{e}^{\mathrm{T}},\\ \boldsymbol{X}_{\mathrm{r}}=\operatorname{diag}\left(\boldsymbol{\sigma}_{x}\right) \hat{\boldsymbol{\varDelta}}+\overline{\boldsymbol{x}} \boldsymbol{e}^{\mathrm{T}}。\end{gathered} $ | (14) |
至此,基于因子分析的负荷曲线样本基本分量与随机分量的提取完成。
3.2 基于随机分量的异常数据3σ判定准则母线负荷的随机波动来源于数据采集、传输及储存等过程中的高斯噪声,异常数据的产生是由于量测系统故障或者受到外界随机干扰以及电力系统本身故障运行导致,因此正常母线负荷曲线各时刻随机分量满足正态分布,异常曲线则不然。据此,笔者提出了基于负荷曲线随机分量的异常数据判定准则:若曲线各时刻负荷随机分量满足正态分布的拉依达(3σ)准则,即判定该数据正常,否则判定该数据异常。
下面对负荷曲线样本随机分量的正态分布参数进行估计,含n条负荷曲线的样本随机分量矩阵为
| $ \boldsymbol{X}_{\mathrm{r}}=\left[\begin{array}{cccc} \varepsilon_{11} & \varepsilon_{12} & \cdots & \varepsilon_{1 n} \\ \varepsilon_{21} & \varepsilon_{22} & \cdots & \varepsilon_{2 n} \\ \vdots & \vdots & & \vdots \\ \varepsilon_{p 1} & \varepsilon_{p 2} & \cdots & \varepsilon_{p n} \end{array}\right], $ | (15) |
式中εij表示样本中第j条负荷曲线第i时刻负荷的随机分量,已经过逆标准化处理还原为带量纲负荷数据。据此,样本随机分量的正态分布均值ε和标准差σε的各分量为
| $ \left\{\begin{array}{l} \bar{\varepsilon}_{i}=\frac{1}{n} \sum\limits_{j=1}^{n} \varepsilon_{i j}, \\ \sigma_{\varepsilon_i}=\sqrt{\frac{1}{n-1} \sum\limits_{j=1}^{n}\left(\varepsilon_{i j}-\bar{\varepsilon}_{i}\right)^{2}}。\end{array}\right. $ | (16) |
在正态分布假设下,按照拉依达(3σ)准则,各负荷曲线第i时刻随机分量正常波动范围为
| $ \begin{aligned} &\boldsymbol{X}_{\mathrm{r-lower}}=\left(\overline{\boldsymbol{\varepsilon}}-3 \boldsymbol{\sigma}_{\varepsilon}\right) \boldsymbol{e}^{\mathrm{T}} ,\\ &\boldsymbol{X}_{\mathrm{r-upper }}=\left(\overline{\boldsymbol{\varepsilon}}+3 \boldsymbol{\sigma}_{\varepsilon}\right) \boldsymbol{e}^{\mathrm{T}}。\end{aligned} $ | (17) |
因此,母线负荷曲线随机分量Xr不满足下列关系的负荷数据即可判定为异常数据,即
| $ \boldsymbol{X}_{\text {r-lower }} \leqslant \boldsymbol{X}_{\mathrm{r}} \leqslant \boldsymbol{X}_{\text {r-upper }}。$ | (18) |
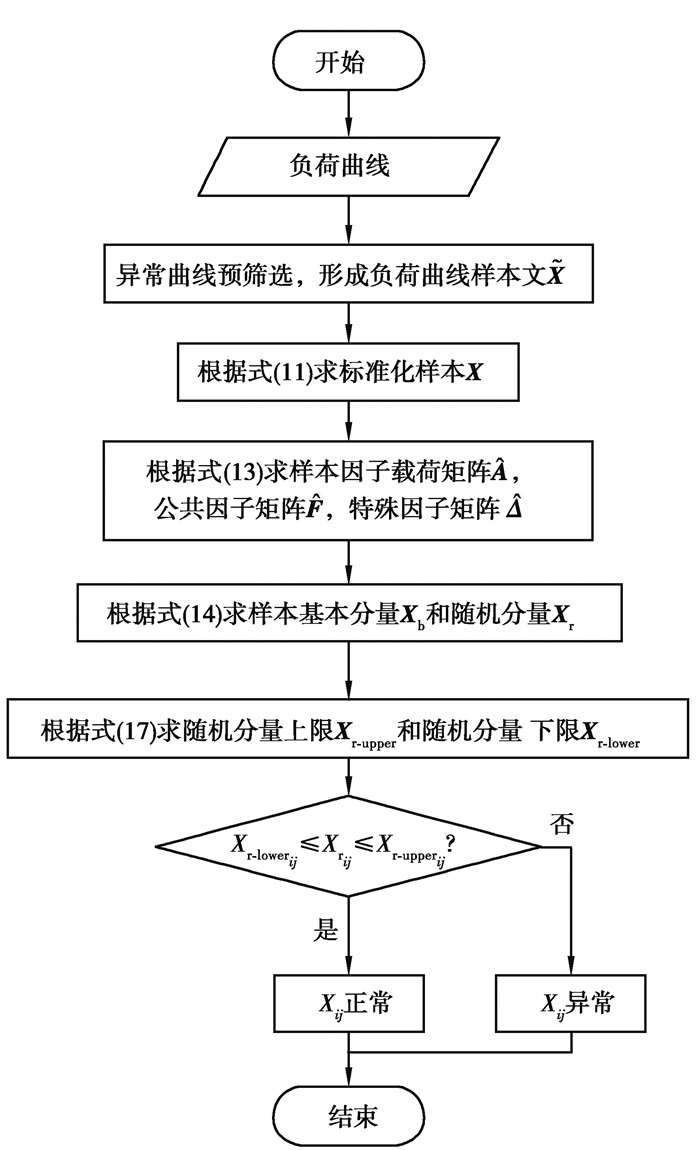
所提基于因子分析的母线负荷异常数据辨识方法流程步骤如下:
1) 首先对待辨识曲线进行预筛选,排除因量测和通信设备故障导致的连续定值异常曲线,形成负荷曲线样本
2) 根据式(11)对负荷曲线样本
3) 对标准化样本X进行因子分析,根据式(13)求得样本因子载荷矩阵
4) 根据式(14)取公共因子线性组合为样本曲线基本分量Xb,取特殊因子为样本曲线随机分量Xr,并对二者进行逆标准化处理。
5) 根据随机分量的分布规律,按式(17)确定负荷曲线样本随机分量波动下限
6) 将样本曲线各时刻随机分量
上述步骤的流程图如图 3所示。
|
图 3 基于因子分析的母线负荷异常数据辨识方法流程图 Fig. 3 Flow chart of bus load abnormal data identification method based on factor analysis |
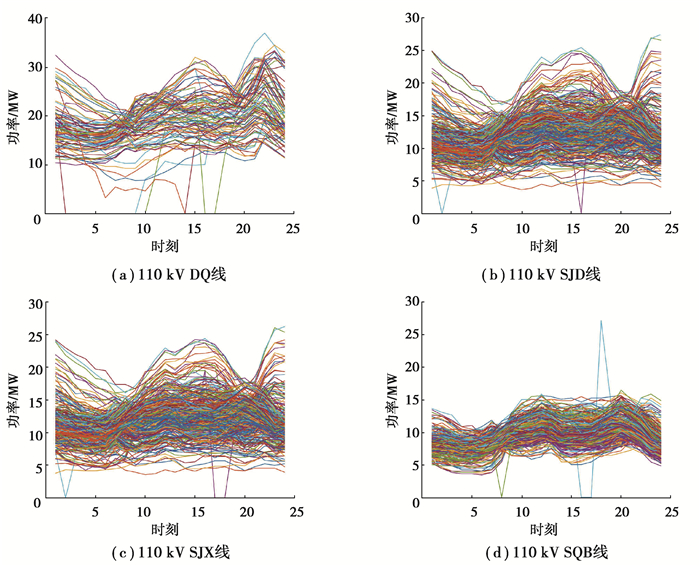
为验证笔者所提方法的合理性和有效性,以重庆市某供电公司4条110 kV母线2015年1 h分辨率的负荷数据为样本进行算例分析。原始数据基本信息如表 1所示,负荷曲线簇绘制如图 4所示。
| 表 1 4条110 kV母线负荷数据样本 Table 1 Load data of four 110 kV buses |
|
图 4 4条110 kV母线全年负荷曲线簇 Fig. 4 Annual load curve group of four 110 kV buses |
基于因子分析的异常负荷数据辨识方法有两点假设:一是负荷曲线基本分量能表征负荷曲线的正常时序变化特征,与正常负荷曲线基本吻合;二是样本中少量的异常数据对样本基本分量提取的影响可忽略不计。现对上述两点假设的合理性进行论证。
针对假设一,可对全正常曲线样本进行因子分析,若全正常样本提取的基本分量与各曲线有良好的吻合度,则可证实该假设成立。笔者引用均方根误差(
| $ C_{\mathrm{RMSE}}=\sqrt{\frac{1}{n p} \sum\limits_{i=1}^{n} \sum\limits_{j=1}^{p}\left(\frac{\tilde{x}_{i j}-x_{\mathrm{b}ij}}{x_{\mathrm{b}ij}}\right)^{2}}, $ | (19) |
| $ C_{\mathrm{MAE}}=\frac{1}{n p} \sum\limits_{i=1}^{n} \sum\limits_{j=1}^{p}\left|\frac{\tilde{x}_{i j}-x_{\mathrm{b}ij}}{x_{\mathrm{b}ij}}\right|, $ | (20) |
式中:
以原始负荷数据样本为基础,剔除样本中异常负荷曲线,只保留符合一般时序变化规律的正常曲线,剔除异常曲线后正常曲线样本基本信息如表 2所示。
| 表 2 剔除异常曲线后的正常数据样本 Table 2 Normal data samples with abnormal curves removed |
根据式(19)(20)计算全正常曲线样本基本分量与各样本曲线均方根误差(CRMSE)和绝对值误差(CMAE),计算结果如表 3所示。据表 3可见各样本CRMSE和CMAE值均不超过8%,表明基本分量与正常负荷曲线吻合程度高,即基本分量能表征负荷曲线的正常时序变化特征。
| 表 3 正常曲线样本与基本分量的相对误差 Table 3 The relative error between each normal curve sample and the basic component |
针对假设二,需对含少量异常负荷曲线的样本进行因子分析,若样本基本分量和样本中正常样本曲线的吻合程度与全正常曲线样本高度接近,则可判定假设成立。
排除异常数据占比大的DQ母线,以异常数据占比小的SJD、SJX、SQB 3条母线负荷曲线为样本。同时为验证异常数据比例增加时方法的鲁棒性,在不改变异常数据占比较少(10%以内)的大前提下,适当增加样本中异常数据的比例。增加异常数据比例后的母线负荷数据如表 4所示。
| 表 4 增加异常数据比例的母线负荷数据 Table 4 Bus load curves with increased proportion of abnormal data |
依旧采用均方根误差(CRMSE)和绝对值误差(CMAE)来衡量含异常曲线样本基本分量与样本中正常曲线的吻合度,但因计算的是基本分量与正常曲线的吻合程度,计算误差时要剔除样本中的异常曲线。计算可得含异常曲线样本基本分量与样本中正常曲线的均方根误差(CRMSE)和绝对值误差(CMAE)如表 5所示。可见各样本基本分量与全正常曲线样本高度接近,即证实少量异常数据对样本基本分量提取的影响可忽略。
| 表 5 含异常曲线样本中基本分量与正常曲线的相对误差 Table 5 The relative error between the basic component and the normal curve sin the sample with abnormal curves |
将110 kV SJD母线各类负荷曲线与其基本分量绘制如图 5所示。
|
图 5 110 kV SJD母线各类负荷曲线及其基本分量 Fig. 5 Various load curves and basic components of 110 kV SJD bus |
综上所述,基于因子分析分解得到的基本分量与正常负荷曲线高度吻合,表征了负荷曲线的正常时序变化规律。且这一结论在样本中含有少量异常曲线的条件下也成立。因此,通过随机分量(基本分量与原始曲线的差距)来判断曲线是否异常的方案是合理的。
4.2 所提方法的有效性论证将所提方法分别与基于傅里叶离散傅里叶变换和小波变换的母线负荷异常数据辨识方法进行对比,以验证所提方法的有效性。
选取基于混淆矩阵[19]的精确率(precision, P)、召回率(recall, R)和F1(F)值为指标评估各方法辨识效果。以表 4中SJD、SJX、SQB 3条母线负荷数据为样本,分别基于因子分析、离散傅里叶变换和小波变换的3种辨识方法的辨识效果如表 6所示。
| 表 6 3种辨识方法的效果对比 Table 6 Comparison of three identification methods |
由表 6可知,笔者所提基于因子分析方法相比于傅里叶法和小波分析法在精确率和召回率上都有明显优势,综合评价指标F1值也明显优于其他两种方法,具体而言,基于离散傅里叶变换的异常数据辨识方法仅提取了负荷曲线日周期分量和周周期分量,难以对原始负荷曲线进行精确复原,导致辨识精确率低,误报情况严重,而基于小波变换的辨识方法侧重于对突变点的检测,能够在一定程度上实现对毛刺异常数据的辨识。由于部分负荷的随机扰动和突变点特征相似,小波变换方法极易将这种正常随机扰动误辨识为异常数据,而笔者所提出基于因子分析的母线负荷异常数据辨识方法则能够兼顾各类异常数据的情况,适应性较好。
综上所述,基于因子分析的异常负荷数据辨识方法能够有效地辨识出母线负荷的各类异常数据,且所提方法优于基于离散傅里叶变换和小波变换方法的辨识效果。
4.3 所提方法的普适性分析笔者以110 kV母线历史负荷数据对所提方法进行了仿真分析,结果表明所提方法对110 kV母线负荷数据有良好的辨识效果。对于110 kV之下的10 kV母线负荷曲线由于其用电规律性相对较弱,可能不满足所提方法的2个假设条件,故所提方法对110 kV以下母线负荷异常数据辨识的实用性有待深入研究。而对于110 kV以上电压等级母线负荷异常数据辨识,一般而言,由于该电压等级负荷更加集中,用户用电行为规律性更强,更容易满足所提方法的2个假设条件。据此,所提方法对110 kV以上电压等级母线负荷异常数据辨识亦有效。
5 结论考虑传统母线负荷异常数据辨识方法的局限性,提出了基于因子分析的母线负荷异常数据辨识方法,主要研究结论如下:
1) 所提方法提取的母线负荷曲线基本分量表征了曲线的主要正常时序变化特征,且少量异常数据不影响负荷曲线基本分量的提取;母线负荷曲线的随机分量表征了曲线的数据异常和随机波动特征,可根据随机分量波动是否越线判断曲线是否含有异常数据。
2) 所提方法关于负荷曲线基本分量能表征负荷曲线的基本时序变化特征且与正常负荷曲线基本吻合,以及样本中少量异常数据对样本基本分量提取的影响可忽略不计的假设均经算例验证合理。
3) 所提方法能够兼顾各类母线负荷异常数据的情况,有效地辨识出母线负荷异常数据,适应性较好,且辨识效果优于传统的基于离散傅里叶变换和小波变换的方法。
| [1] |
徐文远, 雍静. 电力扰动数据分析学: 电能质量监测数据的新应用[J]. 中国电机工程学报, 2013, 33(19): 93-101. Xu W Y, Yong J. Power disturbance data analytics -new application of power quality monitoring data[J]. Proceedings of the CSEE, 2013, 33(19): 93-101. (in Chinese) |
| [2] |
厉超, 卫志农, 倪明, 等. 计及PMU量测的分步线性状态估计模型[J]. 电网技术, 2014, 38(6): 1700-1704. Li C, Wei Z N, Ni M, et al. A PMU measurement based stepwise linear state estimation model[J]. Power System Technology, 2014, 38(6): 1700-1704. (in Chinese) |
| [3] |
颜宏文, 李欣然. 基于差分进化的含分布式电源母线净负荷预测[J]. 电网技术, 2013, 37(6): 1602-1606. Yan H W, Li X R. Uncertainty analysis on net load forecasting for busbar containing distributed energy sources based on differential evolution and rough sets reduction[J]. Power System Technology, 2013, 37(6): 1602-1606. (in Chinese) |
| [4] |
张林, 王浩, 邓强, 等. 考虑公司经营状况和全网现状的高压配电网工程精细化事前评估方法[J/OL]. 重庆大学学报, 2020: 1-11[2020-11-06]. http://kns.cnki.net/kcms/detail/50.1044.N.20190927.1502.006.html. Zhang L, Wang H, Deng Q, et al. Precision pre-evaluation method for high-voltage distribution network project considering business status and overall situation of the whole network[J/OL]. Journal of Chongqing University, 2020: 1-11[2020-11-06]. http://kns.cnki.net/kcms/detail/50.1044.N.20190927.1502.006.html. (in Chinese) |
| [5] |
唐文左, 段磊, 王鹏举, 等. 基于B样条函数的不良负荷数据改进辨识方法[J]. 电力系统及其自动化学报, 2015, 27(8): 37-42. Tang W Z, Duan L, Wang P J, et al. Improved load curve bad data identification method based on B-spline function[J]. Proceedings of the CSU-EPSA, 2015, 27(8): 37-42. (in Chinese) DOI:10.3969/j.issn.1003-8930.2015.08.07 |
| [6] |
Huang C C, Tsao Y T, Hsu J Y J. Abnormality detection by model-based estimation of power consumption[C]//2012 Fifth IEEE International Conference on Service-Oriented Computing and Applications (SOCA), December 17-19, 2012, Taipei, Taiwan, China. IEEE, 2012: 1-6.
|
| [7] |
孟建良, 刘德超. 一种基于Spark和聚类分析的辨识电力系统不良数据新方法[J]. 电力系统保护与控制, 2016, 44(3): 85-91. Meng J L, Liu D C. A new method for identifying bad data of power system based on Spark and clustering analysis[J]. Power System Protection and Control, 2016, 44(3): 85-91. (in Chinese) |
| [8] |
刘莉, 王刚, 翟登辉. k-means聚类算法在负荷曲线分类中的应用[J]. 电力系统保护与控制, 2011, 39(23): 65-68, 73. Liu L, Wang G, Zhai D H. Application of k-means clustering algorithm in load curve classification[J]. Power System Protection and Control, 2011, 39(23): 65-68, 73. (in Chinese) |
| [9] |
蒋雯倩, 李欣然, 钱军. 改进FCM算法及其在电力负荷坏数据处理的应用[J]. 电力系统及其自动化学报, 2011, 23(5): 1-5. Jiang W Q, Li X R, Qian J. Application of improved FCM algorithm in outlier processing of power load[J]. Proceedings of the Chinese Society of Universities for Electric Power System and Its Automation, 2011, 23(5): 1-5. (in Chinese) DOI:10.3969/j.issn.1003-8930.2011.05.001 |
| [10] |
孔祥玉, 胡启安, 董旭柱, 等. 引入改进模糊C均值聚类的负荷数据辨识及修复方法[J]. 电力系统自动化, 2017, 41(9): 90-95. Kong X Y, Hu Q A, Dong X Z, et al. Load data identification and correction method with improved fuzzy C-means clustering algorithm[J]. Automation of Electric Power Systems, 2017, 41(9): 90-95. (in Chinese) |
| [11] |
常鲜戎, 孙景文. 基于改进的模糊C均值聚类的负荷预处理[J]. 华北电力大学学报(自然科学版), 2014, 41(1): 27-32. Chang X R, Sun J W. Data processing based on improved fuzzy C-means clustering[J]. Journal of North China Electric Power University (Natural Science Edition), 2014, 41(1): 27-32. (in Chinese) DOI:10.3969/j.ISSN.1007-2691.2014.01.05 |
| [12] |
Chen X Y, Kang C Q, Tong X, et al. Improving the accuracy of bus load forecasting by a two-stage bad data identification method[J]. IEEE Transactions on Power Systems, 2014, 29(4): 1634-1641. DOI:10.1109/TPWRS.2014.2298463 |
| [13] |
康仁. 基于小波分析的母线负荷预测不良数据检测[J]. 中国电力, 2011, 44(8): 5-8. Kang R. Bad data identification based on wavelet in bus load forecasting[J]. Electric Power, 2011, 44(8): 5-8. (in Chinese) DOI:10.3969/j.issn.1004-9649.2011.08.002 |
| [14] |
李慧, 杨明皓. 小波分析在电力系统不良数据辨识中的应用[J]. 继电器, 2005, 33(3): 10-14, 20. Li H, Yang M H. Application of wavelet analysis to bad data identification for power system[J]. Relay, 2005, 33(3): 10-14, 20. (in Chinese) |
| [15] |
李丹. 考虑时空相关性的源荷功率概率建模和概率预测方法[D]. 重庆: 重庆大学, 2017. Li D. Research on the probabilistic modeling and prediction method of source & load power considering temporal-spatial correlation[D]. Chongqing: Chongqing University, 2017. (in Chinese) |
| [16] |
高惠璇. 应用多元统计分析[M]. 北京: 北京大学出版社, 2005. Gao H X. Applied multivariate statistical analysis[M]. Beijing: Peking University Press, 2005. (in Chinese) |
| [17] |
颜伟, 李丹, 朱继忠, 等. 月前日负荷曲线的概率预测和随机场景模拟[J]. 电力系统自动化, 2017, 41(17): 155-162. Yan W, Li D, Zhu J Z, et al. Probabilistic forecasting and stochastic scenario simulation of month-ahead daily load curve[J]. Automation of Electric Power Systems, 2017, 41(17): 155-162. (in Chinese) DOI:10.7500/AEPS20160908017 |
| [18] |
Wang Y, Chen Q X, Kang C Q, et al. Sparse and redundant representation-based smart meter data compression and pattern extraction[J]. IEEE Transactions on Power Systems, 2017, 32(3): 2142-2151. DOI:10.1109/TPWRS.2016.2604389 |
| [19] |
李航. 统计学习方法[M]. 北京: 清华大学出版社, 2012. Li H. Statistical learning methods[M]. Beijing: Tsinghua University Press, 2012. (in Chinese) |
 2021, Vol. 44
2021, Vol. 44


