2. ABB新会低压开关有限公司, 广东 江门 529000
2. ABB Xinhui Low Voltage Switchgear Co., Ltd., Jiangmen, Guangdong 529000, P. R. China
交流接触器是一种广泛使用的低压电气开关,随着电气产品的发展,对接触器的性能指标要求也越高。接触器通电时,动静触头产生的碰撞弹跳现象引起电弧对触头的烧蚀作用会降低接触器的电寿命[1-2]。故准确分析并掌握其动态特性变化规律,有效减少和抑制触头弹跳,对于交流接触器的优化设计具有重要的意义[3-4]。
目前,国内外学者对交流接触器进行了大量的研究和优化工作。在文献[5-8]中,作者通过可控电磁反力,对交流接触器进行了仿真分析,得到了部分有益结果。文献[9-12]基于ANSYS有限元法,对合闸过程中的电磁力进行了仿真分析,但并未考虑摩擦和碰撞阻尼的影响。文献[13-14]的作者建立接触器数学模型,并进行合闸过程的动态分析,但有关触头碰撞前后的弹跳研究较少。文献[15]运用遗传算法对接触器进行了优化设计,但该文采用了均匀磁场来模拟电磁吸力,对模型做了大量简化,使得误差偏大。文献[16-18]利用ADAMS软件建立交流接触器的三维动态仿真模型,分析了触头弹跳的相关影响因素,由于对电磁力进行了大量线性化处理,使得仿真结果不能准确反映触头弹跳过程。
综上所述,国内外少有结合机械结构本身考虑的触头弹跳问题,由于触头弹跳也是触头系统的振动过程,笔者通过接触器触头弹跳行为规律,将ADAMS软件与遗传算法相结合,对触头系统的参数进行优化设计。
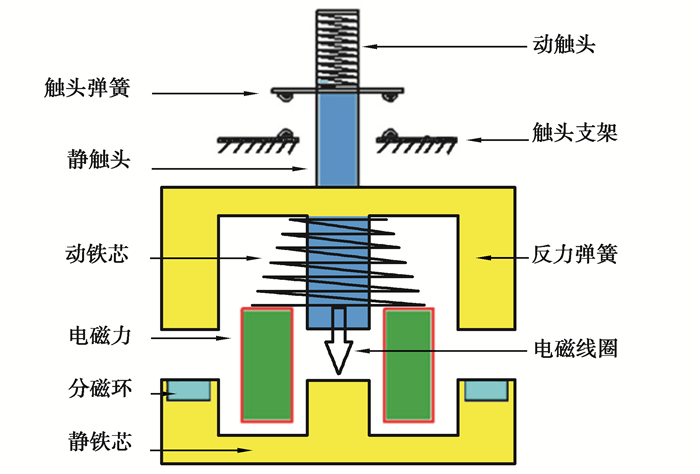
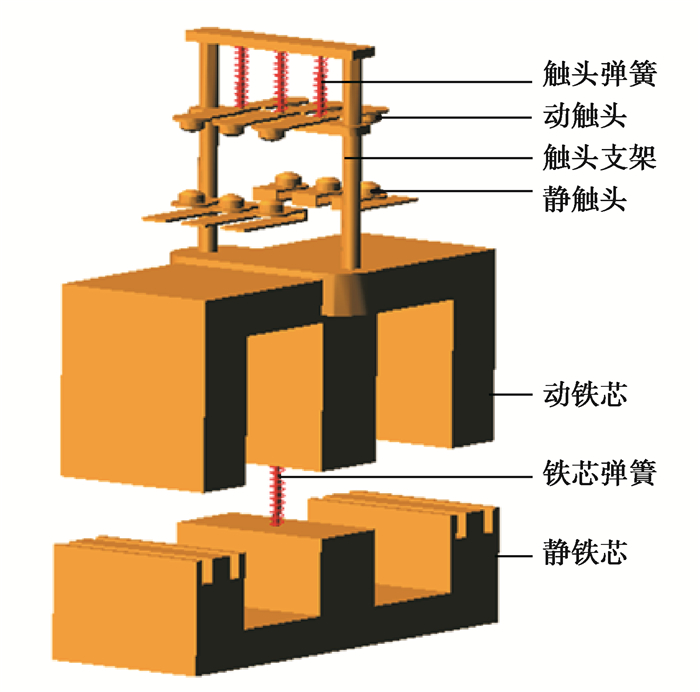
1 接触器触头模型建立与规律分析交流接触器由触头系统、电磁系统和触头支架3部分组成(见图 1)。接触器工作时,先给电磁线圈通电,当电磁力大于反力弹簧作用力时,动铁芯通过触头支架使动触头向下运动,由于动静触头间距小于动静铁芯间距,使得动触头先于动铁芯发生撞击和弹跳。此时动铁芯继续向下运动,直至动静铁芯发生碰撞[19]。
|
图 1 交流接触器结构图 Fig. 1 Schematic diagram of the AC contactor |
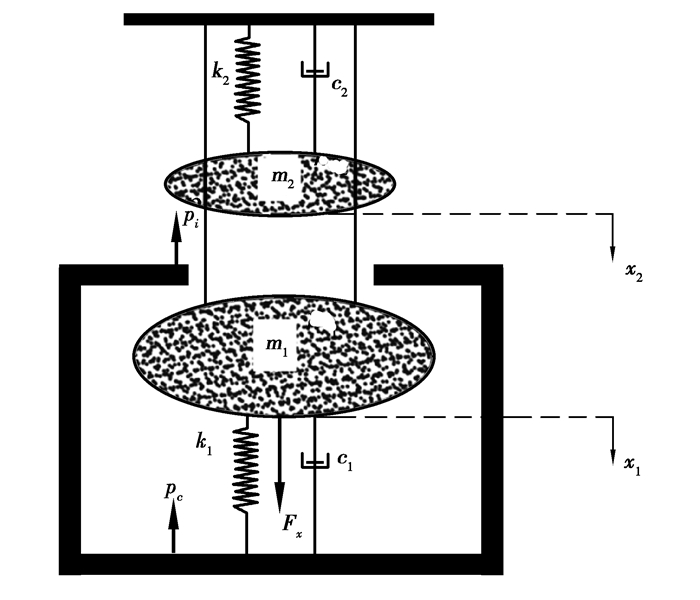
触头弹跳引起的机械振动现象存在于交流接触器整个工作过程中,由于动、静触头以及动、静铁芯间的碰撞接触均具有间断特征,使交流接触器的动力学特性出现不连续性现象。其运动模型如图 2所示。
|
图 2 交流接触器运动模型 Fig. 2 Motion model of AC contactor |
设m1、m2分别为动铁芯和动触头质量;x1、x2分别为动铁芯和动触头位移;c1、c2分别为电磁机构和触头系统等效阻尼;k1、k2分别为反力弹簧和触头弹簧刚度系数;Fx为电磁力;pi、pc分别为触头以及铁芯碰撞时的接触力。
接触器合闸运动过程中,考虑动静触头碰撞接触力pi,动静铁芯碰撞接触力pc。其运动微分方程分别为
| $ \left.\begin{array}{l} m_{1} \ddot{x}_{1}+c_{1} \dot{x}_{1}+c_{2}\left(\dot{x}_{1}-\dot{x}_{2}\right)+k_{1} x_{1}+k_{2}\left(x_{1}-x_{2}\right)=F_{x}-P_{c}, \\ m_{2} \ddot{x}_{2}+c_{2}\left(\dot{x}_{2}-\dot{x}_{1}\right)+k_{2}\left(x_{2}-x_{1}\right)=-P_{i}。\end{array}\right\} $ | (1) |
电磁力作为整个电磁机构动力来源,计算的准确程度会对整个装置的运动过程产生很大影响,为了确保电磁力计算的准确性,本文中采用的电磁铁动态吸力公式为
| $ F_{x}=\frac{\mu_{0} S(N i)^{2}}{2 k^{2} \delta^{2}}, $ | (2) |
式中:
为进一步分析接触器二自由度分段耦合系统中影响因素,假定系统的激励为简谐形式,即
|
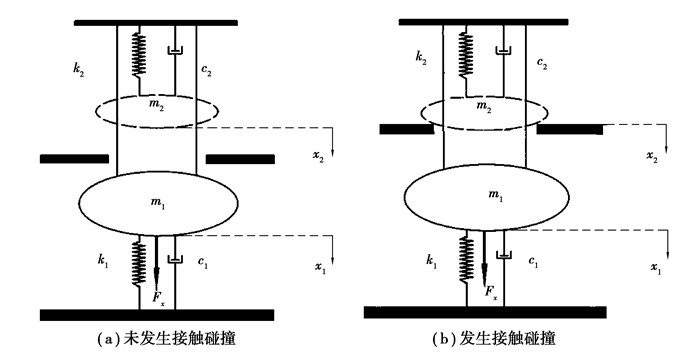
图 3 分段简化模型 Fig. 3 Piecewise simplified model |
阶段1,当动静触头和动静铁芯均未发生接触时,动触头与动铁芯由于通过触头支架相连,所以共同向下运动。如图 3(a)所示,其方程可表示为
| $ \left.\begin{array}{l} m_{1} \ddot{x}_{1}+c_{1} \dot{x}_{1}+c_{2}\left(\dot{x}_{1}-\dot{x}_{2}\right)+k_{1} x_{1}+k_{2}\left(x_{1}-x_{2}\right)=F_{0} \sin \omega t ,\\ m_{2} \ddot{x}_{2}+c_{2}\left(\dot{x}_{1}-\dot{x}_{2}\right)+k_{2}\left(x_{2}-x_{1}\right)=0。\end{array}\right\} $ | (3) |
假设其解的形式为
| $ X_{1}=\left(-\omega^{2} m_{2}+{\rm{i}} \omega c_{2}+k_{2}\right) F_{0} /\left\{\left[-\omega^{2} m_{1}+{\rm{i}} \omega\left(c_{1}+c_{2}\right)+k_{1}+k_{2}\right]\left(-\omega^{2} m_{2}+{\rm{i}} \omega c_{2}+k_{2}\right)-\left({\rm{i}} \omega c_{1}+k_{1}\right)^{2}\right\}, $ | (4) |
| $ X_{2}=-\left(\mathrm{i} \omega c_{1}+k_{1}\right) F_{0} /\left\{\left[-\omega^{2} m_{1}+\mathrm{i} \omega\left(c_{1}+c_{2}\right)+k_{1}+k_{2}\right]\left(-\omega^{2} m_{2}+\mathrm{i} \omega c_{2}+k_{2}\right)-\left(\mathrm{i} \omega c_{1}+k_{1}\right)^{2}\right\}。$ | (5) |
阶段2,当动静触头接触,动静铁芯未接触时,此时动触头和动铁芯分离,只有动铁芯向下运动,如图 3(b)所示,假设系统的运动是简谐的,即
| $ m_{2} \ddot{x}+c_{2} \dot{x}+k_{2} x=-m_{2} \omega^{2} F_{0} \sin \omega t。$ | (6) |
由此可以得出稳态解的振幅为
| $ x(t)=F_{0} \omega^{2}\left\{\left[\left(k_{2}-m_{2} \omega^{2}\right)^{2}+c_{2}^{2} \omega^{2}\right]^{\frac{1}{2}}\right\}\left(\omega t-\arctan \frac{c_{2} \omega}{k_{2}-m_{2} \omega^{2}}\right)。$ | (7) |
以ABB公司A9-30-10型电磁接触器为例,将各项参数带入到上述方程中求解,表 1给出了各项参数值。
| 表 1 接触器结构参数表 Table 1 Parameters of the contactor |
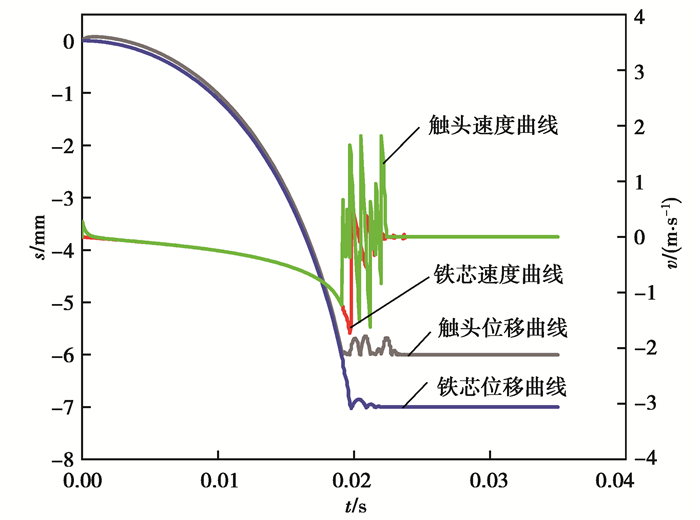
求解结果如图 4所示。从图 4可知,动触头从开始移动到发生初次碰撞的时间为0.019 0 s,其碰撞瞬间速度为1.293 m/s,在0.021 9 s时达到稳定合闸状态;动铁芯在0.019 7 s发生初次碰撞,其碰撞瞬间速度为1.687 mm/s,在0.021 1 s时达到稳定接触。对比可知:动触头开始弹跳时间早于动铁芯,这是由于动静触头距离小于动静铁芯距离,导致动触头先于动铁芯发生撞击和弹跳。
|
图 4 触头和铁芯弹跳响应曲线 Fig. 4 Bounce response curve of contact and core |
由动铁芯位移曲线可知,动铁芯的弹跳次数和最大位移均小于动触头,这是由于动铁芯撞击时接触面积较大,在弹跳过程中受到电磁力作用,且动铁芯质量较大,进一步阻止了动铁芯的弹跳,使得其弹跳次数和时间远小于动触头。分析可知,触头初次碰撞时的最大位移较小,其碰撞时的最大位移出现于动铁芯初次撞击时刻,这是由于动静铁芯的碰撞进一步加剧了触头弹跳,使得其弹跳最大位移增加。
2 仿真模型的建立 2.1 电磁力ANSYS仿真在实际电磁力计算中,由于线圈中的交变电流产生磁场,动铁芯的运动又会在线圈中产生感应电流,使得线圈中磁场分布变得非常复杂,以往研究者多采用简化算法,通过公式直接计算电磁力,使得计算量较大且精度偏低。
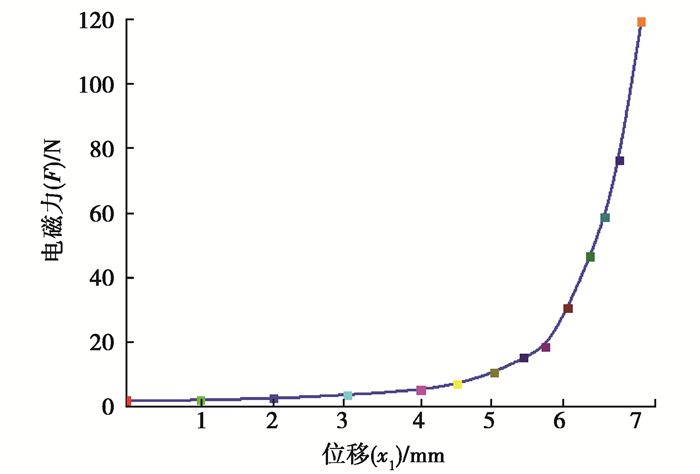
利用多物理场分析软件ANSYS,对动静铁芯间的电磁力进行仿真计算。有限元仿真分析遵循静态电磁场原理,不存在时变效应。通过对物体表面的麦克斯韦电磁应力张量进行表面积分,可获得静态场条件下作用在物体上的电磁力。ANSYS有限元分析软件建立了交流接触器有限元模型,然后利用SOURC36单元创建了3D跑道型线圈,线圈匝数设置为1 600闸,施加了磁力线边界条件,仿真得到的电磁力曲线如图 5所示。
|
图 5 电磁力仿真 Fig. 5 Electromagnetic force simulation |
由图 5可知交流接触器的电磁吸力随着动铁芯位移的增大而增大。当电磁系统中其他参数一定时,由式(2)可知,线圈匝数N的增大使得电磁吸力Fx增大,过大的电磁吸力使得铁芯碰撞速度快,导致碰撞加剧。当线圈匝数较小时,电磁力又不能保证接触器快速合闸、稳定吸合,电磁吸力大小与线圈匝数N的圈数成正比关系。
2.2 接触器ADAMS模型建立根据ABB公司A9-30-10型电磁接触器为参考,采用ADAMS动力学分析软件对交流接触器合闸全过程进行动态仿真。运用二元函数插值法,将上述ANSYS仿真得到离散的磁链和电磁吸力数据用样条函数的方法输入到ADAMS中。通过插值法迭代的方式对函数值进行求解,并将求解结果作为交流接触器机械模型的驱动力,从而实现对交流接触器动态合闸过程的仿真。
为了提高计算精度,仿真过程中还考虑了碰撞阻尼和摩擦力等因素的影响。对静铁芯和静触头施加固定副,动铁芯和动触头施加移动副,对动静触头以及动静铁芯接触面均施加接触副,设置模型中各个部件的结合参数与材料属性,仿真时长为0.035 s,以步长500步进行动态合闸仿真。ADMAS中的仿真模型如图 6所示。
|
图 6 接触器仿真模型 Fig. 6 Contactor simulation model |
遗传算法(genetic algorithm,GA)是一种仿照生物遗传和进化的算法,其本质是根据适应度函数值来评价问题解的优劣,从而实现对解空间的搜索。GA具有强鲁棒性和高效的全局搜索能力,目前已被成功运用于解决多峰值、非线性、高复杂度等工程实际。GA可以用一个五维向量组来描述,即
| $ \boldsymbol{X}_{\mathrm{GA}}=\left[N_{\mathrm{pop}}, N_{\mathrm{gen}}, P, f_{\text {eval }}, f_{\text {set }}\right], $ | (8) |
式中:Npop为种群规模,Ngen为迭代次数,p为遗传算子(交叉pk和变异pz),feval为适应度函数,fsel表示再生选择规则。
由于GA早熟收敛和算法参数敏感,使得算法进化后期搜索效率较低,并且GA需要人为设定3个遗传参数,即所选群体的大小n、交叉概率pk与变异概率pz)。Sriniva等因此首次提出AGA算法,该算法可使得交叉变异概率实现适应度值动态调整,从而获取适合当前个体的最佳交叉变异概率,使搜索能力和效率大幅提高。
3.2 改进的自适应遗传算法 3.2.1 群体生成与子代产生机制采用解空间的均匀采样法,先在解空间中随机均匀生成一定数目的个体,按照适应度值的大小进行排序,挑选出优秀个体组成初始群体。
遗传算法主要通过选择、交叉和变异等操作来产生子代个体,但经过这些操作产生的子代并不一定优于父代中的个体,会造成父代中优良个体的丢失。因此,对子代产生机制进行改进,将子代群体的产生分成3部分:首先采用精英保持策略,将父代群体中前10%的优良个体直接保持到子代,使得父代中的最优解可不被交叉和变异破坏;其次采用随机生成方式,产生10%的子代个体,补充种群中基因型的多样性;第三部分采用选择、交叉、变异产生剩余子代的80%;最后采用该方法可使群体中优良个体得以保存,同时增加和维持了群体的多样性。
3.2.2 算子改进机制AGA对传统GA中的交叉变异概率进行了改进,使交叉变异概率不再是人为设定的固定值,而是可以随着种群中个体的相似度进行动态调整。当种群中父代个体相似度较高时,执行交叉操作就很难产生新的个体,可以有效避免局部最优的情况,抑制早熟收敛现象的发生;当种群中个体的相似度较低时,说明此时种群多样性较高,可以防止种群中的优良基因结构遭到破坏。
AGA算法中交叉变异概率的值是个体适应度和最大适应度的差值成正比关系,最大适应度与平均适应度的差值成反比关系,当群体中某个体适应度值与该代中个体最大适应度值相等时,将导致交叉变异概率为零,使优化问题早熟[20]。AGA算法使得交叉概率和变异概率可以根据个体适应度取到合理的值。具体计算公式为
| $ p_{k}=\left\{\begin{array}{l} \frac{p_{k 1}\left(f_{\mathrm{avg}}-f\right)+p_{k 2}\left(f-f_{\min }\right)}{f_{\mathrm{avg}}-f_{\min }}, f \leqslant f_{\mathrm{avg}} ,\\ \frac{p_{k 2}\left(f_{\max }-f\right)+p_{k 3}\left(f-f_{\mathrm{avg}}\right)}{f_{\max }-f_{\mathrm{avg}}}, f>f_{\mathrm{avg}}, \end{array}\right. $ | (9) |
| $ p_{z}=\left\{\begin{array}{l} \frac{p_{z 1}\left(f_{\mathrm{avg}}-f\right)+p_{z 2}\left(f-f_{\min }\right)}{f_{\mathrm{avg}}-f_{\min }}, f \leqslant f_{\mathrm{avg}}, \\ \frac{p_{z 2}\left(f_{\max }-f\right)+p_{z 3}\left(f-f_{\mathrm{avg}}\right)}{f_{\max }-f_{\mathrm{avg}}}, f>f_{\mathrm{avg}}, \end{array}\right. $ | (10) |
式中:f为个体的适应度值,fmax为群体中最大适应度值,fmin为群体中最小适应度值,favg为群体平均适应度值,其中pk1>pk2>pk3∈(0, 1),pz1>pz2>pz3∈(0, 1)。
3.3 设计变量及约束条件影响触头弹跳的主要因素包括动触头m1、动铁芯m2、动铁芯位移x1、动触头位移x2、触头弹簧刚度系数k1、反力弹簧刚度系数k2、触头系统等效阻尼c1、电磁机构等效阻尼c2、电磁力Fx(可用线圈匝数N代替)。
因此选取对触头弹跳影响的9个参数作为此次接触器的优化变量,具体公式为
| $ \boldsymbol{X}=\left[m_{1}, m_{2}, x_{1}, x_{2}, c_{1}, c_{2}, k_{1}, k_{2}, N\right]^{\mathrm{T}}, $ | (11) |
为了保证算法能得到可靠合理的解,必须对交流接触器模型各设计变量施加约束条件。具体数值及变化范围如表 2所示。
| 表 2 设计变量原始值及其变化范围 Table 2 Original value of design variable and its variation range |
在保证交流接触器正常工作的前提下,以触头合闸和触头弹跳时间作为优化目标,则此次接触器优化的目标函数为
| $ \min f(\boldsymbol{X})=[T(\boldsymbol{X}), \Delta T(\boldsymbol{X})]^{\mathrm{T}}, $ | (12) |
式中:T(X)为触头合闸时间,ΔT(X)为触头弹跳时间。
当接触器运行时,运行函数为f(X),具体表达式为
| $ f(\boldsymbol{X})=\operatorname{step}\left(x, x_{0}, h_{0}, x_{1}, h_{1}\right), $ | (13) |
式中step为ADAMS自带函数。
将以上各个单项优化目标函数按照线性加权的方法,统一成如下综合目标的适应度函数
| $ \min F(x)=w_{1} \frac{T(x)}{T_{0}}+w_{2} \frac{\Delta T(x)}{\Delta T_{0}}, $ | (14) |
式中,w1+w2=1。其中w1、w2为目标函数的加权因子,T0、ΔT0为优化前的各目标函数的值。
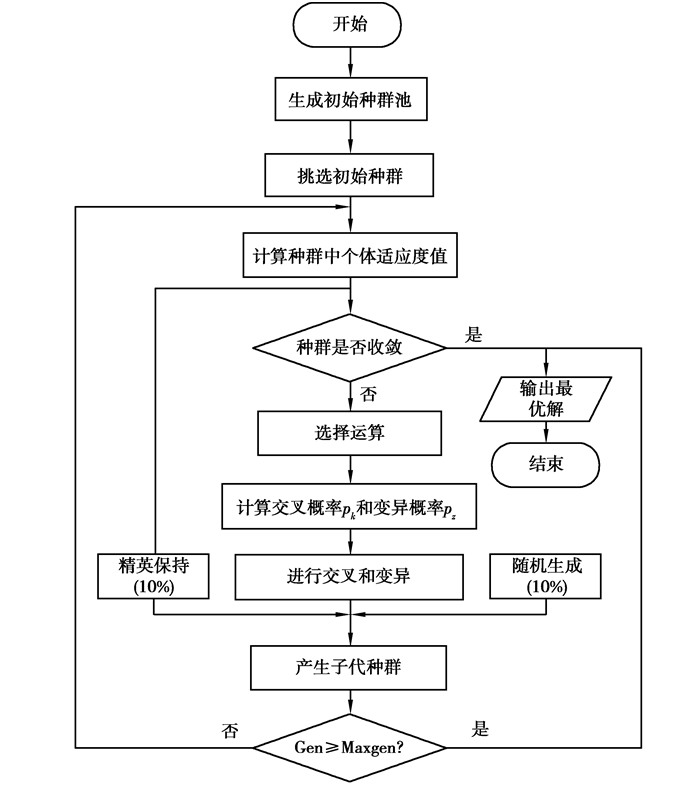
3.5 算法优化流程针对交流接触器中的触头质量、铁芯质量、触头弹簧以及电磁线圈匝数等参数优化,算法流程如图 7所示。
|
图 7 改进遗传算法流程图 Fig. 7 AGA algorithm flow chart |
STEP1:设定改进自适应遗传算法的初始参数,包括编码类型、初始种群大小、遗传迭代数和交叉变异概率等初始参量。
STEP2:采用解空间均匀采样法,均匀随机生成初始种群池,挑选初始种群。
STEP3:对初始种群进行适应度计算,首先采用精英保持策略,将初始种群中前10%优秀个体直接保持到子代。其次判断种群是否满足收敛条件。若满足,输出结果,否则执行STEP4。
STEP4:进行遗传操作,选择80%的父代个体,根据群体中个体适应度值,计算个体的交叉变异概率,进行交叉和变异操作。
STEP5:将采用精英保持策略,随机生成机制,运用选择、交叉和变异操作产生的个体构成新的子代种群。
STEP6:判断种群遗传代数是否超过设定值,若是,输出结果,否则遗传代数加1,返回STEP3。
4 基于AGA算法的接触器优化 4.1 遗传算法程序在ADAMS中的动态链接使用C语言编写遗传算法代码,利用VC++6.0调试器编译添加程序生成动态链接库文件,实现对自编译的算法的注册。通过设置“USER1”接口,将遗传算法添加到ADAMS中。经过算法优化后,将新获得的参数供ADAMS/View调用。
4.2 优化结果及分析在ADAMS/View的菜单栏中,选择“Simulate”中的“Design Evaluation Tools”选项,然后选择“Optimizer”,进入到“求解器设置”对话框中的“Algorithm”选择用户自定义的“USER1”接口,对样机模型进行优化。
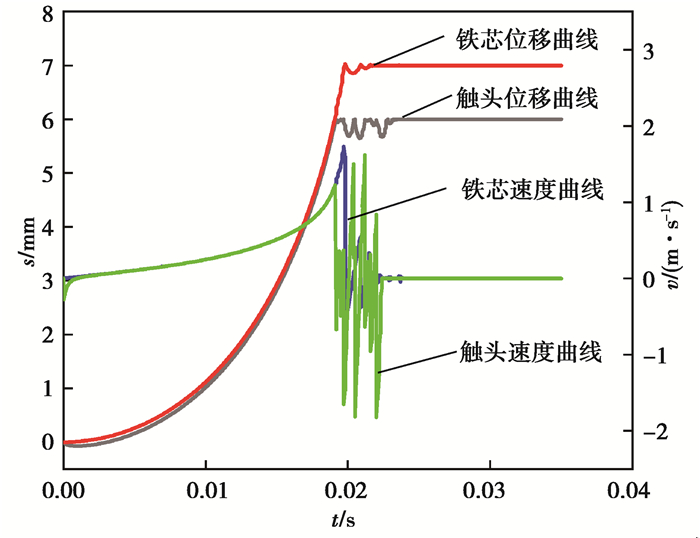
图 8为遗传算法优化前触头弹跳曲线。从图 8可以看出优化前接触器动触头从通电到初次合闸所需时间为19.71 ms,其弹跳过程中的最大位移为0.284 1 mm,碰撞瞬间速度为1.293 m/s,弹跳的总时间为2.9 ms,动触头弹跳4次后慢慢趋于稳定,由于动静触头之间存在Hertz接触,故弹跳曲线向后延伸了一小段。动铁芯于20.8 ms时发生初次碰撞,其弹跳过程中的最大位移为0.124 1 mm,弹跳的总时间为1.7 ms,碰撞瞬间速度为1.687 mm/s,在0.021 9 s时达到稳定合闸状态,动铁芯弹跳2次后即达到了稳定状态。
|
图 8 遗传算法优化前触头弹跳曲线 Fig. 8 Contact bounce curve before optimization of genetic algorithm |
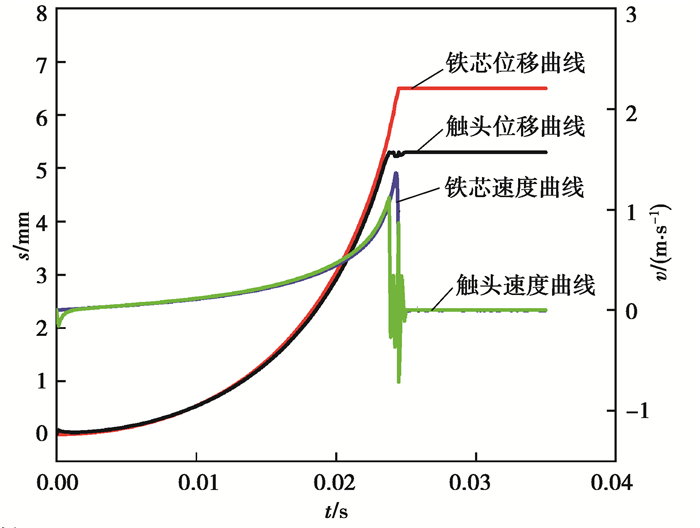
图 9为遗传算法优化后触头弹跳曲线。从图 9中可以看到优化后动触头微小弹跳就达到了稳定合闸状态,动铁芯并未发生明显弹跳,碰撞瞬间为1.187 mm/s;动触头合闸所需时间为23.32 ms,动触头碰撞瞬间速度为1.352 mm/s,其弹跳过程中的最大位移为0.021 2 mm,触头弹跳总时间为0.32 ms。对比图 8可知,通过遗传算法优化后,接触器动触头弹跳总时间降低了89%,最大位移降低了93%,碰撞瞬间速度为降低了8.9%;动铁芯弹跳总时间降低了95%,最大位移降低了83%,碰撞速度降低了19.9%,接触器整体性能得到了大幅提高。
|
图 9 遗传算法优化后触头弹跳曲线 Fig. 9 Contact bounce curve after optimization of genetic algorithm |
接触器优化前后的各项参数如表 3所示,由表 3中优化前后对比可知,显然优化后动铁芯质量减小,动触头质量增加;动铁芯和动触头位移均减小;电磁机构和触头系统等效阻尼均增大;反力弹簧和触头弹簧刚度系数均增大;线圈匝数减小,即电磁力减小,样机动态特性得到了大幅提高。
| 表 3 参数优化结果对比表 Table 3 Comparison of optimization results |
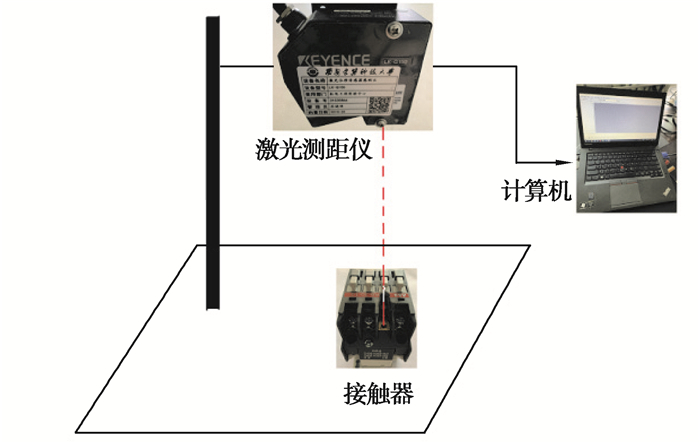
本实验依托ABB江门公司实验平台,对优化后的模型进行验证。首先,将优化后的模型参数按1 ∶1进行实际生产,其生产过程中,触头所用材料为AgNi15,触桥所用材料为CuZn15,铁芯所用材料为50W600。为了精确测量并标记触头弹跳过程的动触头位移变化,使用Ke-Yence的LK-G150型激光位移器对上述电磁接触器的一组触头进行实验。激光位移器能够实现位移数据的实时采集。为了充分掌握接触器运行时的状态,激光位移器需一直处于实时监测状态。在测试过程中,让其位移传感器放置在接触器的正上方,感测头垂直对准该主触头进行零点标记。平台主要布置如图 10所示。
|
图 10 实验平台布置图 Fig. 10 Layout of experimental platform |
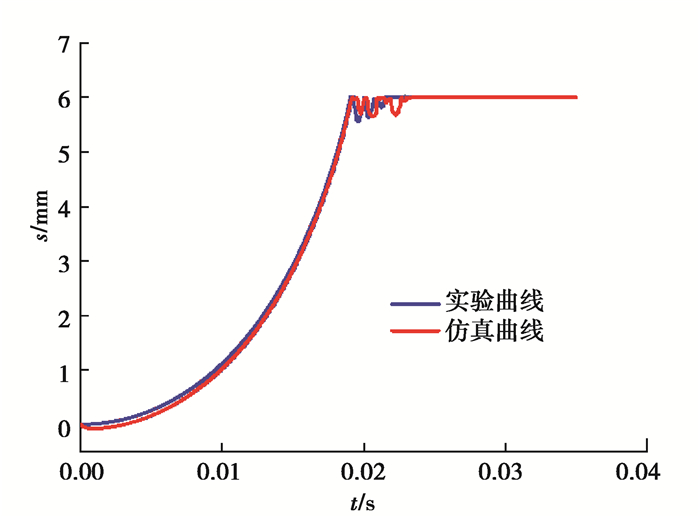
实验所得的数据由电脑直接记录,将Excel表格数据导入到MATLAB中进行1.2准则坏点剔除、间隔取样值和散点函数曲线拟合。将标定取得的触头弹跳过程位移曲线与仿真得到的曲线进行对比,结果如图 11所示。
|
图 11 理论与实验结果对比图 Fig. 11 Comparison of simulation and experimental results |
由图 11可知,仿真曲线设定实验测得交流接触器动触头稳定闭合时间为19.71 ms,弹跳过程中的最大位移为0.284 1 mm;实验得到的交流接触器动触头稳定闭合时间为19.90 ms,弹跳过程中的最大位移为0.280 2 mm;得到:1)触头合闸时间误差为0.96%;2)弹跳时间误差为1.37%,且对于触头弹跳总时间和接触器合闸闭合时间的实验与理论相差都在2%以下,由此证明了该计算方法完全适用于交流接触器弹跳特性的计算和分析。
6 结论通过对触头系统二自由度分段耦合微分方程进行化简求值,对接触器触头弹跳行为规律进行分析,利用ADAMS提供的接口,在ADAMS/View实现了遗传算法程序的调用。进而得出以下结论:
1) 动触头开始弹跳时间略早于动铁芯,动触头弹跳的次数和最大位移均大于动铁芯,触头初次碰撞时的最大位移较小,其碰撞时的最大位移出现于动铁芯初次撞击时刻。
2) 通过AGA型算法优化后,接触器合闸所需时间为23.32 ms,触头碰撞瞬间速度减小为1 187 mm/s,其弹跳过程中的最大位移为0.021 2 mm,弹跳总时间为0.32 ms,与优化前对比,触头弹跳时间和最大位移分别降低了89%和93%。
3) 使用激光测距仪进行的实验,理论与试验结果误差在2%以下,验证了遗传算法在交流接触器设计应用中的可行性和有效性,研究结果为进一步全面优化接触器样机提供了新方法。
| [1] |
Shu L, Wu L, Wu G C, et al. A fully coupled frame-work of predicting the dynamic characteristics of permanent magnet contactor[J]. IEEE Transactions on Magnetics, 2016, 52(8): 8001607. |
| [2] |
Biagini V, Bolognesi P, Mechler G, et al. Multi-domain mechatronic approach for the design of a vacuum contactor actuation drive[C]//2016 XXII International Conference on Electrical Machines, September 4-7, 2016, Lausanne, Switzerland. IEEE, 2016: 1126-1131.
|
| [3] |
Cheng S, Cai Z Y. Design and optimization of energy-saving wind power grid-connected contactor based on Nano two-phase composite magnetic materials[C]//2017 4th International Conference on Electric Power Equipment-Switching Technology, October 22-25, 2017, Xi'an, China. IEEE, 2017: 209-212.
|
| [4] |
Klymenko B V, Pantelyat M G. Electromagnetic actuators for medium voltage vacuum switching devices: classification design controlling[C]//2017 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering, September 14-16, 2017, Lodz, Poland. IEEE, 2017: 1-2.
|
| [5] |
陈德为, 陈文桂, 吕伯钦, 等. 具有电磁可控反力的智能交流接触器的实现与动态分析[J]. 中国电机工程学报, 2016, 36(13): 3660-3666. Cheng D W, Chen W G, Lü B Q, et al. Realization and dynamic analysis of the intelligent AC contactors with electromagnetic controllable force[J]. Proceedings of the CSEE, 2016, 36(13): 3660-3666. (in Chinese) |
| [6] |
陈德为, 张培铭. 基于高速摄像机的智能交流接触器动态测试与分析技术[J]. 仪器仪表学报, 2010, 31(4): 878-884. Chen D W, Zhang P M. High-speed camera-based intelligent AC contactor dynamic testing and analysis techniques[J]. Chinese Journal of Scientific Instrument, 2010, 31(4): 878-884. (in Chinese) |
| [7] |
贺开华, 荣命哲, 吴翊, 等. 三气隙永磁接触器电磁特性分析[J]. 低压电器, 2012(13): 6-10. He K H, Rong M Z, Wu Y, et al. Analysis of electromagnetic characteristics for three gaps permanent magnet contactor[J]. Low Voltage Apparatus, 2012(13): 6-10. (in Chinese) |
| [8] |
Jin P, Lin H Y, Fang S H, et al. A rapid magnetic analysis and dynamic prediction model for permanent magnet contactor[J]. Proceedings of the Chinese Society for Electrical Engineering, 2010, 30(36): 16-21. |
| [9] |
Ren W B, Zhai G F, Cui L. Contact vibration characteristic of electromagnetic relay[J]. IEICE Transactions on Electronics, 2006, E89-C(8): 1177-1181. DOI:10.1093/ietele/e89-c.8.1177 |
| [10] |
Ren W B, Chen Y H, Zhai G F. Modeling and simulation of hermetically sealed electromagnetic relay under mechanical environment[J]. IEICE Transactions on Electronics, 2007, E90-C(7): 1448-1454. DOI:10.1093/ietele/e90-c.7.1448 |
| [11] |
舒亮, 吴桂初, 朱翔鸥, 等. 基于偏微分弱解式方程的三维电磁力计算及其在接触器中的应用研究[J]. 中国电机工程学报, 2013, 33(6): 176-182. Shu L, Wu G C, Zhu X O, et al. 3D magnetic force calculation based on PDE weak form equations and applications in contactors[J]. Proceedings of the CSEE, 2013, 33(6): 176-182. (in Chinese) |
| [12] |
林抒毅, 许志红. 晃电故障下交流接触器的工作特性分析[J]. 中国电机工程学报, 2011, 31(24): 131-137. Lin S Y, Xu Z H. Performance characteristics of AC contactor during voltage sag[J]. Proceedings of the CSEE, 2011, 31(24): 131-137. (in Chinese) |
| [13] |
杨文英, 邵帅, 周敬, 等. 基于Ansys大功率接触器振动特性仿真研究[J]. 电器与能效管理术, 2018(4): 25-28. Yang W Y, Shao S, Zhou J, et al. Vibration characteristic simulation study of high power contactor based on Ansys[J]. Electrical and Energy Management Technology, 2018(4): 25-28. (in Chinese) |
| [14] |
杨文英, 刘兰香, 翟国富. 热场影响下新能源用接触器弹跳特性研究[J]. 电工技术学报, 2019, 34(22): 4687-4698. Yang W Y, Liu L X, Zhai G G. The bounce characteristics of contactors for new energy under the influence of thermal field[J]. Transactions of China Electrotechnical Society, 2019, 34(22): 4687-4698. (in Chinese) |
| [15] |
林抒毅, 许志红. 交流接触器三维动态过程数值计算与分析[J]. 中国电机工程学报, 2014, 34(18): 2967-2975. Lin S Y, Xu Z H. Simulations and numerical analysis on 3D dynamic process of alternating current contactors[J]. Proceedings of the CSEE, 2014, 34(18): 2967-2975. (in Chinese) |
| [16] |
Gao X T, Yang D S, Cui E C, et al. Study on uninterrupted switching topology and its control strategy of voltage sag protection[C]//2017 IEEE Industry Applications Society Annual Meeting, October 1-5, 2017. Cincinnati, OH, USA. IEEE, 2017: 1-9.
|
| [17] |
何晓燕, 许志红. 交流接触器虚拟样机设计技术[J]. 电工技术学报, 2016, 31(14): 148-155. He X Y, Xu Z H. Virtual prototyping technology of AC contactor[J]. Transactions of China Electrotechnical Society, 2016, 31(14): 148-155. (in Chinese) DOI:10.3969/j.issn.1000-6753.2016.14.017 |
| [18] |
汪先兵, 费树岷, 王祥傲, 等. 基于遗传算法的双E型永磁接触器仿真优化设计[J]. 低压电器, 2013(8): 11-16. Wang X B, Fei S M, Wang X A, et al. Simulation and optimization design for double-E type permanent magnet contactor based on genetic algorithm[J]. Low Voltage Apparatus, 2013(8): 11-16. (in Chinese) |
| [19] |
李亚峰, 王发展, 王雁琨, 等. 接触器触头系统弹跳行为仿真及影响因素分析[J]. 机械科学与技术, 2019, 网络首发, doi: 10.13433/j.cnki.1003-8728.20200016. Li Y F, Wang F Z, Wang Y K, et al. Bumping behavior simulation and influencing factors analysis of contact system in contactor[J]. Mechanical Science and Technology for Aerospace Engineering, 2019, pubulised on line, doi: 10.13433/j.cnki.1003-8728.20200016.(inChinese) |
| [20] |
Yan M F, Hu H S, Otake Y, et al. Improved adaptive genetic algorithm with sparsity constraint applied to thermal neutron CT reconstruction of two-phase flow[J]. Measurement Science and Technology, 2018, 29(5): 055404. DOI:10.1088/1361-6501/aaaea4 |
 2021, Vol. 44
2021, Vol. 44


