2. 东北石油大学 电气信息工程学院, 黑龙江 大庆 163318
2. School of Electrical Engineering and Information, Northeast Petroleum University, Daqing, Heilongjiang 163318, P. R. China
中性点箝位式(neutral point clamped, NPC)三电平逆变器因其较好的谐波输出特性、低电压变化率以及相较于更高电平而言较小的计算复杂度而被广泛应用于电驱、光伏并网系统中[1]。但是,多电平逆变器中存在较大的共模电压(common-mode voltage,CMV)[2]。在电驱系统中,幅值过大的共模电压往往伴随着较大的电压变化率,不仅将导致轴承故障进而影响电机的使用寿命[3],还带来电磁干扰问题[4]。此外,NPC三电平还存在直流侧中点电位(neutral-point potential,NPP)偏移的问题,当中点电位发生偏移时会导致逆变器开关管无法均匀分担母线电压,易出现开关管两端过压的情况,将大大减少开关管的使用寿命;同时中点电位波动还会影响逆变器的输出性能,增加输出电压、电流的谐波畸变率,降低输出波形质量。因此,共模电压和中点电位偏移成为NPC逆变器着重优化的热点[5]。
在针对降低共模电压的研究中,文献[6]详细阐述了减小共模电压幅度及其快速变化的技术,但该方案引入了硬件设施,增加了系统的体积和成本;Jun等[7]通过优化脉宽调制(pulse width modulation,PWM)策略降低共模电压负面影响,该方法成本低且方法更加灵活;郭磊磊等[8]针对共模电压尖峰的特性调整开关管的动作时间降低共模电压,但是增加了计算复杂度。这些研究没有在降低共模电压的同时兼顾改善NPC逆变器的中点电位性能。马星河等[5]通过优化虚拟空间矢量实现共模电压和中点电位的平衡控制,该方法虽然能达到零共模电压但中点电位波动的消除效果并不理想;王萍等[9]重新划分扇区并在不同扇区的空间矢量合成过程中添加不同的零序电压分量以达到共模电压和中点电位的协同控制,但该方法在低调制度区间效果有所降低。笔者提出了一种基于虚拟空间矢量脉宽调制(virtual space vector PWM,VSVPWM)的优化策略,该方法的优点在于通过重构VSVPWM策略的参考电压矢量减小共模电压的影响,同时利用闭环控制抑制中点电位波动,更好地改善NPC逆变器的输出电压质量。
1 NPC三电平逆变器原理及特性分析 1.1 NPC三电平逆变器NPC三电平三相逆变拓扑结构如图 1所示,Vdc为直流侧母线电压,其下跨接2个容值相等的分压电容C1和C2;逆变器主电路包括绝缘栅双极型晶体管(insulated gate bipolar transistor,IGBT)、二极管和三相负载[10];P和N分别为直流侧和负载侧中性点,G为接地点。以A相为例,上桥臂开关S1和S2导通时输出电压VA为+Vdc/2;S3和S4导通时VA为-Vdc/2;若S2与S3导通则VA=0。记上述3种工作状态对应的输出电压为电平p、n、o。该状态同样适用于B相和C相,根据每相的电压输出状态,三电平NPC逆变器可共组合成27种空间电压矢量,如图 2所示,其中包含[p p n]在内6个大矢量、[p o n]等6个中矢量[11]、[p p o]等12个小矢量以及[p p p]、[o o o]和[n n n]共3个零矢量。
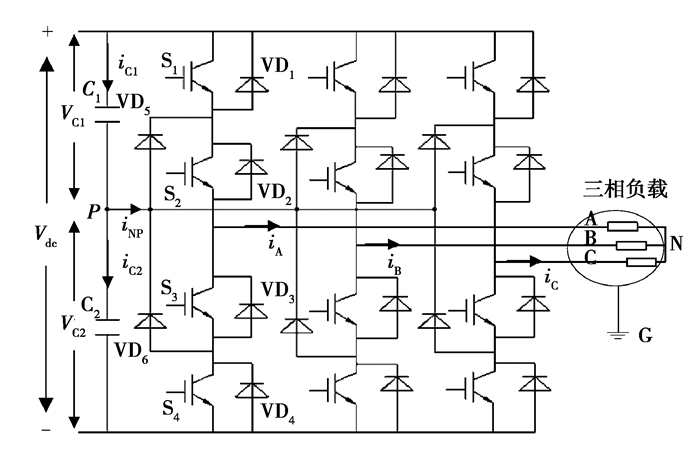
|
图 1 三电平NPC逆变器拓扑结构 Fig. 1 Three-level NPC inverter topology |
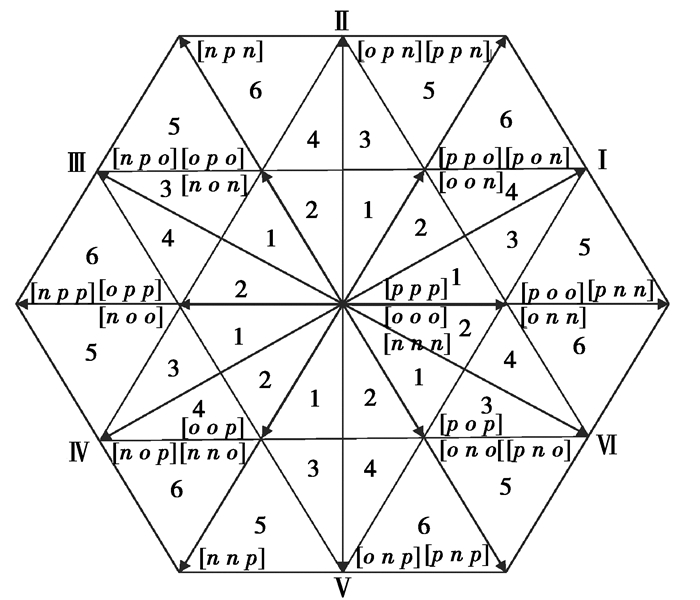
|
图 2 空间电压矢量图 Fig. 2 Space voltage vector diagram |
如图 1所示,逆变器外接负载时,共模电压VCM=VN-P-VG-P,因VG-P值较小可忽略不计,于是共模电压VCM可由式(1)表示[12]。根据式(1)可计算出27种开关组合下每个空间电压矢量的共模电压值,如表 1所示。其中所有中矢量和零矢量[o o o]的作用不会产生共模电压[13],因此在优化PWM策略时应尽可能多地使用中矢量和零矢量[o o o]以减小共模电压值;同时也应尽可能地避免选取小矢量,防止增加共模电压值。
| $ V_{\mathrm{CM}}=\left(V_{\mathrm{A}}+V_{\mathrm{B}}+V_{\mathrm{C}}\right) / 3 $ | (1) |
| 表 1 各电压矢量共模电压值 Table 1 CMV of all voltage vectors |
对于中性点电位而言,如果电流iP≠0,则跨接电容将处于充放电状态,从而导致中性点电位波动[5]。能对中点电位产生影响的是中矢量和小矢量,所以传统的SVPWM策略可以通过调节成对出现且对中点电位作用相反的正、负小矢量来抑制中点电位波动[9],但该方法增大了共模电压并产生低频振荡。因此利用原有电压矢量重构中矢量的VSVPWM技术应运而生。笔者正是在VSVPWM策略抑制中点电位波动的基础上对其进行优化使其同时具有抑制共模电压的能力,进一步提高三电平NPC逆变器的性能。
2 VSVPWM技术及优化 2.1 VSVPWM原理分析传统VSVPWM利用SVPWM的电压矢量定义了虚拟中矢量和虚拟小矢量[14],确保在一个开关周期TS内流入P处的平均电流为零[15]。以VSVPWM的第I大扇区为例,如图 3所示,VVM1为合成的虚拟中矢量,VV0、VVS1、VVS2为虚拟小矢量,VVL1和VVL2代表虚拟大矢量。
各虚拟矢量的表达式如式(2)所示。
| $ \left\{\begin{array}{l} \boldsymbol{V}_{\mathrm{v} 0}=\left[\begin{array}{lll} o & o & o \end{array}\right] , \\ \boldsymbol{V}_{\mathrm{vS} 1}=\left(\left[\begin{array}{lll} p & o & o \end{array}\right]+\left[\begin{array}{lll} o & n & n \end{array}\right]\right) / 2, \\ \boldsymbol{V}_{\mathrm{vS} 2}=\left(\left[\begin{array}{lll} p & p & o \end{array}\right]+\left[\begin{array}{lll} o & o & n \end{array}\right]\right) / 2, \\ \boldsymbol{V}_{\mathrm{VM} 1}=\left(\left[\begin{array}{lll} o & n & n \end{array}\right]+\left[\begin{array}{lll} p & p & o \end{array}\right]+\left[\begin{array}{lll} p & o & n \end{array}\right]\right) / 3, \\ \boldsymbol{V}_{\mathrm{VL} 1}=\left[\begin{array}{lll} p & n & n \end{array}\right], \\ \boldsymbol{V}_{\mathrm{VL} .2}=\left[\begin{array}{ll} p & p & n \end{array}\right]_{\circ} \end{array}\right. $ | (2) |
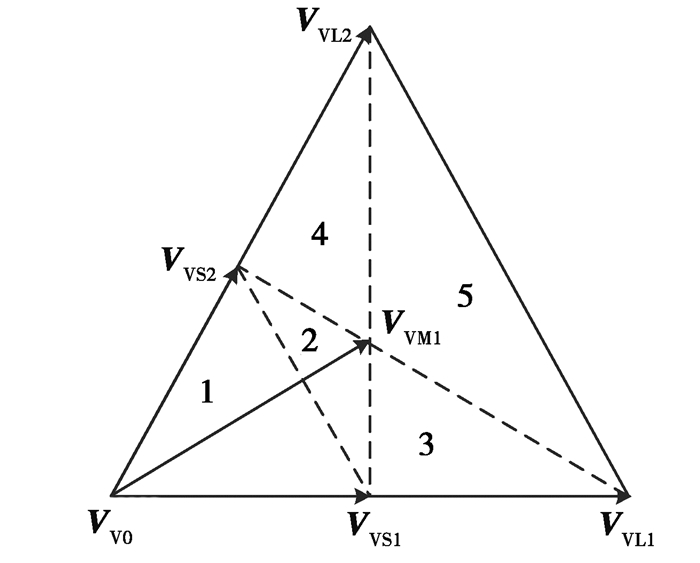
|
图 3 扇区I的虚拟空间矢量 Fig. 3 Virtual space vectors of Sector I |
由式(2)可知,虚拟中矢量由可产生中点电流分别为iA、iB和iC的基本矢量[o n n]、[p o n]和[p p o]组成,因此在TS时间内可以满足iA+iB+iC=0,即流入P的平均电流等于0。但是传统VSVPWM策略在合成虚拟空间矢量时引入了小矢量,导致共模电压最大可达Vdc/3。
2.2 VSVPWM策略的优化VSVPWM策略的优化重点在于虚拟空间矢量的重构,重构的虚拟空间矢量的合成表达式如式(3)。由式(3)可知,重构后的虚拟矢量不含小矢量,虚拟小矢量在零矢量和大矢量的作用下流入中点的电流为零;而合成虚拟中矢量的[o p n]、[p n o]和[p o n]在中点处产生的电流分别为iA、iC和iB,因此在开关周期内的平均电流也为零,不存在中点电位波动。
| $ \left\{\begin{array}{l} \boldsymbol{V}_{\mathrm{V} 0}^{\prime}=\left[\begin{array}{lll} o & o & o \end{array}\right], \\ \boldsymbol{V}_{\mathrm{VS} 1}^{\prime}=\left(\left[\begin{array}{lll} p & n & n \end{array}\right]+\left[\begin{array}{lll} o & o & o \end{array}\right]\right) / 2, \\ \boldsymbol{V}_{\mathrm{vS} 2}^{\prime}=\left(\left[\begin{array}{lll} p & p & n \end{array}\right]+\left[\begin{array}{lll} 0 & o & o \end{array}\right]\right) / 2, \\ \boldsymbol{V}_{\mathrm{VM} 1}^{\prime}=\left(\left[\begin{array}{lll} o & p & n \end{array}\right]+\left[\begin{array}{lll} p & n & o \end{array}\right]+\left[\begin{array}{lll} p & o & n \end{array}\right]\right) / 3, \\ \boldsymbol{V}_{\mathrm{VL} 1}^{\prime}=\left[\begin{array}{lll} p & n & n \end{array}\right], \\ \boldsymbol{V}_{\mathrm{VL} .2}^{\prime}=\left[\begin{array}{lll} p & p & n \end{array}\right]_{\circ} \end{array}\right. $ | (3) |
式(3)定义的虚拟空间矢量重构方式是基于中点电位为零这一理想状态,而在实际运行过程中,中点电位不可避免地出现波动,若波动程度超出可接受范围,或者实际应用场合对中点电位波动有较严格的要求,则需要VSVPWM根据实际情况对中点电位进行实时动态调节。改善这一情况的有效手段是加入反馈环节,实时调整虚拟空间矢量并对中点电压进行控制。为此引入动态调节因子γ二次优化虚拟中矢量,其优化后的表达式如式(4)所示。
| $ \boldsymbol{V}_{\mathrm{VM} 1}^{\prime \prime}=\gamma\left(\left[\begin{array}{lll} o & p & n \end{array}\right]+\left[\begin{array}{lll} p & n & o \end{array}\right]\right)+(1-2 \gamma)\left[\begin{array}{lll} p & o & n \end{array}\right], \quad 0<\gamma<0.5 。$ | (4) |
在
在计算组成参考电压矢量的各虚拟矢量的作用时间时,需在g-h坐标系下将参考电压矢量进行转换,同时结合伏秒平衡原理来求解[16],其他大扇区的参考电压矢量的作用时间也遵循该求解方法。VSVPWM的另一个重点在于开关作用顺序的分配,在传统的VSVPWM策略中,要求开关作用顺序的设定能够保证参考电压矢量的平滑切换,即电平p与电平n只能与o进行切换。而本研究中还需要考虑共模电压的抑制问题,因此,需要结合共模电压的大小重新规划开关作用顺序。根据前文分析,开关作用顺序的确定应以尽量使用中矢量、零矢量[o o o]为准则,虚拟中矢量的重构也正是基于尽量使用中矢量的原则;同时为了减少共模电压,共模电压值为±Vdc/3的小矢量应避免被选取,而正负小矢量是成对出现的,意味着优化的VSVPWM策略中将不再出现小矢量,改进后虚拟电压矢量产生的共模电压最大值仅为Vdc/6,相比于传统SVPWM,共模电压可减少50%。在此基础上,得到优化的VSVPWM的开关作用顺序,以第I扇区为例,各小扇区的电压矢量作用顺序如表 2所示。优化的电压矢量作用顺序为九段式,可以在减少共模电压的同时削减输出电压的谐波成分,相应地也增加了开关管的开关次数。
| 表 2 扇区I的电压矢量作用顺序 Table 2 Sequences of voltage vectors in Sector I |
虽然中矢量不会对共模电压产生负面影响,但是中矢量的投切将会在一定程度上影响中点电压波动,尤其在传统VSVPWM策略设定的调制比m较大时,中矢量作用时间较长,对中点电压波动的影响更加显著。传统的三电平逆变器直流侧中点电位平衡控制仅以降低中点电位波动为目标,将中点电位波动值作为反馈进而调节中点电位。而我们的闭环控制策略的目的是在兼顾降低共模电压的同时实现中点电位的有效抑制。为了在现有降低共模电压方案的基础上同时获得较好的NPP抑制效果,以虚拟中矢量的动态调节因子γ为优化变量,采用闭环控制策略。该策略的核心是根据设定的中点电压波动范围ΔV动态调整γ值,进而通过中矢量的变化动态调节流入、流出NPC逆变器中点的电荷量,从而抑制中点电位的波动。该策略的控制示意图如图 4所示。
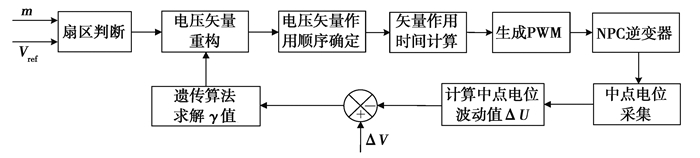
|
图 4 优化的VSVPWM闭环控制策略 Fig. 4 Closed-loop control strategy of optimized VSVPWM |
记直流侧上、下电容两侧的电压差值ΔU为中点电位波动值,在调制比及变压器负载确定后,当|ΔU| < ΔV时,说明中点电位的波动在设定的范围内,此时不需要额外的调节,但应使γ为1/3,中点在一个开关周期内流出电荷为0;当ΔU < -ΔV时,说明电容C1两侧的电压VC1值过小,需要增加流出中点的电荷量以提高VC1,结合一个周期内流过中点处的电荷量可知,若iB>0,则γ∈(0, 1/3),否则γ∈(1/3, 1/2)。当ΔU>ΔV时,说明电容C1两侧的电压VC1值过大,需要增加流入中点的电荷量来减小VC1,若iB>0, 则γ∈(1/3, 1/2),否则γ∈(0, 1/3)。通过锁定γ大致范围,可有效缩短寻优空间,有利于快速确定γ最优值。为了进一步确定γ的最优值,建立关于中点电位的目标函数F(γ),如式(5)所示,然后采用遗传算法对该目标函数求解,得到满足条件的γ的最优值,限于篇幅原因,遗传算法的基本原理不再赘述。
| $ F(\gamma)=\min (|\Delta U|-\Delta V) 。$ | (5) |
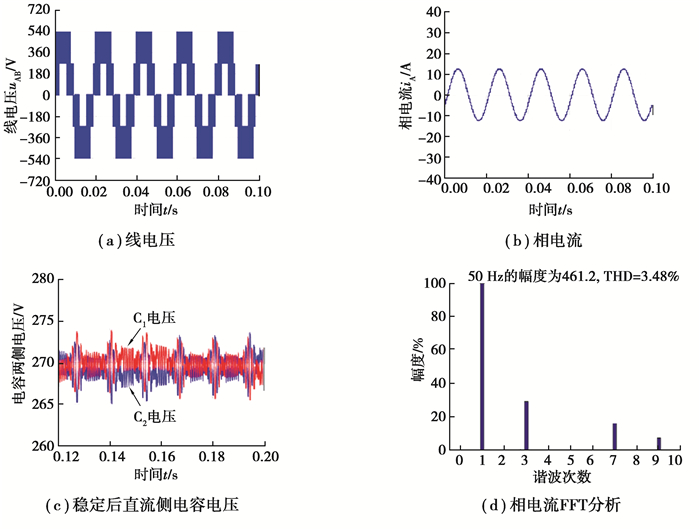
针对所提出的改进VSVPWM策略,通过Matlab对其有效性进行仿真,主要仿真参数设置如下:Vdc为540 V,电容C1与C2电容值为1 100 μF,基波频率和采样频率分别为50 Hz和5 kHz,三相负载的电阻为15 Ω、电感为20 mH,调制度设定位0.8。图 5和图 6展示了传统VSVPWM和改进的VSVPWM的线电压uAB和相电流iA以及稳定状态时的直流侧电容电压。
|
图 5 传统VSVPWM仿真结果 Fig. 5 Simulation results of traditional VSVPWM |
|
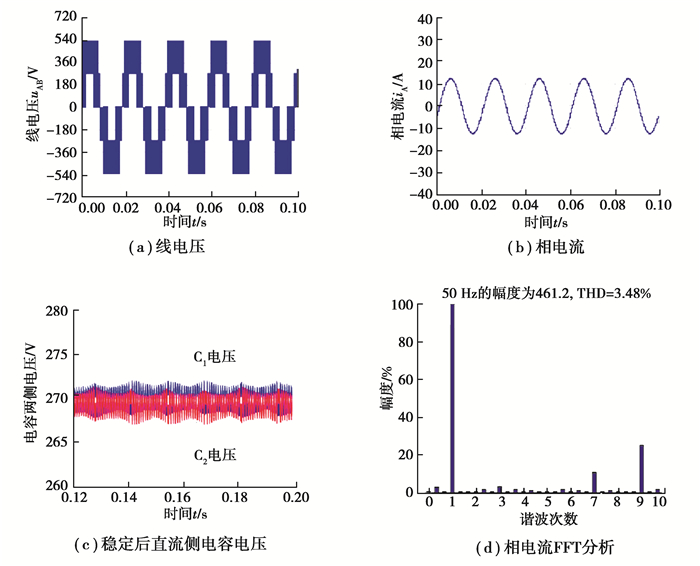
图 6 优化的VSVPWM仿真结果 Fig. 6 Simulation results of optimized VSVPWM |
由图 5和图 6可知,传统的VSVPWM和改进后的VSVPWM的都能输出稳定的线电压,且相电流也均呈较理想的正弦波,但改进的VSVPWM的相电流具有更小的谐波含量,其总谐波失真(total harmonic distortion,THD)为2.94%,而传统的VSVPWM的相电流THD=3.48%。同时,从图 5(c)和图 6(c)所示的直流侧电容电压可明显看出,传统的VSVPWM作用下的电容电压的波动范围为265.7~274.1 V,而改进的VSVPWM控制下电容电压波动范围为267.3~272.6 V,中点电位波动得到改善,其电位波动小于3 V。。
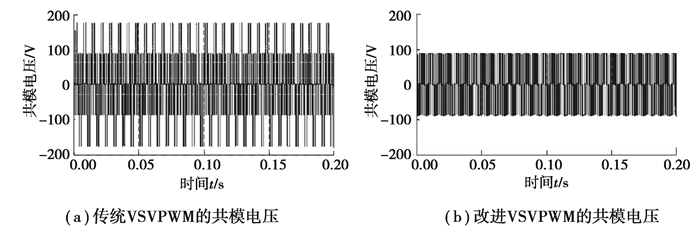
图 7展示了传统的VSVPWM和改进后的VSVPWM作用下的共模电压值,根据前文的理论分析,传统VSVPWM和改进VSVPWM策略的共模电压最大值应分别为±Vdc/3和±Vdc/6,即±180 V和±90 V,与图 7中的电压值相对应,说明改进的VSVPWM策略能够将共模电压值减小50%,该方法能够有效抑制共模电压。
|
图 7 两种VSVPWM策略的共模电压值 Fig. 7 CMV of (a)traditional and (b)optimized VSVPWM strategy |
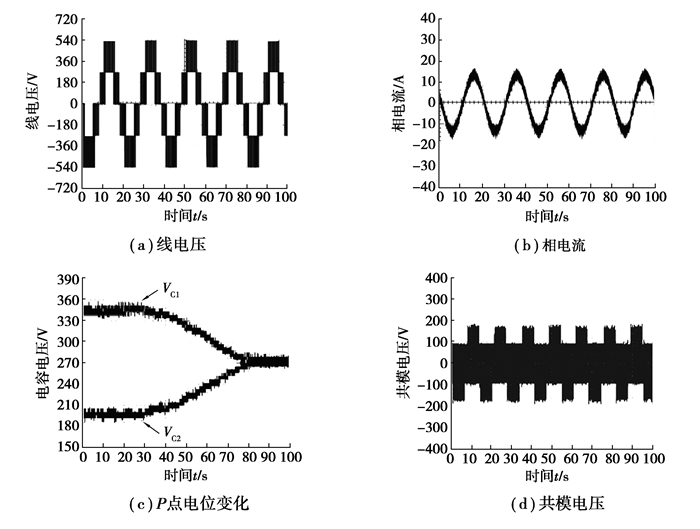
为进一步验证改进的VSVPWM策略在抑制中点电位和共模电压方面的有效性,建立了基于三电平NPC逆变器的实验平台,主控制器型号为TMS320F2812,负载参数与仿真环节的参数相同。传统VSVPWM和改进VSVPWM策略的实验验证结果如图 8和图 9所示。
|
图 8 传统VSVPWM策略的实验结果 Fig. 8 Experiment results of traditional VSVPWM strategy |
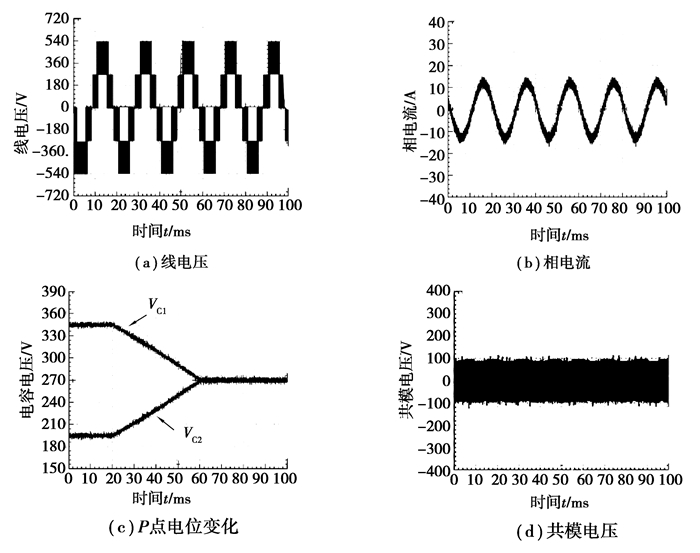
|
图 9 改进VSVPWM策略的实验结果 Fig. 9 Experiment results of optimized VSVPWM strategy |
由试验验证图可知,线电压与相电流波形与仿真波形一致,且电流波形呈正弦波,谐波较少。图 9所示的改进VSVPWM策略控制下中点电位在60 ms达到平衡状态,且维持在270 V,电位波动范围控制在5 V内,近似于仿真中的3 V波动范围;而传统VSVPWM则需要80 ms达到270V的稳定状态,且电容电压波动明显高于改进的VSVPWM策略,说明在改进VSVPWM策略下,中点电位得到有效、快速的控制;同时,图 8(d)所示的传统VSVPWM策略的共模电压最大值约为±180 V,而图 9(d)所示的共模电压幅值在±90 V左右,与理论推导和仿真分析结果吻合。上述试验结果充分说明改进的VSVPWM策略能够有效抑制中点电位波动,同时降低共模电压值,具有较好的抑制效果。
4 结论针对NPC三电平逆变器的中点电位波动和共模电压问题,在VSVPWM策略的基础上重构了基本电压矢量,优化电压矢量的作用顺序,剔除了小矢量对共模电压的影响,使得共模电压较传统VSVPWM减小50%,同时保证中点电位具有较小的波动幅度;为进一步控制共模电压,引入了闭环控制策略,通过负反馈实时监测中点电位和中点电流流向,动态调整中矢量形式,将中点电位控制在给定的波动范围内。通过搭建仿真和实验平台,验证了本文提出的改进方法在同时抑制中点电位波动和共模电压方面的有效性和准确性。
| [1] |
Ramasamy P, Krishnasamy V. Minimization of common-mode voltage for five-phase three-level NPC inverter using SVPWM strategy[J]. Iranian Journal of Science and Technology, Transactions of Electrical Engineering, 2020, 44(3): 1221-1232. DOI:10.1007/s40998-019-00304-5 |
| [2] |
Bharatiraja C, Jeevananthan S, Munda J L, et al. Improved SVPWM vector selection approaches in OVM region to reduce common-mode voltage for three-level neutral point clamped inverter[J]. International Journal of Electrical Power & Energy Systems, 2016, 79: 285-297. |
| [3] |
Baik J H, Yun S W, Kim D S, et al. SVPWM technique for common-mode voltage elimination of dual-winding fault-tolerant permanent magnet motor drives[J]. Journal of Power Electronics, 2020, 20(3): 710-719. DOI:10.1007/s43236-020-00062-2 |
| [4] |
吴可丽, 夏长亮, 张云, 等. 二极管钳位型三电平逆变器共模电压抑制[J]. 电工技术学报, 2015, 30(24): 110-117, 170. Wu K L, Xia C L, Zhang Y, et al. Common-mode voltage suppression for neutral-point-clamped three-level inverter[J]. Transactions of China Electrotechnical Society, 2015, 30(24): 110-117, 170. (in Chinese) DOI:10.3969/j.issn.1000-6753.2015.24.015 |
| [5] |
马星河, 马亚光, 刘志怀, 等. 三电平逆变器共模电压及中性点电压平衡策略[J]. 电力电子技术, 2020, 54(8): 82-85. Ma X H, Ma Y G, Liu Z H, et al. Common mode voltage and neutral point balance strategy of three-level inverter[J]. Power Electronics, 2020, 54(8): 82-85. (in Chinese) DOI:10.3969/j.issn.1000-100X.2020.08.023 |
| [6] |
牛学洲, 侯蕊欣. 降低共模电压的三电平变流器SVPWM策略[J]. 合肥工业大学学报(自然科学版), 2020, 43(7): 919-926. Niu X Z, Hou R X. A novel virtual space vector modulation with reduced common mode voltage and eliminated neutral point voltage oscillation for neutral point clamped three-level inverter[J]. Journal of Hefei University of Technology (Natural Science), 2020, 43(7): 919-926. (in Chinese) DOI:10.3969/j.issn.1003-5060.2020.07.010 |
| [7] |
Jun E S, Park S Y, Kwak S. A comprehensive double-vector approach to alleviate common-mode voltage in three-phase voltage-source inverters with a predictive control algorithm[J]. Electronics, 2019, 8(8): 872. DOI:10.3390/electronics8080872 |
| [8] |
郭磊磊, 金楠, 韩东许. 电压源逆变器模型预测共模电压尖峰抑制方法[J]. 太阳能学报, 2020, 41(3): 282-290. Guo L L, Jin N, Han D X. Model predictive common-mode voltage spike suppression method for voltage source inverter[J]. Acta Energiae Solaris Sinica, 2020, 41(3): 282-290. (in Chinese) |
| [9] |
王萍, 戚银, 张云. NPC三电平逆变器共模电压及中点电位波动协同抑制方法[J]. 电力系统及其自动化学报, 2018, 30(10): 28-33. Wang P, Qi Y, Zhang Y. Co-inhibition method of common mode voltage and neutral point potential fluctuation for NPC three-level inverter[J]. Proceedings of the CSU-EPSA, 2018, 30(10): 28-33. (in Chinese) DOI:10.3969/j.issn.1003-8930.2018.10.004 |
| [10] |
Le Q A, Park D H, Lee D C. Common-mode voltage elimination with an auxiliary half-bridge circuit for five-level active NPC inverters[J]. Journal of power electronics, 2017, 17(4): 923-932. |
| [11] |
Guo L L, Zhang X, Yang S Y, et al. A model predictive control-based common-mode voltage suppression strategy for voltage-source inverter[J]. IEEE Transactions on Industrial Electronics, 2016, 63(10): 6115-6125. DOI:10.1109/TIE.2016.2574980 |
| [12] |
Monge S B, Somavilla S, Bordonau J, et al. Capacitor voltage balance for the neutral-point-clamped converter using the virtual space vector concept with optimized spectral performance[J]. IEEE Transactions on Power Electronics, 2007, 22(4): 1128-1135. DOI:10.1109/TPEL.2007.900547 |
| [13] |
胡存刚, 王群京, 李国丽, 等. 基于虚拟空间矢量的三电平NPC逆变器中点电压平衡控制方法[J]. 电工技术学报, 2009, 24(5): 100-107. Hu C G, Wang Q J, Li G L, et al. A neutral-point potential balancing algorithm for three-level inverter based on virtual-space-vector[J]. Transactions of China Electrotechnical Society, 2009, 24(5): 100-107. (in Chinese) DOI:10.3321/j.issn:1000-6753.2009.05.017 |
| [14] |
Jiang W D, Du S W, Chang L C, et al. Hybrid PWM strategy of SVPWM and VSVPWM for NPC three-level voltage-source inverter[J]. IEEE Transactions on Power Electronics, 2010, 25(10): 2607-2619. DOI:10.1109/TPEL.2010.2041254 |
| [15] |
Wu X, Tan G J, Ye Z B, et al. Virtual-space-vector PWM for a three-level neutral-point-clamped inverter with unbalanced DC-links[J]. IEEE Transactions on Power Electronics, 2018, 33(3): 2630-2642. DOI:10.1109/TPEL.2017.2692272 |
| [16] |
王志强, 邓臣臣, 谷鑫, 等. 基于中点钳位型三电平逆变器的改进型虚拟空间矢量调制策略[J]. 电工技术学报, 2017, 32(18): 230-238. Wang Z Q, Deng C C, Gu X, et al. The improved virtual space vector modulation strategy based on neutral-point-clamped three-level inverter[J]. Transactions of China Electrotechnical Society, 2017, 32(18): 230-238. (in Chinese) |
 2021, Vol. 44
2021, Vol. 44


