关节臂式坐标测量机是一种非笛卡儿式的柔性测量系统,通常在大型加工现场对不便移动的复杂零部件进行几何尺寸的快速测量[1],因其可操作性、灵活性和便捷性在工业生产与科学研究中得到广泛的应用。由于其串联式连杆机构,测量机的测量误差会被累积并放大,同时机械加工精度、装配误差、磨损及环境因素等都对各连杆的几何参数造成影响,与传统的正交式坐标测量机相比,整体测量精度还存在较大差距。因此,测量机的误差模型的分析及参数标定方法对于减少测量误差有着重大意义。
目前已有众多国内外学者针对关节臂式坐标测量机参数标定方法做了多方面研究。一类通过借助更高精度的测量仪器,如激光跟踪仪、三坐标测量机[2],或布置复杂的装夹装置[3]。例如:Acero等[4]研究了激光跟踪仪作为参考仪器在AACMM参数标定中的可行性,但这类方法普遍成本高昂,系统复杂,时间效率较低且容易产生二次误差[5]。另一类通过算法进行参数标定,一般为最小二乘法和智能寻优算法,例如:Santolaria等[6]使用一维球列作为标准件,采用Levenberg-Marquarat法(最小二乘法)对Faro的关节式坐标测量机进行了标定;Seyedhosseini等[7]应用改进的模拟退火算法对测量臂运动学参数的标定值进行了辨识。但采用标定算法对参数进行辨识时,常用的标定算法如最小二乘法在求解过程中存在初始值是非可行点时无法收敛、参数较多的复杂计算易产生积累误差等问题,而寻优算法的局部搜索能力较差、容易陷入局部最小值。
针对关节式坐标测量机的参数标定问题,笔者提出了一种混合优化算法对测量机结构参数进行辨识。首先对最小二乘法求解中的Jacobian矩阵进行变换消除其中冗余参数,通过设定判定准则并实现模拟退火算法和最小二乘法的混合,结合两者全局优化性能和高效局部的优化能力进行参数标定,提高测量机的测量精度。
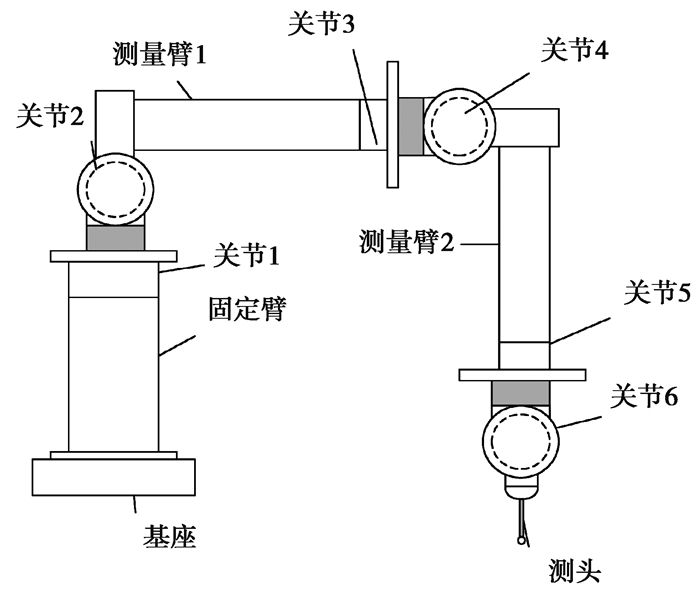
1 关节臂式坐标测量机模型关节臂式坐标测量机是仿人手臂的六自由度非正交坐标测量机,由机座、关节臂和测头通过旋转关节串联连接构成[8],结构参数名义值如表 1所示,其结构如图 1所示。
| 表 1 结构参数的标称值 Table 1 Nominal values of structural parameters |
|
图 1 关节臂式坐标测量机结构示意图 Fig. 1 Configuration of articulated arm coordinate measuring machine |
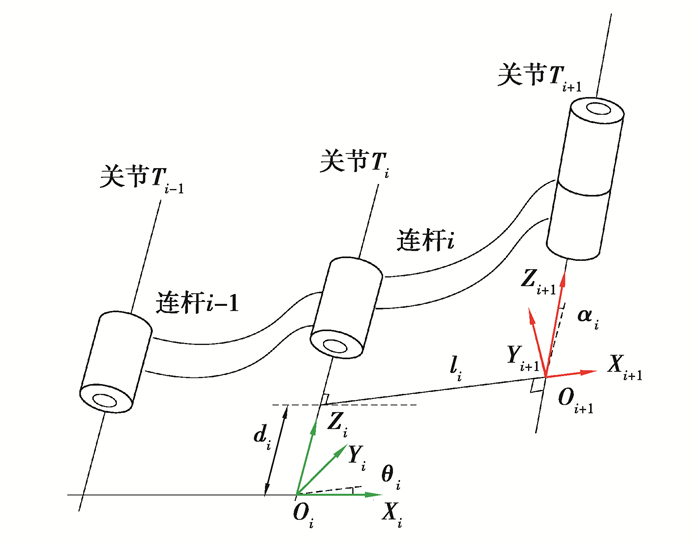
1956年,Denavit和Hartenberg提出D-H方法描述相邻连杆的变换关系,使用4个参数进行描述,分别是关节旋转角θi,杆件的长度ai,杆件偏移量di,杆件扭转角度βi。基于D-H模型的关节坐标转换示意图如图 2所示。
|
图 2 基于D-H模型的关节坐标转换示意图 Fig. 2 Coordinate transformation diagram by D-H model |
根据图 2可知,坐标系(xi-1, yi-1, zi-1)转至下个坐标系(xi, yi, zi)的坐标的变换过程,需要经过2次旋转2次平移得到,坐标转换关系为
| $ \boldsymbol{A}_{i-1, i}=\operatorname{Rot}\left(z_{n}, \theta_{n+1}\right) \operatorname{Trans}\left(0,0, d_{n+1}\right) \operatorname{Trans}\left(a_{n+1}, 0,0\right) \operatorname{Rot}\left(x_{n+1}, \beta_{n+1}\right)。$ | (1) |
相邻坐标系的齐次变换矩Ai-1, i为
| $ \boldsymbol{A}_{i-1, i}=\left[\begin{array}{cccc} \cos \theta_{i} & -\cos \beta_{i} \sin \theta_{i} & \sin \beta_{i} \sin \theta_{i} & \mathrm{a}_{i} \cos \theta_{i} \\ \sin \theta_{i} & \cos \beta_{i} \cos \theta_{i} & -\sin \beta_{i} \cos \theta_{i} & \mathrm{a}_{i} \sin \theta_{i} \\ {\bf{0}} & \sin \beta_{i} & \cos \beta_{i} & \mathrm{~d}_{i} \\ {\bf{0}} & {{\bf{0}}} & {\bf{0}} & {\bf{1}} \end{array}\right] 。$ | (2) |
此时,由于第7个坐标系是以测头为中心,由第6个坐标系平移,设测头中心在坐标系下坐标为(Bx, By, Bz),坐标转换矩阵B为
| $ \boldsymbol{B}=\left[\begin{array}{llll} \boldsymbol{B}_{x} & \boldsymbol{B}_{y} & \boldsymbol{B}_{z} & {\bf{1}} \end{array}\right]^{\mathrm{T}}。$ | (3) |
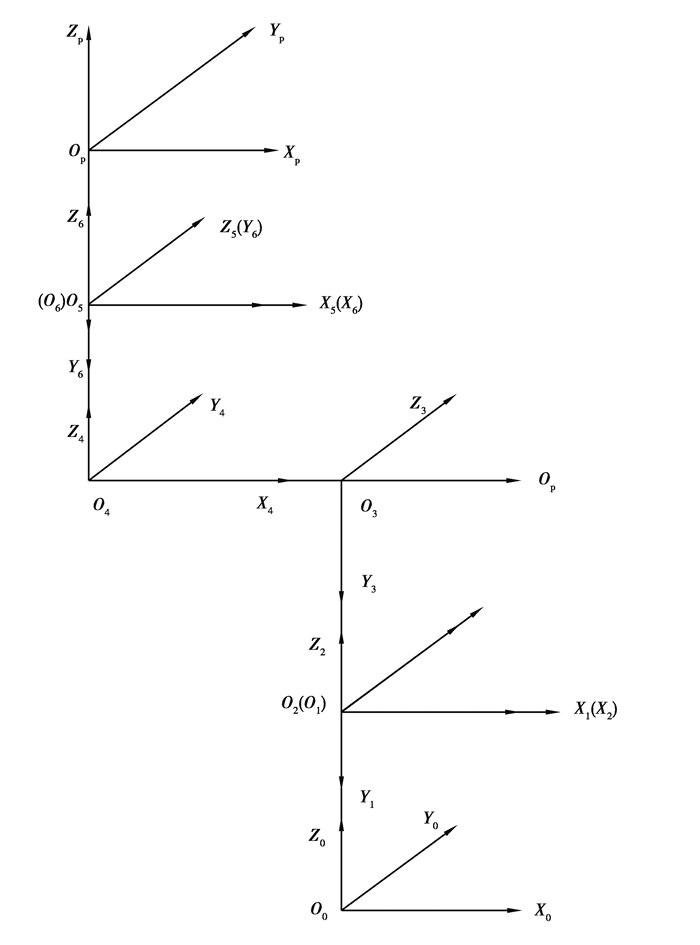
基于D-H方法的关节臂式坐标测量机的坐标系统如图 3所示,根据公式(3),六自由度关节臂式坐标测量机末端测头相对于基座坐标系的数学模型可表达为
| $ \boldsymbol{T}_{\mathrm{Model}}^{\mathrm{S}}=\boldsymbol{A}_{0,1} \times \boldsymbol{A}_{1,2} \times \boldsymbol{A}_{2,3} \times \boldsymbol{A}_{3,4} \times \boldsymbol{A}_{4,5} \times \boldsymbol{A}_{5,6} \times \boldsymbol{B}=\prod\limits_{i=1}^{6}\left[\begin{array}{cccc} \cos \theta_{i} & -\cos \beta_{i} \sin \theta_{i} & \sin \beta_{i} \sin \theta_{i} & \mathrm{a}_{i} \cos \theta_{i} \\ \sin \theta_{i} & \cos \beta_{i} \cos \theta_{i} & -\sin \beta_{i} \cos \theta_{i} & \mathrm{a}_{i} \sin \theta_{i} \\ {\bf{0}} & \sin \beta_{i} & \cos \beta_{i} & \mathrm{~d}_{i} \\ {\bf{0}} & {\bf{0}} & {\bf{0}} & {\bf{1}} \end{array}\right]\left[\begin{array}{c} B_{x} \\ B_{y} \\ B_{z} \\ {\bf{1}} \end{array}\right]。$ | (4) |
|
图 3 基于D-H模型的关节臂式坐标测量机的坐标系统简图 Fig. 3 Coordinate system diagram of AACMM based on the D-H model |
从公式(4)可以看出,测量机末端测头的坐标值通过参数进行描述,则末端测头中心坐标误差与参数误差{Δai,Δdi,Δβi,Δθi,ΔBi}有关。从式中可知共有27个参数误差,Δai,Δdi,Δβi分别是关节的长度误差、关节偏移量误差和关节扭转角度误差,Δθi表示初始零点处的关节变量θi的零位误差,ΔBi是测头的装配误差。根据理论测量模型的参数误差种类建立总误差模型为
| $ \begin{gathered} \boldsymbol{T}_{\mathrm{Model}}^{\mathrm{S}}=\boldsymbol{A}_{0,1}^{\mathrm{S}} \times \boldsymbol{A}_{1,2}^{\mathrm{S}} \times \boldsymbol{A}_{2,3}^{\mathrm{S}} \times \boldsymbol{A}_{3,4}^{\mathrm{S}} \times \boldsymbol{A}_{4,5}^{\mathrm{S}} \times \boldsymbol{A}_{5,6}^{\mathrm{S}} \times \boldsymbol{B}^{\mathrm{S}}= \\ \prod\limits_{i=1}^{6}{\left[\begin{array}{cccc} \cos \left(\theta_{i}+\Delta \theta_{i}\right) & -\cos \left(\beta_{i}+\Delta \beta_{i}\right) \sin \left(\theta_{i}+\Delta \theta_{i}\right) & \sin \left(\beta_{i}+\Delta \beta_{i}\right) \sin \left(\theta_{i}+\Delta \theta_{i}\right) & \left(a_{i}+\Delta a_{i}\right) \cos \left(\theta_{i}+\Delta \theta_{i}\right) \\ \sin \left(\theta_{i}+\Delta \theta_{i}\right) & \cos \left(\beta_{i}+\Delta \beta_{i}\right) \cos \left(\theta_{i}+\Delta \theta_{i}\right) & -\sin \left(\beta_{i}+\Delta \beta_{i}\right) \cos \left(\theta_{i}+\Delta \theta_{i}\right) & \left(a_{i}+\Delta a_{i}\right) \sin \left(\theta_{i}+\Delta \theta_{i}\right) \\ {\bf{0}} & \sin \left(\beta_{i}+\Delta \beta_{i}\right)&\cos \left(\beta_{i}+\Delta \beta_{i}\right) & d_{i}+\Delta d_{i} \\ {\bf{0}} & {\bf{0}} & {\bf{0}} &{\bf{1}} \end{array}\right] \times}\\ \left[\begin{array}{c} B_{x}+\Delta B_{x} \\ B_{y}+\Delta B_{y} \\ B_{z}+\Delta B_{z} \\ {\bf{1}} \end{array}\right]。\end{gathered} $ | (5) |
设测量机理论上测头的坐标值为(xm, ym, zm),测量坐标误差为(Δxm, Δym, Δzm),则含测量误差的末端侧头的坐标相对于TModelS为
| $ \left[\begin{array}{l} x_{r}+\Delta x \\ y_{r}+\Delta y \\ z_{r}+\Delta z \end{array}\right]=\boldsymbol{T}_{\mathrm{Model}}^{\mathrm{S}}。$ | (6) |
将公式(5)中的测头坐标改写为函数形式,对3组函数进行全微分数学解析,并将左右两侧分别展开写成矩阵的形式,可得
| $ \begin{aligned} \left[\begin{array}{c} \mathrm{d} x_{m} \\ \mathrm{~d} y_{m} \\ \mathrm{~d} z_{m} \end{array}\right]=&\left[\begin{array}{c} \frac{\partial f_{x}}{\partial a_{1}} & \cdots & \frac{\partial f_{x}}{\partial a_{6}} & \frac{\partial f_{x}}{\partial d_{1}} & \cdots & \frac{\partial f_{x}}{\partial d_{6}} & \frac{\partial f_{x}}{\partial \beta_{1}} & \cdots & \frac{\partial f_{x}}{\partial \beta_{6}} & \frac{\partial f_{x}}{\partial \theta_{1}} & \ldots & \frac{\partial f_{x}}{\partial \theta_{6}} & \frac{\partial f_{x}}{\partial B_{x}} & \frac{\partial f_{x}}{\partial B_{y}} & \frac{\partial f_{x}}{\partial B_{z}} \\ \frac{\partial f_{y}}{\partial a_{6}} & \cdots & \frac{\partial f_{y}}{\partial a_{6}} & \frac{\partial f_{y}}{\partial d_{1}} & \cdots & \frac{\partial f_{y}}{\partial d_{6}} & \frac{\partial f_{y}}{\partial \beta_{1}} & \ldots & \frac{\partial f_{y}}{\partial \beta_{6}} & \frac{\partial f_{y}}{\partial \theta_{1}} & . . & \frac{\partial f_{y}}{\partial \theta_{6}} & \frac{\partial f_{y}}{\partial B_{x}} & \frac{\partial f_{y}}{\partial B_{y}} & \frac{\partial f_{y}}{\partial B_{z}} \\ \frac{\partial f_{z}}{\partial a_{1}} & \cdots & \frac{\partial f_{z}}{\partial a_{6}} & \frac{\partial f_{z}}{\partial d_{1}} & \ldots & \frac{\partial f_{z}}{\partial d_{6}} & \frac{\partial f_{z}}{\partial \beta_{1}} & \ldots & \frac{\partial f_{z}}{\partial \beta_{6}} & \frac{\partial f_{z}}{\partial \theta_{1}} & \ldots & \frac{\partial f_{z}}{\partial \theta_{6}} & \frac{\partial f_{z}}{\partial B_{x}} & \frac{\partial f_{z}}{\partial B_{y}} & \frac{\partial f_{z}}{\partial B_{z}} \end{array}\right] \times\\ &\ \ \left[\begin{array}{llllllllllllllll} \mathrm{d} a_{1} & \ldots & \mathrm{d} a_{6} & \mathrm{~d} d_{1} & \ldots & \mathrm{d} d_{6} & \mathrm{~d} \beta_{1} & \ldots & \mathrm{d} \beta_{6} & \mathrm{~d} \theta_{1} & \ldots & \mathrm{d} \theta_{6} & \mathrm{~d} B_{x} & \mathrm{~d} B_{y} & \mathrm{~d} B_{z} \end{array}\right]^{\mathrm{T}}, \end{aligned} $ | (7) |
式(7)等号右侧3×27的Jacobian矩阵可用J表示,假设全部结构参数误差足够小,公式(6)可近似为
| $ \left[\begin{array}{llllllll} \Delta x_{m} & \Delta y_{m} & \Delta z_{m} \end{array}\right]=\boldsymbol{J} \times\left[\begin{array}{llllll} \Delta a_{1} \ldots \Delta a_{6} & \Delta d_{1} \ldots \Delta d_{6} & \Delta \beta_{1} \ldots \Delta \beta_{6} & \Delta \theta_{1} \ldots \Delta \theta_{6} & \Delta B_{x} & \Delta B_{y} & \Delta B_{z} \end{array}\right], $ | (8) |
对式(8)进行简化:
关节式坐标测量机在测量同一点时,根据理论模型在不同的姿态时坐标值应该保持不变[9],但结构参数与理论参数因多种因素存在误差,此外,测量误差还与空间位置有关[10],所以标定时测量机应该在不同的位置进行多姿态的测量,坐标值的误差大小和波动范围都是测量机精度的体现。因此笔者结合两者作为目标函数,采用设计的混合算法求取结构参数的实际值。
2.1 目标函数根据上述内容,对锥窝进行不同姿态的测量,记录所得的角度数据得到坐标值,设该点的真实值为多次测量数据的平均值,即
| $ \bar{x}=\frac{1}{N} \sum\limits_{i=1}^{N} x_{i}, \bar{y}=\frac{1}{N} \sum\limits_{i=1}^{N} y_{i}, \bar{z}=\frac{1}{N} \sum\limits_{i=1}^{N} z_{i}。$ | (9) |
该点的误差平均值是
| $ e=\frac{1}{N} \sum\limits_{i=1}^{N} e_{i}=\sqrt{\left(x_{i}-\bar{x}\right)^{2}+\left(y_{i}-\bar{y}\right)^{2}+\left(z_{i}-\bar{z}\right)^{2}}。$ | (10) |
该点的标准差为
| $ \sigma=\sqrt{\frac{1}{N} \sum\limits_{i=1}^{N}\left(e_{i}-e\right)^{2}}。$ | (11) |
关节臂式测量机的整体测量精度通过e和σ的组合来表示,目标函数为
| $ O A=e+3 \sigma $ | (12) |
通过目标函数的值来判定测量机计算所得的结构参数是否接近真实值。
2.2 去除冗余参数的最小二乘法根据公式(8),运用最小二乘法计算可得
| $ \Delta \boldsymbol{S}=\left(\boldsymbol{J}^{\mathrm{T}} \times \boldsymbol{J}\right)^{-1} \times \boldsymbol{J}^{\mathrm{T}} \times \Delta \boldsymbol{M}。$ | (13) |
根据式(13)计算出ΔS后对系统参数进行修正,通过修正后的参数计算出新一轮的理论坐标值及误差矩阵,判定修正后参数的误差小于设定的阈值ε,不满足条件就继续迭代;满足条件则运算结束,输出最终的参数。
当上述公式中雅克比矩阵J为奇异阵时,如果矩阵中有部分参数为线性关系,会对参数误差的求解造成干扰。因此对误差模型ΔS的等式左侧进行变换分析:
| $ \Delta \boldsymbol{S}=\left(\boldsymbol{J}^{\mathrm{T}} \times \boldsymbol{J}\right)^{-1} \times \boldsymbol{J}^{\mathrm{T}} \times \Delta \boldsymbol{M} \leftrightarrow \Delta \boldsymbol{M} \leftrightarrow\left(\boldsymbol{J}^{\mathrm{T}} \times \boldsymbol{J}\right) \times \Delta \boldsymbol{S}=\boldsymbol{J}^{\mathrm{T}} \times \Delta \boldsymbol{M}。$ | (14) |
令式(14)中K= (JT×J)-1,并对其进行奇异值分解:
| $ \boldsymbol{K}=\boldsymbol{P} \times\left[\begin{array}{ll} \boldsymbol{O} & \bf{0} \\ \bf{0} & \bf{0} \end{array}\right] \times \boldsymbol{Q}^{\mathrm{T}}, $ | (15) |
式中: P, Q为正交阵; Λ表示对角阵(Λ=diag(φ1, φ2, ..., φr)), 则对角阵的秩r即为Jacobian矩阵的秩。将矩阵K代回式(15)可得
| $ \boldsymbol{Q}^{\mathrm{T}} \cdot \Delta \boldsymbol{S}=\left[\begin{array}{ll} \boldsymbol{O} & \bf{0} \\ \bf{0} & \bf{0} \end{array}\right] \cdot \boldsymbol{P}^{-1} \cdot \boldsymbol{J}^{\mathrm{T}} \cdot \Delta \boldsymbol{M}。$ | (16) |
根据对式(16)中的矩阵分析,得知结构参数中有25-r个参数有线性关系。由于式(15)中K是对称矩阵,那么有对应的关系式QT=P-1,因此Q阵属于旋转矩阵,对式(16)的误差ΔS模型进行旋转变换,将所有呈线性相关的结构参数处在相同的零平面上[12]。随后将QT中后25-r行的部分做初等行变换从而提取矩阵中有线性关系的误差参数,最终所得结果为
| $ \Delta a_{6}=B_{z} \cdot \Delta \theta_{6}, \Delta d_{6}=-B_{z} \cdot \Delta \beta_{6}。$ | (17) |
由于Bz已知,因此公式(17)中参数a6,θ6,d6,β6无法同时进行标定,选择2个参数作为冗余参数并在Jacobian矩阵及参数误差矩阵ΔS中去除对应参数的矩阵,可得新的结构参数误差公式,其中矩阵ΔS为r行1列,矩阵J为3n行r列,矩阵ΔS为3n行1列,即
| $ \Delta \boldsymbol{S}_{r}=\left(\boldsymbol{J}_{r}^{\mathrm{T}} \cdot \boldsymbol{J}_{r}\right)-1 \cdot \boldsymbol{J}_{r}^{\mathrm{T}} \cdot \Delta \boldsymbol{M}。$ | (18) |
模拟退火是模拟统计物理学中的固体退火过程[12-13],适用于求解不同的非线性复杂问题,算法有解空间、能量函数和初始解3部分,它的解题思路是在对初始解随机扰动产生新解,代入能量函数判断是否满足Metropolis准则,根据冷却系数让温度下降使能量函数达到平衡状态;Metropolis抽样准则具有概率性地跳出局部最优“陷阱”的优点[14]。
为计算出优化权值,将上文的目标函数设为能量函数E=f=e+3σ。
算法步骤如下:
Step 1 设定初始值。给定初始温度T0始权参数w(0)=w0,设置终止检验精度e,终止温度Tmin,马尔可夫链的链长L,令初始最优解w =w0,迭代次数i=0。
Step 2 产生新解。令ωβ=ω(k)+R×E产生新解,其中R为区间[-1, 1]的随机数, 符合Cauchy分布。
Step 3 求优化函数指标。计算ΔE=E(wβ)-E[w(k)]。
Step 4 接受判断。如果ΔE≥0,计算接受概率r=exp[-E(εβ)/T],如果r>p,则w(k+1)=wβ,否则w(k+1)=w(k),p为区间[0, 1]上的随机数;如果ΔE<0,则w(k+1)=wβ,w =wβ。
Step 5 稳定性判别。k=k+1,如果k>L,则转到step 5,否则转到步骤2。
Step 6 降温T=Ti+1=αTi,i=i+1。
Step 7 结束判别。如果(E<e or T<Tmin),则转到Step 8,否则转到Step 2。
Step 8 输出最终最优解w*,中止算法。
融合算法的关键在于如何选择两者算法的转折点[15],最通用的方法是选择固定的温度次数,虽然简便但针对不同模型具有通用性,往往须通过大量的实际经验才能得到大致范围。因此,采取判定适应度的方式融合两种算法,如果同一温度的多个不同最优值之间的差值小于某一设定值,那么结束模拟退火算法转入最小二乘法。
适应度公式为
| $ P=\frac{1}{1+f} 。$ |
转换准则为
| $ \left|s_{0} P_{m}^{t}-\sum\limits_{j=1}^{s_{0}} P_{m-j}^{t}\right| \frac{1}{1+P_{m}^{t}} \leqslant \varepsilon_{1}, $ |
式中:Pmt为当前温度t下的最优适应度值;Pm-jt为当前温度t下的Pmt之后的第j个最优适应度值;s0为当前温度t内选取的最优适应度值个数,小于当前温度的迭代次数。
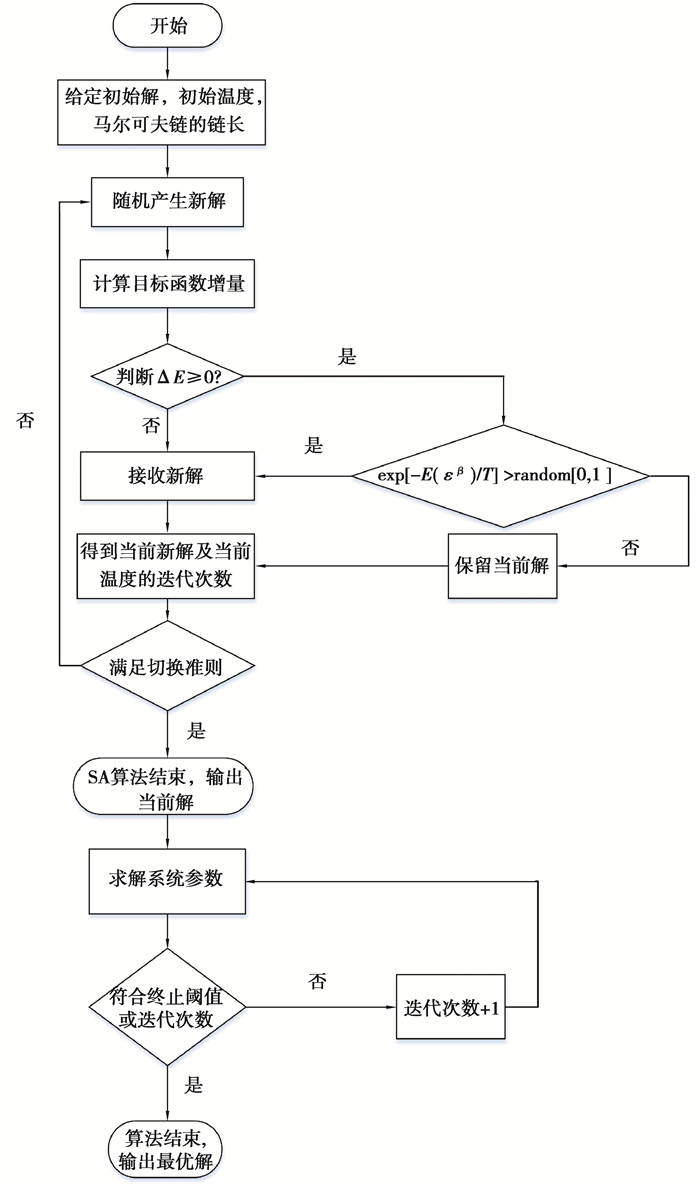
由上可知,融合算法的过程如下:先采用SA算法计算,若满足切换准则表明进入全局最优解的区域,退出SA算法,将满足准则的解作为LM算法的初值代入,通过运算得到最优解,具体的流程图如图 4所示。
|
图 4 混合算法的流程图 Fig. 4 Flow chart of the hybrid algorithm |
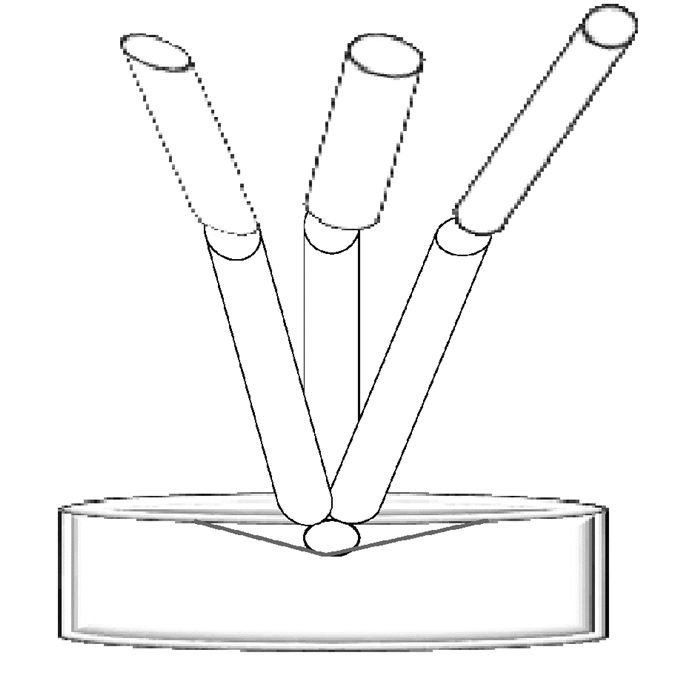
为了减少随机误差的影响,对锥窝中心点进行测量,关节臂式坐标测量机从不同方向上测量同一点(即改变各关节旋转角度)获得空间三维坐标数据,测量结束后改变锥窝的空间位置重复上述步骤,测量示意图如图 5所示。运用最小二乘法通过分析线性相关的结构参数,将其中2个不参与标定的参数设为理论值,而装配测头参数误差(ΔBx, ΔBy, ΔBz)中前两项为0,设Bz的值为100 mm,故整个关节臂式坐标测量机的结构参数误差共有23个。为了减少温度误差的影响,室温保持20 ℃,根据表 1的名义参数和测得的角度数据得到坐标值,用混合算法进行误差参数标定,计算所得的结构参数误差如表 2所示。
|
图 5 测量示意图 Fig. 5 Schematic diagram of the measurement |
| 表 2 基于混合算法标定的各项结构参数误差 Table 2 Errors of structural parameters based on hybrid algorithm calibration |
为了验证所提算法得到的误差参数的准确性,将计算得出的参数误差代入结构参数名义值,得到修正后的测量机结构参数。分别采用辨识前后的参数,对两者的误差进行对比。关节臂式坐标测量机对锥窝进行测量获得角度数据,每测10次数据后锥窝换一次位置,设该点坐标真值为多次测量值的平均值,计算单点重复性误差;此外,长度误差也是测量机整体精度的重要部分,为了验证标定算法的有效性,关节臂式测量机先对锥窝进行多次测量,然后改变锥窝的位置再测多次,获得数据后计算空间每组两点之间的长度测量误差,公式为
| $ \begin{gathered} d_{\text {error }}=\frac{1}{n} \sum\limits_{N=1}^{n}\left(\sqrt{\left(x_{i N}-x_{j N}\right)^{2}+\left(y_{i N}-y_{j N}\right)^{2}+\left(z_{i N}-z_{j N}\right)^{2}}=\right. \\ \left.-\sqrt{\left(\bar{x}_{i}-\bar{x}_{j}\right)^{2}+\left(\bar{y}_{i}-\bar{y}_{j}\right)^{2}+\left(\bar{z}_{i}-\bar{z}_{j}\right)^{2}}\right)。\end{gathered} $ | (19) |
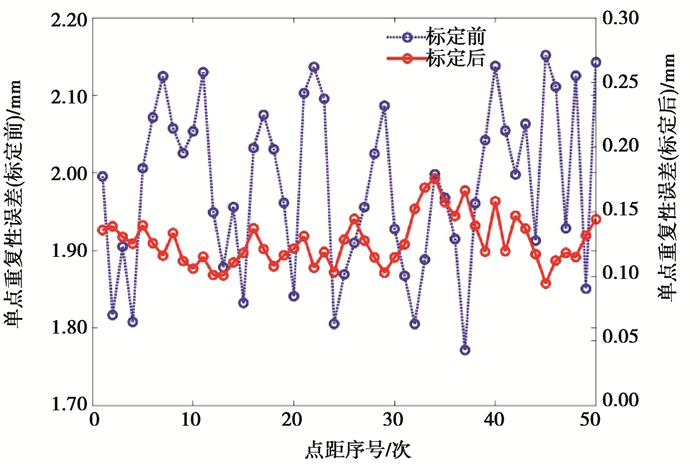
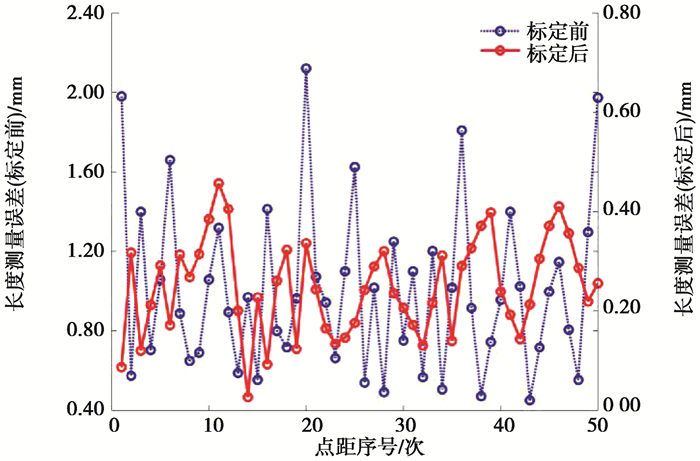
由图 6~7分析可知,参数辨识前,测量机的单点重复性误差范围在1.571 ~2.136 mm,平均值为1.873 mm,标准差为0.106 mm;参数辨识后,测量机的单点重复性误差在0.097 ~ 0.166 mm,平均值为0.127 mm,标准差为0.019 mm。参数辨识前长度误差范围在0.486 ~ 2.116 mm,平均值为1.038 mm,标准差为0.426 mm,参数辨识后长度误差范围在0.025 ~ 0.448 mm,平均值为0.092 mm,标准差为0.097 mm。实验结果表明,混合优化算法有效地提高了测量机的测量精度。
|
图 6 参数辨识前后单点重复性误差 Fig. 6 Single point repeatability error based on different structural parameters |
|
图 7 参数辨识前后长度误差 Fig. 7 Length error based on different structural parameters |
在关节臂式坐标测量机测量模型分析的基础上对标定算法进行了研究,结论如下:
1) 采用最小二乘法标定结构参数过程中,针对呈线性相关的误差参数无法准确地求出参数误差解的问题,对Jacobian矩阵变换分析,去除了方程中的冗余参数,提高了标定精度也减少了计算量。
2) 基于模拟退火算法与最小二乘法的优缺点,通过设定判定准则来混合两种算法,既充分利用了SA的全局优化性能和最小二乘法算法的高效局部优化特点,又解决了最小二乘法初值设定问题。
3) 通过实验结果分析,运用混合优化算法补偿了关节臂式坐标测量机结构参数误差后,测量机的准确性和重复性都得到了显著的提升,测量误差得到了进一步的抑制。
| [1] |
Brau A, Valenzuela M, Santolaria J, et al. Evaluation of different probing systems used in articulated arm coordinate measuring machines[J]. Metrology and Measurement Systems, 2014, 21(2): 233-246. DOI:10.2478/mms-2014-0020 |
| [2] |
Chen B Y, Lei H, Shen H D, et al. A hybrid quantum-based PIO algorithm for global numerical optimization[J]. Science China Information Sciences, 2019, 62(7): 1-12. DOI:10.1007/s11432-018-9546-4 |
| [3] |
Zhang H W, Xie J W, Ge J A, et al. Hybrid particle swarm optimization algorithm based on entropy theory for solving DAR scheduling problem[J]. Tsinghua Science and Technology, 2019, 24(3): 282-290. DOI:10.26599/TST.2018.9010052 |
| [4] |
Acero R, Brau A, Santolaria J, et al. Verification of an articulated arm coordinate measuring machine using a laser tracker as reference equipment and an indexed metrology platform[J]. Measurement, 2015, 69: 52-63. DOI:10.1016/j.measurement.2015.03.023 |
| [5] |
赵磊, 赵新华, 王收军, 等. 柔性测量臂的RPY建模与误差标定[J]. 光学精密工程, 2016, 24(2): 365-371. Zhao L, Zhao X H, Wang S J, et al. RPY modeling and error calibration of flexible measuring arm[J]. Optics and Precision Engineering, 2016, 24(2): 365-371. (in Chinese) |
| [6] |
Santolaria J, Jiménez R, Rada M, et al. Error compensation method for improving the accuracy of biomodels obtained from CBCT data[J]. Medical Engineering & Physics, 2014, 36(3): 397-404. |
| [7] |
Seyedhosseini S M, Esfahani M J, Ghaffari M. A novel hybrid algorithm based on a harmony search and artificial bee colony for solving a portfolio optimization problem using a mean-semi variance approach[J]. Journal of Central South University, 2016, 23(1): 181-188. DOI:10.1007/s11771-016-3061-9 |
| [8] |
Zheng D T, Xiao Z Y, Xia X. Multiple measurement models of articulated arm coordinate measuring machines[J]. Chinese Journal of Mechanical Engineering, 2015, 28(5): 994-998. DOI:10.3901/CJME.2015.0716.095 |
| [9] |
杨欣东, 李国勇. 基于遗传与粒子群混合优化算法的分布式模型预测控制系统结构分解[J]. 科学技术与工程, 2019, 19(25): 262-267. Yang X D, Li G Y. GA-PSO based decomposition of distributed model predictive control systems[J]. Science Technology and Engineering, 2019, 19(25): 262-267. (in Chinese) DOI:10.3969/j.issn.1671-1815.2019.25.039 |
| [10] |
邹德龙, 王宝华. 一种混合优化算法面向高维函数优化的研究[J]. 计算机工程与应用, 2019, 55(20): 122-127. Zou D L, Wang B H. Hybrid optimization algorithm for high dimensional function optimization[J]. Computer Engineering and Applications, 2019, 55(20): 122-127. (in Chinese) DOI:10.3778/j.issn.1002-8331.1808-0105 |
| [11] |
蒋林利, 李洁, 吴建生. 利用PSO-SA混合优化支持向量回归的径流预报模型研究[J]. 计算机应用研究, 2019, 36(9): 2599-2603. Jiang L L, Li J, Wu J S. Runoff forecasting based on hybrid optimized SVR using PSO-SA[J]. Application Research of Computers, 2019, 36(9): 2599-2603. (in Chinese) |
| [12] |
袁小芳, 刘晋伟, 陈秋伊, 等. 并行混沌与和声搜索的多目标混合优化算法[J]. 湖南大学学报(自然科学版), 2018, 45(4): 96-103. Yuan X F, Liu J W, Chen Q Y, et al. A multi-objective hybrid optimization algorithm based on parallel chaos and harmony search[J]. Journal of Hunan University (Natural Sciences), 2018, 45(4): 96-103. (in Chinese) |
| [13] |
潘志康, 祝连庆, 郭阳宽. 基于内点法实现关节式坐标测量机参数标定[J]. 仪器仪表学报, 2018, 39(3): 117-123. Pan Z K, Zhu L Q, Guo Y K. Parameter calibration of joint CMM Based on interior point method[J]. Chinese Journal of Scientific Instrument, 2018, 39(3): 117-123. (in Chinese) |
| [14] |
王学影, 王华, 陆艺, 等. 关节臂式坐标测量机参数标定方法[J]. 农业机械学报, 2016, 47(6): 408-412. Wang X Y, Wang H, Lu Y, et al. Parameter calibration method of articulated arm coordinate measuring machine[J]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(6): 408-412. (in Chinese) |
| [15] |
王勇, 李秀娟. 某四自由度机械臂建模与MATLAB仿真研究[J]. 电子测量技术, 2015, 38(2): 32-36. Wang Y, Li X J. Modeling and simulation of 4-DOF manipulator based on MATLAB[J]. Electronic Measurement Technology, 2015, 38(2): 32-36. (in Chinese) DOI:10.3969/j.issn.1002-7300.2015.02.008 |
 2021, Vol. 44
2021, Vol. 44


