b. 重庆大学 山地城镇建设与新技术教育部重点实验室, 重庆 400045
b. The Key Laboratory of New Technology for Construction of Cities in Mountain Area, Ministry of Education, Chongqing University, Chongqing 400045, P. R. China
结构参数和荷载的识别对结构健康监测、有限元模型更新等具有重要作用。在假设荷载已知的情况下,基于最小二乘估计[1-2]、扩展卡尔曼滤波(EKF)[3-4]、无味卡尔曼滤波(UKF)[5-7]、粒子滤波(PF)[5, 8-9]等众多时域方法被广泛应用于非线性系统的参数识别。当已知结构参数时,可采用卡尔曼滤波[10-13]等对荷载激励进行辨识。在土木结构服役过程中,结构参数的变化和荷载激励往往都是未知的,将结构参数识别和荷载辨识分开进行研究较难满足土木工程的实际需求。为解决这一难题,各国学者逐步发展了结构参数与荷载同步识别方法,丁勇等[14]运用正交分解法建立荷载方程,带入状态空间方程,再运用改进UKF算法识别参数和荷载,在三层非线性框架的数值模拟中,可成功识别刚度、阻尼等结构参数和随机荷载;万志敏等[15]在运用改进粒子滤波算法识别结构参数的同时,运用最小二乘估计求得荷载,数值模拟表明,该法同时识别参数和荷载的效果较好。以上解决方案都采用了2种不同的算法,流程相对复杂。同步识别结构参数与荷载还面临另一个难题,当仅运用加速度进行长时间荷载识别时,其结果随着时间的推移逐渐发生偏移,这是基于时域方法的荷载识别过程中难以避免的现象[15]。虽然可以将速度或位移作为观测值来解决这一问题[5],但在结构健康监测系统的实际应用中,由于较难测量结构的动态速度或位移,一般仅将加速度作为观测值;另一种可行的方法是通过额外的步骤,如虚拟测量技术对位移进行调整[11]。
文中将结构参数、荷载、速度和位移同时作为状态值[16],构造状态空间方程,采用粒子滤波算法直接对结构参数与荷载进行识别,步骤相对简单。同时,针对荷载辨识结果漂移的问题,将加速度数据进行梯形积分和零相位高通滤波,求得速度和位移的计算值,利用计算值来更新由粒子滤波求得的速度和位移状态值,长时间确保荷载识别的准确性。
1 状态空间方程一般来说,土木结构的状态空间方程为
| $ \left\{\begin{array}{l} x_{k+1}=f\left(x_{k}, u_{k}\right)+\omega_{k}, \\ y_{k}=h\left(x_{k}, u_{k}\right)+\nu_{k}, \end{array}\right. $ | (1) |
其中,xk、uk和yk分别是第k时间步的状态值(包括位移和速度)、荷载激励和结构响应;ωk和νk分别是第k时间步的过程噪声和观测噪声;f(·)和h(·)是非线性函数,描述了状态值和结构响应随时间变化的关系。
为实现结构参数和荷载的同步识别,可将结构参数mk、荷载激励uk与原有的状态值xk组成新的状态向量zk[16]。
| $ \boldsymbol{z}_{k}=\left[\begin{array}{l} x_{k} \\ m_{k} \\ u_{k} \end{array}\right]。$ | (2) |
新的状态向量zk与结构响应yk组成新的状态空间方程:
| $ \left\{\begin{array}{l} \boldsymbol{z}_{k}=\left[\begin{array}{c} x_{k} \\ m_{k} \\ u_{k} \end{array}\right]=\left[\begin{array}{c} f\left(x_{k-1}, m_{k-1}, u_{k-1}\right) \\ m_{k-1} \\ u_{k-1} \end{array}\right]+\left[\begin{array}{c} \omega_{k} \\ \theta_{k} \\ \eta_{k} \end{array}\right] \\ y_{k}=h\left(x_{k}, m_{k}, u_{k}\right)+\nu_{k} \end{array}。\right. $ | (3) |
式中,θk和ηk分别是结构参数与荷载激励的过程噪声。文中所有噪声均假设为零均值高斯噪声。
2 粒子滤波与加速度更新方法 2.1 粒子滤波算法以式(3)为例,粒子滤波的流程如下:
1) 初始化:通过已知的初始状态分布p(z0)生成粒子集合{z0i: i=1, …, N},各粒子的权值为1/N。其中,上标i表示第i个粒子;N为粒子数量。
2) 预测:用k-1时间步的粒子集{zk-1i: i=1, …, N}生成k时间步的粒子集{zki: i=1, …, N}:
| $ \boldsymbol{z}_{k}^{i}=\left[\begin{array}{c} x_{k}^{i} \\ m_{k}^{i} \\ u_{k}^{i} \end{array}\right]=\left[\begin{array}{c} f\left(x_{k-1}^{i}, m_{k-1}^{i}, u_{k-1}^{i}\right) \\ m_{k-1}^{i} \\ u_{k-1}^{i} \end{array}\right]+\left[\begin{array}{c} \omega_{k}^{i} \\ \theta_{k}^{i} \\ \eta_{k}^{i} \end{array}\right]。$ | (4) |
3) 更新权值:计算每一个粒子的权值wki:
| $ w_{k}^{i} \propto \widetilde{w}_{k-1}^{i} p\left(y_{k} \mid z_{k}^{i}\right)。$ | (5) |
将wki归一化得
| $ \widetilde{w}_{k}^{i}=\frac{w_{k}^{i}}{\sum\nolimits_{j=1}^{N} w_{k}^{j}}。$ | (6) |
计算有效粒子数Neff:
| $ N_{{\rm{e f f}}(k)}=\frac{1}{\sum\nolimits_{i=1}^{N}\left(\widetilde{w}_{k}^{i}\right)^{2}}。$ | (7) |
4) 若Neff(k)小于阈值NT,则对粒子集合进行重采样,通过复制大权值粒子和去除小权值粒子更新{zki: i=1, …, N}。重采样之后,各粒子的权值{
5) 计算估计值
| $ \widehat{\boldsymbol{Z}}_{k}=\sum\limits_{i=1}^{N} \widetilde{w}_{k}^{i} \boldsymbol{Z}_{k}^{i}。$ | (8) |
土木结构通常仅能得到加速度响应{ak: k=1, …, n},采用梯形积分得到k时间步的速度vk:
| $ v_{k}=v_{k-1}+\frac{a_{k-1}+a_{k}}{2} \times T $ | (9) |
其中,T是采样周期。
采用零相位高通滤波去除速度值{vk: k=1, …, n}的漂移,再采用计算所得的速度值,通过梯形积分和零相位高通滤波计算得到各时间步的位移值。最后,每隔一定的时间间隔Δt,以该时刻的速度、位移计算值,取代该时刻在公式(4)中的状态值{xk-1i: i=1, …, N}。需注意的是,针对不同的情况,需要合理设置调整时间间隔Δt,在数值算例中展开相关讨论。
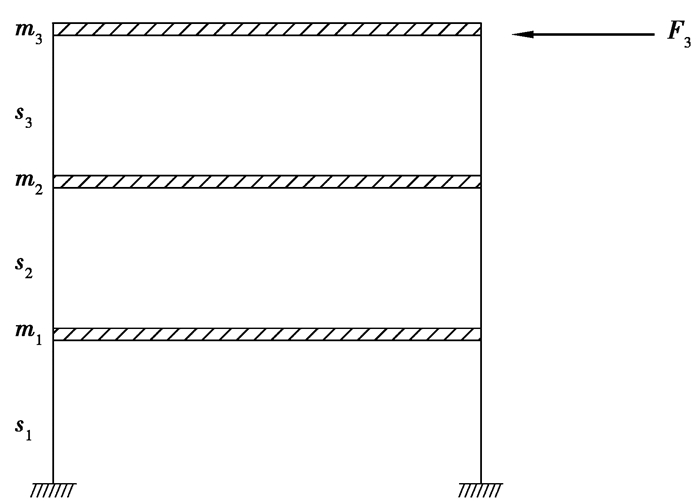
3 数值模拟 3.1 三层框架结构采用如图 1所示的三层框架对文中方法进行验证,每层的刚度s1=s2=s3=500 N/m,每层的质量m1= m2=m3=20 kg。通过集中质量矩阵和刚度矩阵计算得到前三阶的自振频率:f1=2.225 rad/s,f2=6.235 rad/s,f3=9.010 rad/s,假设第一阶阻尼比ξ1、第三阶阻尼比ξ3均为0.05,结构阻尼为瑞利阻尼,可通过式(10)求得瑞利阻尼参数为α=0.178,β=0.009。
| $ \left[\begin{array}{l} \alpha \\ \beta \end{array}\right]=\frac{2 f_{1} f_{3}}{f_{3}{ }^{2}-f_{1}^{2}}\left[\begin{array}{cc} f_{3} & -f_{1} \\ -1 / f_{3} & 1 / f_{1} \end{array}\right]\left[\begin{array}{l} \varepsilon_{1} \\ \varepsilon_{3} \end{array}\right] $ | (10) |
|
图 1 三层框架数值模拟 Fig. 1 The three-storey frame in simulation |
以NS方向的El-centro地震波生成外部荷载F3,水平作用在第三层上,最大值为34.87 N。
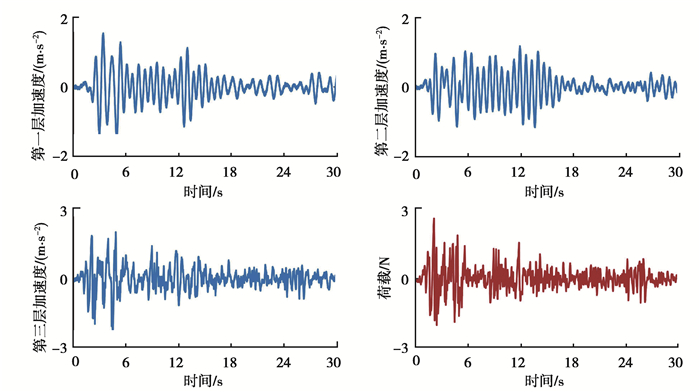
采样频率设置为200 Hz,通过Newmark-β法计算得到结构前30 s的加速度数据。假定观测噪声是零均值高斯噪声,其标准差为加速度响应数据的5%均方根值。计算所用的荷载及各层加速度如图 2所示。
|
图 2 加速度与外部荷载 Fig. 2 The acceleration and external force |
图 1所示三层框架结构的动力学方程为
| $ \left[\begin{array}{ccc} m_{1} & 0 & 0 \\ 0 & m_{2} & 0 \\ 0 & 0 & m_{3} \end{array}\right]\left[\begin{array}{l} \ddot{x}_{1} \\ \ddot{x}_{2} \\ \ddot{x}_{3} \end{array}\right]+\left[\begin{array}{ccc} s_{1}+s_{2} & -s_{2} & 0 \\ -s_{2} & s_{2}+s_{3} & -s_{3} \\ 0 & -s_{3} & s_{3} \end{array}\right]\left[\begin{array}{l} x_{1} \\ x_{2} \\ x_{3} \end{array}\right]+\left\{\begin{array}{ccc} \alpha\left[\begin{array}{ccc} m_{1} & 0 & 0 \\ 0 & m_{2} & 0 \\ 0 & 0 & m_{3} \end{array}\right]+ \\ \beta\left[\begin{array}{ccc} s_{1}+s_{2} & -s_{2} & 0 \\ -s_{2} & s_{2}+s_{3} & -s_{3} \\ 0 & -s_{3} & s_{3} \end{array}\right] \end{array}\right\}\left[\begin{array}{l} \dot{x}_{1} \\ \dot{x}_{2} \\ \dot{x}_{3} \end{array}\right]=\left[\begin{array}{c} 0 \\ 0 \\ F_{3} \end{array}\right], $ | (11) |
其中,x、ẋ和ẍ分别表示位移、速度和加速度。
当对结构刚度、荷载同时进行识别时,公式(11)可转换为离散化的状态空间方程[5]:
| $ \begin{array}{c} \left[\begin{array}{c} \dot{x}_{1(k)} \\ \dot{x}_{2(k)} \\ \dot{x}_{3(k)} \\ x_{1(k)} \\ x_{2(k)} \\ x_{3(k)} \\ s_{1(k)} \\ s_{2(k)} \\ s_{3(k)} \\ F_{3(k)} \end{array}\right]=\left[\begin{array}{c} \dot{x}_{1(k-1)}+T \ddot{x}_{1(k-1)}+\omega_{1(k)} \\ \dot{x}_{2(k-1)}+T \ddot{x}_{2(k-1)}+\omega_{2(k)} \\ \dot{x}_{3(k-1)}+T \ddot{x}_{3(k-1)}+\omega_{3(k)} \\ x_{1(k-1)}+T \dot{x}_{1(k-1)}+\omega_{4(k)} \\ x_{2(k-1)}+T \dot{x}_{2(k-1)}+\omega_{5(k)} \\ x_{3(k-1)}+T \dot{x}_{3(k-1)}+\omega_{6(k)} \\ s_{1(k-1)}+\theta_{1(k)} \\ s_{2(k-1)}+\theta_{2(k)} \\ s_{3(k-1)}+\theta_{3(k)} \\ F_{3(k-1)}+\eta_{(k)} \end{array}\right]\\ \left[\begin{array}{l} \ddot{x}_{1(k)} \\ \ddot{x}_{2(k)} \\ \ddot{x}_{3(k)} \end{array}\right]=\left[\begin{array}{l} \nu_{1(k)} \\ \nu_{2(k)} \\ \nu_{3(k)} \end{array}\right]+ \left[\begin{array}{l} \left\{-\left[\alpha m_{1}+\beta\left(s_{1(k)}+s_{2(k)}\right)\right] \dot{x}_{1(k)}+\beta s_{2(k)} \dot{x}_{2(k)}\right. \\ \left.-\left(s_{1(k)}+s_{2(k)}\right) x_{1(k)}+s_{2(k)} x_{2(k)}\right\} / m_{1} \\ \left\{\beta s_{2(k)} \dot{x}_{1(k)}-\left[\alpha m_{2}+\beta\left(s_{2(k)}+s_{3(k)}\right)\right] \dot{x}_{2(k)}+\beta s_{3(k)} \dot{x}_{3(k)}\right. \\ \left.+s_{2(k)} x_{1(k)}-\left(s_{2(k)}+s_{3(k)}\right) x_{2(k)}+s_{3(k)} x_{3(k)}\right\} / m_{2} \\ \left\{F_{3(k)}+\beta s_{3(k)} \dot{x}_{2(k)}-\left(\alpha m_{3}+\beta s_{3(k)}\right) \dot{x}_{3(k)}\right. \\ \left.+s_{3(k)} x_{2(k)}-s_{3(k)} x_{3(k)}\right\} / m_{3} \end{array}\right], \end{array} $ | (12) |
其中,{ωi: i=1, …, 6}、{θi: i=1, 2, 3}和η是过程噪声,{υi: i=1, 2, 3}为观测噪声,T=0.005 s。图 1中的三层框架是线性结构,由于式(12)中存在未知参数与未知速度、位移相乘的情况,该公式是非线性方程[5, 9],故采用粒子滤波进行参数识别。
运用梯形积分和截止频率为0.1 Hz的零相位高通滤波,可通过加速度求得速度、位移计算值。在此数值模拟中,取Δt =1 s,即每隔1 s对速度、位移状态值进行调整。在粒子滤波算法中,重采样的阈值NT取0.5,粒子个数N=16 000。初始刚度在400~800 N/m的范围内随机取值,荷载、位移和速度的初始值均取0。假设各过程噪声均为独立的零均值高斯噪声,根据试算,速度、位移的过程噪声的标准差分别取速度、位移计算值的0.2%均方根值,刚度、荷载的过程噪声的标准差分别取0.1、2.5。
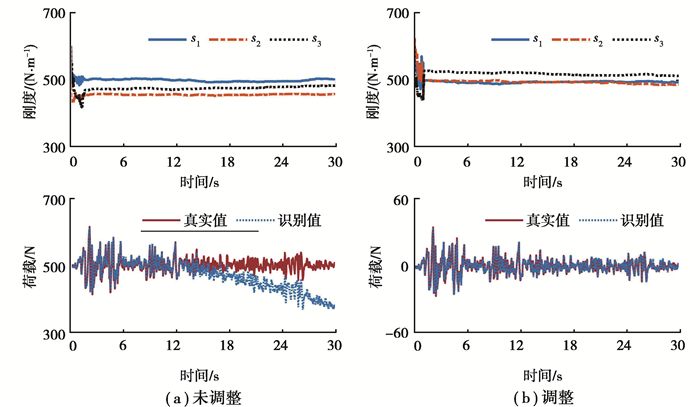
3.3 识别结果分析分别将不调整速度、位移状态值以及按文中方法进行调整后的结果绘制于图 3中,其纵坐标代表在16 000个粒子中刚度或荷载的均值。
|
图 3 结构参数与荷载辨识过程 Fig. 3 Estimation for parameters and force |
将最后一步的均值作为参数识别结果,并用相对误差(RE)来评价各参数识别结果的精度:
| $ \mathrm{RE}=\frac{s_{\mathrm{e}}-s_{\mathrm{r}}}{s_{\mathrm{r}}} \times 100 \%, $ | (13) |
其中,se表示刚度识别结果;sr表示刚度真实值。
用均方误差(MSE)来评价荷载识别的精度:
| $ \mathrm{MSE}=\frac{1}{M} \sum\limits_{k=1}^{M}\left(F_{e(k)}-F_{r(k)}\right)^{2}, $ | (14) |
其中,Fe(k)表示第k步的荷载识别值;Fr(k)表示第k步的荷载真实值;M是时间步长。
由图 3(a)和表 1可知,当不调整速度、位移状态值时,1.5 s左右结构参数收敛,识别结果较好;但在大约10 s后,荷载辨识值发生漂移,程度越来越严重。此时,刚度识别值已接近真实值,故刚度值的辨识误差不是荷载出现漂移的原因。正如文献[11]所述,这是仅用加速度数据进行长时间荷载辨识过程中难以避免的现象。从图 3(b)和表 1可知,对结构参数而言,文中方法的参数识别收敛时间、精度和传统方法基本一致;但对于荷载识别而言,全过程中未出现漂移现象,有效解决了传统方法的不足。
| 表 1 参数识别和荷载识别结果 Table 1 Estimation result of parameters and force |
由于初始值、噪声的影响,识别结果具有一定的随机性,在同样的情况下再对同一组数据进行9次识别,计算结果如表 2所示。从表 2可知,结构参数识别的最大误差为-14.60%,最小误差为0.26%;荷载激励识别的最大均方误差为1.88,最小均方误差为0.79。
| 表 2 结构参数与荷载10次同步识别的结果 Table 2 Estimation results of ten runs |
为研究调整时间间隔Δt对结构参数、荷载识别的影响,选取{Δt =0.1, 0.3, 0.5, 1, 1.5, 2, 3}共7种情况各进行10次运算,不同Δt时的参数相对误差的绝对值的均值、10次荷载识别均方误差的均值如图 4所示。

|
图 4 不同时间间隔Δt的识别情况 Fig. 4 Estimation under different time intervals Δt |
由图 4可知,当Δt较短(如0.1 s、0.3 s)时,第3层的刚度s3的误差和荷载识别的均方误差相对较大。因为在该时段内结构参数识别尚未收敛,此时用带有误差的速度、位移计算值来调整状态值,参数识别受到的影响相对较大;同时,误差相对较大的s3会对荷载识别造成影响。随着Δt逐渐增大,各刚度识别的误差基本保持不变,但荷载识别的均方误差会逐渐增大。各参数趋于收敛或已收敛,计算值的误差对参数识别的影响相对较小;同时,由于不能及时修正速度和位移,荷载识别值会逐渐漂移,故其均方误差会随时间间隔的增大而增大。综上所述,为同时保持结构参数和荷载识别的精确性,应合理设置Δt,不宜过长或过短,建议以参数收敛所需的时间(数值模拟算例的1.5 s)来设置间隔Δt。
4 结束语为了土木工程结构不仅能测试结构的加速度响应,同时还能识别结构参数和输入荷载,文中将结构参数和荷载扩充为状态值并建立状态空间方程,基于粒子滤波算法进行结构参数和荷载的同步识别。同时,利用测试的加速度响应,通过梯形积分和零相位高通滤波计算各时间步的速度、位移,然后将该值以一定时间间隔Δt用于更新对应状态识别值。三层框架结构的数值算例结果表明:
1) 文中方法可同时识别结构参数与荷载,识别结果较为准确、稳定。
2) 采用积分和零相位高通滤波所得的速度、位移计算值来调整速度、位移状态值可克服荷载辨识值出现偏移这一问题。
3) 应合理设置速度、位移的时间间隔Δt,不宜过长或过短,建议根据结构参数识别收敛所需的时间来设置Δt的大小。
| [1] |
Lin J W, Betti R, Smyth A W, et al. On-line identification of non-linear hysteretic structural systems using a variable trace approach[J]. Earthquake Engineering & Structural Dynamics, 2001, 30(9): 1279-1303. |
| [2] |
周念成, 谭桂华, 赵渊, 等. 一种计及参数误差的电网谐波状态估计方法[J]. 重庆大学学报, 2009, 32(2): 146-150. Zhou N C, Tan G H, Zhao Y, et al. A method for considering parameter errors in power system harmonic state estimation[J]. Journal of Chongqing University, 2009, 32(2): 146-150. (in Chinese) |
| [3] |
Corigliano A, Mariani S. Parameter identification in explicit structural dynamics: performance of the extended Kalman filter[J]. Computer Methods in Applied Mechanics and Engineering, 2004, 193(36/37/38): 3807-3835. |
| [4] |
Ghosh S J, Roy D, Manohar C S. New forms of extended Kalman filter via transversal linearization and applications to structural system identification[J]. Computer Methods in Applied Mechanics and Engineering, 2007, 196(49/50/51/52): 5063-5083. |
| [5] |
Chatzi E N, Smyth A W. The unscented Kalman filter and particle filter methods for nonlinear structural system identification with non-collocated heterogeneous sensing[J]. Structural Control and Health Monitoring, 2009, 16(1): 99-123. DOI:10.1002/stc.290 |
| [6] |
Chatzis M N, Chatzi E N, Smyth A W. An experimental validation of time domain system identification methods with fusion of heterogeneous data[J]. Earthquake Engineering & Structural Dynamics, 2015, 44(4): 523-547. |
| [7] |
Liu L J, Lei Y, He M Y. A two-stage parametric identification of strong nonlinear structural systems with incomplete response measurements[J]. International Journal of Structural Stability and Dynamics, 2016, 16(4): 1640022. DOI:10.1142/S0219455416400228 |
| [8] |
苗强, 崔恒娟, 谢磊, 等. 粒子滤波在锂离子电池剩余寿命预测中的应用[J]. 重庆大学学报, 2013, 36(8): 47-52,60. Miao Q, Cui H J, Xie L, et al. Remaining useful life prediction of the lithium-ion battery using particle filtering[J]. Journal of Chongqing University, 2013, 36(8): 47-52,60. (in Chinese) |
| [9] |
Olivier A, Smyth A W. Particle filtering and marginalization for parameter identification in structural systems[J]. Structural Control and Health Monitoring, 2017, 24(3): 1874. DOI:10.1002/stc.1874 |
| [10] |
Lourens E, Reynders E, De Roeck G, et al. An augmented Kalman filter for force identification in structural dynamics[J]. Mechanical Systems and Signal Processing, 2012, 27: 446-460. DOI:10.1016/j.ymssp.2011.09.025 |
| [11] |
Naets F, Cuadrado J, Desmet W. Stable force identification in structural dynamics using Kalman filtering and dummy-measurements[J]. Mechanical Systems and Signal Processing, 2015, 50/51: 235-248. DOI:10.1016/j.ymssp.2014.05.042 |
| [12] |
方明新, 杨志勇, 郅伦海. 超高层建筑横风向荷载反演分析[J]. 振动与冲击, 2015, 34(22): 35-41. Fang M X, Yang Z Y, Zhi L H. Inverse analysis of across-wind loads on super tall buildings[J]. Journal of Vibration and Shock, 2015, 34(22): 35-41. (in Chinese) |
| [13] |
郅伦海, 余攀. 基于卡尔曼滤波的高层建筑风荷载反演研究[J]. 武汉理工大学学报, 2016, 38(2): 57-63,81. Zhi L H, Yu P. Wind load estimation of tall building by a Kalman filtering based inverse method[J]. Journal of Wuhan University of Technology, 2016, 38(2): 57-63,81. (in Chinese) |
| [14] |
Ding Y, Zhao B Y, Wu B, et al. Simultaneous identification of structural parameter and external excitation with an improved unscented kalman filter[J]. Advances in Structural Engineering, 2015, 18(11): 1981-1998. DOI:10.1260/1369-4332.18.11.1981 |
| [15] |
Wan Z M, Wang T, Li S D, et al. A modified particle filter for parameter identification with unknown inputs[J]. Structural Control and Health Monitoring, 2018, 25(12): 2268. DOI:10.1002/stc.2268 |
| [16] |
Naets F, Croes J, Desmet W. An online coupled state/input/parameter estimation approach for structural dynamics[J]. Computer Methods in Applied Mechanics and Engineering, 2015, 283: 1167-1188. DOI:10.1016/j.cma.2014.08.010 |
 2021, Vol. 44
2021, Vol. 44

