b. 天津大学 建筑学院, 天津 300072;
c. 天津大学 建筑工程学院, 天津 300072
b. School of Architecture, Tianjin University, Tianjin 300072, P. R. China;
c. School of Civil Engineering, Tianjin University, Tianjin 300072, P. R. China
模块建筑是以单个房间为模块单元,在工厂完成预制,运输至现场安装,以可靠的连接方式组装成整体的建筑形式。模块建筑作为一种新兴的建造体系,在经济、环保、节能及建造周期等方面优势突出,具有广阔的发展前景,是建筑领域重点发展方向之一。Lawson等[1-2]介绍了模块建筑平面布置、空间组合以及模块单元功能,在建筑结构方面对多高层模块化建筑结构体系进行了研究,提出可依据建筑中整体功能性的不同要求决定模块单元的组合方式、模块的布置及安装顺序,最终形成一种混合装配式模块轻钢结构。国内外学者[3-8, 13-17]在模块建筑结构性能和优化算法上做了很多研究。王蔚等[9]从建筑学的角度对箱体空间体积与尺寸限值和箱体的组合问题进行了研究,提出了合理的设计优化策略和建筑设计方法。陈志华等[10-11]分析了钢框架模块结构体系,将模块单元间的节点连接分为铰接与刚接2种形式,对其进行了有限元对比分析。申杰[12]在建筑组团、单体建筑和局部构件3个不同尺度的设计层次,实现了建筑组团室外风环境优化、单体建筑节能优化和外遮阳构件优化3个具体应用。
我国在模块建筑参数化设计、平面多目标优化体系和模块整体结构优化等方面的研究起步较晚,急需对钢结构模块建筑进行结构和性能等多个层次的系统性研究,针对钢结构模块建筑从建筑方案、结构设计和多目标优化等方面形成一套相对成熟的方法和技术,为钢结构模块建筑的产业化和标准化奠定基础,推动多学科交叉在模块建筑中的应用。
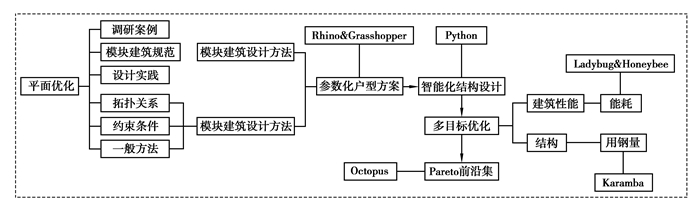
实现结构设计的智能优化,重在保证高质量的同时最大限度地降低工程的造价。而在设计阶段,用钢量和能耗成为结构和建筑性能影响造价的2个重要指标。文中在实现结构智能化设计的基础上通过对用钢量和能耗的参数优化来降低造价,为建筑方案设计提供指导和借鉴。优化流程如图 1所示。
|
图 1 钢结构模块建筑参数化平面优化及结构智能化设计流程 Fig. 1 The process of parameterized plane optimization and intelligent design on modular steel building |
1) 模块间节点连接方式合理,结构传力路径明确,受力合理;
2) 不同建筑类型使用合理的结构体系(如商业区选用框架体系,住宅可选用纯模块单元),根据结构体系划分模块单元;
3) 尽可能减少模块单元种类,采用标准化程度较高的模块单元;
4) 建筑空间及平面功能分区合理,流线明确,具有环境艺术效果;
5) 增大室内利用率与空间灵活度,减少不必要的模块单元空间;
6) 满足防火、疏散、防护等使用安全要求。
1.2 钢结构模块建筑参数化平面自动生成逻辑形体生成的一般规则是在功能限定条件下基于整数规划算法的建筑平面生成,其本质是将建筑布局问题转化为整数规划算法下的数理限定条件,通过设定目标函数求出符合要求的建筑问题。通过制定几何布局的数学问题与一组变量、目标和约束,优化算法可用于解决布局设计的问题。布局规划需考虑尺寸约束和功能约束。尺寸约束限制每个房间的大小,而功能约束根据不同房间的使用功能确定每个模块单元的位置。文中以五层模块住宅为例,通过分析和研究形成一套尺寸按一定模数变化的模块系列,形成典型的模块化住宅建筑方案,使其在满足建筑布置灵活性的基础上也能符合工业化标准化制造的要求,推动模块建筑的应用。
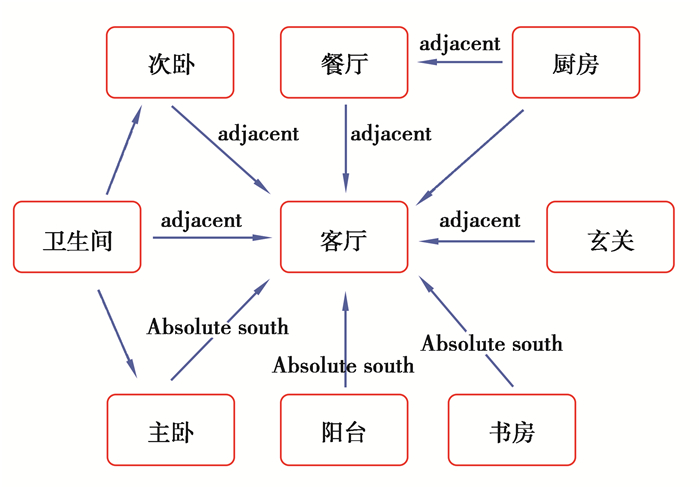
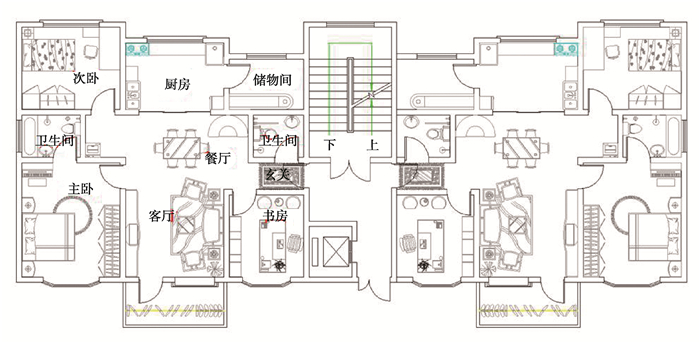
设计师可以根据需求确定建筑类型和规模,假设每户均为一家三口模块住宅户型,包括3种模块单元:私密模块单元、公共模块单元和交通模块单元,如图 2所示。使用功能房间包括主卧、次卧、主卧配置卫生间、客厅、餐厅、厨房、阳台、书房、储物间、公共卫生间和走廊等,这些房间分别包含在3种模块单元之中。根据使用功能所属性质进行分类,每个模块单元包括3~4个房间,使用功能相近的房间布置在同一模块单元中。如图 3所示,以客厅为中心,根据邻接关系和房间使用功能组成模块化户型,但房间长宽尺寸受限。考虑到主卧和次卧属于私密性较强的两个房间,可以把主卧、次卧和主卧配置卫生间放置于私密模块,而主卧应该在阳面,次卧在阴面,主卧配置卫生间则在主卧与次卧之间的位置;公共模块一般为家庭活动或接待客人的场所,私密性较弱,可以将客厅、餐厅、厨房和阳台归为一类,放置在公共模块中,阳台在阳面,阳台北边为客厅,与客厅邻接关系的是餐厅,餐厅的邻接为厨房;交通模块顾名思义应该是进出的通道,将剩下的房间布置在交通模块中,玄关和走廊要布置在入口处,书房位于阳面采光通风良好的位置,储物间可放于阴面,旁边布置公共卫生间。如图 4所示为各房间位置分布图,设计师也可根据自己的需求对各房间位置做出调整,这样每个房间的位置和与其他房间的邻接关系是确定的,但是房间尺寸是变化的,可以通过目标函数来寻找最优方案。

|
图 2 单户型模块单元组成图 Fig. 2 Single-family modular unit composition diagram |
|
图 3 各使用功能房间邻接关系 Fig. 3 Adjacent relationship between each function room |
|
图 4 一梯两户户型方案平面图 Fig. 4 Floor plan of a two-family plan |
从图 4整个建筑方案中提取1户进行研究,3个模块单元类型尺寸大小可互不相同,但一梯两户中每户户型是相同的,也就是说整个建筑仅使用3种模块单元加上楼梯间走廊模块共4种尺寸不同的模块单元即可完成,极大地减少了工厂模块单元制造程序,实现了模块建筑的标准化生产。同时该建筑方案也适用于一梯四户的住宅建筑,设计者可以根据住宅的使用规模及需求进行合理的设计。
计算机依据设计师所提供的预设信息,如功能定义、连接关系定义、房间总数等条件产生符合特定设计目标的拓扑关系。选取单个户型进行平面布置优化,整个户型被定义在12 m×10.8 m边界内,各功能房间根据规范符合表 1中的尺寸限值要求,模数变化取3M的倍数。
| 表 1 房间尺寸限制 Table 1 Room size restrictions |
根据模块建筑及房间之间约束关系的特点,私密模块尺寸主要由主卧决定,主卧房间长和宽为自变量,私密模块中其余房间长度为因变量,随主卧变化而变化,宽度为自变量;公共模块尺寸大小由客厅决定,客厅长和宽为自变量,公共模块中其余房间长度为因变量,随客厅变化而变化,宽度为自变量;交通模块的书房尺寸由自身使用规模控制,走廊长度由书房长度决定,宽度为自变量在限值内变化。
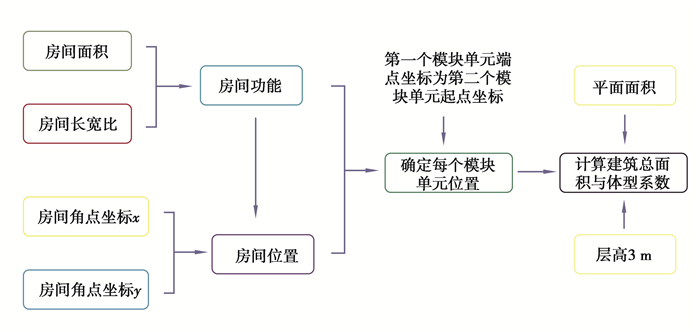
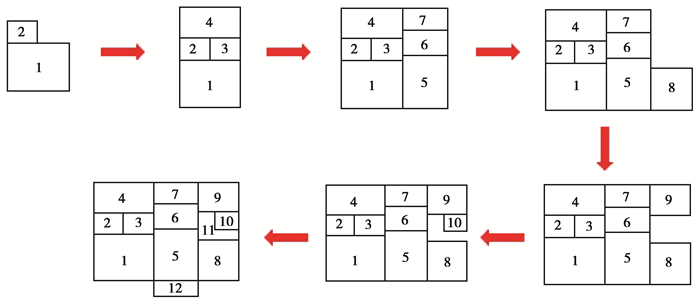
1.3 建立GH模型Grasshopper为Rhino下一款参数化设计插件,实现节点可视化编程,通过参数变化实现建模。首先,按照各房间的使用功能、约束条件和邻接关系等确定模块建筑的生成逻辑和建模方法。使用Rhino & Grasshopper的矩形电池在长宽尺寸和房间面积等约束条件下依次建立各使用功能矩形房间,房间位置取决于各房间角点坐标和附近房间邻接关系。在各房间的使用功能和位置确定的情况下,可形成3个模块单元,确定各模块单元位置关系,最终确定整个模块建筑户型,如图 5所示。房间生成逻辑如图 6所示,建模方式采用参数化建模。
|
图 5 建模过程 Fig. 5 Modeling process |
|
图 6 房间生成逻辑 Fig. 6 Room generation logic |
以房间1左下角点为起始坐标(0, 0),其他房间在所属模块单元与房间1相对关系基础上建模。第1个模块单元长度由主卧1决定,其余房间长度为因变量,宽度均为自变量,卫生间2长宽均为自变量,走廊3宽度由与主卧1相连的卫生间2决定。第2个模块单元长度由客厅5决定,其余房间长度为因变量,宽度均为自变量。第3个模块单元长度由书房8决定,储物间9长度为因变量,宽度均为自变量,卫生间10长宽由走廊11长宽和整个模块单元长宽限值决定。
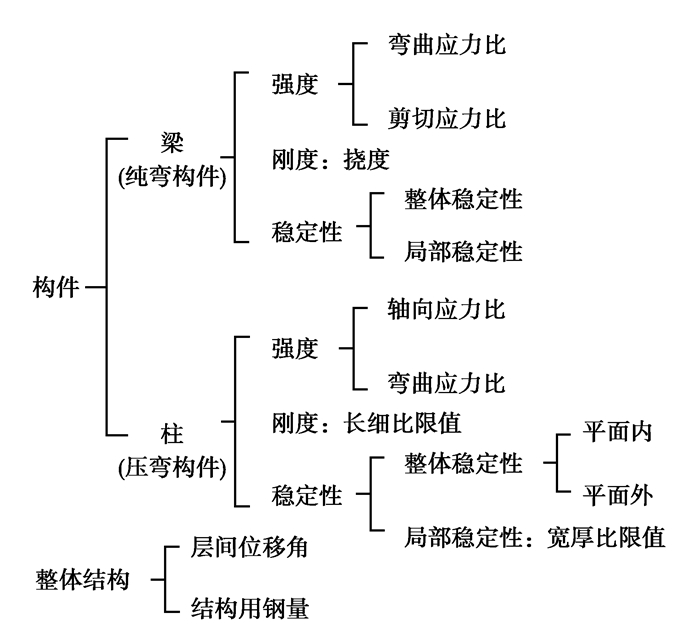
2 钢结构模块建筑结构设计的智能优化方法在进行参数化结构设计时,需考虑结构的安全性和可靠性,是否能在确保结构安全的条件下满足使用需求,其次是结构的使用年限是否满足规范[18-19]的要求。在确保结构是否安全时需要考虑构件和整体结构的安全性,模块建筑的结构受力框架主要是由模块梁、模块柱和连接的角件组成,需要验算受弯构件(梁)和弯压构件(柱)的重要指标。构件的验算根据规范主要考虑构件的强度、刚度、稳定性和整体结构的层间位移角等重要指标,同时满足要求的条件下,认为构件是安全的,如图 7所示。在满足规范的同时尽量实现经济性,即减少结构的用钢量。
|
图 7 构件验算指标 Fig. 7 Checking indexes for members |
层间位移角是按弹性方法计算的风荷载或遇地震标准值作用下的楼层间最大水平位移与层高之比,用来确保高层结构应具备的刚度,是对构件截面大小、刚度大小的宏观控制指标。主要为限制结构在正常使用条件下的水平位移,避免产生过大的位移而影响结构的承载力、稳定性和使用要求。根据规范要求,多高层钢结构位移角限值应控制在1/250之内,结构用钢量没有明确的限制要求,是确保结构经济合理的重要指标。在保证结构安全可靠的前提下,用钢量越少则经济性越好。经过智能优化后结果可导入结构分析软件Midas中进行验证。
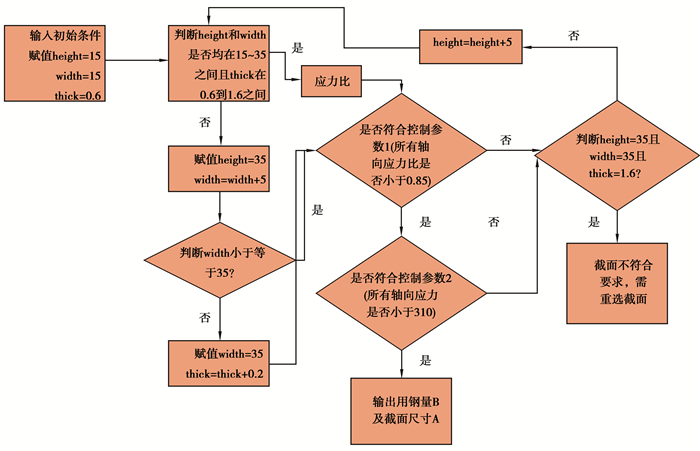
智能化结构优化的流程如图 8所示。首先,赋予截面初始尺寸,尺寸大小可由设计师估计大概范围,判断是否在合理的尺寸范围之内,否的话调整截面尺寸直到合理为止,是的话直接计算结构构件应力比和整体结构指标,将所有计算结果与规范限值比较,全部满足则截面设计合理。若不满足则增大截面尺寸,再重新判断是否在合理尺寸范围之内,对上一步进行循环判断,将满足条件的合理截面尺寸输出,统计整理所有满足要求的数值。选取建筑用钢量最小的截面类型作为结构优化的结果,整个优化设计过程为智能化结构优化设计。理论上,一种建筑形态会对应1个最小用钢量,这个最小用钢量是在保证结构安全条件下的数值。
|
图 8 智能化结构优化设计流程 Fig. 8 The process of intelligent structure optimization design |
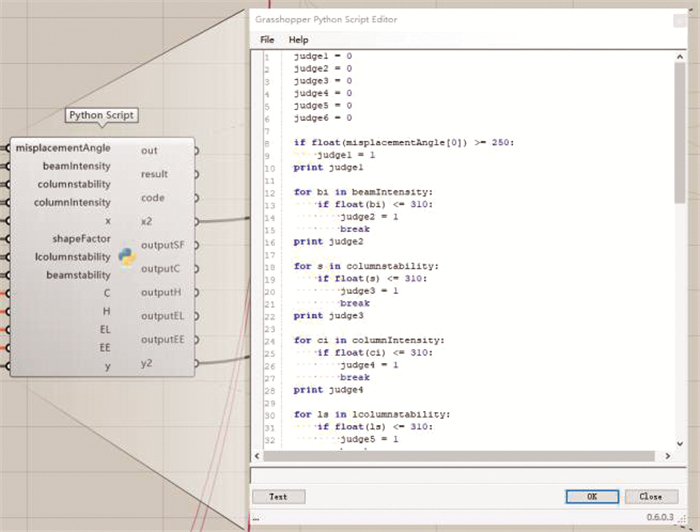
将循环逻辑以脚本语言的形式传输给Python电池块,电池及内部脚本如图 9所示。梁柱构件的强度、稳定性计算结果应小于310,刚度应满足构件长细比的要求,整体结构位移角的倒数应大于250,这几个指标应同时满足要求,当同时满足时,输出结果即截面尺寸、用钢量、建筑户型尺寸和建筑体形系数等参数,最后能计算出所有满足要求的设计结果。
|
图 9 智能优化Python电池及脚本语言 Fig. 9 Intelligent optimization of Python and scripting language |
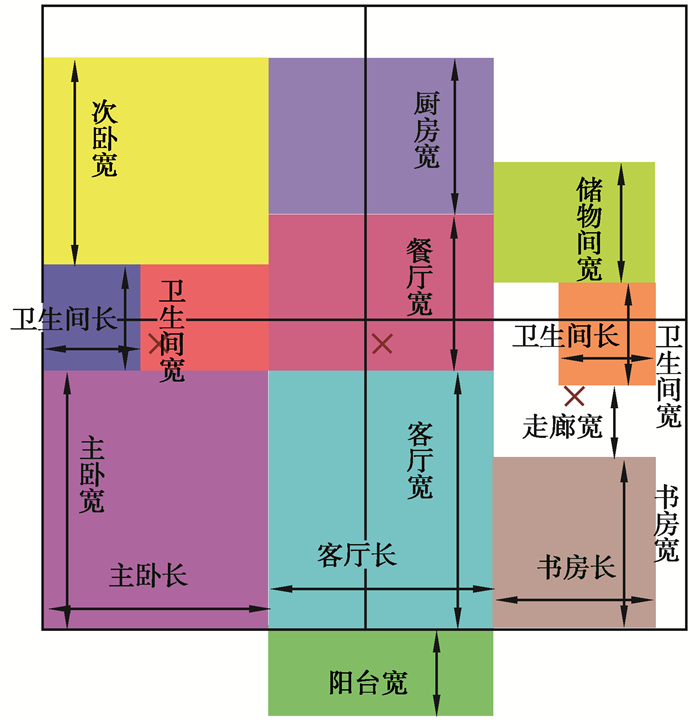
基于生成的参数化户型形体,以建筑各房间长宽尺寸和构件尺寸为变化参数,各房间长宽尺寸参数如图 10所示,构件尺寸取值范围可根据设计师经验选取最优的解集区间,文中取值如表 2~表 4所示。以结构用钢量最低和建筑总能耗最小为目标函数,进行多目标优化。分别建立结构和能耗模型,改变建筑外轮廓和各构件截面尺寸,优化结构用钢量和建筑能耗。
|
图 10 优化变量参数图 Fig. 10 Optimized variable parameter graph |
| 表 2 首层构件尺寸范围值 Table 2 Ground floor component size range value |
| 表 3 标准层构件尺寸范围值 Table 3 Standard floor component size range value |
| 表 4 顶层构件尺寸范围值 Table 4 Top floor component size range value |
能耗模型借助Rhinoceros和Grasshopper软件平台Karamba和Ladybug & Honeybee插件,设计师通过调节建筑不同使用功能房间的尺寸,滑动滑块调节设计参数,可以快速修改建筑体量。文中只研究不同房间尺寸和构件截面尺寸变化下的多目标优化,设置建筑外围护材料参数、内部空调负荷、窗户尺寸和人员设备时间工作表等参数指标为定值,通过改变不同房间长宽尺寸,优化建筑总耗能。优化结果在性能测评的基础上,对2个优化目标即用钢量与建筑总能耗进行综合评价,达到2个目标优化的一种理想状态。在整个优化过程中,从一种形态到另一种形态的变化过程,在没有任何优化目标衰减的前提下,使得至少一种优化目标变得更好。
3.1 参数化模型的建立在探索节能的过程中,将建筑、结构与建筑技术运用在模块建筑中,发现用钢量和建筑能耗2个目标函数之间并没有明显的相关关系,不存在2个目标同时达到最优的状况。因此,多目标优化以建筑总能耗和结构用钢量为目标,在结构安全的前提下提高建筑经济性。建筑能耗受多方面因素的影响,重点讨论在不同房间尺寸和结构构件尺寸变化下对建筑总能耗的影响。取围护结构等参数指标为常量,不同房间长宽尺寸和结构构件尺寸为变化参数,结构构件尺寸是保证结构安全性的重要参数,分析房间长宽尺寸对结构用钢量和建筑总能耗的影响,形成最优方案集,帮助建筑师选择合理的最优方案。
首先,建立5层模块建筑结构模型(见图 11)和能耗模型(见图 12),建筑使用功能为住宅,在满足结构安全的条件下观察建筑平面尺寸和结构构件尺寸的变化,各参数对建筑总能耗和结构用钢量的影响及体形系数与目标函数的相关性,并得到Pareto最优解集。

|
图 11 模块建筑结构模型 Fig. 11 Modular building structure model |

|
图 12 模块建筑能耗模型 Fig. 12 Model building energy consumption model |
整个建筑为纯模块体系,有5层,层高为3 m,无地下室,每层包括7个模块单元,总共35个模块单元。建筑结构使用年限为50年,结构安全等级为二级。根据《建筑抗震设计规范》(GB 50011—2010)及相关地质资料,抗震设防烈度为7度,基本地震加速度为0.15 g,地震分组为第2组,建筑属丙类建筑,抗震等级为三级,场地类别为Ⅲ类,对应特征周期为0.55 s。根据《建筑结构荷载规范》(GB 50009—2001)基本风压为0.50 kN/m2,地面粗糙度为B类。外墙采用石膏板加岩棉的做法,内墙采用波纹板加岩棉的做法,楼板采用压型钢板混凝土组合楼板,根据计算填充墙荷载为4.0 kN/m,如表 5所示。
| 表 5 荷载信息 Table 5 Load information |
模块单元的承重结构为钢框架,由角部的4根模块柱、底梁、顶梁以及次梁构成,外侧墙体采用波纹板。模块单元从模块骨架的制作到模块内部的保温、机电、装修均在工厂内预制生产,完成后运输至现场,并通过可靠的连接方式组装成为建筑整体。
构件材料均选取Q345钢材,角件采用尺寸为200 mm×200 mm,厚度6 mm的方钢管,节点采用铰接建模。模块构件的尺寸可根据设计师的经验确定取值范围,取值如表 2~表 4所示。上述构件梁、柱、短梁等均需检验构件的强度、刚度、稳定性3个重要指标以确保结构的安全性。上天花板梁尺寸的变化对结构用钢量影响较小,取恒定且较为保守的尺寸,在保证结构安全的前提下,尽量减少自变量的个数,便于计算与分析。从计算用钢量电池中输出整个结构的总用钢量,对结果进行处理,将总用钢量除以建筑总面积,即为建筑每平米的用钢量。
3.1.2 建立能耗模拟模型能耗模拟采用Honeybee调用Energyplus引擎来实现,每个房间划分为1个区域, 每户共12个区域,人员、设备、照明的作息均按Energyplus软件中默认设定。建筑层高3 m,区分内外墙。根据《公共建筑节能设计标准》GB 50189—2005[20]中对于窗墙比的规定,假设建筑南侧窗墙比0.6,北侧窗墙比0.3,东西面不开窗;窗台高0.8 m,窗高1.5 m,玻璃种类选择6透明+12A+6透明。外挑阳台不封闭,不计算室内面积和能耗。分别建立楼面、屋面、外窗、外墙围护结构参数和遮阳系数等参数。将建筑主入口设置在正南方向,建筑围护结构构造形式及传热系数如表 6所示。
| 表 6 建筑材料热工参数和门窗类型表 Table 6 Table of thermal parameters of building materials and types of doors and windows |
空调系统采用EnergyPlus中的理想负荷HVAC空调系统,内部得失热(包括人类自身、照明得热、渗透得失热等)和采暖供冷的设定值根据相关要求设置;其他空调参数按经验值设定,参照设备运行以及人员活动时间表、人员密度等规范[20]中的规定值进行设置。调用Energyplus引擎计算建筑能耗,分别将空调制冷、采暖能耗、人工照明能耗和设备使用能耗相加,可得到户型样本的全年总能耗。
3.2 多目标优化多目标优化是设计者在进行多目标性能优化的子流程中,通过作为评价条件的建筑性能和结构设计指标以及进行参数优化设计的参量,利用进化算法在解集空间中搜索出帕累托最优解集的过程。
3.2.1 优化插件参数设置对优化目标的数据交互接口进行连接,将2个目标函数连接至Octopus模块的O端,各参数变量连接至Octopus模块的G端,在Octopus主界面将种群数量设置为100, 变异率设置为0.100, 交叉率设置为0.800,精英比例设置为0.500,最大代数设置为100,然后进行优化。实验选取SPEA2寻优算法与Polynomial变异算法进行搭配。
3.2.2 惩罚函数的定义惩罚函数是一类制约函数,为了淘汰不满足要求的解,即结构安全指标不合理的解。由于结构计算有不同指标,从安全的角度必须满足强度、刚度、稳定性和层间位移角的要求,从经济性角度可以控制用钢量的高低,用钢量越小越好,但不是强制的,而安全指标一定要满足,所以把满足要求的解筛选出来再进行优化提高计算效率。可以在程序内部做出判断,如果解不满足要求,那么它的输出值就加上一个足够大的数值,这个数值可以是正常范围的3~4倍。遗传算法的基本原理就是通过基因组合淘汰那些表现不好的解(输出值大的解),表现不好的解被保留到下一代中的概率就会减小,算法会根据这样的原则自动进行淘汰。本例惩罚因子取为3。
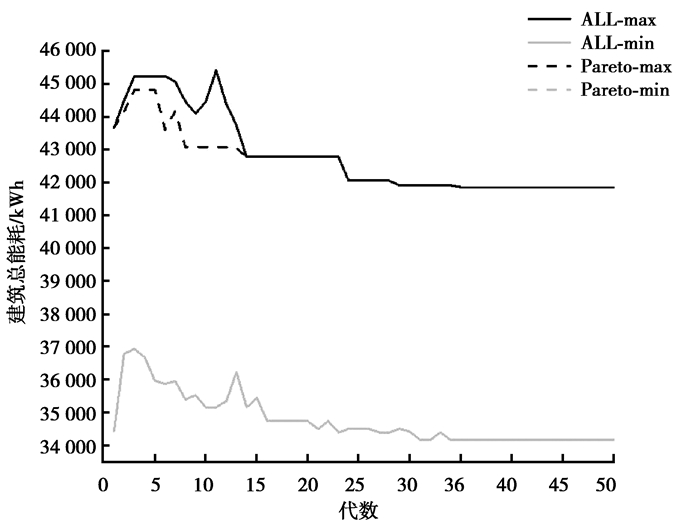
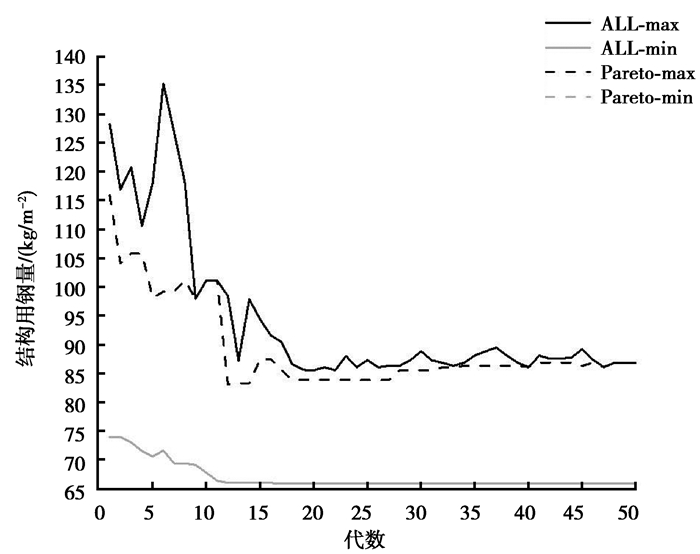
3.2.3 分布状况及收敛过程实验共进行了50次迭代计算,共获得93个优化方案。图 13和图 14分别表示的是1~50代建筑总能耗目标函数和结构用钢量收敛图,每一代解与真实Pareto最优解之间在目标函数上的差距揭示了进化的收敛过程,收敛结果良好,表明2个目标之间存在较大的优化空间。优化过程是为得到目标函数的最小值,所以出现了全部解边界最小值和Pareto最优解边界最小值重合的现象。但对于2种解集边界的最大值而言,往往在最初阶段全部解集的变化曲线会包裹住Pareto最优解集的变化曲线,随着进化过程的推进,2条曲线的重合率越来越高,这种情况表明:一是Pareto最优解在所有解中占比例增加;二是各代的支配集越来越趋近Pareto最优解。而建筑总能耗目标函数值的收敛图与用钢量目标函数不一致,该目标函数值的所有解边界的最大值和Pareto最优解边界的最大值在13代之后几乎重合,这是由于优化算法在最初就找到了Pareto最优解在这一目标函数上的最大值,并且支配解在该函数上的值也都小于它,在13代之前的Pareto变化趋势先于最大值的变化趋势。此外,结构用钢量目标函数的Pareto最优解边界最大值在18代之前变化幅度与最大值的变化幅度相似且小于最大值,并在最初几代呈增大、减小反复变化趋势,而后呈现正常状态,这种反复变化的情况并非不收敛,只能说明该目标函数的分布范围在发生变化。
|
图 13 建筑总能耗收敛图 Fig. 13 Convergence graph of total building energy consumption |
|
图 14 结构用钢量收敛图 Fig. 14 Convergence graph of structural steel consumption |
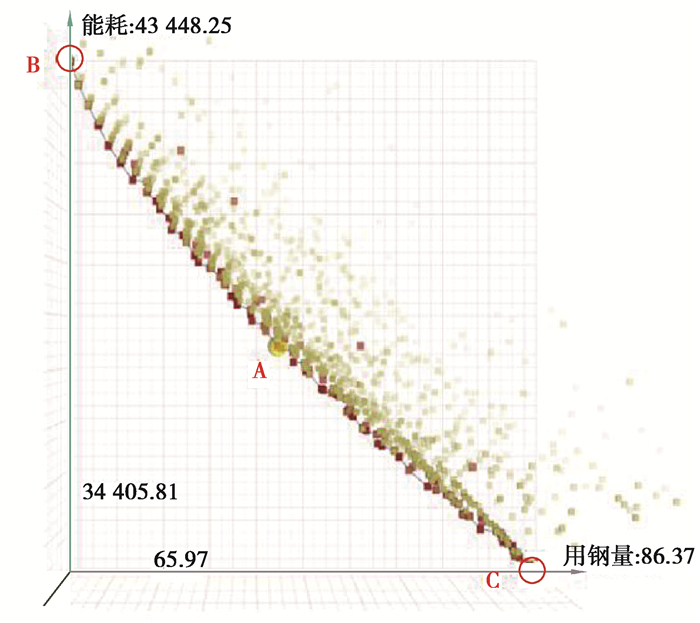
模拟共进行了50次迭代,Pareto最优解由93种形态的参数化方案组成,用于评价优化质量的Hypervolume值为0.89且已经趋于稳定,共耗时6d 16h 33min。由第50代优化得出的最优解组成的Pareto前沿分布情况如图 15所示。图 16为A、B、C 3点对应的方案示意图(在模拟过程中A点具有重要意义,其2个目标均达到较优效果,即A点是Pareto最优解的集合中距离原点最近的点)。图 15显示了进化过程的Pareto最优解、所有代数的支配解在二维空间中的情况,红色的解为Pareto最优解的集合。可以看出,在横轴方向上越靠近原点,其用钢量结果越明显:在纵轴方向上越靠近原点,其建筑总能耗结果越好。以此为依据,挑选Pareto前沿解上的A、B、C 3点。就每组而言,B点是建筑用钢量最小值的点,C点是建筑总能耗最小值的点,A点是距离原点直线距离最近的点,其综合优化结果较优。Pareto前沿面是优化结果在目标函数空间的表现形式,同时也是直接指导设计的工具,设计师或业主可以选择在Pareto前沿面上最为接近能耗和用钢量期望的一个或几个点,对应的目标函数值为这种期望下的最优解,对应的方案可作为设计参考。
|
图 15 Pareto前沿分布图 Fig. 15 Pareto frontier distribution |
|
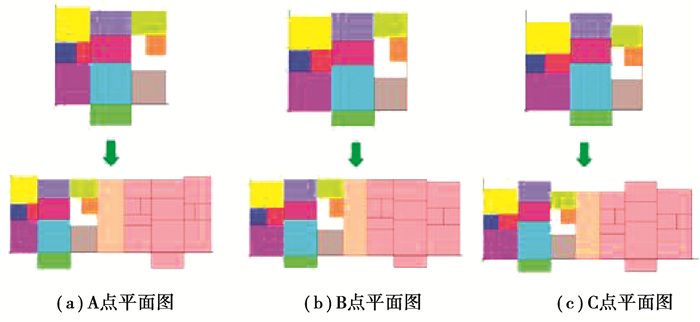
图 16 Pareto前沿分布图中A、B、C 3点对应的平面样式图 Fig. 16 Pareto frontal distribution diagram of the three points corresponding to the A, B, C flat style |
就单个目标而言,由B点对应形式可知用钢量优化最为明显,达到最小值65.97 kg/m2,总能耗为43.45 Wkwh。由于建筑总能耗和体形系数成正比,体形系数越大,则建筑总能耗越大,而第2个模块单元的变化对体形系数影响较大,改变模块单元1和3比较合适,主卧的长宽尺寸对建筑总能耗影响最大,适当减少主卧尺寸,会增加建筑总能耗。建筑总能耗C点对应形式可知第3组建筑总能耗优化最为明显,达到34.17 Wkwh,用钢量为86.90 kg/m2。对于2个优化目标而言,A点对应的数值是用钢量和建筑总能耗综合最优的情况,用钢量优化为73.88 kg/m2,总能耗为38.94 Wkwh,方案的选择要进一步结合建筑审美需求等因素。
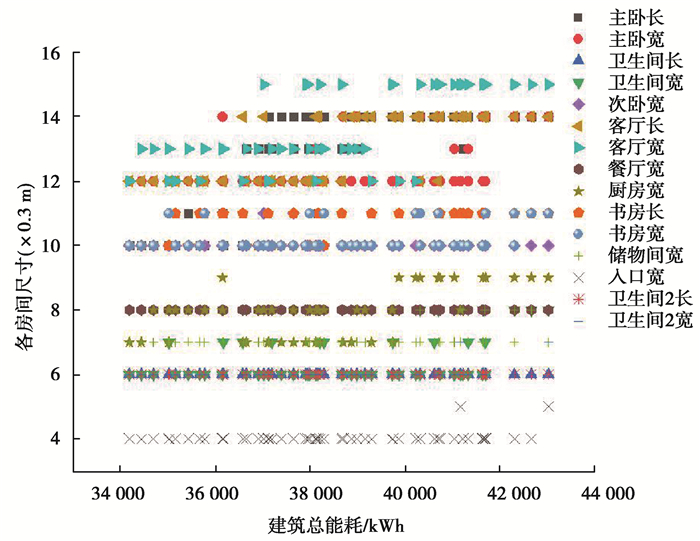
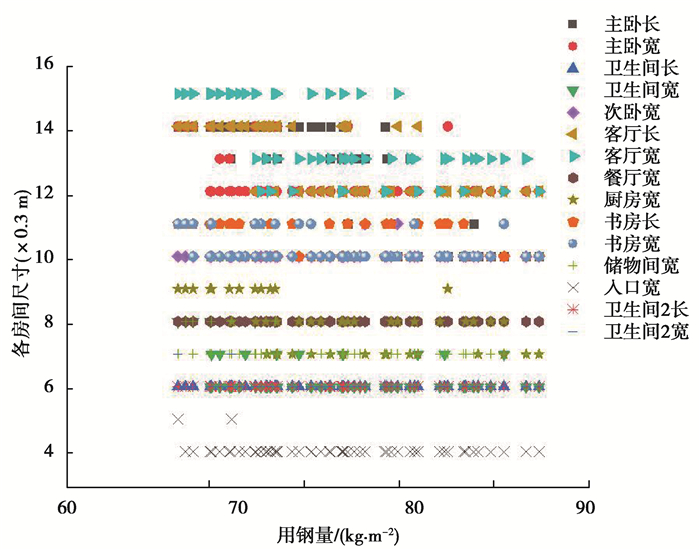
3.2.5 Pareto最优解集方案选择图 17反映了2个实验方案,在不同变量组成下,各房间尺寸变量与2个目标函数值对应的关系。设计师可以根据不同目标函数值选择所需的模块建筑标准化尺寸,也可以根据已确定的变量尺寸得到目标函数值。由图可知,在建筑总能耗目标中(见图 17),第1个模块单元主要尺寸变量的主卧长为3 m,宽为3.6 m,次卧宽3 m;第2个模块单元主要变量的客厅长宽均为3.6 m;第3个模块单元主要变量的书房长宽均为3 m时建筑总能耗是较低的。在结构用钢量目标中(见图 18),第1个模块单元主要尺寸变量的主卧长宽均为4.2 m,次卧宽3 m;第2个模块单元主要变量的客厅长为4.2 m,宽为4.5 m;3个模块单元主要变量的储物间宽均为2.1 m时,结构用钢量较低。
|
图 17 最优解集中建筑总能耗与各房间尺寸参数对应关系 Fig. 17 Correspondence between the total energy consumption of buildings and the size parameters of each room |
|
图 18 最优解集中结构用钢量与各房间尺寸参数对应关系 Fig. 18 Correspondence between the steel consumption of buildings and the size parameters of each room |
可以看出,不同实验方案在解的多样性上具有各自的优势和劣势,设计人员可以根据实际需求选择更为合适的解。
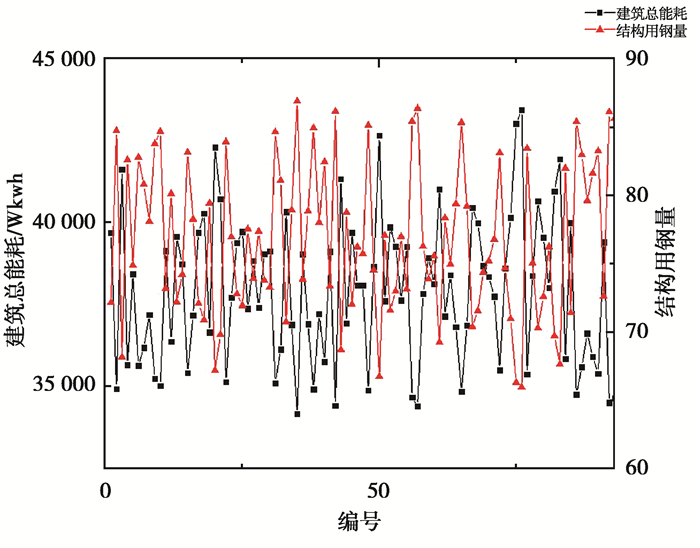
图 19表示Pareto最优集对应的93个多目标优化解的结果,从统计结果可以看出,模拟2个目标函数值的波动范围在65.97~86.90 kg/m2与34.17~43.45 Wkwh之间,用钢量目标最大值与最小值之差控制在21 kg/m2以内,建筑总能耗控制在20%,提高了设计阶段目标优化和方案确定的效率。
|
图 19 模拟Pareto前沿解的多目标优化结果 Fig. 19 Multi-objective optimization results of simulated Pareto frontier solutions |
经过50代优化,每代种群数量为100,总共可以得到4 911组满足承载力要求的数值,将数据提取导入SPSS软件进行统计分析。通过分析得到目标优化时,目标函数与参数之间相关性,各模块单元对应的自变量与目标函数的相关性系数。通过分析可知,第1个模块单元,主卧长与建筑能耗之间呈负相关的关系,显著性程度最强,为-0.706,其他变量均与建筑总能耗呈负相关的关系。主卧长与用钢量之间呈负相关的关系,其他变量均与用钢量呈正相关的关系,次卧宽度对用钢量的影响程度较为明显,为0.299;第2个模块单元,各变量尺寸对建筑总能耗影响均呈负相关,其中客厅长与建筑总能耗之间相关性程度最大,为-0.546,显著性程度中等;各变量尺寸对用钢量影响均呈负相关,其中客厅宽度与用钢量之间相关性系数较大,为-0.259,显著性程度较低;第3个模块单元,各变量尺寸对建筑总能耗影响均呈负相关,其中书房长与总能耗之间相关性系数最大,为-0.407,显著性程度中等。各变量尺寸对用钢量影响均呈负相关,其中储物间宽与用钢量之间相关性系数最大,为-0.474,显著性程度中等。
4 结论模块建筑作为一种新兴的建造体系,在经济、环保、节能及建造周期效率等方面都有明显的优势,具有广阔的发展前景,文中主要研究了模块建筑住宅在建筑方案设计阶段的参数化建模方法、智能化结构设计和多目标优化3个主要方面,得到了户型尺寸方案的优化解集。
1) 提出一种模块建筑参数化建模方法和平面生成逻辑,并通过优化形成1组Pareto最优解,这种生成及优化方法适用于不同类型体系的钢结构模块建筑。
2) 将建筑设计、建筑技术与建筑结构相结合运用在模块建筑住宅中,生成符合模块建筑特有的多目标优化方案户型集,供设计师选择最佳方案。经过优化,可以得到结构用钢量最小为65.97 kg/m2,对应的建筑总能耗为43.45 Wkwh;建筑总能耗最小为34.17 Wkwh,对应的用钢量为86.90 kg/m2。考虑用钢量和建筑总能耗综合最优的情况,用钢量优化为73.88 kg/m2,总能耗为38.94 Wkwh,具体整个优化解集中方案选择可以根据设计师的需求来权衡。
3) 在Pareto最优集对应的93个多目标优化解的结果,模拟2个优化目标的波动范围为65.97~86.90 kg/m2与34.17~43.45 Wkwh,用钢量目标最大值与最小值之差控制在21kg/m2以内,建筑总能耗控制在20%,大大提高了设计阶段目标优化和方案确定的效率。
4) 设计师可以根据不同目标函数值选择所需的模块建筑标准化尺寸,也可以根据已确定的变量尺寸来得到目标函数值。在建筑总能耗目标中,第1个模块单元主要的尺寸变量为主卧长3 m,宽3.6 m,次卧宽为3 m;第2个模块单元主要变量为客厅长宽均为3.6 m;第3个模块单元主要变量书房长宽均为3 m时,建筑总能耗较低。在结构用钢量目标中,第1个模块单元主要的尺寸变量主卧长宽均为4.2 m,次卧宽为3 m;第2个模块单元主要变量为客厅长4.2 m,宽4.5 m;3个模块单元主要变量储物间宽均为2.1 m时,结构用钢量较低。
| [1] |
Lawson R M, Ogden R G, Bergin R. Application of modular construction in high-rise buildings[J]. Journal of Architectural Engineering, 2012, 18(2): 148-154. DOI:10.1061/(ASCE)AE.1943-5568.0000057 |
| [2] |
Lawson R M, Ogden R G, Bergin R. Application of modular construction in high-rise buildings[J]. Journal of Architectural Engineering, 2012, 18(2): 148-154. DOI:10.1061/(ASCE)AE.1943-5568.0000057 |
| [3] |
Zitzler E, Thiele L. Multiobjective evolutionary algorithms: a comparative case study and the strength Pareto approach[J]. IEEE Transactions on Evolutionary Computation, 1999, 3(4): 257-271. DOI:10.1109/4235.797969 |
| [4] |
Annan C D, Youssef M A, El-Naggar M H. Analytical investigation of semi-rigid floor beams connection in modular steel structures[C]. General Conference of the Canadian Society for Civil Engineering, 2005.
|
| [5] |
Lu N. The current use of offsite construction techniques in the United States construction industry[C]//Construction Research Congress 2009. April 5-7, 2009, Seattle, Washington, USA. Reston, VA, USA: American Society of Civil Engineers, 2009: 946-955.
|
| [6] |
Lee W H, Kim K W, Lim S H. Improvement of floor impact sound on modular housing for sustainable building[J]. Renewable and Sustainable Energy Reviews, 2014, 29: 263-275. DOI:10.1016/j.rser.2013.08.054 |
| [7] |
Ha T H, Cho B H, Kim H, et al. Development of an efficient steel beam section for modular construction based on six-sigma[J]. Advances in Materials Science and Engineering, 2016, 2016: 1-13. |
| [8] |
Coello C C A, Lamont G B, Van Veldhuizen D A. Evolutionary Algorithms for Solving Multi-Objective Problems[M]. Second Edition. New York: Springer, 2007.
|
| [9] |
王蔚. 模块化策略在建筑优化设计中的应用研究[D]. 长沙: 湖南大学, 2013. Wang W. Research on the application of mod-ular strategy in optimized architectural desig-n[D]. Changsha: HuNan University, 2013. (in Chinese). |
| [10] |
陈志华, 周子栋, 刘佳迪, 等. 多层钢结构模块建筑结构设计与分析[J]. 建筑结构, 2019, 49(16): 59-64. Chen Z H, Zhou Z D, Liu J D, et al. Structural design and analysis of multi-storey steel structure module structures[J]. Building Structure, 2019, 49(16): 59-64. (in Chinese) |
| [11] |
曲可鑫. 钢结构模块化建筑结构体系研究[D]. 天津: 天津大学, 2014. Qu K X. Study on steel structural system in modular buildings[D]. TianJin: TianJin University, 2014. (in Chinese). |
| [12] |
申杰. 基于Grasshopper的绿色建筑技术分析方法应用研究[D]. 广州: 华南理工大学, 2012. Shen J. Research on methods of using technical analysis in grasshopper for green building design[D]. Guangzhou: South China University of Technology, 2012. (in Chinese) |
| [13] |
李垚. 钢结构模块建筑建造技术和空间设计研究[D]. 重庆: 重庆大学, 2017. Li Y. Research on modular building construction system and space design[D]. Chongqing: Chongqing University, 2017. (in Chinese). |
| [14] |
杜信池. 一种建筑空间生成机理研究的参数化方法[D]. 杭州: 浙江大学, 2017. Du X C. A parametric method for the research in the generation mechanism of architectural space[D]. Hangzhou: Zhejiang University, 2017. (in Chinese) |
| [15] |
陈航. 基于多目标优化算法的寒冷地区办公建筑窗口设计研究[D]. 天津: 天津大学, 2016. Chen H. Window design of office buildings in cold climate area based on multi-objective optimization algorithm[D]. Tianjin: Tianjin University, 2016. (in Chinese) |
| [16] |
吴闻. 夏热冬冷地区装配式建筑体形系数对能耗影响的研究[D]. 合肥: 安徽建筑大学, 2018. Wu W. Study on the influence of building shape coefficient on energy consumption in hot summer and cold winter area[D]. Hefei: Anhui Jianzhu University, 2018. (in Chinese) |
| [17] |
邝达. 多目标遗传算法中解集分布度保持策略的研究[D]. 湘潭: 湘潭大学, 2006. Kuang D. Researches on strategies to keep diversity in multi-objective genetic algorithms[D]. Xiangtan: Xiangtan University, 2006. (in Chinese). |
| [18] |
中国工程建设标准化协会. 钢结构模块建筑技术规程T/CECS 507-2018[S]. 北京: 中国计划出版社, 2018. China Engineering Construction Standardization Association. Technical specification for steel modular buildings. T/CECS 507-2018[S]. Beijing: China Planning Press, 2018. (in Chinese) |
| [19] |
中华人民共和国住房和城乡建设部, 中华人民共和国国家质量监督检验检疫总局. 中华人民共和国国家标准: 钢结构设计规范GB 50017-2003[S]. 北京: 中国计划出版社, 2003. Ministry of Housing and Urban-Rural Development of the People's Republic of China, General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China. National Standard (Mandatory) of the People's Republic of China: Code for design of steel structures. GB 50017-2003[S]. Beijing: China Planning Press, 2003. (in Chinese) |
| [20] |
中华人民共和国住房和城乡建设部, 中华人民共和国国家质量监督检验检疫总局. 中华人民共和国国家标准: 公共建筑节能设计标准GB 50189-2005[S]. 北京: 中国建筑工业出版社. Ministry of Housing and Urban-Rural Development of the People's Republic of China, General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China. National standard (mandatory) of the People's Republic of China: design standard for energy efficiency of public buildings. GB 50189-2005[S]. Beijing: China Architecture & Building Press. (in Chinese) |
 2021, Vol. 44
2021, Vol. 44


