2. 重庆大学 土木工程学院, 重庆 400045
2. School of Civil Engineering, Chongqing University, Chongqing 400045, P. R. China
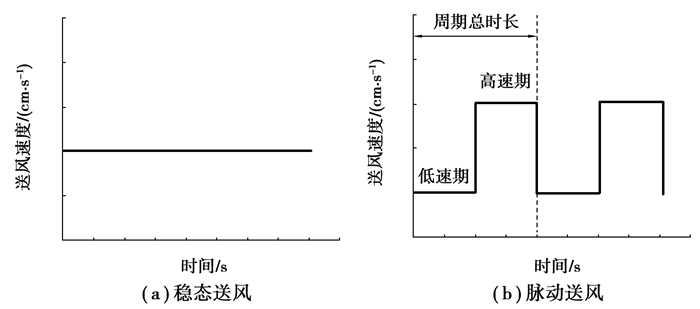
提升空调室温可降低空调系统能耗,降低建筑能耗[1]。层式通风是一种可行的“高温空调”解决方案,适用于中小空间[2]。它通过将送风口布置在侧墙略高于人体头部,直接将清洁空气水平送入人体呼吸区,形成充满呼吸区的“新鲜空气层”,直接有效冷却热舒适决定性部位——头部,最大化通风效率[3]。与传统的混合通风和置换通风相比,层式通风的能耗可以分别降低44%和25%,为室内人员提供可接受的空气品质和热舒适[4-5]。然而,层式通风作为一种新型通风策略,热舒适仍有待提高。如图 1所示,稳态送风下,送风速度随时间保持不变;动态送风下,送风速度随时间变化。脉动送风是动态送风的一种,其中,送风速度较低的时期为低速期,送风速度较高的时期为高速期。研究表明,脉动送风有潜力降低稳态送风下的吹风感[6],提升人体热舒适,改善“病态建筑综合征”[7]。
|
图 1 送风方式示意图 Fig. 1 Schematic diagram of air supply modes |
综上所述,脉动送风与层式通风耦合,在节能的同时提供良好的热舒适。由于送风参数对热舒适起决定性作用,为了实现这一目标,需要为“脉动送风耦合层式通风”策略选用合适的送风参数,如周期时长、送风速度、送风口与受试者之间的距离、送风温度等[7-8]。目前,利用脉动送风耦合层式通风提供良好的热舒适,送风参数应该如何设计,仍然有待研究。
文中采用经实验数据验证的非定常计算流体动力学(CFD)数值模拟方法,改变脉动送风参数,即周期总时长(高速期与低速期时长之和),高速期与低速期的送风速度,高速期与低速期时长之比,探究送风参数对热舒适的影响。利用多目标优化方法得到热舒适综合评价最优的送风参数,为脉动送风耦合层式通风工程设计提供指导。
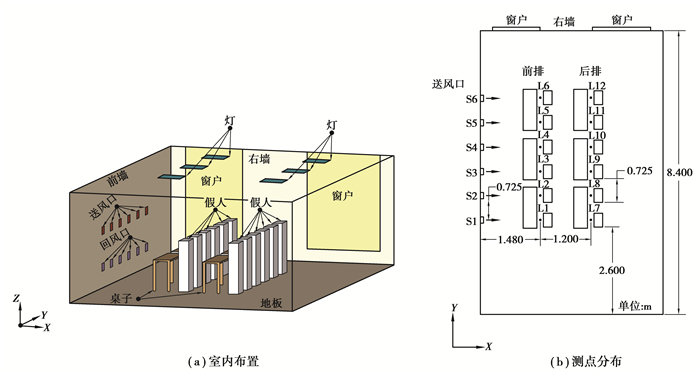
1 研究方法 1.1 模型CFD数值模拟时采用文献[9]中的几何模型,如图 2(a)所示。教室的尺寸为8.4 m(长)×5.4 m(宽)×2.6 m(高)。12个座位被分为2排,编号为1~12。送风口和回风口尺寸均为0.17 m×0.17 m。房间的右外墙上有2扇窗户,其他内墙可视为绝热。室内假人由一个尺寸为0.4 m(长)×0.25 m(宽)×1.2 m(高)的长方体表示。每个假人中都放置了1个100 W的灯泡,模拟人体散热。此外,室内热源还有6盏功率为29 W的白炽灯。图 2(b)中L1~L12是12条测量铅垂线,均在假人前方0.1 m处布置。每条测量线上有3个测点,高度分别为0.1 m(脚踝)、0.6 m(坐姿腹部)和1.1 m(坐姿头部)。测点L1-1.1指的是测量线L1上1.1 m高度的测点,文中的测点命名都参照这一原则。
|
图 2 实验平台 Fig. 2 The experiment platform |
CFD模拟采用软件ANSYS Fluent 19。旨在对房间内的换热和流动进行数值计算,流体为空气。在空气的物性设置上,空气为不可压缩牛顿流体,采用Boussinesq假设来估计温度变化引起的空气密度变化[14]。此外,空气中的粘性耗散忽略不计,除密度外其他物性为常数。采用非定常雷诺平均法(URANS),湍流模型为RNG k-ε。比起雷诺平均法(RANS),URANS的计算方程中增加了时间项,用于室内动态环境的模拟,可得到较好的预测结果[10-13]。原理上,LES更适用于计算非定常流场[10]。对于室内动态速度场和温度场的预测,使用URANS的RNG k-ε模型和LES的结果足够接近[11],而LES的计算需求高出URANS约100倍[10]。因此,使用URANS可以在不牺牲精确度的同时,提高计算效率。对于近壁面区域的湍流流动,采用标准壁面函数[14]。对于辐射,采用DO(discrete ordinate)模型来计算不同壁面(外墙、外窗、人体表面、灯)之间的热传递[4]。控制方程的数学表达式详见文献[10]。对于计算求解的设置,采用有限体积法用于控制方程离散化[15],SIMPLE法作为压力速度耦合算法[14],二阶迎风格式用于物理量的空间离散化,二阶隐式格式用于时间离散化[11]。经过测试不同的时间步长,0.01 s的大小足以保证解的收敛。在模拟过程中,动量残差的收敛准则设为10-4,质量残差、湍流动能残差、湍流耗散残差、能量残差和辐射强度残差的收敛准则设为10-6 [12]。
表 1给出了数值模拟中使用的边界条件。所有的实体表面都设定为固定墙体(no-slip wall)。外墙和外窗的壁面温度值参照之前的现场测量值确定[9]。送风口设置为速度入口(velocity-inlet)[16]。送风速度和温度根据计算工况进行设置。对于稳态送风,送风速度为定值;对于脉动送风,送风速度与时间有关,通过用户定义函数(UDF)设定。回风口设置为自由出流(outflow)。
| 表 1 CFD模拟计算边界条件 Table 1 Boundary conditions of CFD simulation |
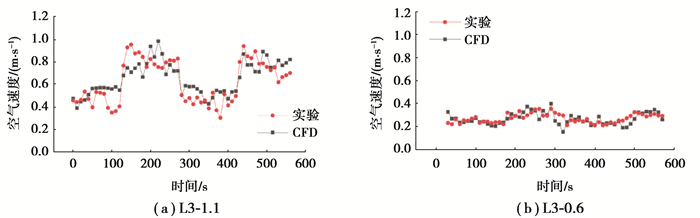
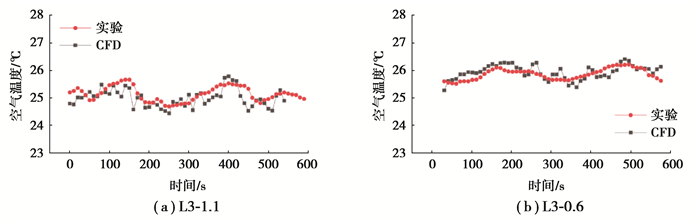
文中利用ICEM软件进行网格划分,网格为六面体网格[12]。风口、热源及热壁面的局部网格得到了细化,这些位置的速度和温度梯度比较大[12]。经过网格独立性验证后,采用网格数量为2、161、376的网格进行计算。为保证数值模拟的可靠性,利用1组实验工况(文献[9]中的工况A)的数据对CFD模型进行了验证。对2个脉动送风周期内(600 s)的空气速度和空气温度的变化趋势进行对比。测点选为文献[9]中的L3-1.1和L3-0.6,如图 3和图 4所示。
|
图 3 空气速度的实验和模拟对比结果 Fig. 3 Comparison of the experimental and simulation results of air velocities |
|
图 4 空气温度的实验和模拟对比结果 Fig. 4 Comparison of the experimental and simulation results of air temperatures |
把周期总时长设为5 min和2 min,高速期时长和低速期时长之比设为1∶1,2∶1,1∶2,4∶1,1∶4。由于房间负荷不变,对于所有工况,送风温度均为21.5 ℃,周期平均送风速度均为1.5 m/s。为了区别高速期和低速期的空气速度,送风速度差最小为0.3 m/s,而最大不限。根据以上原则,确定了周期平均送风速度、周期总时长、高速期时长与低速期时长之比后,其他参数可以根据式(1)进行计算:
| $ \bar v \times {L_{{\rm{total }}}} = {v_{\rm{h}}} \times {L_{\rm{h}}} + {v_1} \times {L_1}, $ | (1) |
式中: v是周期平均送风速度,m/s;Ltotal是周期总时长,s;vh是高速期送风速度,m/s;Lh是高速期时长,s;vl是低速期送风速度,m/s;Ll是低速期时长,s。模拟工况共26个,如表 2所示。
| 表 2 模拟工况 Table 2 Simulated cases |
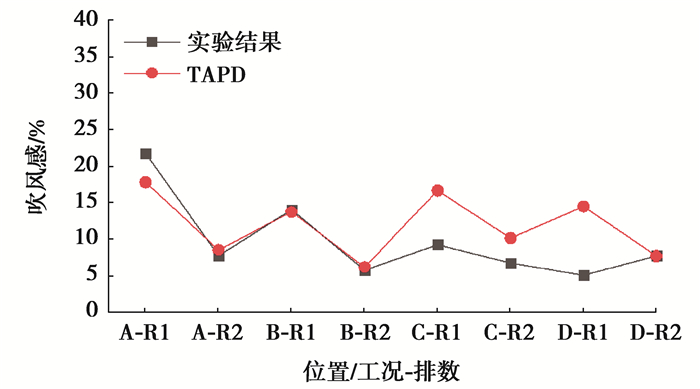
文中利用热感觉和吹风感来评价热舒适。已有研究表明,TAPMV(时间平均预测平均投票)可以较准确预测脉动送风耦合层式通风下的热感觉[9]。对于吹风感,图 5显示了脉动送风耦合层式通风下的TAPD(时间平均吹风感)和吹风感主观实验结果,所对应的实验工况为文献[9]中的工况。TAPD和吹风感主观实验结果最大差异为9.4%,平均差异为3.2%,吻合较好。因此,可采用TAPD进行脉动送风耦合层式通风下的吹风感预测。TAPMV和TAPD的详细计算见文献[9, 17]。
|
图 5 TAPD和吹风感主观实验结果的对比 Fig. 5 The comparison of TAPD and the subjective experimental results |
最优工况的筛选有2方面,一是高速期和低速期各自的TAPMV最接近中性,TAPD最接近0;二是高速期和低速期的TAPMV差异和TAPD差异最大,从而刺激人体的冷热感受器,带来较舒适的感觉[7]。在参数优化中,评价指标采用高速期TAPMV,高速期TAPD,低速期TAPMV,低速期TAPD,高速期和低速期的TAPMV差异,以及高速期和低速期的TAPD差异。
1.6 多目标优化文中采用的多个热舒适评价指标的结果有可能出现矛盾,即对于同一工况,一项指标较好,而另一项指标较差,具体分析见2.2节。需要进行多目标优化,得到综合的热舒适结果。综合热舒适最优的工况即为最优送风工况。
首先,运用熵权法进行权重的计算[18]。计算过程如下:
步骤一:高优指标(越大越好)保持数值不变,低优指标(越小越好)采用“取倒数”的方法转化为高优指标,形成矩阵Yij。
步骤二:对Yij进行标准化处理,形成Zij为
| $ Z_{i j}=\boldsymbol{Y}_{i j} \div \sqrt{\sum\limits_{i=1}^{n}\left(\boldsymbol{Y}_{i j}\right)^{2}} \text { 。} $ | (2) |
步骤三:计算第j项指标的熵值bj为
| $ {b_j} = \frac{{\sum\limits_{i = 1}^n {{Z_{ij}}} \ln {Z_{ij}}}}{{\ln n}}。$ | (3) |
步骤四:计算第j项指标的冗余度为
| $ a_{j}=1-b_{j}。$ | (4) |
步骤五:计算第j项指标的熵权wj为
| $ {w_j} = \frac{{{a_j}}}{{m - \sum\limits_{j = 1}^m {{b_j}} }}。$ | (5) |
对于多目标优化,采用TOPSIS法(technique for order preference by similarity to an ideal solution)。TOPSIS广泛应用于能耗、室内环境等多指标问题的求解[19-20]。该方法的基本思想是最优方案与最优解的距离最短,与最不利解的距离最远。以各工况的第j项指标的最优值Zj+作为最优解,以各工况的第j项指标的最不利值Zj-作为最不利解。
TOPSIS的计算过程如下[20]:
步骤一:计算每一个评价对象与最优解的欧式距离Di+和最不利解的欧氏距离Di-:
| $ D_i^ + = \sqrt {\sum\limits_{j = 1}^m {\left[ {{{\left( {{w_j}\left( {{Z_{ij}} - Z_j^ + } \right)} \right]}^2}} \right.} } , $ | (6) |
| $ D_i^ - = \sqrt {\sum\limits_{j = 1}^m {{{\left[ {{w_j}\left( {{Z_{ij}} - Z_j^ - } \right)} \right]}^2}} } 。$ | (7) |
步骤二:计算各评价对象与最优解的相对接近度Ci:
| $ {C_i} = \frac{{D_i^ - }}{{D_i^ - + D_i^ + }}。$ | (8) |
步骤三:将Ci值按照大小排序。Ci值越大,热舒适水平越好。
2 结果及分析 2.1 脉动送风耦合层式通风下的热舒适表 3展示了26个工况下的热舒适计算结果,前排TAPMV和TAPD是根据L1~L6的1.1 m高度的6个点数据计算的平均结果,后排TAPMV和TAPD是根据L7~L12的1.1 m高度的6个点数据计算的平均结果,整体TAPMV和TAPD是根据L1~L12的1.1 m高度的12个点数据计算的平均结果。由表 3可见,对于前排、后排和整体,高速期的TAPMV比低速期的TAPMV分别低1.26~0.08,0~0.53和0.08~0.90,高速期的TAPD比低速期的TAPD分别高1.1%~18.1%,0.1%~6.9%和0.8%~12.5%,说明设计的工况可以实现高速期和低速期的热舒适差异。然而,低速期,部分工况下的TAPMV高于0.5,可能造成过热;高速期,部分工况下的TAPMV低于-0.5,可能造成过冷。各工况的热舒适水平不同,说明送风参数对热舒适存在影响。为了达到热舒适最优,送风参数需要进行优化选择。
| 表 3 26个模拟工况下的热舒适结果 Table 3 The thermal comfort results of 26 simulation cases |
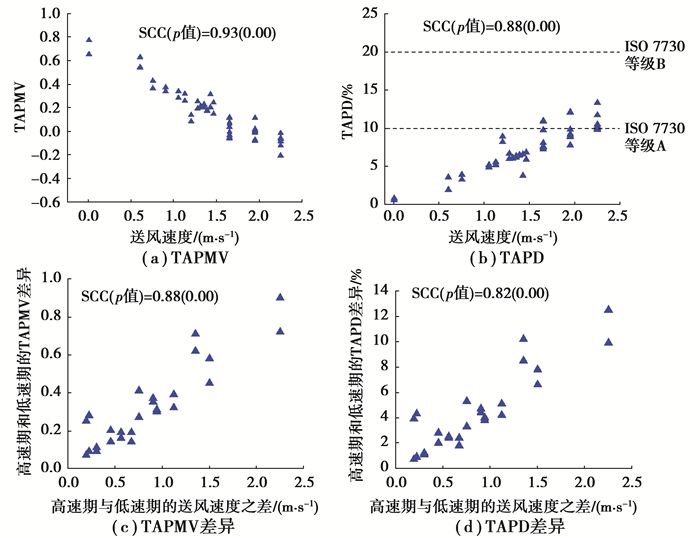
对于送风周期总时长,Wilcoxon检验显示,在0.05的水平,周期总时长5 min和总时长2 min的工况的热舒适各项指标没有显著差异,说明周期总时长对热舒适影响不显著。对于其他送风参数,用斯皮尔曼相关系数(SCC)来评价它们和热舒适指标的相关性,p值小于0.05则认为两者相关。SCC为正,即为正相关,反之则反。SCC的绝对值越大,说明相关性越强烈。由图 6(a)可知,送风速度越高,TAPMV越低(SCC < 0)。由图 6(b)可知,送风速度越高,TAPD越高(SCC>0)。因为送风速度升高,空气速度升高,空气温度降低,进而TAPMV降低,TAPD升高。由图 6(c)和图 6(d)可知,送风速度之差越大,高速期和低速期的TAPMV差异和TAPD差异越大(SCC>0)。
|
图 6 热舒适指标随送风速度的变化 Fig. 6 The variation of thermal comfort indexes with the supply air velocity |
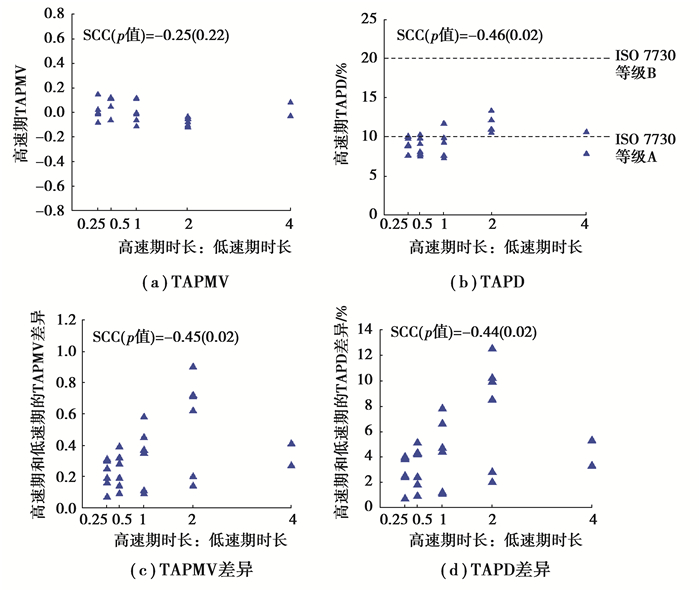
因为高速期的送风速度为1.65、1.95、2.25 m/s,而低速期的送风速度范围较大且不相等,此处只研究了高速期时长与低速期时长之比对高速期热舒适的影响。由图 7(a)可知,高速期时长与低速期时长之比对TAPMV无显著影响(p>0.05)。由图 7(b)可知,高速期时长与低速期时长之比越高,TAPD越高(SCC>0)。因为高速期时长较长时,空气温度降低更多,TAPD升高更多。由图 7(c)和图 7(d)可知,高速期时长与低速期时长之比越高,高速期和低速期的TAPMV差异和TAPD差异越大(SCC>0)。这是因为高速期与低速期时长之比越高,由公式(1)可见,高速期与低速期速度之差会变大,导致高速期和低速期的TAPMV差异和TAPD差异越大。
|
图 7 热舒适指标随高速期时长和低速期时长之比的变化 Fig. 7 The variation of thermal comfort indexes with the ratio of the high-velocity duration to the low-velocity duration |
值得注意的是,高速期时长与低速期时长之比越高,高速期TAPD升高,热舒适水平降低;另一方面,高速期和低速期的TAPMV差异和TAPD差异增大,热舒适水平升高。因此,送风参数对不同热舒适指标的影响存在矛盾性,需要多目标优化。
2.3 脉动送风优化方案确定文中把热舒适可行工况认作高速期和低速期的前后排TAPMV均在-0.5~0.5的范围内,TAPD小于20%,即ISO 7730标准中规定的B等级热环境[21]。通过直接观察筛选,26个工况中共有17个工况可行,即工况1,2,7,8,9,12~16,20~26。最优工况在17个可行工况中进行选择。首先,利用熵权法计算各项指标的权重,结果如表 4所示,再利用TOPSIS法进行多目标优化,得到各个工况的排名,结果如表 5所示。工况2排名最高,说明工况2下,高速期和低速期分别的TAPMV和TAPD较好,且高速期与低速期的TAPMV差异、TAPD差异较大。工况2下,周期总时长为5 min,高速期时长与低速期时长之比为1,高速期的速度为1.95 m/s,低速期的送风速度为1.05 m/s,这一送风工况即为热舒适最优工况。
| 表 4 熵权法确定指标权重 Table 4 The weight of indexes determined by entropy weight method |
| 表 5 排名结果 Table 5 The ranking results |
1) 脉动送风可以在前后排都实现高速时期和低速时期的热舒适差异,热感觉TAPMV和吹风感TAPD的差异,从而刺激人体的冷热感受器官,带来较舒适的感觉。
2) 送风速度越高,TAPMV越低,TAPD越高;高速期时长与低速期时长之比越高,高速期TAPD越高,高速期和低速期的TAPMV差异和TAPD差异越大。
3) 利用TOPSIS法进行多目标优化可知,当高速期时长与低速期时长之比为1,高速期的速度为1.95 m/s,低速期的送风速度为1.05 m/s时,热舒适综合评价最优。
| [1] |
何璇, 罗缘, 刘猛, 等. 昆明市地铁站设备与管理用房冬季室内热环境实测分析[J]. 土木与环境工程学报(中英文), 2019, 41(6): 158-166. He X, Luo Y, Liu M, et al. Measurement and analysis of winter indoor thermal environment of facility room in subway stations in Kunming[J]. Journal of Civil and Environmental Engineering, 2019, 41(6): 158-166. (in Chinese) |
| [2] |
Cheng Y, Fong M L, Yao T, et al. Uniformity of stratum-ventilated thermal environment and thermal sensation[J]. Indoor Air, 2014, 24(5): 521-532. DOI:10.1111/ina.12097 |
| [3] |
Zhang S, Cheng Y, Huan C, et al. Modeling non-uniform thermal environment of stratum ventilation with supply and exit air conditions[J]. Building and Environment, 2018, 144: 542-554. DOI:10.1016/j.buildenv.2018.08.063 |
| [4] |
Kong X F, Xi C, Li H, et al. A comparative experimental study on the performance of mixing ventilation and stratum ventilation for space heating[J]. Building and Environment, 2019, 157: 34-46. DOI:10.1016/j.buildenv.2019.04.045 |
| [5] |
Kong X F, Xi C, Li H, et al. Multi-parameter performance optimization for whole year operation of stratum ventilation in offices[J]. Applied Energy, 2020, 268: 114966. DOI:10.1016/j.apenergy.2020.114966 |
| [6] |
WigÖ H. Effects of intermittent air velocity on thermal and draught perception during transient temperature conditions[J]. International Journal of Ventilation, 2008, 7(1): 59-66. DOI:10.1080/14733315.2008.11683799 |
| [7] |
Zhu Y X, Luo M H, Ouyang Q, et al. Dynamic characteristics and comfort assessment of airflows in indoor environments: a review[J]. Building and Environment, 2015, 91: 5-14. DOI:10.1016/j.buildenv.2015.03.032 |
| [8] |
狄育慧, 王善聪. 动态条件下不同气流组织形式对人体热舒适的影响[J]. 暖通空调, 2014, 44(8): 106-109. Di Y H, Wang S C. Impact of different air distribution forms on human thermal comfort under dynamic conditions[J]. Heating Ventilating & Air Conditioning, 2014, 44(8): 106-109. (in Chinese) |
| [9] |
Tian X, Zhang S, Lin Z, et al. Experimental investigation of thermal comfort with stratum ventilation using a pulsating air supply[J]. Building and Environment, 2019, 165: 106416. DOI:10.1016/j.buildenv.2019.106416 |
| [10] |
Chen Q Y. Ventilation performance prediction for buildings: a method overview and recent applications[J]. Building and Environment, 2009, 44(4): 848-858. DOI:10.1016/j.buildenv.2008.05.025 |
| [11] |
van Hooff T, Blocken B. Mixing ventilation driven by two oppositely located supply jets with a time-periodic supply velocity: a numerical analysis using computational fluid dynamics[J]. Indoor and Built Environment, 2020, 29(4): 603-620. DOI:10.1177/1420326X19884667 |
| [12] |
Wu C F, Ahmed N A. A novel mode of air supply for aircraft cabin ventilation[J]. Building and Environment, 2012, 56: 47-56. DOI:10.1016/j.buildenv.2012.02.025 |
| [13] |
Koufi L, Younsi Z, Cherif Y, et al. A numerical study of indoor air quality in a ventilated room using different strategies of ventilation[J]. Mechanics & Industry, 2017, 18(2): 221. |
| [14] |
Shao X L, Wang K K, Li X T, et al. Potential of stratum ventilation to satisfy differentiated comfort requirements in multi-occupied zones[J]. Building and Environment, 2018, 143: 329-338. DOI:10.1016/j.buildenv.2018.07.029 |
| [15] |
马建垒. 三种主要通风空调送风方式下室内热舒适性模拟[D]. 重庆: 重庆大学, 2015. Ma J L. Comparison of indoor thermal comfort with three main air supply modes[D]. Chongqing: Chongqing University, 2015. (in Chinese) |
| [16] |
Assaad D A, Habchi C, Ghali K, et al. Effectiveness of intermittent personalized ventilation in protecting occupant from indoor particles[J]. Building and Environment, 2018, 128: 22-32. DOI:10.1016/j.buildenv.2017.11.027 |
| [17] |
Wang H Q, Huang C H, Liu Z Q, et al. Dynamic evaluation of thermal comfort environment of air-conditioned buildings[J]. Building and Environment, 2006, 41(11): 1522-1529. DOI:10.1016/j.buildenv.2005.06.002 |
| [18] |
杨振宏, 李盼. 基于熵权法-TOPSIS法的建筑施工人员风险感知水平研究[J]. 建设科技, 2020(Z1): 133-137. Yang Z H, Li P. Research on risk perception level of construction workers based on entropy weight-TOPSIS method[J]. Construction Science and Technology, 2020(Z1): 133-137. (in Chinese) |
| [19] |
Mao N, Song M J, Deng S M. Application of TOPSIS method in evaluating the effects of supply vane angle of a task/ambient air conditioning system on energy utilization and thermal comfort[J]. Applied Energy, 2016, 180: 536-545. DOI:10.1016/j.apenergy.2016.08.011 |
| [20] |
Zhang S, Lin Z, Ai Z T, et al. Multi-criteria performance optimization for operation of stratum ventilation under heating mode[J]. Applied Energy, 2019, 239: 969-980. DOI:10.1016/j.apenergy.2019.01.248 |
| [21] |
ISO 7730: Ergonomics of the Thermal Environment-Analytical Determination and Interpretation of Thermal Comfort Using Calculation of the PMV and PPD Indices and Local Thermal Comfort Criteria[S]. ISO, Geneva, Switzerland, 2005.
|
 2021, Vol. 44
2021, Vol. 44


