2. 重庆大学 计算机学院, 重庆 400044
2. College of Computer Science, Chongqing University, Chongqing 400044, P. R. China
物流配送对规模和时效性要求越来越高,物流车辆路径优化问题显得极其重要,合理的车辆路径规划方案可以为企业节省大量配送成本。另一方面,传统物流车辆已造成严重的污染物排放问题,而物流汽车电动化是解决排放治理的重要手段,但电动物流车最大的问题在于配送里程焦虑。考虑物流总路程、用户时间窗口、总时间的条件下,提出一种加权AP聚类的非支配排序遗传算法(AP-NSGA-Ⅱ)来解决电动物流车的路径优化配送问题。
电动物流车物流配送大部分关注的是路径优化。葛显龙等[1]运用混合模拟退火算法研究了灵活充电策略带时间窗口的电动物流车的配送问题,Schneider和Stenger等[2]在VRP条件下,通过车载电池容量的增加,搭建了电动物流车的车辆路径优化问题,并建立电动汽车数量最小和路径最短的多目标,寻求最优行驶路径。Lim和Kuby[3]基于公共设施的选址问题,提出电动汽车的能源补充设施选址模型。冯智泉等[4]应用蚁群算法对分段路线进行优化,在全局充电方案中加入行驶路径的约束,将两部分结合形成全局的最优行驶路径。文展等[5]提出一种改进的粒子群优化算法解决离散域的组合优化问题及车辆路径规划。但这些方法普遍存在以下问题:1)随着配送点的增加,车辆路径可行解呈阶乘增长,使用启发式或者亚启发式算法的求解效率低,且容易陷入局部最优,贪婪随机自适应搜索算法等[6-10];2)大多数车辆路径问题的优化目标函数较少,不切合现实场景需求,未考虑相关变量的相互关系,导致实际应用的局限性[11-14]。3)电动物流车的里程焦虑问题,限制了每辆电动物流车路径规划的最长距离,导致电动物流车的用车数量增加,综合用车成本增加[15-17]。
研究提出一种改进的非支配遗传算法(AP-NSGA-Ⅱ)解决大规模物流电动车的路径规划问题,根据配送点的分布,采用先聚类再并行优化的方式解决多目标问题,聚类采用带权AP算法,并行多目标优化采用改进的非支配排序算法得到初始配送方案。避免了初始配送方案的随机性和盲目性,同时也降低了算法的执行复杂度。在初始路径规划的基础上执行邻近配送点搜索进行局部重构,以获得最终配送方案。最后根据配送点的权值大小,优选配送路途充电策略。
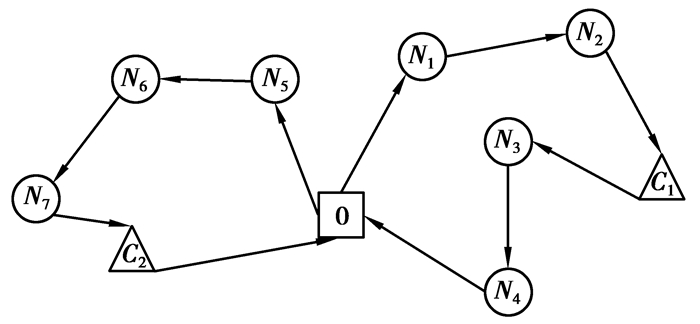
1 问题描述在已知区域内有一定数量的配送点和充电站,从物流中心出发,若干辆电动物流车对所有配送点进行双向货物配送,在配送过程中,要综合考虑配送点的分布和充电站的地理位置,当电动物流车的电池余量不足完成剩余配送,则寻求最适合的充电站进行充电,以满足配送任务,考虑总路程、时间窗口和总时间的多目标优化问题。图 1展示了典型电动物流车的配送场景,其中0为配送中心,N1~N7为配送点,C1, C2为充电站。
|
图 1 途中充电策略示意图 Fig. 1 An illustration of en-route charging strategy |
实际场景中大规模电动物流车配送问题较为复杂,比如路况拥堵,电池衰减、货物体积容量,人力成本计算等,这些都是影响配送结果的因素。为了简化模型,做如下假设:
1) 每辆电动物流车从配送中心出发最终回到配送中心,形成环路;
2) 每个配送点的送货量和取货量不能大于电动物流车的最大载货量;
3) 仅考虑货物的重量,不考虑货物的体积容量;
4) 每辆电动物流车的电池容量、行驶速度、充电系数等参数配置一致;
5) 电动物流车的行驶距离、充电时长与电池容量呈线性关系;
6) 每个充电站能多次被访问,且无等待时间
7) 不考虑交通拥堵、车辆故障等特殊因素,且配送过程的车速是均匀的;
8) 每个配送点的装卸货时长为0,仅考虑路途时间和充电时间。
AP-NSGA-Ⅱ算法的思想:以充电桩为重要潜在聚类中心,根据各配送点的取送货量为权值,执行加权AP算法以获得配送点的聚类中心,各簇执行NSGA-Ⅱ多目标算法,并考虑电池笑话以获得最终配送方案。数学符号如表 1所示。
| 表 1 数学符号及含义 Table 1 Mathematical symbols and meaning |
AP(affinity propagation)算法称为邻近传播算法或者亲和度传播算法,其基本思想是将所有数据点看成潜在的聚类中心,根据点与点之间的距离自主划分聚类区域,算法中每一个点的权重等值。作为大规模的电动物流车的配送问题,区域划分可以明显降低计算复杂度。由于配送点和充电站的权重不等价,在考虑配送和充电方案时,区域的划分不能简单自主聚类,通过设置每个点的权重来控制AP聚类结果。配送点i的权重设置为送货量和取货量之和,即Di+Ri,充电桩的权值设置为所有配送点权值的最大值max{Di+Ri}, i∈N∪C。加权AP算法的初始化相似度矩阵S的各元素为
| $ s(i, k)=-\frac{\sqrt{\left(x_{i}-x_{k}\right)^{2}+\left(y_{i}-y_{k}\right)^{2}}}{\left(D_{i}+R_{i}\right) \times\left(D_{k}+R_{k}\right)}, i \neq k, $ | (1) |
式中:s(i, k)表示第i个配送点到第k个配送点的带权欧式距离的负值,当i=k时,更新相似度矩阵S对角线的值为相似度矩阵中所有值的最小值;
初始化吸引度矩阵R为0矩阵,其中r(i, k)描述了配送点k作为配送点对象i的聚类中心的程度,初始化归属度矩阵A为0矩阵,其中a(i, k)描述了配送点i选择配送点k作为聚类中心的合适程度。
更新吸引度矩阵R
| $ r_{t+1}(i, k)=\left\{\begin{array}{c} s(i, k)-\max \limits_{j \neq k}\left\{a_{t}(i, j)+r_{t}(i, j)\right\}, i \neq k \\ s(i, k)-\max \limits_{j \neq k}\{s(i, j)\}, i=k \end{array},\right. $ | (2) |
式中:t为迭代序号;j表示除配送点k的任意一个配送点;r(i, k)表示配送点k成为配送点i的聚类中心的证明,如果r(i, k)>0,越大表示配送点k成为聚类中心的能力越强。
更新归属度矩阵A,
| $ a_{t+1}(i, k)=\left\{\begin{array}{c} \min \left\{0, r_{t+1}(k, k)+\sum\limits_{j \neq i, k} \max \left\{r_{t+1}(j, k), 0\right\}\right\}, i \neq k \\ \sum\limits_{j \neq k} \max \left\{r_{t+1}(j, k), 0\right\}, i=k \end{array},\right. $ | (3) |
式中:a(i, k)分为两种情况: 当i≠k时,取所有大于0的吸引度累加,加配送点k作为聚类中心的可能性与0之间的小值; 当i=k,表示所有其他配送点传递给配送中心k的正吸引度的累加。
根据衰减系数λ对吸引度矩阵和归属度矩阵进行更新,所述衰减系数λ为[0, 1]之间的正数;
| $ \begin{aligned} &r_{t+1}(i, k)=\lambda \times r_{t}(i, k)+(1-\lambda) \times r_{t+1}(i, k) \\ &a_{t+1}(i, k)=\lambda \times a_{t}(i, k)+(1-\lambda) \times a_{t+1}(i, k) \end{aligned}, $ | (4) |
重复执行式(2)~式(4),直到吸引度矩阵R和归属度矩阵A稳定并不再更新,当r(k, k)+a(k, k)>0就认为是配送点k是一个聚类中心,再根据其他配送点到聚类中心的最短欧式距离划分各簇,最终划分为M个簇。
2.3 电动物流车路径规划利用加权AP算法把大规模的配送点和充电桩进行划分后,在簇内执行考虑充电策略的改进NSGA-Ⅱ算法。建立以簇内电动物流车的总路程、簇内电动物流车行驶总时间、簇内时间惩罚成本为最小的多目标优化函数。
| $ f_{1}=\sum\limits_{k \in K, i \in N, j \in N} x_{i j k}, $ | (5) |
| $ f_{2}=\sum\limits_{k \in K, i \in N, j \in N} \frac{d_{i j}}{s} x_{i j k}+\sum\limits_{i \in C} t f_{i}, $ | (6) |
| $ f_{3}=e_{p} \sum\limits_{i \in N} \max \left(t_{i}-e_{i}, 0\right)+l_{p} \sum\limits_{i \in N} \max \left(l_{i}-t_{i}, 0\right), $ | (7) |
| $ \text { s.t. } \sum\limits_{j \in N, i \neq j} x_{i j k}=1, \forall i \in N, k \in K, $ | (8) |
| $ \sum\limits_{j \in V, i \neq j} x_{0 j k} 1, k \in K , $ | (9) |
| $ \sum\limits_{i \in V, i \neq j} x_{j i k}-\sum\limits_{i \in V, i \neq j} x_{i j k}=0, \forall j \in V, k \in K, $ | (10) |
| $ L_{i-1}+\left(R_{i}-D_{i}\right) L, \forall i \in N, $ | (11) |
| $ Q_{i} \sum\limits_{j \in V} c a \cdot d_{i j} \cdot x_{i j k}, \forall i \in V, k \in K , $ | (12) |
| $ Q_{i}+g \cdot t f_{i} Q, \forall i \in C, $ | (13) |
| $ x_{i j k} \in\{0 ; 1\}, \forall i \in V, \forall j \in V, k \in K, $ | (14) |
| $ y_{i k} \in\{0 ; 1\}, \forall i \in V, k \in K, $ | (15) |
式(5)~式(7)分别为目标函数f1电动物流车的总路程; 目标函数f2电动物流车配送过程花费的时间; 目标函数f3时间惩罚成本的计算;式(8)表示每个配送点仅被电动物流车k服务一次,式(9)表示电动物流车k从配送中心出发只服务一条配送线路,式(10)表示电动物流车k进入某个节点后必须离开。式(11)表示电动物流车在进入配送点i之前的装车容量要满足配送点j的货送货之差。式(12)表示配送车辆k从节点i出发的剩余电池容量Qi要满足到达节点i;式(13)表示电动物流车在充电站i充电后的电池容量不能大于电池最大容量;式(14)和(15)是决策比变量约束。
2.4 非支配排序遗传算法 2.4.1 编码方式本算法采用的智能编码方式为自然数编码,所有节点的编码方式为自然数,配送中心为0,对配送点和充电站依次进行编码:1, 2, 3, 4, 5, …, m。在某个簇的配送网络中,如有10个配送点编号依次为1到10,2个充电站编号为11和12,若使用2辆电动物流车进行配送活动,一条完整个体编码形式为:0→8→3→12→4→0→1→10→11→5→7→9→6→2→0,其中,0→8→3→12→4→0和0→1→10→11→5→7→9→6→2→0分别表示两条完整的配送环路,前一条环路展示了电动物流车从配送中心0出发,依次经过了配送点8和3,然后在充电站12进行充电后,再经配送点4,最后返回配送中心。
| NSGA-Ⅱ的工作原理的伪代码所示,算法如下 |
初始化个体编码的基本思想为:以电动物流车所在位置的作为参照中心,随机选取离车辆最近的h个配送点的其中一个进行配送,按照同一规则依次把配送点加入个体序列,再根据电动物流车的载货量和电池容量,分配车辆和插入充电站,具体步骤如下:
步骤1:获取配送中心和簇内各配送点的坐标信息,计算簇内各配送点之间的欧式距离
步骤2:车辆从配送中心出发,从最近的h个配送点随机选取1个作为下一个配送点,即vm1=rand(
步骤3:然后再从vm1出发,按照步骤2规则,选取下一个配送点vm2,直到遍历完簇m内所有的配送点,最后回到配送中心,形成一条环路;
步骤4:根据电动物流车的载货量和电池容量约束以及充电站的位置信息,进行车辆分配和插入充电站,生成一条符合配送要求的个体;
步骤5:重复操作步骤2~4,生成满足约束条件的
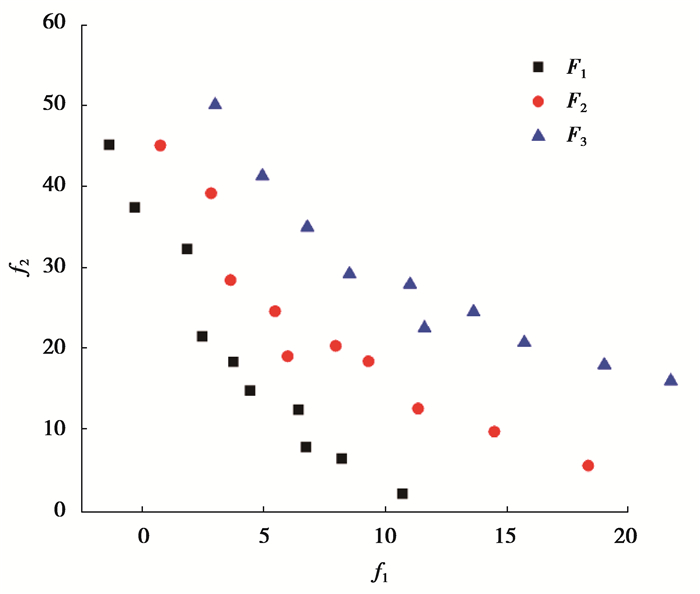
根据式(5)~式(7)的目标函数,比较任意2个体之间的支配和非支配关系,找到种群中所有支配个体数为0的个体,并保存在当前集合F1中,对于F1中的每一个个体i其所支配的个体集合为Si,遍历Si中的每一个个体b,执行递减步骤,如果执行完毕,将个体b保存在集合中H;在F1中得到的个体为第一个非支配层个体,并以H作为当前集合,重复操作得到F2, F3…,直到初始种群的个体关系被全部分层,示意图如2所示。
|
图 2 初始种群的个体关系 Fig. 2 Individual relations of the initial population |
遗传操作包括:个体的选择、交叉、变异,从而产生新种群。由于考虑充电策略和充电站的分布,遗传操作首先是删除充电站进行操作,最后再根据耗电量插入序列。
a) 选择操作尽量选择质量较优的父代个体,以ps的概率选择父代,根据各层的非支配关系,选择概率为pF1s>pF2s>pF3s,其中pF1s表示的集合F1选择父代个体的概;
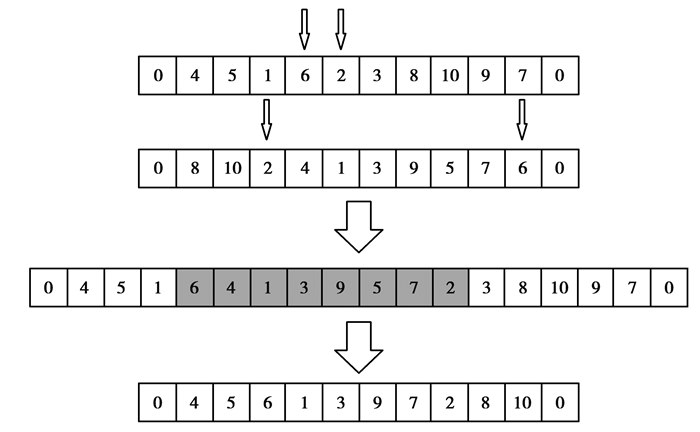
b) 交叉操作:从父代中选择差异性最大2个的父代交叉产生下一代个体,交叉的原则以一个父代中节点i和j为相邻最近的配送点,另外一个父代中节点i和j为相邻最远的2个配送点,如图 3所示,2个父代的区域进行交换,把序列最长的子代随机删除重复配送点后得到新的子代;
|
图 3 交叉操作 Fig. 3 Cross-over operation |
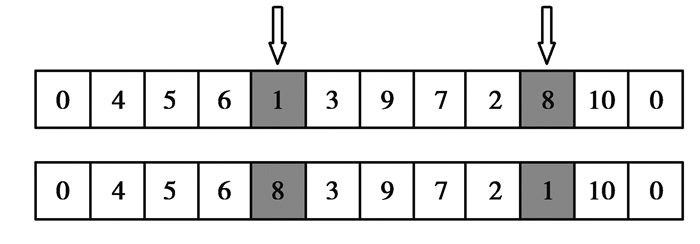
c) 变异操作:父代的序列按照概率pm随机生成2不相等的自然数,进行变异操作,把父代中的两个配送点的位置调换,得到新的子代,如图 4所示;
|
图 4 变异操作 Fig. 4 Mutation operation |
如果遗传操作后新子代的目标函数小于之前的子代则保留,否则丢弃,依次生成N个,得到新一代种群,把父代和新一代种群合并形成2N的候选种群;
2.4.5 拥挤距离计算拥挤距离的计算保证了种群多样性,同时也是为了使得多目标的解在目标中间更加均匀。首先分别在3个目标函数下计算个体i在同一层中与相邻2个个体的平均距离,即以个体i+1和i-1为对角线形成的长度。如果长度越大则表示个体i与相邻点的拥挤距离越大,即多样性越好,就越应该保留,以防止局部最优的出现。通过遗传操作生成新的子代也使得pareto前沿更均匀。
3 仿真分析与验证 3.1 实验方法及算例场景设计为验证本算法对路径规划和充电策略的有效性, 在考虑实际场景容量和规模的情况下, 指定1个配送中心、随机生成90个配送点和10个充电站,以及配送点对应的装卸货物量、服务的起止时间进行仿真分析。主要条件包含:电动物流车的最大载货量为4 t,车载电池的最大容量Q为40 kWh; 每辆电动物流车的最大行驶距离Dis=150 km, 而配送车辆的电能消耗与行驶距离成正比,消耗速率ca为3.75 km/KWh; 电动物流车的行驶速度s为40 km/h。时间窗惩罚成本系数ep为10元/h; lp为20元/h,时间窗口小于0.5 h忽略惩罚,大于0.5 h记为1 h。部分节点如表 2所示:其中0代表配送中心,序号表示配送点。
| 表 2 部分节点的详细信息 Table 2 Details of some nodes |
为了验证实验的有效性,并定性分析与其他方法的优势,加权AP聚类算法与NSGA-Ⅱ的参数设置如下:衰减系数设置为0.5,聚类算法最大迭代次数为200次,聚类中心无变化,迭代为15次。最近距离的配送点h设置为5,每个簇初始化种群数为100个,各层选择操作的ps值为0.8,每次递减0.1,交叉系数设置为0.8,变异系数设置为0.5,与NSGA-Ⅱ比较的其他优化算法的参数设置为:MOEA/D[18],COEA[19],AMOSA[20],MOEA/D的初始种群数大小为100,每一个子问题对应的领域大小为20,COEA外部档案大小为100,AMOSA外部档案大小也为100,初始温度为100,冷却系数为0.95,结束温度为2.5×10-6。
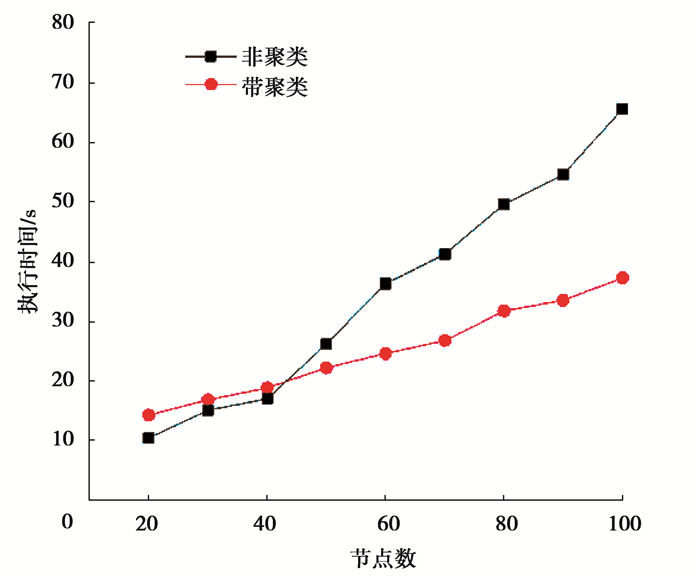
3.3 加权AP聚类算法分析聚类是为了降低多目标优化的计算复杂度。在不考虑充电站的情况下,分析带聚类算法的多目标优化与不带聚类算法的差异。验证聚类方法对路径规划算法的优越性。实验分别以配送点数量为200以下规模来测试带聚类算法的NSGA-Ⅱ与不带聚类算法的NSGA-Ⅱ的时间复杂度的区别。NSGA-Ⅱ分别独立执行50次的平均时间为基准,多目标优化的运行时间分别如图 5所示:可以明显看出,不带聚类的NSGA-Ⅱ运行时间与带聚类的算法,当配送点在40个以下差异小,当配送点40数量在以上时,NSGA-Ⅱ的计算复杂度为O(N2)呈指增长,增长速度,带聚类算法呈线性增长。
|
图 5 聚类与非聚类的执行时间比较 Fig. 5 Comparison of execution time between clustering and non-clustering |
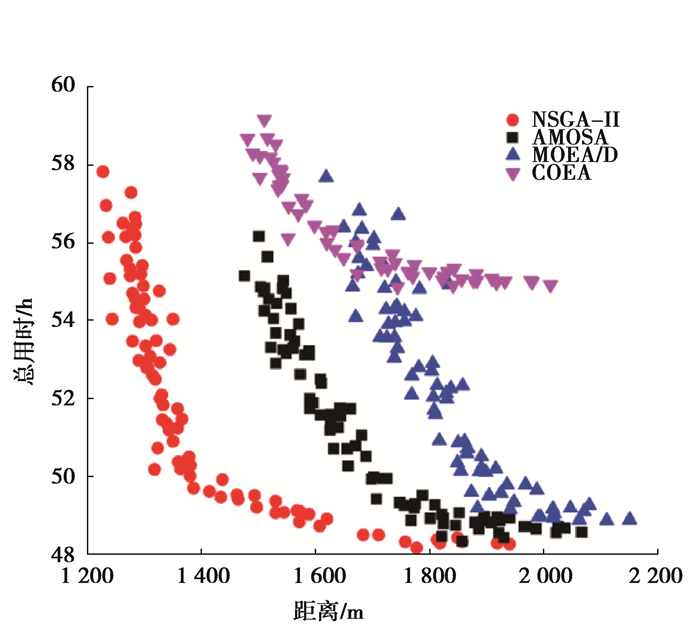
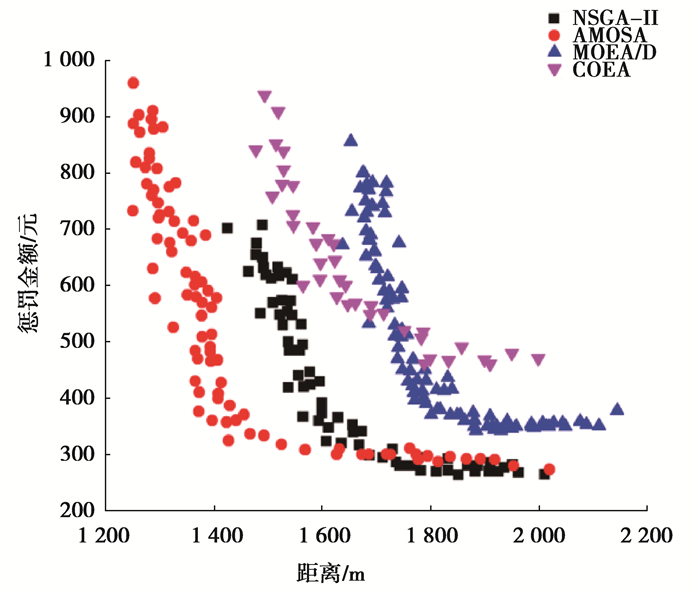
4个多目标优化算法设置为电动物流车到达充电站后,执行满充操作。图 6给出了4种算法在f1~f2和f1~f3从三维映射到二维平面最终非支配解集前沿,在f1~f2总距离和总用时的关系图中可以看出,带AP聚类的NSGA-Ⅱ算法求解路径规划时能在收敛性和多样性上取得较好的效果,该算法的前沿要明显优于其他3种算法,在前沿的两端,优化集合中最短总路径能达到1 277 km,总用时为57.2 h,当优先考虑总用时的情况下,总用时为48.26 h,总距离为1 938.75, km,而其他3种算法AMOSA优化集中最短路径为1 475.59 km,MODEA/D的前沿的最短路径为1 648.4 km,COEA则为1 490.2 km,由此可以分析得出该算法比其他3种算法更好平衡距离和总用时的关系。同样,图 7是f1~f3距离和总惩罚金额的非支配解集前沿,AP-NSGA-Ⅱ大部分的前沿优于其他算法,虽然在总距离区间[1 800-2 000]的惩罚金额,AMOSA算法稍优于AP-NSGA-Ⅱ算法,但是总体来说,本算法在3个目标函数上表现优于其他算法。
|
图 6 距离与总时间的关系 Fig. 6 The relationship between distance and total time |
|
图 7 距离与惩罚金额的关系 Fig. 7 The relationship between distance and penalty amount |
电动物流车在配送过程中,满充情况下势必增加单条路径时间和总时间,时间的增加会带来惩罚成本的增加。考虑满充电情况的执行效果,根据充电站的位置和聚类程度,把它当成配送量为0的配送站进行访问,不单独考虑它为充电站,当经过充电站后进行满充操作以保证后续的行驶。为考察充电策略下的对目标函数的影响,将充电站节点不规划到多目标的路径中,以行驶距离消耗电量为条件,寻找最近的充电站,以满足后续配送的方式进行配送。
按照聚类结果选取3条典型的配送子线路,按照满充和部分充电来分析不同充电策略对配送的影响,结果如表 3所示。
| 表 3 满充电和部分充电策略的比较 Table 3 Comparison of full charge and partial charge strategies |
对于车辆编号1的线路,在满充情况下,行驶距离为204.32 km,总用时为5.79 h,到达编号100的充电站后,执行100%充电后进行完成剩余线路;在部分充电情况下,编号1车辆的原始规划路线为0→42→22→1→90→63→35→6→5→55→3→56→40→16→0,在到达编号56的配送点后,再去适配充电站,编号100的充电站加入节点56和40之间,电动物流车的充电率为18.56%,行驶距离为177.83 km,用时为4.81 h。相同地,车辆编号2满充和部分充电率为分别是100%和23.32%,距离分别为184.98 km和160.35 km,用时分别为5.20 h和5.09 h。车辆编号3在满充设置下编号92被规划到路径中,在部分充电情况下,由于行驶距离小于150 km而不需要充电,他们的行驶距离分别是109.74 km和104.74 km,时间分别为3.39 h和2.62 h。
4 结论基于聚类非支配排序算法(AP-NSGA-Ⅱ)来解决电动物流车的多目标路径优化问题,建立了一种充电策略,通过设计加权AP聚类划分配送簇,避免了初始种群的随机性和盲目性,同时,聚类簇内配送点的规模降低了非支配排序算法的运行时间和复杂度,并根据充电站的分布和距离关系,电动物流车执行部分充电策略。最后,通过仿真实验证明该算法的有效性,比较了电动物流车满充和部分充电条件的差异性。
| [1] |
葛显龙, 李祖伟, 葛小波. 考虑灵活充电策略的带时间窗物流配送路径优化研究[J]. 控制理论与应用, 2020, 37(6): 1293-1301. Ge X L, Li Z W, Ge X B. Research on logistics distribution route optimization with time window considering flexible charging strategy[J]. Control Theory & Applications, 2020, 37(6): 1293-1301. (in Chinese) |
| [2] |
Keskin M, Akhavan-Tabatabaei R, Çatay B. Electric vehicle routing problem with time windows and stochastic waiting times at recharging stations[J]. 2019 Winter Simulation Conference (WSC), 2019, 1649-1659. |
| [3] |
Lim S, Kuby M. Heuristic algorithms for siting alternative-fuel stations using the Flow-Refueling Location Model[J]. European Journal of Operational Research, 2010, 204(1): 51-61. DOI:10.1016/j.ejor.2009.09.032 |
| [4] |
冯智泉, 黄亦翔, 李杰, 等. 蚁群算法求电动汽车最优行驶路径与充电方案[J]. 机电一体化, 2013, 19(8): 43-48. Feng Z Q, Huang Y X, Li J, et al. Ant colony algorithm for EV path and charging optimization[J]. Mechatronics, 2013, 19(8): 43-48. (in Chinese) DOI:10.3969/j.issn.1007-080x.2013.08.007 |
| [5] |
文展, 唐康健, 李文藻. 一种改进粒子群优化算法在车辆路径问题的应用研究[J]. 重庆邮电大学学报(自然科学版), 2020, 32(5): 891-897. Wen Z, Tang K J, Li W Z. Research on application of vehicle routing problem using an enhanced particle swarm optimization[J]. Journal of Chongqing University of Posts and Telecommunications (Natural Science Edition), 2020, 32(5): 891-897. (in Chinese) |
| [6] |
Pillac V, Gendreau M, Guéret C, et al. A review of dynamic vehicle routing problems[J]. European Journal of Operational Research, 2013, 225(1): 1-11. DOI:10.1016/j.ejor.2012.08.015 |
| [7] |
Mourão M C, Almeida M T. Lower-bounding and heuristic methods for a refuse collection vehicle routing problem[J]. European Journal of Operational Research, 2000, 121(2): 420-434. DOI:10.1016/S0377-2217(99)00045-4 |
| [8] |
Bräysy O, Gendreau M. Vehicle routing problem with time windows, part I: route construction and local search algorithms[J]. Transportation Science, 2005, 39(1): 104-118. DOI:10.1287/trsc.1030.0056 |
| [9] |
Kritikos M N, Lappas P Z. Computational intelligence and combinatorial optimization problems in transportation science[J]. Advances in Core Computer Science-Based Technologies, 2021, 325-367. DOI:10.1007/978-3-030-41196-1_15 |
| [10] |
钱小宇, 葛洪伟, 周竞, 等. 基于扩容和双距离决策的多目标粒子群优化算法[J]. 重庆邮电大学学报(自然科学版), 2020, 32(3): 368-376. Qian X Y, Ge H W, Zhou J, et al. Multi-objective particle swarm optimization algorithm based on expansion and dual distance[J]. Journal of Chongqing University of Posts and Telecommunications (Natural Science Edition), 2020, 32(3): 368-376. (in Chinese) |
| [11] |
潘斌斌. 多目标路径规划问题的算法综述[J]. 重庆工商大学学报(自然科学版), 2012, 29(5): 78-84. Pan B B. Review of the algorithms of multi-objective routing programming problems[J]. Journal of Chongqing Technology and Business University (Natural Science Edition), 2012, 29(5): 78-84. (in Chinese) DOI:10.3969/j.issn.1672-058X.2012.05.016 |
| [12] |
Rabani M, Manavizadeh N, Boostani A, et al. A multi-objective model for the residential waste collection location-routing problem with time windows[J]. Journal of Industrial and Systems Engineering, 2020, 12(4): 227-241. |
| [13] |
Mirabi M, Shokri N, Sadeghieh A. Modeling and solving the multi-depot vehicle routing problem with time window by considering the flexible end depot in each route[J]. International Journal of Supply and Operations Management, 2016, 3(3): 1373-1390. |
| [14] |
Miranda D M, Branke J, Conceição S V. Algorithms for the multi-objective vehicle routing problem with hard time windows and stochastic travel time and service time[J]. Applied Soft Computing, 2018, 70: 66-79. DOI:10.1016/j.asoc.2018.05.026 |
| [15] |
Erdelić T, Carić T. A survey on the electric vehicle routing problem: variants and solution approaches[J]. Journal of Advanced Transportation, 2019, 2019: 1-48. |
| [16] |
Raeesi R, Zografos K G. The electric vehicle routing problem with time windows and synchronised mobile battery swapping[J]. Transportation Research Part B: Methodological, 2020, 140: 101-129. DOI:10.1016/j.trb.2020.06.012 |
| [17] |
Breunig U, Baldacci R, Hartl R F, et al. The electric two-echelon vehicle routing problem[J]. Computers & Operations Research, 2019, 103: 198-210. |
| [18] |
Zhang Q F, Li H. MOEA/D: a multiobjective evolutionary algorithm based on decomposition[J]. IEEE Transactions on Evolutionary Computation, 2007, 11(6): 712-731. DOI:10.1109/TEVC.2007.892759 |
| [19] |
Goh C K, Tan K C. A competitive-cooperative coevolutionary paradigm for dynamic multiobjective optimization[J]. IEEE Transactions on Evolutionary Computation, 2009, 13(1): 103-127. DOI:10.1109/TEVC.2008.920671 |
| [20] |
Bandyopadhyay S, Saha S, Maulik U, et al. A simulated annealing-based multiobjective optimization algorithm: AMOSA[J]. IEEE Transactions on Evolutionary Computation, 2008, 12(3): 269-283. DOI:10.1109/TEVC.2007.900837 |
 2021, Vol. 44
2021, Vol. 44

