2. 成都文理学院, 成都 610400;
3. 重庆工程学院, 重庆 400065
2. Chengdu College of Arts and Sciences, Chengdu 610400, P. R. China;
3. Chongqing Institute of Engineering, Chongqing 400065, P. R. China
近年来, 云计算凭借其低成本、配置灵活和资源利用效率高的优势, 正在以极快的速度兴起。在云计算[1-2]中, 其资源的分配一直是研究的重点, 云计算的用户可以根据自己的需求来付费和购买适合的资源,从而最大程度节省了成本,给用户带来了更好体验。因此,就如何规划、利用庞大的云计算资源问题, 国内外学者从自己的研究中提出了相应的观点。方秋义等[3]采用一种满足一定条件下的低成本和低负载的资源分配策略,以此实现系统的负载均衡;李志敏等[4]通过在云计算资源算法中引入人工蜂群算法,算法收敛精度提高,使云计算资源分配的效率提升;魏杰等[5]将针对数据密集型应用的虚拟资源分配, 提出云环境下时延敏感的虚拟机放置方法, 该方法可以有效地降低总数据传输时延和最大数据传输时延,获得较优的云计算资源,从而节省运营成本;蔡晓丽等[6]设计了一种改进的粒子群算法,通过改进粒子迭代过程中社会项系数和认知项系数的权重变化, 使算法更符合最优解的求解规律, 避免陷入局部最优解,以此提高资源分配的准确性;王英等[7]提出了一种基于生产函数的云服务提供商收益最大化同时兼顾用户满意度的资源调度算法,合理规划云服务器所有资源, 最大程度优化配置资源; 然后结合用户请求,解决了云数据中心资源利用率低、云服务提供商收益低的问题。
这些算法虽然能够成功地完成云计算的资源分配, 但由于云计算技术的飞速发展,用户对其使用的需求日益提高,用户在关注任务是否能完成的同时,更加注重于完成调度的成本和时间等。在现有研究基础之上,将传统蚁群算法进行改良得到改进的蚁群优化算法(improved ant colony optimization algorithm), 使算法的效率明显提高。在处理云计算资源分配方面的问题时有了明显的提升,在减少成本的同时节省了任务所需要的时间,仿真模拟实验说明算法在处理云计算资源分配方面问题时拥有较好的优越度[8]。
1 调度算法描述调度算法是云计算资源调度的核心技术,优秀的调度算法可以保证云计算资源调度的高效性和合理性,因此引入传统的蚁群算法,并对其进行优化和改进,实现高效资源调度[9-13]。
蚁群算法(AG)[14-20]是一种模拟蚂蚁觅食行为的模拟优化算法,它是由意大利学者Dorigo M等于1991年首先提出,并首先使用在解决TSP(旅行商问题)上。自然界中的蚂蚁从巢穴出发觅食,通常会在通过的路径上留下大量的信息素来引导后面的蚂蚁,路径上信息素积累的越多,其使之后的蚂蚁选择该路径的概率也就越大,传统的蚁群算法到最后往往会出现几条路径的信息素高于其他路径的情况,如果每只蚂蚁都将任务分配给信息素浓度最高的节点处理,那么就会出现搜索停滞现象。也就是算法收敛速度过快导致的局部最优解,从而无法得到全局最优解。因此需要对传统的蚁群算法进行改进和优化,以发现全局最优解。在传统的蚁群算法运算的前期阶段中各路径的信息素含量差距不明显,则蚂蚁就更倾向于选择路程较短的路径,这就让距离较短的路径更容易被后来的蚂蚁选择, 导致盲目而局部的搜索,因此为了避免这种情况的出现,为此,在传统的蚁群算法基础之上加入随机选择机制, 扩大全局寻优能力,增加解的多样性, 设置由参数q0控制伪随机比率,表示如下
| $ z=\left\{\begin{array}{l} \arg _{i \in {\rm { allowe }}d_k} \max \left[\tau_{i j}^{\alpha}(t) \eta_{i j}^{\beta}(t)\right], q \leqslant q_{0} \\ C q>q_{0} \end{array},\right. $ | (1) |
式中:q0在[0, 1]范围内并且是属于正态分布的随机数,q是属于[0, 1]区间的一个常量,当q≤q0时,选择下一节点为所有可选择节点中的τijα(t)ηijβ(t)最大值,当q>q0C根据下面的概率转移公式(2)计算选择到下一个节点的概率。
| $ P_{i j}^{k}(t)=\left\{\begin{array}{l} \frac{\left[T_{i j}(t)\right]^{\alpha}\left[\eta_{i j}(t)\right]^{\beta}}{\sum\limits_{s \in {\rm { allowe }}d_k}\left[T_{i s}(t)\right]^{\alpha}\left[\eta_{i s}(t)\right]^{\beta}}, j \in \text { allowe } d_{k} \\ 0, \text { otherwise } \end{array}\right. $ | (2) |
| $ \tau_{i j}(t+1)=(1-\rho) \tau_{i j}(t)+\sum\limits_{k=1}^{m} \varDelta \tau_{i j}^{k}(t), $ | (3) |
式中:Pijk(t)表示在t时刻, 第k只蚂蚁从节点i移动到节点j的过程变化;α和β分别表示启发式因子。ρ表示信息素的挥发系数,τij(t)表示第k只蚂蚁从路径i到j上的信息素增量。
2 云计算任务分配问题云计算任务分配问题是将n个任务通过采用的调度算法合理地分配到m个可利用的虚拟节点资源上,并使得任务执行时间最短,所消耗成本最低,同时满足用户Qos需求的过程[21-25]。
2.1 云计算任务模型常见的云计算任务调度算法是将一个任务划分成几个相对独立的子任务,再将每个子任务分配到相应的虚拟资源同时进行计算,最后再将每个计算的结果进行汇总处理,得到最终结果,研究只对上述情况中相对独立的子任务并行计算的情况做出分析, 任务T是包含n个元素的任务集,表示为:T={Task1, Task2…Taski}, Taski代表用户需要处理的任务。
2.2 云计算资源模型云资源模型的计算环境是由一系列结构不同的处理器实例组成[26-30],可表示为:vm={vm1, vm2…, vmj}; vmj为第j个虚拟资源,表示为:vm={vmji·p,vmji·t}, 其中vmji·p和vmji·t分别表示任务Taski在虚拟节点vmj上的执行费用和时间跨度。
2.3 Qos模型在文献[11]中提到,云计算的服务质量(Qos)是衡量用户对云计算满意程度的一种标准。研究将用户的开销需求、任务完成时间需求和任务结果是否有效可用这3个方面的Qos需求纳入考虑范围内,分别建立开支需求适应度因子(payment)、任务完成时间适应度因子(time)和任务结果有效可用性适应度因子(usable)。
2.3.1 用户开支需求适应度因子在分配云计算资源时,假设调度任务到被分配的虚拟节点上,则虚拟节点集合vm={vm1, vm2…, vmj},其中任务Taski对应vmj,且调度任务所需要的费用不得超过用户规定的开支,故资源的分配需要满足以下约束条件
| $ G P=\sum\limits_{i=1}^{n} v m_{i j} \cdot p \leqslant L P, $ | (4) |
式中:GP表示执行任务所需的费用,LP表示用户设置的开支约束, vmij·p表示任务Taski在被分配的虚拟节点上vmj的执行费用。
在资源分配过程中,用户会优先选择执行费用少的虚拟节点资源进行任务。假设所有虚拟节点的费用都是固定的,且各自对应的单位时间价格为cj。故有计费公式:vmji.p=cj·vmji·t,则任务Taski在虚拟节点vmj上的执行费用适应度因子为
| $ \int_{j}^{i} \text { payment }=\left\{\begin{array}{l} \frac{v m_{i j} \cdot p}{p a y_{\max }^{i}-p a y_{\min }^{i}}, p a y_{\max }^{i}-p a y_{\min }^{i} \neq 0 \\ 0, \mathrm{else} \end{array},\right. $ | (5) |
式中:paymaxi和paymini分别表示执行任务Taski的最大开支和最小开支,即paymaxi=max{vmji·p},paymini=min{vmji·p}。故由式(5)得:∫jipayment越小,任务Taski在虚拟节点资源vmj上所需要的费用也就越低。
2.3.2 任务完成时间需求适应度因子在分配云计算资源时,假设调度任务到被分配的虚拟节点上,则虚拟节点集合vm={vm1, vm2,…, vmj},其中任务Taski对应vmj,且调度任务完成时间不得超过用户设置的完成时间需求,故资源的分配需要满足以下约束条件
| $ G T=\sum\limits_{i=1}^{n} v m_{i j} \cdot t \leqslant L T $ | (6) |
式中:GT表示任务实际完成时间;LT表示用户设置的时间长度约束;vmij·t表示任务Taski在被分配的虚拟节点上vmj的完成时间。
在资源分配过程中,用户会优先选择所需完成时间较短的虚拟节点资源进行任务。假设TnE表示的是任务Taski在虚拟节点vmj上预计理想的完成时间长度,starti为任务在虚拟节点上开始执行的时间点,故
| $ \int_{j}^{i} \text { time }=\left\{\begin{array}{l} \frac{v m_{i j} \cdot t}{T_{\max }^{i}-T_{\min }^{i}}, T_{\max }^{i}-T_{\min }^{i} \neq 0 \\ 0, \text { else } \end{array}。\right. $ | (7) |
式中:Tmaxi和Tmini分别表示执行任务Taski的最长完成时间和最短完成时间,即Tmaxi=max{vmij·t},Tmini=min{vmij·t}。故由上式得∫jitime越小,任务Taski在虚拟节点资源vmj上的任务执行的完成时间也就越短。
2.3.3 任务结果有效可用性适应度因子在分配云计算资源时,假设调度任务到被分配的虚拟节点上,则虚拟节点集合vm={vm1, vm2…, vmj},其中任务Taski对应虚拟机vmj,且最终虚拟节点得出的任务结果的有效性和可用程度不得低于用户提出的有效可用性需求,故任务集所用的虚拟节点资源的执行任务的有效可用性必须满足
| $ \mathrm{GU}=\sum\limits_{i=1}^{n} v m_{i j} \cdot u \geqslant \mathrm{LU}, $ | (8) |
其中:GU表示任务集所选的虚拟节点资源运算结果的有效可用性;LU表示用户提出的有效可用性约束;vmij·u表示任务Taski被分配的虚拟节点上vmj计算得到结果的有效可用性。在资源分配过程中,用户会优先选择任务结果有效可用性高的虚拟节点进行资源调度,故任务Taski在经虚拟节点资源vmj运行得出结果的有效可用性适应度因子为
| $ \int_{j}^{i} \mathrm { usable }=\left\{\begin{array}{l} \frac{v m_{i j} \cdot u}{\mathrm { usable }_{\max }^{i}-\mathrm { usable }_{\min }^{i}}, \mathrm { usable }_{\max }^{i}-\mathrm { usable }_{\min }^{i} \neq 0 \\ 0, \text { else } \end{array},\right. $ | (9) |
式中:usablemaxi,usablemini分别表示任务Taski经虚拟节点资源vmj运行得出的结果最大有效可用性和最小有效可用性,表达式为
| $ \operatorname{usable}_{\min }^{i} =\min \left\{\tau m_{i j} \cdot u\right\}, $ | (10) |
| $ \operatorname{usable}_{\max }^{i} =\max \left\{v m_{i j} \cdot u\right\}, $ | (11) |
则∫jiusable的值越大,则任务Taski在虚拟节点资源上运行得出的结果的有效可用性就越强。
2.4 云计算资源调度的综合适应度函数模型综上对用户的QoS需求的分析,根据所得的用户开支需求适应度因子、任务完成时间需求适应度因子和任务结果有效可用性适应度因子,可以得到执行任务、分配虚拟节点资源的综合适应度函数模型如下
| $ F_{j}^{i}=M \cdot \int_{j}^{i} \text { payment }+N \cdot \int_{j}^{i} \text { time }+O \cdot \int_{j}^{i} \text { usable }, $ | (12) |
其中M、N、O分别表示用户开支需求适应度函数(其中0<M<1)、任务完成时间需求适应度函数(其中0<N<1)和任务结果有效可用性适应度函数(其中0<O<1)在总调度因子中所占的权重,并且M+N+0=1。M, N, O表示用户对执行开销、任务完成时间和结果有效可用性的偏向程度。故Fji的值越小,综合了完成时间、执行费用和有效可用性的虚拟节点资源的性能就越好,则当
至此,以资源调度的适应度因子作为引导因子来改进传统的蚁群算法,得到改进的蚁群算法公式如下
| $ P_{i j}^{k}(t)=\left\{\begin{array}{l} \frac{F_{j}^{i}\left[\tau_{i j}^{\alpha}(t)\right]\left[\eta_{i j}^{\beta}(t)\right]}{\sum\limits_{s \notin \text { tabu} _k} F_{j}^{i}\left[\tau_{i s}^{\alpha}(t)\right]\left[\eta_{i s}^{\beta}(t)\right]}, j \notin \operatorname{tabu}_{k}\\ 0, \text { other } \end{array},\right. $ | (13) |
式中:tabuk表示已经通过的路径。
3 算法流程1) 初始化:根据虚拟节点的计算能力、带宽、内存等基础参数对蚁群优化算法的各项参数进行初始化,其中包括信息素的初始化、虚拟节点初始价格的初始化、迭代次数的初始化、信息素浓度的初始化和任务执行时间的初始化。创建禁忌列表tabuk用于记录蚂蚁已经走过的路径。
2) 将若干个蚂蚁随机部署在各起始节点处, 设置包含n个需要执行的任务和m个虚拟节点资源,根据任务不同的QoS需求,设置相应的参数值,根据公式(12)计算任务Taskn在虚拟节点vmm上的综合权重Fji值。
3) 根据改进公式(13)计算每一只蚂蚁选择下一个相邻节点的转移概率,根据计算结果将任务分配到相应的虚拟资源节点上。
4) 当任务被分配到虚拟资源节点上以后,更新在本次迭代过程中蚂蚁通过路径上的信息素,并将已通过的路径添加进禁忌表tabuk中。
5) 重复执行步骤2)~ 4),使整个蚁群任务集都找到最优的路径为止。
6) 根据步骤3)得到的综合权重Fji和该云计算资源调度改进算法公式(13),并计算出最优的路径;
7) 对所有路径上的信息素进行全局更新。
8) 迭代次数累加,判断是否达到最大迭代次数,若未达到,则继续执行步骤2), 若已达到最大迭代次数,则停止搜索,得到的结果即是云计算资源分配的最优解。
4 实验测试与结果分析CloudSim 3.0是墨尔本大学的网络实验室和Gridbus项目推出云计算仿真软件。为了验证本文设计的改进蚁群优化算法在处理云计算资源调度问题时的有效性和可行性,使用CloudSim 3.0平台,在相同的条件和环境下进行实验,并与传统的蚁群算法以及CloudSim 3.0自带的Min-Min调度算法的任务分配结果进行对比。
实验中,对CloudSim 3.0模拟器进行参数设置,设置20个任务中心,每个任务中心部署10个虚拟节点资源,随机设置虚拟节点的性能,设置虚拟节点能力为[1000, 2000]MIP, 内存为[512, 2048]MB, 带宽为[5000, 10000]b/s, 用户任务数量为200~1000个,在[500, 3800]间随机设置任务长度,最大迭代次数为60次。
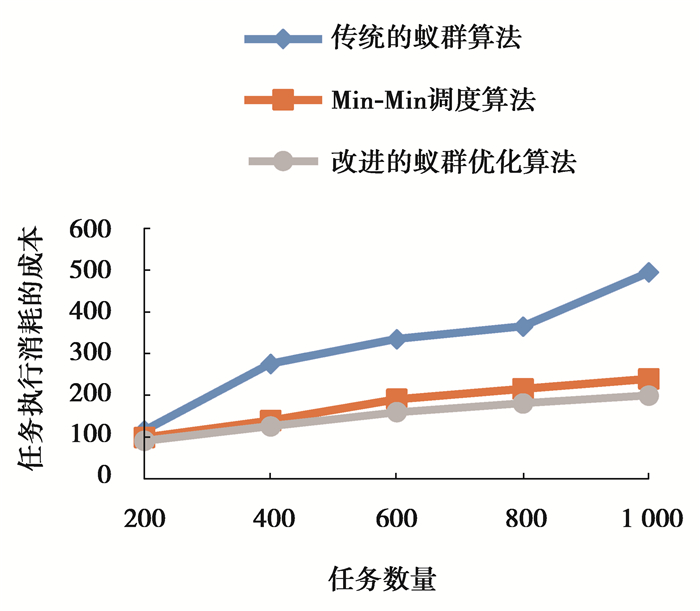
1) 通过进行模拟实验1,对比相同条件下传统的蚁群算法、CloudSim 3.0自带的Min-Min调度算法和的改进蚁群优化算法的任务执行成本,在实验1中主要考虑以任务执行成本为主要目标,设置改进的蚁群优化算法的初始参数
|
图 1 算法运行的成本比较 Fig. 1 Cost comparison of algorithm operation |
从图 1中可以看出当任务数量较少时,传统的蚁群算法、Min-Min调度算法和改进的蚁群优化算法在完成云计算资源调度方面所消耗的成本大致差别不大,但随着任务数量的增多,传统的蚁群算法在云计算资源调度方面所消耗的成本快速上升,而改进的蚁群算法在此方面仍维持较低的成本支出且始终低于Min-Min算法的消耗,这说明提出的改进蚁群优化算法有效地降低了成本消耗。
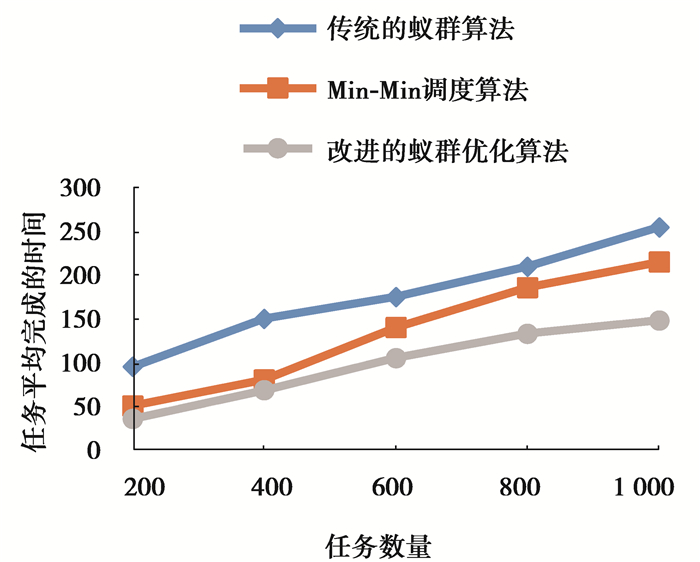
2) 通过进行模拟实验2,对比相同条件下传统的蚁群算法、CloudSim 3.0自带的Min-Min调度算法和设计的改进蚁群优化算法的任务完成时间,在实验2中主要考虑任务执行时间为主要目标,设置改进的蚁群优化算法的初始参数
|
图 2 算法运行时间的比较 Fig. 2 Comparison of running time of algorithms |
从图 2中可以看出,虽然Min-Min调度算法在任务和改进的蚁群优化算法在任务数量较少时完成调度的时间相差不大,且都低于传统的蚁群算法所需要的时间,但在任务数量增加后,改进的蚁群优化算法在消耗时间方面的涨幅相对更小,上升曲线也更平稳,故说明提出的改进蚁群优化算法在任务完成时间方面有较好优势。
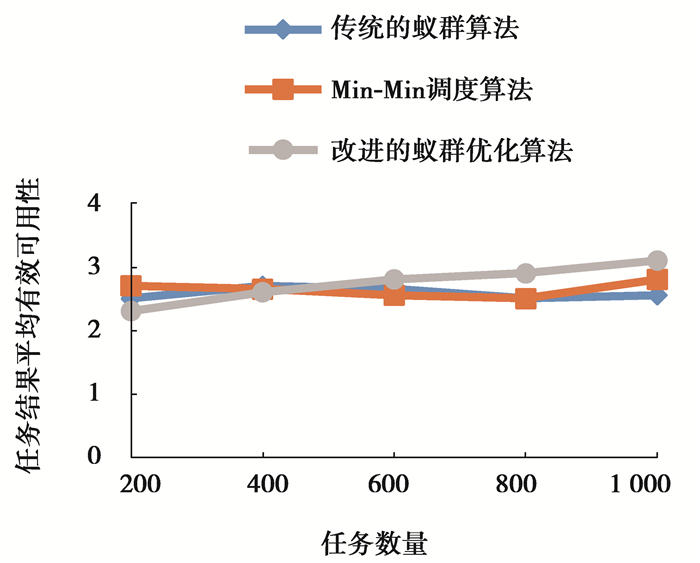
3) 通过进行模拟实验3,对比相同条件下传统的蚁群算法、CloudSim 3.0自带的Min-Min调度算法和本文设计的改进蚁群优化算法得到的任务结果的有效可用性,在实验3中以任务结果的有效可用情况为主要目标,设置改进的蚁群优化算法的初始参数
|
图 3 算法得出结果的有效可靠性比较 Fig. 3 Comparison of effective reliability of results obtained by algorithms |
从图 3中可以看出,在任务数量较少时提出的蚁群优化算法得出结果的有效性低于传统的蚁群算法和Min-Min调度算法得出结果的有效性,但随着任务数量的增加,改进的蚁群优化算法得出结果的有效性成正比例上升,并且高于其余2个算法得出结果的有效性,而其他2个算法虽然在任务数量较低时有更高的任务结果有效性,但增长曲线更波折、不稳定,故说明提出的改进的蚁群优化算法在得出的任务结果的有效性方面也具有明显优势。
5 结语针对一般云计算资源调度问题没有全面的考虑用户QoS需求的情况,引入引导因子对传统的蚁群算法进行优化和改良,得到一种改进的蚁群优化算法,该算法充分的考虑了任务完成时间、任务所需成本和任务结果的有效性,以此来综合得出用户对服务的满意程度。并对改进算法进行模拟仿真实验,实验表明,该算法在任务完成时间、任务所需成本和任务结果的有效可用性3个方面均具有明显的优势,但在满足基于用户QoS需求这3个方面的同时,要求能高效地进行任务调度方面还略有不足,应该考虑负载均衡的问题。
| [1] |
甘云志. 并行计算的一体化研究现状与发展趋势[J]. 电子技术与软件工程, 2019(7): 134. Gan Y Z. Research status and development trend of parallel computing integration[J]. Electronic Technology & Software Engineering, 2019(7): 134. (in Chinese) |
| [2] |
姜栋瀚, 林海涛. 云计算环境下的资源分配关键技术研究综述[J]. 中国电子科学研究院学报, 2018, 13(3): 308-314. Jiang D H, Lin H T. A summary of key techniques research on resource allocation in cloud computing environment[J]. Journal of China Academy of Electronics and Information Technology, 2018, 13(3): 308-314. (in Chinese) DOI:10.3969/j.issn.1673-5692.2018.03.013 |
| [3] |
方义秋, 郑剑, 葛君伟. 一种云环境下基于QoS约束的资源分配策略[J]. 计算机应用与软件, 2015, 32(1): 34-38. Fang Y Q, Zheng J, Ge J W. A resource allocation strategy in cloud environment based on QoS constraint[J]. Computer Applications and Software, 2015, 32(1): 34-38. (in Chinese) DOI:10.3969/j.issn.1000-386x.2015.01.009 |
| [4] |
李志敏, 张伟. 基于差分进化人工蜂群算法的云计算资源调度[J]. 计算机工程与设计, 2018, 39(11): 3451-3455. Li Z M, Zhang W. Clouding computing resource scheduling based on differential evolution artificial bee colony algorithm[J]. Computer Engineering and Design, 2018, 39(11): 3451-3455. (in Chinese) |
| [5] |
魏杰. 时延敏感的云计算虚拟资源调度方法研究[D]. 北京: 北京邮电大学, 2018. Wei J. Research on virtual resource allocation with latency awareness in cloud computing[D]. Beijing: Beijing University of Posts and Telecom, 2018. (in Chinese) |
| [6] |
蔡晓丽, 钱诚. 基于改进的粒子群算法的云资源调度策略[J]. 微电子学与计算机, 2018, 35(6): 28-30, 35. Cai X L, Qian C. Cloud resource schedling strategy based on improved particle swarm optimization[J]. Microelectronics & Computer, 2018, 35(6): 28-30, 35. (in Chinese) |
| [7] |
王英, 秦丁, 刘杰, 等. 基于生产函数的效用优化云计算资源调度算法[J]. 计算机应用研究, 2017, 34(2): 397-400, 452. Wang Y, Qin D, Liu J, et al. User utility optimization of cloud computing resource scheduling algorithm based on production function[J]. Application Research of Computers, 2017, 34(2): 397-400, 452. (in Chinese) DOI:10.3969/j.issn.1001-3695.2017.02.017 |
| [8] |
陈暄, 龙丹. 基于改进的鸡群算法在云计算资源调度中的研究[J]. 计算机应用研究, 2019, 36(9): 2584-2587. Chen X, Long D. Based on improved chicken swarm optimization in cloud computing resource scheduling[J]. Application Research of Computers, 2019, 36(9): 2584-2587. (in Chinese) |
| [9] |
周斌斌. 基于云计算的资源调度和负载均衡的研究[D]. 成都: 西南交通大学, 2018. Zhou B B. Research on resourcescheduling and load balancingbased on cloud computing[D]. Chengdu: Southwest Jiaotong University, 2018. (in Chinese) |
| [10] |
邓晓衡, 关培源, 万志文, 等. 基于综合信任的边缘计算资源协同研究[J]. 计算机研究与发展, 2018, 55(3): 449-477. Deng X H, Guan P Y, Wan Z W, et al. Integrated trust based resource cooperation in edge computing[J]. Journal of Computer Research and Development, 2018, 55(3): 449-477. (in Chinese) |
| [11] |
郑万波. 低可靠环境中云计算系统的服务质量预测与优化调度研究[D]. 重庆: 重庆大学, 2017. Zheng W B. On quality-of-service prediction and optimal scheduling of cloud computing systems in unreliability environment[D]. Chongqing: Chongqing University, 2017. (in Chinese) |
| [12] |
丁丁, 艾丽华, 罗四维, 等. 基于用户行为反馈的云资源调度机制[J]. 系统工程与电子技术, 2018, 40(1): 209-216. Ding D, Ai L H, Luo S W, et al. User behavior-based resource scheduling mechanism for cloud computing with feedback control[J]. Systems Engineering and Electronics, 2018, 40(1): 209-216. (in Chinese) |
| [13] |
郭煜. 可信云体系结构与关键技术研究[D]. 北京: 北京交通大学, 2017. Guo Y. Research of trusted cloud architecture and the key technologies[D]. Beijing: Beijing Jiaotong University, 2017. (in Chinese) |
| [14] |
单好民. 基于改进蚁群算法和粒子群算法的云计算资源调度[J]. 计算机系统应用, 2017, 26(6): 187-192. Shan H M. Cloud computing resource scheduling based on improved ant colony algorithm and particle swarm algorithm[J]. Computer Systems & Applications, 2017, 26(6): 187-192. (in Chinese) |
| [15] |
赵俊普, 殷进勇, 金同标, 等. 遗传蚁群算法在云计算资源调度中的应用[J]. 计算机工程与设计, 2017, 38(3): 693-697. Zhao J P, Yin J Y, Jin T B, et al. Application of genetic ant colony algorithm in cloud computing resource scheduling[J]. Computer Engineering and Design, 2017, 38(3): 693-697. (in Chinese) |
| [16] |
萨日娜. 基于蚁群粒子群优化算法的云计算资源调度方案[J]. 吉林大学学报(理学版), 2017, 55(6): 1518-1522. Sa R N. Cloud computing resource scheduling scheme based on ant colony particle swarm optimization algorithm[J]. Journal of Jilin University (Science Edition), 2017, 55(6): 1518-1522. (in Chinese) |
| [17] |
陈文庆, 程雪颖. 云计算环境下的资源调度和优化方法[J]. 激光杂志, 2016, 37(6): 115-118. Chen W Q, Cheng X Y. Resource scheduling and optimization method in cloud computing environment[J]. Laser Journal, 2016, 37(6): 115-118. (in Chinese) |
| [18] |
崔雪娇, 曾成, 徐占然, 等. 基于贪心算法的云计算资源调度策略[J]. 微电子学与计算机, 2016, 33(6): 41-43, 48. Cui X J, Zeng C, Xu Z R, et al. Resource scheduling strategy in cloud computing based on greedy algorithm[J]. Microelectronics & Computer, 2016, 33(6): 41-43, 48. (in Chinese) |
| [19] |
贾嘉, 慕德俊. 基于粒子群优化的云计算低能耗资源调度算法[J]. 西北工业大学学报, 2018, 36(2): 339-344. Jia J, Mu D J. Low-energy-orientated resource scheduling in cloud computing by particle swarm optimization[J]. Journal of Northwestern Polytechnical University, 2018, 36(2): 339-344. (in Chinese) DOI:10.3969/j.issn.1000-2758.2018.02.020 |
| [20] |
邹燕飞, 刘淑英. 改进蚁群算法的云计算资源调度模型[J]. 吉林大学学报(理学版), 2017, 55(3): 679-683. Zou Y F, Liu S Y. Resources scheduling model of cloud computing based on improved ant colony algorithm[J]. Journal of Jilin University (Science Edition), 2017, 55(3): 679-683. (in Chinese) |
| [21] |
Agarwal M, Srivastava G M S. A genetic algorithm inspired task scheduling in cloud computing[C]//2016 International Conference on Computing, Communication and Automation (ICCCA). April 29-30, 2016, Greater Noida, India: IEEE, 2016: 364-367.
|
| [22] |
Wang T T, Liu Z B, Chen Y, et al. Load balancing task scheduling based on genetic algorithm in cloud computing[C]//2014 IEEE 12th International Conference on Dependable, Autonomic and Secure Computing. August 24-27, 2014, Dalian, China: IEEE, 2014: 146-152.
|
| [23] |
Sheng X D, Li Q. Template-based genetic algorithm for QoS-aware task scheduling in cloud computing[C]//2016 International Conference on Advanced Cloud and Big Data (CBD). August 13-16, 2016, Chengdu, China: IEEE, 2016: 25-30.
|
| [24] |
Song W Z, Yang B, Zhao X H, et al. A fast and scalable supervised topic model using stochastic variational inference and MapReduce[C]//2016 IEEE International Conference on Network Infrastructure and Digital Content (IC-NIDC). September 23-25, 2016, Beijing, China: IEEE, 2016: 94-98.
|
| [25] |
Chen X, Song W F, Li Z G. Research of resource scheduling based on ACA-GA in the cloud computing[J]. International Journal of Grid and Distributed Computing, 2016, 9(6): 1-12. DOI:10.14257/ijgdc.2016.9.6.01 |
| [26] |
Ku-Mahamud K R, Din A M, Nasir H J A. Enhancement of ant colony optimization for grid load balancing[J]. European Journal of Scientific Research, 2011, 64(1): 42-50. |
| [27] |
Ramesh D, Krishnan A. Optimal parameter identification in ant colony optimization for load balancing in grid computing[J]. European Journal of Scientific Research ISSN, 2012, 370-376. |
| [28] |
Mondal B, Dasgupta K, Dutta P. Load balancing in cloud computing using stochastic hill climbing-a soft computing approach[J]. Procedia Technology, 2012, 4: 783-789. DOI:10.1016/j.protcy.2012.05.128 |
| [29] |
Alakeel A M. A guide to dynamic load balancing in distributed computer systems[J]. International Journal of Computer Science and Information Security, 2010, 10(6): 153-160. |
| [30] |
Zhan S B, Huo H Y. Improved PSO-based task scheduling algorithm in cloud computing[J]. Journal of Information & Computational Science, 2012, 9(13): 3821-3829. |
 2021, Vol. 44
2021, Vol. 44

