2. 大唐中南电力试验研究院, 郑州 450006;
3. 重庆大学 期刊社, 重庆 400044
2. DaTang Centrol-China Electric Power Test Research Institute, Zhengzhou 450006, P. R. China;
3. Journal Department, Chongqing University, Chongqing 400044
随着互联网应用深化,中国面临的网络安全问题日益复杂。网络安全风险评估技术通过感知并预测网络系统中的安全风险,通过遏制网络风险传播以控制网络安全态势,对于改善网络安全现状有着十分重要的意义。目前已有一些学者提出网络风险评估方法:如基于层次分析法的网络安全风险评估方法,根据专家主观经验为每个安全要素加权,并基于线性或非线性函数进行加权求和。但这类方法过于依赖专家主观经验,缺乏统一量化评估标准;如基于线性或非线性时序分析的网络安全风险预测方法,依据前一时隙内的网络安全风险,分析安全风险短期时序变化规律。但该方法仅适用于短时宏观风险变化分析。
不仅如此,上述网络风险评估方法均未考虑网络风险传播带来的影响。由于网络风险并非静态的,而是以威胁源为中心向周边节点投射[1]。网络风险传播受网络拓扑、威胁源分布等因素的影响,并且单次网络风险传播行为存在一定随机性,使得网络风险传播行为在时空上难以预测,给网络风险评估带了挑战。虽然已有一些方法在宏观层面量化评估当前的网络风险,并预测未来短时风险变化规律,但这类方法难以细粒度地分析网络风险传播及其分布。
针对上述问题,提出一种RiskRank网络风险传播分析方法。基于DNS日志数据,计算网络节点间的相似关系和临近关系,以构建网络风险传播图谱,通过标记图谱中已知风险的网络节点,基于随机游走方法迭代计算网络风险传播模型,以分析网络风险传播,并量化评估网络风险程度,最后采用密度聚类算法识别高风险簇,通过隔离高风险簇从而控制网络安全态势。
研究的贡献包括:1)构建网络风险传播图谱,以表示2种网络风险传播途径:相似网络节点间传播和临近网络节点间传播;2)基于网络风险传播图谱,提出一种基于随机游走方法的网络风险传播模型,量化评估网络风险程度;3)实验结果表明,提出的RiskRank网络风险传播模型的准确率为97.4%、精度为98.1%、召回率为86.4%。
1 国内外研究现状 1.1 网络安全风险评估与预测Cai等[2]通过提取网络安全关键要素,并基于层次分析法对网络安全关键要素进行加权,以综合评估网络安全风险程度,但在评估过程中该方法过于依赖主观经验,缺乏统一量化评估标准。Ghosh等[3]从损失成本和响应成本的角度分析了网络安全风险。Almohri等[4]基于概率图模型分析网络中发生攻击的概率。Wang等[5]提出一种网络安全性评估模型用于分析网络系统脆弱性带来的风险。潘顺荣等[6]对网络风险传播过程等进行了探讨。田飞等[7-8]分析网络病毒传播规律。
1.2 随机游走方法张良富等[9]综述了随机游动方法的时间复杂度、空间复杂度、计算精确度以及可扩展性并在此基础上总结了这些算法所对应的计算场景。Alamgir等[10]采用随机游走方法实现基于兴趣点的局部聚类,该方法从兴趣点开始随机游走,访问其他可达顶点,直到满足停止条件。郭景峰等[11]在转移概率模型的基础上提出了一种基于两类节点的随机游走算法, 以得到较高质量的随机游走序列。马慧芳等[12]在关键词提取中基于随机游走算法计算节点的重要性分数。Su等[13-14]通过描述高斯反向传播的消息传递过程,提出了新的置信度初始化设置方法。
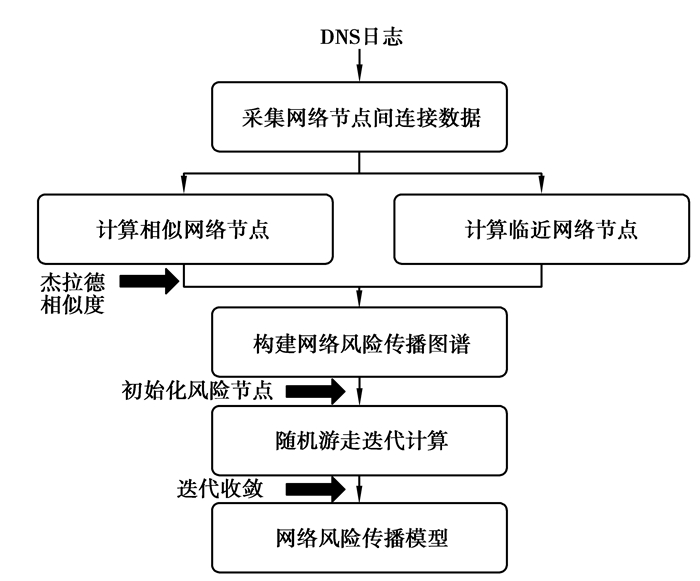
2 RiskRank网络风险传播分析方法笔者提出的RiskRank网络传播分析方法,从DNS日志数据中提取网络节点间的连接,采用杰卡德距离计算节点间相似关系,并结合网络拓扑中节点间临近关系,构建网络风险传播图谱,如图 1所示,图中的节点表示网络节点,图中的边表示两两网络节点之间的相似关系和临近关系[15]。通过标记已知风险的网络节点以初始化风险值,并基于随机游走方法迭代计算网络风险传播模型,最后基于收敛稳定的模型评估图谱中所有节点的风险程度。
|
图 1 网络风险传播分析方法 Fig. 1 Analysis method of network risk propagation |
网络风险传播主要是指网络中的威胁源向周边邻接节点投射风险,如利用恶意网站、攻击服务器、移动介质等,通过诱导或主动等方式,向周边邻接节点实施攻击行为,包括植入恶意软件、控制受控主机、拒绝服务攻击等,使得网络风险从威胁源投射至周边邻接节点。由于越脆弱的网络节点和越有价值的网络节点,越容易遭受攻击,因此高风险的节点在网络拓扑中呈现密集连接现象。
网络风险传播途径主要包括相似节点间传播和临近节点间传播:1)网络风险之所以在相似节点间传播是由于相似节点会具有相似的网络行为,它们关联着共同的域节点和服务器等,如果这些域节点和服务器等是威胁源,那么威胁源会向这些相似的网络节点传播风险。2)网络风险之所以在临近节点间传播是由于临近节点在网络拓扑中存在较短连接路径,容易通过网络通信或移动介质传播风险。
根据DNS数据中的节点间通信,计算相似网络节点与相近网络节点,对其进行关联,以构建网络风险传播图谱,该图谱描述了相近和相似节点之间的关联关系。定义无向图G=(V, E, S0)为网络风险传播图谱,其中V={v1, v2, ……, vn}表示网络节点,E={e1, e2, ……, en}表示连接相似和相近网络节点之间的边(关系),分为两种,一种相似关系、一种临近关系。相似关系是指两网络节点和其他网络节点之间的连接关系存在相似性,临近关系是指两网络节点存在直接的通信连接。采用杰拉德距离计算网络节点间的相似性,相似度公式如公式(1)所示,其中,vi和vj分别表示网络节点i和网络节点j所关联的其他网络节点集合。vi和vj的交集vi∩vj表示两网络节点共同连接的其他网络节点数,vi和vj的并集vi∪vj表示2网络节点连接的其他网络节点总数。vi和vj的相似度sim(vi, vj)表示两网络节点共同连接的其他网络节点数在连接的其他网络节点总数中的占比,如果sim(vi, vj)大于阈值0.5(sim(vi, vj)>0.5),那么说明vi和vj具有相似性。
| $ {\mathop{\rm sim}\nolimits} \left( {{v_i}, {v_j}} \right) = \frac{{{v_i} \cap {v_j}}}{{{v_i} \cup {v_j}}}。$ | (1) |
网络风险传播图谱的构建算法如表 1所示。S0={s1, s2, …, sn}表示网络节点的初始化风险值。基于风险传播模型迭代更新网络节点的风险值,S={s′1, s′2, …, s′n}表示模型收敛后的网络节点风险值,当si′>threshold时,网络节点vi为高风险网络节点,threshold为风险临界阈值,用于判定vi是否为高风险节点。
| 表 1 网络风险传播图谱构建算法 Table 1 Algorithm for constructing network risk propagation map |
通过构建网络风险传播图谱,基于随机游走方法提出一种RiskRank网络风险传播模型,通过分析网络风险在网络空间中随机动态传播过程,以评估网络中的潜在安全风险。对于未知风险的网络节点,通过初始化部分已知节点风险值,基于随机游走迭代计算图谱中所有节点的风险值,待风险传播图谱迭代收敛后,所有未知风险的节点均被标记上风险值,该风险值作为这些节点的潜在风险值。根据公式(2)迭代计算未知节点的风险值,其中score(xi)为节点xi的风险值,α=0.85为阻尼系数,In(xi)是xi的入度,Out(xi)是xi的出度。网络风险传播图谱各节点的风险值经初始化后,根据公式(2)迭代其他节点的风险值,每次迭代计算完成,计算所有节点迭代前和迭代后2次风险值之间的平均差作为收敛误差,当收敛误差小于一定阈值(如小于0.05)时,则说明网络风险传播模型收敛,迭代计算结束。
| $ {\mathop{\rm score}\nolimits} \left( {{x_i}} \right) = (1 - \alpha ) + \alpha \cdot \frac{1}{{{n_{xj}}_{ \in \ln (xi)}}} \cdot \frac{1}{{{n_{xk \in {\mathop{\rm Out}\nolimits} \left( {{x_j}} \right)}}}} \cdot \sum\limits_{{x_j} \in \ln (xi)} {\sum\limits_{xk \in } {\sum\limits_{{\mathop{\rm Out}\nolimits} \left( {{x_j}} \right)} {{\mathop{\rm score}\nolimits} } } } \left( {{x_k}} \right) \cdot {\mathop{\rm score}\nolimits} \left( {{x_j}} \right)。$ | (2) |
通过设定阈值以区分高风险节点和低风险节点,由于阈值的设定会影响风险评估的精度和召回率,设置合理的阈值以获得较高精度和召回率。设置风险临界阈值的原则为:提升精度的条件下同时尽可能不降低召回率。经实验分析,当阈值为0.8时,方法具有高精度和较高的召回率。
2.2 高风险簇检测方法由于高风险网络节点可能是正在被攻击的网络系统,也可能是存在较大风险但还未被攻击的网络系统,因此为了能更加准确的隔离风险源,通过对高风险网络节点进行聚类分析从而隔离由高风险网络节点形成的“团簇”(密集区域),以隔离风险源、抑制网络安全风险传播,如图 2所示。采用上述网络风险传播模型迭代更新网络风险传播图谱G=(V, E, S0),直到网络风险传播模型收敛,得到G=(V, E, Sv),其中Sc={s′1, s′2, …, s′n}表示模型收敛后的风险值。遍历所有网络节点,选择所有si>0.8的网络节点作为高风险网络节点集合Vs={v′1, v′2, ……, v′m}。任意选择一高风险网络节点v′i,遍历所有相邻的高风险网络节点,如果高风险网络节点vi′相邻的网络节点{v′j}的数量大于阈值ρ,则将这些高风险网络节点聚类成簇ci,如果当前生成的簇与之前生成的簇存在交集,则将两簇合并成一个新的簇。遍历所有高风险网络节点聚类形成的簇,如果某簇ci中高风险网络节点总数大于阈值N(根据选取的实验数据,N=10),那么该簇为高风险簇,高风险簇往往是由威胁源向邻接节点投射风险形成。

|
图 2 高风险簇聚类算法 Fig. 2 High-risk cluster clustering algorithm |
利用真实环境中的DNS数据进行实验,以验证所提出方法的有效性。首先介绍实验环境和实验数据,并分析风险传播模型的准确性,同时分析阈值选取对准确性的影响,最后讨论该模型的时间开销。
实验中涉及的方法均采用相同的编译环境和配置环境中,其中,计算机CPU为2 Xeon 4116 12C/85W/2.1GHz,内存为256 G DDR4 2 666 MHz,硬盘为2×480G SSD,操作系统为Ubuntu 16.04,编译器采用Eclipse 3.5/JRE 1.8。
采用的DNS数据来源于国网河南省电力公司数据中心,数据规模超过230万条,包含源地址、目的地址、端口号、域名、时间等字段。安全中心标记了其中1 767个异常节点作为黑名单,包括1 623个恶意域节点以及144个异常主机节点,同时标记了8 556个正常网络节点作为白名单。进行10组实验,测试验证方法采用K(K=10)折交验证法,每组实验都在黑名单中随机选取50%黑和50%白样本作为已知的高风险和低风险网络节点用于迭代计算,剩下50%黑和50%白样本作为验证集中“未知”的网络节点用于测试。
3.1 准确性分析采用准确度(ACC)、精度(PRE)、召回率(REC)来评估网络风险传播模型的预测效果,如公式(3)、公式(4)和公式(5)所示。其中,TP(true positive)表示验证集中被模型正确识别的高风险网络节点数量,FP(false positive)表示验证集中被模型错误识别的高风险网络节点数量,TN(true negative)表示验证集中被模型正确识别的低风险网络节点数量,FN(false negative)表示验证集中被模型错误识别的低风险网络节点数量。根据TP、FP、TN、FN,计算准确度(ACC)、精度(PRE)、召回率(REC)。
| $ {{\rm{ACC}} = \frac{{{\rm{TP}} + {\rm{TN}}}}{{{\rm{TP}} + {\rm{FN}} + {\rm{TN}} + {\rm{FP}}}}},$ | (3) |
| $ {{\rm{PRE}} = \frac{{{\rm{TP}}}}{{{\rm{TP}} + {\rm{FN}}}}},$ | (4) |
| $ {{\rm{REC}} = \frac{{{\rm{TP}}}}{{{\rm{TP}} + {\rm{FP}}}}}。$ | (5) |
从数据集中随机选取部分已知高风险网络节点进行初始化,高风险网络节点的风险值初始化为1.0,其他网络节点初始化风险值为0.0,作为“未知”风险的网络节点。通过构建网络风险传播图谱,迭代计算RiskRank网络风险传播模型,该模型计算所有未知节点的风险值。通过设置风险阈值(设置0.8),提取所有风险值大于阈值的节点并潘定为高风险网络节点,并与验证集中的标签进行比对,从而评估预测网络风险传播模型的准确率、精度和召回率。实验结果表明,提出的基于RiskRank的网络风险传播模型的准确度为97.4%,精度为98.1%,召回率为86.4%。
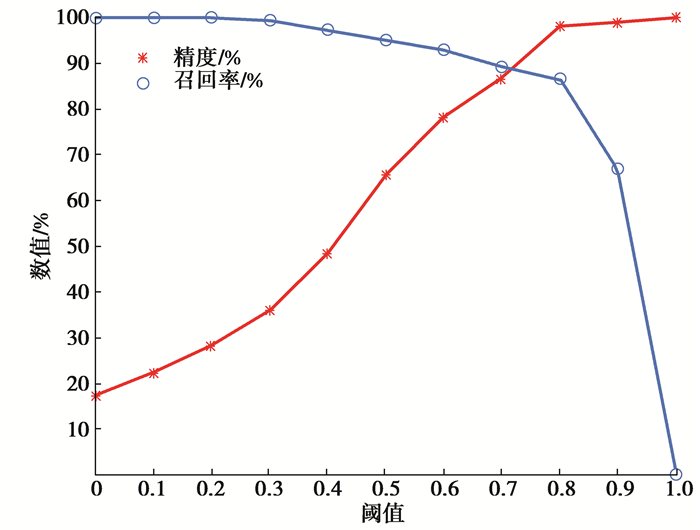
3.2 阈值分析由于不同的阈值会影响风险传播模型的准确性,因此通过设置不同的阈值,以比较分析出较优的风险阈值。不同阈值下精度和召回率实验结果如图 3所示,从中看出:总体趋势上,随着阈值不断增大,精度随之提升,召回率随之下降,反之,随着阈值不断减小,精度随之下降,召回率随之提升。当精度趋近于稳定时,即阈值为0.8时,尽管阈值不断增大,由于精度趋近100%,提升幅度有限,而召回率急剧下降。因此,当阈值大于0.8时,虽然精度有较小提升,但召回率急剧下降,当阈值小于0.8时,虽然召回率较高,但精度明显不足。因此,设定阈值为0.8,在确保精度的情况下,尽可能不降低召回率,即当精度趋近于稳定且召回率仍较高时的临界阈值。
|
图 3 不同阈值下的精度和召回率曲线 Fig. 3 Accuracy and recall curves under different thresholds |
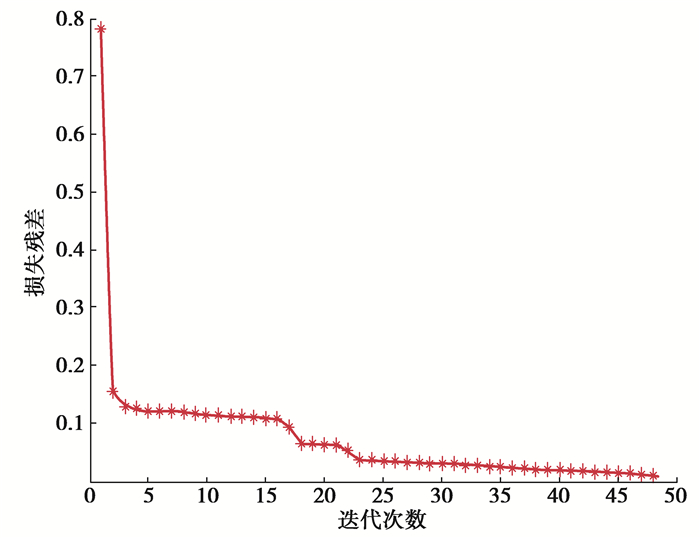
提出RiskRank网络风险传播分析方法是基于随机游走进行收敛的,收敛过程需要多次迭代计算。实验如图 4所示,网络风险传播模型收敛时的平均迭代次数为48次,平均时间开销为62.3 s。结果表明:随着迭代次数的增加,风险传播模型的损失在不断减小,说明风险传播图谱中网络节点的风险值趋近于稳定,收敛时的风险传播模型处于动态平衡状态,该状态下网络节点的风险值即为预测的风险值。进行第一次迭代后,风险传播模型收敛速率较大,反映出风险传播模型可以快速收敛,同时表明提出的风险传播理论依据合理,即网络风险在相似节点和相近节点间进行传播,如果一个网络节点关联更多高风险节点,则说明该网络节点存在较高的安全风险,反之,如果一个网络节点关联更少高风险节点,则说明该网络节点存在较低的安全风险。
|
图 4 风险传播模型收敛过程 Fig. 4 Convergence process of risk propagation model |
针对传统网络安全风险评估方法缺乏考虑网络风险动态传播影响的问题,提出一种RiskRank网络安全风险传播模型,以预测网络安全风险传播态势。通过采集网络DNS数据,基于相似网络节点和相近网络节点构建网络风险传播图谱,以分析网络风险传播行为,基于随机游走理论,构建网络风险传播模型,迭代计算潜在网络风险分布。并提出一种基于密度聚类的高风险簇识别方法,用于隔离高风险簇以控制安全态势。实验测试结果表明,提出RiskRank网络安全风险传播模型具有97.4%的准确率、98.1%的精度和86.4%的召回率。
| [1] |
龚俭, 臧小东, 苏琪, 等. 网络安全态势感知综述[J]. 软件学报, 2017, 28(4): 1010-1026. Gong J, Zang X D, Su Q, et al. Survey of network security situation awareness[J]. Journal of Software, 2017, 28(4): 1010-1026. (in Chinese) |
| [2] |
Cai X D, Zhang H Y, Li T. Network security threats situation assessment and analysis technology study[C]//Proceedings of 2013 2nd International Conference on Measurement, Information and Control. August 16-18, 2013, Harbin, China. IEEE, 2013: 643-646.
|
| [3] |
Ghosh N, Chokshi I, Sarkar M, et al. NetSecuritas: an integrated attack graph-based security assessment tool for enterprise networks[C]//Proceedings of the 2015 International Conference on Distributed Computing and Networking. Goa India. New York, NY, USA: ACM, 2015: 1-10.
|
| [4] |
Almohri H M J, Watson L T, Yao D F, et al. Security optimization of dynamic networks with probabilistic graph modeling and linear programming[J]. IEEE Transactions on Dependable and Secure Computing, 2016, 13(4): 474-487. DOI:10.1109/TDSC.2015.2411264 |
| [5] |
Wang L Y, Jajodia S, Singhal A, et al. K-zero day safety: a network security metric for measuring the risk of unknown vulnerabilities[J]. IEEE Transactions on Dependable and Secure Computing, 2014, 11(1): 30-44. DOI:10.1109/TDSC.2013.24 |
| [6] |
潘顺荣, 崔博, 乐美龙, 等. 系统论视角下的网络风险传播研究[J]. 系统科学学报, 2019, 27(1): 102-107. Pan S R, Cui B, Le M L, et al. Research on network risk communication from the perspective of system theory[J]. Chinese Journal of Systems Science, 2019, 27(1): 102-107. (in Chinese) |
| [7] |
胡宝安, 李兵, 李亚玲. 具有时滞的SIR计算机病毒传播模型[J]. 计算机工程, 2016, 42(5): 168-172. Hu B A, Li B, Li Y L. SIR computer virus propagation model with time delay[J]. Computer Engineering, 2016, 42(5): 168-172. (in Chinese) DOI:10.3969/j.issn.1000-3428.2016.05.029 |
| [8] |
田飞, 陈翰雄, 黄雅云, 等. 重置概率可变的自适应网络病毒传播研究[J]. 计算机技术与发展, 2015, 25(10): 140-144. Tian F, Chen H X, Huang Y Y, et al. Research on epidemic spreading on adaptive network with varied resetting probability[J]. Computer Technology and Development, 2015, 25(10): 140-144. (in Chinese) |
| [9] |
张良富, 李翠平, 陈红. 大规模图上的SimRank计算研究综述[J/OL]. 计算机学报, 2019: 1-23[2019-12-07]. http://kns.cnki.net/kcms/detail/11.1826.TP.20190515.1510.002.html. Zhang L F, Li C P, Chen H. A review of studies on SimRank calculation on large scale maps[J/OL]. Journal of Computer Science, 2019: 1-23[2019-12-07]. http://kns.cnki.net/kcms/detail/11.1826.TP.20190515.1510.002.html. |
| [10] |
Alamgir M, Von Luxburg U. Multi-agent random walks for local clustering on graphs[C]//2010 IEEE International Conference on Data Mining. December 13-17, 2010. Sydney, Australia. IEEE, 2010: 18-27.
|
| [11] |
郭景峰, 董慧, 张庭玮, 等. 主题关注网络的表示学习[J/OL]. 计算机应用, 2019: 1-9[2019-12-07]. http://kns.cnki.net/kcms/detail/51.1307.TP.20191106.1321.012.html. Guo J F, Dong H, Zhang T W, et al. The topic focuses on the presentation learning of the web[J/OL]. Computer Application, 2019: 1-9[2019-12-07]. http://kns.cnki.net/kcms/detail/51.1307.TP.20191106.1321.012.html. |
| [12] |
马慧芳, 王双, 李苗, 等. 融合图结构与节点关联的关键词提取方法[J]. 中文信息学报, 2019, 33(9): 69-78. Ma H F, Wang S, Li M, et al. A keywords extraction method via graph structure and nodes association[J]. Journal of Chinese Information Processing, 2019, 33(9): 69-78. (in Chinese) DOI:10.3969/j.issn.1003-0077.2019.09.009 |
| [13] |
Su Q L, Wu Y C. On convergence conditions of Gaussian belief propagation[J]. IEEE Transactions on Signal Processing, 2015, 63(5): 1144-1155. DOI:10.1109/TSP.2015.2389755 |
| [14] |
Yedidia J S, Freeman W T, Weiss Y. Constructing free-energy approximations and generalized belief propagation algorithms[J]. IEEE Transactions on Information Theory, 2005, 51(7): 2282-2312. DOI:10.1109/TIT.2005.850085 |
| [15] |
侯湘, 黄晋, 桑军, 等. 多维度融合的文献作者亲密度计算[J]. 情报学报, 2021, 40(8): 846-853. Hou X, Huang J, Sang J, et al. Calculation of author intimancy based on multi-dimensional fusin[J]. Journal of the China Society for Scientific and Technical Information, 2021, 40(8): 846-853. |
 2021, Vol. 44
2021, Vol. 44

