线损是考察供电企业技术力量及经济效益的重要指标之一,如何有效降低线路损耗是各级电力企业迫切需要解决的问题。随着线损管理深入推进,高损排查与降损治理成为基层供电单位工作的主要内容[1-2]。配网线损治理是基于用电信息采集系统数据,目前仍然需要大量的手动分析工作,治理效果因人而异,工作效率和质量均难以得到有效保证[3-5]。
当前针对线损精益化管理的研究主要集中在理论线损计算和线损的系统排查方法。文献[6]提出了将映射数据与计量数据建立关联映射的算法;文献[7]采用平均电流损耗时间法计算理论线损,具有算法简单的优势;文献[8]提出一种基于模糊聚类基态修正的计算方法,对线损标杆值进行优化设计;文献[9]从制度、组织管理角度阐述了线损管理策略;文献[10]在现场排查方面提出了分相分段法。
上述方案仅针对单线路进行线损管理,而未从网络的角度来思考线损治理。造成线损异常的原因除了窃电及其他管理因素外[11-12],还包括线路的供电负荷特性,网络中负荷分布情况等[13-15]。因此,文章提出考虑线损电量优化分布的配电网线路最优组合模型,针对配电网线路的高损问题,以实现各条线路的线损率均满足要求为目标,将高损线路与低损线路进行组合,实现线损电量合理分布,为配电网网络重构、网络规划等工作提供依据,从网络的角度制定降损措施。
1 问题场景分析从供电负荷的角度分析,线损率的高低受负荷特性、负荷大小等因素的影响。在负荷特性方面,不同的用电类别或行业类型会造成线损率差异,如工业生产用户,其动力负荷导致的低功率因数可能导致线路高损,而居民生活用电的负荷特性决定了其线损率保持较低水平;在负荷大小方面,重载线路容易发生高损,轻载线路的线损率则一般保持较低水平。不同台区的负荷类型、负荷大小、线路类型、拓扑结构上的较大差异,导致其线损率长期存在显著差异,且针对由于负荷特性导致长期高损的台区,采用基于单线路或单台区的降损策略难以得到理想的效果。
针对上述问题,需要考虑基于网络的降损措施。依据配电网线路供电异常情况下的网络解决方案,短期异常采用网络重构的方式进行联络线的负荷转供;长期异常需要通过规划手段进行负荷切改。基于上述方法构建配电网高线损率解决方案,在单线路单台区降损措施的基础上,通过改变负荷供电方式,将低功率因数、高耗能等导致线路高损的负荷向低损供电线路进行转移和分摊,实现线路共同满足线损率要求。
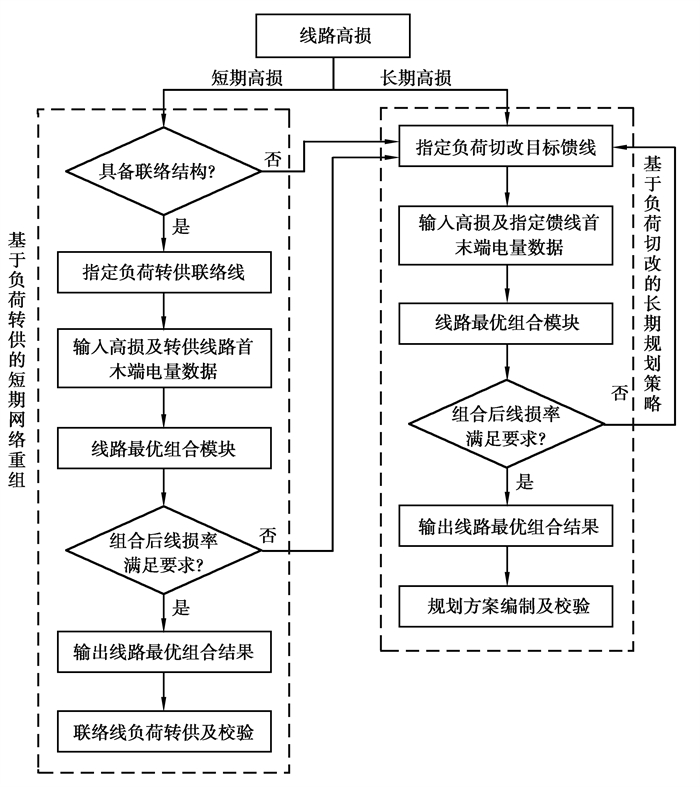
2 模型概述根据上述场景分析,构建配电网线路最优组合模型,通过使网络中线损电量合理分布,确定线路最优组合方式,为高损负荷转供或负荷切改提供依据,实现尽可能多的线路满足线损率要求的目标,模型的结构如图 1所示。
|
图 1 配电网线路最优组合模型框图 Fig. 1 Block diagram of optimal combination of distribution network lines |
根据场景分析中供电异常情况下的网络解决方案所述,模型分为2个组成部分。
2.1 短期高损针对短期高损的情况,首先考察该线路是否具有联络结构。不具有联络结构的情况需借助负荷切改的方式解决;具有联络线的情况,则根据实际情况指定负荷转供联络线,并基于配电网数据采集现状,利用高损线路及转供联络线在高损时段内的首末端电量数据,在线路最优组合模块中进行计算,算法在第3节详细描述。若计算后高损线路及转供线路仍有线损率不满足要求的情况,则需借助于负荷切改手段解决;若线损率均满足要求,则可根据结果进行负荷转供和网络重构方案的制定,以及静态安全校核等评估。
2.2 长期高损针对长期高损的情况,需要通过规划手段进行解决,将线路组合范围扩大到能够进行合理负荷切改的其他馈线,指定可组合的馈线,并利用这些馈线与高损线路的首末端电量数据进行线路最优组合计算,若计算结果中有线路线损率不满足要求,则重新选择切改馈线或规划新增线路;若线损率均符合要求,则依据组合结果进行规划方案的编制及静态安全校核、经济型评估等校验。
3 线路最优组合模块 3.1 线路组合问题的数学描述将以上所描述的线路最优组合问题以数学模型的形式来描述如下:指定配电网络中有n条线路参加优化组合分析,即n个对象,每个对象有属性A、属性B,其中A、B分别为线路的首端电量与末端电量,定义线损率
| $ C = \frac{{A-B}}{A}, $ | (1) |
式中,C的合理区间是[0, L],其中L为该网络的线损率考核上限。如果C不在合理区间内,则定义对象不合格。对于不合格对象可以在满足约束条件的情况下,与其他参与优化组合计算的任意对象进行组合,组合后每组的对象数量均不能大于N,组合后
| $ {A_{p - q}} = {A_p} + {A_l} + \ldots + {A_q}, $ | (2) |
| $ {B_{p - q}} = {B_p} + {B_l} + \ldots + {B_q}, $ | (3) |
| $ {C_{p - q}} = {\rm{ }}\frac{{{A_{p - q}} - {B_{p - q}}}}{{{A_{p - q}}}}, $ | (4) |
式中:Ap-q为优化分组后组内包含的由p到q各线路首端电量之和;Bp-q为组内各线路末端电量之和;Cp-q为该组的整体线损率。只需要Cp-q的区间在[0, L]之间,则该组内由p到q的所有线路均视为合格。若原始数据共有n条线路,通过优化组合后有m条线路合格,那么优化组合的目的是使m最大化,并记录最优时的组合情况。
3.2 线路最优组合算法根据3.1节关于考虑线损电量优化分布的线路组合问题数学描述,提出线路组合优化算法,如式(5)所示。
| $ \left\{ {\begin{array}{*{20}{l}} {{\rm{max}}\left[ {\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{x_{ij}}} } } \right], }\\ {{\rm{s}}.{\rm{t}}.}\\ {{x_{11}}\left( {{a_1} - {b_1} - L{a_1}} \right) + {x_{12}}\left( {{a_2} - {b_2} - L{a_2}} \right) + \ldots + {x_{1n}}\left( {{a_n} - {b_n} - L{a_n}} \right) \le 0, }\\ {{x_{21}}\left( {{a_1} - {b_1} - L{a_1}} \right) + {x_{22}}\left( {{a_2} - {b_2} - L{a_2}} \right) + \ldots + {x_{2n}}\left( {{a_n} - {b_n} - L{a_n}} \right) \le 0, }\\ \vdots \\ {{x_{n1}}\left( {{a_1} - {b_1} - L{a_1}} \right) + {x_{N2}}\left( {{a_2} - {b_2} - L{a_2}} \right) + \ldots + {x_{nn}}\left( {{a_n} - {b_n} - L{a_n}} \right) \le 0, }\\ {{x_{11}}\left( {{a_1} - {b_1}} \right) + {x_{12}}\left( {{a_2} - {b_2}} \right) + \ldots + {x_{1n}}\left( {{a_n} - {b_n}} \right) \ge 0, }\\ {{x_{21}}\left( {{a_1} - {b_1}} \right) + {x_{22}}\left( {{a_2} - {b_2}} \right) + \ldots + {x_{2n}}\left( {{a_n} - {b_n}} \right) \ge 0, }\\ \vdots \\ {{x_{n1}}\left( {{a_1} - {b_1}} \right) + {x_{n2}}\left( {{a_2} - {b_2}} \right) + \ldots + {x_{nn}}\left( {{a_n} - {b_n}} \right) \ge 0, }\\ {{x_{11}} + {x_{12}} + {x_{13}} + \ldots + {x_{1n}} \le N, }\\ {{x_{21}} + {x_{22}} + {x_{23}} + \ldots + {x_{2n}} \le N, }\\ \vdots \\ {{x_{n1}} + {x_{n2}} + {x_{n3}} + \ldots + {x_{nn}} \le N, }\\ {{x_{11}} + {x_{12}} + {x_{13}} + \ldots + {x_{1n}} \le 1, }\\ {{x_{21}} + {x_{22}} + {x_{23}} + \ldots + {x_{2n}} \le 1, }\\ \vdots \\ {{x_{n1}} + {x_{n2}} + {x_{n3}} + \ldots + {x_{nn}} \le 1, }\\ {{x_{ij}} \in \left\{ {0, 1} \right\}}。\end{array}} \right. $ | (5) |
设参与最优组合计算的线路总数为n, 当每条线路均满足线损率要求,即所有线路单独成组时,计算结果的分组数量最大,可见分组数量最大值也为n。由此构建以n×n维系数矩阵的约束方程组为主体的优化模型,i, j分别为该系数矩阵的行号和列号。其中:i为线路所在分组的组号,j为线路编号,二者取值范围均为0到n。
目标函数中:xij为第i组中第j条线路的线路分组结果标志,xij=1代表经过最优组合计算后,在分组i中,线路j被选中,其线损率可视为满足要求;xij=0代表经过最优组合计算后,在分组i中,线路j未被选中。目标函数是xij之和最大,即最优组合计算后所有分组中被选中的线路数量最多,也就是满足线损率考核要求的线路数量最多。
约束条件将第3.1节问题的数学描述中给出的限定条件逐一进行约束,分为5个部分。
1) 组合后的线损上限约束。保证每个分组内被选中的线路,即组内系数满足xij=1的线路满足式(6),表征组内整体线损率低于考核上限,对应式(4)中Cp-q的上限L约束,
| $ \frac{{\Sigma {a_j} - \Sigma {b_j}}}{{\Sigma {a_j}}} \le L。$ | (6) |
2) 组合后的线损下限约束。保证每个分组内被选中的线路,即组内系数满足xij=1的线路,满足式(7),表征组内整体线损率高于考核下限,对应式(4)中Cp-q的下限0的约束,
| $ \frac{{\Sigma {a_j} - \Sigma {b_j}}}{{\Sigma {a_j}}} \ge 0。$ | (7) |
3) 每组的线路数量上限约束。根据实际需求,最优组合计算后,每组选中的线路数量上限为N。
4) 线路出现次数约束。保证在最优组合结果中,每条线路在所有分组中只出现一次。
5) 线路结果标志的取值约束。将线路结果标志的取值约束为整数1或0,分别代表经过最优组合计算后,该线路在当前分组中被选中或未被选中。
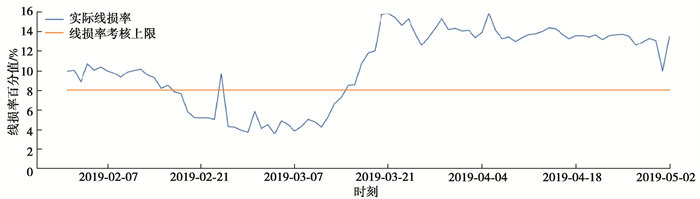
4 算例分析采用2019年2~4月重庆市某地区配网中选取的高损线路作为测试对象,其线损率情况如图 2所示。
|
图 2 高损线路的线损率情况 Fig. 2 Line loss rate of high-loss lines |
由此可见,在给定时间范围内线损率长期高于考核上限,原因是其供电负荷存在大用户,线路长期处于较高负载率运行且功率因数较低。由于不具有负荷转供的联络线,因此考虑制定规划方案,进行负荷切改。在临近区域指定5条线路,作为负荷切改的备选线路,取3月15日~4月30日高损的时间区间作为算例的时间域,形成线路最优组合计算的输入数据,如表 1所示。
| 表 1 线路最优组合计算的输入数据 Table 1 Input data for optimal combination calculation of the line |
根据该地区线损率考核标准,线损率上限为8%。参与最优组合计算的5条线路中,线损异常线路数量为1条,给定组合后每组选中的线路数量上限为3条,因此该算例的实际最优组合计算的简写表达式为
| $ \left\{ {\begin{array}{*{20}{l}} {{\rm{max}}\left[ {\sum\limits_{i = 1}^5 {\sum\limits_{j = 1}^5 {{x_{ij}}} } } \right], }\\ {{\rm{s}}.{\rm{t}}.}\\ {\forall i, \sum\limits_{j = 1}^5 {{x_{ij}}\left( {{a_j} - {b_j} - 0.08{a_j}} \right) \le 0} , }\\ {\forall i, \sum\limits_{j = 1}^5 {{x_{ij}}\left( {{a_j} - {b_j}} \right) \ge 0, } }\\ {\forall i, \sum\limits_{j = 1}^5 {{x_{ij}} \le 3, } }\\ {\forall j, \sum\limits_{i = 1}^5 {{x_{ij}} \le 1, } }\\ {{x_{ij}} \in \left\{ {0, 1} \right\}}。\end{array}} \right. $ | (8) |
利用GAMS(general algebraic modeling system)建模工具进行建模计算,得到最优组合结果,原始的5条线路被重新组合为3组,每组的整体线损率均满足考核要求,该结果中春季工作日和春季休息日数据集经计算得到的分组结果相同,如表 2所示。
| 表 2 线路最优组合计算结果 Table 2 Line optimal combination calculation result |
由分组结果可见,所有参与最优组合计算的线路,通过自成一组或者若干线路组合后,所有线路均满足3.1节中的模型所定义的合格标准,且高损线路1的负荷在规划中的转移方向是线路2和线路4。因此,在规划方案编制时可以考虑将线路1中的大用户负荷转移至线路2和4,使线路1的线损电量能够在线路1、2和4之间优化分布,线损率均满足考核要求。由此可见,该模型能够通过线损电量优化分布使组合后各条线路线损率均满足考核要求,帮助配网线损管理人员快速、高效地找到导致高损的负荷的合理切改方向,为后续的负荷转供、负荷切改以及相关校验提供依据。
5 结束语文章提出了考虑线损电量优化分布的配电网线路最优组合模型,以实现各条线路的线损率均满足要求为目标,将高损线路与低损线路进行组合,从而为高损负荷转移方案的制定提供依据。该模型的意义在于:
1) 从网络的角度提出了线损治理方案,能够进一步解决在特定负荷类型、线路负载率等情况下,传统基于单线路线损管理难以有效降损的问题;
2) 能够为线损电量优化分布实现过程中的负荷转供、负荷切改、线路规划等提供准确可靠的依据。
在该模型的基础上,根据最优组合结果进行网络重构或网络规划方案的制定,以及静态稳定校验、经济型评估等工作将是接下来的研究重点。
| [1] |
Queiroz L M O, Roselli M A, Cavellucci C, et al. Energy losses estimation in power distribution systems[J]. IEEE Transactions on Power Systems, 2012, 27(4): 1879-1887. DOI:10.1109/TPWRS.2012.2188107 |
| [2] |
Goswami S K, Basu S K. A new algorithm for the reconfiguration of distribution feeders for loss minimization[J]. IEEE Transactions on Power Delivery, 1992, 7(3): 1484-1491. DOI:10.1109/61.141868 |
| [3] |
Price W W, Chiang H D, Clark H K, et al. Load representation for dynamic performance analysis (of power systems)[J]. IEEE Transactions on Power Systems, 1993, 8(2): 472-482. DOI:10.1109/59.260837 |
| [4] |
蒋利民, 霍大伟, 闫华光, 等. 配电网理论线损计算方法的数值分析[J]. 电测与仪表, 2012, 49(9): 47-51. Jiang L M, Huo D W, Yan H G, et al. The numerical analysis in the technical loss of distribution network[J]. Electrical Measurement & Instrumentation, 2012, 49(9): 47-51. (in Chinese) DOI:10.3969/j.issn.1001-1390.2012.09.011 |
| [5] |
董楠, 杨柳, 吴鸿亮, 等. 地区电网理论线损计算需求数据合成方法研究[J]. 电力系统保护与控制, 2015, 43(9): 47-53. Dong N, Yang L, Wu H L, et al. Demand data synthesis method of regional power grid theoretical line loss calculation[J]. Power System Protection and Control, 2015, 43(9): 47-53. (in Chinese) |
| [6] |
付学谦, 陈皓勇. 平均电流损耗时间法在配网线损计算中的应用[J]. 电工技术学报, 2015, 30(12): 377-382. Fu X Q, Chen H Y. Energy losses estimation using equivalent time of average current loss method[J]. Transactions of China Electrotechnical Society, 2015, 30(12): 377-382. (in Chinese) DOI:10.3969/j.issn.1000-6753.2015.12.047 |
| [7] |
安晓华, 欧阳森, 冯天瑞, 等. 中压馈线理论线损率标杆值的优化设计方法及应用[J]. 电网技术, 2016, 40(1): 199-206. An X H, Ouyang S, Feng T R, et al. An optimal design method of theoretical line loss rate benchmark value for medium voltage feeders and its application[J]. Power System Technology, 2016, 40(1): 199-206. (in Chinese) |
| [8] |
彭宇文, 刘克文. 基于改进核心向量机的配电网理论线损计算方法[J]. 中国电机工程学报, 2011, 31(34): 120-126. Peng Y W, Liu K W. A distribution network theoretical line loss calculation method based on improved core vector machine[J]. Proceedings of the CSEE, 2011, 31(34): 120-126. (in Chinese) |
| [9] |
李滨, 杜孟远, 韦维, 等. 基于准实时数据的智能配电网理论线损计算[J]. 电力自动化设备, 2014, 34(11): 122-128, 148. Li B, Du M Y, Wei W, et al. Calculation of theoretical line loss based on quasi real-time data of smart distribution network[J]. Electric Power Automation Equipment, 2014, 34(11): 122-128, 148. (in Chinese) DOI:10.3969/j.issn.1006-6047.2014.11.019 |
| [10] |
Sabath F, Garbe H. Radiation analysis of PCB layout using a hybrid MoM-MTL method[J]. IEEE Transactions on Electromagnetic Compatibility, 2003, 45(2): 424-435. DOI:10.1109/TEMC.2003.811295 |
| [11] |
Ling S H, Leung F H F, Lam H K, et al. Short-term electric load forecasting based on a neural fuzzy network[J]. IEEE Transactions on Industrial Electronics, 2003, 50(6): 1305-1316. DOI:10.1109/TIE.2003.819572 |
| [12] |
MacQueen C N, Irving M R. An algorithm for the allocation of distribution system demand and energy losses[J]. IEEE Transactions on Power Systems, 1996, 11(1): 338-343. DOI:10.1109/59.486115 |
| [13] |
卢志刚, 李爽. 基于直接神经动态规划的电网状态估计及理论线损计算[J]. 电网技术, 2008, 32(23): 50-55. Lu Z G, Li S. Power system state estimation and theoretical line loss calculation based on direct neural dynamic programming[J]. Power System Technology, 2008, 32(23): 50-55. (in Chinese) |
| [14] |
李姝, 龚佳怡, 莫颖涛. 10 kV及以下电网线损精细化管理[J]. 供用电, 2009, 26(3): 65-68, 77. Li S, Gong J Y, Mo Y T. Meticulous management for the line loss of 10 kV and below power network[J]. Distribution & Utilization, 2009, 26(3): 65-68, 77. (in Chinese) DOI:10.3969/j.issn.1006-6357.2009.03.021 |
| [15] |
Shannon C E. A mathematical theory of communication[J]. ACM SIGMOBILE Mobile Computing and Communications Review, 2001, 5(1): 3. DOI:10.1145/584091.584093 |
 2022, Vol. 45
2022, Vol. 45

