2. 重庆大学 输配电装备及系统安全与新技术国家重点实验室, 重庆 400044;
3. 国家电网重庆市电力公司 南岸供电分公司, 重庆 401336
2. State Key Laboratory of Power Transmission Equipment & System Security and New Technology, Chongqing University, Chongqing 400044, P. R. China;
3. State Grid Chongqing Nan'an Power Supply Company, Chongqing 401336, P. R. China
经济社会的飞速发展在改善居民生活质量的同时,也对电力能源提出了越来越高的要求。化石能源消耗量的飞速增长不仅加剧了全球能源的紧张的局势,而且对环境问题提出了新的挑战[1]。分布式发电技术(DG, distributed generation)的出现,实现了风能、光能、潮汐能等新能源的有效利用。相比于传统的发电方式,分布式发电具有清洁环保、装配便捷、可靠性高等优势[3]。然而,由于分布式发电受环境条件的随机性和波动性影响较大,分布式电源大规模并网会改变电网正常的潮流分配[13],严重时甚至威胁主网运行的稳定性和安全性。而微电网通过对分布式发电进行整合管理,在保障系统稳定性的同时大大地提高了可再生能源的利用率。微电网与大电网之间由公共连接点(PCC, point of common coupling)相连。当PCC节点连通时,微电网运行于并网模式下,主网能够通过注入或吸收功率为微电网提供电压和频率支撑;当PCC点断开时,微电网从并网模式切换到孤岛模式运行,由于缺少了主网的支撑,以及环境等不确定因素的影响,微电网内部运行环境更加复杂,因此孤岛微电网的运行问题成为研究的热点[4-5]。目前,对于微电网控制技术的研究已逐渐成熟,在保证微电网安全稳定运行的同时,学者们开始对微电网运行的经济性展开深入的研究。
经济调度问题的实质是实现微电网内部各资源的最优配置,在保证微电网安全稳定运行的前提下,通过将负载功率合理分配到每个分布式发电单元,从而保证微电网运行的经济性最优[6]。张双乐等[7-8]在考虑分布式电源的经济型特性的基础上,建立以微电网运行成本最小化为目标的优化模型,采用改进变尺度混沌优化算法求解,仿真结果验证了该方法的可行性。为了平抑可再生能源出力对微电网的影响,文献[9-10]基于约束规划建立了孤岛微电网的经济调度模型,对于模型中的机会约束条件,通过生成可再生能源发电的概率性序列将其转化成等价的确定性约束,仿真验证了该方法快速稳定的优点。针对含冷热出力单元的经济调度问题同时存在凸和非凸的情况,Bhattacharya等[11]通过将差分进化算法和生物地理学优化算法进行结合来求解,并且考虑了爬坡率和禁止作业区等限制,仿真表明新的算法提升了解的质量和收敛速度。为了研究储能装置在优化过程中的作用,文献[12]以电池SOC(SOC, sate of charge)和折旧成本为微电网优化调度的目标函数,采用启发式调整策略与粒子群算法相结合的方法对优化模型进行求解。
目前,越来越多的研究开始将需求响应作为经济调度的一种重要资源。结合分时电价机制,在微电网中配置合适的可调负载,让可调负载响应电价变化一同参与微电网经济调度,不仅能够减轻微电网发电侧的压力,而且还可以增加负荷侧用户的收益[13]。在需求响应信号来临时,用户通过调整用电设备的用电状态或用电模式,来改变当前时刻的电能消耗。在电力价格信号较高时,用户侧通过减少电能消耗节约用电费用,同时也减轻系统发电侧的压力。在电力价格信号较低时,还可以通过可调负载的接入,促进不可再生能源发电的消纳[14]。在直接负载控制方面,Luo等[15]对居民热舒适度进行精确估计,并采用模糊自适应帝国主义竞争算法对直接负荷控制模型进行求解,该方法充分考虑了居民的舒适度感受。Ma等[16]提出一种基于价格的智能电网峰负荷控制策略,使得消费者能够根据电价在电力成本和负荷削减成本之间权衡,并采用一种分布式能量控制算法进行求解,结果表明该策略能够有效消除峰值负荷。Tuan等[17]在电力系统非管制条件下,充分考虑了负载位置、功率因数等因素提出基于最优潮流框架的模型,来对可中断负荷进行实时选择投切。Zhang等[18]提出一种解耦需求响应机制来对家庭中3种负荷进行管理,针对可调节负荷,提出一种基于学习算法的需求响应策略,来最小化用户的用电成本。Wang等[19]建立一种多智能体系统,并以异构家庭代理和零售商代理为主对住宅需求响应状况进行评价,同时建立2种代理的实时价格预测模型,通过最优控制算法求解,从而得到最优的住宅需求响应策略。
综上所述,在研究含有需求响应的调度方法时,现有文献大多只考虑了提高用户侧利益,而没有考虑发电侧的成本。因此,为了实现发电侧和用户侧双赢的局面,笔者建立了一种考虑需求响应的孤岛微电网多目标经济调度模型。首先,研究结合微型燃气轮机发电成本函数构建微电网发电侧总成本目标函数;然后,引入分时电价机制,构造由用电效用函数和用电费用函数组成的总收益函数,从而建立同时考虑发电侧成本和用户侧收益的多目标经济调度模型。最后,搭建运行于孤岛模式下的微电网的仿真平台,在分时电价机制下测试所提出的微电网经济调度模型的性能。
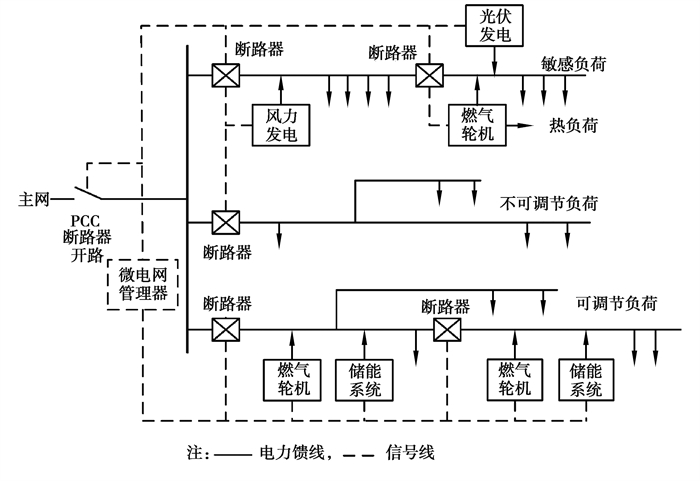
1 需求响应经济调度模型典型的微电网结构如图 1所示,该微电网系统由微型燃气轮机(MT, micro turbine),光伏(PV, photovoltaic cell)、风机(WT, wind turbine)等可再生能源发电单元,以及储能系统(ESS, energy storage system)组成。微电网系统中包含2类负载,分别为可调负载和不可调负载。微电网PCC节点处与主网断开,处于孤岛运行模式下,由系统内部的各分布式电源对负载进行供电。
|
图 1 微电网系统结构图 Fig. 1 Topological structure of microgrid system |
微电网的发电成本一般忽略可再生能源的发电成本,而主要考虑微型燃气轮机MT的发电成本。一般的微型燃气轮机MT的发电成本与传统柴油发电机的发电成本相似,其发电成本是关于有功出力的二次凸函数[20],为
| $ {F_{i, {\rm{mt}}}} = {a_{i, {\rm{mt}}}}p_{i, {\rm{mt}}}^2 + {b_{i, {\rm{mt}}}}{p_{i, {\rm{mt}}}} + {c_{i, {\rm{mt}}}}, $ | (1) |
式中:ai, mt>0,bi, mt>0,ci, mt>0均表示第i个MT的发电成本参数;pi, mt表示第i个MT的有功出力;Fi, mt表示第i个MT的发电成本。
微电网发电侧成本最小即所有MT的发电成本之和最小,为
| $ {\rm{Min}}F = \sum\nolimits_{i = 1}^n {{F_{i, {\rm{mt}}}}\left( {{p_{i, {\rm{mt}}}}} \right)} , $ | (2) |
式中:n表示微电网中MT的总数;F表示发电侧的总成本。
第i个MT的增量成本λi, mt定义为成本函数Fi, mt的一阶导数[21]为
| $ {\lambda _{i, {\rm{mt}}}} = {\rm{ }}\frac{{\partial {F_{i, {\rm{mt}}}}\left( {{p_{i, {\rm{mt}}}}} \right){\rm{ }}}}{{\partial {p_{i, {\rm{mt}}}}}} = 2{a_{i, {\rm{mt}}}}{p_{i, {\rm{mt}}}} + {b_{i, {\rm{mt}}}} $ | (3) |
由等微增率准则可知,当每台MT的增量成本保持一致时,此时的增量成本为所有MT的最优增量成本[20],这时整个微电网的发电成本最小。
1.2 负荷侧收益函数对于用户侧,引入用电成本函数和用电效用函数来建立其效益目标函数。用电成本函数表示用户侧电能消耗的成本费用[21]。根据分时电价机制,在峰时阶段电价较高,用户侧可调负载接入量将减少,从而降低用户的用电费用,同时因为总负荷的减少,可控发电单元的出力也会相应减少,使得发电侧的成本也相应降低。
用户侧在t时刻的用电费用可表示为
| $ C\left( t \right) = \Sigma \left( {{c_f}\left( t \right)\cdot l_i^{fl}\left( t \right) + {c_{in}}\cdot l_i^{ifl}\left( t \right)} \right), $ | (4) |
式中:cf(t)表示t时刻的分时电价;lifl(t)表示可调负载i在t时刻的负载接入量大小;cin表示基准电价;liifl(t)表示在t时刻的不可调负载的接入量大小;C(t)表示用户侧在t时刻电能消耗的总成本费用。
用电效用函数是用于描述负载电能消耗质量的二次函数,为了表征不同负载电能消耗质量的差异,在用电效用函数中引入参数αk>0和βk>0,负载k在t时刻的效用函数可表示为
| $ {u_k}\left( t \right) = {\alpha _k}{l_k}\left( t \right) - {\beta _k}l_k^2\left( t \right), $ | (5) |
式中:αk>0和βk>0为区分不同负载之间电能消耗质量的参数,由负载的种类决定;lk(t)为负载k在t时刻的负载接入量;uk(t)为负载k的效用函数,它随αk线性增加,随βk二次性递减。
综合用户侧成本函数以及效用函数,可以得到在t时刻,用户侧的收益函数可以表示为
| $ {\rm max}\Sigma {u_k}\left( t \right) - C\left( t \right) = \Sigma \left( {{\alpha _k}{l_k}\left( t \right) - {\beta _k}l_k^2\left( t \right)} \right) - \Sigma \left( {{c_f}\left( t \right)\cdot l_i^{fl}\left( t \right) + {c_{in}}\cdot l_i^{fl}\left( t \right)} \right)。$ | (6) |
笔者同时考虑发电侧发电成本和用户侧收益,建立实现微电网发电侧和用户侧双赢的多目标函数。
1.3 约束条件在微电网系统的运行过程中,引入一系列约束条件,保证微电网在实现经济调度的同时保证系统的安全稳定运行。约束条件分为不等式约束和等式约束两大类。满足等式约束即满足微电网内部发电侧与用户侧的供需平衡,这是系统稳定运行的前提。不等式约束主要考虑微型燃气轮机的出力限制,以及可调负载接入量的限制。
1.3.1 功率平衡约束为了保证微电网在孤岛模式下稳定运行,系统中可再生能源发电、储能电源以及微型燃气轮机的出力总和应与用户侧接入负载总和保持平衡,为
| $ \Sigma {p_{i, {\rm{mt}}}}\left( t \right) + \Sigma {p_{i, {\rm{res}}}}\left( t \right) + {p_{{\rm{ess}}}}\left( t \right) = \Sigma {l_k}\left( t \right), $ | (7) |
式中:pess(t)表示t时刻储能系统的出力大小;pi, res(t)表示t时刻第i个可再生能源发电的输出功率。
1.3.2 微型燃气轮机出力约束为了保证微电网功率平衡,微电网中的微型燃气轮机工作于PQ控制模式下,补偿负载与可再生能源出力之间的功率缺额。由于微型燃气轮机自身物理条件的限制,在微型燃气轮机正常运行时,其出力大小受限制如下
| $ {\rm{min}}({p_{i, {\rm{mt}}}}) \le {p_{i, {\rm{mt}}}}\left( t \right) \le {\rm{max}}({p_{i, {\rm{mt}}}}), $ | (8) |
式中,min(pi, mt)和max(pi, mt)表示第i个微型燃气轮机出力的上下限制。
1.3.3 可调负载接入量约束文中的可调负载可根据经济调度方案的需要调整负载的接入量,从而实现相应的经济调度目标,其接入量限制为
| $ {\rm{min}}(l_i^{fl}) \le l_i^{fl}\left( t \right) \le {\rm{max}}(l_i^{fl}), $ | (9) |
式中,min(lifl)和max(lifl)分别表示第i个可调负载接入量的上下限值。
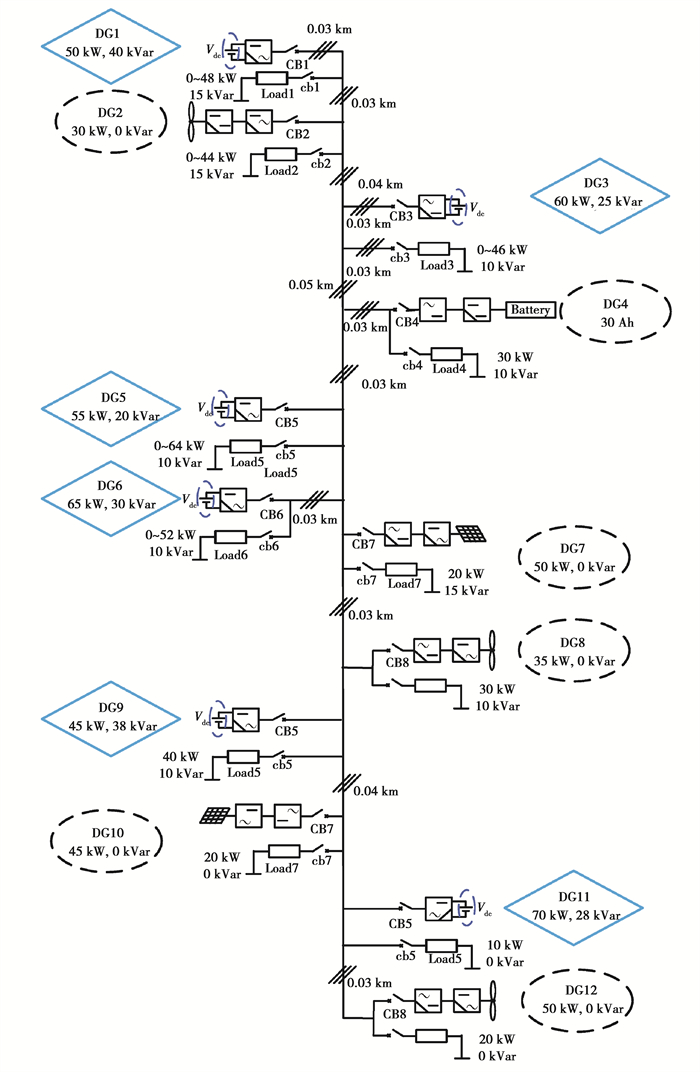
2 仿真平台及参数设置 2.1 仿真平台搭建在建立上述孤岛微电网的经济调度模型的基础上,在Simulink中建立包含可再生能源发电、微型燃气轮机、储能系统,以及负载的孤岛微电网仿真平台如图 2所示。
|
图 2 孤岛微电网拓扑图 Fig. 2 Topology of a radial MG |
对经济调度模型的有效性进行测试微电网由12个分布式发电单元和12个负载组成,其中分布式发电单元又包含微型燃气轮机、可再生能源发电(PV和WT)和储能系统。微型燃气轮机{Gi|i=1, 3, 5, 6, 9, 11}都工作于PQ控制模式,而可再生能源发电{Gi|i=2, 7, 8, 10, 12}工作于最大功率追踪点(MPPT, maximum power point tracking)模式。由于微电网处于孤岛模式没有主网的支撑,因此储能电源G4工作于V/F控制模式下,通过补偿微电网发电侧与需求侧的功率缺额来保证电压和频率的稳定[21]。此外,储能电源由于自身物理条件的限制,在充放电时瞬间输出也受上下限限制,文中假设储能装置的容量足够大,能够满足微电网的瞬时功率缺额。
微电网中的负载包括可调负载和不可调负载2种类型,其中不可调负载{Li|i=4, 7, 8, 9, 10, 11, 12}不会随着电价的变化而改变其接入量,只能够接入或切除。在引入需求响应时,可调负载{Li|i=1, 2, 3, 5, 6}的接入量大小能够随着分时电价的变化而进行调整,以提高用户侧的收益大小。
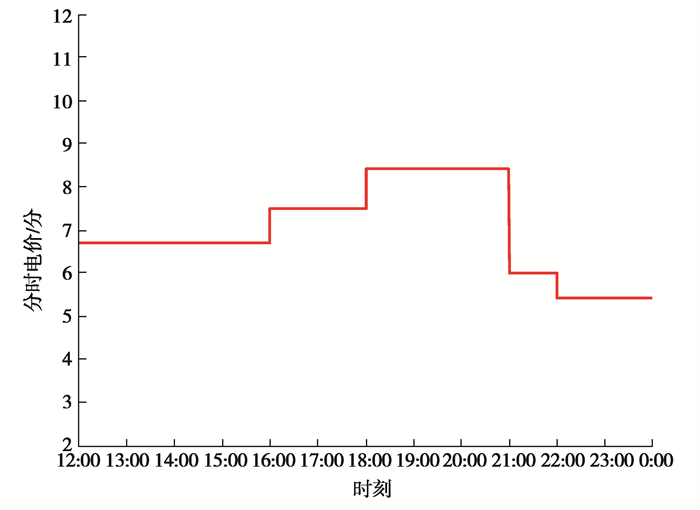
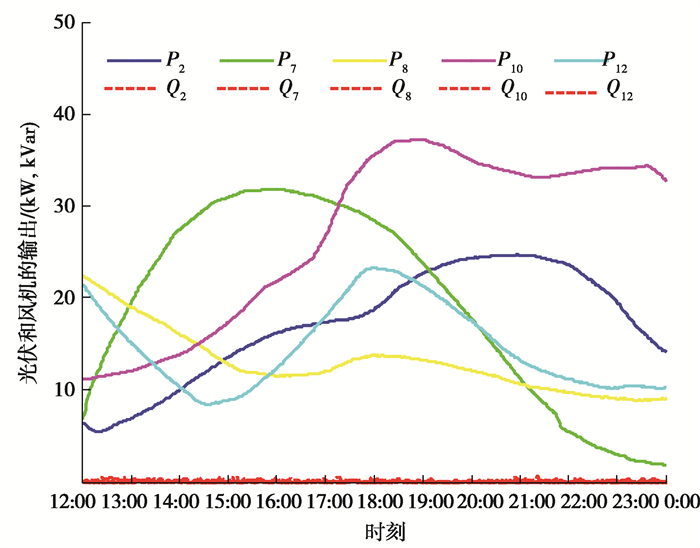
2.2 参数设置根据文献[22]设置分时电价如图 3所示,图 4为不可控再生能源发电的出力曲线,微电网中各分布式发电单元的控制方式以及相关参数列于表 1,表 2为负载的类型及相关参数。
|
图 3 分时电价设置 Fig. 3 Setup of Time-of-use rate |
|
图 4 可再生能源发电出力曲线 Fig. 4 Outputs of all PVs and WTs |
| 表 1 DG相关参数 Table 1 Relevant parameters of DGs |
| 表 2 负载相关参数 Table 2 Relevant parameters of Loads |
在微电网仿真模型中,系统线电压和频率分别设置为380 V和50 Hz,同时考虑线路阻抗,设置为0.169+ j0.07 Ω/km[23]。为了验证方法的有效性,设置再生能源发电不产生无功功率,同时考虑微电网中存在负载变化,设置不可调负载变化如图 5所示。
|
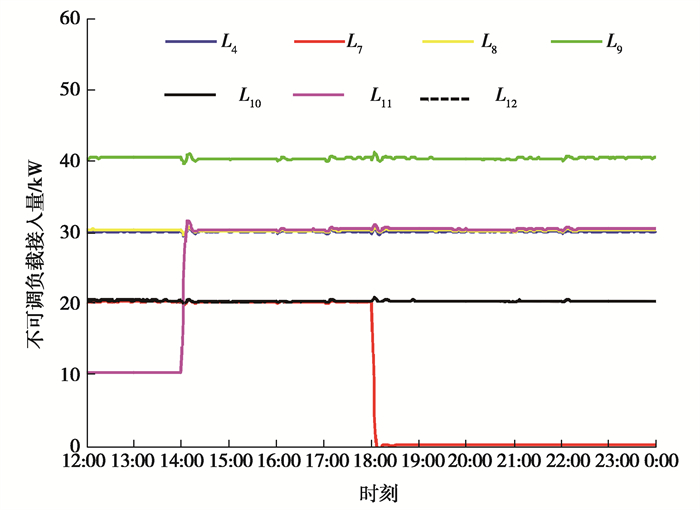
图 5 不可调负载接入量 Fig. 5 The participant amount of fixed load |
1) t=14:00时,不可调负载L11有功功率增加20 kW;
2) t=18:00时,不可调负载L7从微电网中切除。
2.3 经济调度模型求解方法在Simulink中搭建微电网仿真模型后,添加user-defined functions library中的MATLAB Function模块,在MATLAB Function模块中进行编程,对文中第2节中所建立的微电网需求响应经济调度模型进行求解,具体步骤如下:
1) 读入当前时刻各节点的分布式发电单元出力大小、负荷大小、电价。
2) 根据当前的分时电价,在MATLAB Function中调用fmincon优化函数,对提出的优化模型进行求解,可得到用户侧收益最大的可调负载接入方案。
3) 将储能系统的输出功率根据可控微型燃气轮机的容量大小分配给各微型燃气轮机,避免储能系统的过充过放情况。
4) 根据等微增率准则,重新分配各微型燃气轮机的出力大小,保证每台微型燃气轮机的增量成本一致,从而实现发电侧成本最小。
5) 更新可调负载的接入情况和微型燃气轮机的出力大小,等待下一时刻电价信号的到来。
3 仿真算例在建立仿真平台的基础上,设计2个仿真算例对提出的考虑需求响应的微电网多目标经济调度模型进行测试。第一个仿真算例研究分时电价机制对于用户侧收益以及微电网系统运行的影响;第二个仿真算例研究在分时电价机制下,引入需求响应对于用户侧收益以及微电网系统运行的影响。
3.1 算例1:分时电价对用户侧收益的影响在本算例中,考虑发电侧成本,负荷侧不引入需求响应,在分时电价机制下,以及在不可调负载和环境条件波动的情况下,研究分时电价机制对用户侧效益的影响,仿真结果如图 6所示。
|
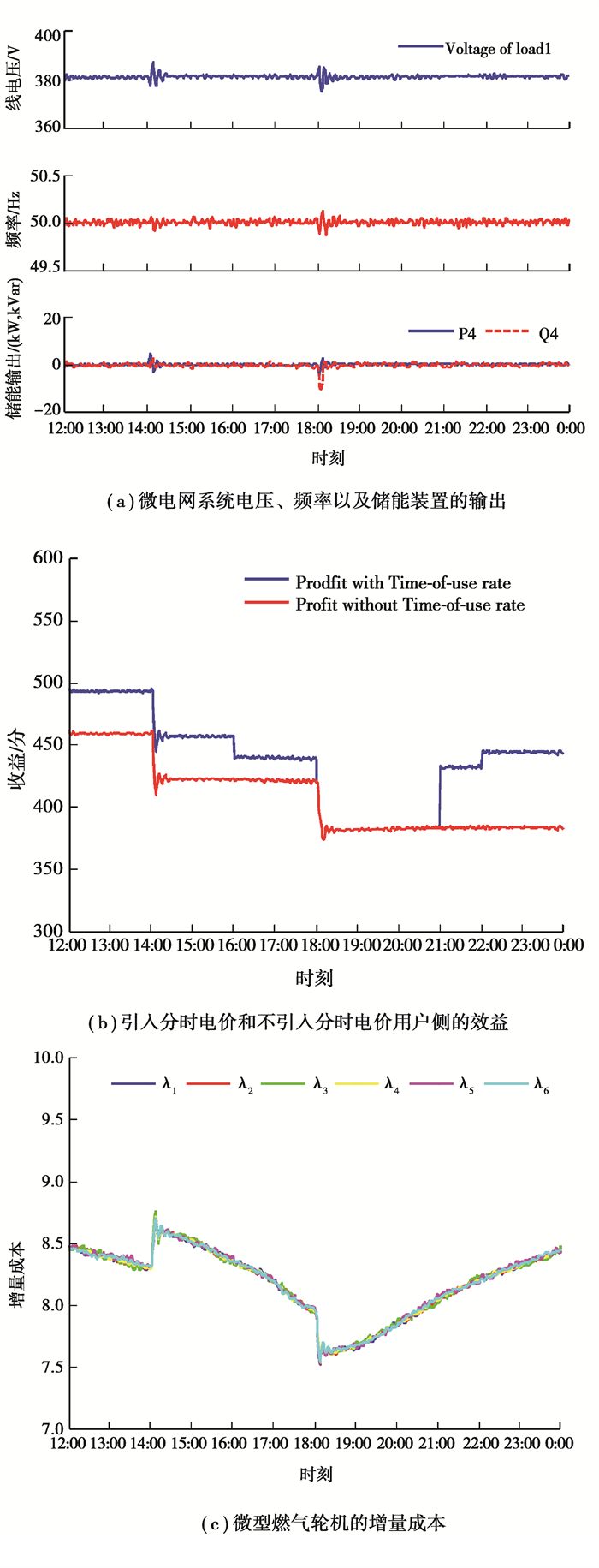
图 6 分时电价对用户效益影响的仿真结果 Fig. 6 Simulation results of impacts of Time-of-use rate on consumers' profit |
图 6(a)为微电网系统电压和频率以及储能装置的输出,可以看出在不可调负荷变化时,储能装置输出或吸收功率维持微电网的功率平衡,而这部分功率又很快被微型燃气轮机所分担,系统的电压和频率在不可调负载变化时有短暂的波动,在其他时刻都是稳定的。图 6(b)为在固定电价和分时电价机制下,用户侧的收益情况比较。根据式(2)~式(6)可得,由于未引入需求响应,可调负载的接入量始终保持一致,用电效用保持不变,而用电费用随着电价的降低而减少,因此用户的总收益将增加。在14:00时,由于不可调负载L7有功增加了20 kW,而用电效用增量又低于用电费用增量,所以用户侧的收益在这个时刻降低了45分左右;在18:00时,不可调负载L7切除,由于L7的用电效用高于其用电费用,所以切除后,用户侧效益降低了40分左右;在22:00时,分时电价达到最低值5.4分/kWh,因此可调负载用电费用达到最低,而用户侧的收益达到最大值445分。由于不可调负载的变化导致用户侧效益总体下降了85分,所以22:00用户侧效益较13:00不可调负载变化之前低。
从图 6(b)可以看出,引入分时电价机制能够提高用户侧的收益,在相同的可调负载接入量的情况下,分时电价价格越低,用户的收益越高。图 6(d)为微型燃气轮机的增量成本曲线,可以看出各微型燃气轮机的增量成本趋于一致,根据等微增率准则可知,此时发电侧的成本趋于最小。
3.2 算例2:需求响应对于优化调度结果的影响在分时电价机制下,考虑需求响应,使得可调负载L1-3和L5-6能够根据电价的变化调整其接入量的大小,在不可调负载和环境条件波动下,研究需求响应对于用户侧效益的影响,仿真结果如图 7所示。
|
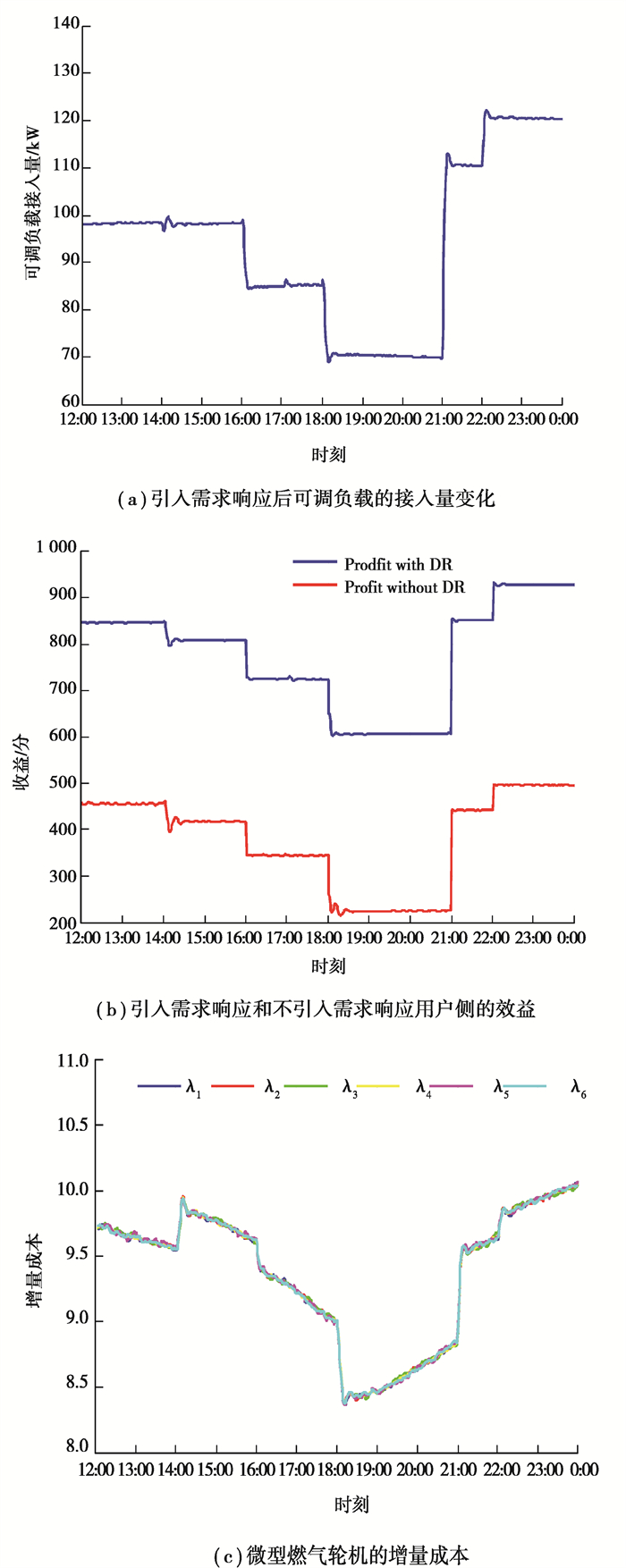
图 7 引入需求响应对用户效益影响的仿真结果 Fig. 7 Simulation results of impacts of DR on consumers' profit |
图 7(a)为可调负载的接入总量,在仿真过程中,保证整个仿真时段内含需求响应和不含需求响应的可调负载接入总量一致。图 7(b)为用户侧收益情况。可以看出:在含需求响应的12:00~21:00期间,随着分时电价价格的升高,此时可调负载的用电费用增加量大于用电效用增加量,所以可调负载的接入量逐渐减少,在18:00时,分时电价达到最大值8.4分/kWh,可调负载接入总量达到最小值70 kW;在21:00~0:00期间,分时电价价格开始降低,由于此时可调负载的用电效用的增益高于其用电费用的增益,因此为了提高用户侧的总收益,可调负载的接入量增大。在22:00时分时电价达到最低值5.4分,可调负载的接入量达到最大值120 kW,此时可调负载的用电效用远大于用电费用,用户侧收益也达到最大值930分。而未引入需求响应时,由于可调负载的接入量不会随着分时电价的变化而变化,保持为93 kW,所以随着分时电价的降低到最低值,用户侧的收益增益较小,最大收益仅为500分。
在分时电价机制下,引入需求响应与未引入需求响应的结果进行对比。从图 7(b)中可以看出,在22:00时,分时电价达到最低值5.4分/kWh,未引入需求响应时,负载接入总量保持不变;而引入需求响应后,可调负载的接入总量增加到120 kW,此时可调负载的用电效用远大于用电费用,此时,引入需求响应比未引入需求响应的用户侧效益增加了430分。在整个仿真时段,未引入需求响应的用户侧收益曲线均位于引入需求响应的用户侧收益曲线之下,在整个仿真时段内,引入需求响应之后用户的总收益较引入需求响应之前提高了104%。
4 结论文章提出一种考虑需求响应的孤岛微电网多目标经济调度模型,在分时电价机制下,实现微电网在运行过程中发电侧和用户侧双赢。在此模型中,首先构建了孤岛微电网发电侧成本的目标函数;接着在分时电价机制下引入需求响应,构建由用电效用和用电成本组成的用户侧效益目标函数,并设置了包含功率平衡约束、微型燃气轮机出力约束和可调负载接入限制的约束条件,从而建立以发电侧成本最小和用户侧效益最大为目标的多目标经济调度模型。求解上述模型,通过调整微型燃气轮机的出力,使其等微增率达到一致,实现发电侧成本最小化。另外,基于分时电价优化可调负载的接入量,实现用户侧收益的最大化。
为了检验所提出模型的性能,搭建孤岛微电网仿真平台进行测试。仿真结果显示,分时电价机制能够提高用户侧的收益,且分时电价越低,用户侧的收益越高。同时所提出的经济调度模型能够在可再生能源和不可调负荷波动的情况下,使得分布式电源增量成本趋于一致,实现发电侧成本最小,同时,使得用户侧的效益达到最大,并且保证微电网能够稳定运行。与分时电价机制下未引入需求响应的结果相比,引入需求响应后的用户侧效益提升了104%。
| [1] |
白建华, 辛颂旭, 刘俊, 等. 中国实现高比例可再生能源发展路径研究[J]. 中国电机工程学报, 2015, 35(14): 3699-3705. Bai J H, Xin S X, Liu J, et al. Roadmap of realizing the high penetration renewable energy in China[J]. Proceedings of the CSEE, 2015, 35(14): 3699-3705. (in Chinese) |
| [2] |
沈鑫, 曹敏. 分布式电源并网对于配电网的影响研究[J]. 电工技术学报, 2015, 30(S1): 346-351. Shen X, Cao M. Research on the influence of distributed power grid for distribution network[J]. Transactions of China Electrotechnical Society, 2015, 30(S1): 346-351. (in Chinese) |
| [3] |
Walling R A, Saint R, Dugan R C, et al. Summary of distributed resources impact on power delivery systems[J]. IEEE Transactions on Power Delivery, 2008, 23(3): 1636-1644. DOI:10.1109/TPWRD.2007.909115 |
| [4] |
杨新法, 苏剑, 吕志鹏, 等. 微电网技术综述[J]. 中国电机工程学报, 2014, 34(1): 57-70. Yang X F, Su J, LYU Z P, et al. Overview on micro-grid technology[J]. Proceedings of the CSEE, 2014, 34(1): 57-70. (in Chinese) |
| [5] |
郑晶, 李赓, 张艳华, 等. 微电网研究综述[J]. 电气开关, 2016, 54(2): 1-3, 25. Zheng J, Li G, Zhang Y H, et al. Summary of micro-grid[J]. Electric Switchgear, 2016, 54(2): 1-3, 25. (in Chinese) DOI:10.3969/j.issn.1004-289X.2016.02.001 |
| [6] |
Abido M A. A novel multiobjective evolutionary algorithm for environmental/economic power dispatch[J]. Electric Power Systems Research, 2003, 65(1): 71-81. DOI:10.1016/S0378-7796(02)00221-3 |
| [7] |
张双乐, 李鹏, 陈超, 等. 基于改进变尺度混沌优化算法的微网优化运行[J]. 电力自动化设备, 2013, 33(1): 70-74. Zhang S L, Li P, Chen C, et al. Economic operation of microgrid based on improved mutative scale chaotic optimization[J]. Electric Power Automation Equipment, 2013, 33(1): 70-74. (in Chinese) DOI:10.3969/j.issn.1006-6047.2013.01.013 |
| [8] |
李鹏, 李涛, 张双乐, 等. 基于混沌二进制粒子群算法的独立微网系统的微电源组合优化[J]. 电力自动化设备, 2013, 33(12): 33-38. Li P, LI T, Zhang S L, et al. Combinatorial optimization of micro-sources in standalone microgrid based on chaotic binary particle swarm optimization algorithm[J]. Electric Power Automation Equipment, 2013, 33(12): 33-38. (in Chinese) DOI:10.3969/j.issn.1006-6047.2013.12.006 |
| [9] |
金鹏, 艾欣, 许佳佳. 基于序列运算理论的孤立微电网经济运行模型[J]. 中国电机工程学报, 2012, 32(25): 52-59. Jin P, Ai X, Xu J J. An economic operation model for isolated microgrid based on sequence operation theory[J]. Proceedings of the CSEE, 2012, 32(25): 52-59. (in Chinese) |
| [10] |
罗毅, 刘明亮. 计及风险备用约束的孤网系统环保经济调度[J]. 电网技术, 2013, 37(10): 2705-2711. Luo Y, Liu M L. Research on environmental and economic dispatch for isolated microgrid system taken risk reserve constraints into account[J]. Power System Technology, 2013, 37(10): 2705-2711. (in Chinese) |
| [11] |
Bhattacharya A, Chattopadhyay P K. Hybrid differential evolution with biogeography-based optimization for solution of economic load dispatch[J]. IEEE Transactions on Power Systems, 2010, 25(4): 1955-1964. DOI:10.1109/TPWRS.2010.2043270 |
| [12] |
石庆均, 江全元. 包含蓄电池储能的微网实时能量优化调度[J]. 电力自动化设备, 2013, 33(5): 76-82. Shi Q J, Jiang Q Y. Real-time optimal energy dispatch for microgrid with battery storage[J]. Electric Power Automation Equipment, 2013, 33(5): 76-82. (in Chinese) DOI:10.3969/j.issn.1006-6047.2013.05.014 |
| [13] |
王明俊. 市场环境下的负荷管理和需求侧管理[J]. 电网技术, 2005, 29(5): 1-5. Wang M J. Load management and demand side management in electricity market environment[J]. Power System Technology, 2005, 29(5): 1-5. (in Chinese) DOI:10.3321/j.issn:1000-3673.2005.05.001 |
| [14] |
郭鸽. 考虑风光消纳的源荷联合多目标优化调度研究[D]. 西安: 西安理工大学, 2017. Guo G. Study on source-load joint multi-objective optimal scheduling for promoting wind power, photovoltaic consumption[D]. Xi'an: Xi'an University of Technology, 2017. (in Chinese) |
| [15] |
Luo F J, Zhao J H, Dong Z Y, et al. Optimal dispatch of air conditioner loads in southern China region by direct load control[J]. IEEE Transactions on Smart Grid, 2016, 7(1): 439-450. DOI:10.1109/TSG.2014.2388233 |
| [16] |
Ma K, Hu G Q, Spanos C J. Distributed energy consumption control via real-time pricing feedback in smart grid[J]. IEEE Transactions on Control Systems Technology, 2014, 22(5): 1907-1914. DOI:10.1109/TCST.2014.2299959 |
| [17] |
Tuan L A, Bhattacharya K. Competitive framework for procurement of interruptible load services[J]. IEEE Transactions on Power Systems, 2003, 18(2): 889-897. DOI:10.1109/TPWRS.2003.810998 |
| [18] |
Zhang D, Li S H, Sun M, et al. An optimal and learning-based demand response and home energy management system[J]. IEEE Transactions on Smart Grid, 2016, 7(4): 1790-1801. DOI:10.1109/TSG.2016.2552169 |
| [19] |
Wang Z L, Paranjape R. Optimal residential demand response for multiple heterogeneous homes with real-time price prediction in a multiagent framework[J]. IEEE Transactions on Smart Grid, 2017, 8(3): 1173-1184. DOI:10.1109/TSG.2015.2479557 |
| [20] |
Wood A J, Wollenberg B F, Sheblé G B. Power generation, operation and control[M]. New Jersey: Wiley, 1984.
|
| [21] |
夏海波. 含需求响应的孤岛微电网经济运行与优化调度方法研究[D]. 重庆: 重庆大学, 2018. Xia H B. Economic operation and optimal dispatch methods for islanded microgrids considering demand response[D]. Chongqing: Chonqing University, 2018. (in Chinese) |
| [22] |
Tomar V, Tiwari G N. Techno-economic evaluation of grid connected PV system for households with feed in tariff and time of day tariff regulation in New Delhi-a sustainable approach[J]. Renewable and Sustainable Energy Reviews, 2017, 70: 822-835. DOI:10.1016/j.rser.2016.11.263 |
| [23] |
Li Q, Peng C B, Wang M L, et al. Distributed secondary control and management of islanded microgrids via dynamic weights[J]. IEEE Transactions on Smart Grid, 2019, 10(2): 2196-2207. DOI:10.1109/TSG.2018.2791398 |
 2022, Vol. 45
2022, Vol. 45


