利用清洁能源发电是未来的趋势,而光伏发电是新能源的一种重要方式。但光伏发电方式的光功率受日照强度、温度等诸多因素影响,故发电量会随时间有较大的波动。而设备产生的电能直接被并入电网,这样势必会给电网调峰和调度带来巨大压力。因此,正确地预测光伏发电系统在某个时间段内光功率变化情况,对电网的稳定运行具有重要意义,也受到学术界和产业界的广泛关注[1]。
现有的光功率预测方法大致可以分为统计分析方法和人工智能方法2类。其中,基于套索算法[2]、基于统计升尺度[3]和基于整合移动平均自回归模型[4-5]的系列方法都属于统计分析方法。此类方法中模型较为简单,不能适应气象数据的随机变化,故其总体预测能力较差。人工智能方法主要基于各种神经网络、支持向量机、马尔可夫模型等,也有研究人员利用集成学习和信息融合的思想来解决问题[6-8]。目前,基于神经网络的方法是此问题领域最常见的解决方法,这是因为神经网络具有拟合未知的复杂函数关系的能力,善于处理分类与预测问题。求解未来的光功率问题既是一个预测问题,又可以转化为对发电量等级进行预测的分类问题,故神经网络非常适用于此领域。现有神经网络中反向传播神经网络[9-10] (BPNN, back propagation neural networks)、长短期记忆网络(LSTM, long short term memory)[11-12]、自组织神经网络[13]、径向基神经网络[14]、模糊神经网络[15],以及极限学习机等类神经网络方法都被应用到了光伏发电量预测问题中,并取得良好的效果。例如,白会杰[16]与田义[17]将一些人工智能基础模型用于光伏发电量预测,经过实验对比发现神经网络的判别能力高于传统统计学的ARIMA模型、决策回归树、支持向量回归算法及梯度提升树。基于此,研究人员也提出了许多对基础神经网络进行优化或改进的新方法[18-21],来预测复杂环境下的光伏发电量。
在现有的基于神经网络的光伏发电预测方法中,BPNN和LSTM是2种常用模型。这是因为BPNN是最具普适性的神经网络,可以拟合各种类型、各种特征的数据[22]。LSTM则适用于处理序列数据,尤其是时间序列数据,它更能关注样本数据在时间维度上所具有的特征,可以应对实际时序数据分类问题中,各种因素在实际发挥作用时的迟滞性问题与影响累积性问题[23]。光伏设备所采集的环境数据恰是时间序列数据,所以LSTM和BPNN能够取得更好的预测结果。
然而以上方法都是从单个视角出发,或是注重全局拟合,或是仅关注时序特征,未能同时发挥各种神经网络的优势,使预测模型受采集数据的变化影响较大,导致预测结果精度较低、稳定性较差。基于此,文中提出了一种基于双深度神经网络的光功率预测方法,利用长短期记忆网络LSTM与前馈神经网络BPNN的各自优势学习光伏发电时序数据,并通过遗传算法优化神经网络待定结构参数,最大化模型整体目标函数精度来搜索最优解,得到更加准确和鲁棒的预测结果。
1 相关技术文中算法以BPNN和LSTM为基础判别器,通过遗传算法将二者融合为更高精度的双深度神经网络光功率预测方法。本节对文中用到的BPNN、LSTM和遗传算法等基础知识进行简单介绍。
1.1 反向传播神经网络BPNNBPNN为使用反向传播算法的人工神经网络[22], 其中每个计算单元可以抽象为一个非线性函数,对传来的数据进行如式(1)的处理,该表达式以数学形式还原了人脑中神经元间化学信号转换为神经元上电信号的类似激活过程。
| $ \begin{array}{c} z^{(l)}=\boldsymbol{W}^{(l)} \cdot a^{(l-1)}+\boldsymbol{b}^{(l)}, \\ a^{(l)}=f_{l}\left(z^{(l)}\right), \end{array} $ | (1) |
式中:上标和下标l表示该神经元所处的层;a(l)表示神经元的输出;W(l)表示网络权重;b(l)为对应偏置向量;fl(·) 表示使用的激活函数,常用的激活函数有非线性修正单元(RELU,rectified linear unit)、挤压函数(sigmoid型)等。
要训练BPNN神经网络使其能够学习数据的规律,就要为其设置一个损失函数,用来衡量神经网络输出值与目标输出值(标签)之间的差距。通过使用反向传播的梯度下降法,不断地修正神经网络中各计算单元的可调参数W、b,可以使损失函数达到极小化。此时,模型输出值已达到最接近目标输出值的状态。模型训练完毕,可以用来对其他数据进行预测或分类。
1.2 长短期记忆网络LSTM循环神经网络(RNN, recurrent neural network)是一种具有一定记忆能力的人工神经网络[23]。在RNN中某一时刻t隐藏层与其上一时刻t-1的隐藏层间存在反馈连接,此连接将上一时间段内的信息——外部状态ht-1传入当前时刻,来实现记忆功能。在RNN中,每个计算单元可以用如下函数表达:
| $ \begin{array}{c} z_{t}=\boldsymbol{U} h_{t-1}+\boldsymbol{W} x_{t}+\boldsymbol{b}, \\ h_{t}=f_{l}\left(z_{t}\right), \end{array} $ | (2) |
式中:zt表示t时刻隐藏层的净输入值;ht为隐藏层状态值;U是状态权重矩阵。每一时刻网络的净输入不仅与当前的样本数据有关,也与上一时刻隐藏层的信息输入有关。
长短期记忆网络(LSTM)是RNN最常用的变体形式,它引入了门机制,可以解决标准RNN模型在样本数据过多时所产生的一些问题。每个LSTM计算单元中包含3个控制信息流量的“门”,分别为输入门it, 遗忘门ft和输出门ot,每种门在(0, 1)之间取值。LSTM还引入了内部状态ct,它专门用于隐藏层间循环信息传递,同时也输出信息给隐藏层的外部状态。内部状态与外部状态共同影响下一时刻。其单元结构如图 1所示。
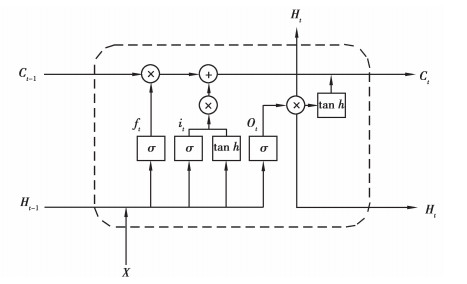
|
图 1 长短期记忆网络(LSTM)的单元结构 Fig. 1 Unit structure of long short-term memory network (LSTM) |
遗传算法[24]源自生物学领域“适者生存”的思想, 它模拟生物种群在繁衍时基因的随机自由组合以及DNA交叉、突变、异位等变异过程,常被用于参数选择、组合优化、规划设计等问题。遗传算法对要进行优化的参数进行编码,编码串可视为基因,经过个体间每代繁衍过程的基因随机组合和变异,会得到众多新的参数取值及参数组合形式。这些参数在适应函数(即优化的目标函数)下的值,就是该个体的适应度。每代仅保留一定数量的优秀个体,适应度较高的个体有更大的概率被保留,这样可以保证在优秀解的基础上逐步向最优解靠近。
遗传算法的本质是在给定的参数取值范围内进行非线性地、随机地搜索,找到使目标函数达到最优的一组解。可将其用于寻找文中模型融合的最佳比例系数。
2 基于双深度神经网络的预测方法不同来源的光伏发电的数据虽在采集属性、频次和参数单位等方面等存在差异,但都是标准的时间序列数据。LSTM具有记忆功能,可以探寻相邻的序列沿时间维度的特征,而BPNN从数据整体出发去拟合样本的真实分布,从而能够做出正确判别。LSTM和BPNN的特点决定了其擅于处理时间序列问题,2种网络各有侧重,将二者的决策进行有效融合能达到优势互补的作用,进而可以得到具有更高判别能力的鲁棒模型。因此,融合BPNN和LSTM的特点,文中提出了基于双深度神经网络的光功率预测方法,如图 2所示。首先,对采集到的光功率数据进行预处理,使其满足BPNN和LSTM 2个深度神经网络;然后,训练、优化BPNN和LSTM 2个深度神经网络,分别预测光功率数据结果;最后,利用遗传算法优化2个深度神经网络的融合系数,得到更加准确的光功率预测结果。具体过程如图 2所示。
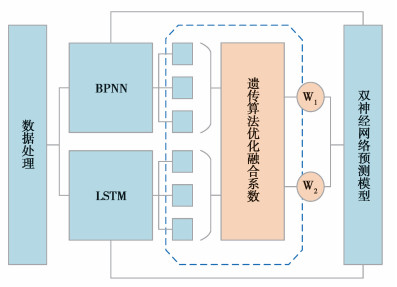
|
图 2 双深度神经网络融合算法结构图 Fig. 2 Schematic diagram of double deep neural network fusion algorithm |
BPNN可以拟合各种类型、各种特征的数据,因此可以用其拟合预测光伏发电序列数据。在本模型使用的BPNN结构中,使用交叉熵损失函数与梯度下降法优化更新网络的结构参数,完成光功率序列数据的预测,具体函数求解过程如下:
首先,定义交叉熵损失函数定义:
| $ J(y, \hat{y} \mid \boldsymbol{W}, \boldsymbol{b})=-y \log (\hat{y}), $ | (3) |
然后,利用梯度下降法计算各层梯度:
| $ \begin{array}{l} \frac{\partial J(y, \hat{y})}{\partial W^{(l)}}=\frac{\partial J(y, \hat{y})}{\partial z^{(l)}} \cdot \frac{\partial z^{(l)}}{\partial W^{(l)}}, \\ \frac{\partial J(y, \hat{y})}{\partial b^{(l)}}=\frac{\partial J(y, \hat{y})}{\partial z^{(l)}} \cdot \frac{\partial z^{(l)}}{\partial b^{(l)}}, \end{array} $ | (4) |
在反向传播过程中,对各层参数进行更新:
| $ \begin{array}{c} W_{n+1}^{(l)}=W_{n}^{(l)}-\alpha \cdot \frac{\partial J(y, \hat{y})}{\partial W_{n}^{(l)}}, \\ b_{n+1}^{(l)}=b_{n}^{(l)}-\alpha \cdot \frac{\partial J(y, \hat{y})}{\partial b_{n}^{(l)}} 。\end{array} $ | (5) |
最后,利用优化更新好的BPNN神经网络预测光功率数据值。
2.2 LSTM神经网络优化求解LSTM是一种典型的适用于处理序列数据尤其是时间序列数据的模型,可以应对时序数据分类问题中,各种因素在实际发挥作用时的迟滞性与影响累积性问题。光伏设备所采集的环境数据恰是时间序列数据,因此可以通过优化更新LSTM预测光功率数据值。同BPNN神经网络一样,循环神经网络也使用反向传播学习方法——随时间反向传播算法,优化更新整个深度预测网络。在具体优化更新过程中,主要计算3种门(遗忘门ft、输入门it、输出门ot)、节点状态及激活值,为
| $ {{f_t} = \sigma \left( {{W_f}{\chi _{(t - 1)}} + {U_f}{h_t} + {b_f}} \right),} $ | (6) |
| $ {{i_t} = \sigma \left( {{W_i}{\chi _{(t - 1)}} + {U_i}{w_t} + {b_i}} \right),} $ | (7) |
| $ {{a_t} = \tan {\rm{h}}\left( {{W_a}{\chi _{(t - 1)}} + {U_a}{w_t} + {b_a}} \right),} $ | (8) |
| $ {{C_t} = {C_{(t - 1)}} \odot {f_t} + {i_t} \odot {a_t},} $ | (9) |
| $ {{o_t} = \sigma \left( {{W_o}{\chi _{(t - 1)}} + {U_o}{w_t} + {b_o}} \right),} $ | (10) |
| $ {{h_t} = {o_t} \odot \tanh \left( {{C_t}} \right),} $ | (11) |
式中:权重W*、U*为各门处的权重b*为偏置;⊙表示向量元素乘。最后利用优化好的LSTM预测光功率数值。
2.3 双深度神经网络融合预测寻找融合的比例参数问题本质上是一种目标优化问题,利用遗传算法的搜索功能,可以找到使两者融合效果达到最佳的比例参数。用遗传算法寻找最佳融合系数,每代个体的适应度应为融合后的多模态模型所具有的判别精度。适应度函数为
| $ f\left( {{{\tilde \omega }_1},{{\tilde \omega }_2}} \right) = a(g(\mathit{\boldsymbol{X}})), $ | (12) |
式中:a(·)是正确率统计函数;g(X)为多模态模型给出的对数据集X中每个样本所属等级的判断,定义为
| $ g\left( {\mathit{\boldsymbol{X}}\mid {{\tilde \omega }_1},{{\tilde \omega }_2}} \right) = {\tilde \omega _1} \cdot B(\mathit{\boldsymbol{X}}) + {\tilde \omega _2} \cdot R(\mathit{\boldsymbol{X}}), $ | (13) |
式中:B(X)是BPNN对输入X的判别结果;R(X)是RNN对输入X的判别结果。
在得到遗传算法的双深度网络融合优化结果后,即可得到文中提出模型的最终预测值。由于遗传算法是在解空间内进行随机的搜索,每次将获得的不同的最优解,所以遗传算法的缺点是带有一定的不可重复性。对于文中光功率预测问题,由于融合结果对融合系数即遗传算法的待优化参数相对不敏感,所以遗传算法的缺点很难体现出来。加之,构成此算法的基础单模态模型都是由具有容错能力的神经网络来实现的,所以文中算法具有一定的鲁棒性。算法详细操作过程如表 1所示。
| 表 1 双深度网络融合算法 Table 1 Double deep neural network fusion algorithm |
在表 1的基于双深度神经网络的光功率预测中,第1~7步训练优化模型中的2个深度预测网络BPNN和LSTM,随机初始化2个网络的参数,并根据式(3)~式(11)优化更新网络中的各参数,直到2个网络达到最优;第8~17步根据遗传算法优化调整2个深度网络的融合权重,根据式(12)和式(13)设定遗传算法的适应度函数,并对其进行迭代更新,得到融合模型最优结果Y=g(X|$\tilde \omega $1*, $\tilde \omega $2*)=$\tilde \omega $1*·B(X)+$\tilde \omega $2*·R(X),根据得到的融合模型预测每个时刻的发电量等级。
3 实验针对文中提出的基于双深度神经网络的光功率预测方法进行实验分析,在具体的实验中选用东北电网的光伏发电历史数据,包括东北电网全网、辽宁电网、吉林电网、黑龙江电网和蒙东地区电网,进行BPNN和LSTM2个深度网络的融合预测模型分析,并通过预测正确率指标验证文中提出融合模型和各单深度网络模型(BPNN和LSTM)的精度。以下将对实验数据选取和预处理,以及实验过程调试和实验结果分析进行详细介绍。
3.1 实验数据实验数据来自东北电网电力研究所:包含东北电网全网、辽宁电网、吉林电网、黑龙江电网和蒙东地区电网的光伏发电历史数据。每个地区的数据包含辐照度、风速、实发电量等实时采用数据。数据的采用间隔为15 min,采样时间范围为2019年1月1日~11月3日。此外,由于光伏发电情况受温度等环境因素影响,在实验中从网络上获取了上述地区在该段时间的历史天气情况,使用每天的最高气温和最低气温作为实验数据的附加指标。
将上述的辐照度、风速、实发电量采样数据,每4个为一组取平均值,获得每小时的时均参数,得到每天24小时的数据。将获取的每天最高最低气温,插值到24个小时。认为最高温度出现在12时,最低温度出现在0时。
在实发电量的最高值和最低值间取2个阈值,将实发电量划分为高、中、低三个等级,此实际应用问题转化为了三分类问题。借鉴“相似日”思想[18],实际发电量可以反映当前很多不可测量因素对发电能力及发电设备效率的综合影响,所以对每条数据来说,其上一时段的实发电量也是有价值的数据,可将其作为本时刻的一维属性。
综上,数据集共有307×24=7 368条数据,每条时间序列共有4条属性和1个标签,属性即辐照度、风速、温度、上一时间段内实发电量。将数据划分为测试集和训练集,供实验使用,具体如表 2所示。
| 表 2 数据集描述 Table 2 Dataset description |
按照文中提出算法的步骤进行实验,分别将2个基础神经网络模型BPNN和LSTN训练优化至最佳状态。此时,2种神经网络的主要参数如表 3所示。
| 表 3 BPNN和LSTM在最佳状态下的参数 Table 3 Parameters of BPNN and LSTM in the best state |
当2个深度神经网络调整至最优时,利用遗传算法优化选择2个深度网络的融合权重,得到最后权重后,可以获取最优的双深度神经网络融合预测结果。在用遗传算法优化2种深度模型的融合加权系数过程中,为了更好地完成随机搜索,将用于融合的待优化参数由2个分裂为4个,赋予其不同的参数范围限制。在实验中对优化参数在设定范围内进行随机初始化,并对遗传算法进行20代繁衍,得到加权系数的最优解。
表 4和图 3展示了BPNN和LSTM 2种深度网络分别在各测试集的判别精度和2种深度网络在遗传算法作用下的融合判别精度,以及遗传算法给出的2个深度网络的归一化融合系数。
| 表 4 实验比较结果 Table 4 Experimental results |
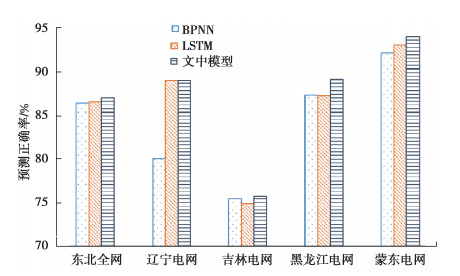
|
图 3 各算法比较结果 Fig. 3 Comparison results of different methods |
从图 3可以看出,对于东北、吉林、黑龙江和蒙东电网等大多数数据集,2种基本的神经网络判别能力相近,融合后的模型正确率高于任一种单视图判别模型。当2种基本模型的判别能力相差较大时,如辽宁电网数据集,BPNN和LSTM的正确率相差达9%,此时融合后的结果也不会比单视图模型中的最大精度值低。由此双神经网络模型可以将正确率稳定在单神经网络的最佳状态。
如表 4所示,通过遗传算法求解的模态网络参数在不同数据集上表现有所不同,致使不同深度网络在不同数据集结果预测上起到的作用也不尽相同。例如,在东北全网数据集上BPNN网络在融合预测结果中起到了较大作用,占到0.656的比重,而在辽宁电网数据集上,BPNN网络的比重只占到0.33。这说明,面对不同电网数据集时,由于数据特点的不同,深度神经网络的选择对预测结果影响巨大,如果预测网络选择不当将严重影响预测结果的精度。例如,如果在辽宁电网数据集上,只是用BPNN网络进行预测,得到结果的正确率仅为80.05%;而选择融合网络对数据进行预测,结果精度可以达到89.01%。即使单神经网络选择相对合理时能够得到相对较高的预测精度,如东北全网、吉林、黑龙江、蒙东电网等单网络预测结果,但数据中也可能存在部分数据不适用于选择的网络,因此选择双网融合预测能够得到更加有效和鲁棒的预测结果,例如,使用双网融合得到的结果全部优于单网预测结果(如表 4最后一列所示)。
综上,文中提出的基于双深度神经网络的光功率预测方法能够有效融合2个深度网络的优点,使其适应于不同数据集,得到更加有效和稳定的数据预测结果。
4 结论文章针对由气象因素和历史发电数据预测光伏发电光功率存在的问题,提出了基于BPNN和LSTM的双深度神经网络融合模型,该模型结合了两者在时序数据处理上的数据拟合与特征学习的能力,可以获得较高的光功率预测精度和稳定的预测结果。在东北电网实际数据集上的实验结果表明,文中提出的模型能够充分融合2种深度网络的特点,其判别能力强于单一深度网络模型,且具有一定的鲁棒性。
| [1] |
Yang M, Huang X. Ultra-short-term prediction of photovoltaic power based on periodic extraction of PV energy and LSH algorithm[J]. IEEE Access, 2018, 6: 51200-51205. DOI:10.1109/ACCESS.2018.2868478 |
| [2] |
刘金裕, 赵磊, 朱道立. 基于LASSO的光伏发电功率短期时间序列预测[J]. 电力科学与工程, 2019, 35(7): 13-22. Liu J, Zhao L, Zhu D L. Short-term time series prediction of photovoltaic power generation based on LASSO[J]. Electrical Science and Engineering, 2019, 35(7): 13-22. (in Chinese) DOI:10.3969/j.ISSN.1672-0792.2019.07.003 |
| [3] |
陈颖, 孙荣富, 吴志坚, 等. 基于统计升尺度方法的区域风电场群功率预测[J]. 电力系统自动化, 2013(7): 1-5. Chen Y, Sun S F, Wu Z J, et al. A regional wind power forecasting method based on statistical upscaling approach[J]. Automation of Electric Power Systems, 2013(7): 1-5. (in Chinese) |
| [4] |
赵滨滨, 王莹, 王彬, 等. 基于ARIMA时间序列的分布式光伏系统输出功率预测方法研究[J]. 可再生能源, 2019, 37(6): 820-823. Zhao B B, Wang Y, Wang B, et al. Research on the output power prediction method of distributed photovoltaic system based on ARIMA time series[J]. Renewable Energy, 2019, 37(6): 820-823. (in Chinese) DOI:10.3969/j.issn.1671-5292.2019.06.006 |
| [5] |
连立军, 王艳君, 邓林, 等. 基于多元统计分析的光伏发电量预测[J]. 河北农业大学学报, 2017, 40(1): 111-116. Lian L J, Wang J, Deng L, et al. Prediction of photovoltaic power generation based on multivariate statistical analysis[J]. Journal of Hebei Agricultural University, 2017, 40(1): 111-116. (in Chinese) |
| [6] |
彭曙蓉, 郑国栋, 黄士峻, 等. 基于XGBoost算法融合多特征短期光伏发电量预测[J]. 电测与仪表, 2020, 57(24): 76-83. Peng S R, Zheng G D, Huang S J, et al. Multiple-feature short-term photovoltaic generation forecasting based on XGBoost algorithm[J]. Electrical Measurement and Instrumentation, 2020, 57(24): 76-83. (in Chinese) |
| [7] |
李英姿, 曾万昕, 戴玉, 等. 基于D-S证据理论的光伏发电量预测[J]. 电气应用, 2019, 38(2): 102-107. Li Y Z, Zeng WX, Dai Y, et al. Prediction of photovoltaic power generation based on D-S evidence theory[J]. Electrical Applications, 2019, 38(2): 102-107. (in Chinese) |
| [8] |
Wang Z, Zhang M, Wang D, et al. Failure prediction using machine learning and time series in optical network[J]. Optics Express, 2017, 25(16): 18553-18565. DOI:10.1364/OE.25.018553 |
| [9] |
郝宁, 王新娜, 宁博扬, 等. 基于BP神经网络的配网系统光伏输出功率平滑控制分析[J]. 电子测量技术, 2019, 42(16): 62-65. Hao N, Wang X N, Ning B Y, et al. Smooth control analysis of photovoltaic output power of distribution network system based on BP neural network[J]. Electronic Measurement Technology, 2019, 42(16): 62-65. (in Chinese) |
| [10] |
Song H, Chen Y, Zhou N, et al. Electricity consumption forecasting for smart grid using the multi-factor back-propagation neural network[C]//Sensors and Systems for Space Applications XII. International Society for Optics and Photonics, 2019.
|
| [11] |
黄滇玲, 迟学斌, 许可, 等. 基于长短时记忆网络的光伏发电功率预测[J]. 科研信息化技术与应用, 2019, 10(2): 31-41. Huang D L, Chi X B, Xu K, et al. Photovoltaic power generation prediction based on long and short time memory network[J]. Scientific Research Information Technology and Application, 2019, 10(2): 31-41. (in Chinese) |
| [12] |
Zhang C, Wang M, Zhang M, et al. Adaptive failure prediction using long short-term memory in optical network[C]//201924th Optoelectronics and Communications Conference (OECC) and 2019 International Conference on Photonics in Switching and Computing (PSC). IEEE, 2019: 1-3.
|
| [13] |
López M, Valero S, Senabre C, et al. Application of SOM neural networks to short-term load forecasting: The Spanish electricity market case study[J]. Electric Power Systems Research, 2012, 91: 18-27. DOI:10.1016/j.epsr.2012.04.009 |
| [14] |
Zeng J, Qiao W. Short-term solar power prediction using an RBF neural network[C]//2011 IEEE Power and Energy Society General Meeting. IEEE, 2011: 1-8.
|
| [15] |
张玉, 万成伟. 基于模糊神经网络的光伏发电量短期预测[J]. 电子设计工程, 2017, 25(2): 150-153. Zhang Y, Wan C W. Short-term prediction of photovoltaic power generation based on fuzzy neural network[J]. Electronic Design Engineering, 2017, 25(2): 150-153. (in Chinese) |
| [16] |
白会杰. 基于人工智能的光伏发电短期功率预测技术[D]. 北京: 北京交通大学, 2019. Bai H J. Short-term photovoltaic power prediction technology based on artificial intelligence[D]. Beijing: Beijing Jiaotong University, 2019. |
| [17] |
田义. 基于深度学习的光伏发电功率预测技术研究[D]. 北京: 北方工业大学, 2019. Tian Y. Research on prediction technology of photovoltaic power based on deep learning[D]. Beijing: North China University of Technology, 2019. |
| [18] |
李燕斌, 万亚宁, 肖俊明, 等. 基于PSO优化BP神经网络的光伏发电量预测[J]. 中原工学院学报, 2019, 30(4): 75-79. Li Y B, Wan Y N, Xiao J M, et al. Prediction of photovoltaic power generation based on optimized BP neural network based on PSO[J]. Journal of Zhongyuan Institute of Technology, 2019, 30(4): 75-79. (in Chinese) |
| [19] |
黄鹏. 基于变分模态分解和神经网络的光伏发电功率短期预测[D]. 南宁: 广西大学, 2019. Huang P. Short-term prediction of photovoltaic power generation based on variational mode decomposition and neural network[D]. Nanning: Guangxi University, 2019. (in Chinese) |
| [20] |
Yun G, Zhang B, Yan X Y. Accurate short-term forecasting for photovoltaic power method using rbm combined LSTM-RNN structure with weather factors quantification[C]//2019 IEEE Sustainable Power and Energy Conference (iSPEC). IEEE, 2019: 797-802.
|
| [21] |
李芬, 宋启军, 蔡涛, 等. 基于PCA-BPNN的并网光伏电站发电量预测模型研究[J]. 可再生能源, 2017, 35(5): 689-695. Li F, Song Q J, Cai T, et al. Research on power generation prediction model of grid-connected photovoltaic power station based on PCA-BPNN[J]. Renewable Energy, 2017, 35(5): 689-695. (in Chinese) |
| [22] |
Zeng Y R, Zeng Y, Choi B, et al. Multifactor-influenced energy consumption forecasting using enhanced back-propagation neural network[J]. Energy, 2017, 127: 381-396. |
| [23] |
Greff K, Srivastava R K, Koutník J, et al. LSTM: a search space odyssey[J]. IEEE Transactions on Neural Networks and Learning Systems, 2016, 28(10): 2222-2232. |
| [24] |
Bharathi C, Rekha D, Vijayakumar V. Genetic algorithm based demand side management for smart grid[J]. Wireless Personal Communications, 2017, 93(2): 481-502. |
 2022, Vol. 45
2022, Vol. 45

