谐振接地系统经消弧线圈接地方式具有易熄灭电弧和减小过电压危害等优势,广泛应用于3~60 kV的中压配电网中,由于消弧线圈的补偿作用,导致故障电流微弱,零序电流方向不定[1]和出现“虚幻接地”[2]或“换相”[3]的现象,未彻底解决谐振接地系统故障选线问题,制约了配电网安全可靠供电运行。目前,主要利用故障信号暂态量实现故障选线[4-7],以零序电流的能量、电压或电流幅值,极性和突变量为依据筛选故障线路。文献[8]以“能量最大”为标准确定零序电流的特征频带,提出相对能量法实现故障选线;文献[9]通过比较相邻监测点故障电流的极性判别故障线路;文献[10]根据故障时相电压和相电流突变量之间的关系,提出一种故障定位方法。上述方法受到故障电流微弱、方向不定或换相影响出现选线失误,因此,仅利用故障电流某一方面的特征构造选线依据具有片面性,当故障特征不明显时,易出现误判。配电线路发生单相接地故障时,故障线路与非故障线路间零序电流波形明显区别于非故障线路间零序电流波形,从零序电流波形相似度出发,可将图像相似度识别方法[11-14]应用在单相接地故障选线中。为此,提出一种接地故障选线新方法,该方法以线路间零序电流波形的相似程度为选线依据,对零序电流应用希尔伯特黄变换(HHT, Hilbert Huang transform)得到Hilbert时频谱,再用时频谱带通滤波法重构各频带的零序电流,计算得到各线路故障电流的时频能量矩阵,求得综合相似系数矩阵完成故障选线。
1 时频能量矩阵 1.1 HHT算法HHT的处理对象是具有非平稳、非线性特性的零序电流信号,其步骤中的EMD(empirical mode decomposition)在分解故障信号时,获得IMF分量随着原始信号而变化,出现模态混叠问题[15]。因此,采用时频谱带通滤波法处理零序电流信号来解决上述问题,具体处理步骤见文献[16]。
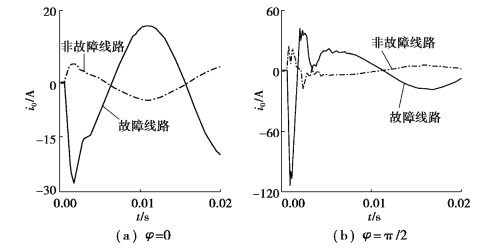
1.2 零序电流波形特征在不同故障角下,馈线与母线故障时线路的零序电流波形,如图 1和图 2所示。
|
图 1 不同故障角下线路的零序电流波形 Fig. 1 Zero-sequence current waveform of the circuit at different fault angles |
|
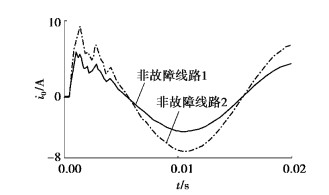
图 2 母线接地时线路的零序电流波形 Fig. 2 Zero-sequence current waveform of the circuit on bus-bar earthed fault |
在φ=0时,零序电流主要是低频感性电流;在φ=π/2时,零序电流主要是高频电容分量,其余时刻,零序电流由2个不同频率的电流合成[8]。由图可知,馈线故障时,故障线路与非故障线路间零序电流波形差异明显,相似度低;母线故障时,非故障线路的零序电流波形在相同时刻所对应的相位基本相同,只是幅值略有差异,各线路的零序电流波形相似度较高。因此,在任意故障角下,均可采用文中方法实现故障选线。
1.3 时频能量矩阵对经HHT处理的各线路电流波形使用时频谱带通滤波法得到M(i=1, 2, …, M)个不同频带的原始信号分量,将各频带原始信号分量按时间轴进行K等分,得到l个具有相同频带宽度和时间间隔的时频小块,对每个时段进行P等分。定义所有分量时频小块的能量为
| $ {e_{il}} = \sum\limits_{m = 1}^p {\left| {{a_{il}}(m)\Delta t} \right|} , $ | (1) |
式中:ail(m)为子频带i在时频小块l内m个数据点的幅值;Δt为每等分所占的时间。求出所有时频小块的幅值,可获得各线路零序电流的时频能量矩阵为
| $ \mathit{\boldsymbol{E}} = \left[ {\begin{array}{*{20}{c}} {{e_{11}}}&{{e_{12}}}& \cdots &{{e_{1l}}}\\ {{e_{21}}}&{{e_{22}}}& \cdots &{{e_{2l}}}\\ \vdots & \vdots &{}& \vdots \\ {{e_{M1}}}&{{e_{M2}}}& \cdots &{{e_{Ml}}} \end{array}} \right]。$ | (2) |
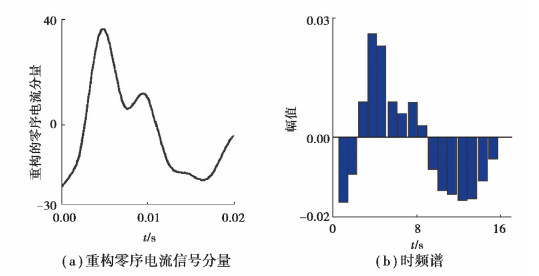
采用时频谱带通滤波法将各条线路的零序电流波形分解到16个不同的频带内, 取频带宽度Δf=300 Hz,子频带的频率范围是[(i-1)Δf, iΔf](i=1, 2, …, M),将每个子频带内的重构零序电流信号按时间轴等间距划分为16个时间段,可以得到16×16个时频小块,据式(1)计算所有时频小块的能量值,即时频能量矩阵中的元素。重构的某一子频带内零序电流信号分量及其时频谱,如图 3所示。
|
图 3 Hilbert子频带时频谱 Fig. 3 Time-frequency spectrum for Hilbert sub-band |
设EA、EB分别是2条不同线路零序电流信号的时频能量矩阵,则故障波形间的相似度ρAB为
| $ {\rho _{{\rm{AB}}}} = \frac{{\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^K {{\mathit{\boldsymbol{E}}_A}} } (i,j){\mathit{\boldsymbol{E}}_B}(i,j)}}{{\sqrt {\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^K {\mathit{\boldsymbol{E}}_A^2} } (i,j)\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^K {\mathit{\boldsymbol{E}}_B^2} } (i,j)} }}, $ | (3) |
式中,ρAB值越接近于1,即2条线路的故障波形越相似;ρAB值越小,说明2条线路的故障波形相似度越低。
2.2 接地故障选线判据根据相似度矩阵求出线路i和其他线路间的综合相似系数ki[16],与阈值kset比较判断故障线路,经过多次仿真表明kset取值0.1。
发生单相接地故障选线判据如下:
1) 如果线路i均有ki>kset,i=1,2,…,H,则是母线故障;
2) 如果有ki<kset,i=1,2,…,H,则是线路i故障。
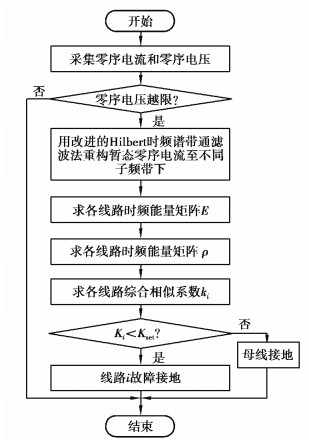
故障选线方法流程,如图 4所示。
|
图 4 故障选线方法流程 Fig. 4 Flowchart of fault line detection |
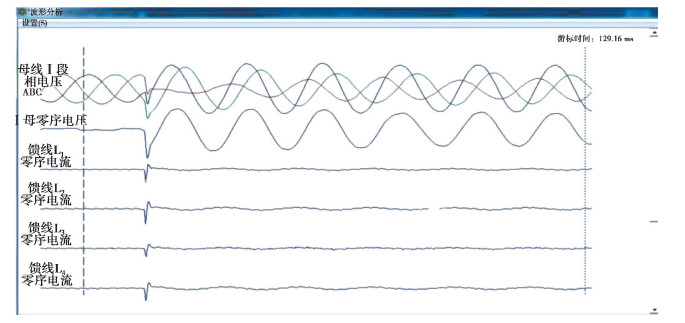
某地区110 kV/10 kV的变电站有L1~L4配电线路,其母线故障和馈线故障的采样波形数据[17]分别如图 5和图 6所示,用来验证文中方法的选线准确性。
|
图 5 母线故障的实测录波波形 Fig. 5 Measured recorded waveform of bus-bar fault |
|
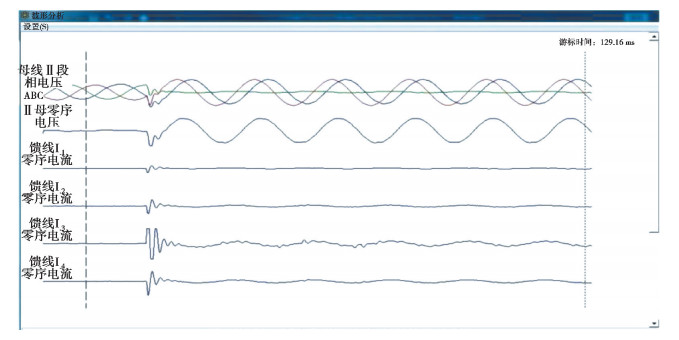
图 6 馈线L3故障的实测录波波形 Fig. 6 Measured recorded waveform of feeder L3 fault |
2013年2月10日,母线发生单相接地故障,计算每条线路零序电流的综合相似系数,结果如下:
| $ k_{1}=0.976, k_{2}=0.995, k_{3}=0.993, k_{4}=0.995 。$ |
将综合相似系数与阈值0.1比较,k1、k2、k3和k4的值均大于0.1,所以判定母线故障,判定结果与实际情况相符合。
3.1.2 馈线故障2013年5月1日,馈线L3发生单相接地故障,计算每条线路零序电流的综合相似系数,结果如下:
| $ k_{1}=0.643, k_{2}=0.651, k_{3}=-0.975, k_{4}=0.640 。$ |
将综合相似系数与阈值0.1比较,k3<kset=0.1,其他馈线的综合相似系数均大于0.1,所以故障线路是L3,判定结果与实际情况相符合。
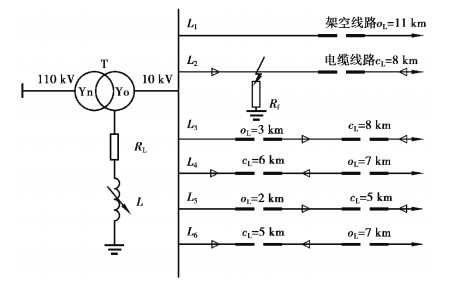
3.2 方法适应性分析考虑线路类型对故障选线的影响,用MATLAB搭建缆线混合线路的谐振接地系统,其模型如图 7所示。图中OL、CL分别为架空线路和电缆线路长度。消弧线圈的补偿度取5%,电感L取值0.35 H,得到RL=0.03 ωL=3.3 Ω,每条馈线的负荷大小是0.5+j0.25 MVA。仿真模型中主变压器和馈线参数分别如表 1和表 2所示。
|
图 7 谐振接地系统仿真模型 Fig. 7 Simulation model of resonant earthed system |
| 表 1 主变压器的参数 Table 1 Parameters of the main transformer |
| 表 2 馈线参数 Table 2 Parameters of the feeder |
为了验证文中方法在不同故障情况下的选线有效性,改变馈线类型、故障位置、接地电阻和故障角几种因素完成仿真分析。不同故障情况下接地故障的选线结果如表 3所示。表中:Li是故障线路;lf是故障位置(故障点到母线的距离);Rf是接地电阻;θ是故障角;[k1k2 k3 k4 k5 k6] 是综合相似系数矩阵。
| 表 3 接地故障选线结果 Table 3 Results of earthed fault line detection |
由表 3可知,当线路故障时,故障线路的综合相似系数均小于阈值kset(kset=0.1);当母线故障时,所有线路的综合相似系数均大于0.1,不同条件下均正确选线。
3.2.2 噪声干扰设置线路L1和线路L3发生单相接地故障,故障信号中加入高斯白噪声(信噪比为30 dB)时,仿真结果如表 4所示。
| 表 4 高斯白噪声影响的选线结果 Table 4 Results of fault line detection with Gaussian white noise |
由表 4可知,该方法在噪声干扰下准确选线,抗干扰能力强。假设线路3在故障角为90°时,不对零序电流作HHT分解,得到的直接计算结果是[0.537 0.536-0.947 0.528 0.553 0.543],选线结果正确但选线裕度较低,适应性不强。
3.2.3 两点接地故障设置线路L2在lf=7 km和线路L4在lf=5 km处发生B相接地故障,接地电阻是20 Ω,其仿真选线结果如表 5所示。结果表明,此方法在线路同时和不同时发生两点接地故障均正确选线,适应性较好。
| 表 5 两点接地故障时的选线结果 Table 5 Results of fault line detection with two earthed faults |
当消弧线圈处于过补偿状态时,谐振接地系统发生单相接地故障时零序电流减小,其减小量与补偿度有关,而且零序电流波形特征的持续时间短暂,因此,设置线路L1末端在故障角接近0,接地电阻是2 kΩ时发生接地故障,选用不同补偿度p下,不同暂态时间范围内的零序电流波形,其仿真选线结果如表 6所示。由表 6可知,此方法在消弧线圈处于过补偿状态,即使零序电流波形特征的持续时间短暂,仍可正确选线。
| 表 6 不同暂态时间范围的故障选线结果 Table 6 Results of fault line detection with different transient time ranges |
假设故障线路是L3,在接地电阻Rf=20 Ω、故障位置lf=3 km和故障角θ=0时,故障信号中加入高斯白噪声(信噪比为30 dB)进行仿真,分别用文中方法、基于EMD的选线方法[7]和基于小波包的选线方法[8]进行选线,结果如表 7所示。
| 表 7 故障选线结果 Table 7 Results of different methods of fault line detection |
由表 7可知,在恶劣的故障环境下零序电流幅值会受到影响而减小,影响故障特征提取,引起基于EMD选线方法失误。而基于小波包的选线方法虽然选线正确,但小波包选线方法中的小波基函数的确定具有主观性,选线效果依赖于小波基函数的确定,在恶劣复杂的故障工况下会出现误选。文中所用HHT自适应分解零序电流,利用时频带通滤波法重构零序电流,解决了HHT分解故障信号存在的模态混叠问题,实现正确的故障选线。
4 结论利用故障后各线路零序电流波形图像的相似度,结合各线路电流波形的时频能量矩阵,提出一种配电线路的接地故障选线新方法。
1) 采集零序电流波形数据实现接地故障选线,充分利用幅值和极性等故障信息,克服了单一型选线依据的片面性所造成的选线错误问题。
2) 该方法有效放大了故障电流特征,可以区分母线故障和馈线故障,在外界噪声干扰和发生两点接地故障情况下其适应性较好。
3) 采用复杂的时频能量矩阵相似度实现故障选线,解决了仅利用波形相似度选线需提取整个频带故障信号特征时所忽略的故障信号时变性问题。
| [1] |
龙茹悦, 黄纯, 汤涛, 等. 一种谐振接地系统的配电线路接地故障选线新方法[J]. 电力系统保护与控制, 2019, 47(21): 21-29. Long R Y, Huang C, Tang T, et al. A new method of grounding fault line selection for distribution line in resonant grounding system[J]. Protection and Control of Power System, 2019, 47(21): 21-29. (in Chinese) |
| [2] |
束洪春. 谐振接地系统虚幻接地的辨识和综合选线方法[J]. 电力自动化设备, 2016, 36(6): 122-129. Shu H C. Identification and comprehensive line selection method of illusory grounding in resonant grounding system[J]. Electric Power Automation Equipment, 2016, 36(6): 122-129. (in Chinese) |
| [3] |
束洪春. 配网选线保护与故障定位[M]. 北京: 科学出版社, 2016: 28-30. Shu H C. Line selection protection and fault location of distribution network[M]. Beijing: Science Press, 2016: 28-30. (in Chinese) |
| [4] |
Cheng S W, Fu Z X. Single-phase ground fault line selection for distribution network based on frequency domain parameter identification method[J]. IOP Conference Series: Earth and Environmental Science, 2019, 267(4): 147-151. DOI:10.1088/1755-1315/267/4/042130 |
| [5] |
刘谋海, 王媛媛. 基于暂态相电流特征分析的故障选线新方法[J]. 电力系统及其自动化学报, 2017, 29(1): 30-36. Liu M H, Wang Y Y. A new fault line selection method based on transient phase current characteristics analysis[J]. Proceedings of the CSU-EPSA, 2017, 29(1): 30-36. (in Chinese) DOI:10.3969/j.issn.1003-8930.2017.01.006 |
| [6] |
Wei X, Yang D. An adaptive fault line selection method based on wavelet packet comprehensive singular value for small current grounding system[C]//20155th International Conference on Electric Utility Deregulation and Restructuring and Power Technologies (DRPT). IEEE, 2015.
|
| [7] |
王清亮, 杜辉. 基于固有模态能量的暂态量选线方法[J]. 工矿自动化, 2013, 39(9): 92-95. Wang Q L, Du H. Line selection method with transient state based on intrinsic mode energy[J]. Industrial and Mining Automation, 2013, 39(9): 92-95. (in Chinese) |
| [8] |
束洪春, 彭仕欣. 配网缆-线混合线路故障选线相对能量法[J]. 电力自动化设备, 2009, 29(11): 1-5. Shu H C, Peng S X. Relative energy method for fault line selection of distribution cable hybrid line[J]. Electric Power Automation Equipment, 2009, 29(11): 1-5. (in Chinese) DOI:10.3969/j.issn.1006-6047.2009.11.001 |
| [9] |
庞清乐, 刘昱超, 李希年, 等. 基于电流极性比较的主动配电网故障定位方法[J]. 电力系统保护与控制, 2018, 46(20): 107-114. Pang Q Y, Liu Y C, Li X N, et al. The fault location method based on current polarity comparison in active distribution network[J]. Protection and Control of Power System, 2018, 46(20): 107-114. (in Chinese) |
| [10] |
常仲学, 宋国兵, 黄炜, 等. 基于相电压电流突变量特征的配电网单相接地故障区段定位方法[J]. 电网技术, 2017, 41(7): 2363-2369. Chang Z X, Song G B, Huang W, et al. The single-phase grounding fault location method based on the sudden change characteristics of phase voltage and phase current for distribution network[J]. Power System Technology, 2017, 41(7): 2363-2369. (in Chinese) |
| [11] |
Xu X. Underwater target recognition based on time-frequency matrix[C]//International Conference on Intelligent Human-machine Systems & Cybernetics. IEEE, 2012.
|
| [12] |
Xiao X, Xu F, Yang H. Short duration disturbance classifying based on S-transform maximum similarity[J]. International Journal of Electrical Power And Energy Systems, 2009, 31(7/8): 374-378. |
| [13] |
李泽文, 贺子凝, 郭田田, 等. 基于时频矩阵相似度的输电线路暂态保护方法[J]. 电力系统自动化, 2019, 43(5): 121-134. Li Z W, He Z N, Guo T T, et al. Transmission line transient protection method based on time-frequency matrix similarity[J]. Automation of Electric Power Systems, 2019, 43(5): 121-134. (in Chinese) |
| [14] |
Yuan Y, Chen X, Yang L, et al. A novel fault line selection method of resonant grounding system[C]//2017 IEEE Conference on Energy Internet and Energy System Integration (EI2). Beijing: IEEE, 2017: 1-5.
|
| [15] |
蒋海峰, 张曼, 赵斌炎, 等. 基于改进Hilbert-Huang变换的电网故障诊断[J]. 电工技术学报, 2019, 34(S1): 336-342, 351. Jiang H F, Zhang M, Zhao B Y, et al. Power network fault diagnosis based on improved Hilbert-Huang transform[J]. Journal of Electrical Technology, 2019, 34(S1): 336-342, 351. (in Chinese) |
| [16] |
Guo M F, Yang N C, Chen W F. Deep-Learning-based fault classification using Hilbert-Huang transform and convolutional neural network in power distribution systems[J]. IEEE Sensors Journal, 2019, 1. |
| [17] |
张宁. 小电流接地选线方法研究与装置研制[D]. 北京: 华北电力大学, 2017. Zhang N. Method research and equipment development of small current grounding line selection[D]. Beijing: North China Electric Power University, 2017. (in Chinese) |
 2022, Vol. 45
2022, Vol. 45


 ,
,