2. 湖南大学 电气与信息工程学院, 长沙 410082
2. College of Electrical Engineering, Hunan University, Changsha 410082, P. R. China
准确的负荷预测是保障电网稳定、解决电量偏差、节约能源的有效途径[1]。随着存储技术和数据采集技术的发展,通过历史数据搭建预测模型进行负荷预测的方式广受关注[2]。传统的时间序列预测方法主要包括最小二乘回归法[3]、回归分析法[4]等,由于负荷数据的非线性、非平稳性和自相关性等特征[5-6],这些方法难以达到电力市场的精度要求。神经网络算法具有较强的非线性特征提取能力,能够有效提高预测模型的精度。目前,已有大量的神经网络算法应用在负荷预测模型中,主要包括BP神经网络[7]、支持向量机(support vector machine,SVM)[8]、长短期记忆神经网络(long short-term memory,LSTM)[9]、极限学习机(extreme learning machine,ELM)[10]、极限梯度提升(extrme gradient boosting, XGBoost)[11]等。文献[12]针对风电功率的随机性和波动性特征,建立了基于遗传算法优化后的核极限学习机预测模型,具有较好的泛化性能与预测精度。文献[13]针对负荷数据不确定性动态特征,提出了一种基于约束并行长短期记忆神经网络分位数回归的短期电力负荷概率预测模型,该模型有效提高了预测效率和预测精度。文献[14]提出了一种基于贝叶斯深度学习的多任务概率预测模型框架,通过群集池化的方式增加该框架处理数据的多样性和数量,不仅解决了过拟合问题,还改善了预测性能。
由于负荷数据作为一种时间序列存在较强的自相关性,在构建预测模型时有必要针对负荷数据进行时序分析。混沌时序分析一直是时序数据因果的研究热点,它通过延迟时间和嵌入维度对时序数据进行自相关分析。此外,负荷数据易受温度、湿度等因素的影响而存在非平稳性,在进行数据时序分析时有必要进行信号分解。变分模态分解算法相比较小波分解、经验模态分解等信号处理技术,能够有效克服断点效应和模态混叠两大弊端[15]。文中针对负荷数据自相关、非平稳特征对预测精度的影响,提出了一种基于多粒度核极限学习机(multi-granularity kernel extreme learning machine, MG-KELM)的负荷预测模型。首先,原始负荷的时间复杂度较高,导致负荷数据存在较强的非平稳特征,通过变分模态分解算法将原始负荷数据分解为时间复杂度较低且频率相对平稳的主要特征分量、中频细节分量和高频随机分量。其次,不同频率的模态分量的自相关性强弱不同,导致输入数据的时间窗取值影响着模型的预测精度,文中通过混沌时序分析方法,求解各个模态输入预测模型时的时间窗大小。最后,通过融合多个频率粒度的核极限学习机的预测结果,实现负荷多粒度预测。结果表明,文中模型通过变分模态分解算法和混沌时序分析方法,使预测模型能更有效提取负荷数据中的时序特征,提高模型的预测精度。
1 基本理论 1.1 混沌时间序列分析混沌理论对原始数据进行重构,将原始数据扩展到高维空间,以高维的方式将非线性系统中隐含的特征信息表现出来[16]。根据混沌学Takens的延迟嵌入定理,时间序列可以通过相空间重构恢复到原系统。对于单变量时间序列X∈{x1, x2, …, xn},通过嵌入维度d和延迟时间τ进行相空间重构,拓扑结构为
| $ X=\left\{x_{i}, x_{i+\tau}, \cdots, x_{i+(d-1) \tau}\right\}, i \in[1, n] 。$ | (1) |
进行相空间重构时需要对嵌入维度d和延迟时间τ进行求解,其中交互信息法和虚假近邻法是计算这2个参数的有效方法。
1.1.1 交互信息法求解延迟时间交互信息法是一种通过信息论和遍历论求解非线性系统混沌时间序列延迟时间τ的一种有效方法。对于时间序列X∈{x1, x2, …, xn},延迟时间τ的交互信息公式为
| $ I(\tau)=H[x(i)]+H[x(i+\tau)]-H[x(i), x(i+\tau)], $ | (2) |
式中:I(τ)为x(i+τ)对于x(i)的依赖程度。当I(τ)为0时,说明x(i+τ)和x(i)完全不相关,而I(τ)的第1个极小值表示x(i+τ)和x(i)的最大可能不相关,相空间重构时I(τ)的第1个极小值为最优的延迟时间。
1.1.2 虚假近邻法求解嵌入维度虚假近邻法在相空间重构方面是计算嵌入维数的有效方法。随着嵌入维度的增大,混沌运动轨迹逐渐打开,低维空间相邻的2个数据在高维可能相距很远,那么这2个点便是虚假近邻点。针对时间序列X∈{x1, x2, …, xn},令a(i, d)代表维度变换距离之差:
| $ a(i, d)==\left\|x_{i}(i+d \tau)-x_{j}(i+d \tau)\right\|^{2} 。$ | (3) |
如果a(i, d)(典型值为[10,50]),则认为这2个数据是由于高维混沌吸引子中2个不相邻的数据投影到低维空间中变成虚假近邻点。嵌入维数从2开始,随着嵌入位数d的增大,直到虚假临近点的数量少于某一值或者虚假临近点的数量不再改变时,此时的嵌入维度d便是最小嵌入维度。
1.2 变分模态分解变分模态分解算法(variational mode decomposition,VMD)能够将原始非平稳信号S分解为k个具有不同中心频率和有限带宽的相对平稳子信号{μ1, μ2, …, μn}。每一个子信号作为原始信号的一种带限固有模态分量(band-limited intrinsic mode function,BLIMF)[15],能够反映原始信号在不同时间尺度下的结构特征。
| $ S(t)=\sum\limits_{i=1}^{k} \boldsymbol{\mu}_{i}(t) , $ | (4) |
| $ \boldsymbol{\mu}_{i}(t)=A_{i}(t) \cos \left(\varphi_{i}(t)\right), $ | (5) |
式中:Ai表示模态分量μi的幅值;φi表示模态分量μi的相位。
文中将原始负荷数据经VMD分解为不同模态分量,考虑不同模态分量的自相关性强弱不同,针对每一模态分量建立各自的预测模型,以提高预测精度。文中模型用于短期负荷预测,在短时间内温度波动幅度较小,温度分解对短期预测模型的预测精度影响较小,故不对温度数据进行VMD分解,以减小模型的复杂度。
1.3 核极限学习机极限学习机是一种高效的单隐含层前馈神经网络,广泛应用在预测回归和分类领域。极限学习机的输入为[x1, x2, …, xn],输入层与隐藏层之间是全连接。若隐藏单元的个数是m,则隐藏层的输出矩阵为
| $ \boldsymbol{H}(x)=\left[h_{1}(x), h_{2}(x), \cdots, h_{k}(x)\right] 。$ | (6) |
隐藏单元的输出是输入节点乘上隐藏节点的权值w加上偏差b,经过一个非线性函数将所有输入节点求和得:
| $ h_{i}(x)=\sum\limits_{j=1}^{n} g\left(w_{i j} \times x_{i j}+b_{i j}\right)。$ | (7) |
其中:g是激活函数,常用的有Sigmoid函数、Gaussian函数等。
从隐藏层到输出层也是全连接,输出层的结果为
| $ o_{i}(x)=\sum\limits_{i=1}^{k} \beta_{i} h_{i}(x)=H(x) \beta 。$ | (8) |
文中选取均方根误差(RMSE),平均绝对误差(MAE)和决定系数(R2)作为预测模型的评价指标。假设,预测值为
| $ \mathrm{RMSE}=\sqrt{\frac{1}{n} \sum\limits_{i=1}^{n}\left(\widehat{y}_{i}-y_{i}\right)^{2}}, $ | (9) |
式中,RMSE的范围是[0,+∞],该指标越小,说明预测值越贴近真实值。
| $ \mathrm{MAE}=\frac{1}{n} \sum\limits_{i=1}^{n}\left|\widehat{y}_{i}-y_{i}\right|, $ | (10) |
式中,MAE的范围是[0,+∞],该指标越小,说明预测值越贴近真实值。
| $ R^{2}=1-\frac{\sum\limits_{i=1}^{n}\left(\widehat{y}_{i}-y_{i}\right)^{2}}{\sum\limits_{i=1}^{n}\left(y_{i}-\bar{y}\right)^{2}}, $ | (11) |
式中:y是真实值y的均值;R2的范围是[0, 1],该指标越大,说明预测模型拟合程度越高。
2 负荷多粒度预测模型 2.1 负荷预测中的时间窗大小取值问题负荷作为一种时序数列,具有较强的自相关性。此外,用户用电过程中受温度因素的影响,导致负荷与温度之间存在潜在的互相关性。针对多变量单值预测模型,其数学模型为
| $ y_{t+m}=f(X, Z), $ | (12) |
| $ X=\left\{x_{t}, x_{t-1}, \cdots, x_{t-k_{x}}\right\}, $ | (13) |
| $ Z=\left\{z_{t+h}, z_{t+h-1}, \cdots, z_{t+h-k_{z}}\right\}, $ | (14) |
式中:t表示时刻;m表示预测步长;f表示预测模型;X表示历史负荷数据;Z表示预测温度数据;y表示预测负荷。
由式(12)所代表的负荷预测模型可知,预测质量不仅与预测模型拟合的函数f有关,还与输入数据的时间窗大小kX和kZ有关。文中分析负荷数据的自相关性以及负荷数据与温度数据之间的互相关性,研究输入数据的时间窗大小对模型预测精度的影响。
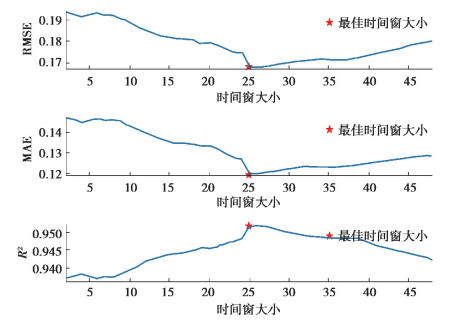
选择核极限学习机作为预测模型,采用1.4节中的评价指标衡量模型的预测质量。当预测步长较小时,负荷数据的自相关性对预测模型影响较大。设置预测步长大小为1,预测温度时间窗kZ大小为24,预测质量与输入负荷时间窗大小的关系曲线如图 1所示。由图 1可知,当输入负荷时间窗大小为25时,模型的预测质量最高,说明合适的负荷时间窗大小能够提高模型的预测精度。
|
图 1 预测质量与输入负荷时间窗大小的关系曲线 Fig. 1 Relationship between the prediction quality and the size of the input load-time window |
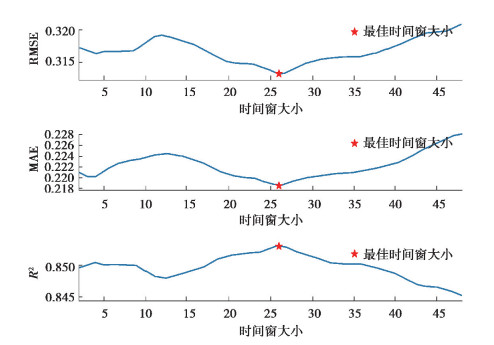
当预测步长较大时,负荷数据与温度数据之间的互相关性对预测模型影响较大。设置预测步长为5,预测负荷时间窗kX大小为25,预测质量与输入温度时间窗大小的关系曲线,如图 2所示。由图 2可知,当输入温度时间窗为26时,模型的预测质量最高,说明合适的温度时间窗大小能够提高模型的预测质量。
|
图 2 预测质量与输入温度时间窗的关系曲线 Fig. 2 Relationship between prediction quality and the size of input temperature-time window |
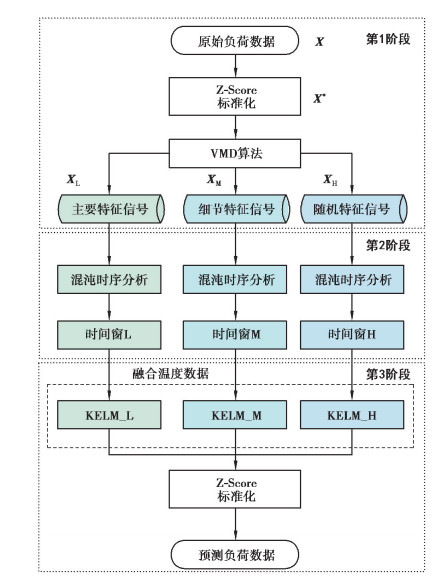
文中提出的基于MG-KELM的负荷预测模型的总体框架,如图 3所示,该模型包括3个阶段:信号分解阶段、时间窗求解阶段和多粒度预测阶段。
|
图 3 基于MG-KELM的多粒度预测模型的总体框架 Fig. 3 Framework of the prediction model based on MG-KELM |
第1阶段:信号分解阶段。与其它时序信号比较,台区负荷的频率分量相对较少。为此,将负荷信号X分解为3个中心频率递增的子信号:主要特征信号XL,细节特征信号XM和随机特征信号XH。可根据经验得到负荷信号分解的个数,实验发现分解个数为3比较合理。如果原始信号最优的分解个数为2或者4,则需相应建立数量为2或者4的子信号预测模型,文中模型作相应修改即可。
第2阶段:时间窗求解阶段。通过混沌时序分析,利用嵌入维度和延迟时间求解每个模态在进行预测时的时间窗。
1) 混沌特性分析。在进行相空间重构时,延迟时间τ和嵌入维度m由于数据时间长度有限导致求解时不存在。此外,混沌系统具有对初始值的极端敏感性,即2个差别很小的初值经过混沌系统处理后产生的差距将越来越大,并且呈现指数级分离,Lyapunov指数是描绘这一现象的方法。只要最大Lyapunov指数大于0便可判定该系统存在混沌特性。因此,一个系统是否具有混沌特性可以从2个方面判断:在一定条件下延迟时间和嵌入维度是否可解,最大Lyapunov指数是否大于0。
2) 时间窗求解。在数据Xi处,理想时间窗的窗内数据与之时序相关,窗外数据与之时序无关。根据数据是否具有混沌特性,时间窗的计算方法分为2种情况。
情况一:数据具有混沌特性。在单变量相空间重构过程中,延迟时间τ和嵌入维度m使得{xi, xi-τ, …, xi-(m-1)τ}中,数据之间保持相互独立但又不完全随机。由于时间窗的大小与延迟时间和嵌入维度有关,由混沌时间序列中延迟时间τ和嵌入维度m,得到混沌时间序列中数据之间最大不相关的时间尺度T的最终表达式为
| $ T=(m-1) \tau \text { 。} $ | (15) |
情况二:数据不具有混沌特性。对于不具有混沌特性的系统,无法进行相空间重构,说明该数据系统的时序相关性较弱。若数据不具有混沌特性,则将时间窗大小设为定值24。
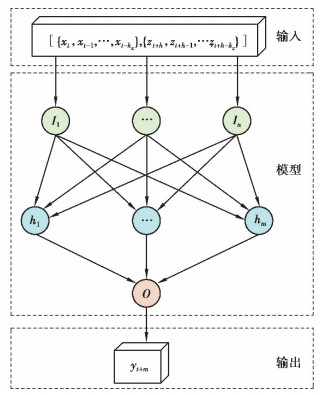
第3阶段:多粒度预测阶段。针对每个模态建立不同时间窗大小的KELM预测模型,再对各个预测模型进行累加求和,最终反标准化得出预测负荷数据。多粒度预测阶段的目的是针对不同频率的模态分量,建立不同时间窗大小的KELM预测模型,基于KELM的单一模态分量预测模型,如图 4所示。
|
图 4 基于KELM的单一模态分量的预测模型 Fig. 4 Prediction model of single-mode function based on KELM |
Step1:构建多粒度数据。根据上一阶段时间窗求解方法,分别计算主要特征分量XL、细节特征分量XM、随机特征分量XH和温度数据的时间窗大小kXL、kXM、kXH和kZ。因此,多粒度训练数据的结构为
| $ y_{t+m}=\left[x_{t}, \cdots, x_{t-k_{x}}, z_{t+h}, \cdots, z_{t+h-k_{z}}\right] 。$ | (16) |
Step2:多粒度训练。根据Step1中的多粒度训练数据,建立各个模态分量的KELM训练模型。由于ELM只需设定隐藏层节点个数和激活函数类型,参照文献[17]的方法进行设置。
Step3:多粒度预测。累加各个模态分量的KELM模型的输出值,通过反标准化得出最终预测结果。
3 案例分析着重考虑负荷自相关性和非平稳性对于预测模型精度的影响,选取欧盟互联电网(europe electricity transmission system operator,ENTSO)公布的台区负荷数据作为案例,验证文中模型的有效性。数据类型包括负荷数据和温度数据,采样时间为2015年1月1日至2017年5月1日,采样间隔为1 h。训练数据的样本规模为15 000,测试数据的样本规模为2 000。
3.1 时间窗有效性分析为了验证时间窗大小对预测精度的影响,各个模态分量通过不同大小的时间窗,以MG-KELM模型进行预测实验。表 1为原始数据以及VMD分解后各个模态分量的混沌特性分析,根据最大李雅普诺夫指数判断,都具有混沌特性。因此,以延迟时间和嵌入维度求解的时间窗进行负荷预测。
| 表 1 数据混沌特性分析 Table 1 Chaotic characteristics of data |
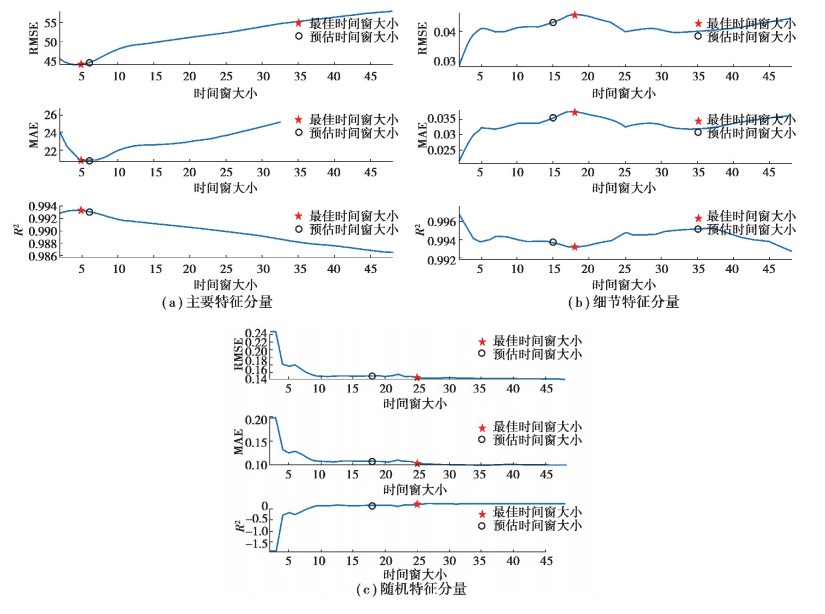
时间窗大小与模型预测精度关系,如图 5所示,图中蓝色曲线为不同时间窗大小时模型的预测结果,红色五角星是使预测模型预测质量最高时的时间窗大小,黑色圆圈是根据混沌时序分析预估的时间窗大小。从图 5可知,最佳时间窗大小使得预测精度最高,在图中表现为RMSE、MAE和R2的极值点,说明时间窗大小能够影响模型的预测精度。
|
图 5 时间窗大小与模型预测精度关系 Fig. 5 Relationship between the size of the time window and model prediction accuracy |
当时间窗过大,模型提取时序特征存在冗余;当时间窗较小,模型提取时序特征较不完整。此外,各个模态分量的最佳时间窗大小不同,说明数据中不同模态分量的时序特征不同,表达其时序特征所需的序列长度也不同。对比表 1可知,根据混沌相时序分析求解的时间窗取值接近最佳时间窗, 说明文中方法能够有效预估时间窗的大小。
3.2 预测模型对比为了验证文中模型的有效性,采用长短期神经网络(LSTM)作为对比实验。根据原始负荷是否通过VMD分解,设立如表 2所示的4种对比试验。其中,与ELM相关的预测模型的隐藏层数量设为100,激活函数设置为径向基函数(RBF)类型;与LSTM相关的预测模型的隐藏层单元数量设置为100,梯度阈值设置为1,迭代次数设置为150,激活函数设置为S型函数(Sigmoid)类型。为了消除随机因素的影响,所有预测模型进行20次仿真实验,去除各自实验结果中最坏和最好的情况后,以平均值作为最终的预测结果。
| 表 2 实验对照组 Table 2 Experimental control group |
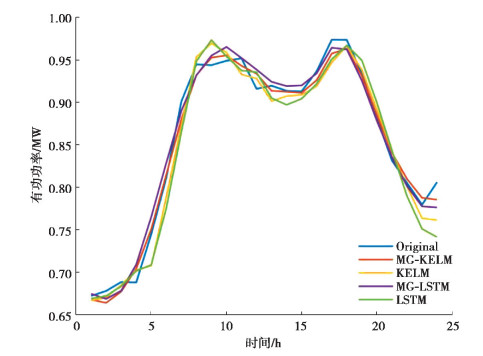
当预测步长为1时,各个模型预测结果的评价指标如表 3所示,滑动预测24 h的结果如图 6所示。由表 3可知,MG-ELM在所有预测模型中的RMSE指标值和MAE指标值最小,说明文中模型的单点预测值与实际值最为接近;MG-ELM在所有预测模型中的R2系数最大,说明文中模型的整体拟合度最高。观察图 6中各个模型预测数据形成的曲线形态,所有模型在进行单步预测时均能较好地拟合出原始负荷数据的曲线形态,但在9:00、16:00、24:00等时刻ELM和LSTM的预测值与原始值存在较大差异。
| 表 3 预测步长为1时的预测评价指标对比 Table 3 Prediction and evaluation indicators when the prediction step is 1 |
|
图 6 预测步长为1时各个模型的预测结果 Fig. 6 Prediction results of each model when the prediction step is 1 |
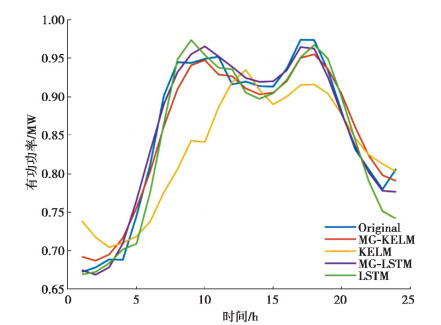
当预测步长为7时,各个模型预测结果的评价指标如表 4所示,滑动预测24 h的结果如图 7所示。由表 4可知,随着预测步长的增大,各个模型的预测精度均有下滑,但是MG-LELM和MG-LSTM均保持较好的预测质量。观察图 7中各个模型预测数据形成的曲线形态,ELM与原始负荷数据形态差异最大;LSTM与原始负荷数据虽然形态相似,但是各个时刻的负荷值相差较大;MG-ELM和MG-LSTM不仅与原始负荷形态相似,所预测的负荷大小也与原始负荷大小相近。表明通过变分模态分解算法和混沌时序分析方法,针对负荷数据进行多粒度的时序特征处理,能够提升原有模型的多步长预测精度。
| 表 4 预测步长为7时的预测评价指标对比 Table 4 Prediction and evaluation indicators when the prediction step is 7 |
|
图 7 预测步长为7时各个模型的预测结果 Fig. 7 Prediction results of each model when the prediction step is 7 |
文中MG-KELM模型通过变分模态分解建立时间多粒度的极限学习机进行短期负荷预测,考虑负荷数据存在时序数列的自相关性,通过混沌时序分析方法计算时间窗的大小。不同模态分量的中心频率不同,不同模态的自相关性强弱也不同,针对每一种模态分量进行混沌相空间时序分析,建立各自的预测模型。这种多粒度的负荷预测模型,可以提高所有模态的拟合程度,最终提升对原始负荷数据的预测精度。结果表明,通过变分模态分解的方法进行多粒度时序预测可以提升原始预测模型的精度,通过混沌时序分析方法可以估算最佳时间窗,提高各个模态的预测精度。
| [1] |
张昀, 周湶, 任海军, 等. 改进人工免疫网络算法在电力短期负荷预测中的应用[J]. 重庆大学学报, 2013, 36(4): 33-38. Zhang Y, Zhou Q, Ren H J, et al. Application and research of improved artificial immune network to power short-term load forecasting[J]. Journal of Chongqing University, 2013, 36(4): 33-38. (in Chinese) |
| [2] |
李闯, 孔祥玉, 朱石剑, 等. 能源互联环境下考虑需求响应的区域电网短期负荷预测[J]. 电力系统自动化, 2021, 45(1): 71-78. Li C, Kong X Y, Zhu S J, et al. Short-term load forecasting of regional power grid considering demand response in energy interconnection environment[J]. Automation of Electric Power Systems, 2021, 45(1): 71-78. (in Chinese) |
| [3] |
王雁凌, 吴梦凯. 经济新常态下基于偏最小二乘回归的中长期负荷预测模型[J]. 电力自动化设备, 2018, 38(3): 133-139. Wang Y L, Wu M K. Medium and long term load forecasting model based on partial least-square regression under new normal economy[J]. Electric Power Automation Equipment, 2018, 38(3): 133-139. (in Chinese) |
| [4] |
Mahmud M A. Isolated area load forecasting using linear regression analysis: practical approach[J]. Energy and Power Engineering, 2011, 3(4): 547-550. DOI:10.4236/epe.2011.34067 |
| [5] |
Amjady N. Short-term bus load forecasting of power systems by a new hybrid method[J]. IEEE Transactions on Power Systems, 2007, 22(1): 333-341. DOI:10.1109/TPWRS.2006.889130 |
| [6] |
Fan S, Chen L. Short-term load forecasting based on an adaptive hybrid method[J]. IEEE Transactions on Power Systems, 2006, 21(1): 392-401. DOI:10.1109/TPWRS.2005.860944 |
| [7] |
Bian H H, Zhong Y Q, Sun J S, et al. Study on power consumption load forecast based on K-means clustering and FCM-BP model[J]. Energy Reports, 2020, 6: 693-700. |
| [8] |
王保义, 王冬阳, 张少敏. 基于Spark和IPPSOLSSVM的短期分布式电力负荷预测算法[J]. 电力自动化设备, 2016, 36(1): 117-122. Wang B Y, Wang D Y, Zhang S M. Distributed short-term load forecasting algorithm based on Spark and IPPSOLSSVM[J]. Electric Power Automation Equipment, 2016, 36(1): 117-122. (in Chinese) |
| [9] |
Abdel-Nasser M, Mahmoud K. Accurate photovoltaic power forecasting models using deep LSTM-RNN[J]. Neural Computing and Applications, 2019, 31(7): 2727-2740. DOI:10.1007/s00521-017-3225-z |
| [10] |
Zhang C, Zhou J Z, Li C S, et al. A compound structure of ELM based on feature selection and parameter optimization using hybrid backtracking search algorithm for wind speed forecasting[J]. Energy Conversion and Management, 2017, 143: 360-376. DOI:10.1016/j.enconman.2017.04.007 |
| [11] |
Zheng H T, Yuan J B, Chen L. Short-term load forecasting using EMD-LSTM neural networks with a xgboost algorithm for feature importance evaluation[J]. Energies, 2017, 10(8): 1168. DOI:10.3390/en10081168 |
| [12] |
王浩, 王艳, 纪志成. 基于SAIGM-KELM的短期风电功率预测[J]. 电力系统保护与控制, 2020, 48(18): 78-87. Wang H, Wang Y, Ji Z C. Short-term wind power forecasting based on SAIGM-KELM[J]. Power System Protection and Control, 2020, 48(18): 78-87. (in Chinese) |
| [13] |
李丹, 张远航, 杨保华, 等. 基于约束并行LSTM分位数回归的短期电力负荷概率预测方法[J]. 电网技术, 2021, 45(4): 1356-1364. Li D, Zhang Y H, Yang B H, et al. Short time power load probabilistic forecasting based on constrained parallel-LSTM neural network quantile regression mode[J]. Power System Technology, 2021, 45(4): 1356-1364. (in Chinese) |
| [14] |
Yang Y D, Li W, Gulliver T A, et al. Bayesian deep learning-based probabilistic load forecasting in smart grids[J]. IEEE Transactions on Industrial Informatics, 2020, 16(7): 4703-4713. DOI:10.1109/TII.2019.2942353 |
| [15] |
Dragomiretskiy K, Zosso D. Variational mode decomposition[J]. IEEE Transactions on Signal Processing, 2014, 62(3): 531-544. DOI:10.1109/TSP.2013.2288675 |
| [16] |
黎静华, 黄玉金, 黄乾. 基于改进混沌时间序列的风电功率区间预测方法[J]. 电力自动化设备, 2019, 39(5): 53-60, 68. Li J H, Huang Y J, Huang Q. Interval prediction method of wind power based on improved chaotic time series[J]. Electric Power Automation Equipment, 2019, 39(5): 53-60, 68. (in Chinese) |
| [17] |
鲁迪, 王星华, 贺小平. 基于混合粒子群算法和多分位鲁棒极限学习机的短期风速预测方法[J]. 电力系统保护与控制, 2019, 47(5): 115-122. Lu D, Wang X H, He X P. Hybrid population particle algorithm and multi-quantile robust extreme learning machine based short-term wind speed forecasting[J]. Power System Protection and Control, 2019, 47(5): 115-122. (in Chinese) |
 2022, Vol. 45
2022, Vol. 45

