2. 中国原子能科学研究院放射化学研究所,北京 102413
2. Department of Radiochemistry, China Institute of Atomic Energy, Beijing 102413, P. R. China
近十年来,中国核电规模持续高速发展,预计到2030年,中国将累积贮存近2.4万吨的乏燃料[1]。目前国际上对乏燃料处置有“一次通过”和“闭式循环”两种战略,“一次通过”战略[2]将进行乏燃料的地质处置,该战略的铀利用率小于1%,导致宝贵的铀资源大量浪费。天然铀资源是不可再生的,而通过乏燃料后处理回收铀、钚等有用核燃料材料再循环使用,可使铀资源的利用率提高50~60倍。因此,利用面向核资源回收的乏燃料后处理技术,建立闭式燃料循环体系,已成为核能可持续发展的重要方向之一。乏燃料组件切割是乏燃料后处理的第一步,组件由多根燃料芯管组成[1],单根芯管由元件管和燃料芯组成,由于其较高的放射性,科研试验中常采用不锈钢管与脆性材料作为模拟组件来替代[3]。
与激光切割和等离子切割相比,机械剪切是一种快速、可靠的切割方法[4-5]。目前,对不锈钢管剪切的关注较多,涉及到脆性材料剪切的研究仍比较少。受试验技术和条件限制,有限元分析是脆性材料结构研究的有效途径[6-8]:刘亚忠等[9]利用脆性断裂力学理论,建立断裂分析模型,模拟了陶瓷材料在切削过程中的断裂过程,但主要用于脆性拉伸破坏为主要破坏方式的材料;曲蒙等[10]将损伤塑性模型和模糊裂缝模型联合应用,数值模拟了混凝土的损伤、断裂全过程,在一定程度上尝试了损伤与断裂结合应用于脆性材料试件的失效过程分析,但仅针对于混凝土单轴拉伸试验;周芬等[11]基于ANSYS二次开发,编写考虑损伤后混凝土D-P(Drucker-Prager)本构模型应用于剪力墙及混凝土立方体块模型,并通过与未考虑损伤的D-P模型对比,验证其合理性,但并未进行试验验证。
目前国内外关于脆性材料剪切的研究极少,对脆性材料剪切数值模型以及剪切产生的最大剪切力、剪切工艺参数研究也比较少,而最大剪切力对乏燃料剪切设备及刀具设计十分重要。笔者借助于成熟的非线性有限元技术,选用考虑损伤的D-P模型,即采用Drucker-Prager模型与Shear Damage模型相结合建立脆性材料剪切本构模型,选取脆性材料的典型代表砂浆进行剪切试验验证,对其受剪产生的剪切力进行数值分析,并探究剪切速度与刀具间隙对剪切力的影响,为单根芯管及乏燃料组件的剪切研究提供了理论基础,并为乏燃料剪切设备及刀具设计提供参考。
1 脆性材料剪切本构模型在脆性材料剪切有限元分析中,因其材料本身的特殊性而相对复杂,需要高效的建模方法和合理的材料本构模型[11]。笔者选用目前广泛使用的Drucker-Prager本构模型,并选择Shear Damage模型定义损伤,将损伤与断裂联合应用于脆性材料剪切。
D-P模型在von Mises模型的基础上改进与发展,与Mohr-Coulomb模型相似[11]。D-P模型[12]不考虑温度变化的影响,但考虑了由屈服引起的体积膨胀。故广泛应用于岩石、陶瓷、混凝土等脆性材料,其能够反映脆性材料的强度特征在多轴应力状态下的变化趋势。
材料受到荷载之后,逐渐由弹性变形变为非弹性变形,即开始发生塑性变形,这个由弹性转变到非弹性的条件就是屈服条件。线性Drucker-Prager模型的屈服面函数为
| F=t−ptanβ−d=0, | (1) |
| t=F(k)√J2, | (2) |
| d=(1−1/3tanβ)σc, | (3) |
| p=−I1/√3。 | (4) |
式中:t为偏应力;p为平均应力;J2是偏应力张量的第二不变量;I1是主应力张量的第一不变量;β是屈服面在应力空间上的倾斜角,是材料的内摩擦角;d是强化函数,根据单轴抗压强度σc定义;k是三轴拉伸强度与三轴压缩强度之比,体现了主应力对屈服的影响,控制屈服面在偏平面上的形状。考虑便利性与保密性,笔者参考C30混凝土,选用配合比(水∶水泥∶砂,质量比)为0.56∶1.00∶2.47的砂浆材料进行验证本构模型的合理性,根据文献[13],为确保屈服面外凸,将k值取为0.78,内摩擦角β取为53.7°。
在屈服之后控制着塑性流动的法则称作流动法则。其中,对于金属采用关联流动法则已经得到了广泛的认可,对于砂浆等脆性材料,多数学者认为应该采用非关联的流动法则,即塑性势面与屈服面不同。塑性势面函数为
| G=t−ptanψ, | (5) |
屈服面大小的变化通过给出σ与等效塑性应变εpl的关系来控制,σ取为单轴抗压强度σc,等效塑性应变为
| ˉεpl=∫Δˉεpldt, | (6) |
| dˉε−pl=|dεpl11|。 | (7) |
由于有限元方法是基于连续介质力学的,所研究的是连续的物体,即在空间中物质域是连续的。在这样的理论假设框架下,单元是不会消失的。而在实际情况中,一些单元势必会因为损伤、断裂的存在而消失或者失效,为了模拟这种情况,选择剪切损伤模型(Shear Damage)来定义损伤,模拟材料断裂过程。剪切损伤模型已成功运用于剪切工艺中,并能与实际结果吻合良好。
剪切损伤模型需要设定断裂应变(fracture strain)与破坏位移(displacement at failure)。断裂应变衡量材料从何时开始进入损伤,对应损伤开始时的等效塑性应变值。当材料的损伤达到1时最终失效,选择位移控制材料损伤演化,损伤最大为1时所对应的塑性位移值为破坏位移。
故笔者结合Drucker-Prager模型与Shear Damage模型建立脆性材料剪切有限元模型。
2 砂浆基体块剪切有限元模型根据所设计的剪切试验装置在ABAQUS/Explicit中建立如图 1所示的有限元模型,由试件、剪切刀、压紧头和固定刀组成,试件为直径为16 mm,长为56 mm的砂浆基体块。
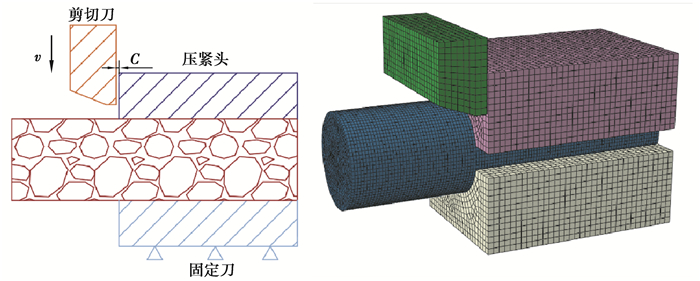
|
图 1 砂浆基体块剪切模型 Fig. 1 Shear model of mortar block |
为了计算方便,减小计算量,压紧头、固定刀与剪切刀均设置为离散刚体,剪切刀简化并且适量减小,压紧头、固定刀设置边界条件时,各方向位移均设置为0,剪切刀施加向下的速度载荷v为40 mm/s,刀具间隙即剪切刀与固定刀的间隙为C。剪切速度、刀具间隙均是可变参数,在试验中改变刀具间隙十分繁琐,因此在数值模型中设置了不同间隙下的剪切仿真,探究刀具间隙对其剪切力的影响,刀具间隙在0.1~1.6 mm范围内变动。
固定刀、压紧头与剪切刀的单元类型为四节点壳单元类型R3D4,网格大小设置为1 mm×1 mm,砂浆基体块单元类型如表 1所示,选择8节点等参减缩积分单元C3D8R,网格大小设置为0.5 mm×0.5 mm。
| 表 1 有限元模型单元类型 Table 1 Element type of finite element model |
为了使砂浆基体块网格单元沿径向划分,如图 2(a)所示,将基体块切分为内圆柱、外圆管两部分进行网格划分,内外边界单元尺寸分别为0.5,0.6 mm。保证离散刚体网格尺寸大于砂浆基体块,防止节点穿透导致计算错误。划分后,网格数为92 400万。

|
图 2 砂浆基体块模型 Fig. 2 Mortar block model |
砂浆基体块设置为弹塑性变形体,为提高计算效率,将砂浆基体块沿轴向分为压紧区、剪切区以及分离区3部分,如图 2(b)所示,其本构关系如表 2所示。
| 表 2 砂浆基体块本构关系 Table 2 Constitutive relation of the mortar block |
如表 2所示,每个部分添加相应的本构模型。为使压紧区各节点在剪切过程中保持相对位置稳定,将压紧区设置为刚性约束。剪切区、分离区采用ABAQUS中的Drucker-Prager模型,参考C30混凝土的相应参数[13-15]来进行验证,具体参数如表 3所示。屈服应力σ等效塑性应变εpl关系[16-17]见表 4。
| 表 3 砂浆基体块参数 Table 3 Parameters of the mortar block |
| 表 4 砂浆基体块屈服应力-等效塑性应变关系 Table 4 Relationship between yield stress and equivalent plastic strain of the mortar block |
主要受力变形与断裂均发生在剪切区,还需在剪切区增加剪切损伤模型(Shear Damage),通过删除单元模拟裂纹萌生、扩展至分离的过程,文中采用ABAQUS/Explicit计算拟合得到断裂应变为0.100 00,破坏位移为0.001 35。
3 砂浆基体块剪切试验为证明脆性材料剪切本构模型的正确性,设计了砂浆基体块剪切试验,图 3(a)所示为剪切试验装置,试验所用砂浆基体块如图 3(b)所示,在MTS疲劳试验机上进行剪切试验,剪切试验装置包括剪切刀、固定刀、压紧头和螺钉,剪切刀与固定刀分别由MTS上、下悬臂夹持,压紧头通过螺钉与固定刀连接,并提供压紧力将砂浆基体块压紧。

|
图 3 剪切试验设备 Fig. 3 Shear test device |
MTS上、下两悬臂无相对旋转可保证刀具间隙恒定为0.2 mm,剪切刀随上悬臂以预设速度40 mm/s向下移动,与固定刀形成锋利刃口进行剪切,剪切力与位移由上悬臂的力与位移传感器测量。每种速度设置3组试件剪切,每完成一次剪切后,取下螺钉,更换试件。
4 结果分析 4.1 数值模型与试验结果对比 4.1.1 剪切过程及断口分析如图 4所示为剪切速度40 mm/s的试件受剪过程仿真结果。剪切刀随上悬臂以预设速度向下运动,砂浆基体块先后发生:弹塑性变形-裂纹萌生及扩展-断裂分离。
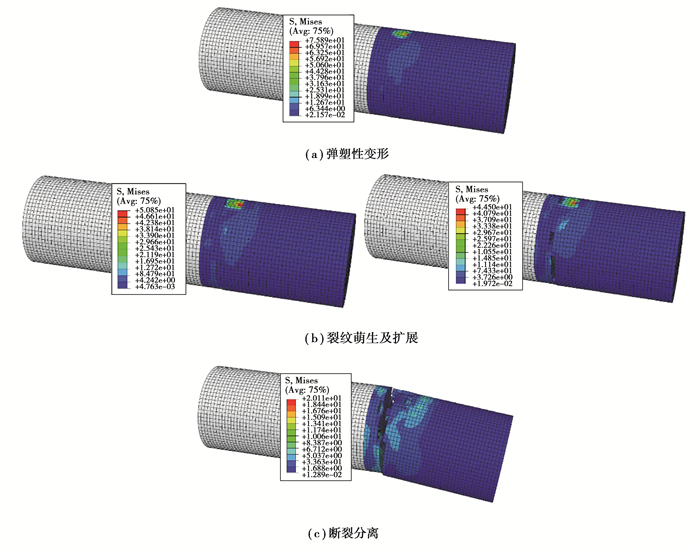
|
图 4 剪切仿真结果 Fig. 4 Simulation results of shearing process |
弹塑性变形:当剪切刀以预设速度向下移动,砂浆基体块与剪切刀接触点产生局部损伤,砂浆基体块开始产生弹性变形、塑性变形,砂浆是脆性材料,在受到较大冲击时,弹塑性变形阶段非常短暂。
裂纹萌生、裂纹扩展:砂浆基体块与剪切刀接触点以及砂浆基体块与固定刀接触点产生裂纹,裂纹迅速由接触点扩展至断裂。
断裂分离:试件沿预定剪切面断开,并产生碎屑,分离段与碎屑在残余动能下继续运动。
图 5为剪切断口对比图。从试验结果可看出,右侧分离区试件与剪切刀接触点发生剥离,分离出小碎屑,压紧区靠近接触点处,产生凸起,砂浆基体块由裂缝迅速扩展并断开,呈现凹凸不平的平面,产生了少量的碎屑及粉末。总体来看,数值模型断口形貌与试验结果相似,证明了砂浆基体块剪切有限元模型的正确性。
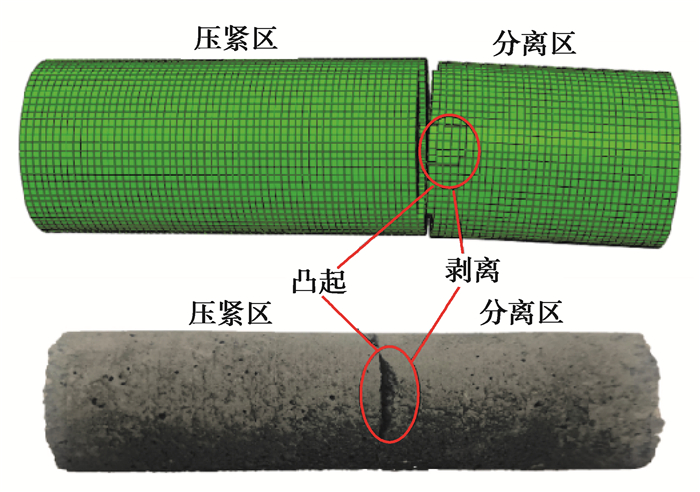
|
图 5 剪切断口对比图 Fig. 5 Contrast diagram of shear fracture |
最大剪切力可以为乏燃料剪切设备及剪切刀具设计提供参考,从图 6所示剪切速度为40 mm/s的剪切力随位移变化曲线可看出,整个试验过程中剪切力只出现了一个峰值,此时开始产生裂纹,之后裂纹迅速扩展至断裂,剪切力急速减小。

|
图 6 剪切力-位移曲线 Fig. 6 Shear force-displacement curve |
与数值模型曲线不同,试验曲线存在大量波动,波动的产生主要是由于在砂浆基体块断裂时,瞬间载荷消失后的冲击震荡逐步衰减,而数值模型未考虑此问题。
从图 6可见,文中数值模型能够真实模拟砂浆基体块断裂过程,所预测的最大剪切力在试验数据的波动范围内,剪切仿真的剪切力-位移曲线与试验曲线趋势一致,证明了砂浆基体块剪切有限元模型的正确性。
4.2 剪切速度对剪切力的影响最大剪切力对刀具的设计十分重要,探究剪切速度对剪切力的影响,可判断组件的剪切速度与刀具设计的关联性。图 7为不同速度下的剪切试验曲线。试验曲线均存在波动,瞬间载荷消失后的冲击震荡逐步衰减,观察可知速度越大,剪切后产生的波动越大,这是由于速度越大,瞬间载荷消失后的冲击震荡越大,从而使力传感器采集到的数据产生波动。
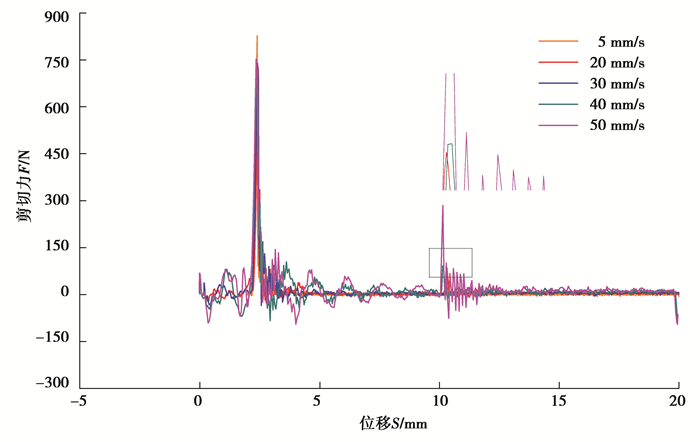
|
图 7 不同速度下的剪切试验曲线 Fig. 7 Shear test curves under different speeds |
在砂浆基体块断裂后,仍会有部分剪切速度(20 mm/s、40 mm/s、50 mm/s)可测量到剪切力,这是由于部分砂浆基体块剪断后,留在剪切试验装置中的试件断口凹凸不平,剪切刀向下运行到中部,剪切断口处凸起时会产生剪切力,数值模型也存在此现象,提取图 6,7中的最大剪切力进行分析,为了安全起见,剪切试验涉及的剪切速度变化范围不大,在一定范围内进行波动。图 8所示,最大剪切力的试验数据具有一定离散性,力与速度的关系有些散乱,试件数量较少是原因之一。因此在后续试验中,可以增加相同速度下的试验组数。
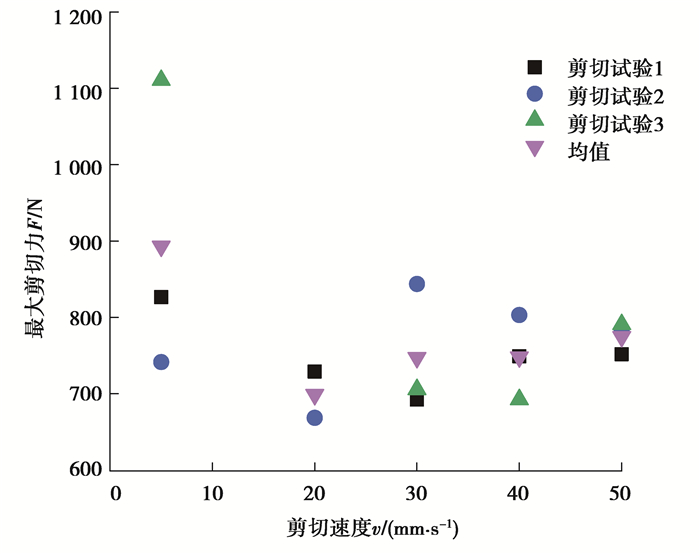
|
图 8 最大剪切力随速度变化趋势 Fig. 8 Changes of maximum shear force with speed |
由于在试验中改变刀具间隙十分繁琐,验证了剪切模型的正确性后,可通过数值仿真进一步研究刀具间隙对最大剪切力的作用。图 9为最大剪切力随刀具间隙变化趋势。
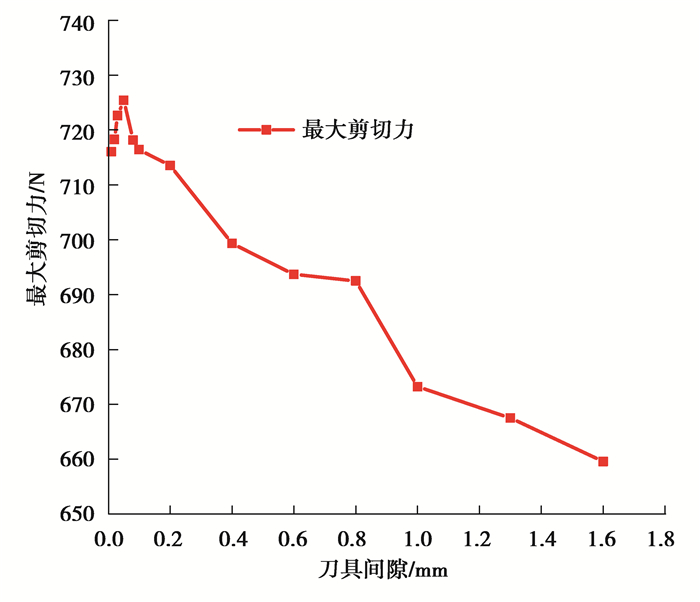
|
图 9 最大剪切力随刀具间隙变化趋势 Fig. 9 Changes of maximum force with tool clearance |
从图 9可知,刀具间隙增加,试件的变形区域会相应增大,不利于组件剪断,也就需要较大的剪切力,当间隙增大到一定程度时,拉应力会变得很大,加快断裂,剪切力大小会随之下降。图 10为不同间隙下剪切试验曲线。
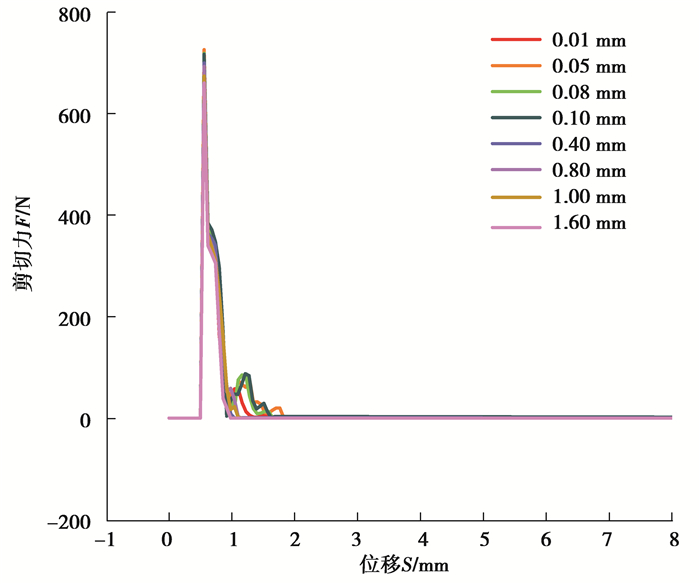
|
图 10 不同间隙下剪切试验曲线 Fig. 10 Shear test curves with different shear clearances |
从图 10可看出随刀具间隙的增大,后续剪切断面时产生的力与最大剪切力的变化趋势一致,后续剪切设备及刀具设计应参考此趋势选择适合的刀具间隙。
5 结论笔者在ABAQUS/Explicit中,通过有限元数值仿真研究了砂浆基体块的剪切过程,将砂浆基体块的剪切过程分为3个阶段、4个步骤,建立了砂浆基体块剪切有限元模型,并通过剪切试验证明了有限元模型与本构模型的正确性,分析了工艺参数中剪切速度、刀具间隙对剪切的影响,得出如下结论:
1) 试验结果与数值模型载荷位移曲线整体趋势基本一致,最大剪切力预测也较为准确,并且仿真得到的断裂形态与剪切试验的断面情况几乎相同,证明了模型的正确性。
2) 将砂浆基体块的剪切过程分为3个阶段、4个步骤,研究了弹塑性变形、裂纹萌生、裂纹扩展和断裂分离的全过程,以及过程中受力变形情况。但采用删除单元的方法模拟剪切过程裂纹的产生及演变,当单元达到设定的载荷极限会删除该单元,而实际剪切过程中裂纹产生源自材料的撕裂,而非材料消失,后续应寻找新的方法模拟其断裂,以完成更精确的模拟分析。
3) 通过目前的剪切试验发现,最大剪切力具有一定的离散性,随速度的变化在一定范围内波动,由剪切模拟可知剪切力随间隙的增大呈现先增大后减小的趋势。
| [1] |
熊江茗, 周杰, 王时龙, 等. 基于Johnson-Cook模型的不锈钢管剪切数值模拟[J]. 中国机械工程, 2020, 31(15): 1877-1884. Xiong J M, Zhou J, Wang S L, et al. Numerical simulation of stainless steel tube shearing based on Johnson-cook model[J]. China Mechanical Engineering, 2020, 31(15): 1877-1884. (in Chinese) DOI:10.3969/j.issn.1004-132X.2020.15.015 |
| [2] |
何敬柯. 中国核电工业燃料循环及其优化研究[D]. 沈阳: 东北大学, 2015. He J K. Research on fuel cycle of nuclear power industry and optimization on structure of fuel cycle in China[D]. Shenyang: Northeastern University, 2015. (in Chinese) |
| [3] |
Yang X H, Han J C, Zhang Y M, et al. Research on ultrasonic vibration grinding of the hard and brittle materials[J]. Chinese Journal of Aeronautics, 2006(B12): 9-13. |
| [4] |
Fishman Y A. Features of shear failure of brittle materials and concrete structures on rock foundations[J]. International Journal of Rock Mechanics and Mining Sciences, 2008, 45(6): 976-992. DOI:10.1016/j.ijrmms.2007.09.011 |
| [5] |
Dong J P, Wang S L, Zhou J, et al. Experimental and numerical investigation on the shearing process of stainless steel thin-walled tubes in the spent fuel reprocessing[J]. Thin-Walled Structures, 2019, 145: 106407. DOI:10.1016/j.tws.2019.106407 |
| [6] |
Chen Z, Li X K, Yang Y B, et al. Experimental and numerical investigation of the effect of temperature patterns on behavior of large scale silo[J]. Engineering Failure Analysis, 2018, 91: 543-553. DOI:10.1016/j.engfailanal.2018.04.043 |
| [7] |
王维, 马丽英. 基于Drucker-Prager模型的振动压实有限元分析[J]. 公路, 2018, 63(2): 40-45. Wang W, Ma L Y. FEM analysis of vibration compaction based on drucker-prager model[J]. Highway, 2018, 63(2): 40-45. (in Chinese) |
| [8] |
Song S H, Choi W C. FEM investigation on thermal effects on force in high-speed blanking of mild steel[J]. International Journal of Precision Engineering and Manufacturing, 2016, 17(5): 631-635. DOI:10.1007/s12541-016-0076-y |
| [9] |
刘亚忠, 马力, 黄姝. 工程陶瓷切削有限元仿真[J]. 机械设计与制造, 2005(4): 108-110. Liu Y Z, Ma L, Huang S. Finite element method of industrial ceramics[J]. Machinery Design & Manufacture, 2005(4): 108-110. (in Chinese) |
| [10] |
曲蒙. 早龄期混凝土损伤断裂的数值分析[D]. 杭州: 浙江大学, 2006. Qu M. Numerical analysis of damage and fracture for early-age concrete[D]. Hangzhou: Zhejiang University, 2006. (in Chinese) |
| [11] |
周芬. 基于ANSYS考虑损伤的混凝土本构模型二次开发算法研究[D]. 西安: 西安建筑科技大学, 2015. Zhou F. Study on the secondary development program of concrete constitutive model with damage based on ANSYS[D]. Xi'an: Xi'an University of Architecture and Technology, 2015. (in Chinese) |
| [12] |
许浒, 余志祥, 赵世春. 混凝土非线性分析中的非协调参数Drucker-Prager模型[J]. 四川大学学报(工程科学版), 2012, 44(4): 75-80. Xu H, Yu Z X, Zhao S C. An incompatible drucker-prager model applied in nonlinear analysis of concrete[J]. Journal of Sichuan University (Engineering Science Edition), 2012, 44(4): 75-80. (in Chinese) |
| [13] |
费康, 张建伟. ABAQUS在岩土工程中的应用[M]. 北京: 中国水利水电出版社, 2013. Fei K, Zhang J W. Application of ABAQUS in geotechnical engineering[M]. Beijing: China Water Power Press, 2013. (in Chinese) |
| [14] |
蔡小玲, 杨俊杰. 基于Drucker-Prager模型的FRP约束混凝土力学性能分析[J]. 结构工程师, 2018, 34(6): 29-37. Cai X L, Yang J J. Structural behaviour of FRP-confined concrete by drucker-prager model[J]. Structural Engineers, 2018, 34(6): 29-37. (in Chinese) |
| [15] |
施利洋. 钢筋混凝土框架—剪力墙结构地震损伤分析[D]. 南京: 南京林业大学, 2016. Shi L Y. Seismic damage analysis of reinforced concrete frame-shear wall structure[D]. Nanjing: Nanjing Forestry University, 2016. (in Chinese) |
| [16] |
Li Q F, Guo W, Kuang Y H. Parameter calculation and verification of concrete plastic damage model of ABAQUS[J]. IOP Conference Series: Materials Science and Engineering, 2020, 794(1): 012036. |
| [17] |
张劲, 王庆扬, 胡守营, 等. ABAQUS混凝土损伤塑性模型参数验证[J]. 建筑结构, 2008, 38(8): 127-130. Zhang J, Wang Q Y, Hu S Y, et al. Parameters verification of concrete damaged plastic model of ABAQUS[J]. Building Structure, 2008, 38(8): 127-130. (in Chinese) |
 2022, Vol. 45
2022, Vol. 45



