2. 中国船舶集团海装风电股份有限公司,重庆 401122
2. CSIC (Chongqing) Haizhuang Windpower Co., Ltd., Chongqing 401122, P. R. China
发展清洁无污染的海上风电被认为是应对全球气候变暖的重要举措。截至2019年底,全球海上浮式风电装机总量已达到66 MW,预测到2030年全球海上浮式风电装机量将在3~ 19 GW之间[1]。然而风、浪具有明显的随机分布特征,两者之间的耦合作用会增加海上浮式风机长期极限响应的复杂性,加之高昂的海上设备运维成本,对海上浮式风机的设计可靠性提出了更高要求,因此开展海上浮式风机长期极限响应预测研究,可以为海上浮式风机结构设计提供理论参考。
目前,针对海上浮式风机长期极限响应预测的研究方法主要有全面长期分析法和环境等值线法。由于全面长期分析法需要至少3 000多种环境工况的仿真计算,造成风机的设计效率低,因此近年来大量学者针对环境等值线法开展了深入研究。Raed等[2]采用基于逆一次可靠度法(IFORM)和蒙特卡罗模拟的环境等值线法评估海上浮式风机长期极限响应的不确定性,结果表明基于不同的环境等值线法产生的工况差异会显著影响极限响应幅值。Li等[3]考虑对多个轮廓面的校核,提出改进的环境等值线法使海上浮式风机系泊锚链张力的预测极值提高了10%。Liu等[4]以13.2 MW海上浮式风机为研究对象,通过2D和3D IFORM环境等值线法得到了浮式风机长期极限响应,结果表明基于3D IFORM环境等值线法可以得到更大的响应极值。Li等[5]利用C-vine copula模型建立了风浪联合分布模型,通过环境等值线法和Rosenblatt变换预测Spar型海上浮式风机结构的长期极限响应,结果表明利用50 a环境等值线得到的海上浮式风机的长期极限响应预测效果更好。周帅等[6]以Spar型海上浮式风机为研究对象,采用IFORM的环境等值线法预测风机的长期极限响应具有较高的计算效率和可靠性。逆二次可靠度法(ISORM)考虑了设计点与失效区域的曲率信息渐进近似,近年来也用于环境等值线法。Giske等[7]通过使用IFORM、ISORM和全面长期分析法对比分析浮桥的极限响应,结果表明ISORM具有较高的预测精度。Chai等[8]基于ISORM的环境等值线法,对波浪统计、风浪统计和第一年冰脊统计进行分析得出ISORM环境等值线计算的结果比IFORM更加可靠。
现有文献主要侧重研究基于IFORM的环境等值线法评估风机长期极限响应,但是IFORM基于设计点线性相似会导致环境等值线存在误差,采用设计点区域渐进相似的ISORM可以有效克服传统IFORM的缺点,使得到的环境等值线更可靠。因此笔者以5 MW半潜式浮式风机为研究对象,根据实测风浪的联合概率分布分别建立了基于IFORM和ISORM的环境等值线模型,通过使用Gumbel极值分布评估海上浮式风机的长期极限响应,并对两种环境等值线下海上浮式风机长期极限响应预测进行了对比分析,为海上浮式风机结构可靠性设计提供一定的理论参考。
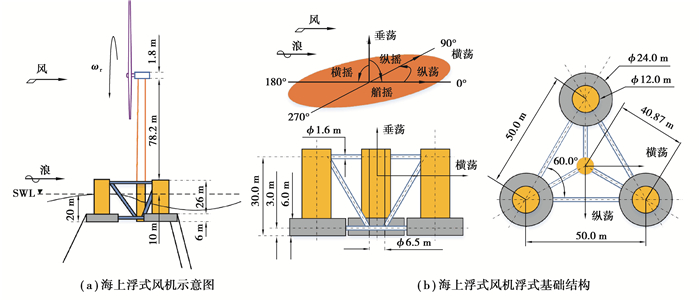
1 海上浮式风机运行原理 1.1 海上浮式风机基本结构以5 MW半潜式海上浮式风机系统为研究对象,如图 1所示,该系统主要由风电机组(叶片、传动链、发电机、控制系统、塔架)、浮式基础及系泊锚链等组成[9-11],海上风电机组主要参数如表 1所示。海上浮式风机主要受风和波浪等环境载荷的影响,风载荷主要作用于风机叶片和塔架,波浪载荷主要作用在浮式基础和系泊锚链。
|
图 1 5 MW半潜式海上浮式风机示意图 Fig. 1 Schematic diagram of 5 MW semi-submersible offshore floating wind turbine |
| 表 1 海上风电机组主要参数 Table 1 Main parameters of offshore wind turbine |
本文的风浪数据来源于中国湛江市某海域,离岸距离20~75 m,水深在60 m左右,海域地形起伏较大,适合部署半潜式海上浮式风机。在测风塔10 m高度处监测并获取风速数据;采用波浪流速剖面仪测量波浪的有义波高和谱峰周期,测量数据历时5 a。
1.2.1 平均风速边缘分布测风塔高度层实测风速与轮毂高度处风速之间的关系如式(1)所示。
| $ u=u_{\mathrm{h}}\left(\frac{z}{h}\right)^\alpha。$ | (1) |
式中:u表示轮毂高度z处平均风速;uh表示在相对高度h处的风速;α表示风切变指数,本研究中的取值0.14。
使用两参数威布尔分布[12]拟合平均风速Uw,如式(2)所示。
| $ f_{U_{\mathrm{w}}}(u)=\frac{\alpha_{\mathrm{U}}}{\beta_{\mathrm{U}}}\left(\frac{u}{\beta_{\mathrm{U}}}\right)^{\alpha_{\mathrm{U}}-1} \exp \left[-\left(\frac{u}{\beta_{\mathrm{U}}}\right)^{\alpha_{\mathrm{U}}}\right], $ | (2) |
式中αU和βU分别表示形状参数和尺度参数,通过极大似然法获取。
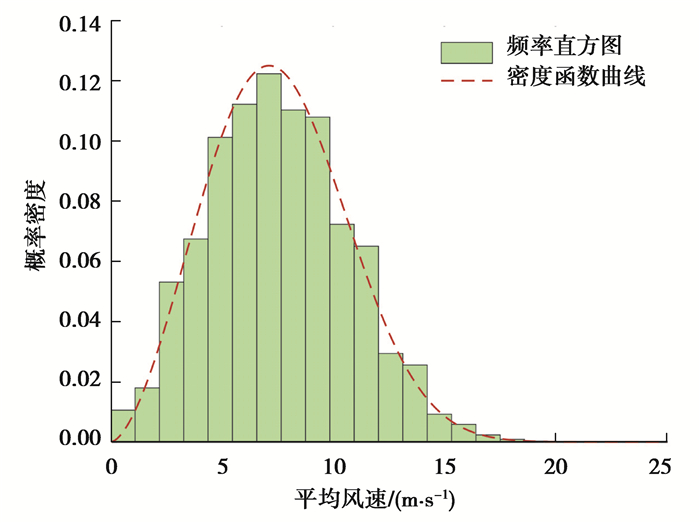
表 2为平均风速的两参数威布尔分布及其参数估计结果,对应的边缘分布概率密度函数如图 2所示。
| 表 2 平均风速的边缘分布类型及其参数估计 Table 2 Marginal distribution of mean wind speed and parameter estimation |
|
图 2 平均风速概率密度函数 Fig. 2 Probability density function of mean wind speed |
有义波高Hs和谱峰周期Tp的联合分布如式(3)所示,Hs和Tp分别采用三参数威布尔分布和对数正态分布拟合[13],概率密度函数如式(4)~(7)所示,对应的参数估计如表 3所示。
| $ f_{H_{\mathrm{s}}, T_{\mathrm{P}}}(h, t)=f_{H_{\mathrm{s}}}(h) f_{T_{\mathrm{p}} \mid H_{\mathrm{s}}}(t \mid h), $ | (3) |
| 表 3 有义波高和谱峰周期分布类型及其参数估计 Table 3 The distribution of the significant wave height and the spectral peak period and parameter estimation |
式中h和t分别表示有义波高和谱峰周期的数据。
| $ f_{H_{\mathrm{s}}}(h)=\frac{\beta_{\mathrm{H}}}{\alpha_{\mathrm{H}}}\left(\frac{h-\gamma_{\mathrm{H}}}{\alpha_{\mathrm{H}}}\right)^{\beta_{\mathrm{H}}-1} \exp \left\{-\left(\frac{h-\gamma_{\mathrm{H}}}{\alpha_{\mathrm{H}}}\right)^{\beta_{\mathrm{H}}}\right\}, $ | (4) |
| $ f_{T_{\mathrm{p}} \mid H_{\mathrm{s}}}(t \mid h)=\frac{1}{\sqrt{2 \pi} \sigma t} \exp \left\{-\frac{(\ln (t)-\mu)^2}{2 \sigma^2}\right\}, $ | (5) |
| $ \mu=E[\ln (t)]=a_0+a_1 h^{a_2}, $ | (6) |
| $ \sigma=\operatorname{std}[\ln (t)]=b_0+b_1 \exp \left(b_2 h\right)_{\circ} $ | (7) |
式中:αH、βH和γH分别表示三参数威布尔分布的尺度参数、形状参数和位置参数,通过最大似然法获取;μ和σ分别表示ln (t)的均值和标准差;系数ai和bi(i=0, 1, 2)通过最小二乘法获取。
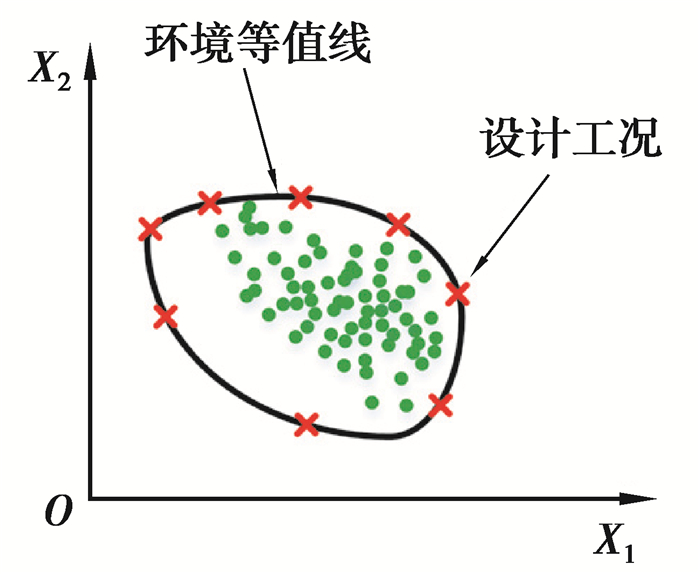
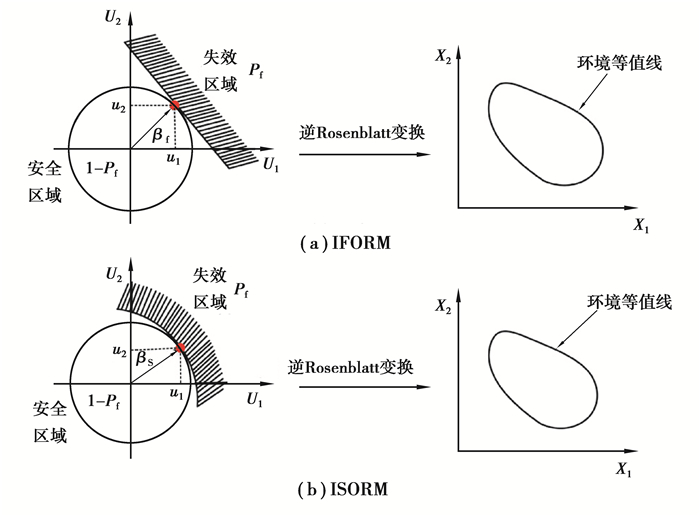
2 环境等值线法环境等值线法可独立于结构响应识别极限环境载荷,如图 3所示,通过在环境等值线上选取设计工况计算响应,大幅减少仿真时间[2]。针对有义波高和谱峰周期,分别采用IFORM和ISORM构造环境等值线,如图 4所示。选择沿着环境等值线上的设计工况组合,并对有限环境工况进行响应分析,从而进一步降低计算成本。
|
图 3 环境等值线法设计 Fig. 3 Design conditions for the environmental contour method |
|
图 4 基于IFORM和ISORM的环境等值线 Fig. 4 Environmental contours based on IFORM and ISORM |
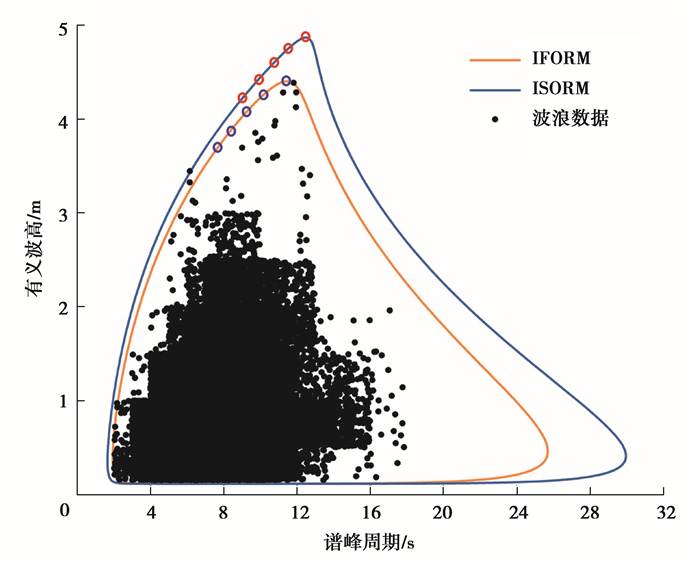
如图 4(a)所示,基于IFORM的环境等值线[14]是根据失效概率Pf,将标准正态空间(U空间)里的集合(u1, u2)通过逆Rosenblatt变换转换为物理空间(X空间)的环境变量,从而得到环境等值线。与IFORM不同,如图 4(b)所示,基于ISORM的环境等值线[8]则是以圆弧切面代替设计点处切平面近似的破坏面,然后通过逆Rosenblatt变换到物理空间的环境等值线。IFORM和ISORM在标准正态空间的半径βf和βs通过式(8)~(10)求得。
| $ P_{\mathrm{f}}=1 /(T \times D \times H), $ | (8) |
| $ {\mathit{\Phi}}\left(\beta_{\mathrm{f}}\right)=1-P_{\mathrm{f}}, $ | (9) |
| $ \chi_n^2\left(\beta_{\mathrm{s}}^2\right)=1-P_{\mathrm{f} }。$ | (10) |
式中:T、D和H分别取值50 a重现周期、365.25 d和24 h;Φ(·)是标准正态累积分布函数; χn2(·)为n自由度的χn2分布函数。
通过式(11)得到标准正态空间的随机变量(u1, u2),然后采用式(12)将标准正态空间集合(u1, u2)转换为物理空间的随机变量,hs和tp通过FHs和FTp|Hs的逆函数求得[15]。依据上述方法得到基于IFORM和ISORM的50 a重现周期环境等值线如图 5所示。
| $ \left\{\begin{array}{l} u_1=\beta_i \cos \theta, \\ u_2=\beta_i \sin \theta ; \end{array}\right. $ | (11) |
| $ \left\{\begin{array}{c} h_{\mathrm{s}}=F_{H_{\mathrm{s}}}^{-1}\left({\mathit{\Phi}}\left(u_1\right)\right), \\ t_{\mathrm{p}}=F_{T_{\mathrm{p}} \mid H_{\mathrm{s}}}^{-1}\left({\mathit{\Phi}}\left(u_2\right)\right)_{\circ} \end{array}\right. $ | (12) |
|
图 5 基于IFORM和ISORM的50 a重现周期环境等值线 Fig. 5 Environmental contours based on IFORM and ISORM of the 50-year return period |
式中:i=f, s;θ为失效边界上的任意夹角0, 360°;
海上浮式风机耦合系统动力学方程[16]如式(13)所示。
| $ \boldsymbol{M} \ddot{x}=\boldsymbol{W}+F_{\text {aero }}+F_{\text {hydro }}+F_{\text {mooring }} \text { 。} $ | (13) |
式中:M为海上浮式风机系统的质量矩阵;
叶片空气动力学载荷Faero采用叶素-动量理论计算,将叶片分割为若干叶素,基于迭代法对叶片每个离散节点的翼型横截面进行载荷计算,叶片法向方向的力Fp和切向方向的力Ft如式(14)~(15)所示。
| $ F_{\mathrm{p}}=\frac{1}{2} \rho_{\mathrm{a}} W^2 n_{\mathrm{b}} c\left(C_1 \cos \varphi+C_{\mathrm{d}} \sin \varphi\right) \Delta_{\mathrm{r}}, $ | (14) |
| $ F_{\mathrm{t}}=\frac{1}{2} \rho_{\mathrm{a}} W^2 n_{\mathrm{b}} c\left(C_{\mathrm{l}} \sin \varphi-C_{\mathrm{d}} \cos \varphi\right) \Delta_{\mathrm{r} \circ} $ | (15) |
式中:ρa为空气密度;W表示入流风速;nb表示叶片数目;c表示叶素弦长;Cl和Cd分别表示升力系数和阻力系数;φ为入流角;Δr表示叶素的长度。
水动力载荷Fhydro用波浪运动学和水动力学[17]求解,波浪动力学模型用Airy波理论计算,水动力学模型采用势流理论和莫里森方程相结合的方法计算,利用三维势流理论求解浮式基础浮筒波浪力,基于莫里森方程求解浮式基础连杆波浪力。
用集中质量法建立了系泊锚链模型[18],将系泊锚链离散为若干均匀等长的有质量节点和弹簧阻尼,系泊锚链载荷Fmooring主要包括内部轴向刚度、阻尼力、重力、浮力、莫里森水动力以及与海床的接触力。
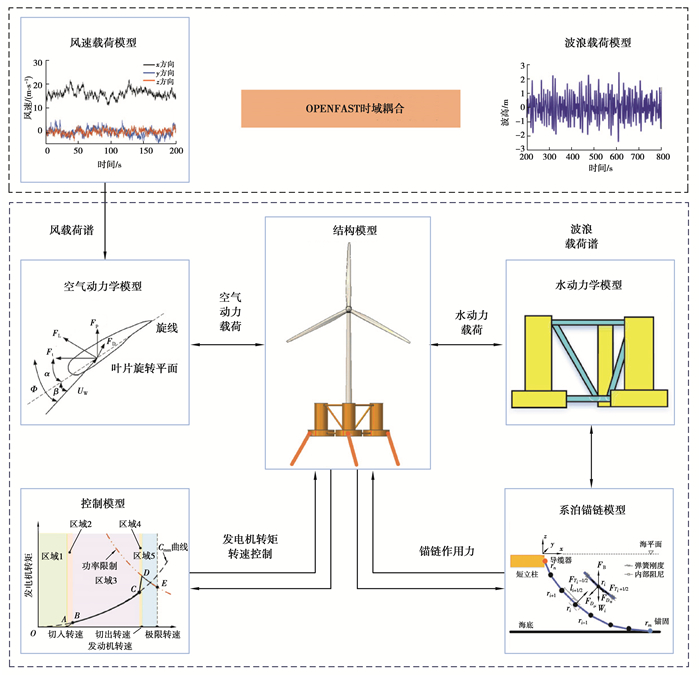
基于OPENFAST[19]建立了海上浮式风机耦合系统动力学模型,各子系统耦合关系如图 6所示。
|
图 6 海上浮式风机耦合系统动力学模型 Fig. 6 Dynamics model of offshore floating wind turbine coupling system |
根据图 5得到基于IFORM和ISORM的环境等值线确定环境工况,如表 4所示。结合IEC61400-3设计标准[20]在基于IFORM和ISORM的环境等值线上选取可能产生响应极值的5组环境工况组合,平均风速在8~16 m/s以间隔2 m/s选取。使用TURBSIM[21]模拟湍流风,采用NTM风载荷模型,湍流风谱使用Kaimal模型,湍流风场设置为170.5 m×170.5 m,湍流强度设置为10%,时间步长设置为0.01 s。波浪谱采用JONSWAP模型,水动力载荷计算步长设置为0.25 s。整机动力学仿真时间设置为3 800 s,时间步长设置为0.01 s,去除前200 s避免海上浮式风机在启动时产生瞬态行为对仿真造成影响。基于海上浮式风机耦合系统动力学模型对每组工况使用100种不同的随机风浪种子仿真得到短期极限响应。
| 表 4 环境工况 Table 4 Environmental conditions |
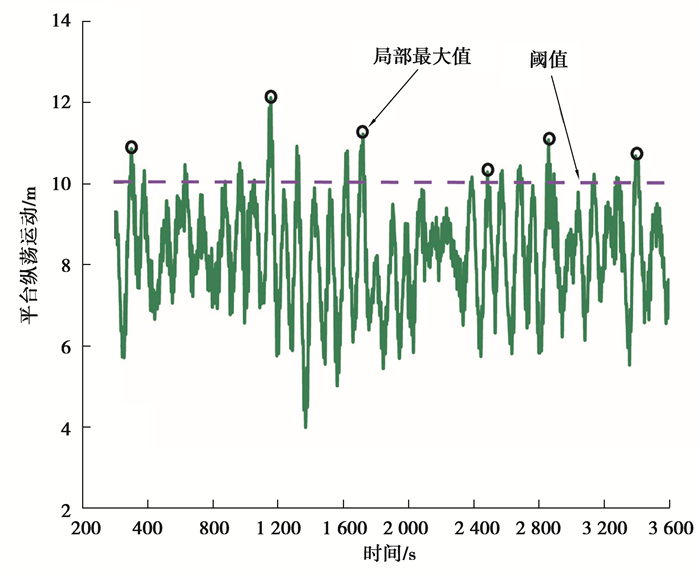
结合分块最大值法和过阈最大值法[22],提取海上浮式风机平台纵荡运动、叶根面外弯矩、塔基前后弯矩以及系泊锚链张力的局部最大值。将每次仿真时间均分成6个等长时间段(600 s),定义每个等长时间段响应的平均值加上1.5倍标准差为阈值,即在每个等长时间段内,提取大于阈值的响应值作为平台纵荡运动局部最大值,如图 7所示。
|
图 7 平台纵荡运动局部最大值 Fig. 7 The local maximum value of platform surge motion |
假设海上浮式风机的结构短期极限响应局部最大值服从Gumbel分布[23],使用卡方检验对短期极限响应局部最大值进行假设检验,基于式(16)对短期极限响应的局部最大值进行参数估计,海上浮式风机各结构50 a重现周期的极限响应[3]如式(17)所示。
| $ F(x) = \exp \left[ { - \exp \left( { - \frac{{x - A}}{B}} \right)} \right], $ | (16) |
| $ {L_{50 - {\rm{yr}}}} = A + B\ln (50 \times 365.25 \times 24)。$ | (17) |
式中:F(x)表示Gumbel的累积分布函数;A和B分别为位置参数和尺度参数。
海上浮式风机的长期极限响应极值L50-yr的95%置信区间[Lci-(n), Lci+(n)]如式(18)所示,极值误差ε如式(19)所示。
| $ {L_{{\rm{ci}} \pm }}(n) = {L_{50 - {\rm{yr}}}} \pm {t_{95\% , n}}\sqrt {{\mathop{\rm var}} (L(n))/n} , $ | (18) |
| $ \varepsilon = \left( {{L_{{\rm{ci + }}}}(n) - {L_{{\rm{ci - }}}}(n)} \right)/{L_{50 - {\rm{yr}}}}。$ | (19) |
式中:n为仿真次数,t95%, n是n自由度学生t分布的95%百分位数,var(·)为数据的方差,本文的极值误差取为5%以内。
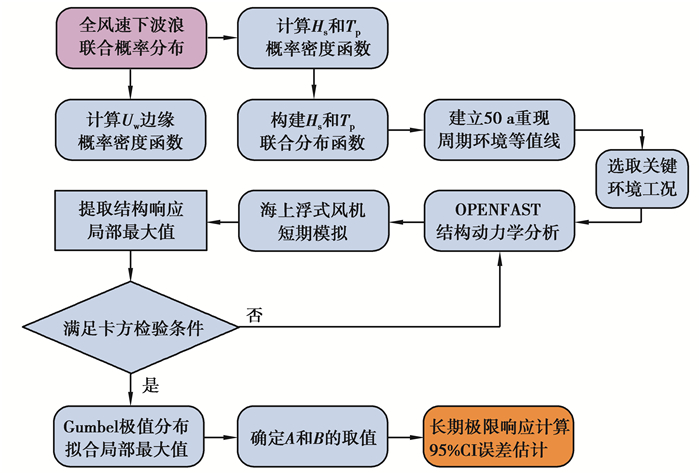
使用环境等值线法评估海上浮式风机长期极限响应的流程如图 8所示。
|
图 8 长期极限响应分析流程图 Fig. 8 The flow chart of the long-term extreme response |
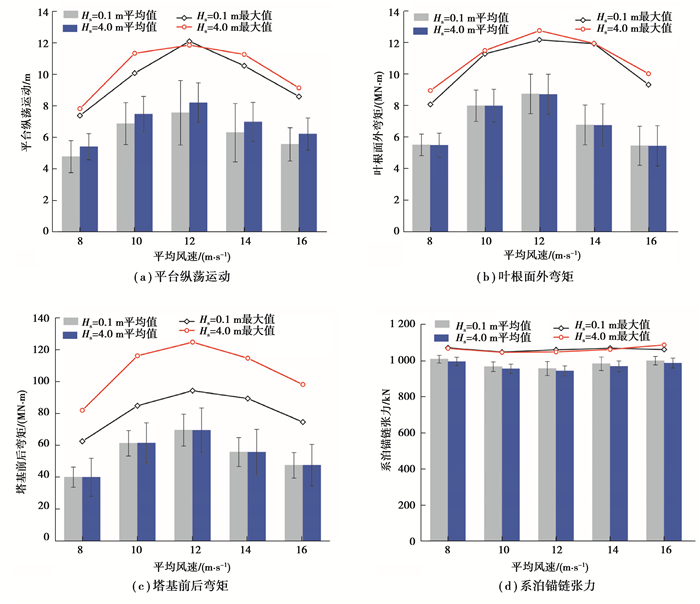
分别选取风速为8, 10, 12, 14, 16 m/s,有义波高为4.0 m和0.1 m,利用海上浮式风机耦合系统动力学模型计算海上浮式风机各结构响应的平均值、最大值和标准差,如图 9所示。随着平均风速增大,平台纵荡运动、叶根面外弯矩和塔基前后弯矩出现了先增大后减少的趋势,在平均风速为12 m/s时各结构响应最大,如图 9(a)~(c)所示。在同一平均风速下,有义波高会显著影响平台纵荡运动的最大值和平均值以及塔基前后弯矩的最大值。如图 9(a)和(c)所示,在平均风速为10 m/s时,有义波高为4.0 m时平台纵荡运动的最大值和平均值比有义波高为0.1 m时分别增加了12.5%和8.9%,塔基前后弯矩的最大值增加了37.1 %。叶根面外弯矩和系泊锚链张力受有义波高的影响较小。
|
图 9 有义波高对海上浮式风机短期极限响应的影响 Fig. 9 The influence of waves on the short-term extreme response of offshore floating wind turbines |
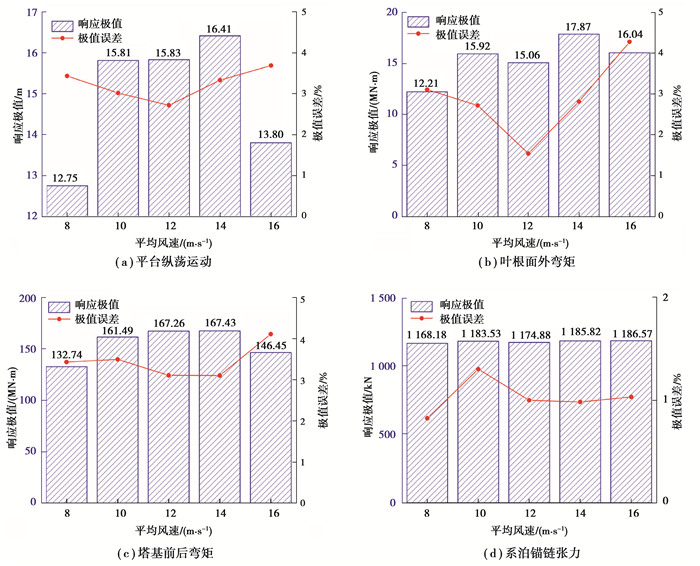
图 10和图 11分别给出了基于IFORM和ISORM的环境等值线计算的海上浮式风机长期极限响应,可以看出,基于IFORM和ISORM的环境等值线计算各结构的长期极限响应变化趋势和短期极限响应基本一致。
|
图 10 基于IFORM的长期极限响应 Fig. 10 Long-term extreme response based on IFORM |
|
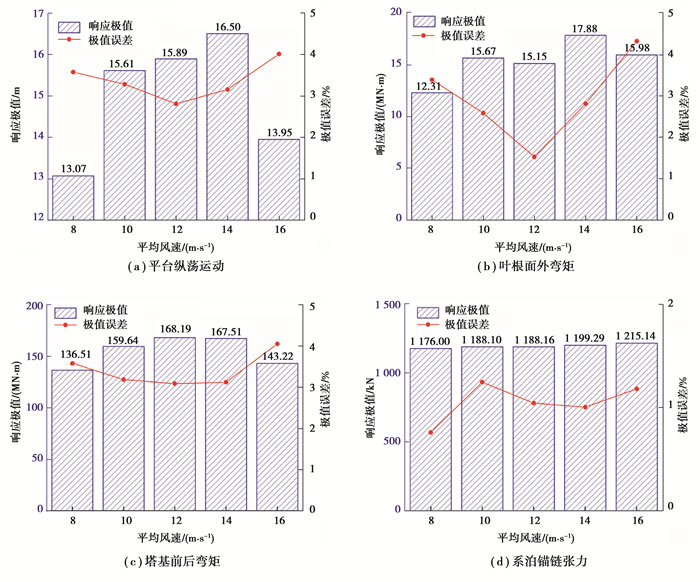
图 11 基于ISORM的长期极限响应 Fig. 11 Long-term extreme response based on ISORM |
从基于IFORM的环境等值线得到了平台纵荡运动、叶根面外弯矩、塔基前后弯矩和系泊锚链张力响应极值和极值误差。平台纵荡运动、叶根面外弯矩和塔基前后弯矩的极值出现了先增大后减小的趋势,响应极值出现在平均风速为14 m/s时,分别为16.41 m、17.87 MN·m和167.43 MN·m;系泊锚链张力的极值出现在平均风速16 m/s时,为1 186.57 kN。基于式(19)计算海上浮式风机各响应的极值误差,各响应的极值误差均小于5%,故满足极值误差的要求。
如图 11所示,基于ISORM的环境等值线法得到平台纵荡运动、叶根面外弯矩、塔基前后弯矩和系泊锚链张力极限响应变化趋势和基于IFORM的环境等值线法的结果基本一致,对应的结构响应极值分别为16.50 m、17.88 kN·m、168.19 MN·m、1 215.14 kN。各响应的极值误差ε均小于5%,两种方法所得到的极值误差变化趋于一致。
表 5列出了采用基于IFORM和ISORM的环境等值线法得到的海上浮式风机各结构长期极限响应之间的偏差,可以看出两种方法的计算结果差异较小,其原因是两种方法选取的代表性环境工况参数相近,有义波高相差0.4 m,谱峰周期相差9 s,因此产生的偏差较小,同时也验证了基于ISORM环境等值线的正确性。从两种方法的计算结果对比可以看出,基于ISORM的环境等值线法计算的长期极限响应普遍大于基于IFORM的结果。
| 表 5 基于IFORM与ISORM法估计的极限响应偏差 Table 5 Deviation results of extreme response based on IFORM and ISORM methods |
通过国内某海域实测风浪的联合概率分布,分别基于逆一次可靠度法和逆二次可靠度法构建了50 a重现周期环境等值线,通过海上浮式风机耦合系统动力学模型获取风机结构短期响应,并结合Gumbel极值分布评估了海上浮式风机平台纵荡运动、叶根面外弯矩、塔基前后弯矩和系泊锚链张力的50 a长期极限响应,主要结论如下:
1) 风浪联合作用下,平台纵荡运动、叶根面外弯矩和塔基前后弯矩随着平均风速的增大,各结构短期极限响应出现了先增大后减少的趋势;在同一风速下,平台纵荡运动的最大值和平均值、塔基前后弯矩的最大值受有义波高的影响较大;而叶根面外弯矩和系泊锚链张力几乎不受波浪的影响。
2) 基于逆一次可靠度法得到平台纵荡运动、叶根面外弯矩、塔基前后弯矩的长期极限响应极值主要出现在平均风速为14 m/s处,各响应的极值误差满足估计误差要求;基于逆二次可靠度法得到的平台纵荡运动、叶根面外弯矩和塔基前后弯矩响应的极值分布与基于逆一次可靠度法的结果基本一致。
3) 基于逆二次可靠度法和逆一次可靠度法的环境等值线形状相似,但是基于逆二次可靠度法的环境等值线法考虑了更多的环境工况组合,浮式风机系泊锚链张力响应极值较高,进一步提高了海上浮式风机结构设计的安全性。
| [1] |
Global Wind Energy Council. Global offshore wind report 2020[R]. Brussels: Global Wind Energy Council, 2020.
|
| [2] |
Raed K, Teixeira A P, Guedes Soares C. Uncertainty assessment for the extreme hydrodynamic responses of a wind turbine semi-submersible platform using different environmental contour approaches[J]. Ocean Engineering, 2020, 195: 106719. DOI:10.1016/j.oceaneng.2019.106719 |
| [3] |
Li L, Yuan Z M, Gao Y, et al. Investigation on long-term extreme response of an integrated offshore renewable energy device with a modified environmental contour method[J]. Renewable Energy, 2019, 132: 33-42. DOI:10.1016/j.renene.2018.07.138 |
| [4] |
Liu J S, Thomas E, Goyal A, et al. Design loads for a large wind turbine supported by a semi-submersible floating platform[J]. Renewable Energy, 2019, 138: 923-936. DOI:10.1016/j.renene.2019.02.011 |
| [5] |
Li X, Zhang W. Long-term assessment of a floating offshore wind turbine under environmental conditions with multivariate dependence structures[J]. Renewable Energy, 2020, 147: 764-775. DOI:10.1016/j.renene.2019.09.076 |
| [6] |
周帅, 王迎光, 李昕雪. Spar型海上浮式风机极端载荷预报[J]. 舰船科学技术, 2018, 40(17): 99-106. Zhou S, Wang Y G, Li X X. Extreme load predictions of a spar-type floating wind turbine[J]. Ship Science and Technology, 2018, 40(17): 99-106. (in Chinese) |
| [7] |
Giske F I G, Kvale K A, Leira B J, et al. Long-term extreme response analysis of a long-span pontoon bridge[J]. Marine Structures, 2018, 58: 154-171. DOI:10.1016/j.marstruc.2017.11.010 |
| [8] |
Chai W, Leira B J. Environmental contours based on inverse SORM[J]. Marine Structures, 2018, 60: 34-51. DOI:10.1016/j.marstruc.2018.03.007 |
| [9] |
Jonkman J, Butterfield S, Musial W, et al. Definition of a 5-MW reference wind turbine for offshore system development: NREL/TP-500-38060 TRN: US200906%%69[R]. Golden, Colorado, United States: U.S. Department of Energy Office of Scientific and Technical Information (OSTI), 2009.
|
| [10] |
Robertson A, Jonkman J, Masciola M, et al. Definition of the semisubmersible floating system for phase Ⅱ of OC4: NREL/TP-5000-60601[R]. Golden, Colorado, United States: U.S. Department of Energy Office of Scientific and Technical Information (OSTI), 2014.
|
| [11] |
Coulling A J, Goupee A J, Robertson A N, et al. Validation of a FAST semi-submersible floating wind turbine numerical model with DeepCwind test data[J]. Journal of Renewable and Sustainable Energy, 2013, 5(2): 557-569. |
| [12] |
Li L, Gao Z, Moan T. Joint distribution of environmental condition at five European offshore sites for design of combined wind and wave energy devices[J]. Journal of Offshore Mechanics and Arctic Engineering, 2015, 137(3): 031901. DOI:10.1115/1.4029842 |
| [13] |
Vanem E, Bitner-Gregersen E M. Stochastic modelling of long-term trends in the wave climate and its potential impact on ship structural loads[J]. Applied Ocean Research, 2012, 37: 235-248. DOI:10.1016/j.apor.2012.05.006 |
| [14] |
Velarde J, Vanem E, Kramhøft C, et al. Probabilistic analysis of offshore wind turbines under extreme resonant response: Application of environmental contour method[J]. Applied Ocean Research, 2019, 93: 101947. DOI:10.1016/j.apor.2019.101947 |
| [15] |
Haselsteiner A F, Ohlendorf J H, Wosniok W, et al. Deriving environmental contours from highest density regions[J]. Coastal Engineering, 2017, 123: 42-51. DOI:10.1016/j.coastaleng.2017.03.002 |
| [16] |
Barooni M, Ale Ali N, Ashuri T. An open-source comprehensive numerical model for dynamic response and loads analysis of floating offshore wind turbines[J]. Energy, 2018, 154: 442-454. DOI:10.1016/j.energy.2018.04.163 |
| [17] |
李修赫, 朱才朝, 谭建军, 等. 风浪不共线对浮式风机基础动态特性影响研究[J]. 振动与冲击, 2020, 39(13): 230-237. Li X H, Zhu C C, Tan J J, et al. Effects of wind-wave misalignment on dynamic characteristics of floating offshore wind turbine foundation[J]. Journal of Vibration and Shock, 2020, 39(13): 230-237. (in Chinese) |
| [18] |
Hall M, Goupee A. Validation of a lumped-mass mooring line model with DeepCwind semisubmersible model test data[J]. Ocean Engineering, 2015, 104: 590-603. DOI:10.1016/j.oceaneng.2015.05.035 |
| [19] |
Jonkman J M, Buhl Jr M L. FAST user's guide: NREL/TP-500-38230[R]. Golden, Colorado, USA: National Renewable Energy Laboratory, 2005.
|
| [20] |
International Electrotechnical Committee. Wind energy generation system - Part 3-2: design requirements for offshore wind turbines: IEC TS 61400-3-2[S]. Geneva: International Electrotechnical Committee, 2019.
|
| [21] |
Jonkman B J. TurbSim user's guide: Version 1.50: NREL/TP-500-46198[R]. Golden, Colorado, USA: National Renewable Energy Laboratory, 2012.
|
| [22] |
赵永生, 杨建民, 何炎平, 等. 张力腿式浮动风力机极限载荷分析[J]. 华中科技大学学报(自然科学版), 2015, 43(4): 113-117. Zhao Y S, Yang J M, He Y P, et al. Extreme load analysis for a TLP-type floating wind turbine under operating conditions[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2015, 43(4): 113-117. (in Chinese) |
| [23] |
Li Q Y, Gao Z, Moan T. Modified environmental contour method to determine the long-term extreme responses of a semi-submersible wind turbine[J]. Ocean Engineering, 2017, 142: 563-576. DOI:10.1016/j.oceaneng.2017.07.038 |
 2022, Vol. 45
2022, Vol. 45


