2. 中国船舶重工集团海装风电股份有限公司,重庆 401121
2. CSIC(Chongqing) Haizhuang Windpower Equipment Co., Chongqing 401121, P. R. China
海上浮式风电机组适用于获取深、远海域(水深大于60 m)风能资源[1-2],但在运行过程中浮式风机在风浪联合作用下的六自由度运动会对浮式风机的性能产生很大影响,导致风机的功率产生周期性波动[3]。这是因为随机风、浪载荷的联合激励,会引起平台和塔架的倾斜运动[4],使整个机组的空间运行姿态产生显著变化[5],进而改变不同桨距角下叶片不同径向位置处的入流风速,增加发电功率波动。因此,研究海上浮式风电机组变桨距控制对保持输出功率稳定具有重要的意义。
目前,国内外学者针对风电机组变桨距控制开展了大量深入研究。Colombo等[6]提出了将叶片桨距角作为控制变量输入的滑膜控制方法,并验证了其闭环收敛性。Yin等[7]提出了风电机组变桨距自适应鲁棒控制策略,提高了系统的鲁棒性。Civelek等[8-10]通过将模糊控制与变桨距控制结合,实现了风电机组恒功率控制。苑晨阳等[11-12]利用人工蜂群算法对风电机组变桨距PID控制器参数进行优化,有效地降低了发电功率和风轮转速波动。虽然上述控制方法在一定程度上可以改善风电机组变桨距控制性能,但是在实际控制过程中由于难以获取精确的控制模型与系统参数,应用局限性大。自抗扰控制(active disturbance rejection control, ADRC)[13-14]不依赖于被控系统精确的数学模型,对控制品质和控制精度有显著提高。目前,已有学者将ADRC应用于风电机组变桨系统[15-18]。然而,目前变桨距ADRC控制研究都将风电机组进行了简化,未考虑风电机组气动力、水动力、结构弹性和变桨距控制之间耦合,并且目前变桨距ADRC控制器的参数整定仍依靠专家经验,造成变桨距ADRC实际应用受限。
综上所述,海上浮式风电机组模型复杂,难以获取精确的控制模型和系统参数,采用不依赖精确数学模型的变桨距ADRC策略可以有效提高控制精度。同时,考虑到ADRC需要整定的参数过多且不利于在实际工程中应用,将ADRC简化为线性自抗扰控制(LADRC)[19],降低了调试难度,更具工程实用性。
笔者针对随机风、浪载荷引起的海上浮式风电机组发电功率波动问题,提出了海上浮式风电机组变桨距线性自抗扰控制策略,将基于5 MW级海上浮式风电机组气-弹-水-控耦合系统动力学模型对带宽整定法和BP神经网络整定法下的LADRC策略功率波动抑制效果进行对比分析,验证变桨距LADRC策略对发电功率波动的抑制效果。
1 海上浮式风电机组变桨距运行原理如图 1所示,海上浮式风电机组整机主要包括叶片、塔架、传动链、机舱、浮动平台以及锚链等。叶片将风能转换为机械能,通过传动链传递到发电机并转化为电能[20]。海上浮式风电机组整机由浮动平台提供支撑,锚链约束其空间运动范围。在风、浪载荷联合激励下,海上浮式风电机组整机将产生6个方向的刚体运动。表 1所示为某5 MW级海上浮式风电机组整机结构参数。
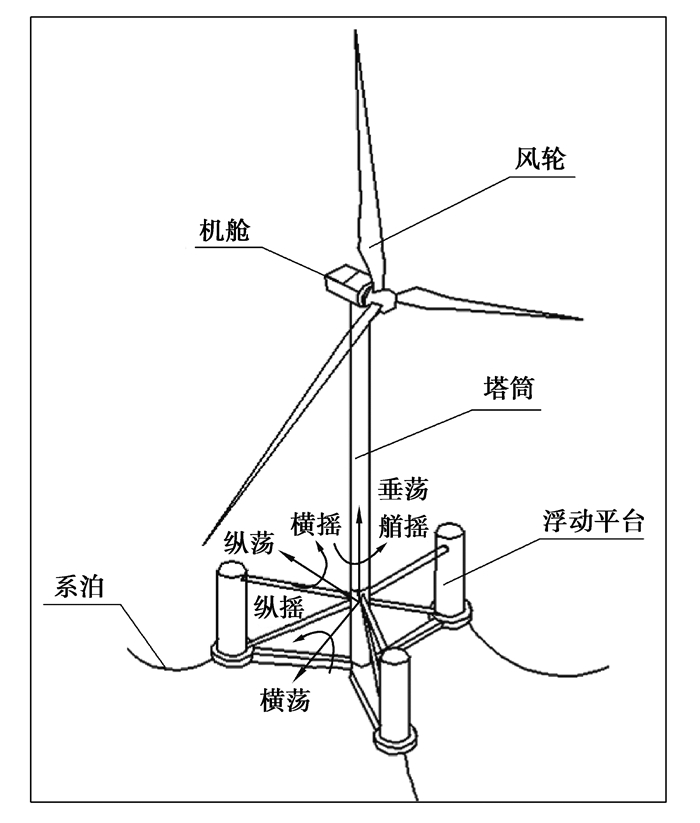
|
图 1 某5 MW级海上浮式风电机组整机结构 Fig. 1 Structure of a 5 MW offshore floating wind turbine |
| 表 1 某5 MW级海上浮式风电机组整机参数 Table 1 Parameters of a 5 MW offshore floating wind turbine |
根据切入、切出和额定风速大小可将变桨距运行分为低风速阶段、过渡阶段和高风速阶段。图 2和图 3分别为不同风速下发电功率和桨距角变化曲线。
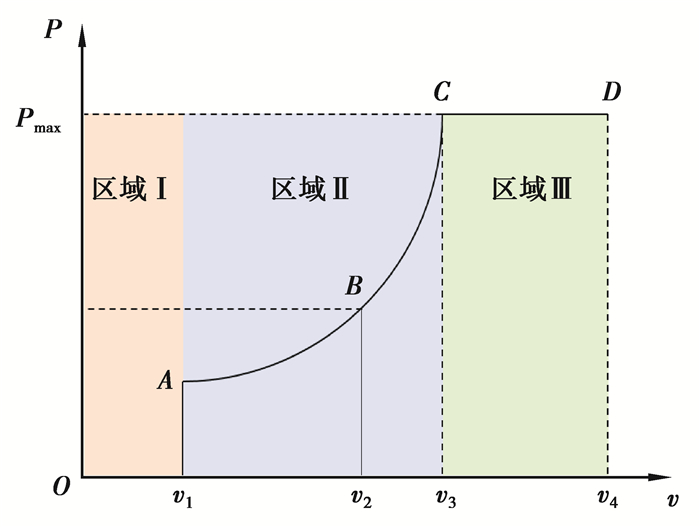
|
图 2 不同风速下发电功率曲线 Fig. 2 Power curve with different wind speeds |
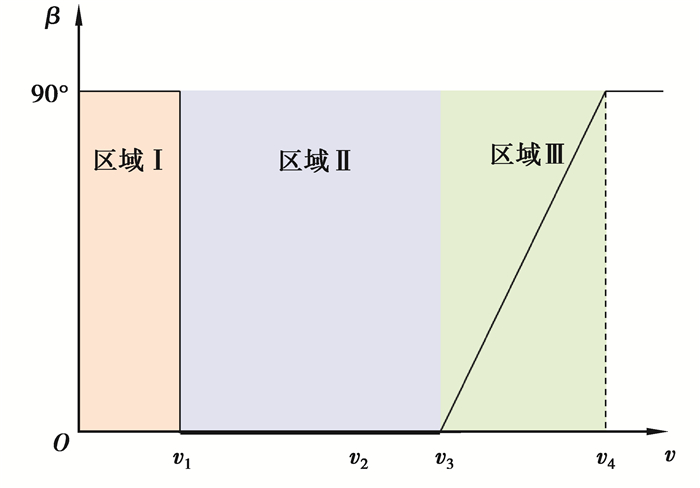
|
图 3 不同风速下桨距角曲线 Fig. 3 Pitch angle curve with different wind speeds |
当风机运行于低风速阶段(区域Ⅰ)时,叶片桨距角保持在90°不变;当风速达到切入风速v1时,变桨执行机构将桨距角控制在零附近,使风轮获得较大的启动转矩;当风速低于额定风速v3时,维持桨距角固定不变,通过调节风轮转速使其工作在最佳叶尖速比处;当风速高于额定风速v3的情况下,变桨执行机构采用改变桨距角的策略,使系统的输出功率稳定于额定功率处。
2 海上浮式风电机组气-弹-水-控耦合系统动力学模型如图 4所示,海上浮式风电机组整机气-弹-水-控耦合系统动力学模型主要包括空气动力学模块、结构动力学模块、水动力学和控制模块[21-23]。
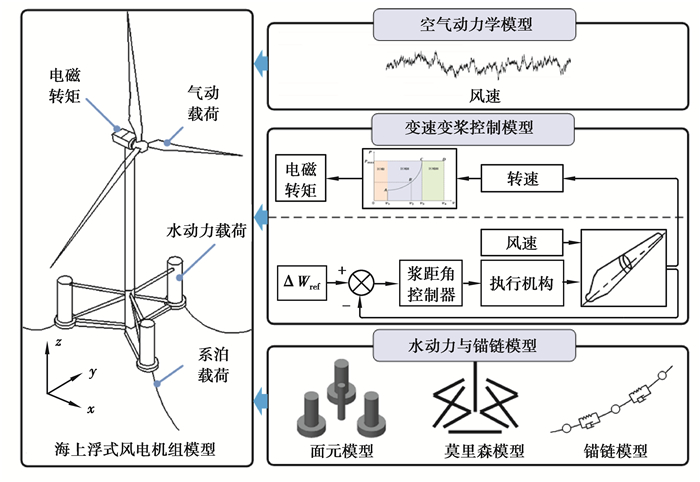
|
图 4 海上浮式风电机组耦合模型 Fig. 4 Coupling model of an offshore floating wind turbine |
将叶片沿展向分成若干叶素单元,通过对作用在各个叶素的气动力沿展向积分,得到作用在整体叶片上的气动力载荷,如图 5所示[23]。
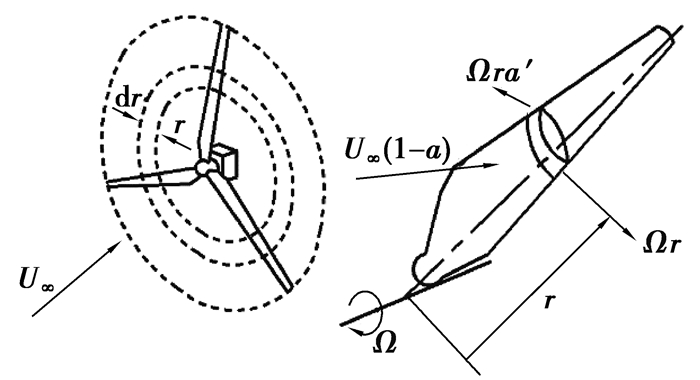
|
图 5 叶素动量理论示意图 Fig. 5 Diagram of blade element-momentum theory |
利用叶素理论计算环形区域中叶素所产生的推力和转矩
| $ \mathrm{d} T=B \frac{1}{2} \rho v^2\left(C_{\mathrm{L}} \cos \varphi+C_{\mathrm{D}} \sin \varphi\right) c \mathrm{~d} r, $ | (1) |
| $ \mathrm{d} Q=B \frac{1}{2} \rho v^2\left(C_{\mathrm{L}} \sin \varphi-C_{\mathrm{D}} \cos \varphi\right) c r \mathrm{~d} r \text { 。} $ | (2) |
式中:dT为环形区域中的叶素推力;dQ为环形区域中的叶素转矩;B为叶片数目;ρ为流体密度;c为翼型弦长;φ为入流角;v为叶素单元速度;CL和CD为叶素升力和阻力系数;r为叶素局部半径。
最后利用动量定理计算环形区域的叶素所产生的推力和转矩
| $ \mathrm{d} T=4 \pi r \rho U_{\infty}^2(1-a) a \mathrm{~d} r, $ | (3) |
| $ \mathrm{d} Q=4 \pi r^3 \rho U_{\infty} \omega(1-a) a^{\prime} \mathrm{d} r。$ | (4) |
式中: U∞为垂直于风轮平面的来流风速;a和a′为轴向和切向诱导因子;ω为风轮转速。
通过结合公式(1)~(4),与二维翼型升阻特性参数,通过数值迭代可以得到风机叶片气动转矩与推力。
2.2 结构动力学模型风轮、传动链、机舱、塔架、浮式平台和锚链耦合系统的动力学方程为[24]
| $ \boldsymbol{M}_t \Delta \ddot{r}_t+\boldsymbol{C}_t \Delta \dot{r}_t+\boldsymbol{K}_t \Delta r_t=\Delta \boldsymbol{R}_t^{\mathrm{E}}, $ | (5) |
式中:Mt为风轮、传动链、机舱、塔架、浮式平台和锚链在t时刻的质量矩阵;Ct为风轮、传动链、机舱、塔架、浮式平台和锚链在t时刻的阻尼矩阵;Kt为风轮、传动链、机舱、塔架、浮式平台和锚链t时刻的刚度矩阵;Δrt为位移增量;
如图 6所示,将浮式平台中浮筒定义为大尺度构件,建立面元模型;将平台连杆定义为小尺度构件,建立莫里森模型[23]。
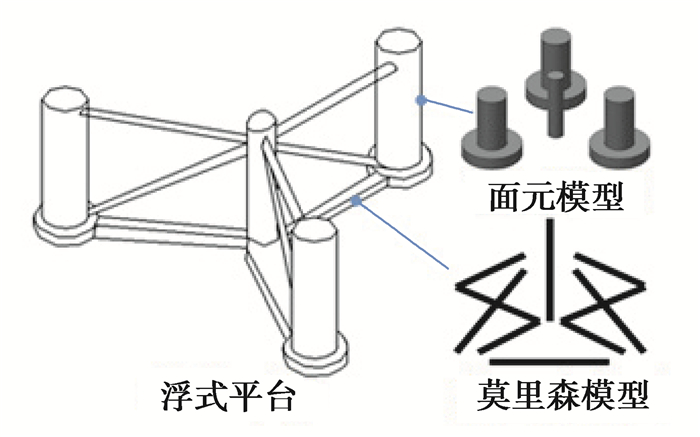
|
图 6 浮式平台模型 Fig. 6 Floating platform model |
在面元模型中,利用三维势流理论计算波浪力, 即
| $ \boldsymbol{F}_{W_i}=-\rho \iint_{s_0}\left(\frac{\partial \varphi_i}{\partial t}\right) \boldsymbol{n}_i \mathrm{~d} S-\rho \iint_{s_0}\left(\frac{\partial \varphi_{\mathrm{d}}}{\partial \mathrm{t}}\right) \boldsymbol{n}_i \mathrm{~d} S, $ | (6) |
式中:FWi为第i自由度下的波浪力;φi为入射波的速度势;S为面积;ni为第i自由度下浮体表面单位外法方向的向量;φd为绕射波速度势。
在莫里森模型中,利用莫里森公式计算波浪力, 即
| $ \mathrm{d} F_{\mathrm{m}}=\rho \frac{\pi D^2}{4}\left(C_{\mathrm{m}} \dot{u}-C_{\mathrm{a}} \ddot{x}\right) \mathrm{d} x+\frac{1}{2} \rho C_{\mathrm{d}} D|u-\dot{x}|(u-\dot{x}) \mathrm{d} x, $ | (7) |
式中:Cm为惯性力系数;Ca为附加质量系数;Cd为拖曳力系数;u为垂直于构件轴线的水质点速度;
如图 7所示,采用集中质量法建立锚链系统模型,锚链由连接节点和弹簧阻尼系统表示[23]。
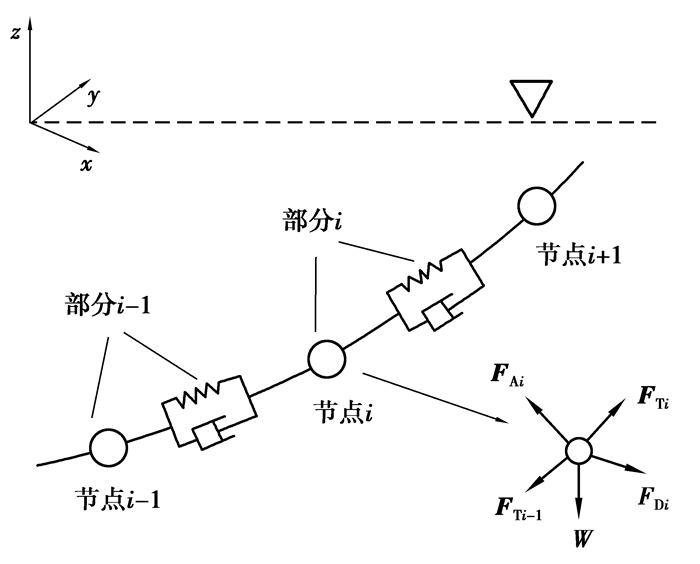
|
图 7 锚链受力分析 Fig. 7 Force analysis of anchor chain |
锚链动力学方程为
| $ \boldsymbol{F}_{\mathrm{DN} i}=\frac{1}{2} \rho C_{\mathrm{DN}} D u_{\mathrm{N}}\left|u_{\mathrm{N}}\right|, $ | (8) |
| $\boldsymbol{F}_{\mathrm{DT} i}=\frac{1}{2} \rho C_{\mathrm{DT}}(\pi D) u_{\mathrm{T}}\left|u_{\mathrm{T}}\right|, $ | (9) |
| $ \boldsymbol{F}_{\mathrm{A} i}=\rho C_{\mathrm{M}} V\left(-\boldsymbol{a}_i\right), $ | (10) |
式中:Mi为节点的质量;ai为节点i的加速度向量;FTi为元素i的张力向量;FTi-1为元素i-1的张力向量;FDNi为节点i的流体法向力;FDTi为节点i的流体切向力;FAi为节点i的流体惯性力;Wi为节点i的重力。
2.4 变桨控制模型如图 8所示,风电机组变桨距控制主要通过变桨执行机构实现,可以将其等效为一阶惯性环节,其传递函数为
| $ \beta=\frac{1}{\tau s+1} \beta_{\mathrm{r}}, $ | (11) |
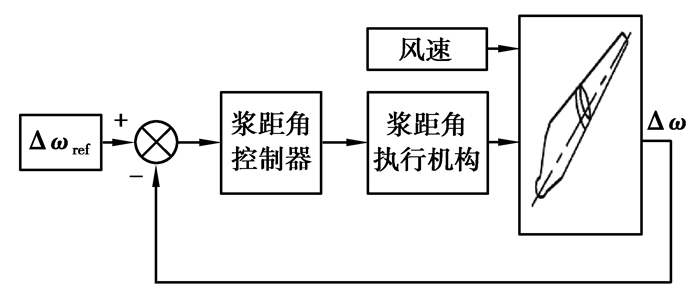
|
图 8 变桨控制图 Fig. 8 Pitch control diagram |
式中:β为实际桨距角;βr为设定桨距角;τ为变桨执行机构时间常数;s表示时间。
2.5 海上浮式风电机组整机气-弹-水-控全耦合动力学模型海上浮式风电机组整机气-弹-水-控动力学全耦合框图如图 9所示。将结构动力学模型与空气动力学模型、水动力模型、锚链模型及变桨控制模型通过双向数据交换,实现海上浮式风电机组气-弹-水-控动力学全耦合[25]。
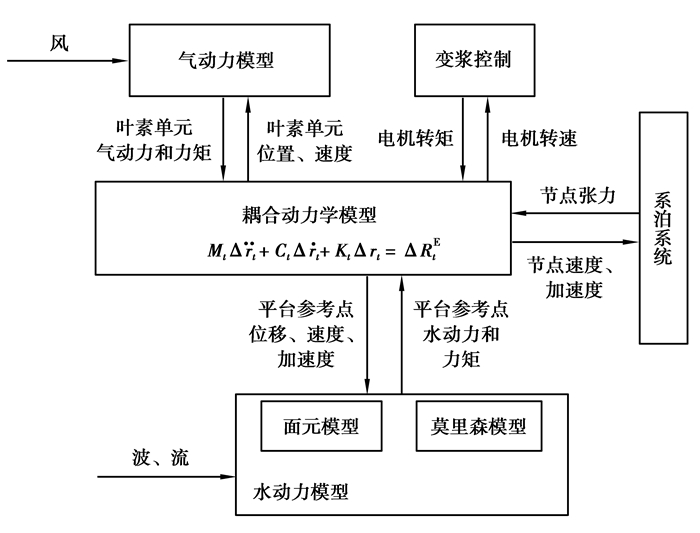
|
图 9 浮式风电机组整机气-弹-水-控全耦合动力学模型 Fig. 9 Full coupled block diagram of gas-elasto-water-control dynamics of a floating wind turbine |
基于海上浮式风电机组气-弹-水-控耦合系统动力学模型,设计变桨距线性自抗扰控制器(LADRC)。LADRC不仅继承了PID控制器简单、有效的优点,还具有强鲁棒性和可实现性。从结构上看,LADRC主要包括线性扩张状态观测器和状态反馈控制率,如图 10所示。图中Δωref为设定的风轮参考转速差,y为实际风轮转速差。u为LADRC输出的桨距角,考虑变桨执行机构的机械特性依次对桨距角进行限速、限幅等,再将其作为海上浮式风电机组耦合系统动力学模型变桨距控制输入信号,最后形成变桨距LADRC控制闭环系统。
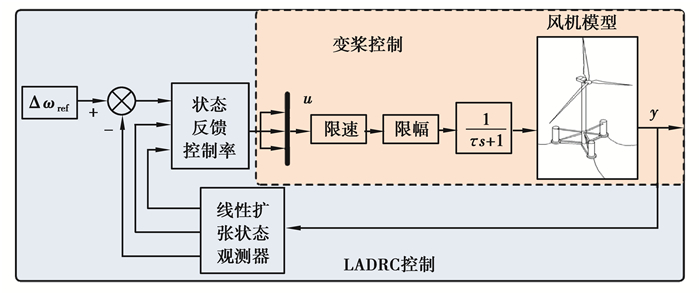
|
图 10 变桨距LADRC Fig. 10 Pitch LADRC |
风电机组发电机电磁转矩通过转速-转矩控制曲线进行调节。变桨距则基于恒转矩控制目标进行控制,其动态方程为
| $ J \dot{\omega}=T_{\text {air }}-T_{\text {gen }}, $ | (12) |
式中:Tair为风轮转矩;Tgen为发电机的电磁转矩;J为风轮转动惯量;ω为风轮转速。
选定风电机组在额定功率处且对应的风能利用率cp最高处作为平衡点,对传动系统进行线性化处理,如式(13)所示。
| $ T_{\mathrm{r}}-T_{\mathrm{ro}}=\frac{\partial T_{\mathrm{r}}}{\partial \omega} \Delta \omega+\frac{\partial T_{\mathrm{r}}}{\partial \beta} \Delta \beta+\frac{\partial T_{\mathrm{r}}}{\partial v} \Delta v+h, $ | (13) |
式中:Tr为发电机电磁转矩;Tro为平衡点处发电机电磁转矩;β为桨距角;v为风速;h为展开高次项。
令
| $ T_{\mathrm{r}}-T_{\mathrm{ro}}=a \Delta \omega+b \Delta \beta+c \Delta v+h, $ | (14) |
以Δω为变桨距LADRC输入,结合式(14)可得
| $ J \Delta \dot{\omega}=J \dot{\omega}-J \dot{\omega}_0=a \Delta \omega+b \Delta \beta+c \Delta v+h \text { 。} $ | (15) |
考虑到桨距角的动态特性,可得
| $ \beta-\beta_0=\Delta \beta=\frac{1}{\tau s+1} \Delta \beta_{\mathrm{r}} 。$ | (16) |
式中Δβr为桨距角控制给定值。
因此,式(15)可转化为
| $ J \Delta \ddot{\omega}=\frac{\tau s-J}{\tau} \Delta \dot{\omega}+\frac{a}{\tau} \Delta \omega+\frac{b}{\tau} \Delta \beta_{\mathrm{r}}+\frac{\tau s+1}{\tau}(c \Delta v+h), $ | (17) |
令
| $ \Delta \ddot{\omega}=\frac{\tau s-J}{J \tau} \Delta \dot{\omega}+\frac{a}{J \tau} \Delta \omega+b_0 \Delta \beta_{\mathrm{r}}+d_{\circ} $ | (18) |
令
| $ \left\{\begin{array}{c} \dot{x}_1=x_2, \\ \dot{x}_2=\frac{\tau s-J}{J \tau} x_2+\frac{a}{J \tau} x_1+b_0 \Delta \beta_{\mathrm{r}}+d , \\ y=x_1 。\end{array}\right. $ | (19) |
根据自抗扰控制理论,基于式(19)可得线性扩张状态观测器状态方程为
| $ \left\{\begin{array}{c} \dot{z}_1=z_2+l_1\left(y-z_1\right),\\ \dot{z}_2=z_3+l_2\left(y-z_1\right)+b \Delta \beta_{\mathrm{r}},\\ \dot{z}_3=l_3\left(y-z_1\right),\\ y=z_{1 }。\end{array}\right. $ | (20) |
式中l1,l2,l3为待调节参数。
3.2 状态反馈控制率设计采用如下状态反馈控制率[25]
| $ u_0=k_1(r-z)+k_2(\dot{r}-\dot{z})+\cdots+k_p\left(r^{(p-1)}-z^{(p-1)}\right), $ | (21) |
式中r为参考信号。
最终控制率为
| $ u=\frac{u_0-z_3}{b_0}=\frac{k_1\left(\Delta \omega_{\mathrm{ref}}-z_1\right)-k_2 z_2-z_3}{b_0} 。$ | (22) |
根据式(12)~(22)设计变桨距LADRC控制器,其控制率为
| $ \left\{\begin{array}{c} \dot{z}_1=z_2+l_1\left(y-z_1\right), \\ \dot{z}_2=z_3+l_2\left(y-z_1\right)+b \Delta \beta_{\mathrm{r}}, \\ \dot{z}_3=l_3\left(y-z_1\right), \\ y=z_1, \\ u_0=K_1\left(\Delta \omega_{\text {ref }}-z_3\right)-K_2 z_2, \\ \Delta \beta_{\mathrm{r}}=\frac{u_0-z_3}{b_0} 。\end{array}\right. $ | (23) |
式中k1,k2,b0为待调节参数。
3.3 控制器参数整定海上浮式风电机组变桨距自抗扰控制器的带调节参数为l1,l2,l3,k1,k2,b0。考虑到海上浮式风电机组机构的复杂性,提出带宽整定法和BP神经网络整定法对LADRC的待调整参数进行整定,以提高抗扰性能和实用性。
3.3.1 带宽整定法由式(23)可知,LADRC有6个参数需要整定,因此对式(23)进行拉式变换,得到系统的闭环传递函数[19]
| $ G_{\mathrm{cl}}(s)=\frac{G_{\mathrm{p}}(s) k_1\left(s^3+l_1 s^2+l_2 s+l_3\right)}{b_0 A_1(s)+G_p(s) A_2(s)} 。$ | (24) |
其中
| $ A_1(s)=s^3+\left(l_1+k_2\right) s^2+\left(l_1 k_2+l_2\right) s, $ | (25) |
| $ A_2(s)=k_1 s^3+\left(l_3+l_2 k_2+l_1 k_1\right) s^2+\left(l_3 k_2+l_2 k_1\right) s+l_3 k_{1 \circ} $ | (26) |
令
| $ \left\{\begin{array}{c} s^3+l_1 s^2+l_2 s+l_3=\left(s+\omega_0\right)^3, \\ s^2+k_2 s+k_1=\left(s+\omega_{\mathrm{c}}\right)^2。\end{array}\right. $ | (27) |
再令k1=ωc2,k2=2ωc,则系统的近似函数为
| $ Y(s)=\frac{\omega_{\mathrm{c}}^2}{s\left(s+\omega_{\mathrm{c}}\right)^2}=\frac{1}{s}-\frac{\omega_{\mathrm{c}}}{\left(s+\omega_{\mathrm{c}}\right)^2}-\frac{1}{s+\omega_{\mathrm{c}}} 。$ | (28) |
故系统的单位阶跃响应为
| $ y(t)=1-\left(1+\omega_{\mathrm{c}} t\right) \mathrm{e}^{-\omega_{\mathrm{c}} t}。$ | (29) |
将式(27)改写为
| $ l_1=3 \omega_0, l_2=3 \omega_0^2, l_3=\omega_0^3 \text { 。} $ | (30) |
由于ω0对线性扩张状态观测器观测速度的影响很小,因此选取
综上所述,带宽整定LADRC的方法是:先确定系统要求的调节时间ts,然后根据ts,调整ωc和ω0的值,再根据式(27)调整l1,l2,l3,k1,k2的值,最后逐渐增大b0值,保证调节时间和超调量满足系统要求。
3.3.2 BP神经网络整定法采用基于BP神经网络的PID控制方法[26],将神经网络输出层的输出等效为二阶LADRC参数[27],即将PID参数转化为二阶自抗扰控制参数,如式(31)所示。
| $ u(t)=\frac{k_1\left(r(t)-z_1(t)\right)+k_2\left(z_2(t)\right)-z_3(t)}{b_0} 。$ | (31) |
由式(31)可知,二阶LADRC包括比例项(k1/b0)(r(t)-z1(t))、微分项(k2/b0)z2(t)以及扰动估计及补偿项(1/b0)z3(t),实际上就是P+I+D的组合,但没有直接采用输出导数和积分,而是利用扩张状态观测器直接进行估计。因此,文中采用基于BP神经网络的PID控制方法对LADRC参数进行整定。
采用3层BP神经网络7-8-3,BP神经网络LADRC算法如图 11所示。
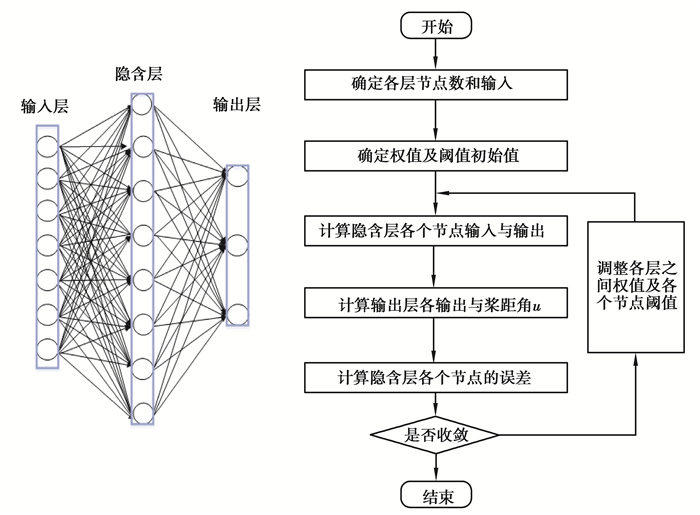
|
图 11 BP神经网络流程图 Fig. 11 Flow chart of BP neural network |
先确定BP神经网络结构,然后选取各层加权系数初值ωij(0)、tli(0)、学习效率和惯性系数,确定输入量,最后计算神经网络输出层,即为LADRC的3个系数
综上所述,BP神经网络整定LADRC的方法是:先根据带宽整定法调整l1,l2,l3的值,再根据BP神经网络整定法确定
利用FAST建立某5 MW级海上浮式风电机组的空气动力学模块、结构动力学模块和水动力学模块。LADRC模块则利用Simulink搭建,通过Level-2 S-Function调用FAST动态链接库,实现与FAST各模块耦合。
如图 12所示,根据IEC标准DLC 1.2工况定义[28],选用平均风速15 m/s的湍流风,并利用TurbSim软件生成时序风速。水动力计算采用白噪声波谱,有效波高为1.264 6 m。仿真时间步长设为0.012 5 s,仿真时间为200 s。图 13~18所示为分别采用带宽整定和BP神经网络整定的变桨距LADRC与PID控制之间的对比分析。
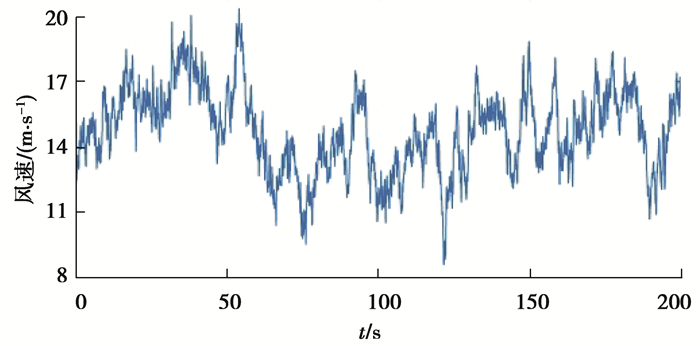
|
图 12 时序随机风速 Fig. 12 Time series random wind speed |
|
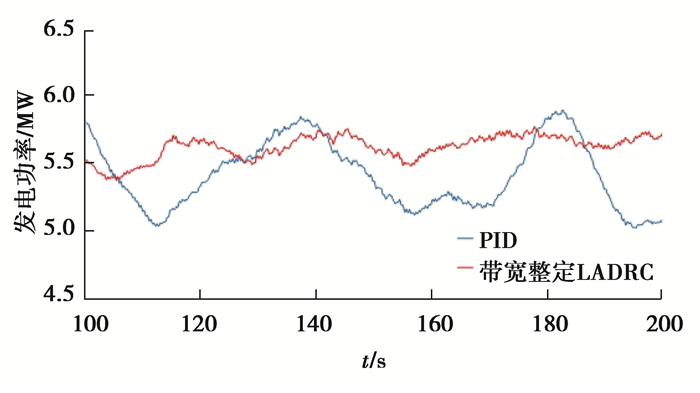
图 13 PID控制和带宽整定LADRC下发电功率对比 Fig. 13 Comparison of generator power between PID control and bandwidth tuning LADRC |
|
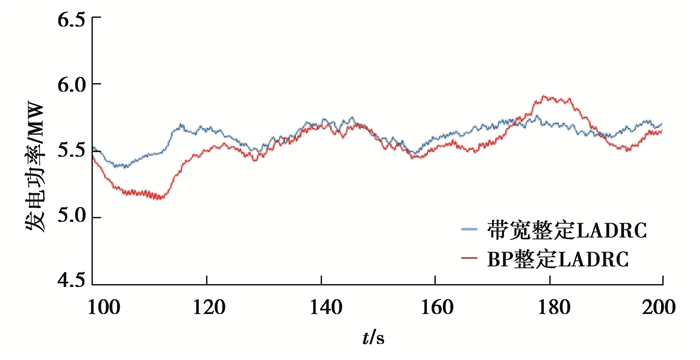
图 14 带宽整定和BP神经网络整定LADRC发电功率对比 Fig. 14 Comparison of generator power between bandwidth setting and BP neural network |
|
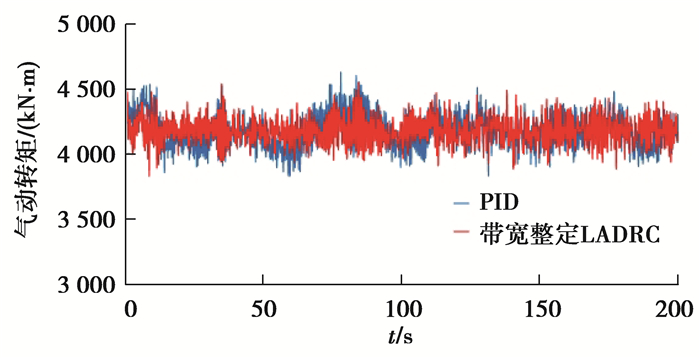
图 15 PID控制和带宽整定LADRC下气动转矩对比 Fig. 15 Comparison of aerodynamic torque between PID control and bandwidth tuning LADRC |
|
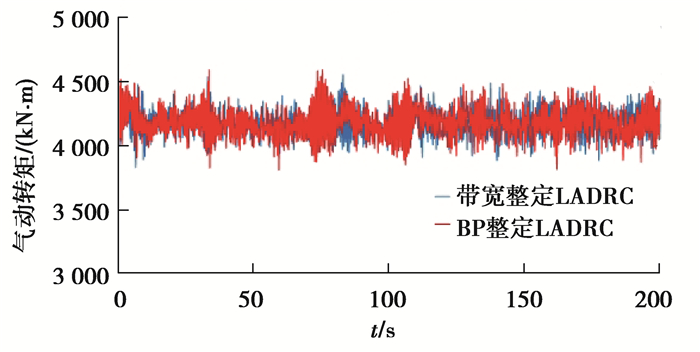
图 16 带宽整定和BP神经网络整定LADRC气动转矩对比 Fig. 16 Comparison of aerodynamic torque between bandwidth tuning and BP neural network tuning LADRC |
|
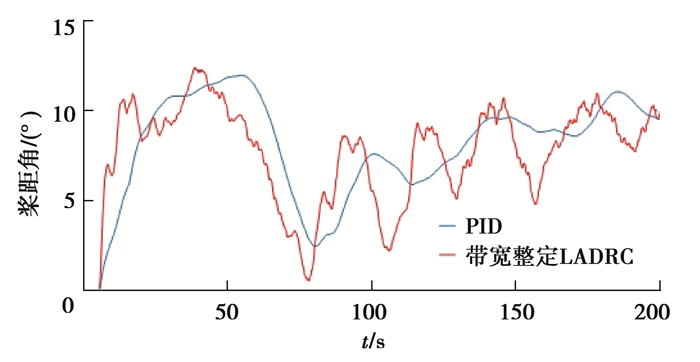
图 17 PID控制和带宽整定LADRC下桨距角对比 Fig. 17 Comparison of pitch angle between PID control and bandwidth tuning LADRC |
|
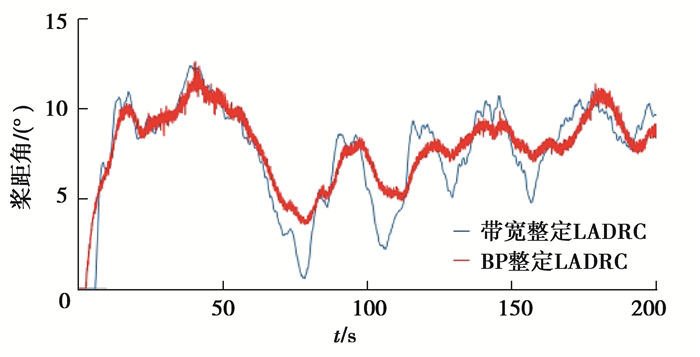
图 18 带宽整定和BP神经网络整定LADRC下桨距角对比 Fig. 18 Comparison of pitch angle between bandwidth setting and BP neural network |
图 13和图 14为风电机组稳定运行状态下100~200 s的发电功率。对比图 13和14可以看出,LADRC和PID都可以稳定发电功率在5 MW附近,但相对于PID,变桨距LADRC的发电功率曲线标准差减少了约30%。
对比图 15和16的气动转矩可以看出,LADRC和PID都将风轮气动转矩稳定在4 180 kN·m附近,但相对于PID,LADRC控制下的气动转矩波动幅值较小,更加稳定,并且基于BP神经网络整定LADRC控制的气动转矩波动幅值略小于带宽整定。
对比图 17和18的桨距角可以看出,针对风速变化,LADRC控制下的桨距角能迅速做出反应,而PID控制的桨距角反应略慢。对比两种参数整定方法可以看出,BP神经网络整定LADRC控制下的桨距角波动幅值小于带宽整定。
此外,根据IEC标准DLC 1.2工况定义,选用3种相同湍流强度NTM B,对比不同平均风速下发电功率,如图 19所示。
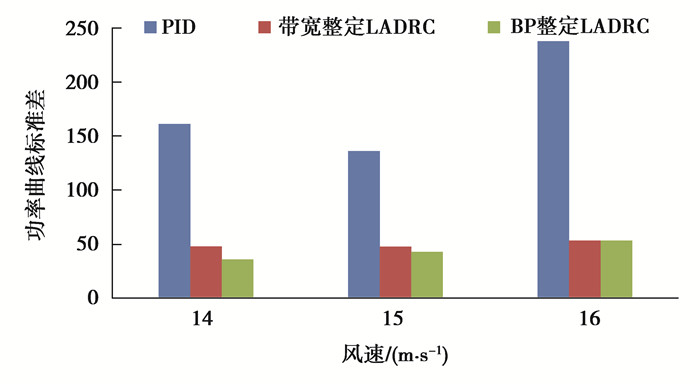
|
图 19 不同风速的功率曲线标准差对比 Fig. 19 Comparison of standard deviations of power curves of different wind speeds |
从图 19中可以看出,LADRC控制下的发电功率波动情况明显小于PID。当平均风速为14 m/s时,相比传统PID控制,采用LADRC的发电功率曲线标准差减少了约60%。在不同平均风速下,采用LADRC的发电功率波动均显著小于PID,而基于BP神经网络整定LADRC的发电功率波动幅值与带宽整定整体相近。由此可得,变桨距LADRC控制器在不同风速条件下均有较好的控制效果。
5 结论以某5 MW级海上浮式风电机组为研究对象,建立了海上浮式风电机组气-弹-水-控耦合系统动力学模型,进而设计了变桨距线性自抗扰控制器,分别采用带宽整定法和BP神经网络参数整定法对控制器进行参数整定,对比分析了变桨距自抗扰控制对发电功率波动的抑制效果,结论如下:
1) 在随机风、浪载荷联合激励下,海上浮式风电机组发电功率将发生大幅波动,传统PID变桨距控制无法有效进行抑制。
2) 所设计的变桨距线性自抗扰控制器可以快速地将海上浮式风电机组发电功率稳定在额定值附近,相比传统PID变桨距控制可有效减少发电功率波动。
3) 提出利用BP神经网络对变桨距线性自抗扰控制器进行参数整定,整定后的控制器对发电功率波动抑制的性能与带宽整定相近,且适应不同风速。
| [1] |
汪胡根, 岳懂, 侯文清. 我国风电装备发展趋势分析[J]. 华东电力, 2014, 42(12): 2665-2667. Wang H G, Yue D, Hou W Q. Analysis of wind power equipment development trend in China[J]. East China Electric Power, 2014, 42(12): 2665-2667. (in Chinese) |
| [2] |
Tan J J, Zhu C C, Song C S, et al. Dynamic modeling and analysis of wind turbine drivetrain considering platform motion[J]. Mechanism and Machine Theory, 2019, 140: 781-808. DOI:10.1016/j.mechmachtheory.2019.06.026 |
| [3] |
王强, 廖康平, 马庆位, 等. 海上浮式风机耦合运动响应的研究[C]//第十九届中国海洋(岸)工程学术讨论会论文集(上), 2019: 250-254. Wang Q, Liao K P, Ma Q W, et al. Research on coupled motion response of floating fans[C]//The 19th China Ocean (Shore) Engineering Symposium (Part Ⅰ), 2019: 250-254. (in Chinese) |
| [4] |
沈涛. 漂浮式海上风力发电机组载荷优化及控制技术研究[D]. 重庆: 重庆大学, 2016. Sheng T. Research on load mitigation and control technology of offshore floating wind turbine system[D]. Chongqing: Chongqing University, 2016. (in Chinese) |
| [5] |
Al-Solihat M K, Nahon M. Flexible multibody dynamic modeling of a floating wind turbine[J]. International Journal of Mechanical Sciences, 2018, 142/143: 518-529. DOI:10.1016/j.ijmecsci.2018.05.018 |
| [6] |
Colombo L, Corradini M L, Ippoliti G, et al. Pitch angle control of a wind turbine operating above the rated wind speed: a sliding mode control approach[J]. ISA Transactions, 2020, 96: 95-102. DOI:10.1016/j.isatra.2019.07.002 |
| [7] |
Yin X X, Zhang W C, Jiang Z S, et al. Adaptive robust integral sliding mode pitch angle control of an electro-hydraulic servo pitch system for wind turbine[J]. Mechanical Systems and Signal Processing, 2019, 133: 105704. DOI:10.1016/j.ymssp.2018.09.026 |
| [8] |
Civelek Z. Optimization of fuzzy logic (Takagi-Sugeno) blade pitch angle controller in wind turbines by genetic algorithm[J]. Engineering Science and Technology, an International Journal, 2020, 23(1): 1-9. DOI:10.1016/j.jestch.2019.04.010 |
| [9] |
Venkaiah P, Sarkar B K. Hydraulically actuated horizontal axis wind turbine pitch control by model free adaptive controller[J]. Renewable Energy, 2020, 147: 55-68. DOI:10.1016/j.renene.2019.08.127 |
| [10] |
Yu H Q, Gao Y, Zhang H. Fuzzy self-adaptive PID control of the variable speed constant frequency variable-pitch wind turbine system[C]//2014 IEEE International Conference on System Science and Engineering. July 11-13, 2014, Shanghai, China. IEEE, 2014: 124-127.
|
| [11] |
苑晨阳, 李静, 陈健云, 等. 大型风电机组变桨距ABC-PID控制研究[J]. 太阳能学报, 2019, 40(10): 3002-3008. Yuan C Y, Li J, Chen J Y, et al. Research on abc-pid pitch control of large-scale wind turbines[J]. Acta Energiae Solaris Sinica, 2019, 40(10): 3002-3008. (in Chinese) |
| [12] |
Yilmaz A S, Özer Z. Pitch angle control in wind turbines above the rated wind speed by multi-layer perceptron and radial basis function neural networks[J]. Expert Systems With Applications, 2009, 36(6): 9767-9775. DOI:10.1016/j.eswa.2009.02.014 |
| [13] |
韩京清. 自抗扰控制器及其应用[J]. 控制与决策, 1998, 13(1): 19-23. Han J Q. Auto-disturbances-rejection controller and its applications[J]. Control and Decision, 1998, 13(1): 19-23. (in Chinese) DOI:10.3321/j.issn:1001-0920.1998.01.005 |
| [14] |
Huang Y, Han J Q. Analysis and design for the second order nonlinear continuous extended states observer[J]. Chinese Science Bulletin, 2000, 45(21): 1938-1944. DOI:10.1007/BF02909682 |
| [15] |
谢景凤, 杨俊华, 刘慧媛, 等. 变速恒频变桨距风力机自抗扰控制[J]. 微特电机, 2010, 38(11): 58-61. Xie J F, Yang J H, Liu H Y, et al. Active-disturbance rejection control for variable speed constant frequency variable pitch wind turbines[J]. Small & Special Electrical Machines, 2010, 38(11): 58-61. (in Chinese) |
| [16] |
Li J, Zhao X, Chen Y. An active disturbance rejection controller for depth-pitch control of an underwater vehicle[J]. International Journal of Innovative Computing Information and Control: IJICIC, 2017, 13(3): 727-739. |
| [17] |
任丽娜, 吕明月, 刘爽爽, 等. 基于蜂群算法优化的变桨距自抗扰控制器[J]. 新型工业化, 2014, 4(6): 43-48. Ren L N, Lv M Y, Liu S S, et al. Pitch control using active disturbance rejection controller based on colony optimization algorithm[J]. The Journal of New Industrialization, 2014, 4(6): 43-48. (in Chinese) |
| [18] |
周蓉, 韩文杰, 谭文. 线性自抗扰控制的适用性及整定[J]. 控制理论与应用, 2018, 35(11): 1654-1662. Zhou R, Han W J, Tan W. On applicability and tuning of linear active disturbance rejection control[J]. Control Theory & Applications, 2018, 35(11): 1654-1662. (in Chinese) |
| [19] |
Gao Z Q. Scaling and bandwidth-parameterization based controller tuning[C]//Proceedings of the 2003 American Control Conference, 2003. Denver, CO, USA. IEEE, 2003 : 4989-4996.
|
| [20] |
陈旭, 朱才朝, 宋朝省, 等. 紧急停机工况下风力发电机系统动态特性分析[J]. 机械工程学报, 2019, 55(5): 82-88. Chen X, Zhu C C, Song C S, et al. Dynamic characteristics analysis of wind turbine under emergency shutdown events[J]. Journal of Mechanical Engineering, 2019, 55(5): 82-88. (in Chinese) |
| [21] |
Li X H, Zhu C C, Fan Z X, et al. Effects of the yaw error and the wind-wave misalignment on the dynamic characteristics of the floating offshore wind turbine[J]. Ocean Engineering, 2020, 199: 106960. |
| [22] |
Ding Q W, Li C, Yu N T, et al. Numerical and experimental investigation into the dynamic response of a floating wind turbine spar array platform[J]. Journal of Mechanical Science and Technology, 2018, 32(3): 1106-1116. |
| [23] |
李修赫, 朱才朝, 谭建军, 等. 风浪不共线对浮式风机基础动态特性影响研究[J]. 振动与冲击, 2020, 39(13): 230-237. Li X H, Zhu C C, Tan J J, et al. Effects of wind-wave misalignment on dynamic characteristics of floating offshore wind turbine foundation[J]. Journal of Vibration and Shock, 2020, 39(13): 230-237. (in Chinese) |
| [24] |
范增辉. 基于全局耦合响应的三浮筒半潜式风机基础的动力响应及疲劳分析[D]. 镇江: 江苏科技大学, 2019. Fan Z H. Dynamic response and fatigue analysis of three-buoy semi-submersible fan foundation based on global coupling response[D]. Zhenjiang: Jiangsu University of Science and Technology, 2019. (in Chinese) |
| [25] |
彭春江. 海上浮式风电机整机全耦合动力学建模及动态激励特性研究[D]. 长沙: 湖南大学, 2017. Peng C J. Full couping dynamics modeling and dynamic excitation characteristics research for offshore floating wind turbine[D]. Changsha: Hunan University, 2017. (in Chinese) |
| [26] |
刘金琨. 先进PID控制MATLAB仿真[M]. 北京: 电子工业出版社, 2004.
|
| [27] |
韩文杰, 谭文. 基于PID参数整定的线性自抗扰控制参数整定[J]. 控制与决策, 2021, 36(7): 1592-1600. Han W J, Tan W. Tuning of linear active disturbance rejection controllers based on PID tuning rules[J]. Control and Decision, 2021, 36(7): 1592-1600. (in Chinese) |
| [28] |
International Electrotechnical Commission. Wind turbines - Part 3: design requirements for offshore wind turbines: IEC 61400-3: 2009[S]. Geneva, Switzerland: IEC, 2009.
|
 2022, Vol. 45
2022, Vol. 45


