2. 郑州宇通集团有限公司, 郑州 450061
2. Zhengzhou Yutong Bus Co., Ltd., Zhengzhou 450061, P. R. China
随着世界范围内化石能源储备量急剧减少,急需寻求新的可替代能源。而氢能具有高效率、可再生和零污染的优点,逐渐进入大众的视野。近些年燃料电池动力系统和燃料电池汽车快速发展[1-3],各国政府也逐渐加大加氢站的建设力度[4]。高压储氢技术由于其实用可靠、成本较低及技术较为成熟等优点成为加氢站的主要储氢方式[5]。但快速充氢过程中,由于氢气的快速压缩、焦耳-汤姆逊负效应及动能向热能的转化会导致气瓶内壁温度急剧上升[6-7],从而对气瓶材料造成损伤甚至失效产生安全隐患,因此需要研究快速加氢控制策略以完成氢气的快速高效安全充装。
当前国内外对于快速加氢的研究主要为通过实验及计算流体动力学CFD(computational fluid dynamics)仿真对加注过程温升机理进行分析和综合考虑加氢站能耗对站内储氢系统参数设置进行分析。文献[8~9]通过建立加注过程中气瓶内部的CFD仿真模型,研究了不同加注参数对气瓶内部氢气状态的影响; 文献[10]研究了储氢瓶进气口结构对加注过程中氢气温度分布的影响,通过设置合理的氢气入口倾斜角度可以减小气瓶内部温差,避免局部温度过高; 文献[11]考虑氢气利用率及加注时间,建立了多目标优化模型,完成了不同压力等级储氢瓶组的供气量策略研究; 文献[12~14]完成了加注完成后气瓶内部氢气温度的预测,为加注策略的制定提供了参考。文献[15]对单级高压储氢系统和多级储氢系统的加注过程进行了对比,虽然单级储氢系统可以提供较快的加注速度,但其会导致氢气温升和运行能耗较高,而采用级联式氢气存储系统可以降低加氢站的压缩能耗,控制氢气预冷可以有效控制氢气温升,制定合理的压力切换及温度控制策略可以有效提高加氢速度,降低预冷能耗[16-17]。
综上所述,目前对于氢气快速加注的研究主要集中于温升机理研究及能耗分析,对实际加注过程中的控制策略研究较少。考虑3级储氢式加氢站,以35 MPa的III型车载储氢瓶为研究对象,建立了级联式储氢系统加注过程的热力学模型,研究了不同压力等级之间的压力切换系数和氢气预冷温度对加氢过程的影响。以冷却能耗、加注时间和氢气瓶SOC为优化目标,建立多目标优化模型,优化结果表明,该方法可以在不同初始条件下以最低的工作能耗,3 min内完成氢气瓶SOC大于85%的氢气快速加注。
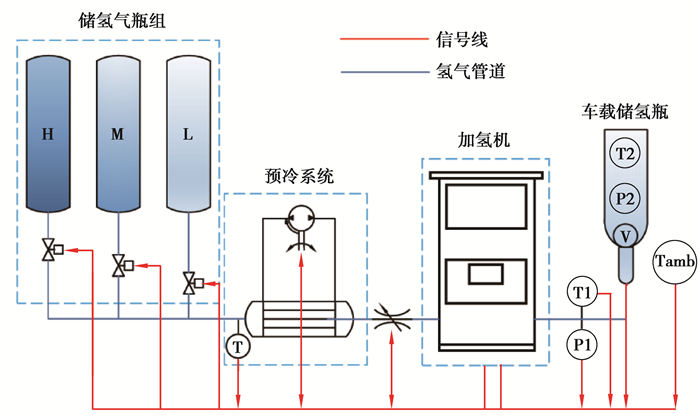
1 系统与模型 1.1 级联式加氢站系统考虑到氢气压缩能耗及氢气利用率,加氢站储氢系统一般采用级联存储系统,其通常由低、中、高压3种压力等级的储氢瓶组组成。图 1为级联式氢气加注系统的原理图,系统部件主要包括高压储氢系统、氢气冷却系统、加氢机及车载储氢瓶等。
|
图 1 级联式加氢站拓扑图 Fig. 1 Diagram of the cascade hydrogen refueling station |
车辆需要补充氢气时,车载氢气瓶首先连接到低压储氢瓶组进行氢气加注,当气瓶内压力达到预设的切换压力水平时,系统切换到中压储氢瓶组,最后切换到高压储氢瓶组;根据实际工作条件确定预冷系统在整个加注过程中是否需要工作;当瓶内压力达到目标压力(35 MPa)或瓶内壁温度高于358 K时,停止氢气加注。加注完成后的氢气状态(SOC)定义为充装结束时的氢气质量与288 K/35 MPa氢气状态下车载氢气瓶所能储存氢气质量的比值如式(1)所示。
| $ S_{\mathrm{OC}}=\frac{m_{\mathrm{c}}}{\rho_{\mathrm{g}} V_{\mathrm{c}}}, $ | (1) |
式中:mc, Vc, ρg分别代表加注完成后气瓶内部氢气质量、氢气瓶容积及288 K/35 MPa下的氢气密度。
1.2 氢气加注模型本节介绍了高压氢气式加氢站在快速加注过程中的建模理论,对所用到的一些理论公式及经验公式进行参数说明。为了得到一个较为简单的氢气状态计算模型,以便完成后续多目标优化过程,在考虑模型准确性的同时做出如下简化及假设。
1) 加注过程中,加氢站用储氢系统中氢气温度、压力恒定;
2) 忽略管道内氢气的热损失及其压降;
3) 假设氢气瓶内的气体温度为氢气瓶壁的最高温度;
4) 假设加注过程中为准稳态过程,车载储氢瓶内部氢气温度、压力均匀分布。
1.2.1 气体状态方程低压氢气(<10 MPa)一般认为是理想气体,适用理想气体状态方程来描述。当氢气压力较高时,气体的物理性质会偏离理想气体状态方程,不再适用于理想气体状态方程。车载氢气瓶的压力通常最低高达35 MPa,而加氢站的储氢瓶组压力甚至更高。为了更真实地模拟氢气的状态,对理想气体状态方程进行修正:将含压缩因子的真实气体状态方程考虑为式(2)[18]。
| $ \begin{aligned} &P V=Z m R_{\mathrm{g}} T, \end{aligned} $ | (2) |
式中:P、V、Z、m、T分别代表气体压力、体积、相对应的压缩因子、质量和温度;Rg表示理想气体常数。
1.2.2 氢气流量计算方程根据气体经过小孔质量流量理论计算公式,如式(3)~(6)所示,公式(4)和(6)分别表示氢气环境中亚音速状态和音速状态下的氢气流量计算公式。
| $ P_{\mathrm{c}} / P_{\mathrm{sto}}>\left(\frac{2}{k+1}\right)^{\frac{k}{k-1}} 。$ | (3) |
质量流量:
| $ q_{\mathrm{m}}=C \rho_{\mathrm{g}} S_{\mathrm{or}}\left(\frac{P_{\mathrm{c}}}{P_{\mathrm{sto}}}\right)^{\frac{1}{k}}\left\{\left(\frac{2 k}{k-1}\right)\left(\frac{P_{\mathrm{c}}}{P_{\mathrm{sto}}}\right)\left[1-\left(\frac{P_{\mathrm{c}}}{P_{\mathrm{sto}}}\right)^{\frac{k-1}{k}}\right]\right\}^{\frac{1}{2}}, $ | (4) |
| $ P_{\mathrm{c}} / P_{\mathrm{sto}} \leqslant\left(\frac{2}{k+1}\right)^{\frac{k}{k-1}} 。$ | (5) |
质量流量:
| $ q_{\mathrm{m}}=C\left(k \rho_{\mathrm{g}} P_{\mathrm{sto}}\right)^{\frac{1}{2}} S_{\mathrm{or}}\left(\frac{2}{k+1}\right)^{\frac{k+1}{2(k-1)}} 。$ | (6) |
式中:qm表示入口氢气质量流量;Pc为车载储氢瓶当前压力;Psto储氢系统氢气压力;C为加氢口节流系数;ρg为储氢系统氢气密度;Sor为加氢口面积,k为氢气的比热比,可由式(7)计算。
| $ k=c_{\mathrm{p}} / c_{\mathrm{v}}, $ | (7) |
式中:cp, cv分别表示氢气的定压热容及定容热容。
1.2.3 质量能量守恒方程将氢气瓶内部单位体积的氢气作为一个热力学控制体积。在质量守恒方程中,
| $ \dot{m}_{\text {in }}=\dot{m}_{\text {out }}=\dot{m}, $ | (8) |
式中:
根据国际标准NIST[19],氢的比内能与温度的简化关系如式(9)所示,其中参数a和b分别为常系数10.51和482.43,氢气焓值的计算方法如式(10)所示。
| $ u=a T-b , $ | (9) |
| $ h=u+p / \rho_{\mathrm{g}} , $ | (10) |
式中u、h、p分别表示单位质量氢气的内能焓值及压力。
由于没有外部功的输入且气体势能变化很小,仅考虑入口氢气的动能及焓值,气瓶内氢气单位控制体积的内能计算如式(11)所示。
| $ \frac{\mathrm{d} U_{\mathrm{c}}}{\mathrm{d} t}=\dot{Q}+\dot{m}_{\text {in }}\left(\frac{V_{\mathrm{in}}^2}{2}+h_{\mathrm{in}}\right), $ | (11) |
式中:Uc表示车载氢气瓶内的氢气内能;t表示时间;
考虑铝内衬的热积累,氢气与铝内衬之间的换热表达式为式(12),氢气瓶外表面向环境的传热可表示为式(13),车载氢气瓶的初始温等于环境温度,根据气瓶壁吸收和散出的热量,利用式(14)计算氢气瓶壁面平均温度。
| $ \dot{Q}_1=k_1 S_{\text {wall }}\left(T_{\mathrm{g}}-T_{\text {wall }}\right), $ | (12) |
| $ \dot{Q}_2=k_2 S_{\text {sur }}\left(T_{\text {wall }}-T_{\text {amb }}\right), $ | (13) |
| $ c m \Delta T_{\text {wall }}=\dot{Q}_1-\dot{Q}_2, $ | (14) |
式中:
根据式热力学第一定律及式(8)~(12),可得车载氢气瓶内部氢气内能计算式为式(15)。
| $ U_{\mathrm{c}}=m u+\int q_{\mathrm{m}} h_{\mathrm{sto}} \mathrm{d} t+\int Q_1 \mathrm{d} t $ | (15) |
式中hsto表示站储氢系统氢气的单位质量焓值。
2 加注过程的参数优化本节介绍了压力切换系数PSC(pressure switching coefficients)的定义和快速加注过程的预冷能耗即冷却需求的计算。随后建立了多目标优化模型,给出了求解算法。
2.1 压力切换系数高压氢气储存在低中高压3级储氢瓶组中,在氢气加注过程中,当车载氢气瓶内压力达到预设的切换压力(Pswit)时,压力源(即连接的氢气源)需切换到较高的压力水平。目前级联式加氢站采用固定压力切换点或等压切换操作,这会导致不同初始条件下的加注过程不可控以及加注时间过长。本研究中压力切换点被设定为可根据工作条件变化的量,通过设置适当的压力切换点可以有效缩短加注时间。压力切换系数(PSC)定义为切换压力值(Pswit)与当前储氢瓶组压力水平(Psto)的比值如式(16)所示,PSC是决定加注时间的重要参数,为实现快速加注将其作为优化的控制参数。
| $ P_{\mathrm{sc}}=P_{\text {swit }} / P_{\text {sto }}。$ | (16) |
为了将氢气瓶内的最终温度控制在可接受范围内,在气体进入氢气瓶之前,需要用冷冻机组对氢气进行预冷。模型中需要计算氢气的制冷量需求,换热器的能量守恒如式(17)(18)所示。
| $ Q_{\mathrm{C}}=\Delta h \dot{m}, $ | (17) |
| $ \Delta h=h_{\text {sto }}-h_{\text {coling }}, $ | (18) |
式中:QC为冷却需求;Δh为单位流量下氢气制冷前后的焓差。
由式(19)可求得冷冻机组所需的能耗值,其中Cop是制冷设备的性能系数。
| $ W=Q_{\mathrm{C}} / C_{\mathrm{op}} \text { 。} $ | (19) |
根据上述分析,在一定初始条件下需要用PSC和预冷温度来计算实际的冷却能耗、加氢时间和SOC。因此以冷却需求、填充时间和SOC为优化目标。以PSC和预冷温度为优化参数x,建立了多目标优化模型,其数学模型如式(20)(21)所示。
| $ \min \left[W(x), t(x), -S_{\mathrm{OC}}(x)\right], $ | (20) |
| $ \text { s.t. } x \in X, $ | (21) |
式中W(x)、t(x)分别表示预冷能耗及氢气加注时间。
此问题优化参数为离散变量且搜索范围较小,为得到全局最优解,减少计算成本,选择顺序搜索算法进行寻优。另外如果对多个目标各自设置权重进行优化,得到的结果过于主观,因此选择将其中2个目标转换为约束条件,多目标优化模型的一般形式可以转化为单目标模型如式(22)~(23)所示。
| $ \min W(x), $ | (22) |
| $ \text { s.t. }\left\{\begin{array}{l} t(x) \leqslant \varepsilon_1, \\ {S_{{\rm{OC}}}}(x) \geqslant \varepsilon_2, \\ x \in X 。\end{array}\right. $ | (23) |
式中:预冷能耗W(x)为优化目标,t(x)和SOC(x)分别表示为加注时间约束和气瓶终态氢气质量约束。加注时间约束为ε1=180 s;SOC的最低值设置为ε2=85%;X域为优化参数PSC和预冷温度的取值范围。根据模型计算结果及级联式储氢系统的氢气利用率和氢气加注时间,PSC取值范围设定0.55~0.95,入口氢气温度可由环境温度预冷至-40 ℃。
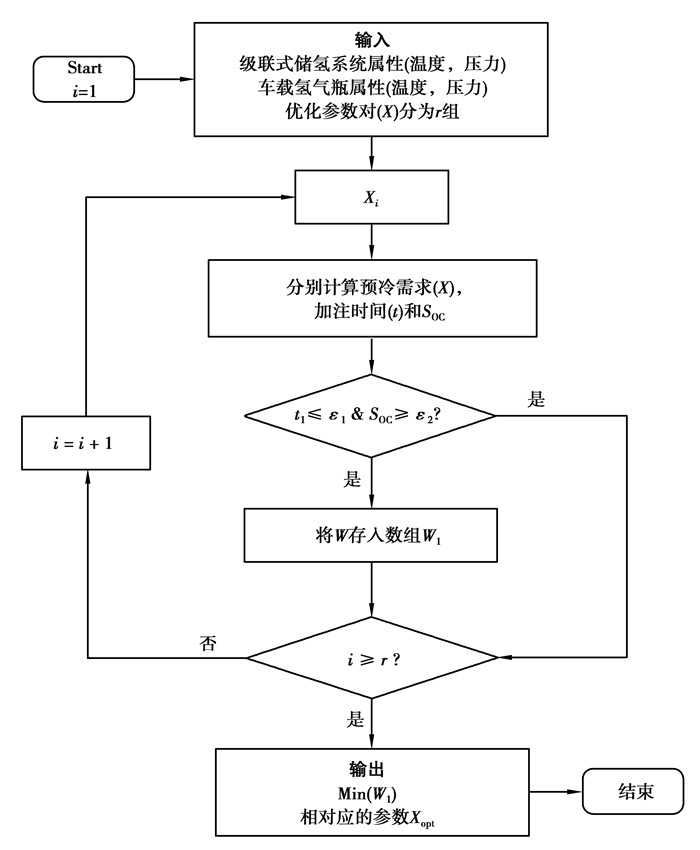
采用顺序搜索算法对单目标优化模型进行求解,计算过程如图 2所示。当车载氢系统与加氢机连接时,车载氢系统通过红外通信将当前气瓶状态传输到加氢机。将参数对X(i)分为r组,例如X(1)=[0.55, -40 ℃]。根据加注模型及级联式储氢系统特性,给定PSC和预冷温度,在每个初始条件下可以计算出系统的能耗、加氢时间和氢气瓶的SOC值,通过加注时间和SOC与约束条件的比较进行参数取舍,然后记录所有满足约束条件的参数对,以能耗最低的参数对为最优解,对不同的初始条件进行参数寻优得到不同工况下的最优控制参数。
|
图 2 优化算法流程框图 Fig. 2 Flow chart of the optimization algorithm |
根据加氢站运行参数,级联式储氢系统的压力等级为高压(40 MPa)、中压(30 MPa)和低压(20 MPa)。研究对象为额定压力35 MPa,140 L的Ⅲ型氢气瓶。本节完成了模型验证,并研究了PSC和预冷温度对充填过程的影响,给出了不同初始条件下多目标优化模型的计算结果。
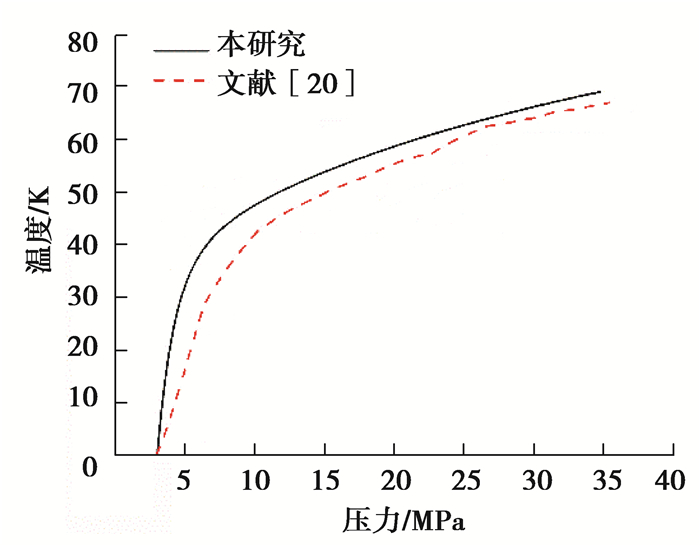
3.1 模型验证本节将模型仿真结果与实验数据进行对比,验证模型的正确性。实验数据来源于文献[20]中针对35 MPa,150 L的Ⅲ型氢气瓶加注实验,初始温度和压力分别为293 K和3 MPa。图 3给出了加氢过程中温升-压力变化的实验结果与仿真结果的对比。可以看出仿真结果与实验数据的变化趋势一致,且具有较好的一致性(填充结束时温升差小于3 K)。低压阶段温度差异较大,由于低压阶段气瓶内外氢气压差较大导致气体流速较快,气瓶内部氢气与瓶壁的热交换及摩擦生热剧烈,而仅考虑了氢气的平均温度且忽略了气体与瓶壁之间的摩擦,由于考虑能量守恒定律及氢气与瓶壁的热交换,导致氢气温度低于实验数据而瓶壁温度高于实验数据,因此造成低压阶段氢气温度差异较为明显,而随着压力升高,气流速度渐缓,而由于瓶壁温度较高导致热交换变慢,模型温升逐渐趋近实验数据。因此模型比较准确可用于进一步研究。
|
图 3 加注过程中实验数据与仿真结果关于温度压力的对比图 Fig. 3 Comparison of experimental results and simulation results for temperature rise vs. pressure increase during filling process |
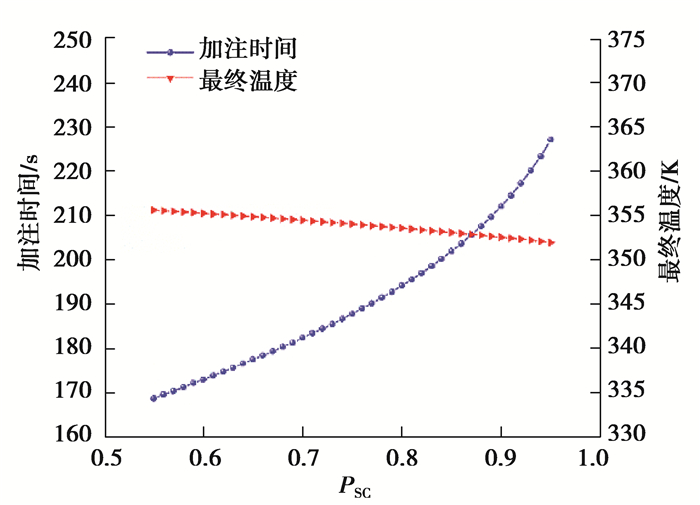
在环境温度293 K、初始压力2 MPa、入口氢气预冷到273 K的初始条件下,取不同PSC值的计算结果如图 4所示。随着PSC的增加,加注时间显著增加,而在PSC的全约束范围内,气瓶内部氢气温度变化小于5 K,这是由于不同控制参数下,气瓶内部氢气温度的差异仅取决于气瓶向外界环境中的散热及气瓶本身的热积累,而加注过程较短(<3 min),所以散热速度及热积累较慢而导致温升变化不大。从以上分析可以看出,选择合适的PSC值可以有效缩短加注时间,且对气瓶内最终温度的影响较小。
|
图 4 PSC对氢气瓶加注时间及最终温度的影响 Fig. 4 The variation of filling time and final temperature with PSC |
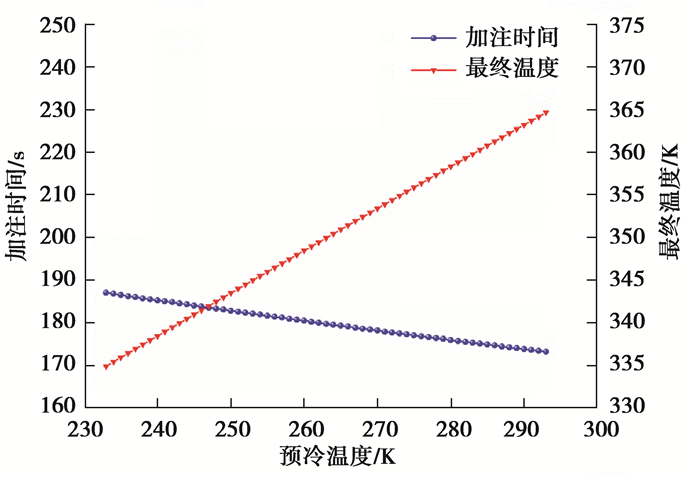
在环境温度293 K、初始压力2 MPa、PSC值为0.65的初始条件下,研究不同入口氢气温度对加注时间和气瓶内最终温度的影响,结果如图 5所示。可以看出,加注时间随氢气预冷温度变化较小,反之气瓶内最终温度随预冷温度变化显著,且近似呈线性关系,这是由于入口氢气温度的降低大大减小了进入气瓶的氢气内能。可看出氢气预冷温度降低2 K,气瓶内的最终温度降低约1 K,为预冷温度的确定提供了思路。
|
图 5 预冷温度对氢气瓶加注时间及最终温度的影响 Fig. 5 The variation of filling time and final temperature with pre-cooling temperature |
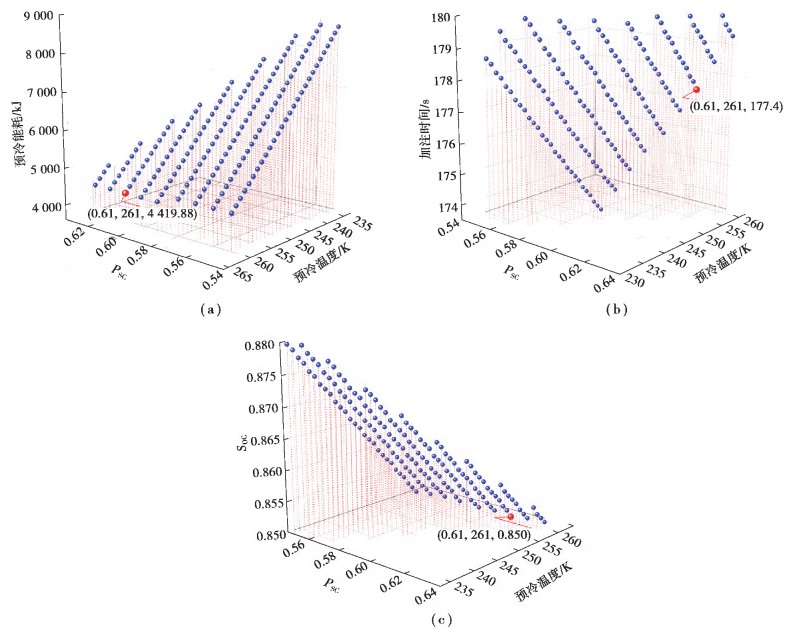
图 6(a)给出了可行域内的不同优化参数在初始压力2 MPa、环境温度293 K下的预冷能耗。随着预冷温度的降低,由于氢气入口焓值的降低,冷却能耗急剧增加,与之相反,随着PSC的增加能耗略有增加,这是由于所加注的氢气质量增加导致预冷能耗略增,当PSC为0.61,预冷温度为261 K时能耗最小。图 6(b)(c)为可行域内不同优化参数下氢气瓶加注时间和SOC值,加注时间均小于180 s(3 min),SOC均大于85%。考虑氢热值为1.4×105 kJ/kg,计算加注氢气能量与预冷能耗进行比较,具体优化参数和目标如表 1所示。
|
图 6 氢气瓶初始压力为2 MPa和环境温度293 K时的优化结果 Fig. 6 Optimized result under initial pressure 2 MPa and ambient temperature 293 K |
| 表 1 初始工况为2 MPa, 293 K时的优化参数及目标 Table 1 Optimized parameters and target under initial condition 2 MPa, 293 K |
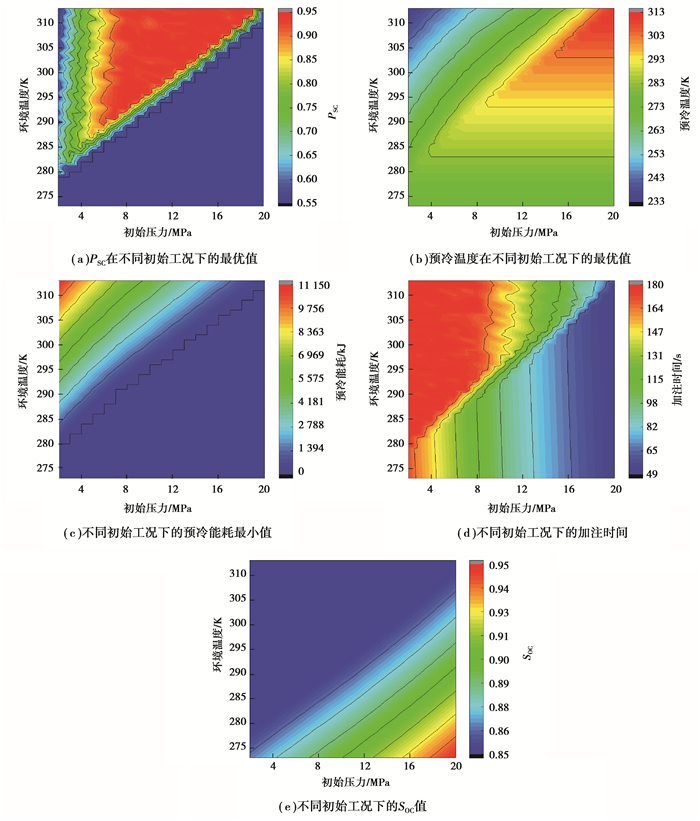
考虑到加氢站的实际运行条件,环境温度(即车载氢气瓶初始温度)取值范围为273~313 K(计算步长取1 K),气瓶内初始压力取值范围为2~20 MPa(计算步长取1 MPa)。通过参数组合共有779种不同初始工况,优化结果如图 7所示。图 7(a)所示不同工况下PSC的最优取值,在初始压力和环境温度较低时取较小的PSC,可以缩短加注时间,在3 min内完成氢气加注;在环境温度较高时,较大的PSC可以延长加注时间降低温升,同时提高SOC;当初始压力较高时,SOC约束容易满足,较小的PSC可以有效地缩短加氢时间。入口氢气的最佳预冷温度如图 7(b)所示,预冷温度与初始压力的变化成正比,与环境温度的变化成反比,环境温度高、初始压力低时,需要较大的预冷能耗,导致预冷温度较低;当环境温度较低而初始压力较高时,进口氢气需要较少的预冷,甚至不需要预冷。
|
图 7 不同初始工况下的优化结果 Fig. 7 Optimized results under different initial conditions |
图 7(c)为不同初始条件(气瓶内初始压力和环境温度)下的最小预冷能耗。当环境温度最高、初始压力最低时,预冷能耗最大,因为在此工作条件会导致气瓶内部温度急剧上升,需要非常低的氢气预冷温度,导致预冷能耗增加。在最优控制参数下的氢气加注时间如图 7(d)所示。从图 7(d)可以看出,氢气加注时间随初始压力的增大而减小,这是由于所加注的氢气质量随瓶内初始压力的增大而减小。环境温度对加注时间影响不大。图 7(e)给出了不同初始状态下加注完成后的瓶内氢气SOC值。结果表明,SOC变化与环境温度成反比,与初始压力成正比。且在高环境温度和低初始压力的极端条件下,SOC的值也可以控制在可接受范围内。
4 结语基于级联式加氢站,考虑实际气体的状态、质量能量守恒等方程,建立了车载氢气瓶快速充装过程的集总参数热力学模型,将模型与其他学者的实验数据进行对比验证了模型的正确性。研究了加注过程中PSC和氢气预冷温度对氢气瓶内部氢气状态的影响。将冷冻机系统的能耗值、加注时间及氢气SOC值作为优化目标,建立了多目标优化模型,考虑优化参数离散性提出顺序搜索算法进行全局寻优,优化结果表明该策略可以有效降低加注过程中的预冷能耗并提高氢气SOC值,实现快速加氢。
| [1] |
Daud W R W, Rosli R E, Majlan E H, et al. PEM fuel cell system control: a review[J]. Renewable Energy, 2017, 113: 620-638. DOI:10.1016/j.renene.2017.06.027 |
| [2] |
Zeng T, Zhang C Z, Hu M H, et al. Modelling and predicting energy consumption of a range extender fuel cell hybrid vehicle[J]. Energy, 2018, 165: 187-197. DOI:10.1016/j.energy.2018.09.086 |
| [3] |
刘宗巍, 史天泽, 郝瀚, 等. 中国燃料电池汽车发展问题研究[J]. 汽车技术, 2018(1): 1-9. Liu Z W, Shi T Z, Hao H, et al. Research on main problems associated with development of fuel cell vehicle in China[J]. Automobile Technology, 2018(1): 1-9. (in Chinese) |
| [4] |
赵俊玮, 陈轶嵩, 方海峰, 等. 我国燃料电池汽车加氢站发展现状分析及对策建议[J]. 汽车工程学报, 2019, 9(3): 201-208. Zhao J W, Chen Y S, Fang H F, et al. Status and countermeasures of hydrogenation station network layout in China for fuel cell vehicles[J]. Chinese Journal of Automotive Engineering, 2019, 9(3): 201-208. (in Chinese) DOI:10.3969/j.issn.2095-1469.2019.03.06 |
| [5] |
Li M X, Bai Y F, Zhang C Z, et al. Review on the research of hydrogen storage system fast refueling in fuel cell vehicle[J]. International Journal of Hydrogen Energy, 2019, 44(21): 10677-10693. DOI:10.1016/j.ijhydene.2019.02.208 |
| [6] |
Kim S C, Lee S H, Yoon K B. Thermal characteristics during hydrogen fueling process of type IV cylinder[J]. International Journal of Hydrogen Energy, 2010, 35(13): 6830-6835. DOI:10.1016/j.ijhydene.2010.03.130 |
| [7] |
Molkov V, Dadashzadeh M, Makarov D. Physical model of onboard hydrogen storage tank thermal behaviour during fuelling[J]. International Journal of Hydrogen Energy, 2019, 44(8): 4374-4384. DOI:10.1016/j.ijhydene.2018.12.115 |
| [8] |
Melideo D, Baraldi D, Galassi M C, et al. CFD model performance benchmark of fast filling simulations of hydrogen tanks with pre-cooling[J]. International Journal of Hydrogen Energy, 2014, 39(9): 4389-4395. DOI:10.1016/j.ijhydene.2013.12.196 |
| [9] |
Melideo D, Baraldi D. CFD analysis of fast filling strategies for hydrogen tanks and their effects on key-parameters[J]. International Journal of Hydrogen Energy, 2015, 40(1): 735-745. DOI:10.1016/j.ijhydene.2014.10.138 |
| [10] |
Melideo D, Baraldi D, de Miguel Echevarria N, et al. Effects of some key-parameters on the thermal stratification in hydrogen tanks during the filling process[J]. International Journal of Hydrogen Energy, 2019, 44(26): 13569-13582. DOI:10.1016/j.ijhydene.2019.03.187 |
| [11] |
Zheng J Y, Ye J J, Yang J, et al. An optimized control method for a high utilization ratio and fast filling speed in hydrogen refueling stations[J]. International Journal of Hydrogen Energy, 2010, 35(7): 3011-3017. DOI:10.1016/j.ijhydene.2009.07.001 |
| [12] |
Cheng J, Xiao J S, Bénard P, et al. Estimation of final hydrogen temperatures during refueling 35 MPa and 70 MPa tanks[J]. Energy Procedia, 2017, 105: 1363-1369. DOI:10.1016/j.egypro.2017.03.505 |
| [13] |
Xiao J S, Bénard P, Chahine R. Estimation of final hydrogen temperature from refueling parameters[J]. International Journal of Hydrogen Energy, 2017, 42(11): 7521-7528. DOI:10.1016/j.ijhydene.2016.05.213 |
| [14] |
Xiao J S, Cheng J, Wang X, et al. Final hydrogen temperature and mass estimated from refueling parameters[J]. International Journal of Hydrogen Energy, 2018, 43(49): 22409-22418. DOI:10.1016/j.ijhydene.2018.10.131 |
| [15] |
Sadi M, Deymi-Dashtebayaz M. Hydrogen refueling process from the buffer and the cascade storage banks to HV cylinder[J]. International Journal of Hydrogen Energy, 2019, 44(33): 18496-18504. DOI:10.1016/j.ijhydene.2019.05.023 |
| [16] |
Talpacci E, Reuβ M, Grube T, et al. Effect of cascade storage system topology on the cooling energy consumption in fueling stations for hydrogen vehicles[J]. International Journal of Hydrogen Energy, 2018, 43(12): 6256-6265. DOI:10.1016/j.ijhydene.2018.02.030 |
| [17] |
Kuroki T, Sakoda N, Shinzato K, et al. Prediction of transient temperature of hydrogen flowing from pre-cooler of refueling station to inlet of vehicle tank[J]. International Journal of Hydrogen Energy, 2018, 43(3): 1846-1854. DOI:10.1016/j.ijhydene.2017.11.033 |
| [18] |
Lemmon E W, Huber M L, Leachman J W. Revised standardized equation for hydrogen gas densities for fuel consumption applications[J]. J Res Natl Inst Stand Technol, 2008, 113(6): 341-350. DOI:10.6028/jres.113.028 |
| [19] |
National Institute of Standards and Technology. NIST chemistry webbook[EB/OL]. [2020-10-18]. http://webbook.nist.gov/chemistry/.
|
| [20] |
Liu Y L, Zhao Y Z, Zhao L, et al. Experimental studies on temperature rise within a hydrogen cylinder during refueling[J]. International Journal of Hydrogen Energy, 2010, 35(7): 2627-2632. DOI:10.1016/j.ijhydene.2009.04.042 |
 2022, Vol. 45
2022, Vol. 45


