2. 先进节能驱动技术教育部工程研究中心,成都 610031
2. Engineering Research Center of Advanced Drive Energy Saving Technologies, Ministry of Education, Chengdu 610031, P. R. China
陆地资源枯竭迫使人类将目光投向了广袤的深海。随着“蛟龙号”“深海勇士”潜水器的相继问世,中国深海勘探技术取得了长足的进步,同时对深海领域液压传动技术提出更高的要求。斜盘式轴向柱塞泵凭借其功率密度大,在高压工况下,容积效率高等突出特点,成为目前深水环境下应用较为广泛的一类油压动力源,柱塞副作为其关键摩擦副之一,在深水环境下,柱塞副油膜的良好润滑性能是提高柱塞泵工作性能的关键。
柱塞副油膜润滑性能受介质属性等影响较大。国内外学者已对柱塞泵柱塞副润滑性能的变化规律进行了大量的理论与实验研究。Yamaguch等[1]假定柱塞不发生偏心和自旋,柱塞与缸孔之间的接触为理想接触,推导获得了表述柱塞运动状态表达式,并搭建简易实验台测量柱塞在缸孔内的往复运动及柱塞副的油膜厚度,但由于早期实验设备较简易,其研究结果有待验证。Fang等[2]采用简化模型来求解柱塞副内的油膜承载能力,并提出以柱塞-缸孔接触比来评估混合润滑条件下柱塞副油膜润滑性能的好坏。Trivedi等[3-4]采用L9正交设计和方差分析方法对负载、速度和温度3个控制因素对活塞杆和缸的摩擦系数的影响进行分析,并搭建往复式试验台进行试验工作,通过实验结果与理论分析相结合分析获得3个控制因素对摩擦的影响程度。Kim等[5-6]提出一种考虑流固耦合的活塞润滑系统建模与分析方法,并采用Craig-Bampton模态约简的方法提高计算速度,数值计算结果表明,柔性体的弹性行为对油膜厚度的计算起着重要的作用,采用MFBD模拟的EHD润滑可以准确地预测活塞的润滑行为。Mechalikh等[7-8]考虑油膜与整个油缸表面界面的滑移条件,建立了修正的雷诺方程,并分析其工作特性,结果表明交界面滑移对油膜的工作特性影响显著,但未考虑热变形和弹性变形等影响因素,研究内容有待进一步深入。
国内学者Song等[9]考虑温度对柱塞副润滑性能的影响建立柱塞与缸体间的接触时间数学模型,表明温度升高时,在一个周期内柱塞与缸体间的接触时间呈双曲正切函数增加,达临界温度时,接触时间将迅速增加。Jiang等[10]建立水压泵中柱塞副的泄漏模型,考虑柱塞偏心的自适应和受力平衡,通过遗传迭代法和有限体积法求解柱塞副内的水膜厚度和水膜压力,显示出口压力、主轴转速和初始密封间隙、柱塞副内水膜压力以及柱塞的微运动密切相关,对柱塞副的泄漏量影响显著。俞奇宽等[11]考虑黏温-黏压效应后, 建立了油膜热-流耦合模型, 并且搭建了一种360°油膜特性试验台, 获得了柱塞副油膜的偏心量随温度变化的变化情况,但未考虑压力变化带来的影响。刘世琦等[12]考虑柱塞间隙内介质黏度以及间隙受压形变的影响,用AMESim软件对超高压水压泵柱塞副在工作压力从0~120 MPa变化时的间隙、泄漏占理论排量的比值进行了计算预测,但计算结果未进行试验验证。
研究的压力补偿式柱塞泵(压力补偿泵)位于薄壁油箱内,假定深水压力未超过泵体所能承受的容许值,不考虑壳体变形,且柱塞-缸体间压差不受水深变化影响。考虑深水环境下柱塞副油液介质属性变化,建立深水环境压力补偿泵柱塞副流体动力润滑模型,构建数值寻优求解方法,获得深水环境下柱塞副的膜厚、压力、间隙泄漏量及轴向摩擦力的变化规律,为深水环境下压力补偿泵摩擦副的性能分析和设计提供理论指导。
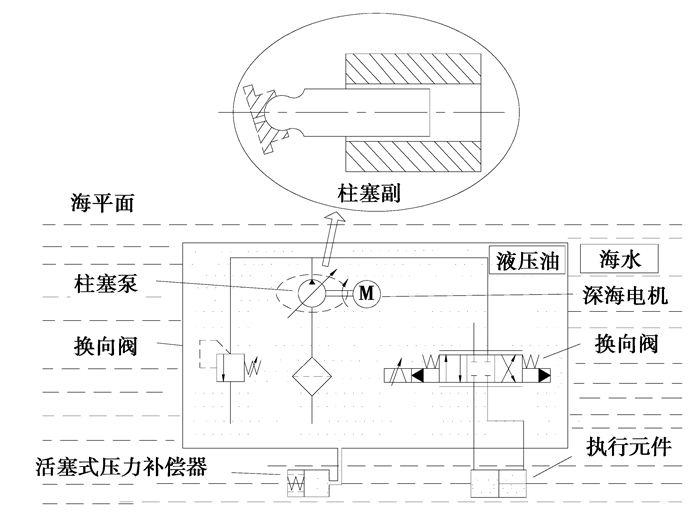
1 压力补偿泵柱塞副动力学分析 1.1 柱塞泵的深水压力补偿原理深水环境下柱塞泵的压力补偿原理如图 1所示,柱塞泵、深海电机、换向阀等元件浸入充满液压油的油箱中,油箱采用薄壁结构,外设有活塞式压力补偿器[13]。当水深变化时,海水压力、温度等环境参数通过压力补偿器和油箱壁面实时传至箱内液压介质和柱塞泵,始终保持箱体内外压力平衡,进而使液压泵工作在深海油压环境中,而执行元件则处在外界海水中。
|
图 1 深水环境下柱塞泵压力补偿原理图 Fig. 1 Schematic diagram of pressure compensation of plunger pump in deep water environment |
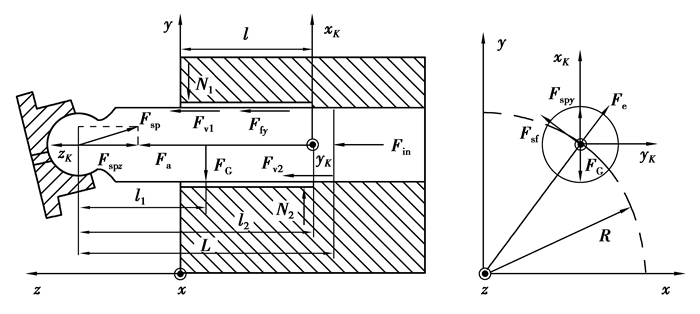
考虑上述工作环境,柱塞副润滑为完全流体动力润滑,在给定工况下,柱塞副的油膜厚度和相对压力分布同大气工况,均由外负载决定。柱塞运动主要包括3部分:自旋、轴向运动以及随泵体的旋转,图 2所示为柱塞受力示意图。
|
图 2 柱塞受力示意图 Fig. 2 Schematic diagram of plunger force |
其中,l1、l2分别表示柱塞球心到质心和端面的距离,m;Fin为柱塞腔入口油液的压力,N;Fa为柱塞轴向往复运动惯性力,N;Ffx、Ffy分别为柱塞圆周和轴向运动引起的黏性摩擦力,N;N1、N2分别表示不同位置柱塞与缸体的固体接触力,N;Fv1、Fv2分别表示不同位置柱塞与缸体接触产生的滑动摩擦力,N;Fsp表示斜盘对柱塞的支撑力,N;Fsf表示柱塞球头滑靴所受摩擦力,N;FG表示柱塞自身重力,N;Fe表示柱塞绕主轴运动的离心力,N。
假定柱塞质心保持在自身轴线上,且不受滑靴旋转的影响,则柱塞轴向往复运动惯性力:
| $ F_{\mathrm{a}}=\left(m_{\mathrm{s}}+m_{\mathrm{p}}\right) \cdot a=\left(m_{\mathrm{s}}+m_{\mathrm{p}}\right) \omega^2 R \tan \beta \cos \varphi, $ | (1) |
式中:ms、mp分别为滑靴和柱塞的质量,kg;a为轴向运动加速度,m/s2;ω为角速度,rad/s;R为柱塞的分布圆半径,m;β为斜盘倾角,(°);φ为柱塞以上死点为参考的顺时针转过的角度,(°)。
在zk轴正方向上的合力:
| $ F_{\mathrm{sp} z}=F_{\mathrm{in}}+F_{\mathrm{a}}+F_{\mathrm{f} y}+F_{v 1}+F_{v 2} 。$ | (2) |
其中,Fv1=N1f,Fv2=N2f,f为柱塞和缸体间的摩擦系数。
柱塞球头端受到斜盘的支撑力可以沿z轴、y轴方向分解,其中沿z轴方向的分力为:
| $ F_{\mathrm{sp} z}=F_{\mathrm{sp}} \cdot \cos \beta $ | (3) |
外力于xK和yK轴方向上的合力、合力矩分别为:
| $ \begin{gathered} F_{\mathrm{s} x}=F_{\mathrm{e}} \cos \varphi+F_{\mathrm{sp}} \sin \beta-F_{\mathrm{G}}+F_{\mathrm{ss}} \sin \varphi, F_{\mathrm{s} y}=F_{\mathrm{e}} \sin \varphi-F_{\mathrm{sf}} \cos \varphi, \\ M_{\mathrm{s} x}=F_{\mathrm{e}} \sin \varphi\left(l_2-l_1\right)-F_{\mathrm{sf}} \cos \varphi l_2, M_{\mathrm{sy}}=\left(F_{\mathrm{G}}-F_{\mathrm{e}} \cos \varphi\right)\left(l_2-l_1\right)-\left(F_{\mathrm{sf}} \sin \varphi+F_{\mathrm{sp}} \sin \beta\right) l_2 \text { 。} \end{gathered} $ | (4) |
式中:
惯性力Fa和离心力Fe与柱塞宏观运动有关。柱塞在轴向力的驱动下沿缸孔的轴线往复运动。在径向力作用下,柱塞在缸孔径向上产生微运动。鉴于油膜的厚度为微米级,柱塞的径向加速度非常小,故忽略径向惯性力。油膜的压力用于平衡所有其他外力,柱塞的力与力矩平衡方程式为:
| $ \begin{gathered} \sum F_x=F_{\mathrm{p} x}+F_{\mathrm{s} x}+\bar{N}_2-\bar{N}_1, \sum F_y=F_{\mathrm{p} y}+F_{\mathrm{s} y} \\ \sum M_x=M_{\mathrm{p} x}+M_{\mathrm{s} x}, \sum M_y=M_{\mathrm{p} y}+M_{\mathrm{s} y}-f \bar{N}_2 r_{\mathrm{p}} / l+f \bar{N}_1 r_{\mathrm{p}} / l+\bar{N}_1 \end{gathered} $ | (5) |
式中:Fpx、Fpy、Mpx、Mpy分别为沿xK、yK轴方向流体对柱塞的作用分力、力矩。
上述柱塞平衡方程为含有4个未知偏心变化e的非线性方程组。在不同位置和姿态,柱塞与缸体的接触间呈动态变化,故方程组(5)的求解实际上为有约束的非线性优化问题,即在给定角度位置φ处,需寻找一组偏心距E=[E1, E2, E3, E4]及相应的固体接触力,满足:
| $ || \vartheta(E)|| \leqslant e_{\mathrm{a}}, $ | (6) |
式中ea表示求解精度,取10-6;当范数小于10-6认为柱塞已达平衡状态。
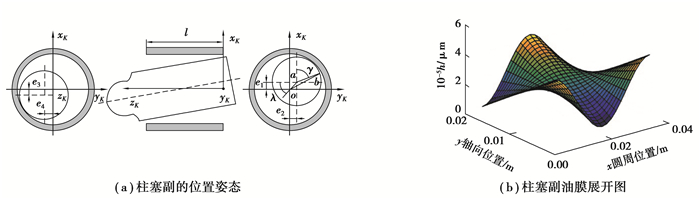
2 柱塞副流体动力润滑模型 2.1 柱塞副的油膜厚度模型柱塞副在缸孔中的位置姿态,如图 3(a)所示,通过柱塞轴线相对缸孔中心偏移值[e1, e2, e3, e4]来衡量其倾斜程度[14]。考虑到油膜厚度相对较小,可沿着缸孔轴线展开,如图 3(b)所示。得到油膜展开前后坐标系的关系:
| $ x=r_{\mathrm{p}} \gamma, y=z_k, z=h\left(\gamma, z_k\right), $ | (7) |
|
图 3 柱塞在缸孔中的倾斜姿态 Fig. 3 Inclined posture of plunger in cylinder bore |
式中:rp为柱塞半径,m;γ为油膜上任意点的角度,(°)。
根据空间几何关系,可得油膜厚度h公式为:
| $ h=c-\left[e_2-\frac{y\left(e_2-e_4\right)}{l}\right] \sin \gamma-\left[e_1-\frac{y\left(e_1-e_3\right)}{l}\right] \cos \gamma 。$ | (8) |
式中:c为平均间隙,m;l为油膜长度,m。
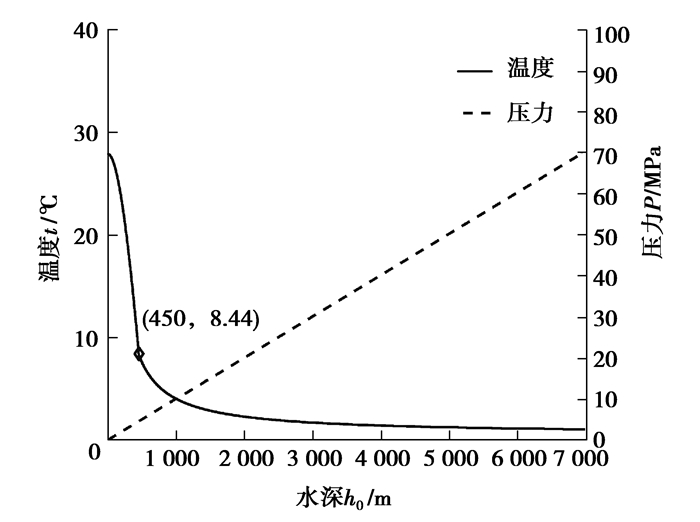
2.2 柱塞副油膜的压力方程 2.2.1 深水环境下油液介质模型参考文献[15]热带海域水温铅直向分布情况,可得环境参数如压力、温度随水深变化呈现如图 4所示的变化。
|
图 4 深水环境参数随水深的变化曲线 Fig. 4 Dynamic change curve of pressure and temperature in deep water environment |
当柱塞泵外部采用图 1所示的带有压力补偿器的薄壁油箱结构时,环境压力、深水温度等通过油箱壁面影响泵内液压介质,引起工作介质属性的变化。根据已有研究成果获得了深水环境参数作用下的油液黏度、密度等介质特性变化规律[16],分别表示为:
| $ \mu=K \exp \left[\frac{B}{T+C}\right] \exp \left[\frac{P}{a_1+a_2 T+\left(b_1+b_2 T\right) P}\right] 。$ | (9) |
式中:K、B、C、a1、a2、b1、b2为黏度参数;T为环境温度,℃;P为压力,MPa。
| $ \rho=\frac{1+\frac{\rho_{\mathrm{g} 0} \alpha}{\rho_{10}(1-\alpha)}}{\frac{1}{\left(c+a p-b p^2\right)-\alpha_t\left(t-t_0\right)}+\frac{p_0}{\rho_{10} p_{\mathrm{sat}}}\left(\frac{p_{\mathrm{sat}}}{p}\right)^{\frac{1}{\kappa}} \frac{T \alpha}{T_0(1-\alpha)}}, $ | (10) |
式中:a、b、c、αt为相应参数;ρ为油液密度,kg/m3;ρg0、ρl0分别表示标准状态下空气和纯油液的密度,kg/m3;α为油液含气率;t为油液温度,℃;t0、T0分别为初始油液温度和环境温度,℃;p0为大气压力,MPa;psat代表饱和状态时的压力,MPa;κ表示空气体积多变指数。式中各参数的取值如表 1、2所示。
2.2.2 深水环境下柱塞副油膜压力方程假定柱塞、缸体为刚性体,不考虑柱塞弹性变形及油膜厚度的影响。对柱塞副油膜的压力方程中,摩擦副表面的粗糙度小于最小油膜厚度,柱塞副间的油液是层流牛顿流体,同一水深下沿厚度方向压力、油液物理属性等保持不变,考虑不同水深下的油液介质属性变化,柱塞副的流体压力控制方程可表示为:
| $ \frac{\partial}{\partial x}\left(\frac{\partial p}{\partial x} \frac{\rho h^3}{\mu}\right)+\frac{\partial}{\partial y}\left(\frac{\partial p}{\partial y} \frac{\rho h^3}{\mu}\right)=6 v_x \frac{\partial \rho h}{\partial x}+6 v_y \frac{\partial \rho h}{\partial y}+12 \frac{\partial \rho h}{\partial t} 。$ | (11) |
式中:vx为柱塞的自转速度,m/s;vy为柱塞轴向运动速度,m/s。
为提高数值结果的通用性和计算过程的稳定性,对压力偏微分方程量纲化:
| $ H=\frac{h}{c}, X=\frac{x}{r_{\mathrm{p}}}, Y=\frac{y}{l}, v_0=\sqrt{v_x^2+v_y^2}, V_x=\frac{v_x}{v_0}, V_y=\frac{v_y}{v_0}, P=\frac{p_{\mathrm{s}} c^2}{6 \mu r_{\mathrm{p}} v_0}, E_i=\frac{e_i}{c}, i=1, 2, 3, 4 。$ | (12) |
式中ps为水下环境压力,MPa。
代入式(11)后,获得深水环境下反映黏-密动态变化的柱塞副压力控制方程:
| $ \frac{\partial}{\partial X}\left(\varepsilon \frac{\partial P}{\partial X}\right)+\frac{r_{\mathrm{p}}^2}{l^2} \frac{\partial}{\partial Y}\left(\varepsilon \frac{\partial P}{\partial Y}\right)=V_x \frac{\partial\left(\rho^* H\right)}{\partial X}+\frac{r_{\mathrm{p}}}{l} V_y \frac{\partial\left(\rho^* H\right)}{\partial Y}+\frac{2 r_{\mathrm{p}} \omega}{v_0} \frac{\partial\left(\rho^* H\right)}{\partial \varphi} 。$ | (13) |
式中:ε=ρ* H3/μ*;μ*表示油液量纲为1的黏度,μ*(x, y)=μ(x, y)/μ0;ρ*表示油液量纲为1的密度,ρ*(x, y)=ρ(x, y)/ρ0。
3 柱塞副润滑模型的数值求解 3.1 油膜厚度的数值求解方法油膜厚度的数值求解过程包括2个环节,即全斜盘转角位置下偏心值求解和全周期内柱塞副的油膜厚度分布的求解。
1) 求解边界:当柱塞与缸孔中心线不重合,且偏离程度较大时,柱塞端部易与缸体内壁产生挤压,视柱塞与缸孔均为刚体,设两表面粗糙度均为Rz=0.05 μm,许用油膜厚度取[h]=0.1 μm。当柱塞副的油膜厚度达到[h]时,认为柱塞与缸孔发生局部接触摩擦。此时,油膜厚度保持[h]不变,偏心量最大。
2) 全斜盘转角位置下偏心值的寻优及求解:
a.先求解某斜盘转角位置的油膜厚度分布,见公式(8),采用坐标轮换法[18]迭代求解柱塞偏心距E,设其迭代初值: Eφ= [1,0, -1,0]。
b.由式(13)求柱塞副的油膜压力场,据数值积分求力与力矩FPX,FPY,MPX,MPY。令ϑ(E)=0,经式(5)变换后获得两端接触力:
| $ \left\{ {\begin{array}{*{20}{l}} {{{\bar N}_1} = - \left[ {\frac{{f{r_{\rm{p}}}}}{l}\left( {{F_{\rm{P}}}X + {F_{{\rm{S}}X}}} \right) + {M_{{\rm{P}}Y}} + {M_{{\rm{S}}Y}}} \right], }\\ {{{\bar N}_2} = {{\bar N}_1} - {F_{{\rm{P}}X}} + {F_{{\rm{S}}Y}}。} \end{array}} \right. $ | (14) |
c.对N1、N2进行迭代判断,交替使用黄金分割法进行一维搜索。
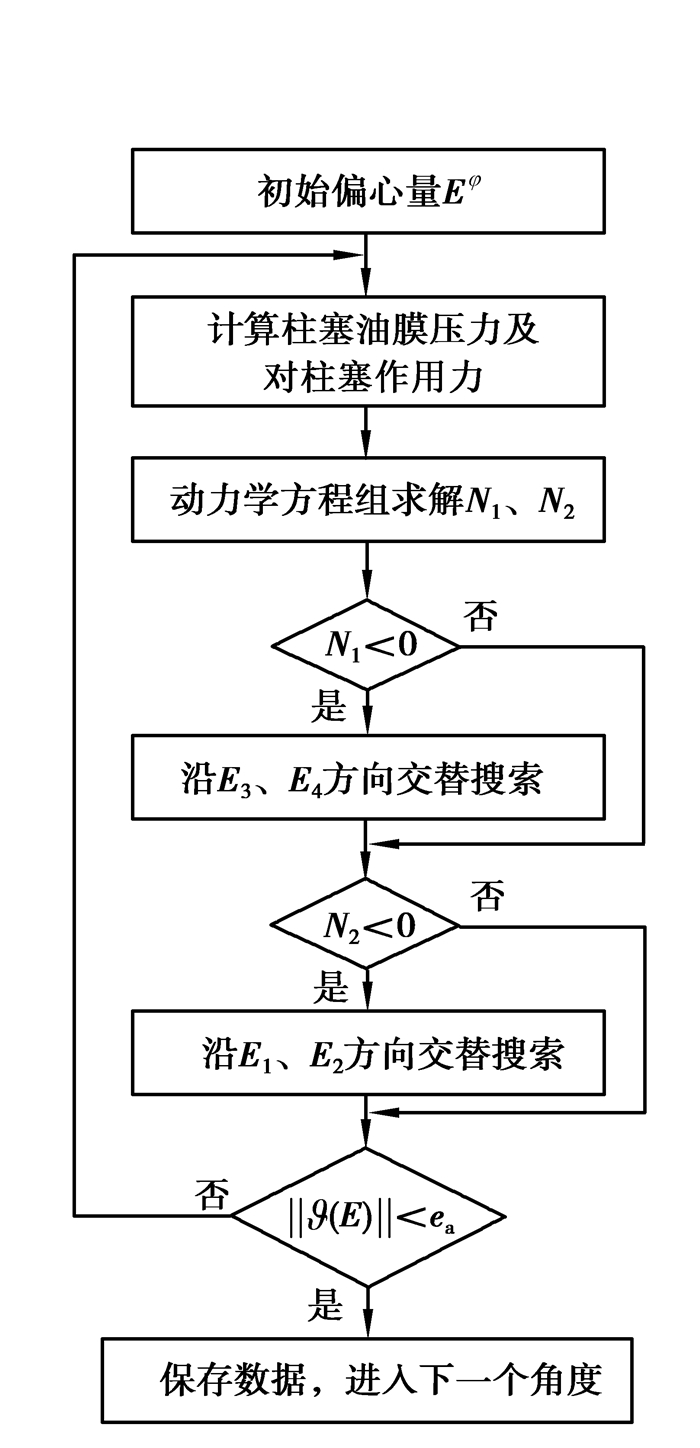
d.计算||ϑ(E)||,判断循环或进入下一角度位置计算,最后获得全转角位置下柱塞的偏心量。如图 5所示为单个角度位置偏心量寻优求解流程图。
|
图 5 单个角度位置偏心量寻优求解流程 Fig. 5 Single angular position eccentricity optimization solution process |
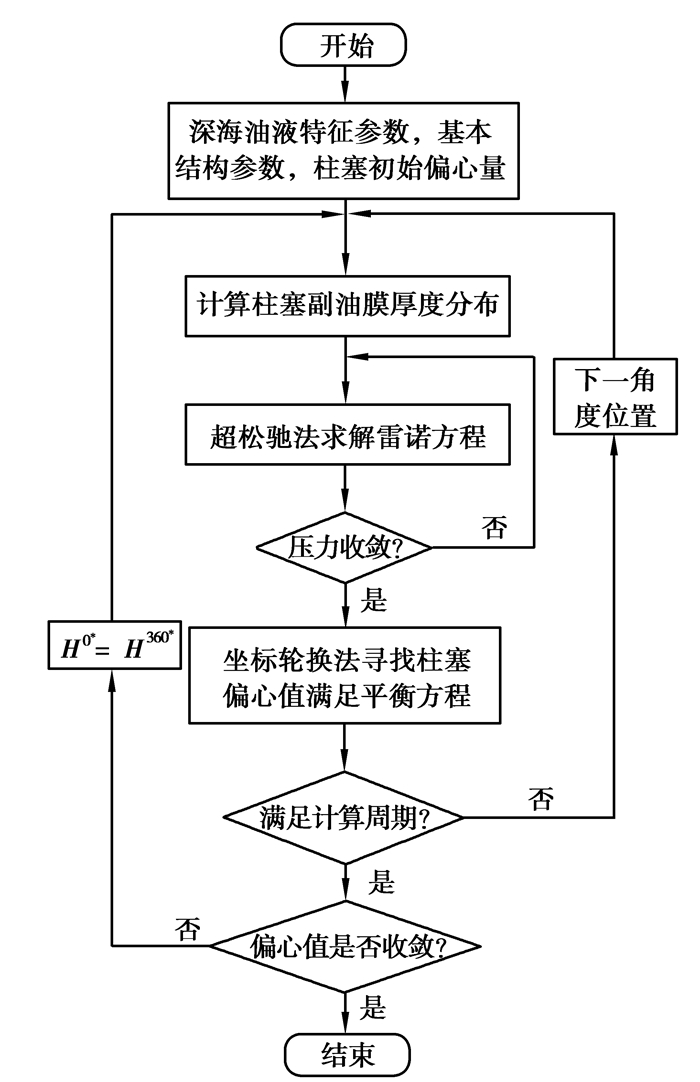
3) 借助该偏心量计算全周期内柱塞副的油膜厚度分布,其求解流程如图 6所示,设定的偏心量收敛条件为:
| $ \sum\limits_{i=1}^4 \frac{\left|E_i\left(0^{\circ}\right)-E_i\left(360^{\circ}\right)\right|}{\left|E_i\left(0^{\circ}\right)\right|} \leqslant 10^{-6} 。$ | (15) |
|
图 6 深水环境下全周期内柱塞副油膜厚度的求解流程 Fig. 6 The solution process of the plunger pair oil film in the full cycle in the deep sea environment |
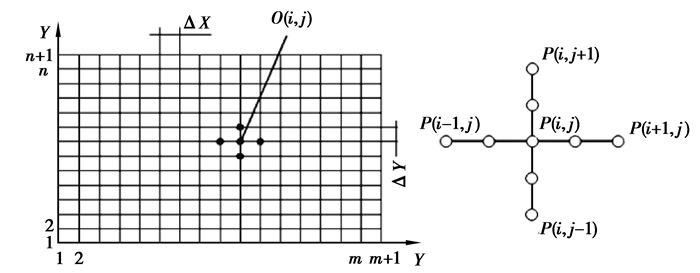
由于压力方程式(13)为椭圆形偏微分方程,有效解析解通过常规计算较难求得,为此采用有限数值差分法[19-21]求解柱塞油膜压力。将流体计算域划分成若干等间距网格,如图 7所示。
|
图 7 流体域的网格划分 Fig. 7 Mesh division of fluid domain |
节点P(i, j)处一阶偏导数中心差分格式:
| $ \frac{\partial\left(\rho^* H\right)}{\partial X}=\frac{\rho_{i+\frac{1}{2}, j}^* H_{i+\frac{1}{2}, j}-\rho_{i-\frac{1}{2}, j}^* H_{i-\frac{1}{2}, j}}{\Delta X} 。$ | (16) |
节点P(i, j)处二阶偏导数中心差分格式:
| $ \frac{\partial}{\partial X}\left(\varepsilon \frac{\partial P}{\partial X}\right)_{i, j}=\frac{\varepsilon_{i+0.5, j}\left(P_{i+1, j}-P_{i, j}\right)-\varepsilon_{i-0.5, j}\left(P_{i, j}-P_{i-1, j}\right)}{\Delta X^2} 。$ | (17) |
油膜挤压项的差分格式为:
| $ \frac{\partial\left(\rho^* H\right)}{\partial \varphi}=\frac{\rho_{i, j}^{* \varphi+1} H_{i, j}^{\varphi+1}-\rho_{i, j}^{* \varphi} H_{i, j}^{\varphi}}{\Delta \varphi} 。$ | (18) |
式中ρi, j*φ、Hi, jφ分别表示节点在上一个角度位置对应的无量纲密度和油膜厚度。
将式(16)~(17)代入到式(13)中,得到压力方程的差分格式为:
| $ \begin{gathered} \frac{\varepsilon_{i+\frac{1}{2}, j}\left(P_{i+1, j}-P_{i, j}\right)-\varepsilon_{i-\frac{1}{2}, j}\left(P_{i, j}-P_{i-1, j}\right)}{\Delta X^2}+\alpha \frac{\varepsilon_{i, j+\frac{1}{2}}\left(P_{i, j+1}-P_{i, j}\right)-\varepsilon_{i, j-\frac{1}{2}}\left(P_{i, j}-P_{i, j-1}\right)}{\Delta Y^2}= \\ V_1 \frac{\rho_{i+\frac{1}{2}, j}^* H_{i+\frac{1}{2}, j}-\rho_{i-\frac{1}{2}, j}^* H_{i-\frac{1}{2}, j}}{\Delta X}+\frac{V_2 r_{\mathrm{p}}}{l} \frac{\rho_{i, j+\frac{1}{2}}^* i_{i, j+\frac{1}{2}}-\rho_{i, j-\frac{1}{2}}^* H_{i, j-\frac{1}{2}}}{\Delta Y}+\frac{2 r_{\mathrm{p}} \omega}{v_0} \frac{\rho_{i, j}^{*, \varphi+1} H_{i, j}^{\varphi+1}-\rho_{i, j}^{* \varphi} H_{i, j}^{\varphi}}{\Delta \varphi}。\end{gathered} $ | (19) |
式中:
进一步整理压力求解可得:
| $ \widetilde{P}_{i, j}^k=\frac{\left(A_{i, j} P_{i+1, j}^k+B_{i, j} P_{i-1, j}^k+C_{i, j} P_{i, j+1}^k+D_{i, j} P_{i, j-1}^k-F_{i, j}\right)}{E_{i, j}} 。$ | (20) |
利用加权求和的方法整理式(20)所得的压力与未修正压力,下一轮压力用此压力进行求解:
| $ P_{i, j}^{k+1}=(1-\lambda) P_{i, j}^k+\lambda \widetilde{P}_{i, j}^k。$ | (21) |
式中:Pi, jk、Pi, jk+1分别为该次迭代的初始压力值、终止压力值;Pi, jk为式(20)求得的修正压力值;λ为松弛因子,取λ=1~2。
压力迭代求解过程的结束条件:
| $ \frac{\sum \sum\left|P_{i, j}^{k+1}-P_{i, j}^k\right|}{\sum \sum P_{i, j}^{k+1}} \leqslant \varepsilon 。$ | (22) |
式中相对精度ε取10-6,此时各节点处压力分布即为柱塞副的压力分布。
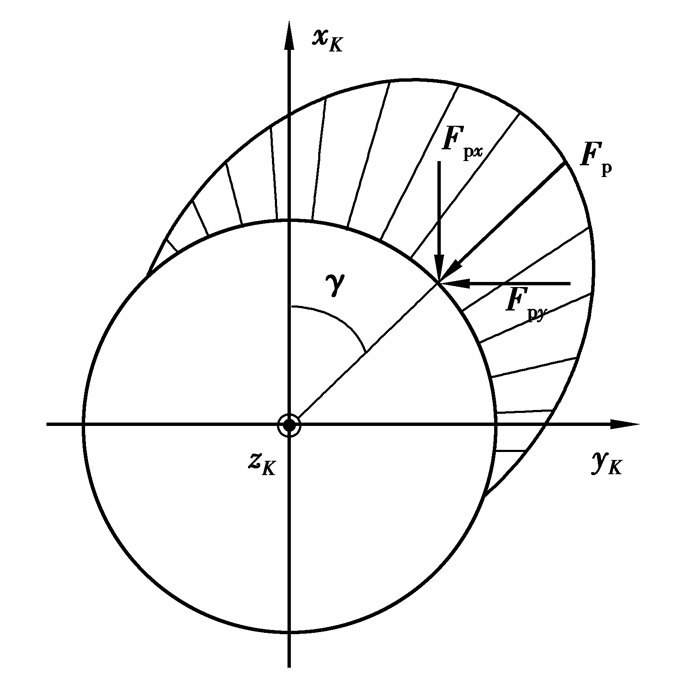
运用数值积分方法求解柱塞副油膜作用力与力矩,如图 8所示,其表达式为:
| $ {F_{{\rm{P}}X}} = {F_{{\rm{p}}x}}\frac{{{c^2}}}{{6\mu r_{\rm{p}}^2{v_0}l}} = \int_0^1 {\int_0^{2 \pi} - } P\cos X{\rm{d}}X{\rm{d}}Y, $ | (23) |
| $ {F_{{\rm{P}}Y}} = {F_{{\rm{p}}y}}\frac{{{c^2}}}{{6\mu r_{\rm{p}}^2{v_0}l}} = \int_0^1 {\int_0^{2 \pi} - } P\sin X{\rm{d}}X{\rm{d}}Y, $ | (24) |
| $ M_{\mathrm{P}X}=M_{\mathrm{p} x} \frac{c^2}{6 \mu r_{\mathrm{p}}^2 v_0 l^2}=\int_0^1 \int_0^{2 \pi}-Y P \sin X \mathrm{d} X \mathrm{d} Y, $ | (25) |
| $ M_{\mathrm{P}Y}=M_{\mathrm{p} y} \frac{c^2}{6 \mu r_{\mathrm{p}}^2 v_0 l^2}=\int_0^1 \int_0^{2 \pi} Y P \cos X \mathrm{d} X \mathrm{d} Y 。$ | (26) |
|
图 8 柱塞副的油膜力作用示意图 Fig. 8 Schematic diagram of oil film force action of plunger pair |
同理,可获得油膜对柱塞的轴向摩擦力及柱塞副间隙的泄漏量,分别表示为:
| $ F_{\mathrm{f} y}=\int_0^{2 \pi r_{\mathrm{p}}} \int_0^l\left(\frac{h}{2} \frac{\partial p}{\partial y}+\mu \frac{v_y}{h}\right) \mathrm{d} x \mathrm{d} y, $ | (27) |
| $ Q=\int_0^{2 \pi r_{\mathrm{p}}}\left(-\frac{\partial p}{\partial y} \frac{h^3}{12 \mu}+v_{\mathrm{p}} \frac{h}{2}\right) \mathrm{d} x 。$ | (28) |
通过与经实践验证的经典计算结果进行对比,以验证上述模型的有效性。设置与文献[2]相同的工况参数,即满足:
| $ \omega_{\mathrm{p}}=0 ; \frac{r_{\mathrm{p}}}{l}=0.2 ; \frac{6 \mu r_{\mathrm{p}} v_0}{p_{\text {in }} c^2}=0.1 。$ | (29) |
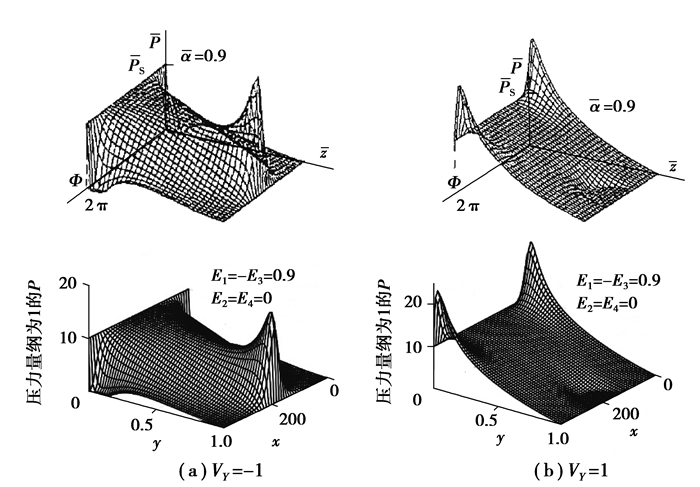
在柱塞不同转角下的模型求解,得油膜压力分布结果(图 9(a)(b)下图)与文献[2](图 9(a)(b)上图)的对比。可知,VY=-1时(图 9(a)), 球头端油膜压力峰值与偏心值成正相关,上、下两三维曲面所示的油膜的分布吻合度高;VY=1(图 9(b)),油液入口处的油膜压力亦与偏心值成正相关,同样上、下两图曲面形貌和趋向亦接近一致,从而验证了本文所建模型及其求解流程的合理性及有效性。
|
图 9 油膜压力求解的结果对比图 Fig. 9 Comparison of the solution results of oil film pressure |
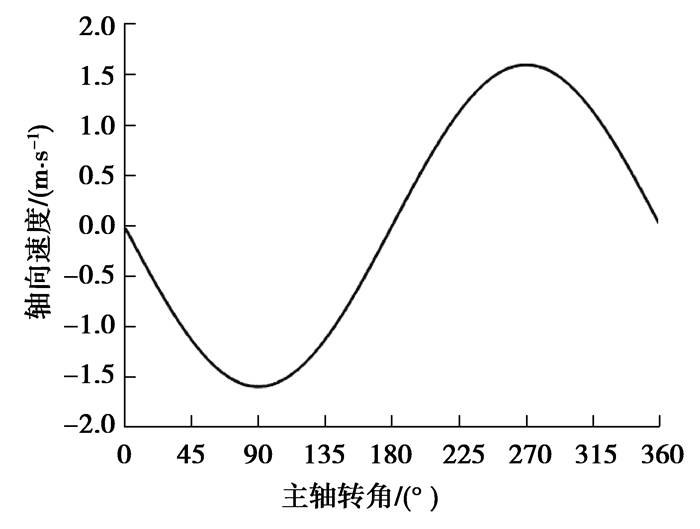
根据图 6所示的全周期内油膜厚度计算流程图编写相应程序,当结果收敛后将各角度下油膜厚度、压力等的分布输出。首先分析给定水深下的柱塞副油膜的润滑特性,初始计算参数如表 3所示。设定柱塞轴向运动速度随主轴转角的变化如图 10所示。
| 表 3 柱塞副相关参数 Table 3 Related parameters of plunger pair |
|
图 10 柱塞轴向运动速度变化曲线 Fig. 10 The changes of the axial movement speed of the plunger |
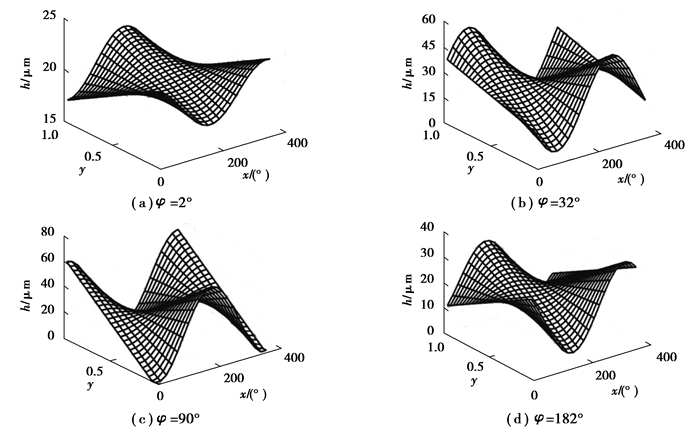
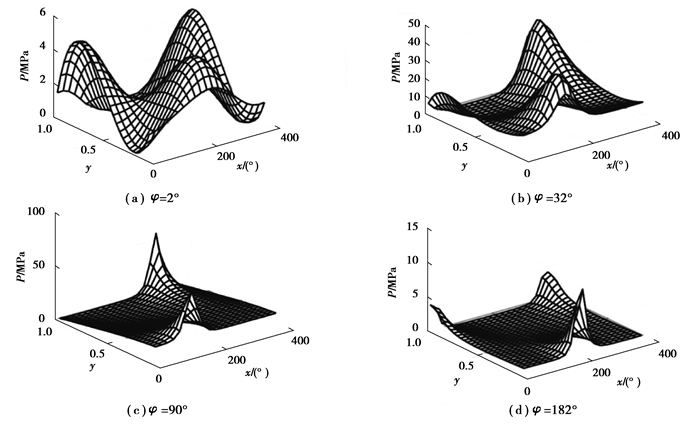
设水深1 000 m,泵轴转速为1 500 r/min,工作压力为16 MPa,斜盘倾角12°,柱塞转角位置分别为2°, 30°, 90°, 182°,其油膜的厚度和压力分布如图 11~12所示。
|
图 11 水深1 000 m下不同转角时柱塞副的油膜厚度分布 Fig. 11 Distribution of oil film thickness of plunger pair at different turning angles at a water depth of 1 000 m |
|
图 12 水深1 000 m下不同转角时柱塞副的油膜压力分布 Fig. 12 Oil film pressure distribution of plunger pair at different rotation angles at a water depth of 1 000 m |
水深1 000 m下不同转角时柱塞副的油膜压力、厚度变化如表 4所示。当泵转角φ=90°时,油压最大峰值达到80 MPa,该位置柱塞偏心达极限,膜厚极薄,极有可能与缸体间发生固体接触。由以上图表可得,柱塞副的油膜压力分布与油膜厚度分布同步变化,油膜压力随着该处油膜厚度的减小而逐渐增大,但两分布的波动均随着柱塞偏载的增大而增大。在柱塞泵工作过程中,由于负载的时变性,柱塞需不断改变自身偏斜程度来动态平衡外负载。
| 表 4 水深1 000 m下不同转角时柱塞副的油膜压力、厚度变化 Table 4 Variations of the oil film pressure and thickness of the plunger pair at different rotation angles at a water depth of 1 000 m |
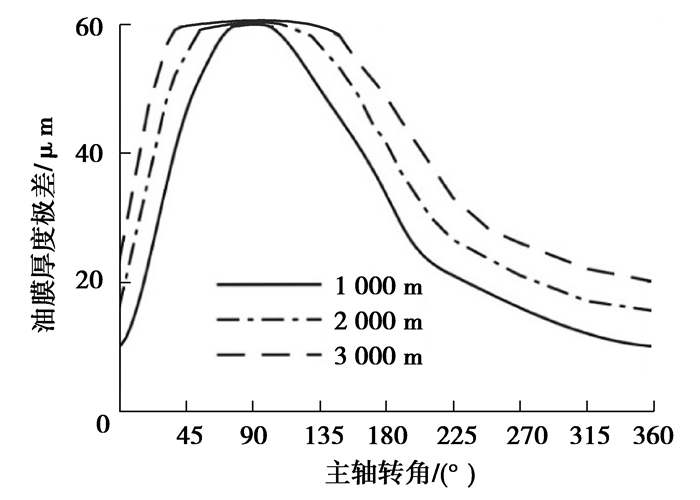
不同水深下油膜厚度极差变化曲线如图 13所示。在转角φ为0°~45°时,油膜厚度极差平稳上升,油膜厚度分布相对均匀;在转角φ=90°左右,油膜厚度极差达到最大值,该区域油膜厚度波动大,柱塞与缸体产生接触;在转角φ为135°~360°时,油膜厚度极差缓慢减小,油膜厚度恢复均匀分布。当水深增加时,油膜厚度整体波动更加剧烈,油膜厚度最大极差转角区间以φ=90°为中心向两边拓宽,柱塞产生固体接触的转角提前,接触转角范围扩大。
|
图 13 不同水深下油膜厚度极差变化曲线 Fig. 13 Variation curve of oil film thickness range under different water depths |
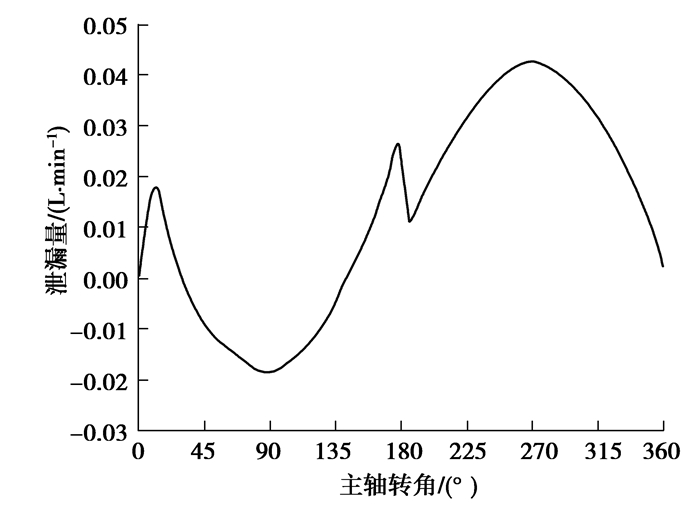
水深1 000 m工况下在一个周期内柱塞副泄漏量变化曲线如图 14所示。上死点是柱塞开始运动的起点,在起始状态柱塞做缩回运动,运动速度逐渐增大,整个过程泄漏量为正;随着运动速度继续增大,柱塞间隙慢慢开始吸收油液,泄漏量出现负值;转角φ=90°时,柱塞运动速度为反向最大,泄漏量最小;转角超过φ=180°后,柱塞进入低压区伸出吸油,运动方向与压力作用方向相同,泄漏量为正,但柱塞副两端压差较小,由于剪切流的作用,泄漏量呈与轴向速度相一致的正弦变化规律,转角φ=270°时,轴向速度达正向最大,泄漏量最大。
|
图 14 水深1 000 m下柱塞副泄漏量变化曲线 Fig. 14 Leakage curve of the plunger pair at a water depth of 1 000 m |
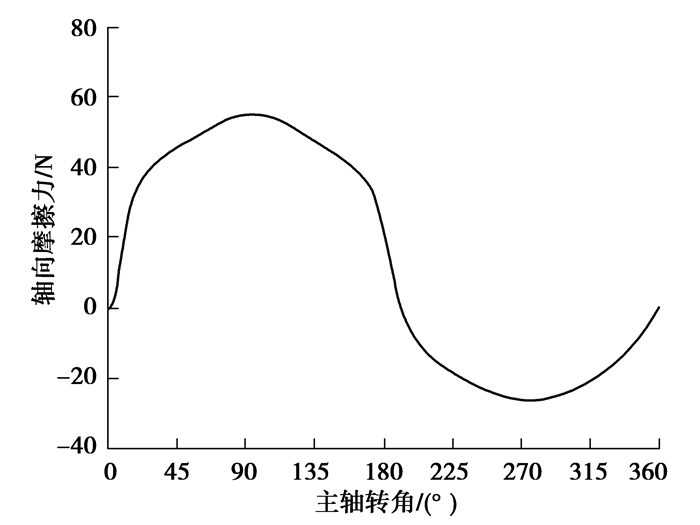
水深1 000 m工况下在一个周期内柱塞轴向摩擦力变化曲线如图 15所示。在一个周期内高压区的轴向摩擦力数值相比于低压区的轴向摩擦力数值要大一些,这是因为在高压区柱塞两端压差较大,此时压差流的存在增大了黏性摩擦力。转角φ=90°时,轴向黏性摩擦力随柱塞轴向运动速度同步达到正向最大;在低压柱塞两端油压偏小,此时压差流的作用效果较小,剪切流主导黏性摩擦力的大小。转角φ=270°时,轴向黏性摩擦力达反向最大。
|
图 15 水深1 000 m下柱塞副轴向摩擦力变化曲线 Fig. 15 Variation curve of axial friction force of plunger pair in water depth of 1 000 m |
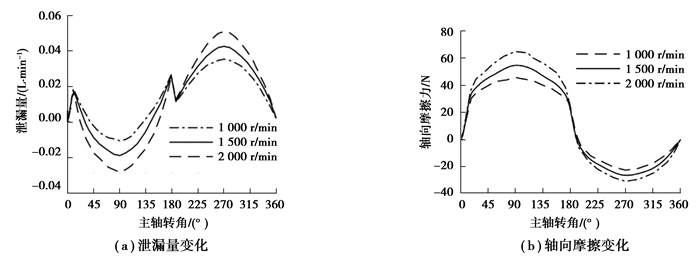
1) 主轴转速的影响。在水深1 000 m,设定工作压力16 MPa,斜盘倾角15°,取泵主轴转速分别为1 000,1 500,2 000 r/min,缸体转动一个周期柱塞副泄漏量和轴向摩擦力的变化如图 16所示。
|
图 16 不同转速下柱塞副泄漏量和轴向摩擦力 Fig. 16 Piston pair leakage and axial friction at different speeds |
如图 16(a)所示,泄漏量曲线变化随着主轴转速的提高而增大。在转角φ=0°~180°范围,柱塞做缩回运动,此时剪切流与压差流方向相反,随着主轴转速的增加,柱塞轴向速度和剪切流占比均增大,泄漏量会减小,甚至出现负值,即出现油液倒吸现象;在转角φ=180°~360°范围,柱塞做伸出运动,此时剪切流与压差流方向相同,主轴转速增加,泄漏量增大。随着主轴转速增加,柱塞副油液速度梯度增大,轴向摩擦力增加,如图 16(b)所示,在高压区和低压区柱塞的运动方向相反,轴向摩擦力存在负值,在变转速工况下,高压区的摩擦力数值变化更为显著。
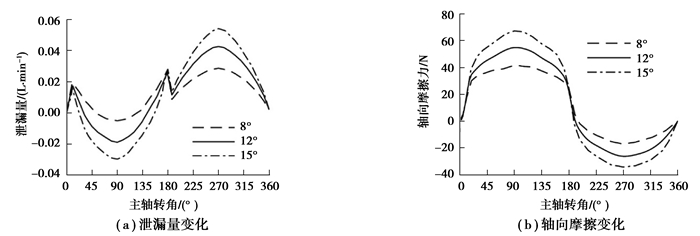
2) 斜盘倾角的影响。在水深1 000 m,设定工作压力16 MPa,泵体转速1 500 r/min,取泵斜盘倾角分别为8°、12°、15°,一个周期内柱塞副油液泄漏量和轴向摩擦力的变化如图 17(a)(b)所示。
|
图 17 不同斜盘倾角下柱塞副泄漏量和轴向摩擦力 Fig. 17 Leakage and axial friction of the plunger pair at different swashplate inclination angles |
如图 17(a)所示,在高压排油区,倾角越大,柱塞副泄漏量越小,在低压吸油区则相反;如图 17(b)所示,柱塞轴向摩擦力变化与斜盘倾角变化呈正相关;这是因为斜盘倾角增加使柱塞轴向往复运动行程、速度均增加,油液速度梯度增大,泄漏量和轴向摩擦都会增大。在一个周期内,斜盘倾角变化对总泄漏量影响较小,而轴向摩擦损失随着倾角的增大而增大。
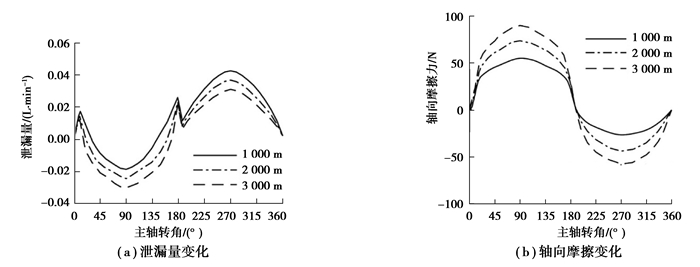
3) 变水深环境的影响。设定泵转速为1 500 r/min,工作压力16 MPa,斜盘倾角12°时,当工作水深分别为1 000,2 000,3 000 m时,一个周期内柱塞副油液泄漏量和轴向摩擦力的变化如图 18(a)(b)所示。
|
图 18 不同水深下柱塞副泄漏量和轴向摩擦力 Fig. 18 Leakage and axial friction in different water depths |
如图 18(a)所示,水深增加,在高压区,间隙从泵体内吸油量增加,低压区,间隙向外泄漏油液减少,整个周期内柱塞副泄漏量减小;这是因为在压力补偿器的作用下,虽然水深增加,但柱塞副出入口的相对压力保持不变,即可保持轴向运动速度和压差不变,由式(9)可知,水深增加使油液黏度增加,导致泄漏量减小。如图 18(b)所示,轴向摩擦力与水深成正相关变化,由式(10)可知,这是由于水深增加以后流体黏性增大,各节点上对应的切应力增大,从而使整个周期内的轴向摩擦力增加。由此可见,深水环境使柱塞副的容积效率提升,但机械效率下降。
5 结论1) 考虑深水环境因素对液压介质黏度、密度等属性的影响,获得表征压力补偿泵柱塞副润滑特性的压力控制方程,与已有经实践验证的计算结果相吻合,表明建立的压力控制方程的有效性。
2) 提出适应于深水工况柱塞副的油膜厚度和压力控制方程的求解方法和数值计算流程,获得表征柱塞副的油膜厚度、压力分布、泄漏量等润滑特性的变化规律,为深水环境下压力补偿泵摩擦副的性能分析和预测打下基础。
3) 深水环境下的研究结果表明,在水深1 000 m,当柱塞泵转角90°左右,柱塞副的油膜压力达最大,此时柱塞偏载达极限,出现膜厚极薄区域,为油膜润滑的危险点。此外,随水深的增加,柱塞副的容积效率提升,但机械效率下降。
| [1] |
Yamaguchi A, Tanioka Y. Motion of pistons in piston-type hydraulic machines: 1st report: theoretical analysis[J]. Bulletin of the JSME, 1976, 19(130): 402-407. DOI:10.1299/jsme1958.19.402 |
| [2] |
Fang Y, Shirakashi M. Mixed lubrication characteristics between the piston and cylinder in hydraulic piston pump-motor[J]. Journal of Tribology, 1995, 117(1): 80-85. DOI:10.1115/1.2830610 |
| [3] |
Trivedi H K, Bhatt D V. Effect of lubricating oil on tribological behaviour in pin on disc test rig[J]. Tribology in Industry, 2017, 39(1): 90-99. DOI:10.24874/ti.2017.39.01.10 |
| [4] |
Trivedi H K, Bhatt D V. An experimental investigation on friction and wear test parameters of cylinder liner and piston ring pair using Taguchi technique[J]. Industrial Lubrication and Tribology, 2018, 70(9): 1721-1728. |
| [5] |
Kim S, Choi J, Rhim S, et al. Numerical modeling and analysis of piston lubrication for flexible bodies through elastohydrodynamics and modal reduction method[C]//Proceedings of ASME 2017 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, August 6-9, 2017, Cleveland, Ohio, USA. 2017.
|
| [6] |
Kim S, Choi J, Kim J G, et al. Coupled simulation of elastohydrodynamics and multi-flexible body dynamics in piston-lubrication system[J]. Advances in Mechanical Engineering, 2019, 11(12): 168781401989585. DOI:10.1177/1687814019895855 |
| [7] |
Mechalikh M, Zidane I, Benhamou A, et al. Modelling and analysis of slip conditions in hydrodynamic lubrication of a piston skirt-cylinder contact[J]. Industrial Lubrication and Tribology, 2020, 72(10): 1181-1187. DOI:10.1108/ILT-11-2019-0483 |
| [8] |
Mechalikh M, Benhamou A, Zidane I, et al. Study of piston thermo-elastic behaviour under thermomechanical solicitations[J]. International Journal of Automotive and Mechanical Engineering, 2019, 16(4): 7287-7298. DOI:10.15282/ijame.16.4.2019.08.0542 |
| [9] |
Song Y H, Ma J M, Zeng S K. A numerical study on influence of temperature on lubricant film characteristics of the piston/cylinder interface in axial piston pumps[J]. Energies, 2018, 11(7): 1842. DOI:10.3390/en11071842 |
| [10] |
Jiang Q, Yang H B, Yu Y, et al. Numerical analysis of the water film characteristics in the eccentric state of a radial piston pump[J]. IEEE Access, 2018,6: 15274-15282. DOI:10.1109/ACCESS.2018.2808298 |
| [11] |
俞奇宽, 王冬云, 李胜虎, 等. 液压泵柱塞副油膜热-流耦合特性研究[J]. 机电工程, 2020, 37(7): 777-782. Yu Q K, Wang D Y, Li S H, et al. Thermal-flow coupling characteristics of hydraulic pump's piston/cylinder interface oil film[J]. Journal of Mechanical & Electrical Engineering, 2020, 37(7): 777-782. (in Chinese) DOI:10.3969/j.issn.1001-4551.2020.07.008 |
| [12] |
刘世琦, 冀宏, 刘银水. 超高压水压泵柱塞副间隙泄漏占比的仿真计算[J]. 液压与气动, 2020(10): 19-25. Liu S Q, Ji H, Liu Y S. Simulation prediction of the clearance leakage ratio of piston couples in ultra-high pressure water hydraulic pump[J]. Chinese Hydraulics & Pneumatics, 2020(10): 19-25. (in Chinese) DOI:10.11832/j.issn.1000-4858.2020.10.004 |
| [13] |
曹学鹏. 深海电液比例液压源关键技术及工作特性研究[D]. 成都: 西南交通大学, 2011. Cao X P. Research on key technologies and working characteristics of electro-hydraulic proportional power source operated in deep-sea[D]. Chengdu: Southwest Jiaotong University, 2011. (in Chinese) |
| [14] |
阮登芳, 高真超, 许金霞, 等. 机体弹性变形对主轴承润滑特性的影响[J]. 重庆大学学报, 2017, 40(1): 1-10. Ruan D F, Gao Z C, Xu J X, et al. Effects of engine block elastic deformation on the lubrication characteristics of main bearings[J]. Journal of Chongqing University, 2017, 40(1): 1-10. (in Chinese) |
| [15] |
叶安乐, 李凤岐. 物理海洋学[M]. 青岛: 青岛海洋大学出版社, 1992. Ye A L, Li F Q. Physical oceanography[M]. Qingdao: Qingdao Ocean University Press, 1992. (in Chinese) |
| [16] |
曹学鹏, 卫昌辰, 赵帅贵, 等. 深海环境下油液密度特性变化规律研究[J]. 润滑与密封, 2020, 45(8): 41-46. Cao X P, Wei C C, Zhao S G, et al. Study on the change law of oil density characteristics based on deep sea environment model[J]. Lubrication Engineering, 2020, 45(8): 41-46. (in Chinese) DOI:10.3969/j.issn.0254-0150.2020.08.006 |
| [17] |
曹学鹏, 周钊强, 王官洪, 等. 基于变深环境模型的油液黏度特性变化规律研究[J]. 润滑与密封, 2017, 42(7): 1-6. Cao X P, Zhou Z Q, Wang G H, et al. Study on change rules of oil viscosity characteristics based on deepening environment model[J]. Lubrication Engineering, 2017, 42(7): 1-6. (in Chinese) DOI:10.3969/j.issn.0254-0150.2017.07.001 |
| [18] |
雍龙泉. 非线性方程牛顿迭代法研究进展[J]. 数学的实践与认识, 2021, 51(15): 240-249. Yong L Q. Advances in Newton's iterative methods for nonlinear equation[J]. Mathematics in Practice and Theory, 2021, 51(15): 240-249. (in Chinese) |
| [19] |
张希, 罗会信, 左兵权, 等. 基于层次模型的雷诺方程自适应变步长差分算法研究[J]. 润滑与密封, 2019, 44(7): 123-130. Zhang X, Luo H X, Zuo B Q, et al. Research on adaptive step-size difference algorithm for Reynolds equation based on hierarchical model[J]. Lubrication Engineering, 2019, 44(7): 123-130. (in Chinese) |
| [20] |
Wang H K, Leaney P G. Modelling and energy efficiency analysis of a hybrid pump-controlled asymmetric (single-rod) cylinder drive system[J]. International Journal of Hydromechatronics, 2020, 3(1): 1-25. |
| [21] |
Kang Y, Wang F, Qiu Z Z, et al. A novel iteration method for estimation of bearing dynamic coefficients in the rotor-bearing system[J]. International Journal of Hydromechatronics, 2021, 4(3): 277-294. DOI:10.1504/IJHM.2021.118007 |
 2022, Vol. 45
2022, Vol. 45

