b. 重庆大学 机械与运载工程学院,重庆 400044
b. College of Mechanical and Vehicle Engineering, Chongqing University, Chongqing 400044, P. R. China
离心鼓风机作为旋转机械中的一种,在现代工业中承担着重要的角色。离心鼓风机结构复杂,系统零部件众多,在高温高压、高负荷、强冲击等恶劣工况下,极易出现各种故障[1],如果不及时采取恰当的维修策略,将很可能导致整个系统停机,甚至造成巨大的经济损失乃至危害人身安全。因此,开展离心鼓风机的故障诊断研究,提高设备的安全性和稳定性具有深远的意义。
随着大数据和机器学习的发展,基于数据驱动的故障诊断研究已得到了广泛应用。常用的诊断方法有支持向量机(SVM, support vector machine)[2],小波变换[3],K最近邻算法[4]等。这些方法都属于浅层学习模型,其诊断精度依赖于人工提取特征的好坏,且在高维大数据情况下,其诊断能力和泛化性能明显不足[5]。不同于浅层机器学习模型,深度学习因其强大的特征提取能力,在图像识别[6]、自然语言处理[7]等领域已经取得了巨大的成就,在故障诊断领域也成为一些学者研究的热点。如Wen等[8]利用卷积神经网络(CNN, convolutional neural network)自动提取振动信号的特征,实现了滚动轴承的故障诊断;胡茑庆等[9]利用经验模态分解(EMD, empirical mode decomposition)对振动信号做预处理,结合深度CNN实现了齿轮箱的故障诊断;Jiang等[10]提出了一种多尺度CNN,有效提取了振动信号的故障特征,提高了风力发电机齿轮箱诊断的准确性。离心鼓风机监测信号种类多且复杂,研究一种能从复杂高维数据中自适应学习故障特征的深度CNN,对于离心鼓风机的故障诊断具有重要意义。
以上学者均是基于单一信号开展的故障诊断研究,而单一信号容错能力不佳,且含有的故障信息有限,多传感器信息融合能够为诊断提供更为丰富的信息,增强诊断系统的鲁棒性与可靠性[11]。如任海锋等[12]将两个测点上的振动信号进行融合,结合SVM实现了某高射机枪自动机裂纹的故障诊断;朱丹宸等[13]提出了一种基于多振动信号与CNN的滚动轴承故障诊断方法,相比于单一振动信号,诊断精确性有了明显提升;Jing等[14]将振动信号、声发射信号、电流信号与瞬时角速度信号进行融合后共同输入构建的深度CNN,实现了滚动轴承的故障诊断,且取得了较好的诊断性能。上述文献都仅是基于多源同类或异类信息融合的故障诊断研究,且融合方式均是将多个信号串行叠加为一个信号,这种融合方式并不能充分地利用各多源信息间的相关性与互补性,且存在一定的数据缺失[15]。经此方式融合后提取的特征关联度差,并不能全面反映出所包含的故障信息,诊断精确性也会因此降低。
离心鼓风机监测信息种类多、数据维度高,既有同类信息,也有异类信息。传统的融合方式忽略了同类信息间的时序相关性,也未考虑异类信息间的空间关联特性,存在一定的信息丢失,影响诊断性能。传统的CNN在处理复杂的多源高维数据时自适应特征提取能力较差,且融合后的特征含有的故障信息不全,会导致较差的分类性能。盲目地增大网络深度又会导致较高的计算成本甚至出现过拟合情况。如何有效地融合这些信息是解决离心鼓风机故障诊断问题的关键。为此,笔者提出了一种基于多源信息融合和自适应深度卷积神经网络(ADCNN, adaptive deep convolutional neural network)的离心鼓风机故障诊断方法。基于相关性方差贡献率法实现了多源同类信息的数据层融合,将多个同类信号融合为一个信号,有效利用了各信号间的相关性与互补性。提出的ADCNN可以根据实际的网络性能优化网络层次结构,以网络收敛速度为评价指标,对网络进行自适应扩展,显著提升了网络的特征学习能力。通过ADCNN自适应地提取各异类信息的故障特征并完成特征融合,实现离心鼓风机的精确故障诊断。
1 离心鼓风机多源信息融合处理 1.1 离心鼓风机多源信息组成离心鼓风机监测量丰富、信号源多,在数据采集层,利用振动传感器、温度传感器、压力传感器以及电流传感器获取4类传感器信息。离心鼓风机的多源传感器信息可分为多源同类信息和多源异类信息两类。多源同类信息是指监测同一部件的多个同类传感器信息,包括转子振动、转子轴承温度与电机三相绕组温度3类。其中,转子振动包括转子水平方向振动信号vh与垂直方向振动信号vv;转子轴承温度包括转子前轴承温度tbf与后轴承温度tbr;电机三相绕组温度包括电机A相绕组温度tpa、B相绕组温度tpb与C相绕组温度tpc。多个同类传感器信号经数据层融合后变为一个信号,融合后的信号构成多源异类信息中的一类。多源异类信息是指不同传感器的监测信息,共有6类,包括融合转子振动vf、融合转子轴承温度tbf、融合电机三相绕组温度tpf、转子推力轴承温度ttb、电机电流im、润油压力po。离心鼓风机的多源信息组成如表 1所示。
| 表 1 离心鼓风机多源信息组成 Table 1 Multi-source information composition of the centrifugal blower |
数据层融合直接融合同类信息的原始数据,能够提供很多细微信息[15]。相关性方差贡献率法有效利用了传感器各信号间的相关性及互补性。此方法以方差贡献率为依据,根据信息间的相关重要程度去分配融合系数,将多个同类信号融合为一个信号,实现了同类信息间的动态融合,从而避免了有效信息的漏频及丢失。
设x(n)和y(n)是2个能量有限的确定性信号,则信号x(n)与y(n)的相关系数为
| $\rho_{x y}=\frac{\sum\limits_{n=0}^{\infty} x(n) y(n)}{\left[\sum\limits_{n=0}^{\infty} x^2(n) \sum\limits_{n=0}^{\infty} y^2(n)\right]^{\frac{1}{2}}}=\frac{R_{x y}}{\overline{E_x E_y}}, $ | (1) |
式中:
假设m个同类传感器信号x1(n), x2(n), …,xm(n),则任意2个信号的互相关性可表示为
| $R_{x_i x_j}(t)=\frac{1}{n-t} \sum\limits_{t_0=1}^{n-t} x_i\left(t_0\right) x_j\left(t_0+t\right), $ | (2) |
式中:n为每个信号数据点的个数;t=0, 1, …,n-1表示信号时间序列。第i个传感器与所有同类传感器信号总的相关能量可表示为
| $E_i=\sum\limits_{j=1, j \neq i}^m E_{i j}=\sum\nolimits_{j=1, j \neq i}^m \sum\nolimits_{t=0}^{n-1}\left[R_{i j}(t)\right]^2, $ | (3) |
式中:
| $y_i=\frac{x_i}{\sqrt{E_i^2}} \text {, }$ | (4) |
式中:xi为第i个传感器在时间T内以一定的采样频率采集到的数据信号序列,其能量归一化信号yi的离散的n个数据值为yi(1), yi(2), …,yi(n),定义其方差贡献率为
| $K_{i l}=\frac{\left[y_i(l)-\mu_i\right]^2}{n \sigma_i^2}, $ | (5) |
式中:yi(l)代表能量归一化信号yi的第l个数据点, l=1, 2, …,n;
由某一时刻m个同类传感器采集到的同类信号的方差贡献率,得到任一传感器信号xi第l个数据点xi(l)的分配系数为
| $k_{i l}=\frac{K_{i l}}{\sum\nolimits_{i=1}^m K_{i l}},$ | (6) |
基于所得的分配系数,m个同类传感器信号被融合为一个信号。融合后所得信号x第l个数据点的值为
| $x(l)=\sum\limits_{i=1}^m k_{i l} y_i(l) 。$ | (7) |
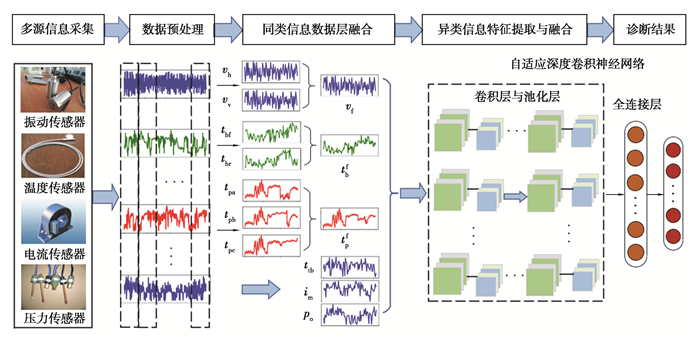
传统的多源信息融合模式是将多个信号串行叠加为一个信号,这种融合模式并不能充分地利用各信号间的相关性与互补性。离心鼓风机监测信号多,既有多源同类信息又有异类信息,综合有效地利用这些信息对于提升离心鼓风机的诊断精确性具有重要意义。基于此,笔者提出了一种数据层与特征层相结合的多源信息融合模式。基于相关性方差贡献率法实现离心鼓风机多源同类信息的数据层融合,将多个同类信号融合成一个信号,利用ADCNN自适应地提取各异类信息的特征并完成特征融合。这种融合模式考虑了同类信号间的相关性及互补性,避免了关键故障信息的丢失。其融合框架如图 1所示。
|
图 1 离心鼓风机多源信息融合框架 Fig. 1 Multi-source information fusion framework of the centrifugal blower |
离心鼓风机多源信息融合框架可分为3个部分:
1) 多源信息采集与数据预处理:利用振动传感器、温度传感器、电流传感器以及压力传感器采集离心鼓风机的多源传感器信息,并将每个信号分割为多个片段。
2) 多源同类信息数据层融合:利用相关性方差贡献率法将离心鼓风机的多个同类传感器信号融合为一个信号。转子水平方向振动信号vh与垂直方向振动信号vv经融合后构成异类信息中的转子振动信息vf;转子前轴承温度tbf与后轴承温度tbr经融合后构成异类信息中的转子轴承温度tbf;电机绕组A相温度tpa、B相绕组温度tpb与C相绕组温度tpc经融合后构成异类信息中的电机三相绕组温度tpf。
3) 异类信息特征提取与融合:将6种异类信息融合为一个6通道的信号输入到构建的ADCNN中,利用ADCNN自动提取各异类信息的故障特征并实现特征融合。
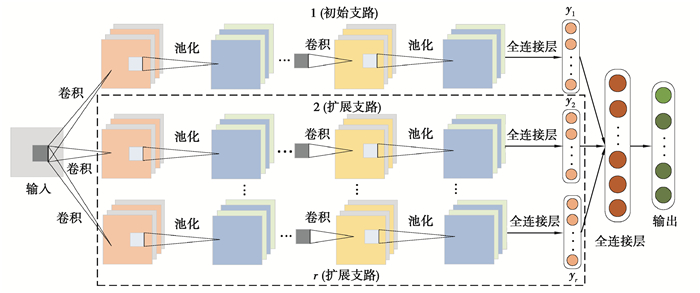
2 基于ADCNN的离心鼓风机故障诊断方法 2.1 ADCNN模型构建传统的CNN在处理多源高维数据时,特征自适应提取能力较差,其性能随着神经元数目增加或网络的加深而相应提高[16]。而卷积运算复杂度较高,盲目增大网络规模,将会耗费大量训练时间,且有时识别精度提升并不明显,因此使用固定的网络深度并不合适。ADCNN可以根据实际网络性能,优化网络层次结构,以收敛速度为评价指标,对网络进行自适应扩展,提取各多源信息的代表性故障特征。笔者利用ADCNN处理融合后的离心鼓风机多源信息并得到诊断结果,其网络结构如图 2所示。
|
图 2 ADCNN结构 Fig. 2 The structure of ADCNN |
卷积层是ADCNN的核心部分,由多个特征图组成,每个特征图通过卷积核与上一层特征图的局部区域相连,通过对各输入特征图的卷积滤波,提取数据特征。卷积层的数学模型可表示为
| $X_j^l=f\left(\sum\nolimits_{i \in M_j} X_i^{l-1} * K_{i j}^l+b_j^l\right), $ | (8) |
式中:Mj为输入特征图;Xjl为l层第j个输出特征图;Kijl为卷积核;bjl为偏置;符号*代表卷积运算;f()为激活函数。
池化层通过对上一层特征图的缩放映射以降低数据维度,同时还能提高网络的鲁棒性。其中,最大池化函数是最常用的池化函数,其数学表达式为
| $P_j=\max\limits_{j \in S} X_j,$ | (9) |
式中:Pj表示池化层的第j个输出;S为池化窗口大小。
如图 2所示,ADCNN共有r条支路,包含初始支路与扩展支路。初始化网络只包含一条初始支路,并以网络收敛速度为评价指标判断是否需要进行自适应扩展。若收敛速度未达到期望阈值则需进行自适应扩展,自适应扩展即在初始网络基础上扩展一条与初始支路相同结构与参数的新支路,当收敛速度满足要求或者r达到预设支路条数的最大值rmax时,自适应扩展则将停止。rmax设为5,收敛速度vcs的定义及应满足的要求如下:
| $v_{\mathrm{cs}}=E_{\mathrm{pre}}-E_{\mathrm{cur}} \geqslant C_{\mathrm{h}}, $ | (10) |
式中:Epre为前一次网络训练平均误差;Ecur为当前网络训练平均误差;Ch为收敛速度的期望阈值,设定为0.1。网络训练平均误差的计算公式为
| $E_{\text {mean }}=\frac{\sum\limits_{j=1}^N \sum\limits_{i=1}^c\left(y_i^j-y_{\mathrm{lab}}^j\right)^2}{N}, $ | (11) |
式中:N为训练样本总数;c为类别数;yij为第j幅训练样本对应的第i个神经元的输出;ylabj为训练样本的真实类别标签。
当进行自适应扩展时,在扩展结构中,需用一个新的全连接层将初始支路和扩展支路的输出结果进行融合,并获得新的输出结果。输出层激励函数融合输出结果为
| $y=f\left(y_1+\sum\limits_{k=2}^r \omega_k y_k\right),$ | (12) |
式中:y1与yk是初始支路与扩展支路k的输出结果;ωk为扩展支路k的输出权值;初始支路输出权值设为1。
ADCNN训练过程中,初始支路的网络结构与相关参数保持不变,先保留其输出结果y1,待扩展支路训练完后再与其输出结果y1进行融合,通过BP算法更新扩展支路的相应权值,当所有扩展支路扩展完毕时,即完成自适应扩展学习。待扩展支路完成后,通过网络输出层得到诊断结果。
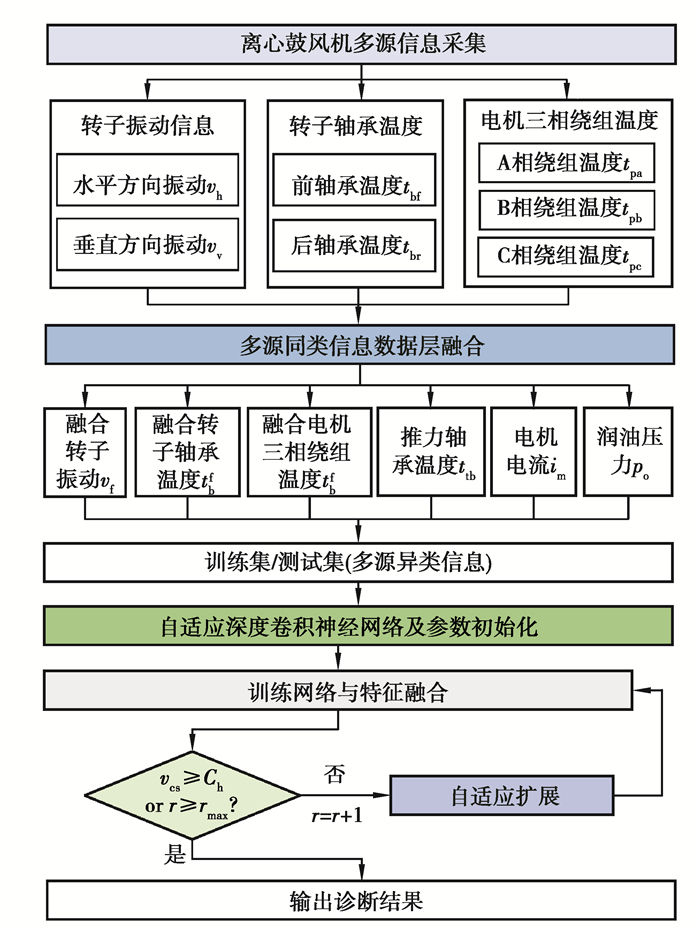
2.2 基于ADCNN的离心鼓风机故障诊断流程离心鼓风机监测信息多,故障类型复杂,多传感器信号融合能够提供更为丰富的故障信息。提出的ADCNN能够自适应地提取各异类信息的特征完成特征融合,并根据网络性能优化网络层次结构,有利于提高诊断的精确性。基于ADCNN的离心鼓风机故障诊断流程如图 3所示。
|
图 3 基于ADCNN的离心鼓风机故障诊断流程 Fig. 3 Flow chart of centrifugal blower fault diagnosis based on ADCNN |
诊断具体步骤如下:
1) 利用振动传感器、温度传感器、电流传感器和压力传感器采集离心鼓风机的多种传感器监测信息,并划分为多源同类信息和多源异类信息。
2) 利用相关性方差贡献率法将多源同类信息中的多个同种传感器信号融合为一个信号,实现数据层融合。vh与vv经融合后构成转子振动信息vf;tbf与tbr经融合后构成转子轴承温度tbf;tpa, tpb与tpc经融合后构成电机三相绕组温度tpf。
3) 将经数据层融合后的多源异类信息按比例设置训练集与测试集,将训练集输入初始的ADCNN并进行参数初始化,r的初始值设为1。
4) 训练网络并根据收敛速度及支路条数判断网络是否需要进行自适应扩展。判断条件vcs≥Ch或r≥rmax是否满足,若条件满足,保存网络模型参数并输出诊断结果。否则r=r+1,对网络进行自适应扩展直至条件成立。
5) 将测试集输入构建的ADCNN,并利用该方法实现离心鼓风机的故障诊断,验证所提故障诊断方法的有效性。
2.3 模型评价指标准确率(Acc),精确率(Precision),召回率(Recall)和F1-score是诊断问题中常用的4个评价指标。为了量化所提方法在离心鼓风机上的诊断表现,使用准确率与F1-score来评估所提故障诊断方法的性能。准确率表示正确分类的样本数与样本总数之比,F1-score是精确率和召回率的加权调和平均,综合反映了两者的结果。2个指标的计算公式为
| $A_{\mathrm{cc}}=\frac{T_{\mathrm{P}}+T_{\mathrm{N}}}{T_{\mathrm{P}}+F_{\mathrm{P}}+T_{\mathrm{N}}+F_{\mathrm{N}}}, $ | (13) |
| $F_{1 \text {-score }}=\frac{2 T_{\mathrm{P}}}{2 T_{\mathrm{P}}+F_{\mathrm{P}}+F_{\mathrm{N}}}, $ | (14) |
式中:TP为某一类别样本yc被正确分类的数目;TN为其他类别样本被正确识别的数目;FP为其他类别样本被错误识别为yc的数目;FN为类别yc的样本被识别错误的数目。
3 案例分析 3.1 实验条件本实验中采用的BCD系列单级离心式鼓风机故障模拟试验台如图 4所示,离心鼓风机故障模拟试验台由转子组件、齿轮箱、电机、润滑装置、数据采集系统及其他辅助零部件等组成。在转子表面的水平与垂直方向上均装有加速度传感器用于采集不同方向上的振动信号;转子的前轴承、后轴承、主推力轴承轴瓦处均装有接触式温度传感器用于获取转子温度信号;电机的A相绕组、B相绕组与C相绕组上也均布置有接触式温度传感器用于获取电机三相绕组温度;电气柜装有电流传感器用于获取电机电流;润油装置上装有压力传感器用于获取润油压力。

|
图 4 离心鼓风机故障试验台 Fig. 4 Centrifugal blower failure experiment platform |
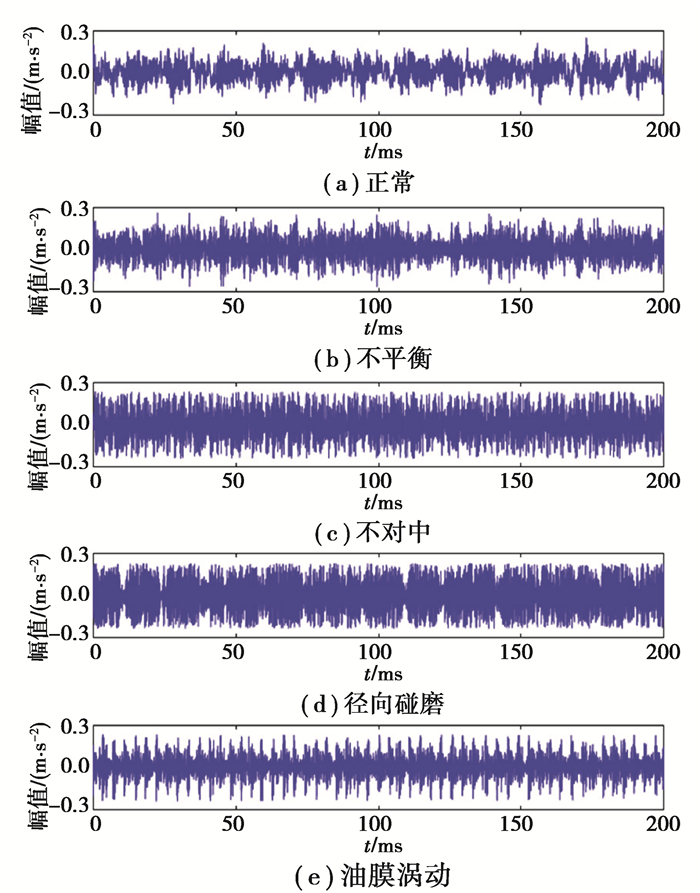
转子是离心鼓风机的核心部件,工作转速一般为10~30 kr/min,长期工作在此高速环境下极易发生故障。因此,笔者在试验台上分别模拟了转子正常、转子不平衡、转子不对中、径向碰磨和油膜涡动5种单一工况健康状态。为了使得离心鼓风机故障试验台模拟的工况更加符合工程应用实际,在实验中,正常与故障情况下共设置了5种变速工况:转速分别为10, 15, 20, 25, 30 kr/min。离心鼓风机故障模拟试验台的运行参数如表 2所示。振动信号含有最为敏感的故障信息,图 5展示了转子水平方向振动信号在每种健康状态下的时域波形。
| 表 2 试验运行参数 Table 2 Experiment operation parameters |
|
图 5 5种健康状态下转子水平振动信号时域图 Fig. 5 Time domain diagram of the rotor's horizontal vibration signal under five health states |
通过上述离心鼓风机故障试验台,在每种转速工况下,分别模拟5种不同的健康状态,采集不同工况不同健康状态下的传感器数据。每种工况下信号连续采样时间为16 s,样本个数均为200。加速度传感器、温度传感器、电流传感器与压力传感器的采样频率均为12.8 kHz,因此,每个样本信号包含1 024个数据点。经数据层融合后的多源异类信息共含有6种信号,将此6种信号按顺序堆叠成一个6通道样本,每个样本数据的维度为1×1 024×6。共设置有5种转速工况,则每种健康状态采集样本数为1 000,共有5种健康状态,因此采集样本总数为5 000。从每类健康状态中随机选择80%的样本作为训练集,其余样本作为测试集,最终得到的数据集如表 3所示。
| 表 3 转子故障数据集描述 Table 3 Rotor failure data set description |
融合后的样本数据集为一维样本,故采用一维ADCNN,通过反复试验调整相关参数,最终得到的初始支路网络模型结构包含3个卷积层、3个池化层和2个全连接层。卷积层参数如表 4所示,所有的卷积层都进行了全零填充处理,避免尺寸的变化,在每层卷积操作后进行Dropout处理,以0.5的概率将网络中的神经元置零,提高ADCNN的泛化性能。池化层采用最大池化,池化大小为2,2个全连接层节点数分别为400与100。第1层卷积层采用较大的卷积核(64×1)可以增大模型输入的感受野。第2层与第3层卷积层采用较小的卷积核(3×1)以及较深的网络结构可以充分挖掘信号中隐含的故障特征。实验结果表明ADCNN的最佳网络支路条数r为3,且每条支路与初始支路具有相同的结构与参数。
| 表 4 ADCNN卷积层参数 Table 4 ADCNN convolutional layer parameters |
为了验证所提多源信息融合模式对离心鼓风机故障诊断的有效性,分别将按所提方法融合的多源信息、按传统方法融合的多源信息、转子振动信号输入构建的故障诊断模型,其中,传统的多源信息融合方法是将多个信号串行叠加为一个信号。共有10种信号信息,每个样本包含1 024个数据点,因此,按照传统的多源信息融合方法其数据输入维度为10 240。为了进一步说明ADCNN的优越性,对比了CNN、BPNN和SVM在不同融合模式下的故障识别能力。其中CNN与ADCNN初始支路结构、参数相同,BPNN对应3种融合模式的结构分别为2 048-600-200-5, 10 240-600-200-5, 6 144-600-200-5,SVM使用高斯径向基函数作为核函数。为了消除偶然误差的影响,每种方法各进行了10次试验。表 5总结了不同方法在测试集上10次试验结果的平均值。
| 表 5 不同故障诊断方法的试验结果 Table 5 Experiment results of different fault diagnosis methods |
从表 5可以看出,多源信息融合相比单一的振动信号有着更为优越的诊断效果,另外,所提出的多源信息融合方法在诊断表现上也明显优于传统的融合模式。以ADCNN为例,3种融合模式的诊断平均准确率分别为81.46%, 89.33%, 99.12%。可见多传感器信号融合可以提供更为丰富的故障诊断信息,且所提融合方法标准差更低,诊断结果更稳定。与CNN及其他的机器学习方法相比,ADCNN实现了99.12%的平均准确率,F1-score为99.11%,其诊断性能普遍优于传统的CNN及其他浅层学习网络,说明基于ADCNN的故障诊断方法可以有效地从多源信息中自适应提取代表性的故障特征并完成故障分类。
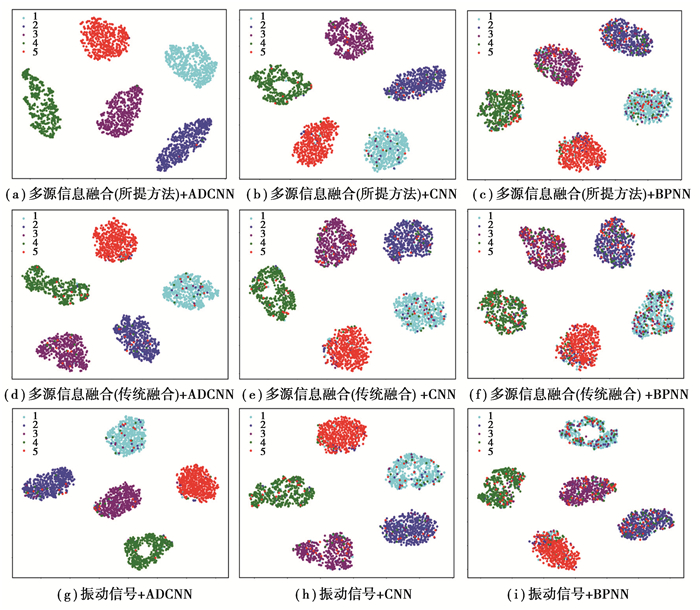
t-SNE是一种非线性降维算法,能够可视化网络学习的特征分布[17]。不同诊断方法提取后的特征经降维后的二维散点图如图 6所示。散点图的两坐标轴均无实际意义,只是表征不同特征间的分布距离。可以发现同一故障状况下的特征被聚集在一起,不同故障状态下的特征彼此分开。与使用单一振动信号和传统的多源信息融合模式相比,所提出的多源信息融合模式展现出更为优越的特征可分性,且仅有较少的故障状态特征被误分类为正常状态。与CNN、BPNN相比,ADCNN也展现出更好的特征学习能力,通过多层卷积运算离心鼓风机各多源信号间的隐含特征被自适应提取。全连接层对特征进行整合处理,增大了不同健康状态下特征分布的距离,使得特征区分更明显,结果表明所提出的方法展现出最佳的诊断性能。
|
图 6 不同诊断方法下的t-SNE特征可视化图 Fig. 6 Visualization of t-SNE features with different diagnosis methods |
1) 笔者分析了离心鼓风机的多源信息组成,提出了一种数据层与特征层相结合的多源信息融合框架,基于相关性方差贡献率法实现了多源同类信息的数据层融合,利用ADCNN自适应地提取各异类信息的特征完成特征融合,有效利用了各信息间的相关互补性。
2) 建立了基于多源信息融合和ADCNN的离心鼓风机故障诊断模型,并在离心鼓风机故障模拟试验台上进行了试验验证,结果表明,ADCNN有着更为优越的自适应特征提取能力,融合了多源信息后的转子故障诊断准确性与稳定性均优于其他方法。
3) 笔者在进行离心鼓风机的故障诊断时只是对所有多源信息做了融合处理,而离心鼓风机各多源信息对故障的敏感程度不同。因此,综合考虑各信息间的关联度对诊断的影响是下一步研究的重点。
| [1] |
Lei Y G, Lin J, He Z J, et al. A review on empirical mode decomposition in fault diagnosis of rotating machinery[J]. Mechanical Systems and Signal Processing, 2013, 35(1/2): 108-126. |
| [2] |
李嫄源, 袁梅, 王瑶, 等. SVM与PSO相结合的电机轴承故障诊断[J]. 重庆大学学报, 2018, 41(1): 99-107. Li Y Y, Yuan M, Wang Y, et al. Fault diagnosis of motor bearings based on SVM and PSO[J]. Journal of Chongqing University, 2018, 41(1): 99-107. (in Chinese) |
| [3] |
Sangeetha B P, S H. Rational-dilation wavelet transform based torque estimation from acoustic signals for fault diagnosis in a three-phase induction motor[J]. IEEE Transactions on Industrial Informatics, 2019, 15(6): 3492-3501. DOI:10.1109/TII.2018.2874463 |
| [4] |
Feng Z P, Chen X W, Zuo M J. Induction motor stator current AM-FM model and demodulation analysis for planetary gearbox fault diagnosis[J]. IEEE Transactions on Industrial Informatics, 2019, 15(4): 2386-2394. DOI:10.1109/TII.2018.2875447 |
| [5] |
Shao H D, Jiang H K, Zhang H Z, et al. Rolling bearing fault feature learning using improved convolutional deep belief network with compressed sensing[J]. Mechanical Systems and Signal Processing, 2018, 100: 743-765. DOI:10.1016/j.ymssp.2017.08.002 |
| [6] |
Chen Y S, Jiang H L, Li C Y, et al. Deep feature extraction and classification of hyperspectral images based on convolutional neural networks[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(10): 6232-6251. DOI:10.1109/TGRS.2016.2584107 |
| [7] |
Young T, Hazarika D, Poria S, et al. Recent trends in deep learning based natural language processing[review article[J]. IEEE Computational Intelligence Magazine, 2018, 13(3): 55-75. DOI:10.1109/MCI.2018.2840738 |
| [8] |
Wen L, Li X Y, Gao L, et al. A new convolutional neural network-based data-driven fault diagnosis method[J]. IEEE Transactions on Industrial Electronics, 2018, 65(7): 5990-5998. DOI:10.1109/TIE.2017.2774777 |
| [9] |
胡茑庆, 陈徽鹏, 程哲, 等. 基于经验模态分解和深度卷积神经网络的行星齿轮箱故障诊断方法[J]. 机械工程学报, 2019, 55(7): 9-18. Hu N Q, Chen H P, Cheng Z, et al. Fault diagnosis for planetary gearbox based on EMD and deep convolutional neural networks[J]. Journal of Mechanical Engineering, 2019, 55(7): 9-18. (in Chinese) |
| [10] |
Jiang G Q, He H B, Yan J, et al. Multiscale convolutional neural networks for fault diagnosis of wind turbine gearbox[J]. IEEE Transactions on Industrial Electronics, 2019, 66(4): 3196-3207. DOI:10.1109/TIE.2018.2844805 |
| [11] |
Olofsson B, Antonsson J, Kortier H G, et al. Sensor fusion for robotic workspace state estimation[J]. IEEE/ASME Transactions on Mechatronics, 2016, 21(5): 2236-2248. DOI:10.1109/TMECH.2015.2506041 |
| [12] |
任海锋, 潘宏侠. 多振动信号的时频相干多分形特征提取[J]. 振动测试与诊断, 2018, 38(6): 1114-1121, 1288. Ren H F, Pan H X. Extraction of time-frequency coherence multifractal features for multiple vibration signals[J]. Journal of Vibration, Measurement & Diagnosis, 2018, 38(6): 1114-1121, 1288. (in Chinese) |
| [13] |
朱丹宸, 张永祥, 潘洋洋, 等. 基于多传感器信号和卷积神经网络的滚动轴承故障诊断[J]. 振动与冲击, 2020, 39(4): 172-178. Zhu D C, Zhang Y X, Pan Y Y, et al. Fault diagnosis for rolling element bearings based on multi-sensor signals and CNN[J]. Journal of Vibration and Shock, 2020, 39(4): 172-178. (in Chinese) |
| [14] |
Jing L Y, Wang T Y, Zhao M, et al. An adaptive multi-sensor data fusion method based on deep convolutional neural networks for fault diagnosis of planetary gearbox[J]. Sensors (Basel, Switzerland), 2017, 17(2): 414. DOI:10.3390/s17020414 |
| [15] |
Gravina R, Alinia P, Ghasemzadeh H, et al. Multi-sensor fusion in body sensor networks: state-of-the-art and research challenges[J]. Information Fusion, 2017, 35: 68-80. DOI:10.1016/j.inffus.2016.09.005 |
| [16] |
Guo X J, Chen L, Shen C Q. Hierarchical adaptive deep convolution neural network and its application to bearing fault diagnosis[J]. Measurement, 2016, 93: 490-502. |
| [17] |
Van der Maaten L, Hinton G. Visualizing data using t-SNE[J]. Journal of machine learning research, 2008, 9(11): 2579-2605. |
 2022, Vol. 45
2022, Vol. 45


