2. 山东高速集团有限公司 建设管理分公司, 济南 250001;
3. 北京工业大学 工程抗震与结构诊治北京市重点实验室, 北京 100124
2. Construction Management Branch of Shandong Expressway Group Co., Ltd., Jinan 250001, P. R. China;
3. Beijing Laboratory of Earthquake Engineering and Structural, Beijing University of Technology, Beijing 100124, P. R. China
火灾作为时空跨度最大的一种灾害,是21世纪多发性灾害中发生概率较高的一种灾害,火灾导致的桥梁坍塌事件为地震导致的桥梁坍塌事件的3倍[1-2]。截至2019年6月,全国机动车总保有量已达3.4亿辆[3],燃料及危险品运输日渐频繁;新能源汽车保有量达344万辆,占汽车总量的1.37%,仅2019年前8个月,新能源汽车燃烧事故就发生了40余起。据不完全统计[1],混凝土梁桥占国内桥梁火灾事故总数的90%以上,主要为预应力混凝土桥。因此,预应力混凝土梁桥过火后的有效预应力的研究具有重要工程意义。近年来,针对预应力混凝土结构的特点,国内外学者开展了不同程度的抗火研究。Kodur等[4-5]综合试验数据,分析了温度与应力路径耦合作用对预应力混凝土梁板抗火性能的影响,提出了考虑热力耦合影响的数值方法。Bailey[6]研究非粘结预应力混凝土单向板的抗火性能,以混凝土骨料类型、板端边界约束等为主参数,分析这些因素对桥梁抗火性能敏感性的影响。结果表明,这些因素对高温下预应力混凝土板的实时变形影响显著。Chhun等[7]研究预应力钢束在不同载荷和温度下的松弛,建立了松弛增量模型,该增量模型能够计算预应力钢束的应变滞后,考虑了温度和加载效应的非线性耦合。Shakya等[8]对低松弛预应力钢绞线力学性能进行试验,发现在20 ℃~800 ℃的温度范围内,预应力钢绞线的强度退化程度高于钢筋。Gales等[9]研究无粘结后张拉(UPT)平板混凝土板在标准火灾中各种温度条件下的潜在预应力松弛行为,通过改变初始预应力水平、混凝土覆盖层与预应力筋、加热长度与总筋长度的比值来研究预应力损失的潜在影响,分析了这些因素对抗弯和抗剪能力的影响,指出建造UPT板时需要特别注意,确保结构的防火安全有足够的混凝土覆盖层。张岗等[10]以ASTM119温升曲线作为预应力混凝土桥梁火灾温度场强度计算标准,利用ANSYS有限元软件,研究高温下钢绞线有效预应力随时间的变化,提出了评估混凝土箱梁预应力时程损失公式。范进等[11-13]分别对高温下及高温后1 570、1 670、1 860级预应力钢绞线(钢丝)进行拉伸试验,获得了钢绞线及钢丝弹性模量、抗拉强度和条件屈服强度随温度的变化规律。王俊等[14]通过实验研究高强预应力筋高温中的蠕变效应,提出了对应的高温蠕变率力学模型及该效应导致的有效预应力损失估算公式,发现对火灾下的预应力混凝土结构须考虑预应力钢筋的高温蠕变作用。针对高温中(后)预应力混凝土有效预应力的研究多以标准升温曲线为出发点。受桥址处大地边界层内空气流动特性、通风因子、可燃烧物表面积、燃烧控制方式等因素影响,较难真实推测桥址温度分布,进而增加快速确定过火后有效预应力的难度。另外,预应力混凝土桥梁常采用水灰比较低的高标号混凝土,即低加热速率下也有高爆裂剥落的敏感性,当混凝土开裂(爆裂)后,裂缝处的温度较未开裂处有所提高,较难通过数值模拟准确计算。
笔者采用理论解析与试验研究相结合的方法,选取国内服役高速公路过火后拆除的实梁作为样本,利用频率法测试钢绞线永存预应力,并使用拉力试验机进行修正,获得了15根钢绞线过火后真实的有效预应力数据。通过回归分析,得到了混凝土剥落深度比与预应力损失比回归公式,通过极限承载能力试验及有限元模拟分析验证该公式的适用性。
1 工程概况某省一座9 m×20 m简支桥面连续预应力混凝土空心板桥,斜交角α=52.74°,混凝土设计强度等级为50 MPa,其中边梁和中梁分别布置15、14根6×ΦJ 15.2低松弛钢绞线,屈服强度设计值为1 860 MPa,张拉控制应力1 395 MPa,立面及边板配筋如图 1所示。该火灾事故详细描述、受损情况分布、火源中心示意及中板配筋图见文献[15]。该桥经检测评估后,对过火的30多片梁拆除替换,为本研究提供了充实的样本。
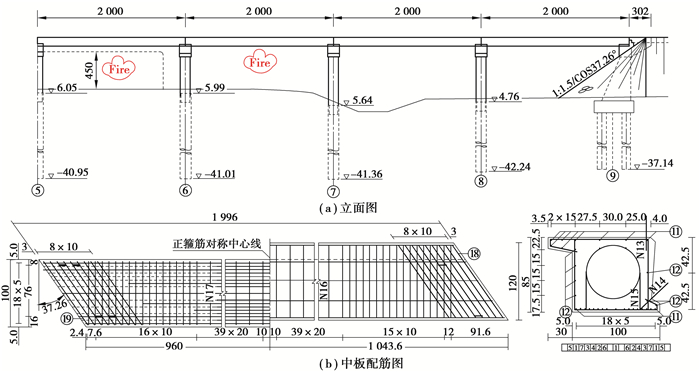
|
图 1 立面及中板配筋 Fig. 1 Elevation and middle plate reinforcement |
因过火剥落后底板呈凹凸不平的状态,测量剥落厚度时,将底板分成20 cm×20 cm的测区,取该测区剥落深度的最大值作为代表值,计算所有测区的平均值作为该区域的平均深度,根据以上方法进行检测,测得空心板跨中附近底板剥落平均深度介于0.9 cm~3.8 cm之间。有2片梁基本未受火焰直接灼烧,可以作为基准梁。典型的剥落情况如图 2所示。

|
图 2 典型底板剥落照片 Fig. 2 Typical floor spalling |
频率法测钢绞线有效预应力测定以弦振动理论作为理论基础。针对张紧的钢绞线,考虑其抗弯刚度,得到拉索微元的动力平衡方程:
| $\frac{\omega}{g} \frac{\partial^2 y}{\partial t^2}+E I \frac{\partial^4 y}{\partial x^4}-T \frac{\partial^2 y}{\partial x^2}=0, $ | (1) |
式中,y为横向坐标(垂直于索长度方向);x为纵向坐标(沿索长度方向);w为单位索长的质量;g为重力加速度;T为索的张力;t为时间;EI为索的抗弯刚度。
若钢绞线两端是铰支,钢绞线作微幅自由振动时,经过分离变量等变换后得到其拉力与第n阶固有频率间的关系为
| $ T=\frac{4 m L^2}{n^2} f_n^2-E I\left(\frac{n {\rm{\mathsf{π} }}}{L}\right)^2, $ | (2) |
式中,T为钢绞线的张力;L为钢绞线的计算长度;EI为钢绞线的抗弯刚度;m为单位钢绞线长的质量;fn为钢绞线的第n阶固有频率。
上述频率法测钢绞线永存应力公式的基本假定为:
1) 钢绞线截面一致、材料均匀、应力应变关系符合胡克定律;2)钢绞线振动时没有外力且为微幅振动;3)钢绞线两端的拉力相等(忽略拉索自重);4)钢绞线两端铰接,振动时不计阻尼影响;5)只考虑几何非线形,不考虑其他非线形。
由假定条件可知,频率法测钢绞线永存应力的主要影响因素是边界条件和抗弯刚度。为减少上述因素的影响,对所选钢绞线频率分别进行2次现场测试。现场测试时,钢绞线计算长度L取1.1 m,将其从梁板凿出后置于拉力试验机进行试验,以便对现场测试结果进行修正。现场及室内测试如图 3和图 4所示。

|
图 3 室内试验室测试 Fig. 3 The laboratory test |

|
图 4 现场测试 Fig. 4 The field test |
通过振动法及室内试验修正,对8片梁跨中附近共计15根钢绞线进行有效预应力测试,典型的信号时程图,如图 5所示;典型的自功率谱幅频曲线,如图 6所示。经回归分析得出预应力损失比与剥落深度与钢绞线净保护层厚度比的公式,见式(3)。原桥R-7-2#梁仅个别区域混凝土被熏黑,未见其他损伤,该梁跨中通过上述方法实测的跨中附近有效预应力均值为1 093 MPa,因该桥的所有梁预制时处于同一批次,施工工艺和环境相同,可将此值作为所有梁未过火前的永存预应力。
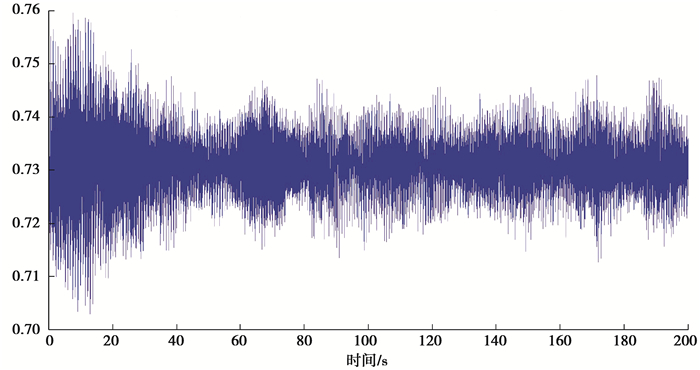
|
图 5 典型振动信号时程图 Fig. 5 The typical time history of typical vibration signals |
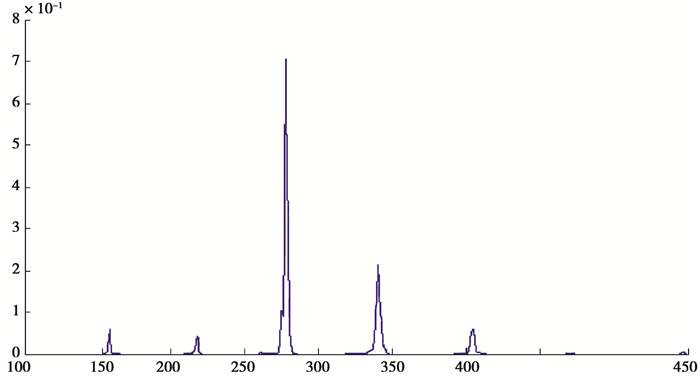
|
图 6 典型的自功率谱幅频曲线 Fig. 6 The typical amplitude-frequency curve of self-power spectrum |
图 7表明,过火后混凝土剥落越深,预应力损失越大;当混凝土剥落深度不超过1/3保护层厚度时,火灾造成的预应力损失小于5%;当剥落深度超过2/3保护层时,预应力损失比大于10%。预应力损失过大,将严重影响结构正常使用,降低结构刚度。
| $ \Delta P_f=0.3385 d_f^{1.2}, $ | (3) |
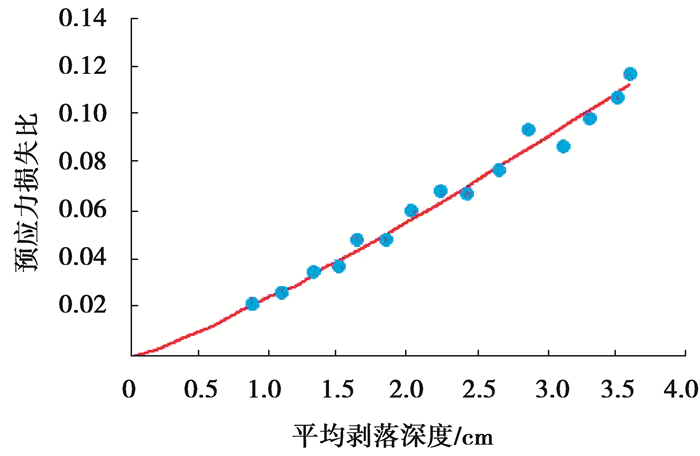
|
图 7 剥落深度与预应力损失比回归图 Fig. 7 The regression diagram of spalling depth and prestress loss ratio |
式中:ΔPf为火灾后预应力损失比;df为火灾后预应钢绞线位置处,因火灾造成的剥落平均深度与钢绞线净保护层厚度比。
钢绞线在火灾中应力损失主要原因如下:
1) 高温中材料弹性模量E下降,导致应力损失,通常在正常使用状态下,钢束没有达到塑性状态,该损失冷却后可恢复[13];2)钢束高温蠕变造成的预应力损失,该损失冷却后无法恢复;3)混凝土在高温下塑性变形导致的预应力损失,该损失冷却后也无法恢复。
4 实例验证因样本数偏少,需通过其他方式验证该公式的适用性。根据文献[16-17]可知,预应力混凝土梁开裂荷载与预应力有效应力、截面抵抗矩塑性影响系数γ及混凝土抗拉强度有关。即当截面、配筋、材料已定,开裂荷载取决于有效预应力,通过实测预应力混凝土梁的开裂弯矩,验证回归公式的适用性。选取一片跨中平均剥落深度为3.625 cm的梁做极限抗弯承载能力试验及有限元模拟分析。
试验加载布置需同时考虑正截面最大弯矩及1/3l~2/3l处截面的抗剪承载能力,最终确定分配梁间距为3 m,加载布置、流程和终止条件详见文献[15],现场试验如图 8所示。

|
图 8 极限承载能力试验 Fig. 8 The bearing capacity test |
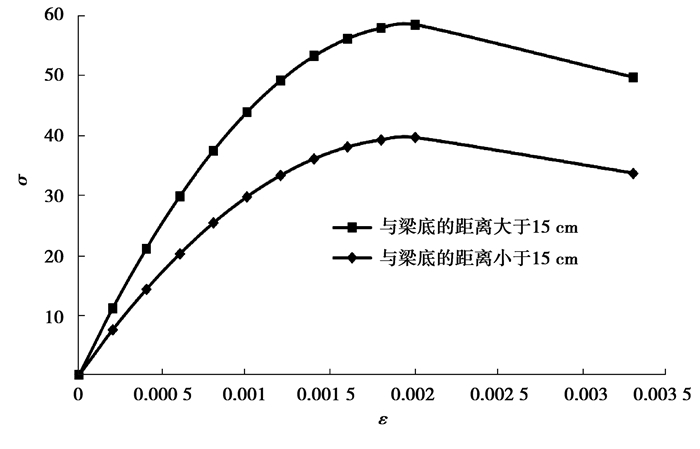
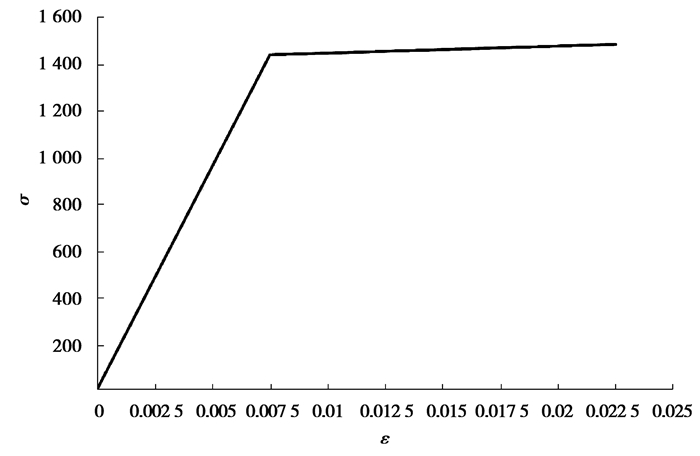
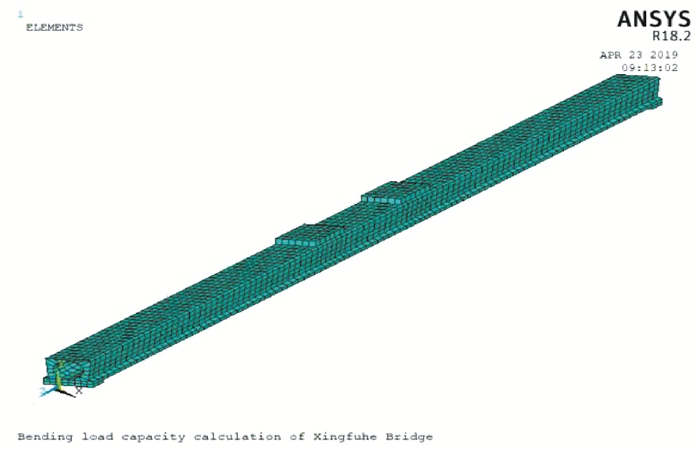
根据有限元软件ANSYS建模,混凝土采用SOLID65单元,混凝土的应力应变关系模型是对混凝土结构进行非线性分析的重要依据,模拟时采用随动硬化模型,混凝土破坏准则中,张开裂缝的剪切传递系数根据相关经验并试算后取0.7,闭合裂缝的剪切传递系数经多次调整后取0.95。混凝土单轴应力应变关系综合了Hognestad和GB 50010—2002的规定。根据文献[15],距梁底15 cm以内的混凝土立方体抗压强度fcu, 下=39.6 MPa,其他区域混凝土立方体抗压强度fcu, 上=58.5 MPa。钢绞线屈服强度取文献[15]中剥落C测区值,即fpk=1 441 MPa,高温后,钢绞线弹性模量几乎可恢复到常温时,故Ep=1.95×105 MPa。混凝土和钢绞线本构如图 9~图 10所示。建模细节见文献[15],模型单元数5 918,节点数8 266,如图 11所示。
|
图 9 混凝土应力应变关系曲线(MPa) Fig. 9 Stress-strain relationship curve of concrete (MPa) |
|
图 10 钢绞线本构(MPa) Fig. 10 The steel strand constitutions (MPa) |
|
图 11 有限元模型 Fig. 11 The finite element model |
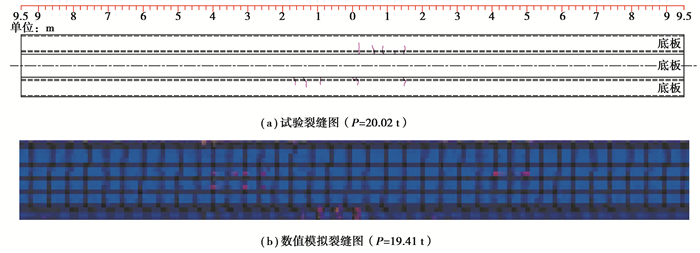
根据文献[17]中的公式,由开裂弯矩反算钢绞线有效预应力的结果,如表 1所示。由表 1可知,回归公式与数值模拟结果基本一致,但与承载能力试验结果差距略大。究其原因,文献公式计算的关建是确定开裂弯矩,而实际加载中,梁开裂初期,裂缝宽度较小,肉眼很难发现,加之荷载分级较大,导致识别的真实加载吨位略大,计算的有效预应力偏大。试验过程中,跨中附近首次开裂裂缝形态如图 12和图 13所示。
| 表 1 过火后有限预应力结果 Table 1 The results of finite prestress after fire |
|
图 12 跨中附近首次开裂裂缝形态 Fig. 12 The fracture morphology of the first crack near the mid-span |

|
图 13 跨中附近裂缝照片 Fig. 13 The photos of cracks near the mid-span |
文中利用频率法对过火后空心板梁钢绞线永存预应力进行测试,使用试验机修正,获得了15根钢绞线过火后真实的有效预应力。通过实测过火后混凝土梁桥钢绞线永存应力,获得了剥落深度比与预应力损失比回归公式,通过极限承载能力试验及有限元模拟分析验证该公式的适用性。
1) 火灾后梁板预应力钢束将出现预应力损失,当混凝土剥落深度超过1/3钢绞线净保护层时,预应力损失不可忽略。
2) 当混凝土剥落深度超过2/3钢绞线净保护层时,预应力损失达10%,严重影响结构刚度。
3) 对于先张法预应力混凝土空心板,底板厚度较薄,用于火灾易发区域时,应严格控制底板尺寸,适当提高钢绞线保护层厚度。
4) 因缺少剥落深度小于0.9 cm的样本,回归公式在此区间的适用性有待深入研究。
| [1] |
徐超. 晚清山东灾害研究[D]. 石家庄: 河北师范大学, 2020. Xu C. Research on Shandong disasters in late qing dynasty[D]. Shijiazhuang: Hebei Normal University, 2020. (in Chinese) |
| [2] |
徐柏刚. 复合灾害应急避难政策及疏散受损评估研究: 以东京新小岩地区为例[D]. 大连: 大连理工大学, 2018. Xu B G. Research on emergency disaster evacuation policy and evacuation damage: based on shin-koiwa of Tokyo[D]. Dalian: Dalian University of Technology, 2018. (in Chinese) |
| [3] |
商讯. 2019上半年全国机动车保有量达3.4亿辆[J]. 商用汽车, 2019(7): 7. The number of motor vehicles in China will reach 340 million In the first half of 2019[J]. Commercial Vehicle, 2019(7): 7. (in Chinese) |
| [4] |
Kodur V K R, Dwaikat M. A numerical model for predicting the fire resistance of reinforced concrete beams[J]. Cement and Concrete Composites, 2008, 30(5): 431-443. DOI:10.1016/j.cemconcomp.2007.08.012 |
| [5] |
Shi X D, Tan T H, Tan K H, et al. Effect of force-temperature paths on behaviors of reinforced concrete flexural members[J]. Journal of Structural Engineering, 2002, 128(3): 365-373. DOI:10.1061/(ASCE)0733-9445(2002)128:3(365) |
| [6] |
Bailey C G, Ellobody E. Fire tests on bonded post-tensioned concrete slabs[J]. Engineering Structures, 2009, 31(3): 686-696. DOI:10.1016/j.engstruct.2008.11.009 |
| [7] |
Chhun P, Sellier A, Lacarriere L, et al. Incremental modeling of relaxation of prestressing wires under variable loading and temperature[J]. Construction and Building Materials, 2018, 163: 337-342. DOI:10.1016/j.conbuildmat.2017.12.123 |
| [8] |
Shakya A M, Kodur V K R. Effect of temperature on the mechanical properties of low relaxation seven-wire prestressing strand[J]. Construction and Building Materials, 2016, 124: 74-84. DOI:10.1016/j.conbuildmat.2016.07.080 |
| [9] |
Gales J, Bisby L A, MacDougall C, et al. Transient high-temperature stress relaxation of prestressing tendons in unbonded construction[J]. Fire Safety Journal, 2009, 44(4): 570-579. DOI:10.1016/j.firesaf.2008.11.006 |
| [10] |
张岗, 刘天龙, 王翠娟, 等. 刚度高温衰变的混凝土箱梁预应力时程损失研究[J]. 武汉理工大学学报, 2015, 37(6): 66-71. Zhang G, Liu T L, Wang C J, et al. Prestress loss of concrete bridges with box girders based on decay of stiffness exposed to high temperature[J]. Journal of Wuhan University of Technology, 2015, 37(6): 66-71. (in Chinese) |
| [11] |
范进, 吕志涛. 高温后预应力钢丝性能的试验研究[J]. 工业建筑, 2002, 32(9): 30-31, 68. Fan J, Lyu Z T. Experimental study on materials'properties of prestressed steel wire post high temperatures[J]. Industrial Construction, 2002, 32(9): 30-31, 68. (in Chinese) DOI:10.3321/j.issn:1000-8993.2002.09.010 |
| [12] |
范进, 吕志涛. 高温(火灾)下预应力钢丝性能的试验研究[J]. 建筑技术, 2001, 32(12): 833-834. Fan J, Lyu Z T. Experimental research on performance of prestressed steel wire in high temperature environment (fire)[J]. Architecture Technology, 2001, 32(12): 833-834. (in Chinese) DOI:10.3969/j.issn.1000-4726.2001.12.018 |
| [13] |
范进. 高温后预应力钢绞线性能的试验研究[J]. 南京理工大学学报(自然科学版), 2004, 28(2): 186-189. Fan J. Experimental study on material properties of prestressed steel strand post high temperatures[J]. Journal of Nanjing University of Science and Technology, 2004, 28(2): 186-189. (in Chinese) DOI:10.3969/j.issn.1005-9830.2004.02.018 |
| [14] |
王俊, 蔡跃, 黄鼎业. 预应力钢筋高温蠕变试验研究及有限元分析应用[J]. 土木工程学报, 2004, 37(11): 1-5, 55. Wang J, Cai Y, Huang D Y. Testing research on thermal creep strain model of prestressing tendons and application of fem analysis[J]. China Civil Engineering Journal, 2004, 37(11): 1-5, 55. (in Chinese) |
| [15] |
郝朝伟, 刘康, 李洪印, 等. 预应力混凝土梁桥过火后的材料性能[J]. 土木与环境工程学报(中英文), 2020, 42(3): 106-114. Hao C W, Liu K, Li H Y, et al. Material properties of prestressed concrete girder bridge after exposed to fire[J]. Journal of Civil and Environmental Engineering, 2020, 42(3): 106-114. (in Chinese) |
| [16] |
JTG 3362-2018, 公路钢筋混凝上及预应力混凝上桥涵设计规范[S]. 北京: 人民交通出版社, 2018. JTG 3362-2018, Specifications for Design of Highway Reinforced Concrete and Prestressed Concrete Bridges and Culverts[S]. Beijing: China communication press, 2018. (in Chinese) |
| [17] |
聂长勇, 王鹏. 考虑预应力筋增量的混凝土梁开裂弯矩计算公式研究[J]. 公路交通技术, 2017, 33(2): 26-30. Nie C Y, Wang P. Study on calculation formula of cracking moment of concrete beam considering prestressed reinforcement increment[J]. Technology of Highway and Transport, 2017, 33(2): 26-30. (in Chinese) |
 2022, Vol. 45
2022, Vol. 45

