近几年来,随着中国建筑行业产业化与绿色化发展,装配式建筑的研究及应用受到广泛关注。预制装配式混凝土剪力墙作为一种高效的抗侧力结构构件,其水平与竖向连接构造的合理性决定了整体结构的抗震性能。目前,剪力墙水平接缝的研究已经取得较多成果,刘家彬等[1]设计出一种采用U型闭合筋连接的预制剪力墙水平接缝构造,基于试验结果研究了采用该水平接缝构造预制剪力墙的抗震性能;赵斌等[2]对一种采用“螺栓钢连接件套筒”水平接缝方案的全装配预制剪力墙进行试验,发现该种全装配预制剪力墙耗能能力弱于现浇剪力墙,但总体抗震性能良好;李宁波等[3]对部分竖向分布钢筋采用套筒挤压连接的预制剪力墙进行试验,发现套筒挤压连接能有效传递钢筋应力,部分竖向钢筋采用套筒挤压连接的预制剪力墙的刚度退化与耗能能力和现浇剪力墙试件相当,但在弹塑性阶段的变形能力较差;Soudki等[4-6]通过一系列足尺试验对比了采用不同构造水平接缝的装配式剪力墙的滞回性能,基于试验结果对这几类预制剪力墙提出抗震设计建议;Kurama等[7]对带水平接缝的无粘结后张法预应力预制剪力墙进行了非线性动力分析,发现这种预制剪力墙在水平荷载作用下侧移较大,但卸载后残余变形较小。文中参考已有的“螺栓连接件螺栓”式水平接缝连接构造[8]全装配混凝土剪力墙(PSW-1),设计了一种“螺栓连接件”式新型水平接缝连接构造装配式混凝土剪力墙(PSW-2),利用ABAQUS软件对PSW-1进行建模并在试验工况[8]下进行单向加载数值模拟,将模拟所得荷载位移曲线与试验结果进行对比,证明文中数值模拟方法的有效性;对PSW-1、PSW-2及对比现浇剪力墙试件(SW-1)进行了有限元建模及低周反复加载模拟,通过对比3类试件数值模拟结果,分析了该新型装配式剪力墙试件的抗震性能。
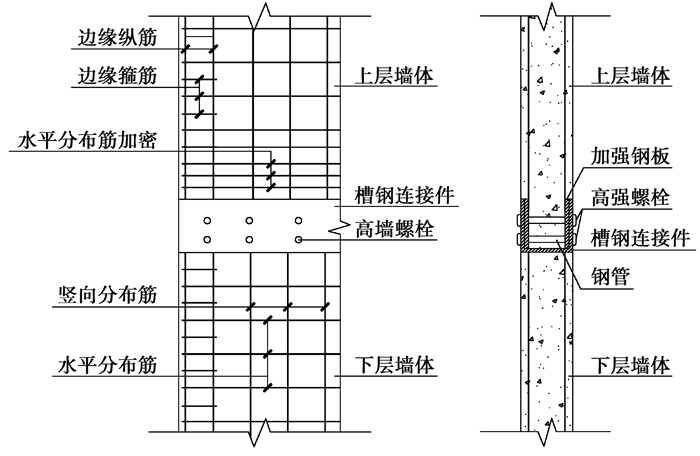
1 新型全装配剪力墙构造参考预制装配式剪力墙水平缝连接构造[8],设计了一种新型“螺栓连接件”式水平缝连接构造装配式剪力墙,其构造如图 1所示。
|
图 1 新型装配式剪力墙构造示意图 Fig. 1 The detail of prefabricated shear wall with innovative horizontal joint |
在该新型“螺栓连接件”式全装配混凝土剪力墙中,上、下层预制剪力墙通过预埋加强钢板、U型槽钢连接件与高强螺栓进行连接。上层预制墙体底部连接端部两侧预埋开孔加强钢板,两侧钢板开孔位置一一对应,对应孔位之间垂直焊接贯穿墙厚的钢管作为预制剪力墙安装对拉螺栓的预留孔道。为提高预制剪力墙底部连接部位的受力性能,对距底部3倍墙厚水平分布筋进行加密处理。下层预制剪力墙墙顶预埋U型槽钢连接件,连接件两侧翼板开有对拉螺栓孔(孔位与上层预制剪力墙底部预埋加强钢板开孔位置一一对应),预制剪力墙体竖向分布筋通过穿孔塞焊与U形槽钢连接件底板焊接连接。现场安装时,上层预制剪力墙底部对应插入下层预制剪力墙顶部预埋U形槽钢连接件内,高强螺栓穿过预埋钢管后对拉拧紧,完成上、下层预制剪力墙的连接安装。
2 试件设计为对比新型“螺栓连接件”式全装配剪力墙水平缝连接构造的抗震性能,文中利用ABAQUS软件对以下3种类型的剪力墙试件进行数值模拟:1)现浇剪力墙试件,编号为SW-1;2)文献[8]中水平缝采用“螺栓连接件螺栓”连接的装配式剪力墙试件,编号为PSW-1;3)文中所设计的水平缝采用“螺栓连接件”连接的新型装配式剪力墙试件,编号为PSW-2。
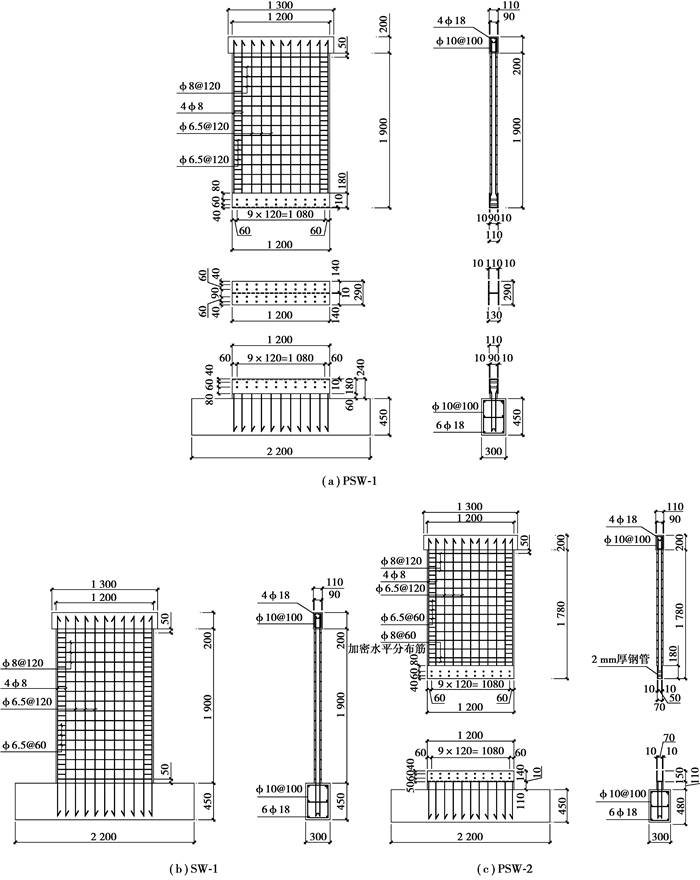
以上试件均由加载梁、墙体及支座梁组成,各试件的加载梁、支座梁及连接端部以上墙体的几何参数保持一致。各类试件具体的几何尺寸与配筋如图 2和表 1所示。PSW-2试件在距底部连接端部270 mm(3倍墙厚)范围内设有ϕ8@60的水平加密分布筋,其余配筋与SW-1与PSW-1保持一致。
|
图 2 各试件几何参数及配筋 Fig. 2 The dimension and reinforcement of shear wall specimens |
| 表 1 剪力墙试件配筋 Table 1 Reinforcement of shear wall specimens |
文中采用有限元软件ABAQUS对试件进行模拟分析。试件SW-1、PSW-1及PSW-2内钢筋及钢板部件均采用HPB235钢材,弹性模量Es取200 GPa,泊松比为0.3。钢筋、钢板屈服强度fy、抗拉强度fu均采用文献[8]中材料强度参数实测值;螺栓采用M16、10.9S高强螺栓,螺栓屈服强度fy与抗拉强度fu分别取940 MPa与1 050 MPa[9]。文中均采用二折线模型对钢材本构关系进行定义。
各剪力墙试件混凝土均采用C35混凝土,泊松比为0.2。混凝土立方体抗压强度fcu实测值为38.9 MPa[8],抗压强度fc、抗拉强度ft及弹性模量Ec按规范[10]进行计算。文中采用混凝土塑性损伤模型(CDP模型)对混凝土材料性能进行模拟,基于张劲等[11]提出的方法计算CDP模型材料本构关系及损伤参数。
3.2 单元类型及接触面定义各剪力墙试件中,钢筋单元采用桁架单元T3DR进行模拟,混凝土、钢板、钢管及螺栓单元均定义为C3D8R单元。钢筋通过“Embedded”约束于混凝土中以协调钢筋与混凝土单元间的变形,不考虑钢筋与混凝土间的粘结滑移[12];连接端部处,PSW-1内嵌钢框、PSW-2加强钢板及钢管表面通过“Tie”与混凝土表面约束;钢筋与钢板间的焊接关系用“Tie”约束进行模拟。连接部位各钢钢接触面及钢混凝土接触面均采用“General Contact”进行模拟(法向接触定义为“Hard Contact”,切向接触定义为“Penalty”,摩擦系数取0.3)。
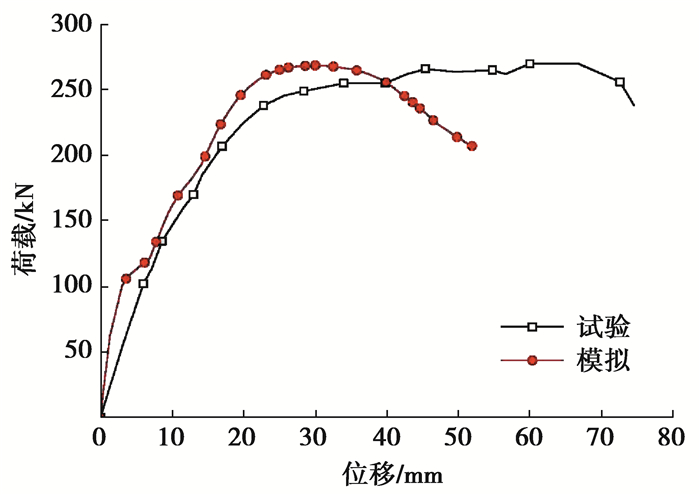
3.3 数值模拟方法验证为检验文中数值模拟方法的准确性及合理性,在文献[8]所述试验工况下对PSW-1进行模拟,并将模拟结果与试验结果进行对比。在轴压比为0.16的情况下,对与试件PSW-1构造及材料完全一致的试件WH-1进行单向加载试验,WH-1极限荷载为270.1 kN,单向加载的荷载位移曲线能维持较长水平段。
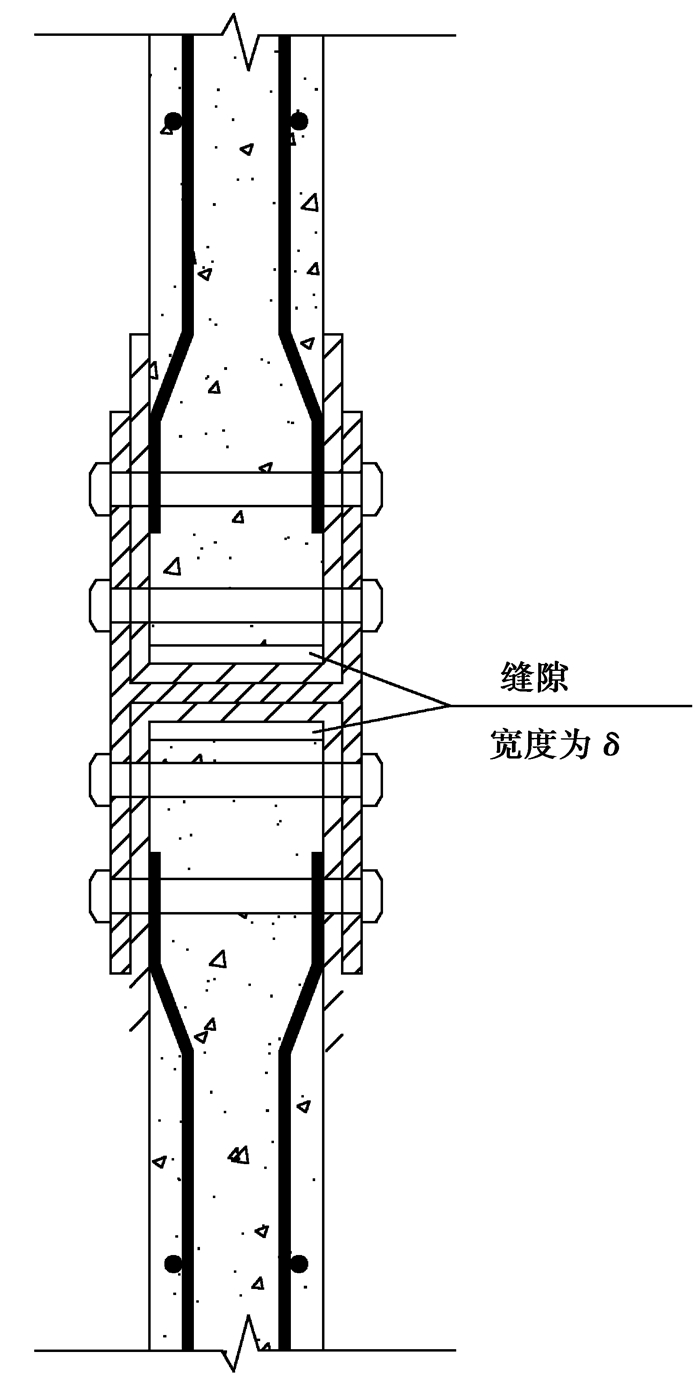
在实际工程中,装配式剪力墙连接端部与连接件腹板间存在一定间隙,设上、下层剪力墙端部与连接件腹板之间的间隙宽度为δ,如图 3所示。δ的大小与试件制作工艺及安装精确度有关。测得试件WH-1的δ=1.5 mm,在相同条件下对PSW-1进行单向加载模拟,试验与模拟所得荷载位移曲线对比如图 4所示。从图 4可知,PSW-1极限承载力模拟结果为268.6 kN,与试验结果相差小于6%。进入弹塑性阶段后,模拟与试验所得荷载位移曲线存在一定差异,原因在于实际试验加载过程中,试件与基础地面间的锚固约束有限,试件与地面间存在滑移,且在加载过程中钢筋与混凝土之间也存在粘结滑移。而数值模拟中试件基础与地面完全锚固且试件钢筋混凝土之间不存在粘结滑移。所以在弹塑性阶段相同水平荷载作用下,实际试验中试件位移大于理想条件下数值模拟试件的水平位移,从荷载位移曲线上看试验试件延性较好。模拟所得荷载位移曲线与试验结果吻合较好,说明文中数值模拟方法有效。
|
图 3 内嵌钢框与连接件间缝隙示意图 Fig. 3 The gap between wall body and steel connector |
|
图 4 PSW-1单向加载荷载位移曲线 Fig. 4 Load-displacement curve of PSW-1 under single-direction lateral load |
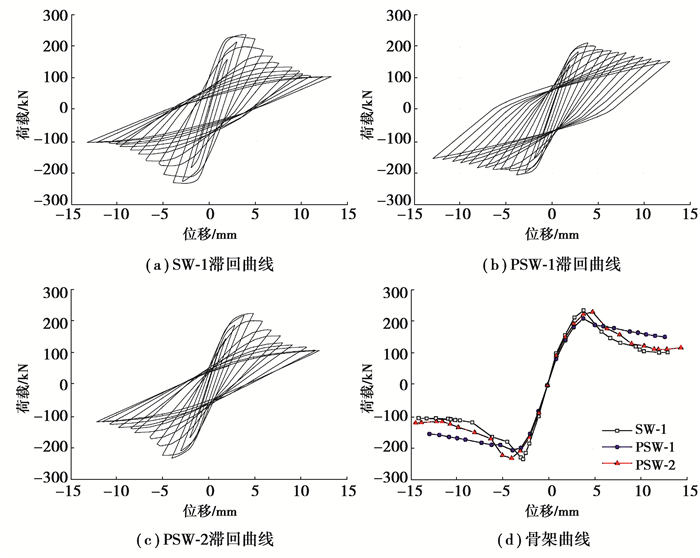
假定装配式剪力墙试件PSW-1及PSW-2的加工及装配精确(即δ=0),在轴压比控制为0.16的情况下对SW-1、PSW-1及PSW-2进行低周反复加载数值模拟分析,图 5为模拟所得各试件滞回曲线及骨架曲线。
|
图 5 各试件滞回曲线及骨架曲线 Fig. 5 Hysteretic curves and skeleton curves of specimens |
由图 5可知,PSW-1的峰值荷载小于其余试件,过峰值点后荷载随位移的增长缓慢下降。试件SW-1与PSW-2在弹性段承载力与刚度较为接近,弹塑性阶段SW-1刚度略大于PSW-2。总体上,试件PSW-2与现浇试件SW-1的骨架曲线基本一致。
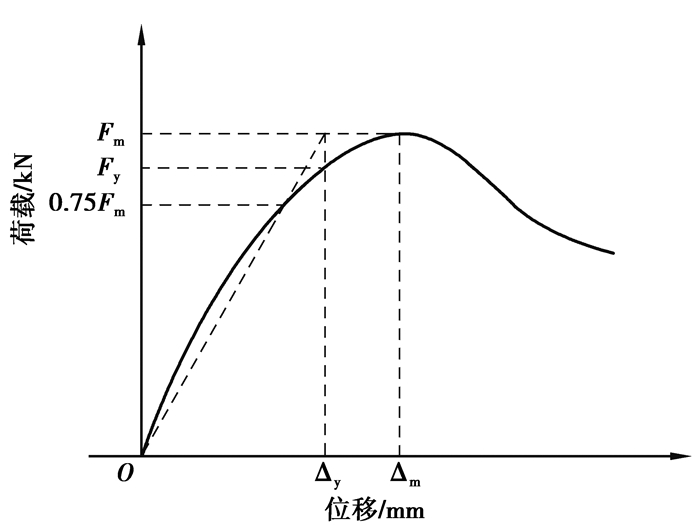
4.1 承载能力如图 6所示,试件屈服位移Δy采用割线刚度法确定[13],Δy在骨架曲线上所对应的荷载即为屈服荷载Fy;各试件峰值水平荷载Fm取骨架曲线荷载最大值;当承载力下降至峰值荷载的85%时认为试件发生极限破坏,即试件极限承载力Fu=0.85Fm。按上述方法得到各试件屈服荷载Fy、峰值荷载Fm与极限荷载Fu,如表 2所示。
|
图 6 割线法计算屈服荷载示意图 Fig. 6 Calculating yield load by secant stiffness method |
| 表 2 剪力墙试件各受力阶段特征荷载 Table 2 Characteristic load of specimens |
由表 2可知,现浇剪力墙SW-1的屈服荷载Fy、峰值荷载Fm与极限荷载Fu均大于预制剪力墙试件PSW-1的相应荷载;试件PSW-2的屈服荷载Fy略小于SW-1,峰值荷载Fm与极限荷载Fu与试件SW-1接近。由于构造原因,PSW-2试件上层墙体在连接端部处混凝土有效截面积小于SW-1试件。但由于PSW-2在连接部位墙体两侧加强钢板间垂直焊接钢管作为螺栓孔道,钢板与钢管之间形成封闭区域约束混凝土的开裂,一定程度上改善了连接端部处混凝土受力性能,有助于提高PSW-2的承载力。
试件PSW-2墙肢正截面理论抗弯承载力按式(1)~式(11)计算[14]:
| $ N \leqslant A_{\mathrm{s}}^{\prime} f_{\mathrm{y}}^{\prime}-A_{\mathrm{s}} \sigma_{\mathrm{s}}-N_{\mathrm{sw}}+N_{\mathrm{c}}, $ | (1) |
| $ N\left(e_0+h_0-\frac{h}{2}\right) \leqslant A_{\mathrm{s}}^{\prime} f_{\mathrm{y}}^{\prime}\left(h_0-a_{\mathrm{s}}^{\prime}\right)-M_{\mathrm{sw}}+M_{\mathrm{c}}, $ | (2) |
| $ N_{\mathrm{c}}=\alpha_1 f_{\mathrm{c}} b x, $ | (3) |
| $ M_{\mathrm{c}}=\alpha_1 f_{\mathrm{c}} b x\left(h_0-\frac{x}{2}\right), $ | (4) |
当x≤ξbh0时,试件在大偏心受压情况下:
| $ \sigma_{\mathrm{s}}=f_{\mathrm{y}}, $ | (5) |
| $N_{\mathrm{sw}}=\left(h_0-1.5 x\right) b_{\mathrm{w}} f_{\mathrm{yw}} \rho_{\mathrm{w}}, $ | (6) |
| $ M_{\mathrm{sw}}=\frac{1}{2}\left(h_0-1.5 x\right)^2 b_{\mathrm{w}} f_{\mathrm{yw}} \rho_{\mathrm{w}}, $ | (7) |
当x>ξbh0时,试件在小偏心受压情况下:
| $ \sigma_{\mathrm{s}}=\frac{f_{\mathrm{y}}}{\xi_{\mathrm{b}}-0.8}\left[\frac{x}{h_0}-\beta_1\right], $ | (8) |
| $ N_{\mathrm{sw}}=0, $ | (9) |
| $M_{\mathrm{sw}}=0, $ | (10) |
| $ \xi_{\mathrm{b}}=\frac{\beta_1}{1+\frac{f_{\mathrm{y}}}{E_{\mathrm{s}} \varepsilon_{\mathrm{cu}}}}, $ | (11) |
式中:a′s为剪力墙受压边缘构件纵筋合力点到受压区边缘的距离;b为剪力墙截面宽度;h为剪力墙截面高度;h0为剪力墙截面有效高度;e0为偏心距;fy、f′y分别为剪力墙边缘构件受拉、受压纵筋强度设计值;fyw为剪力墙墙体竖向分布钢筋强度设计值;fc为混凝土轴心抗压强度设计值;ρw为剪力墙竖向分布钢筋配筋率;ξb为界限相对受压区高度;α1、β1为系数,在混凝土强度等级不超过C50时分别取1.0、0.8;εcu为混凝土极限压应变。
计算得到试件PSW-2在轴压比为0.16的情况下,x=376.21 mm<ξbh0=701.1 mm,试件发生大偏压破坏;截面抗弯承载力M=347.95 kN·m;峰值承载力F=M/H=154.64 kN<Fm= 231.33 kN。可知PSW-2承载力验算满足要求,试件具有一定的安全储备。
4.2 变形能力表 3列出了各剪力墙试件的屈服位移Δy、峰值位移Δm及极限位移Δu;对应的位移转角θ=Δ/H,其中,H为加载梁截面中心距支座梁顶面的垂直距离;试件位移延性系数取μ=Δu/Δy。
| 表 3 试件各受力阶段变形值 Table 3 Lateral displacement and ductility of specimens |
试件PSW-2相比于试件SW-1,在屈服点、峰值点与极限点时加载点的水平位移、对应位移角及位移延性系数略大,试件PSW-2的变形能力比现浇剪力墙试件SW-1略好。在达到峰值荷载后,PSW-1试件的水平荷载随位移增长而缓慢下降,其变形能力优于PSW-2与SW-1。
4.3 耗能文中采用等效粘滞阻尼系数he能量耗散系数E代表试件在地震作用下的耗能能力,he及E的值越大说明试件的耗能能力越强[15]。取试件屈服荷载、峰值荷载与极限荷载所对应的加载循环进行he及E的计算,结果如表 4所示。可见,各试件等效粘滞阻尼系数he和能量耗散系数E的值随水平位移增长而增大。现浇试件SW-1与试件PSW-1、PSW-2在屈服点对应的加载循环处he和E的值相差不大,而在峰值点与极限点对应的加载循环he与E的值均大于其余两试件。上述情况表明,现浇试件SW-1的耗能性能优于试件PSW-1与PSW-2,原因在于SW-1剪力墙体内纵筋直接锚固于基础梁中,在加载过程中纵筋能有效传递应力并在接缝处通过拉压屈服耗能;装配式剪力墙试件PSW-1、PSW-2由于水平接缝构造特点,上层剪力墙体纵筋没有伸入基础梁内进行锚固,剪力墙水平连接接缝处无纵筋贯通,导致PSW-1、PSW-2屈服后的耗能性能不如现浇试件SW-1。
| 表 4 剪力墙试件等效粘滞阻尼系数与能量耗散系数 Table 4 Equivalent viscosity damping of shear wall specimens |
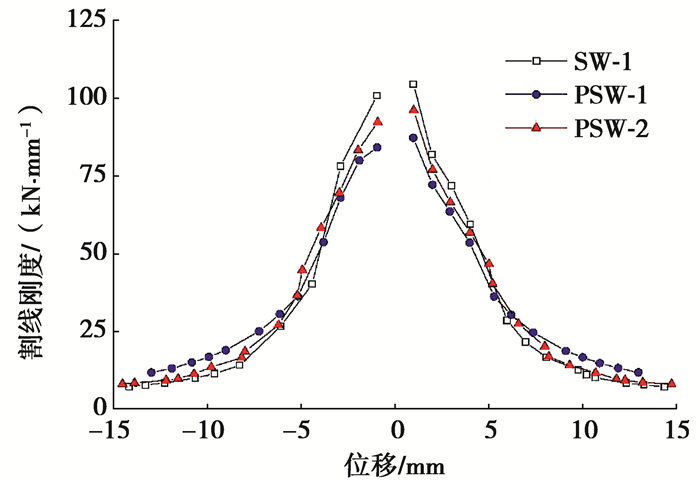
以试件各级循环加载下荷载位移曲线的峰值荷载点对应的割线刚度Kr作为试件在该循环下的刚度代表值,图 7为加载过程中各试件刚度位移曲线。可见,在弹性段试件PSW-1刚度略小于试件SW-1与PSW-2,超过荷载峰值点后其刚度大于试件SW-1与PSW-2且退化趋势缓慢。试件SW-1与试件PSW-2刚度退化曲线较为接近:两者在弹性阶段刚度退化较快,荷载超过峰值后由于混凝土主要裂缝基本形成、混凝土破坏趋于稳定,刚度退化趋缓。
|
图 7 割线刚度退化曲线 Fig. 7 Degradation curves of secant stiffness |
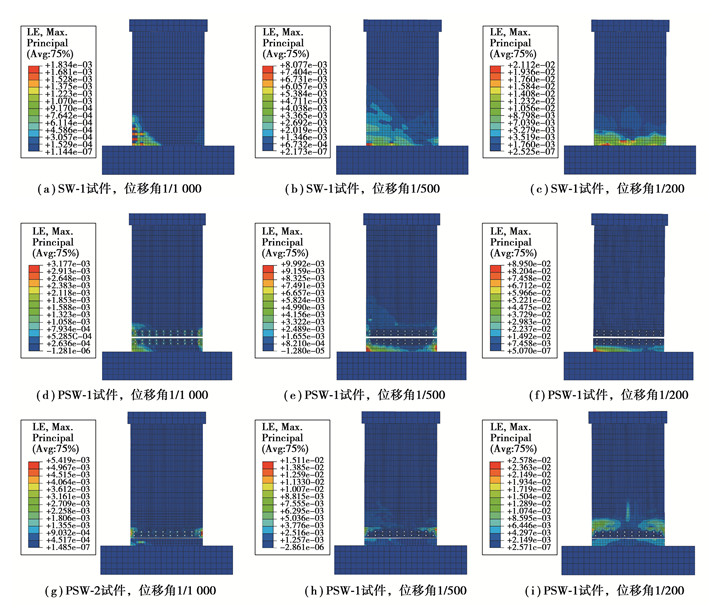
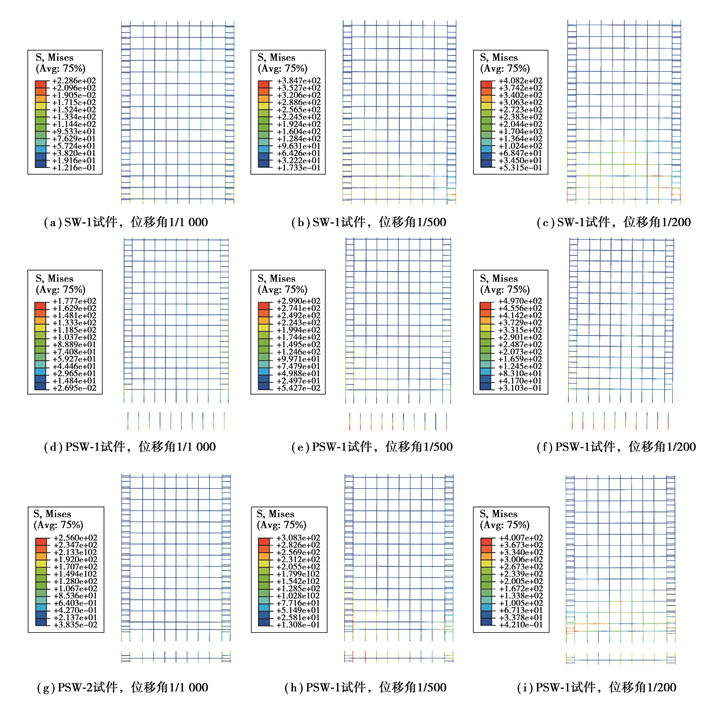
为研究加载过程中试件连接端部的破坏形态,分别导出正向位移角为1/1000、1/500和1/200时SW-1,PSW-1和PSW-2混凝土主应变云图及钢筋Mises应力云图(PSW-1和PSW-2试件的连接件、加强钢板及高强螺栓均已隐藏),如图 8、图 9所示。
|
图 8 混凝土应变云图 Fig. 8 Strain nephogram of concrete |
|
图 9 钢筋应力云图 Fig. 9 Stress nephogram of reinforcement |
由图 8可知,在弹性阶段位移角为1/1000时,各试件受拉侧墙角裂缝主要向水平方向开展,此时试件变形以弯曲变形为主。位移角为1/500时,各试件开裂情况加剧,试件SW-1裂缝沿墙身高度斜向发展,PSW-1裂缝主要集中于墙角部位,PSW-2裂缝主要分布于混凝土截面突变处且由墙身端部向中部发展。当位移角达到1/200时,各试件均已发生极限破坏,SW-1与PSW-2试件破坏形态有所差异:SW-1的主要裂缝集中在距墙体底部1/3墙身高度范围内,墙身底端及两侧墙角破坏较为严重;由于PSW-2构件采用“螺栓连接件”式水平接缝,薄弱部位上移,破坏主要发生在连接件以上墙体角部。由图 9可知,位移角相同时,SW-1与PSW-2上层墙体内钢筋应力分布相近,应力值均大于PSW-1墙体内相应钢筋应力值。在位移角为1/200时,试件SW-1与PSW-2上层墙体受压与受拉边缘纵筋应力值均大于PSW-1相应边缘纵筋应力值,说明发生极限破坏时PSW-1内钢筋材料强度未得到充分发挥。
5 结论参考已有的“螺栓连接件螺栓”式水平接缝连接构造全装配混凝土剪力墙(PSW-1),设计了一种新型“螺栓连接件”式水平接缝连接构造全装配混凝土剪力墙(PSW-2),利用有限元分析软件ABAQUS对2种水平缝连接构造的全装配混凝土剪力墙及现浇剪力墙试件(SW-1)进行有限元建模,并对PSW-1在单向加载工况下进行模拟,对SW-1、PSW-1及PSW-2进行低周反复加载模拟。
1) 单向加载工况下,“螺栓连接件螺栓”式水平接缝连接构造全装配式混凝土剪力墙试件数值模拟所得荷载位移曲线与试验曲线较为吻合,表明文中所采用的数值模拟方法有效。
2) 由于新型“螺栓连接件”式全装配混凝土剪力墙试件连接端部处钢管与加强钢板对混凝土的约束作用,其承载力与现浇剪力墙试件基本一致且满足验算要求,试件具有一定的安全储备。采用“螺栓连接件螺栓”式水平接缝连接构造全装配混凝土剪力墙试件承载力小于其余两试件。
3) 新型“螺栓连接件”式全装配混凝土剪力墙试件在加载过程中,与荷载位移曲线各特征点对应的加载点水平位移、位移转角及延性系数均略大于现浇试件,表明其变形能力略优于现浇剪力墙试件。
4) 新型“螺栓连接件”式全装配混凝土剪力墙试件耗能能力随位移增长而提升,优于采用“螺栓连接件螺栓”式水平连接方法的剪力墙。新型装配式剪力墙试件屈服时的耗能能力与现浇试件基本一致,但屈服后其耗能能力不如现浇试件。
5) 新型“螺栓连接件”式全装配混凝土剪力墙试件、现浇剪力墙试件及采用“螺栓连接件螺栓”式水平连接方法的剪力墙试件屈服前的刚度随位移增长退化较快;进入弹塑性阶段后,各试件刚度退化趋缓。新型装配式剪力墙试件与现浇试件刚度退化曲线较为接近。
6) 弹性阶段,各剪力墙试件变形均以弯曲变形为主,随着位移角增大现浇试件裂缝沿墙身高度方向斜向发展。试件发生极限破坏时,现浇试件墙身底端及墙角破坏较严重;由于采用“螺栓连接件”式水平接缝,新型全装配剪力墙试件薄弱部位上移,发生极限破坏时裂缝主要发生在水平接缝以上墙体角部处,两者破坏形态具有一定差异。
| [1] |
刘家彬, 陈云钢, 郭正兴, 等. 装配式混凝土剪力墙水平拼缝U型闭合筋连接抗震性能试验研究[J]. 东南大学学报(自然科学版), 2013, 43(3): 565-570. Liu J B, Chen Y G, Guo Z X, et al. Test on seismic performance of precast concrete shear wall with U-shaped closed reinforcements connected in horizontal joints[J]. Journal of Southeast University (Natural Science Edition), 2013, 43(3): 565-570. (in Chinese) |
| [2] |
赵斌, 王庆杨, 吕西林. 采用全装配水平接缝的预制混凝土剪力墙抗震性能研究[J]. 建筑结构学报, 2018, 39(12): 48-55. Zhao B, Wang Q Y, Lyu X L. Research on seismic behavior of precast concrete walls with fully assembled horizontal joints[J]. Journal of Building Structures, 2018, 39(12): 48-55. (in Chinese) |
| [3] |
李宁波, 钱稼茹, 刘时伟, 等. 部分竖向分布钢筋套筒挤压连接的预制剪力墙抗震性能试验研究[J]. 土木工程学报, 2016, 49(7): 49: 36-48. Li N B, Qian J R, Liu S W, et al. Experimental study on seismic behavior of pre-cast shear walls with partial vertical distributed steel bars pressed sleeve splicing[J]. China Civil Engineering Journal, 2016, 49(7): 49: 36-48. (in Chinese) |
| [4] |
Soudki K A, West J S, Rizkalla S H, et al. Horizontal connections for precast concrete shear wall panels under cyclic shear loading[J]. PCI Journal, 1996, 41(3): 64-80. DOI:10.15554/pcij.05011996.64.80 |
| [5] |
Soudki K A, Rizkalla S H, LeBlanc B. Horizontal connections for precast concrete shear walls subjected to cyclic deformations part 1: mild steel connections[J]. PCI Journal, 1995, 40(4): 78-96. DOI:10.15554/pcij.07011995.78.96 |
| [6] |
Soudki K A, Rizkalla S H, Daikiw R W. Horizontal connections for precast concrete shear walls subjected to cyclic deformations part 2: prestressed connections[J]. PCI Journal, 1995, 40(5): 82-96. DOI:10.15554/pcij.09011995.82.96 |
| [7] |
Kurama Y, Pessiki S, Sause R, et al. Seismic behavior and design of unbonded post-tensioned precast concrete walls[J]. PCI Journal, 1999, 44(3): 72-89. DOI:10.15554/pcij.05011999.72.89 |
| [8] |
Sun J, Qiu H X, Lu B. Experimental validation of horizontal joints in an innovative totally precast shear wall system[J]. Journal of Southeast University(English Edition), 2015, 31(1): 124-129. |
| [9] |
周赵凤, 沈骅. 高强螺栓抗剪连接有限元分析[J]. 浙江树人大学学报(自然科学版), 2011, 11(3): 37-41. Zhou Z F, Shen H. Finite element analysis of shear behaviorof high-strength bolt connections[J]. Journal of Zhejiang Shuren University (Acta Scientiarum Naturalium), 2011, 11(3): 37-41. (in Chinese) |
| [10] |
中华人民共和国住房和城乡建设部. 中华人民共和国国家标准: 混凝土结构设计规范GB 50010—2010[S]. 北京: 中国建筑工业出版社, 2011. Ministry of Housing and Urban-Rural Development of the People's Republic of China. National Standard (Mandatory) of the People's Republic of China: Code for design of concrete structures. GB 50010—2010[S]. Beijing: China Architecture & Building Press, 2011. (in Chinese) |
| [11] |
张劲, 王庆扬, 胡守营, 等. ABAQUS混凝土损伤塑性模型参数验证[J]. 建筑结构, 2008, 38(8): 127-130. Zhang J, Wang Q Y, Hu S Y, et al. Parameters verification of concrete damaged plastic model of ABAQUS[J]. Building Structure, 2008, 38(8): 127-130. (in Chinese) |
| [12] |
党像梁, 吕西林, 钱江, 等. 底部开水平缝预应力自复位剪力墙有限元模拟[J]. 工程力学, 2017, 34(6): 51-63. Dang X L, Lyu X L, Qian J, et al. Finite element simulation of self-centering pre-stressed shear walls with horizontal bottom slits[J]. Engineering Mechanics, 2017, 34(6): 51-63. (in Chinese) |
| [13] |
中华人民共和国建设部. 中华人民共和国建筑工程标准: 建筑抗震试验方法规程JGJ 101—1996[S]. 北京: 中国建筑工业出版社, 1997. Ministry of Construction of the People's Republic of China. Specificating of testing methods for earthquake resistant building. JGJ 101—1996[S]. Beijing: China Architecture & Building Press, 1997. (in Chinese) |
| [14] |
中华人民共和国住房和城乡建设部. 中华人民共和国建筑工程标准: 高层建筑混凝土结构技术规程JGJ 3—2010[S]. 北京: 中国建筑工业出版社, 2011. Ministry of Housing and Urban-Rural Development of the People's Republic of China. Technical specification for concrete structures of tall building. JGJ 3—2010[S]. Beijing: China Architecture & Building Press, 2011. (in Chinese) |
| [15] |
蒋庆, 叶献国, 连星, 等. 叠合板式剪力墙的耗能分析[J]. 江苏大学学报(自然科学版), 2010, 31(4): 483-487. Jiang Q, Ye X G, Lian X, et al. Analysis on energy dissipation of superimposed slab shear walls[J]. Journal of Jiangsu University (Natural Science Edition), 2010, 31(4): 483-487. (in Chinese) |
 2022, Vol. 45
2022, Vol. 45

