b. 河南理工大学 电气工程与自动化学院, 河南 焦作 454150
b. School of Electrical Engineering and Automation, Henan Polytechnic University, Jiaozuo 454150, Henan, P. R. China
近年来,随着新能源发电技术的不断发展,能源危机和环境问题得到了缓解。新能源发电正朝着规模化和产业化的方向发展,其装机容量在电力系统中所占比例越来越高[1-3]。并网逆变器作为新能源发电系统与电网之间连接的关键部分,其稳定性直接影响到新能源发电并网系统的可靠性[4]。虽然逆变器具有一定的灵活性和可控性,但是并网逆变器主电路是由电力电子器件组成,在运行时易产生谐波,并且在并网时需要电压传感器提供同步信号。
在早期主要是通过在逆变器输出端添加接口电感或LC(LC, inductance capacitance)低通滤波器进行滤波,并提供理想的电压同步点[5]。为了达到更好的滤波效果,有不少学者对滤波器的结构进行了改进,目前主要使用LCL(LCL, inductance capacitance inductance)型和LLCL(LLCL, inductance inductance capacitance inductance)型滤波器,其中LCL型滤波器在并网逆变器中具有更好的滤波性能与稳定性,而LLCL型滤波器更多时间用于单相并网逆变器[6-7]。但是,滤波器会给系统增加额外的体积和功率损耗。随后,又有学者提出了无电压传感器的控制策略,文献[8]采用基于积分谐振电流控制的电网电压估计器,可以在无电压传感器的情况下来重构电网电压。但系统中的LCL滤波器会增加额外的体积。文献[9]研究了基于模型预测控制的无电压传感器控制策略,但每个控制周期仅采用一个电压矢量作用,会产生较大电流谐波。在此基础上,文献[10]提出一种基于改进型滑模观测器的电网电压在线观测方法,以实现无电网电压传感器控制。但是,无电压传感器控制方法通常依赖于线路阻抗数据,而这些数据在并网系统中很难获得。
近些年,虚拟阻抗在并网逆变器的控制系统中得到了广泛应用,文献[11]介绍了目前虚拟阻抗的不同实现方式,对基于虚拟阻抗控制的逆变器进行了系统的总结。文献[12-13]分别从不同方面对虚拟阻抗技术进行全面的介绍,结合自适应虚拟阻抗这一研究热点,探讨了未来的研究趋势和可能遇到的关键问题。但是,很少有文献研究虚拟阻抗在消除接口阻抗和电压传感器方面的应用。
针对以上问题,在逆变器控制系统的基础上,提出了用虚拟接口阻抗代替接口阻抗以及移除电压传感器实现自同步的方法,解决了在启动过程中使用电流传感器进行同步的问题,仅使用虚拟电阻进行自同步的方法,用来降低dq-电流控制算法的计算复杂性。通过仿真和实验结果,验证了这些方法的稳定性和动态性能。
1 并网逆变器系统模型并网逆变器控制系统框图如图 1所示。逆变器的直流侧通常看作理想的直流电压源来提供电能[14]。图中,Vdc为直流母线电压,vI、i分别为逆变器的输出电压和电流,vs为传感点电压,RI、LI分别为接口阻抗的电阻和电感,RG、LG分别为线路上的电阻和电感,vG为电网电压,idq*为参考电流。
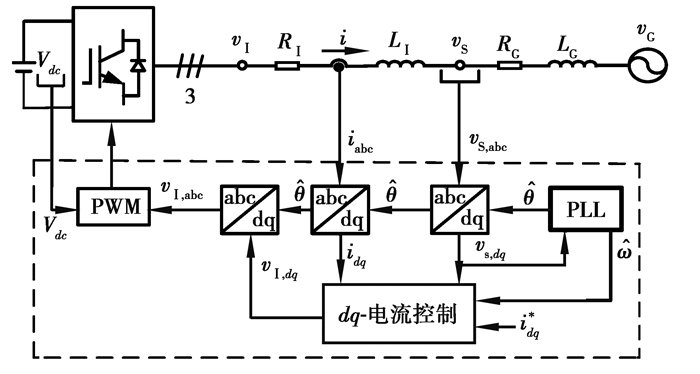
|
图 1 并网逆变器控制系统框图 Fig. 1 Grid-connected inverter control system |
根据图 1可知,逆变器输出电压表达式为
| $ v_{{\rm{I}}, \alpha \beta}=v_{Z_{\rm{I}}, \alpha \beta}+v_{\mathrm{S}, \alpha \beta}=R_{\rm{I}} i_{\alpha \beta}+L_{\rm{I}} \frac{\mathrm{d} i_{\alpha \beta}}{\mathrm{d} t}+v_{\mathrm{S}, \alpha \beta} 。$ | (1) |
经过Park变换之后,可得dq坐标系下的三相逆变器的输出电压方程:
| $ \left\{\begin{array}{l} v_{\mathrm{I}, d}=R_{\mathrm{I}} i_d+L_{\mathrm{I}} \frac{\mathrm{d} i_d}{\mathrm{~d} t}-\hat{\omega} L_{\mathrm{I}} i_q+v_{s, d}, \\ v_{\mathrm{I}, q}=R_{\mathrm{I}} i_q+L_{\mathrm{I}} \frac{\mathrm{d} i_q}{\mathrm{~d} t}+\hat{\omega} L_{\mathrm{I}} i_d+v_{s, q} 。\end{array}\right. $ | (2) |
虚拟阻抗可以模拟接口阻抗实现对并网逆变器的控制。如图 2所示,在电压型逆变器控制中,电流作为输入信号,获得虚拟阻抗ZVI上的压降,将逆变器的输出电压vI变为v′I,其表达式为
| $ v_{\mathrm{I}}^{\prime}=v_{\mathrm{I}}-Z_{\mathrm{VI}} i。$ | (3) |
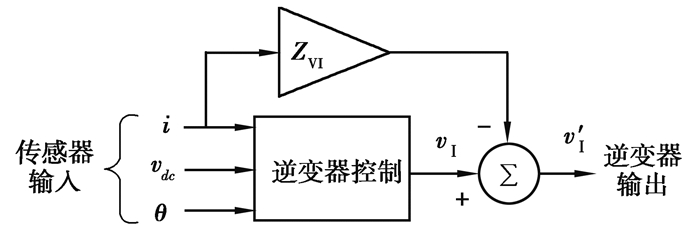
|
图 2 基于虚拟阻抗的逆变器控制框图 Fig. 2 Inverter control based on virtual impedance |
假设逆变器的实际输出电压vI中没有谐波,就可以用虚拟阻抗代替实际接口阻抗来产生压降。用逆变器的输出电压vI(由dq-电流控制计算)减去虚拟阻抗上的压降,生成新的输出电压v′I,并将该电压作为传感点电压,即vS=v′I。
实际上,逆变器受PWM (PWM, pulse width modulation)控制信号驱动会产生大量谐波。但是,PWM模块的输入是逆变器电压的基波分量,所以可以将输入信号当作传感电压,直接反馈到控制系统中。因此,笔者提出了基于虚拟阻抗的无电压传感器的并网逆变器控制方案,其控制框图如图 3所示。
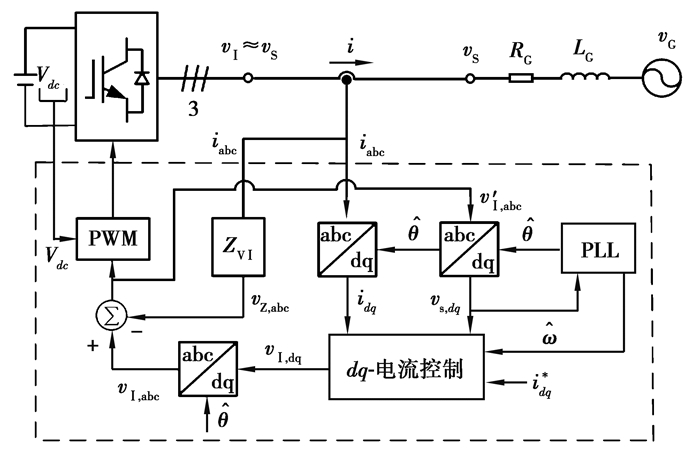
|
图 3 基于虚拟阻抗的无电压传感器的并网逆变器控制框图 Fig. 3 Virtual impedance-based control for grid-connected inverters without voltage sensors |
通过该控制方案,可以移除接口阻抗和电压传感器。但是,在没有电压传感器提供同步信号的情况下,逆变器在启动瞬间可能会产生同步问题。
为了解决逆变器启动同步问题,文中通过在逆变器交流侧的B相和C相之间接入电容CSU、开关SSU和电流传感器,形成闭合回路。其结构如图 4所示。
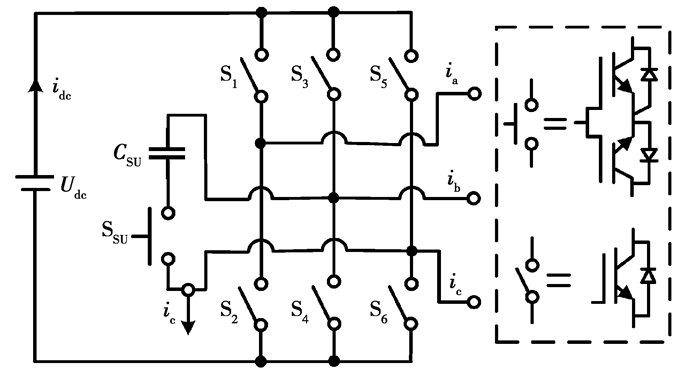
|
图 4 启动同步的电容负载结构图 Fig. 4 Structure diagram of capacitive load for start-up synchronization |
在逆变器启动过程中,开关闭合,将产生电容电流,通过电流传感器采样获得ic,可由单相锁相环获得与A相电压相同的相位。其原理如图 5所示。在同步后,开关SSU自动断开,逆变器控制部分开始产生PWM控制信号,同时启用自同步算法。
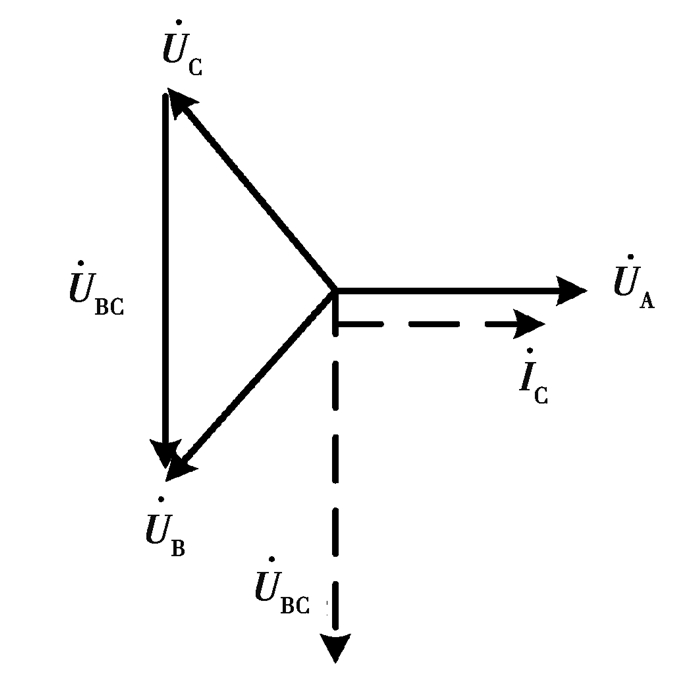
|
图 5 相位的变换原理 Fig. 5 Transformation principle of phase |
为了检测电网电压幅值,可以选择合适的电容CSU,来获得相应的电流,然后计算出电网电压幅值。假设相电流峰值Im (等于电容电流)可以限制在250 mA左右。那么在50 Hz的电网上产生峰值电流为250 mA,并且线电压有效值为380 V时,所需的电容值为1.48 μF,计算公式为
| $ C=\frac{\left|I_C\right|}{\omega\left|U_C\right|}=\frac{0.25}{(2 \pi 50)(380 \sqrt{2})} \approx 1.48 \text { 。} $ | (4) |
单相同步锁相环算法的控制框图如图 6所示[15]。一旦检测到电流幅值后,就可以通过式(4)计算出电压的幅值。
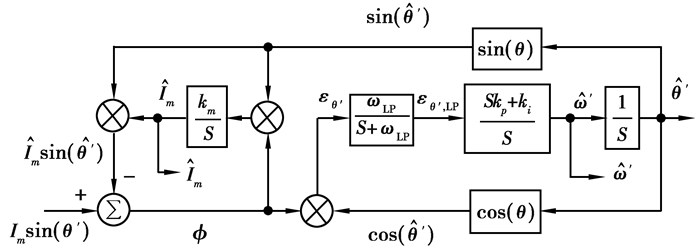
|
图 6 包含幅值检测的单相同步锁相环算法框图 Fig. 6 Single-phase synchronous phase-locked loop algorithm with amplitude detection |
由图 3可知,根据KVL定理,主电路的数学表达式:
| $ v_{\mathrm{S}, \alpha \beta}=v_{\mathrm{G}, \alpha \beta}+R_{\mathrm{G}} i_{\mathrm{G}, \alpha \beta}+L_{\mathrm{G}} \frac{\mathrm{d} i_{\mathrm{G}, \alpha \beta}}{\mathrm{d} t} 。$ | (5) |
经过park变换后,主电路在dq坐标系下的微分方程为
| $ \left\{\begin{array}{l} \frac{\mathrm{d} i_d}{\mathrm{~d} t}=\frac{1}{L_{\mathrm{G}}}\left[v_{\mathrm{S}, d}-R_{\mathrm{G}} i_d-v_{\mathrm{G}, d}-\hat{\omega} L_{\mathrm{G}} i_q\right], \\ \frac{\mathrm{d} i_q}{\mathrm{~d} t}=\frac{1}{L_{\mathrm{G}}}\left[v_{\mathrm{S}, q}-R_{\mathrm{G}} i_q-v_{\mathrm{G}, q}+\hat{\omega} L_{\mathrm{G}} i_d\right]。\end{array}\right. $ | (6) |
虚拟阻抗上的电压表达式为
| $ v_{\mathrm{ZVI}, \alpha \beta}=\left[R_{\mathrm{VI}}+s L_{\mathrm{VI}} \frac{\omega_{\mathrm{C}}}{s+\omega_{\mathrm{C}}}\right] i_{\alpha \beta}, $ | (7) |
式中,ωC为高通滤波器的截止频率。应用拉普拉斯变换的频移特性,经过park变换得式
| $ v_{\mathrm{ZVI}, d q}=R_{\mathrm{VI}} i_{d q}+L_{\mathrm{VI}}(s+j \hat{\omega}) i_{{d q}, \mathrm{LP}}, $ | (8) |
式中,再次引入了一个复杂的低通滤波器。为了适应该低通滤波器,定义附加变量idq, LP,来表示旋转坐标系下低通滤波器电流。使用此低通滤波器变量得
| $ v_{\mathrm{ZVI}, d q}=R_{\mathrm{VI}} i_{d q}+L_{\mathrm{VI}}(s+j \hat{\omega}) i_{d q, \mathrm{LP}}。$ | (9) |
低通滤波器的输入idq和输出idq, LP之间的关系为
| $ \left\{\begin{array}{l} \frac{\mathrm{d} i_{d, \mathrm{LP}}}{\mathrm{d} t}=\omega_{\mathrm{C}} i_d-\omega_{\mathrm{C}} i_{d, \mathrm{LP}}+\hat{\omega} i_{q, \mathrm{LP}}, \\ \frac{\mathrm{d} i_{q, \mathrm{LP}}}{\mathrm{d} t}=\omega_{\mathrm{C}} i_q-\omega_{\mathrm{C}} i_{q, \mathrm{LP}}-\hat{\omega} i_{d, \mathrm{LP} }。\end{array}\right. $ | (10) |
将式(10)代入到式(9)中,可以获得dq坐标系下虚拟阻抗电压的总表达式
| $ \left\{\begin{array}{l} v_{\mathrm{ZVI}, d}=R_{\mathrm{VI}} i_d+\omega_{\mathrm{C}} L_{\mathrm{VI}}\left(i_d-i_{d, \mathrm{LP}}\right), \\ v_{\mathrm{ZVI}, q}=R_{\mathrm{VI}} i_q+\omega_{\mathrm{C}} L_{\mathrm{VI}}\left(i_q-i_{q, \mathrm{LP}}\right)。\end{array}\right. $ | (11) |
对dq-电流控制中的PID控制器进行建模。从PI控制器开始,由于电流的积分产生电荷,可以定义2个变量Qd和Qq,分别表示电流误差信号εd和εq的积分。定义为
| $ \left\{\begin{array}{l} \frac{\mathrm{d} Q_d}{\mathrm{~d} t}=\varepsilon_d=i_d^*-i_d。\\ \frac{\mathrm{d} Q_q}{\mathrm{~d} t}=\varepsilon_q=i_q^*-i_{q }。\end{array}\right. $ | (12) |
由于无电压传感器的虚拟阻抗控制算法在控制环路中加入了少量的微分增益以保证稳定性,所以可以在建立的模型中使用高增益的高通滤波器来实现微分。定义2个变量,即电流误差信号的低通滤波值εd, LP和εq, LP为
| $ \left\{\begin{array}{l} \frac{\mathrm{d} \varepsilon_{d, \mathrm{LP}}}{\mathrm{d} t}=\omega_{\mathrm{D}}\left(\varepsilon_d-\varepsilon_{d, \mathrm{LP}}\right), \\ \frac{\mathrm{d} \varepsilon_{q, \mathrm{LP}}}{\mathrm{d} t}=\omega_{\mathrm{D}}\left(\varepsilon_q-\varepsilon_{q, \mathrm{LP}}\right), \end{array}\right. $ | (13) |
式中,ωD是高通滤波器的截止频率。PID控制器的微分项可以表示为
| $\frac{s \omega_{\mathrm{D}}}{s+\omega_{\mathrm{D}}} K_{d, \mathrm{c}} \varepsilon_{d q}=K_{d, \mathrm{c}} s \varepsilon_{d q, \mathrm{LP}}=K_{\mathrm{d}, \mathrm{c}} \omega_{\mathrm{D}}\left(\varepsilon_{\mathrm{dq}}-\varepsilon_{\mathrm{dq}, \mathrm{LP}}\right) 。$ | (14) |
将定义的变量代入式(3),可得简化后的逆变器输出电压
| $ \left\{\begin{array}{l} v_{I d}=\varepsilon_d k_{p, c}+Q_d k_{i, \mathrm{c}}+\left(\varepsilon_d-\varepsilon_{d, \mathrm{LP}}\right) \omega_{\mathrm{D}} k_{d, \mathrm{c}}-\hat{\omega} L_{\mathrm{I}} i_q+v_{\mathrm{s}, d}, \\ v_{\mathrm{I} q}=\varepsilon_q k_{p, c}+Q_q k_{i, \mathrm{c}}+\left(\varepsilon_q-\varepsilon_{q, \mathrm{LP}}\right) \omega_{\mathrm{D}} k_{d, c}+\hat{\omega} L_1 i_d+v_{\mathrm{s}, q} 。\end{array}\right. $ | (15) |
文中所用到的锁相环主要有单相锁相环和三相锁相环。对单相锁相环进行建模,定义变量εθ′, LP为低通滤波相角误差信号:
| $ \frac{\mathrm{d} \varepsilon_{\theta^{\prime}, \mathrm{LP}}}{\mathrm{d} t}=\omega_{\mathrm{D}}\left(\varepsilon_d-\varepsilon_{\theta^{\prime}, \mathrm{LP}}\right) 。$ | (16) |
定义变量δ来表示低通滤波相位误差信号的积分,对δ进行微分,可得单相锁相环的微分方程:
| $ \frac{\mathrm{d} \delta}{\mathrm{d} t}=\varepsilon_{\theta^{\prime}, \mathrm{LP}}=\frac{I_{\mathrm{m}}}{2}\left(\theta^{\prime}-\hat{\theta}^{\prime}\right)。$ | (17) |
根据以上定义,单相锁相环中PI控制器的输出估计频率
| $ \hat{\omega}^{\prime}=\left(k_{p, \theta^{\prime}} \varepsilon_\theta+k_{i, \theta^{\prime}} \int \varepsilon_{\theta^{\prime}, \mathrm{LP}} \mathrm{d} t\right)=\left(k_{p, \theta^{\prime}} \varepsilon_{\theta^{\prime}, \mathrm{LP}}+k_{i, \theta^{\prime}} \delta\right) 。$ | (18) |
对三相锁相环进行建模,定义一个变量γ,来表示相位误差的积分。对γ进行微分,可以得到三相锁相环的微分方程
| $ \frac{\mathrm{d} \gamma}{\mathrm{d} t}=\varepsilon_\theta=\frac{v_{\mathrm{S}, q}}{\sqrt{v_{\mathrm{S}, d}^2+v_{\mathrm{S}, q}^2}} 。$ | (19) |
根据以上定义,三相锁相环中PI控制器的输出估计频率
| $ \hat{\omega}=\left(k_{p, \theta} \varepsilon_\theta+k_{i, \theta} \int \varepsilon_\theta \mathrm{d} t\right)=\left(k_{p, \theta} \varepsilon_\theta+k_{i, \theta} \gamma\right) 。$ | (20) |
在前几小节中定义了附加状态变量之后,建立各个模块的代数方程,将各种值与状态变量联系起来,用式(6)、(10)、(12)、(13)、(19)组成一个微分方程组来表示逆变器系统。可知该系统是一个9阶的非线性动态系统。
为了验证该非线系统的稳定性,可以运用Lyapunov特征值估计法,通过系统在平衡状态下的雅克比矩阵的特征值来判断系统的稳定性。在平衡工作点处利用交流小信号线性化的方法对系统进行线性化处理,线性化后的系统可表示为
| $ \frac{\mathrm{d} \Delta \boldsymbol{x}}{\mathrm{d} t} \approx \boldsymbol{A} \Delta \boldsymbol{x}+\boldsymbol{B} \boldsymbol{u}, $ | (21) |
式中:矩阵A是雅可比矩阵;状态变量为
在平衡点处的雅可比矩阵A为:
| $ \boldsymbol{A}=\left[\begin{array}{ccccccccc} -\frac{\boldsymbol{R}_{\mathrm{G}}}{\boldsymbol{L}_{\mathrm{G}}} & -\hat{\omega} & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ -\hat{\omega} & -\frac{\boldsymbol{R}_{\mathrm{G}}}{\boldsymbol{L}_{\mathrm{G}}} & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \omega_{\mathrm{C}} & 0 & -\omega_{\mathrm{C}} & \hat{\omega} & 0 & 0 & 0 & 0 & 0 \\ 0 & \omega_{\mathrm{C}} & -\hat{\omega} & -\omega_{\mathrm{C}} & 0 & 0 & 0 & 0 & 0 \\ -1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & -\omega_{\mathrm{D}} & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & -\omega_{\mathrm{D}} & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{array}\right] 。$ | (22) |
求解该矩阵的特征值,可得所有特征值均满足Re(λi) < 0,即雅可比矩阵的特征值均在复平面的左半平面,满足有界输入有界输出稳定性的定义。因此,该系统具有很好的稳定性。
4 虚拟电阻简化电流控制为了降低虚拟电压计算的复杂性以及简化dq-电流控制,此处选择纯虚拟电阻。
简化的dq坐标系下的虚拟阻抗控制系统模型如图 7所示。dq-电流控制仍可通过PID控制器来完成,控制器中的微分项是确保稳定性所必须的。由于现在的虚拟阻抗只是一个电阻,因此动态也会发生变化。
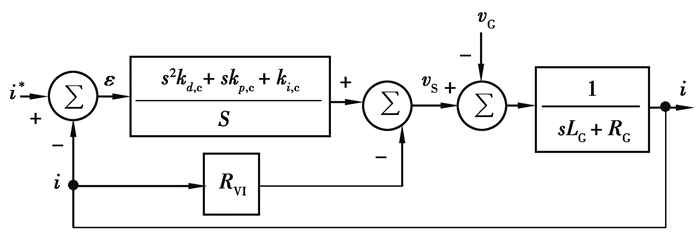
|
图 7 虚拟电阻控制算法的动态系统模型 Fig. 7 Dynamic system model of virtual resistance control algorithm |
在图 7中,感应点电压的正反馈回路已被简化,该系统的闭环传递函数为
| $ \frac{I(s)}{I^*(s)}=\frac{s^2 k_{d, c}+s k_{p, c}+k_{i, c}}{s^2\left(L_{\mathrm{G}}+k_{d, c}\right)+s\left(R_{\mathrm{G}}+R_{\mathrm{VI}}+k_{p, c}\right)+k_{i, c}} 。$ | (23) |
令分母多项式为零,得二阶系统的特征方程分:
| $ s^2\left(L_{\mathrm{G}}+k_{d, c}\right)+s\left(R_{\mathrm{G}}+R_{\mathrm{VI}}+k_{p, c}\right)+k_{i, c}=0 \text { 。} $ | (24) |
其2个根(系统的极点)为:
| $ s_{1, 2}=-\frac{\left(R_{\mathrm{G}}+R_{\mathrm{VI}}+k_{p, c}\right)}{2\left(L_{\mathrm{G}}+k_{d, c}\right)} \pm \sqrt{\frac{k_{i, c}}{L_{\mathrm{G}}+k_{d, c}}} \sqrt{\left(\frac{R_{\mathrm{G}}+R_{\mathrm{VI}}+k_{p, c}}{2 \sqrt{k_{i, c}\left(L_{\mathrm{G}}+k_{d, c}\right)}}\right)^2-1} 。$ | (25) |
上述二阶系统的特征根表达式中,阻尼比恒大于零,即特征根S1和S2均有负实部。因此,该系统具有一定的稳定性。
5 仿真与实验 5.1 仿真验证为了验证文中所提出的基于虚拟电阻自同步的无电压传感器控制策略,在Matlab/Simulink中建立了系统的仿真模型,如图 8所示。
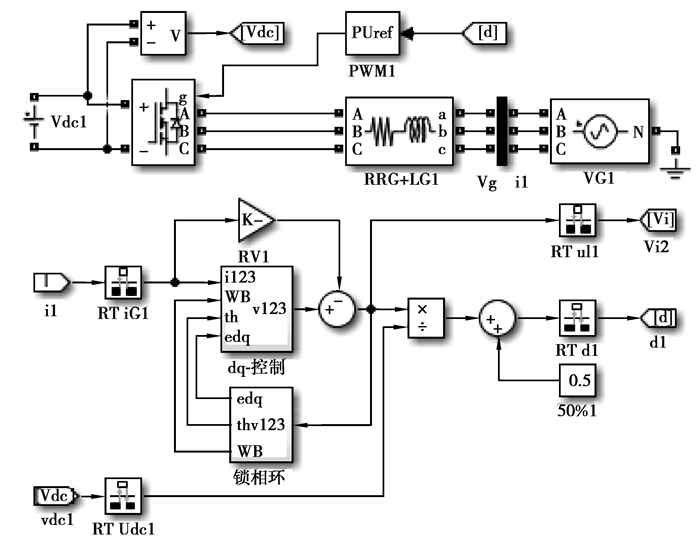
|
图 8 基于虚拟阻抗补偿的无电压传感器的并网逆变器仿真框图 Fig. 8 Simulation of grid-connected inverter without voltage sensor based on virtual impedance compensation |
仿真系统的参数如表 1所示。仿真中,电网相电压幅值(有效值为30 V)和逆变器直流母线电压幅值(100 V)均比正常值小。因为小电流可以增加阻抗对控制系统的影响。调整dq-控制的Tstl, c=50 ms,使电流过阻尼。同时,调整锁相环的Tstl, θ=100 ms,使其有一个临界阻尼。
| 表 1 虚拟电阻的仿真主电路参数 Table 1 Main circuit parameters of virtual resistors in simulation |
在仿真模型中分别施加3种不同的电网扰动。
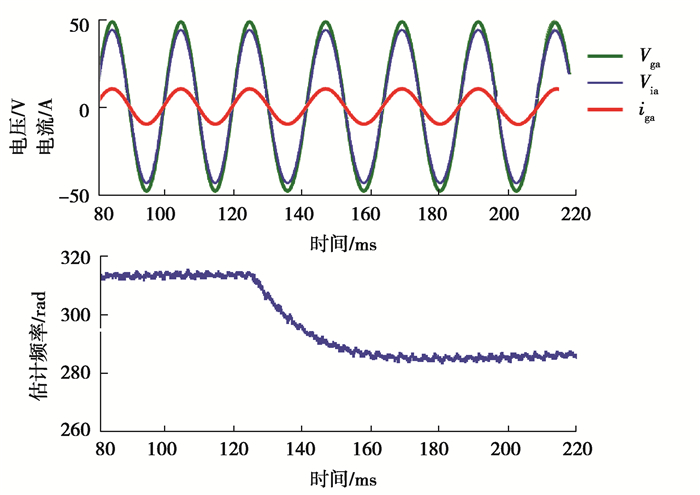
图 9显示了t = 125 ms时, 电网频率变化-5 Hz的仿真结果。
|
图 9 t = 125 ms时, 电网频率变化-5 Hz的仿真结果 Fig. 9 Simulation results for grid frequency change of -5 Hz at t = 125 ms |
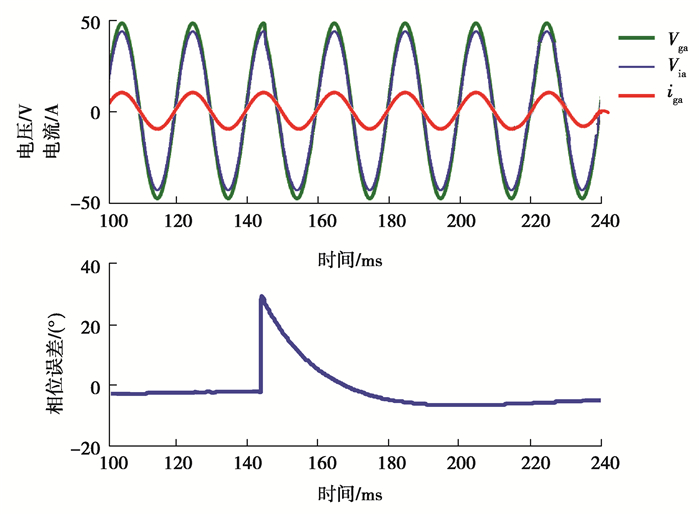
图 10显示了t = 145 ms时, 相角阶跃10%(36°)的仿真的结果。
|
图 10 t = 145 ms时, 相角阶跃10%(36°)的仿真的结果 Fig. 10 Results of the simulation with a phase angle step of 10% (36°) at t = 145 ms |
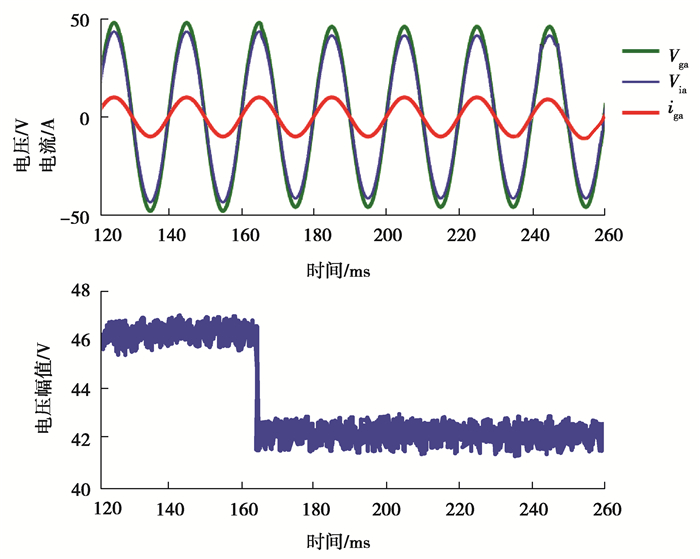
图 11显示了t = 165 ms时, 电网电压下降10% 的仿真的结果。
|
图 11 t = 165 ms时, 电网电压下降10% 的仿真的结果 Fig. 11 Results of the simulation for a 10% drop in grid voltage at t = 165 ms |
由仿真结果可知,在频率跳变和相位角跳变发生后,逆变器输出电压的相位就迅速发生变化,约90 ms后能跟踪电网电压相位,但相位差不能为零,这是因为电网阻抗ZG引起了相位延迟。当电网电压下降10% 后,由于虚拟电阻的响应非常迅速,电流能够得到很好的调节,所以会立即引起逆变器输出电压的幅值发生变化。这些结果表明控制系统具有一定的快速反应能力和高效性。
5.2 实验验证在仿真的基础上搭建了逆变器并网系统,来验证所提出的方案。实验平台如图 12所示,其中包括TDK-Lambda GEN 600-8.5直流电源,碳化硅三相逆变器,额定电流为50 A的1 mH接口电感,1210B -3型自耦变压器和横河DL850型隔离示波器。其中,电源、逆变器、电感器、自耦变压器、示波器以及笔记本电脑通过USB数据线与逆变器主控板连接,用作逆变器控制软件编译、下载和状态检测。5 V直流电源为逆变器的DSP主控板、门极驱动器电路、电流传感器和电压传感器供电。实验参数如表 1所示,与仿真参数保持一致。

|
图 12 虚拟电阻控制算法的实验台 Fig. 12 Experimental bench for virtual resistance control algorithm |
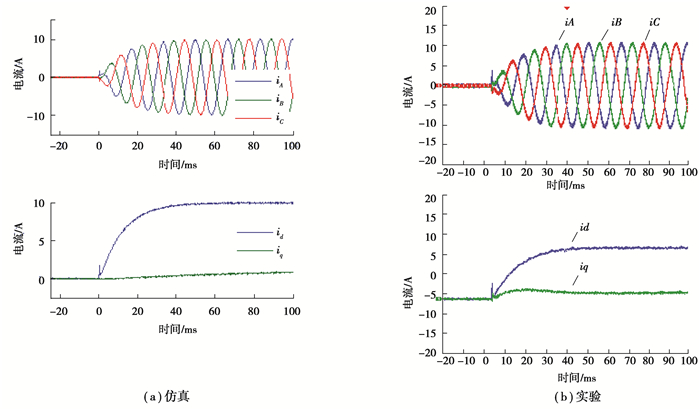
第一个实验是负载(d轴电流)的阶跃变化。将锁相环的PI控制器的系数修改为Kp, θ= 16和Ki, θ= 64,以降低锁相环的动态性能并使Tstl, θ= 500 ms。调节dq-电流控制,设置交流电流Tstl, c= 500 ms。仿真和实验结果如图 13所示,其中id和iq的波形是通过将DSP内实验数据通入计算机内获得。
|
图 13 负载电流阶跃变化的阻尼结果 Fig. 13 Damping results for step change of load current |
从图 13中可以发现,实验结果和仿真结果具有很好的一致性。实验电流的幅值存在一定的稳态误差,这主要是由电流传感器误差引起的。此外,在阶跃变化的瞬间,电流急剧上升,这是由于PID控制器的微分项所致。
在第一个实验参数的基础上,调节PID控制器积分参数和虚拟电阻值:Ki, c=100和RVI=0.1 Ω,以产生类似的电流沉降时间。检查负载电流的阶跃响应,仿真和实验结果对比如图 14所示。
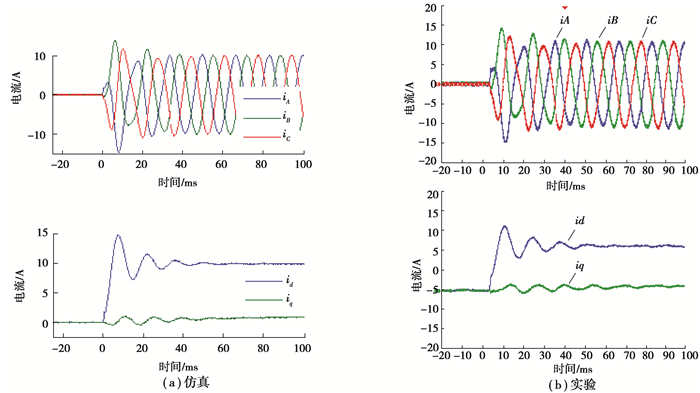
|
图 14 负载电流阶跃变化不足的结果 Fig. 14 Results of insufficient step change in load current |
从图 14中可以发现,实验结果和仿真结果仍具有很好的一致性。但是从图 13和图 14也可以发现,q轴电流不为零,是伴随着d轴电流的产生而出现的,存在稳态误差。这种误差是由于存在电网电感,在电网电压和感测点电压之间产生了相位偏移而引起的。
6 结论文中提出了基于虚拟阻抗的无电压传感器控制方法,进行逆变器并网。在理论分析的基础上,通过虚拟阻抗来获得电网同步信号,省去接口阻抗和交流电压传感器,从而降低了系统的成本、功耗和复杂性。此外,通过构建启动电路,为逆变器提供启动电流,并使用虚拟电阻实现了虚拟阻抗压降的计算,简化了dq-电流控制的计算过程。Matlab/simulink仿真和实验结果证实了运用所提出的方法使系统对电网参数变化具有很好的跟随特性,并且与有接口阻抗的实际系统具有相同的控制效果,达到了设计目的。
| [1] |
Liu J H, Zhou L, Li B, et al. Modeling and analysis of a digitally controlled grid-connected large-scale centralized PV system[J]. IEEE Transactions on Power Electronics, 2017, 33(5): 4000-4014. |
| [2] |
陈燕东. 微电网多逆变器控制关键技术研究[D]. 长沙: 湖南大学, 2014. Chen Y D. Research on the key techniques of multi-inverter control system in microgrid[D]. Changsha: Hunan University, 2014. (in Chinese) |
| [3] |
Boettcher M, Fuchs F W. Power electronic converters in wind energy system-Considerations of reliability and strategies for increasing availability[C]//Proceedings of the 201114th European Conference on Power Electronics and Applications. IEEE, 2011: 1-10.
|
| [4] |
李伟, 张勇军, 肖雄. 实时电感辨识的模型预测并网逆变器控制方法[J]. 电工技术学报, 2018, 33(15): 3450-3460. Li W, Zhang Y J, Xiao X. The model predictive grid-connected inverter control method based on real-time inductance identification[J]. Transactions of China Electrotechnical Society, 2018, 33(15): 3450-3460. (in Chinese) |
| [5] |
Parida N, Das A. A modular multilevel converter with filter capacitor for long-cable-fed drive application[J]. IEEE Transactions on Industry Applications, 2019, 55(6): 7833-7842. DOI:10.1109/TIA.2019.2931674 |
| [6] |
王杰. 多并网逆变器的交互影响分析与控制[D]. 重庆: 重庆大学, 2019. Wang J. Interaction analysis and control of the multipe grid-connected inverters[D]. Chongqing: Chongqing University, 2019. (in Chinese) |
| [7] |
许德志, 汪飞, 阮毅. LCL、LLCL和LLCCL滤波器无源阻尼分析[J]. 中国电机工程学报, 2015, 35(18): 4725-4735. Xu D Z, Wang F, Ruan Y. Passive damping of LCL, LLCL and LLCCL filters[J]. Proceedings of the CSEE, 2015, 35(18): 4725-4735. (in Chinese) |
| [8] |
Tran T V, Kim K H. Grid voltage estimation based on integral resonant current controller for LCL-filtered grid-connected inverter without AC voltage sensors[J]. Electronics, 2020, 9(12): 1-22. |
| [9] |
Yang H T, Zhang Y C, Liang J, et al. Sliding-mode observer based voltage-sensorless model predictive power control of PWM rectifier under unbalanced grid conditions[J]. IEEE Transactions on Industrial Electronics, 2018, 65(7): 5550-5560. DOI:10.1109/TIE.2017.2774730 |
| [10] |
郭磊磊, 金楠, 李琰琰, 等. 并网逆变器无电网电压传感器模型预测控制[J]. 电工技术学报, 2020, 35(12): 2612-2622. Guo L L, Jin N, Li Y Y, et al. Grid voltage sensorless model predictive control for grid-connected inverters[J]. Transactions of China Electrotechnical Society, 2020, 35(12): 2612-2622. (in Chinese) |
| [11] |
Wang X F, Li Y W, Blaabjerg F, et al. Virtual-impedance-based control for voltage-source and current-source converters[J]. IEEE Transactions on Power Electronics, 2015, 30(12): 7019-7037. DOI:10.1109/TPEL.2014.2382565 |
| [12] |
袁敞, 丛诗学, 徐衍会. 应用于微电网的并网逆变器虚拟阻抗控制技术综述[J]. 电力系统保护与控制, 2017, 45(9): 144-154. Yuan C, Cong S X, Xu Y H. Overview on grid-connected inverter virtual impedance technology for microgrid[J]. Power System Protection and Control, 2017, 45(9): 144-154. (in Chinese) |
| [13] |
温春雪, 黄耀智, 胡长斌, 等. 虚拟同步发电机接口变换器并联运行虚拟阻抗自适应控制[J]. 电工技术学报, 2020, 35(S2): 494-502. Wen C X, Huang Y Z, Hu C B, et al. Adaptive control of virtual impedance in parallel operation of virtual synchronous generator interface converter[J]. Transactions of China Electrotechnical Society, 2020, 35(S2): 494-502. (in Chinese) |
| [14] |
董焕宝. 低压微电网多源协调控制策略研究[D]. 沈阳: 沈阳工业大学, 2017. Dong H B. Research on multiple micro-source coordination control strategy of low voltage microgrid[D]. Shenyang: Shenyang University of Technology, 2017. (in Chinese) |
| [15] |
肖辅荣. 单相光伏并网逆变器的运行控制技术研究[D]. 北京: 北京理工大学, 2017. Xiao F R. Research on operational control of single-phase grid-connected inverter[D]. Beijing: Beijing Institute of Technology, 2017. (in Chinese) |
 2022, Vol. 45
2022, Vol. 45

