2. 重庆市轨道交通(集团)有限公司, 重庆 401120
2. Chongqing Rail Transit(Group) Co. Ltd., Chongqing 401120, P. R. China
近年来,在数字城市的推进下,中国的城市轨道交通行业高速发展。为了制定有效的管制措施、合理配置地铁运力、提高运营服务质量,需要准确、高效地对短时间内轨道交通客流量的变化进行预估,因此一个对短时间内客流的准确预测方法对于实现上述措施至关重要。
目前,对于城市轨道交通短时客流起讫点(origin-destination, OD)预测的研究仍在起步阶段[1]。已有的轨道交通短时客流预测方法一般分为参数模型和非参数模型。典型的参数模型中包括历史平均模型、回归分析方法[2]、贝叶斯方法[3]、时间序列模型和卡尔曼滤波模型[4-5]等。典型的非参数模型包括K最近邻算法[6-7]、支持向量机(support vector machine, SVM)模型[8]和神经网络[9]等。上述方法中,客流OD的短时预测通常被看作是时间序列预测的问题,神经网络具有识别复杂非线性系统的特性,因此比较适合用于短期交通流预测[10]。
轨道交通客流OD预测与交通流OD预测原理十分相似,因此很多交通流预测模型如车流量预测等都被用于轨道交通客流预测。Smith等[11]首次在短时交通流的预测研究中应用神经网络模型,通过与其他模型的比较证明了神经网络的良好效果。赵顗等[12]结合小波函数和BP神经网络模型对交通小区的生成交通进行分解后再预测,提高了交通小区生成交通短时预测精度。李洁等[13]提出了客流时间序列的分析和预测方法,构建了基于LSTM的客流预测模型,通过实验证明了该模型的预测性能较优。由于轨道交通尤其是轻轨地铁系统本质上是一个基于图的结构,且为非欧几里得图结构,借助于卷积神经网络对局部结构的建模能力及图上普遍存在的节点依赖关系,图卷积网络(graph convolutional networks, GCN)成为其中最活跃和最重要的一支[14]。陈喜群等[15]考虑路网拓扑结构和交通流时空相关性,提出基于图卷积网络的短时交通流预测模型,具有较高的预测精度,在预测性能上有较大提升。陈镇元等[16]提出一种基于图卷积神经网络的地铁客流预测模型,有效捕捉了地铁网络中复杂的空间依赖,提升了预测的精度。在短时交通客流预测方法中,单一模型适用情况不同,因此许多学者根据实际情况,选用多种单一模型组合使用,从而发挥各种预测方法的优点[17]。刘晓磊等[18]组合图卷积网络和循环神经网络构建了图卷积循环神经网络GCGRU模型;梁强生等[19]分析了短时客流在城市轨道交通网络中的空间关系,建立图卷积神经网络提取不同车站客流的空间交互关系,同时利用循环门控单元捕获客流的时间特征,进而较好地反映路网各车站客流的时空相关性。申慧涛等[20]采用残差神经网络构建新型的生成对抗网络的内部结构,提高了预测精度。以上研究表明了组合模型在轨道交通客流预测方向的优势。
基于此,笔者采用长短期记忆(long short-term memory, LSTM)和GCN建立混合深度学习模型,对连续时间间隔的重庆轻轨全网进出站客流量进行短时客流OD矩阵预测。模型聚焦于挖掘客流的时空特征,通过对基于出站口建立的OD矩阵分析,获取站点的时间相关性以及站点间的空间相关性,最后通过加权融合的方式来对重庆市轻轨的客流OD进行预测。
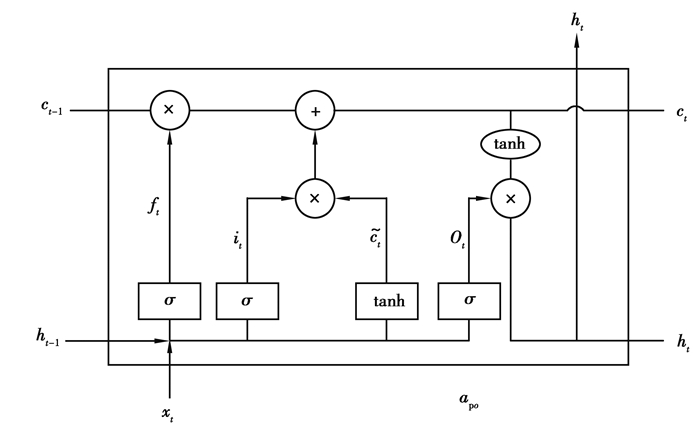
1 相关技术 1.1 长短期记忆网络在时间序列建模方面,LSTM作为一种特殊的循环神经网络(recurrent neural network, RNN)结构,在之前的各种研究[21-22]中已被证明对于时间序列的处理效果优秀,用于建模长期依赖关系。LSTM可以解决长序列训练过程中的梯度消失和梯度爆炸问题。LSTM由4部分构成,输入门、输出门、细胞状态和遗忘门。记忆单元负责记录历史数据中的有用信息,并将其传递到当前任务中;遗忘门则负责删除和遗忘部分信息,解决RNN存在的长期依赖问题。LSTM的结构见图 1所示,其计算过程如式(1)~式(6)所示。
|
图 1 LSTM的结构 Fig. 1 Structure of LSTM |
| $ f_t=\sigma_g\left(\boldsymbol{W}_f x_t+\boldsymbol{U}_f h_{t-1}+b_f\right), $ | (1) |
| $ i_t=\sigma_g\left(\boldsymbol{W}_i x_t+\boldsymbol{U}_i h_{t-1}+b_i\right), $ | (2) |
| $ o_t=\sigma_g\left(\boldsymbol{W}_o x_t+\boldsymbol{U}_o h_{t-1}+b_o\right), $ | (3) |
| $ \tilde{c}_t=\sigma_c\left(\boldsymbol{W}_c x_t+\boldsymbol{U}_c h_{t-1}+b_c\right), $ | (4) |
| $ c_t=f_t * c_{t-1}+i_t * \tilde{c}_t, $ | (5) |
| $ h_t=o_t * \sigma_h\left(c_t\right), $ | (6) |
式中:ft、xt、it、ot、ct、ht分别代表遗忘门、输入数据、输入门、输出门、记忆单元和隐藏状态;W、U是权重矩阵;b是需要在训练中学习的偏置项。初始状态c0=0,h0=0,并使用反向传播算法和优化函数来对参数进行优化,t代表第t个时间间隔。
1.2 图卷积网络GCN主要用于非欧式图结构数据的特征提取。图卷积网络的方法分为两类,分别是基于谱域的方法和基于空域的方法,笔者采用了基于谱域的方法。给定一个无向关系图G=(V, E, A),V表示顶点的合集,E为边的合集;A∈
在GCN网络中,每一个节点下一层的信息都由前一层本身的信息与相邻节点的信息加权求和,再对其进行线性变换和非线性变换得到[23]。令D代表邻接矩阵A中结点的度矩阵,对A进行归一化处理,其中
| $ H^{(l+1)}=\sigma\left(\hat{\boldsymbol{D}}^{-\frac{1}{2}} \hat{\boldsymbol{A}} \hat{\boldsymbol{D}}^{-\frac{1}{2}} H^{(l)} \boldsymbol{W}^{(l)}\right), $ | (7) |
GCN在图的拉普拉斯算子基础上对卷积神经网络对图的卷积运算进行进一步推广,在谱图卷积中使用对称归一化的拉普拉斯矩阵:
| $ \boldsymbol{L}=\boldsymbol{I}-\boldsymbol{D}^{-\frac{1}{2}} \boldsymbol{A} \boldsymbol{D}^{-\frac{1}{2}}。$ | (8) |
图的性质可以由图的拉普拉斯矩阵求得,对图的特征提取则可以等价为对图的拉普拉斯矩阵的特征提取。文中采用k阶切比雪夫多项式作为卷积核,减少参数,从全局卷积变为局部卷积,以降低计算的复杂度。
2 组合预测模型客流OD存在时序特征和空间相关特征[24]。通常站点之间的进出关系即客流出行[25], 客流OD可以看作矩阵时间序列,矩阵的每个元素都表现了单个站点与单个站点间的空间相关性,所有矩阵又表现了所有站点与自身相关的时间特征。根据划分时间长度将一天分为数个时间间隔,每一个时间间隔对应一个OD矩阵,矩阵的行和列代表当前时间间隔下站点与站点间的来往客流。由于行程可能不会覆盖每个时间间隔的所有OD对,因此产生的客流OD矩阵通常是稀疏矩阵[20],如何构建有效的客流OD矩阵与如何提取时间和空间特征是主要研究内容。
2.1 基于出站口的OD预测由于客流OD矩阵并非实时性获得,在某一时刻入站所采集到的AFC(automatic fare collection system)数据在给定的时间间隔内并不一定会完成此次出行得到出站的刷卡数据。但对于出站口,每一个出站所得到的刷卡数据则必定会有一个入站刷卡数据与之对应。文中所述客流OD矩阵是指一个基于整个路网结构和站点建立的矩阵。
给定一个路网,对于每一个站点都将其视作一个拓扑图的节点,则整个站点的集合用V={v1, v2, …, vN}来表示,集合内vi代表第i个站点,N表示站点数。将一整天分为m个时间间隔,令X表示客流OD矩阵,X∈
| $ \boldsymbol{X}_t=\left[\begin{array}{ccc} x_t(1, 1) & \cdots & x_t(1, n) \\ \vdots & & \vdots \\ x_t(n, 1) & \cdots & x_t(n, n) \end{array}\right], $ | (9) |
客流OD预测是指,在获得基于AFC数据得到的历史客流OD条件下,分析数据在时间和空间分布的特征,并对当前路网进行接下来一段时间间隔的客流OD预测。轨道交通客流OD预测的目标就是通过{XT-h, …, XT-2, XT-1}来对XT进行预测。其中h=T-1, …, 1,表示历史时间间隔数。
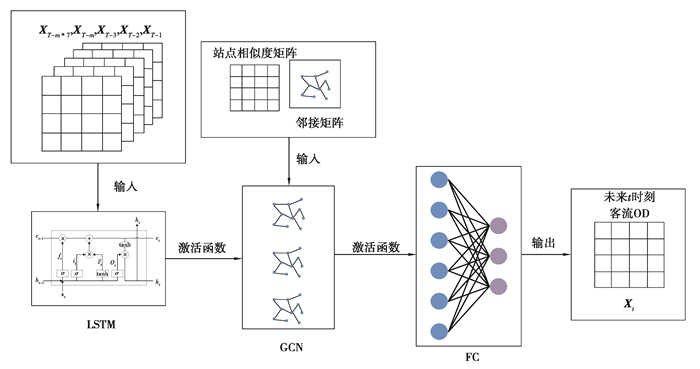
2.2 模型构建由于轨道交通客流OD出发地和目的地存在动态的相关性,且对时间、空间有很强的依赖性,普通的模型无法同时解决这2个问题。组合模型通过提取时间、空间位置关系对历史客流OD进行处理,来预测未来的客流OD。组合模型的结构如图 2所示,包含3个关键模块,分别为时间特征提取模块、空间特征提取模块和全连接模块。
|
图 2 模型结构 Fig. 2 Model architecture |
在时间提取模块中,文章采用单层的LSTM结构,将历史客流OD矩阵转化为序列作为输入;在空间特征提取模块,将LSTM的输出经过激活函数处理,并引入站点相似度矩阵和邻接矩阵进一步获取空间相关特征。文章采用3层GCN结构,如式(10)所示,
| $ f(X, A)=\sigma\left(\hat{A} \sigma\left(\hat{A} \sigma\left(\hat{A} X \theta_0\right) \theta_1\right) \theta_2\right), $ | (10) |
式中:θ0、θ1、θ2为3层卷积的权重矩阵;σ代表层与层之间的激活函数。
根据模型结构设计算法过程如下所示:
算法1:未来第T个时间间隔(即当天第t个时间间隔)客流OD预测。
输入:前一周的第t个时间间隔客流OD矩阵XT-m*7、前一天的第t个时间间隔客流OD矩阵XT-m、同一天前3个时间间隔客流OD矩阵XT-3、XT-2、XT-1、轨道交通路网邻接矩阵、相似度矩阵。
输出:第T个时间间隔客流OD。
步骤1 计算轨道交通路网邻接矩阵;
步骤2 计算不同时刻站点间相似度矩阵;
步骤3 将5个时刻的客流OD矩阵输入模型获取时间相关性;
步骤4 将邻接矩阵与该时刻相似度矩阵输入模型获取空间相关性;
步骤5 结果融合,得到T时刻客流矩阵。
在进行时间特征提取部分,笔者将基于出站口建立的OD矩阵作为输入数据,将每个OD对相关联的历史值作为一个单独的时间序列。为预测第k天的第t个时间段的客流OD,笔者使用第k天的第t-3、t-2、t-1这3个时间段的客流OD,以及第k-1天的第t个时间段和第k-7天的第t个时间段的客流OD输入LSTM模型中,即最近前3个时间间隔数据、一天前的同一时间数据、一周前的同一时间数据。使用LSTM模块来获取的时间特征,最终将作为GCN第0层的隐藏向量。在空间特征提取部分历史客流OD数据由地铁网络得到的表明真实地理信息的邻接图以及每一个时间间隔中站点与站点间的相似性矩阵来进行计算,通过GCN来获取客流OD的空间相关性。根据每一个站点的分布,结合客流OD来形成一个张量。模型中的邻接图由真实地理位置信息得到,即站点与站点之间的邻接关系生成的邻接图,是一个固定的静态图;站点相似度矩阵反映了站点与站点之间的动态相关性,由不同时刻的站点与站点之间的客流OD矩阵决定并根据历史客流OD采用余弦相似度进行计算,数值越大,相似度越高。
这5个时间段的历史客流OD矩阵使用LSTM获取时间相关性,并作为GCN第0层的输入信息,再使用GCN分别对由站点的邻接矩阵构成的静态图和由客流OD构成的动态图进行空间特征的提取,使用平均策略对上述2个结果进行融合来获得更好的结果。
3 实验结果 3.1 数据集来源数据来源于重庆市轨道交通的AFC数据。乘客刷卡进出站时都会生成一条AFC数据,数据中记录了卡ID、刷卡时间、刷卡站点、刷卡事件、数据上传时间。文章采用了2018年10月份31天的重庆轻轨AFC数据来进行模型的训练和预测。系统所采集刷卡记录有105 065 115次,所采集内容有票卡号、交易日期、交易时间、票卡种类、交易事件、交易车站、交易前余额、交易金额、交易后余额、联程交易、卡计数器、设备编号、数据接收时间。关键信息如表 1所示。
| 表 1 AFC数据样例 Table 1 AFC data sample |
按照运营时间,将刷卡时间在6:30前和23:30后的数据去掉,去除工作人员的刷卡记录,只保留票卡号、交易日期、交易时间、交易事件、交易车站,以此生成完整的客流数据,基于出站口,时间间隔为15 min来建立客流OD矩阵。
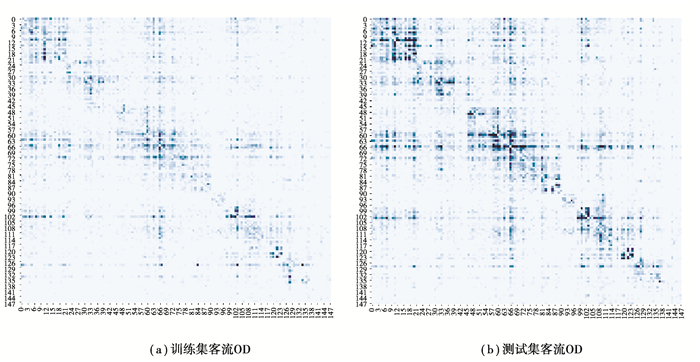
在2018年10月重庆的轻轨站点总共有148个站点,根据站点与站点间的邻接关系建立邻接矩阵。由于国庆节7天假期导致客流并不规律,在这里采用第2周开始到第4周这3周数据,并将数据集分为两部分:前2周作为训练集,最后1周作为测试集。训练集与测试集的OD矩阵以热力图可视化后分别如图 3所示。其中横纵坐标分别对应2018年10月重庆轨道交通路网148个站点的编号,横纵坐标交错位置为由横坐标代表站点去向纵坐标代表站点的客流数量,客流人数越多,颜色越深,在同一站点进出的记录被视为无效记录,对角线位置全部用“0”替代。
|
图 3 训练集与测试集的OD矩阵相关热力图 Fig. 3 Heat map of train set and test set of passenger flow OD |
为评价预测结果的性能,笔者采用均方根误差(root mean square error, RMSE)和平均绝对误差(mean square error, MAE)来进行模型的性能评价。
| $ R_{\text {RMSE }}\left(X_t, \hat{\boldsymbol{X}}_t\right)=\frac{1}{N} \sqrt{\sum_{i=1}^N \sum_{j=1}^N\left(x_{i j}-\hat{x}_{i j}\right)^2}, $ | (11) |
| $ R_{\mathrm{MAE}}=\frac{1}{N^2} \sum_{i=1}^N \sum_{j=1}^N\left|x_{i j}-\hat{x}_{i j}\right|, $ | (12) |
式中:xij是矩阵Xt的第i行第j列个元素,代表第t个时间间隔的真实客流量;
实验采用切比雪夫多项式作为GCN卷积核形式,使用ReLU作为激活函数;在训练模型中,采用Adam优化函数,训练次数设置为200,学习率设置为0.000 1。
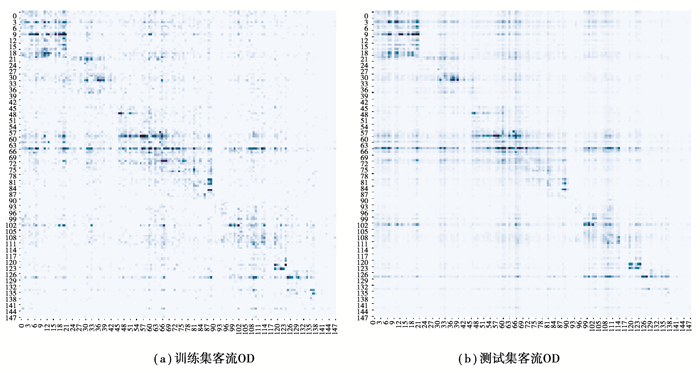
3.4 预测结果分析对于组合模型的预测结果,取同一天的同一个时间间隔的真实值与模型预测值热力图进行对比,如图 4所示。
|
图 4 模型预测值与真实值相关热力图 Fig. 4 Heat map of true value and model predietion of passenger flow OD |
图 4(a)表明了客流OD在10月28日22:15~22:30的真实值,图 4(b)表明了客流OD在同一时刻的模型预测值,其中横纵坐标意义与图 3一致,颜色越深表明从该行代表的站点到该列代表的站点之间的客流量越大,反之越少。从图 4可以看出预测值与真实值之间虽然存在误差,但整体预测效果良好。
针对重庆轻轨交通客流OD数据集,将组合模型预测结果与GCGRU[26]和基于LSTM模型预测的结果对比分析。这3种方法对客流OD的预测误差如表 2所示。
| 表 2 模型短时预测结果对比 Table 2 Comparison of short-term forecast of models |
文中的组合模型的平均绝对误差为1.37,均方根误差为3.43;GCGRU组合模型的平均绝对误差为1.47,均方根误差为3.94;而基于LSTM神经网络的预测模型平均绝对误差为1.49,均方根误差为4.61。可以看出,组合模型结果优于LSTM模型,主要由于深度学习模型有较强的拟合能力。对于轨道交通的客流OD预测,文中组合模型效果也优于GCGRU模型。文中组合模型既可以获取在时间维度上的长时间依赖性,又可以捕获源、目的地之间的依赖关系,根据站点与站点间的空间分布来捕获动态客流流动规律。
4 结束语笔者研究了轨道交通客流OD预测问题的时间、空间依赖关系,通过改进客流OD的处理方式,即基于每一个出站口对客流进行入站口的统计,并使用基于LSTM和GCN的组合模型来对轻轨地铁客流OD进行预测,其中LSTM用于获取交通客流的时间相关性,而GCN则用来提取交通客流的空间位置相关性,经过模型训练后得到预测的结果。为检验模型的预测效果,笔者采用了基于LSTM神经网络的模型和GCGRU作为对比模型,采集实际的轨道交通客流量,以RMSE和MAE作为评价指标,通过实验比较本文模型和其他模型的预测精度。实验表明,基于LSTM和GCN的组合预测模型的精度要优于单独的LSTM神经网络预测模型和GCGRU模型,说明文中构建的预测模型有效。
| [1] |
侯晓云, 邵丽萍, 李静, 等. 基于深度学习的城市轨道交通短时客流起讫点预测[J]. 城市轨道交通研究, 2020, 23(1): 55-58, 115. Hou X Y, Shao L P, Li J, et al. Urban rail transit short-time passenger flow OD forecasting based on deep learning modeling[J]. Urban Mass Transit, 2020, 23(1): 55-58, 115. (in Chinese) |
| [2] |
唐继强, 钟鑫伟, 刘健, 等. 基于时间序列季节分类模型的轨道交通客流短期预测[J]. 重庆交通大学学报(自然科学版), 2021, 40(7): 31-38, 60. Tang J Q, Zhong X W, Liu J, et al. Short term forecast of rail transit passenger flow based on time series seasonal classification model[J]. Journal of Chongqing Jiaotong University (Natural Science), 2021, 40(7): 31-38, 60. (in Chinese) |
| [3] |
Perrakis K, Karlis D, Cools M, et al. A Bayesian approach for modeling origin-destination matrices[J]. Transportation Research Part A: Policy and Practice, 2012, 46(1): 200-212. DOI:10.1016/j.tra.2011.06.005 |
| [4] |
姚向明, 赵鹏, 禹丹丹. 城市轨道交通网络短时客流OD估计模型[J]. 交通运输系统工程与信息, 2015, 15(2): 149-155, 162. Yao X M, Zhao P, Yu D D. Short-time passenger flow origin-destination estimation model for urban rail transit network[J]. Journal of Transportation Systems Engineering and Information Technology, 2015, 15(2): 149-155, 162. (in Chinese) |
| [5] |
Kumar S V. Traffic flow prediction using Kalman filtering technique[J]. Procedia Engineering, 2017, 187: 582-587. DOI:10.1016/j.proeng.2017.04.417 |
| [6] |
Cai P L, Wang Y P, Lu G Q, et al. A spatiotemporal correlative k-nearest neighbor model for short-term traffic multistep forecasting[J]. Transportation Research Part C: Emerging Technologies, 2016, 62: 21-34. DOI:10.1016/j.trc.2015.11.002 |
| [7] |
方琴, 李永前. K近邻短期交通流预测[J]. 重庆交通大学学报(自然科学版), 2012, 31(4): 828-831. Fang Q, Li Y Q. On K-nearest neighbor short-term traffic flow prediction[J]. Journal of Chongqing Jiaotong University (Natural Science), 2012, 31(4): 828-831. (in Chinese) |
| [8] |
傅贵, 韩国强, 逯峰, 等. 基于支持向量机回归的短时交通流预测模型[J]. 华南理工大学学报(自然科学版), 2013, 41(9): 71-76. Fu G, Han G Q, Lu F, et al. Short-term traffic flow forecasting model based on support vector machine regression[J]. Journal of South China University of Technology (Natural Science Edition), 2013, 41(9): 71-76. (in Chinese) |
| [9] |
Liyanage S, Abduljabbar R, Dia H, et al. AI-based neural network models for bus passenger demand forecasting using smart card data[J]. Journal of Urban Management, 2022, 11(3): 365-380. |
| [10] |
吴慰. 短时交通流预测的PSO-PLS组合预测模型研究[D]. 重庆: 重庆大学, 2009. Wu W. Study on PSO-PLS combined forecasting model for short-term traffic flow forecasting[D]. Chongqing: Chongqing University, 2009. (in Chinese) |
| [11] |
Smith B L, Demetsky M J. Short-term traffic flow prediction: neural network approach[J]. Transportation Research Record, 1994, 1453(1453): 98-104. |
| [12] |
赵顗, 沈玲宏, 马健霄, 等. 综合小波分解和BP神经网络的交通小区生成交通短时预测[J]. 重庆交通大学学报(自然科学版), 2021, 40(11): 60-66. Zhao Y, Shen L H, Ma J X, et al. Traffic short-term prediction generated by wavelet decomposition and BP neural network of traffic zone[J]. Journal of Chongqing Jiaotong University (Natural Science), 2021, 40(11): 60-66. (in Chinese) |
| [13] |
李洁, 彭其渊, 文超. 基于LSTM深度神经网络的高速铁路短期客流预测研究[J]. 系统工程理论与实践, 2021, 41(10): 2669-2682. Li J, Peng Q Y, Wen C. Short term passenger flow prediction of high speed railway based on LSTM deep neural network[J]. Systems Engineering-Theory & Practice, 2021, 41(10): 2669-2682. (in Chinese) |
| [14] |
徐冰冰, 岑科廷, 黄俊杰, 等. 图卷积神经网络综述[J]. 计算机学报, 2020, 43(5): 755-780. Xu B B, Cen K T, Huang J J, et al. A survey on graph convolutional neural network[J]. Chinese Journal of Computers, 2020, 43(5): 755-780. (in Chinese) |
| [15] |
陈喜群, 周凌霄, 曹震. 基于图卷积网络的路网短时交通流预测研究[J]. 交通运输系统工程与信息, 2020, 20(4): 49-55. Chen X Q, Zhou L X, Cao Z. Short-term network-wide traffic prediction based on graph convolutional network[J]. Journal of Transportation Systems Engineering and Information Technology, 2020, 20(4): 49-55. (in Chinese) |
| [16] |
陈镇元. 基于图卷积神经网络的地铁客流预测方法[J]. 科学技术创新, 2021(3): 88-89. Chen Z Y. Subway passenger flow forecasting method based on graph convolution neural network[J]. Scientific and Technological Innovation, 2021(3): 88-89. (in Chinese) |
| [17] |
雷斌, 张源, 郝亚睿, 等. 城市轨道交通短期客流预测研究进展[J]. 长安大学学报(自然科学版), 2022, 42(1): 79-96. Lei B, Zhang Y, Hao Y R, et al. Research progress on short-term passenger flow forecast model of urban rail transit[J]. Journal of Chang'an University (Natural Science Edition), 2022, 42(1): 79-96. (in Chinese) |
| [18] |
刘晓磊, 段征宇, 余庆, 等. 基于图卷积循环神经网络的城市轨道客流预测[J]. 华南理工大学学报(自然科学版), 2022, 50(3): 21-27. Liu X L, Duan Z Y, Yu Q, et al. Passenger flow forecast of urban rail transit based on graph convolution and recurrent neural network[J]. Journal of South China University of Technology (Natural Science Edition), 2022, 50(3): 21-27. (in Chinese) |
| [19] |
梁强升, 许心越, 刘利强. 面向数据驱动的城市轨道交通短时客流预测模型[J]. 中国铁道科学, 2020, 41(4): 153-162. Liang Q S, Xu X Y, Liu L Q. Data-driven short-term passenger flow prediction model for urban rail transit[J]. China Railway Science, 2020, 41(4): 153-162. (in Chinese) |
| [20] |
申慧涛, 郑亮, 李树凯, 等. 基于生成对抗网络的地铁OD需求短时预测[J]. 铁道科学与工程学报, 2022, 19(6): 1530-1539. Shen H T, Zheng L, Li S K, et al. Short-term urban metro OD demand prediction with a Generative Adversarial Network[J]. Journal of Railway Science and Engineering, 2022, 19(6): 1530-1539. (in Chinese) |
| [21] |
Sutskever I, Vinyals O, Le Q V. Sequence to sequence learning with neural networks[EB/OL]. [2022-01-01]. https://doi.org/10.48550/arXiv.1409.3215.
|
| [22] |
Sun R, Giles C L. Sequence learning: from recognition and prediction to sequential decision making[J]. IEEE Intelligent Systems, 2001, 16(4): 67-70. |
| [23] |
Kipf T N, Welling M. Semi-supervised classification with graph convolutional networks[EB/OL]. [2021-01-01]. https://doi.org/10.48550/arXiv.1609.02907.
|
| [24] |
林友芳, 尹康, 党毅, 等. 基于时空LSTM的OD客运需求预测[J]. 北京交通大学学报, 2019, 43(1): 114-121. Lin Y F, Yin K, Dang Y, et al. Spatio-temporal LSTM for OD passenger demand prediction[J]. Journal of Beijing Jiaotong University, 2019, 43(1): 114-121. (in Chinese) |
| [25] |
张建旭, 宾科, 蒋雨洋. 考虑轨道出行时空分布的断面客流预测[J]. 重庆理工大学学报: 自然科学, 2022, 36(6): 164-171. Zhang J X, Bin K, Jiang Y Y. Cross-section passenger flow prediction considering the temporal and spatial distribution of rail travel[J]. Journal of Chongqing University of Technology: Natural Science, 2022, 36(6): 164-171. (in Chinese) |
| [26] |
Hu J L, Yang B, Guo C J, et al. Stochastic origin-destination matrix forecasting using dual-stage graph convolutional, recurrent neural networks[C]//2020 IEEE 36th International Conference on Data Engineering. IEEE, 2020: 1417-1428.
|
 2022, Vol. 45
2022, Vol. 45

