随着中国低空空域通航逐渐开放,通航活动越来越频繁,通航(通用航空)运行事故率不断增加。对通航事故机理分析,找出事故诱因间的耦合关系,避免事故链的形成,对于提升通航安全运行保障能力具有重要意义。对事故原因调查中发现,事故发生的诱因分为4类,人的不安全行为、机器的不安全状态、环境的不安全因素以及管理失误。这4种状态之间又会相互碰撞耦合,加大航空事故形成的概率[1],所以,对通航事故诱因预测显得尤为重要。
国内外学者对通航的事故诱因调查与分析做出了很多研究。王春林在2011年基础性地分析了通航运行现状、特点和制约安全运行因素,为通航事故成因的调查奠定了基础[2];陈勇刚于2012年开创性地构建了符合中国通航公司运行现状的安全管理体系,为通航事故成因的分析提供了理论支持[3];Shyur和Huan-Jyh于2008年第一次运用事故和安全指标的数据来量化由人为错误所造成的航空风险,为通航事故的调查提供依据[4]。
通航事故的发生是一种或多种诱因耦合震荡共同作用的结果,该过程较为复杂。模糊认知图可以将系统内部复杂的关系以图的形式展示出来,便于分析研究,因此,使用模糊认知图对通航事故成因进行分析与研究[5-9]。通过对中国2006—2015年10年间所发生的通航事故进行详细地调查与分析,对通航事故影响因素进行了统计与分类,根据事故诱因的基本关系,建立模糊认知图预测模型。结合关联度的分析计算[10-11],各个诱因间的事故关联度,得出导致通航事故的主要诱因。这在一定程度上为预防通航事故的发生奠定了理论基础,减少了事故发生的概率,进一步保障人员的生命和财产安全。
1 影响通航安全要素分析通航事故的发生是一个复杂过程,对事故诱因的预测要从人—机—环—管共同作用的大系统出发。其中,人是指飞行机组人员、航务人员机务人员和后勤保障人员等;机是指在通航运行的过程中所涉及到所有机械设备,包括航空器、签派放行系统及空管指挥系统等;环是指自然环境,工作环境和人文环境等;管是指在通航运行过程中与之相关的培训方案、制度管理与政策法规等[12-13]。通航事故的形成过程是复杂的,在对其事故诱因进行分类研究的同时,分析通航事故发生的主要诱因有哪些,根据这些主要影响因素之间的关联关系挖掘出是哪一个诱因或哪几个诱因相互作用而引发通航事故及事故与这些诱因之间关联度的强弱。模糊认知图是根据事故中不同诱因之间的关联关系,结合专家经验进行修正并推理,从而预测通航事故成因。
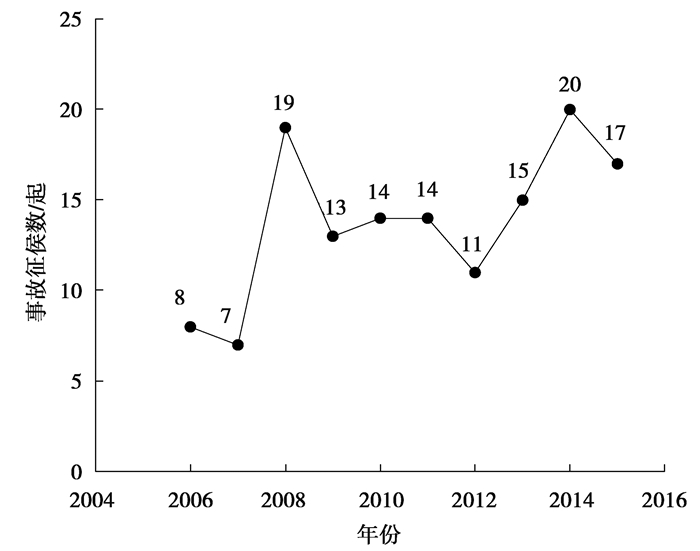
研究对影响通航安全因素的分类和研究主要是依据2006—2015年通航事故统计报告进行分析的。图 1是按照年份给出了2006—2015年通航事故的统计情况。
|
图 1 通航事故的统计情况 Fig. 1 Statistics of general aviation accidents |
对通航事故进行统计分析之后发现,事故诱因可以划分为“人的因素”、“机械因素”、“环境因素”、“管理因素”和一些原因不明的因素,称之为“不明因素”,在这些因素的分类中,其中“人的因素”包括人员的操作失误、专业技术水平较低、飞行前准备不充分、训练程度不成熟等;而“机械因素”包括发动机故障、油门失效、起落架故障、通讯设施故障、机械结构设计不完善等;“环境因素”包括鸟击、恶劣天气、地形复杂等;而“管理因素”主要包括人员培训制度不完善、规章制度不健全、应急预案不充分等[12]。此外,对于一些事故原因不明确的未知情况,将其列为“不明因素”。
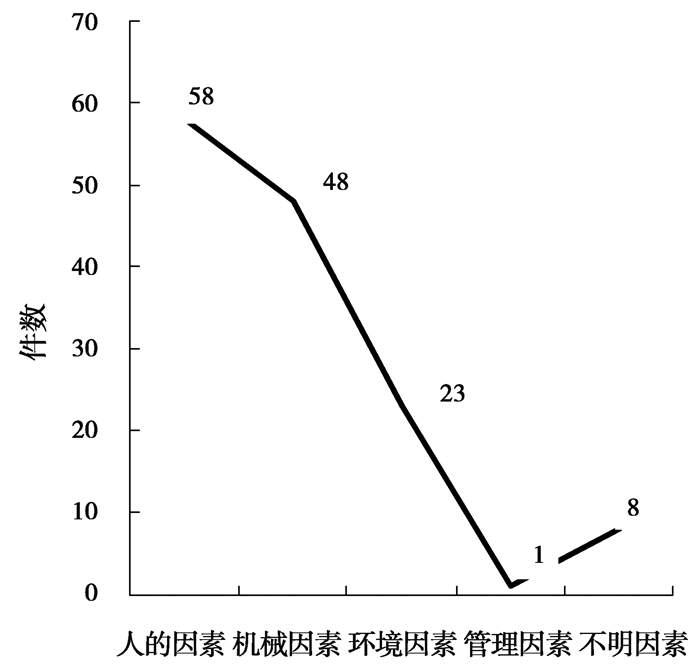
根据以上对于通航事故发生的因素的划分原则,对2006—2015年所发生的138起通航事故进行统计,得到了不同诱因导致的通航事故数量和所占的比例。从下图 2可以看出:这些事故中,由于“人的因素”所引起的事故数为58起,占所有事故数的42%;由于“机械因素”所引起的事故数为48起,占34.8%;由于“环境因素”所引起的事故数为23起,占16.67%;由“管理因素”所引起的事故数为1起,占0.72%;剩余的由“不明因素”所引起的事故数有8起,占5.8%,具体的事故诱因分布表见图 2。
|
图 2 不同诱因导致事故的统计 Fig. 2 Statistics of accidents caused by different inducements |
模糊认知图是由Kosko于1986年在Axelord的认知图基础上,将Zadeh的模糊集理论引入到认知图理论中提出的[7]。模糊认知图是将不同因子间的复杂关联关系以图形的方式展现出来。具体则是利用图形中的节点与有向弧将概念或事务间的关联关系表示出来,从而将系统的复杂动态行为量化,实现较高置信度的预测功能[13]。
模糊认知图的原理如下,即可以用四元组U=(A, E, X, Y)来表示,其中:A={A1, …, An}是模糊认知图中的所有概念集合;E(A×A)=(qij)n×n是模糊认知图的权重矩阵,(Ai,Aj)→qij是一个映射,其中qij∈ E, Ai, Aj∈A, qij是表示从概念Ai到概念Aj的关联关系程度;X:表示节点Ai在某一时刻的状态为xi,X(t)=[x1(t), x2(t), …xn(t)]T表示模糊认知图G在t时刻的状态,根据模糊认知图的推理预测方法,系统在下一时刻的状态可以表示为
| x(t+1)=WxT(t), | (1) |
若模糊认知图中含有n个节点,给出一个阈值函数f(x),每个节点在t+1时刻的值可用下式进行计算
| xi(t+1)=f([∑nxj(t)ωij]), | (2) |
确保所有迭代的节点值都处于[-1, 1]范围内。
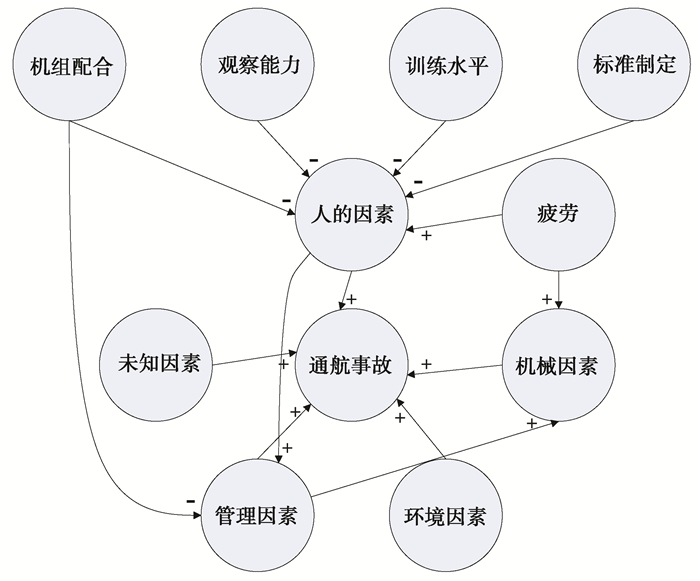
3 预测通航事故主要诱因对可能诱发通航事故形成的因素进行分析,建立事故诱因的预测模型,期望在事故形成前将诱导因素剔除,起到事故预防的作用。在对危险因素进行识别的基础上,可预先采取措施,控制事故的发生,尽可能降低事故发生的概率。因此,可以在通航事故的诱因统计及分类的基础上,将“通航事故”作为因变量,“人的因素”、“机械因素”、“环境因素”、“管理因素”和“不明因素”作为自变量,另外还包括一些其他的因素,如“机组配合”、“观察能力”、“训练水平”、“标准制定”、“疲劳”等因素都可能直接或间接对因变量产生影响,因此,这些因素被定义为随机变量。构建出通航事故诱因预测的模糊认知图如图 3所示。
|
图 3 模糊认知图模型 Fig. 3 Fuzzy cognitive model |
在上述模型中,可以看到3类节点因变量结果的节点,自变量原因的节点和随机变量事件的节点。表 1表示在通航事故诱因预测的模糊认知图模型各个节点的概念及其所对应的具体含义,所以,通航事故诱因预测模型的状态向量可以表示为
| A=[A1,A2,A3,A4,A5,A6,⋮c1,c2,c3,c4,c5,]。 | (3) |
| 表 1 各个节点的概念与具体含义 Table 1 Concept and specific meaning of each node |
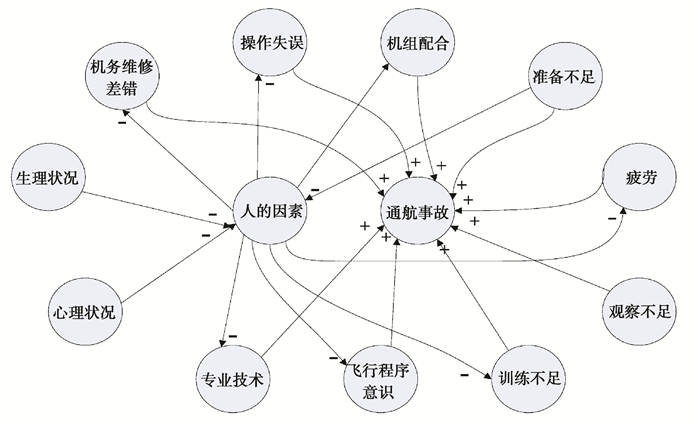
通航运行系统较为复杂,通常情况下人的心理状况较差、生理状况较差、专业技术能力较低、训练程度不足、观察能力较弱等人的因素均会不同程度引发通航事故;而动力系统故障、油门失效、起落架故障、通讯故障等机械因素同样也会引发通航事故[12-14]。因此,需要进一步将图 3中的“人的因素”和“机械因素”进一步划分,建立如图 4和图 5所示模型。这样构建出的模型可以将通航事故诱因追究到最终,更有利于分析得出通航的事故主要诱因及诱因间的关联关系,这为减少通航的事故发生奠定了强有力的保障基础,这是进行通航事故主要诱因预测的目的。
|
图 4 “人的因素”构造的模型 Fig. 4 "Human Factors" Construction Model |
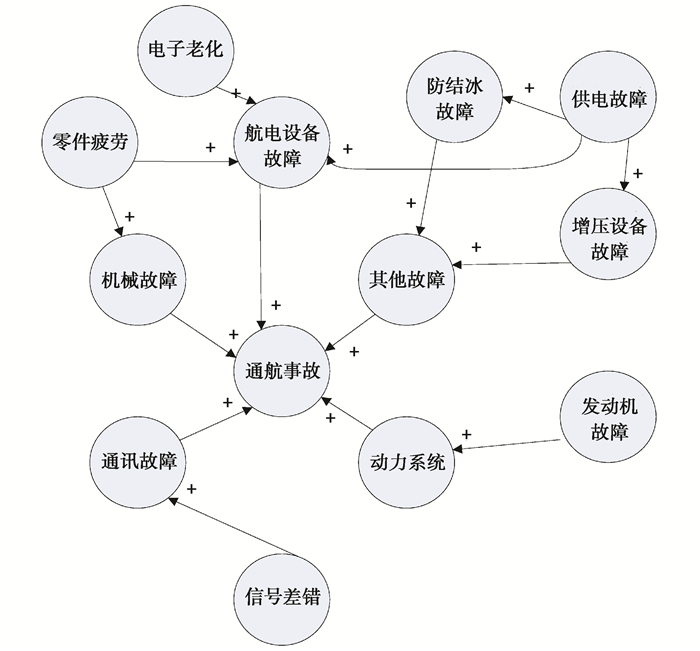
|
图 5 “机械因素”构造的模型 Fig. 5 Structural model of "mechanical factors" |
根据图 3,自变量和因变量并非存在线性关系,可以选择公式(2)进行多次迭代计算完成多变量非线性时间预测,这种预测方法不但需要对每个概念的初始状态进行分析,还分析模糊认知图的邻接矩阵。
选择专家针对通航事故诱因预测模型中的A1至A6节点概念进行打分,经过前期调研,特邀通航安全领域的6位专家,专家1和专家2擅长通航运行系统领域,专家3和专家4擅长通航事故调查,专家5和专家6擅长通航飞行技术。6名专家从专业的角度使用模糊语言对A1至A6节点概念间的关联关系进行描述。根据通航事故发生概率将其定义为7个语义值:很大(HD)、大(D)、偏大(PD)、中等(ZD)、偏小(PX)、小(X)和很小(HX),其模糊形式如表 2所示。
| 表 2 模糊数表示形式 Table 2 Representation of Fuzzy Numbers |
为了准确充分将专家打分利用起来,将使用算数平均法将各个专家的评判结果进行综合计算,假设每位专家的权重一致,最终所得的结果作为模糊认知图中概念A1、A2、A3、A4、A5、A6的权值,表示为式(4)。
| qij=˜pij=(f1ij+f2ij+⋯+fn−1ij+fnij)/N, | (4) |
式中:fijn是第n个专家根据概念i对概念j的影响程度进行判断;
代入式(4)进行计算,可以得出通航事故成因预测模型的邻接矩阵
| W=|000.71000.830000000000000000.530000.530000000000.350000000000.1700000000000000−0.780−0.490000000−0.7000000000−0.75000000000−0.750000000000.70.5800000000|, | (5) |
专家根据初始条件确定初始状态,为了提高预测的准确性,需要将专家提供的全部概念值进行充分利用。因此使用经典的最小最大法对概念值初始化得到初始值,即
| Pl(t0)=(Pl−min | (6) |
假设c1, c2, c3, c4和c5等随机变量仅存在2种状态——“激活”与“不被激活”,且在开始预测时,随机变量并不会对因变量产生影响,即机组配合程度很好,人员的观察能力很强,人员的训练水平很高,标准制定非常完善,人员及机械并未出现疲劳的情况,因此,c1= c2= c3= c4= 1被激活,c5=0不被激活。所以开始时系统的初始状态向量如下
| \boldsymbol{A}\left(t_0\right)=\left[A_1, A_2, A_3, A_4, A_5, A_6, 1, 1, 1, 1, 0\right], | (7) |
依据模糊认知图的理论可知,式(7)和式(5)邻接矩阵做乘法,根据计算结果分析每个概念的状态值,在此结果的基础上将状态值作为下一次计算的输入值,依次迭代计算,直到所有概念的状态值都稳定在某一个值,或状态值呈现周期性变化,预测就进入了期望稳定状态,阈值函数为
| f(x)=\frac{1}{1+e^{-\mu x}}, \mu>0, | (8) |
处于稳定状态中的某概念权值大于某个阈值,则认为其他概念权值中的某一个或几个诱因会在一定程度上导致通航事故的发生,那么该诱因的关联度即可作为通航事故成因预测的最终评价指标。再根据自变量因素概念和因变量概念之间关联程度强弱得出最终结论。
步骤1:将k步预测中A6的所有状态值作为参考序列,记为A0(k);
步骤2:将概念A1,A2,A3,A4和A5在预测过程中的状态值作为比较序列,记为Ai(k),比较序列与参考序列的关联系数χ可以由下面公式求出
| \chi=\frac{\min\limits_i \min \limits_k\left|A_0(k)-A_i(k)\right|+\alpha \max\limits _i \max \limits_k\left|A_0(k)-A_i(k)\right|}{\left|A_0(k)-A_i(k)\right|+\alpha \max\limits _i \max\limits _k\left|A_0(k)-A_i(k)\right|}, | (9) |
式中:α为分辨率系数,α∈(0, 1);k为迭代步数;i=1, 2…,5。如果记序列Ai(k)与序列A0(k)的关联度为γi,则
| {{\gamma }_{i}}=\sum\limits_{k=1}^{N}{\chi }(k)/{{N}_{{}^\circ }} | (10) |
步骤3:比较γi的值,值越大则2个序列间的关系越紧密,该诱因诱发通航事故概率就越大。
4 实例分析为了验证该方法的适用性与有效性,选取一起通航事故,使用方法对其进行分析与计算,将最终所得到的该通航事故的预测原因与实际原因进行对比,验证其有效性。
2011年11月10日,一架塞斯纳208水陆两用型飞机在天津执行物探任务时发生迫降,导致2名机组成员受伤,无人员死亡。经过对事故现场进行调查分析后得出结论:由于飞机发动机空中停车迫降野外,导致飞机螺旋桨变形,机翼明显损伤,油箱燃油泄露严重。依据初始条件对专家给出的初始状态进行整理之后得出
| \boldsymbol{A}\left(t_0\right)=[0, 1, 0, 0, 0, 0, 1, 1, 1, 1, 0], |
其中,取μ=2,将初始状态输入到图 3所示的模糊认知图模型中,输出结果如下表 3所示。
| 表 3 迭代输出值 Table 3 Iteration output value |
从表 3可以看出,迭代到第7步时数据达到固定值,基本保持不变,因此系统的状态为:
| \begin{gathered} A_1=0.1316, A_2=0.7950, A_3=0.4248, \\ A_4=0.5000, A_5=0.5000, A_6=0.7665 , \\ c_1=0.5000, c_2=0.5000, c_3=0.5000, \\ c_4=0.5000, c_5=0.7811 \text { 。} \end{gathered} |
记A6(k)=(0.500 0, 0.693 0, 0.761 2, 0.763 0, 0.765 4, 0.766 1, 0.766 5)为参考数列,取α=0.5,将A1-A5每一步迭代的预测值为Ai(k), i=1, 2,…5,k=7。由公式(11)和(12)计算得出关联度γ1=0.743 3,γ2=0.919 4,γ3=0.893 2,γ4=0.363 5,γ5=0.363 5。
因此,通航事故影响诱因的排序为:γ2>γ3>γ1>γ4=γ5,引发此次通航事故的主要诱因为“机械因素”,而次要诱因则为管理因素。而在实际的事故调查中发现,该通航事故的主要诱因为“机械因素”,计算结果与实际情况相符合。
5 对比分析为了验证使用的方法适用性与有效性较好,选取另外一种算法-DEMATEL方法来进行通航事故诱因的预测[15]。
选用0.1~0.9来表示影响通航事故的各个诱因之间的影响强度,同样使用专家打分的方法得出各诱因之间影响强度的矩阵B=(bij)5×5如下
| \boldsymbol{B}=\left|\begin{array}{ccccc} 0 & 0.1 & 0.6 & 0 & 0 \\ 0 & 0 & 0.1 & 0 & 0 \\ 0.3 & 0.5 & 0 & 0.1 & 0 \\ 0 & 0.2 & 0.3 & 0 & 0 \\ 0 & 0 & 0 & 0.1 & 0 \end{array}\right| \text { 。} |
依据公式(11)对B进行规范化得到
| \tilde{\boldsymbol{B}}=\frac{1}{\max\limits _{1 \leqslant i \leqslant 5} \sum\limits_{j=1}^5 b_{i j}}, | (11) |
| \boldsymbol{B}^{\prime}=\tilde{\boldsymbol{B}}(1-\tilde{\boldsymbol{B}})^{-1}, | (12) |
| \mathit{\boldsymbol{B' = }}\left| {\begin{array}{*{20}{c}} \begin{aligned} & 0.3338 \\ & 0.0538 \\ & 0.4894 \\ & 0.1733 \\ & 0.0191 \end{aligned}&\begin{aligned} & 0.7376 \\ & 0.1012 \\ & 0.9202 \\ & 0.5459 \\ & 0.0600 \\ \end{aligned}&\begin{aligned} & 1.0120 \\ & 0.1631 \\ & 0.4829 \\ & 0.5253 \\ & 0.0578 \\ \end{aligned}&\begin{aligned} &0.111\\ &0.0179\\ &0.1631\\ &0.0578\\ &0.1164 \end{aligned}&\begin{aligned} {\rm{0}}\\ {\rm{0}}\\ {\rm{0}}\\ {\rm{0}}\\ {\rm{0}} \end{aligned} \end{array}} \right|. |
从矩阵B’的结果中得出不同诱因的影响度、被影响度、中心度以及原因度[16],具体值见下表 4。
| 表 4 不同因素的影响度、被影响度、中心度和原因度 Table 4 Influence degree, affected degree, centrality and cause degree of different factors |
根据上表计算得出的中心度比较发现,A3即管理因素的影响最大,所以,可以预测得出通航事故的发生管理因素对其影响最大。
对以上2种方法计算结果进行对比分析后发现,使用FCM建立的通航事故诱因模型与相关度计算结合进行计算的通航事故诱因更为适用且有效。
6 结论1) 对2006—2015年的通航事故进行详细地统计分析之后,提出了通航事故影响因素的划分方法,根据模糊认知图模型建立起通航事故诱因预测模型,利用模糊认知图的表示方法与推理计算可以预测得到通航事故的诱因,根据关联度的计算最终挖掘出通航事故的主要诱因。
2) 通过实例分析验证得出,计算方法对于通航事故诱因的预测是有效的,该方法对事故诱因的预测可以降低由于人的喜好与偏见对事故诱因挖掘的影响,进而可以得到较为有效的预测结果。
| [1] |
王一姮. 通用航空公司安全运行保障能力模型研究[D]. 天津: 中国民航大学, 2014. Wang Y H. Research on model of safe operation assurance capability of general aviation airline[D]. Tianjin: Civil Aviation University of China, 2014. (in Chinese) |
| [2] |
王春林, 罗凤娥. 通用航空运行保障体系建设[C]//第十三届中国科协年会第22分会场[XC半字线. tif; Z*5;Y*5, JZ]中国通用航空发展研讨会论文集, 天津: 中国科技, 2011. Wang C L, Luo F E. Construction of general aviation operation security system[C]//Proceedings of the 22nd session of the 13th China association for science and technolog annual conference-China general aviation development symposium, Tianjing: China A ssociation for Science and Technology, 2011. |
| [3] |
陈勇刚. 我国通用航空安全管理体系建设研究[J]. 中国安全生产科学技术, 2012, 8(6): 216-220. Chen Y G. Study on safety management system of general aviation in China[J]. Journal of Safety Science and Technology, 2012, 8(6): 216-220. (in Chinese) DOI:10.3969/j.issn.1673-193X.2012.06.043 |
| [4] |
Shyur H J. A quantitative model for aviation safety risk assessment[J]. Computers & Industrial Engineering, 2008, 54(1): 34-44. |
| [5] |
Papageorgiou E I, Salmeron J L. A review of fuzzy cognitive maps research during the last decade[J]. IEEE Transactions on Fuzzy Systems, 2013, 21(1): 66-79. DOI:10.1109/TFUZZ.2012.2201727 |
| [6] |
Stylios C D, Groumpos P P. Modeling complex systems using fuzzy cognitive maps[J]. IEEE Transactions on Systems, Man, Cybernetics-Part A: Systems and Humans, 2004, 34(1): 155-162. DOI:10.1109/TSMCA.2003.818878 |
| [7] |
Kosko B. Fuzzy cognitive maps[J]. International Journal of Man-Machine Studies, 1986, 24(1): 65-75. DOI:10.1016/S0020-7373(86)80040-2 |
| [8] |
韩慧健, 韩佳兵, 张锐. 基于模糊认知图的物流需求预测模型研究[J]. 系统工程理论与实践, 2019, 39(6): 1487-1495. Han H J, Han J B, Zhang R. Study on logistics demand forecasting model based on fuzzy cognitive map[J]. Systems Engineering-Theory & Practice, 2019, 39(6): 1487-1495. (in Chinese) |
| [9] |
贺强, 徐艺, 马尧. 基于FCM的无人机飞行安全风险评估[J]. 民航学报, 2018, 2(1): 31-34. He Q, Xu Y, Ma Y. UAS flight safety risk assessment based on fuzzy cognitive maps[J]. Journal of Civil Aviation, 2018, 2(1): 31-34. (in Chinese) |
| [10] |
邱慧, 黄解宇, 董亚兰. 基于灰色系统模型的山西省物流需求预测分析[J]. 数学的实践与认识, 2016, 46(13): 66-70. Qiu H, Huang X Y, Dong Y L. Prediction analysis of logistics demand in Shanxi Province based on grey system model[J]. Mathematics in Practice and Theory, 2016, 46(13): 66-70. (in Chinese) |
| [11] |
陈勇刚. 基于灰熵分析法的航空公司维修安全质量影响因素分析[J]. 安全与环境学报, 2013, 13(1): 267-270. Chen Y G. Analysis of the influential factors of safety and quality maintenance of airline based on the grey relation entropy method[J]. Journal of Safety and Environment, 2013, 13(1): 267-270. (in Chinese) |
| [12] |
朱晓丽. 通用航空公司安全保障能力指标体系构建[D]. 广汉: 中国民用航空飞行学院, 2017. Zhu X L. Build on index system of safe assurance capability of general aviation airline[D]. Guanghan: Civil Aviation Flight University of China, 2017. (in Chinese) |
| [13] |
崔军辉, 魏瑞轩, 崔建汝, 等. 基于FCM的UAV事故成因预测方法[J]. 系统工程理论与实践, 2015, 35(12): 3258-3264. Cui J H, Wei R X, Cui J R, et al. Prediction method of UAV accident causations based on FCM[J]. Systems Engineering-Theory & Practice, 2015, 35(12): 3258-3264. (in Chinese) |
| [14] |
周长春. 航空安全管理[M]. 成都: 西南交通大学出版社, 2011. Zhou C C. Aviation safety management[M]. Chengdu: Southwest Jiaotong University Press, 2011. (in Chinese) |
| [15] |
Lin R J. Using fuzzy dematel to evaluate the green supply chain management practices[J]. Journal of Cleaner Production, 2013, 40: 32-39. |
| [16] |
林松, 刘小弟, 朱建军, 等. 基于模糊认知图的航天商业发射服务竞价影响因素分析[J]. 运筹与管理, 2019, 28(3): 158-165. Lin S, Liu X D, Zhu J J, et al. Analysis of the influencing factors of the bidding for aerospace commercial launching service based on fuzzy cognitive map[J]. Operations Research and Management Science, 2019, 28(3): 158-165. (in Chinese) |
 2022, Vol. 45
2022, Vol. 45



