b. 重庆大学 煤矿灾害动力学与控制国家重点实验室, 重庆 400044;
c. 重庆大学 非均质材料力学重庆市重点实验室, 重庆 400044
b. State Key Laboratory of Coal Mine Disaster Dynamics and Control, Chongqing University, Chongqing 400044, P. R. China;
c. Chongqing Key Laboratory of Heterogeneous Material Mechanics, Chongqing University, Chongqing 400044, P. R. China
PBX(polymer bonded explosives)是含能颗粒与黏结剂组成的多相非均质高能炸药,具有较好的安全性能、较高的能量密度以及易于加工等特性,广泛应用于军事、工业等领域[1-3]。在使役过程中,由于承受复杂的温度和载荷环境,可能会导致界面的损伤,进而影响其安全性能与爆轰性能。由于PBX的细观结构极其复杂,它的热力学属性与微细观结构密切相关[4-6]。为了探究PBX在不同温度与载荷条件下的损伤规律,近年来国内外学者进行了许多相关研究[7]。Wang等[8]利用有限元软件研究PBX在冲击载荷作用下的热力学响应。Walters等[9]通过力学测试与数值模拟探究黏结剂的力学行为以及黏结剂与晶体之间界面的降解。但这些研究中均未建立能反映PBX真实结构的几何模型,没有将细观的损伤与宏观的变形联系起来。为了更深入地认识PBX的损伤机理,将着重于细观层面对PBX的力学性能进行研究。引入Voronoi方法建立能反映PBX细观结构的三维模型,对PBX进行升温和降温以及低压加载,了解PBX微结构以及温度和低压对TATB(三氨基三硝基苯)颗粒与黏结剂界面力学行为的影响。
1 基于Voronoi方法的PBX几何建模PBX颗粒是典型的不规则多面体[10],它的微观结构会直接影响断裂行为[11],建立与真实结构相一致的PBX模型,对探究含能颗粒与黏结剂以及界面对PBX炸药的影响十分重要。目前,PBX的细观几何模型主要为:二维的圆形颗粒与六边形颗粒分布[12]、三维的圆形颗粒分布[13],如图 1所示,但这些模型并不能反映PBX颗粒特征。这里采用Voronoi方法建立PBX模型,构建与真实PBX相一致的细观结构。
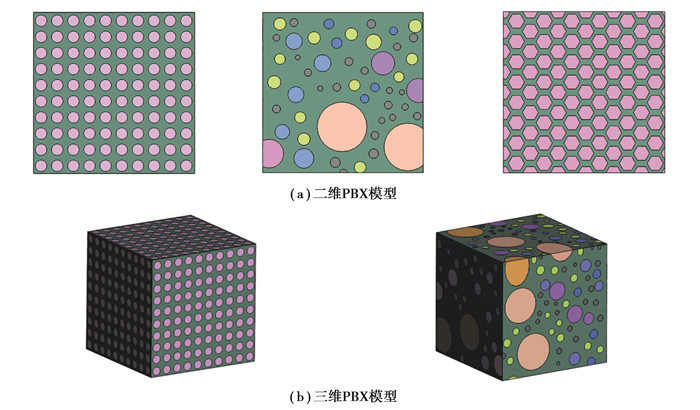
|
图 1 不同分布与形貌的PBX几何模型 Fig. 1 Geometric model of PBX with different distributions and morphologies |
基于Voronoi原理进行几何建模的方法先是在计算几何等相关领域中得到了应用[14]。由于其建模简单并且可控性强,不断地被推广到众多的领域中。如图 2(c)基于Voronoi原理建立的PBX二维模型图与PBX真实的细观形貌[15]图 2(a)极为相似。虽然二维Voronoi细观模型结构与PBX的颗粒形貌和分布相一致,但变形本质上是一个三维的问题,用二维模型去进行数值计算有较大的局限性。其三维细观形貌[16]如图 2(b)所示,因此建立可以反映PBX不规则多面体特性的三维细观模型是极为重要的。
在二维Voronoi模型的基础上,利用Voronoi方法在MATLAB中编程建立了可以反映真实PBX细观结构的三维Voronoi模型,如图 3(a)与(d)。模型能有效区分颗粒与黏结剂,模型I的颗粒分布与黏结剂分别为图 3(b)和(c),模型Ⅱ的颗粒分布与黏结剂分别为图 3(e)和(f)。生成的颗粒的粒径为几十到几百微米不等,与实际情况符合。采用的级配关系图 3(h)和(i)与实际的炸药制备时的级配[17]图 3(g)也较为相近,均为近似的单峰正态分布。
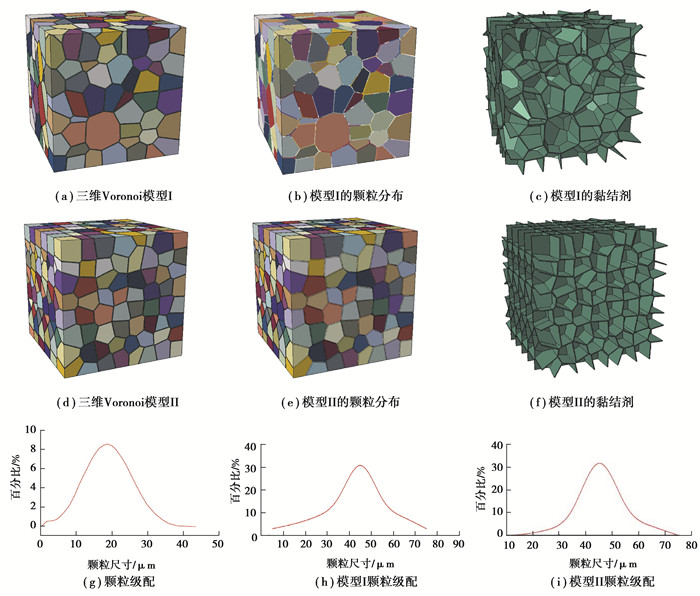
|
图 3 三维Voronoi模型与颗粒级配 Fig. 3 3D Voronoi Model and particle size distribution |
TATB是一种耐热的含能颗粒,具有弹性与塑性材料的特性,因此采用各向同性弹塑性模型对其进行描述。由于TATB具有各向异性的热力学属性,采用正交各向异性的热膨胀系数对其进行描述。结合已有研究者的实验结果[18-19],得到相关的材料参数如表 1所示。
| 表 1 TATB材料参数 Table 1 Material parameters of TATB |
F2314黏结剂具有弹性、黏性和塑性等力学特性,选用黏弹塑性模型[20]对其进行描述,其模型如图 4所示。
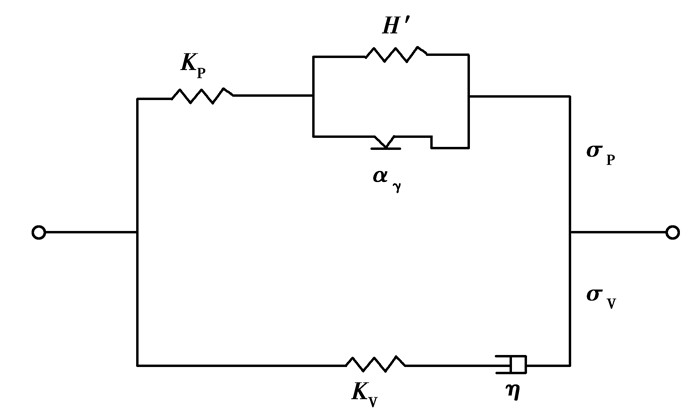
|
图 4 黏弹塑性本构模型 Fig. 4 The viscoelasto-plastic constitutive model |
此模型由2个支路并联而成,分别为弹塑性支路和黏弹性支路。其中,弹塑性支路由塑性元件αγ、线性弹簧KP和H′组成,而黏弹性支路由黏壶η和弹性元件KV组成。2个支路由比例参数f联系在一起,其表示黏性弹性支路中的弹性模量占总模量的比值为
| f=KVKV+KP=KVK0<f<1。 | (1) |
弹塑性支路满足Von-Mises屈服准则,其应力-应变关系如下:
| σP={KPεσP<σS,Rεn1σP⩾σS。 | (2) |
式中:σS为屈服应力; n1为硬化指数;系数R与屈服应变εS、塑性应变εPpl有关。
黏弹支路满足Norton-Hoff法则,其应力-应变关系如下:
| σV=A−1n˙ε1nV, | (3) |
式中A,n为蠕变参数。整合得总应力:
| σ=σP+σV=A−1n˙ε1nv+σP。 | (4) |
总应变为:
| ε=εcl+fεvV+(1−f)εplP=f(εclV+εvv)+(1−f)(εclP+εplP) 。 | (5) |
根据实验研究结果[19],对黏结剂F2314的弹性模量和热膨胀系数进行拟合[18],得到其随温度的变化曲线如图 5所示,其热力学参数见表 2。

|
图 5 F2314的杨氏模量和热膨胀系数与温度的关系 Fig. 5 Temperature dependence of Young's modulus and thermal expansion rate of F2314 |
| 表 2 F2314材料参数 Table 2 Material Parameters of F2314 |
为探究TATB颗粒与F2314黏结剂界面间的损伤,基于Tan等[21]提出的微观内聚力法则,采用双线性内聚力模型[22]进行数值计算。图 6(a)和(b)分别为界面损伤演化模型与界面的双线性内聚力模型,其中abc段为起裂阶段,通过强度准则对损伤的起始进行判断,cde段为损伤阶段,通过能量释放率准则对界面破坏、刚度退化进行判断。
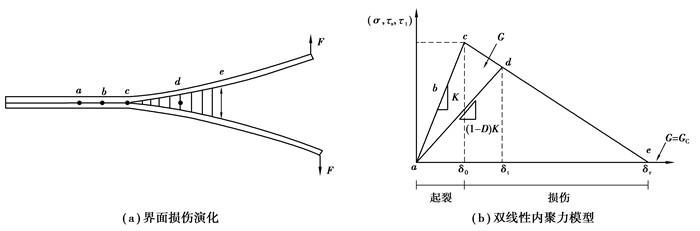
|
图 6 界面损伤模型 Fig. 6 Interface damage model |
强度准则采用最大名义应力准则[23],如式(6)所示。
| d=max | (6) |
式中:σ,τ1,τ2分别为界面3个方向最大应力。当d=1时,界面出现损伤。损伤演化规律描述了达到相应损伤破坏准则时材料刚度衰减速度。能量释放率是判断界面损伤破坏的重要参数,是界面损伤扩展时所需的能量,损伤的模式有张开型、滑开型和撕开型3种。根据能量释放率理论与J积分的能量形式有:
| G = - \frac{{\partial \mathit{\Pi }}}{{\partial a}} = J = \int\limits_0^{\delta_{\rm{t}}} {\sigma (\delta ){\rm{d}}\delta } , | (7) |
式中:Π为总位能;a为损伤界面面积;δt为界面尖端位移;δr为界面完全损伤的临界位移。当δt=δr时能量释放率G等于临界值GC:
| {G_{\rm{C}}} = \int\limits_0^{{\delta _{\rm{r}}}} {\sigma (\delta ){\rm{d}}\delta } 。 | (8) |
界面损伤的过程体现为界面刚度的退化,通过界面的位移定义损伤因子D:
| D=\frac{\delta_{\mathrm{r}}\left(\delta-\delta_0\right)}{\delta\left(\delta_{\mathrm{r}}-\delta_0\right)} 。 | (9) |
当G=0时,D=0,界面未发生损伤;当0<G<GC时,0<D<1,界面开始出现损伤,损伤越严重,D值越大;当G=GC时,D=1,界面完全损伤。损伤后界面的刚度为
| K_{\mathrm{D}}=(1-D) K_0, | (10) |
式中K0为界面未损伤时的界面刚度。根据炸药的拉剪复合试验[24-25]的测试结果,得到TATB颗粒与F2314黏结剂界面的相关力学参数,如表 3所示。
| 表 3 界面材料参数 Table 3 Parameters of crystals-binder interface |
因为三维模型晶体数目较多,数值模拟时计算量大,为了使数值模拟更加方便、结果呈现更加直观,选择模型中0.30 mm×0.30 mm×0.05 mm的区域,将模型导入ABAQUS中进行相关模拟。在进行升温与降温的数值模拟时,选择黏结剂含量为7.4%的PBX模型进行模拟。将PBX的左边界、下边界和后边界进行位移约束并从四周向PBX传热,5 min内将PBX从213 K(-60 ℃)升温至393 K(120 ℃),降温模拟时与升温模拟时的速率保持一致。由于模型尺寸较小,在变温过程中模型中心温度与表面温度温差较小,可以忽略内外温差。
对升温时界面的状态进行分析发现,由于黏结剂的热膨胀系数远小于颗粒的热膨胀系数,升温时,颗粒向四周膨胀,黏结剂将颗粒包覆,由图 7(c)和(d)可看出,界面的法向拉应力为负值,法向压应力为正值,界面整体受到压应力与切向应力作用,但界面的应力值均未达到临界应力,对比图 7(a)界面的初始损伤判据,d的最大值为0.61,等于界面法向拉应力与法向应力临界值的比值,未到达界面损伤初始值1.00,损伤因子D的值为零,因此界面未产生损伤。
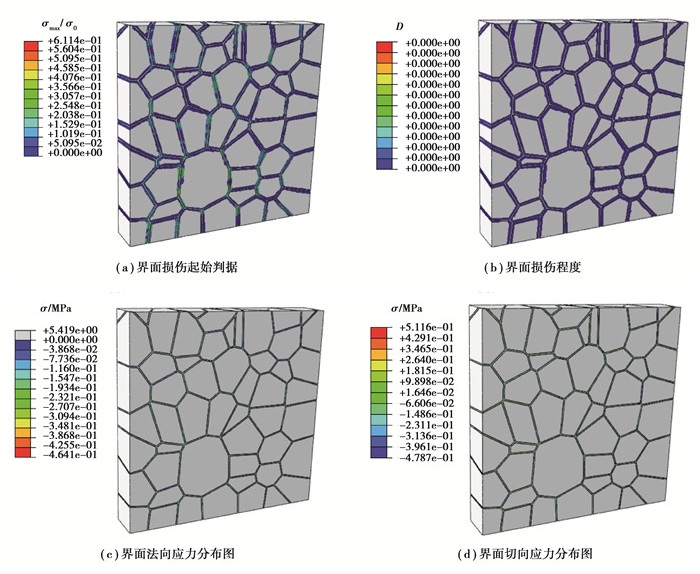
|
图 7 PBX升温过程中的界面状态 Fig. 7 Interface state of PBX during heating |
对图 8中降温过程的界面状态分析发现,颗粒向中心收缩,界面间受到拉伸,界面的最大法向拉应力达到了法向应力临界值0.759 MPa,且主要集中在大颗粒附近。界面的最大切应力为0.96 MPa,小于但接近切向应力临界值0.97 MPa。图 8(a)中界面损伤起始判据,红色区域d的最大值为1.00,该区域界面出现了损伤,对比图 8(b)界面损伤的区域主要集中在大颗粒附近。通过对升温与降温时界面状态的分析可得,与升温相比,降温更容易造成界面的损伤,损伤主要由界面间的法向应力造成。
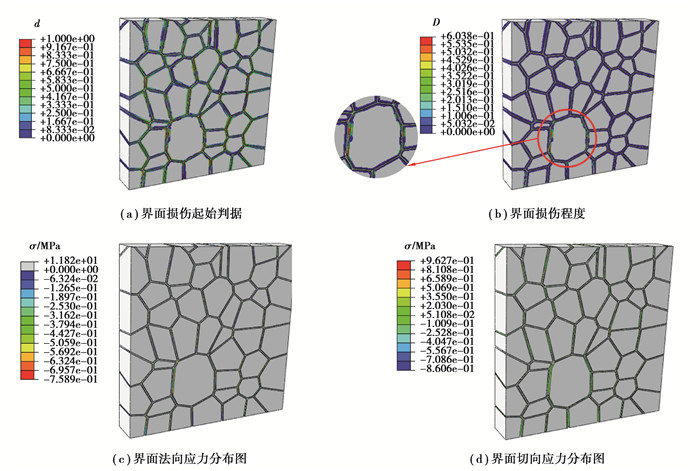
|
图 8 PBX降温过程中的界面状态 Fig. 8 Interface state of PBX during cooling |
一般情况下,PBX中TATB晶体含量大于90%、黏结剂含量小于8%[16, 26]。因此选择黏结剂含量分别为2.5%、3.6%、4.5%、6.2%的4组颗粒分布一致的PBX模型与黏结剂含量为7.4%的粒径较为一致、分布均匀的PBX模型进行模拟。因为降温比升温更易造成界面的损伤且主要由界面间的法向应力造成,所以对模型进行降温处理,得到界面的法向应力分布如图 9所示。
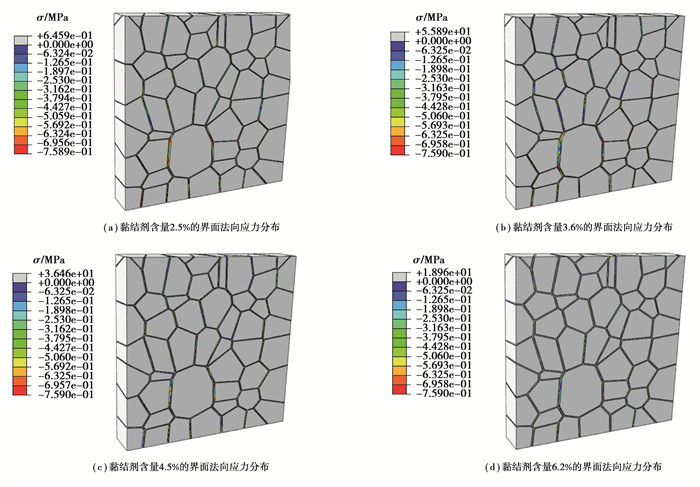
|
图 9 不同黏结剂含量的PBX的界面法向应力分布 Fig. 9 Normal stress distribution of PBX interface with different binder contents |
界面损伤因子与黏结剂含量的关系如图 10所示,随着黏结剂含量的增加,界面上部分法向拉应力转变为法向压应力,界面达到法向拉应力临界值的区域发生改变,损伤因子也随着黏结剂含量的增加而变化,总体呈现下降趋势。这是由于黏结剂对颗粒的包覆性增强,颗粒收缩时约束减小,使得界面的损伤程度减弱。
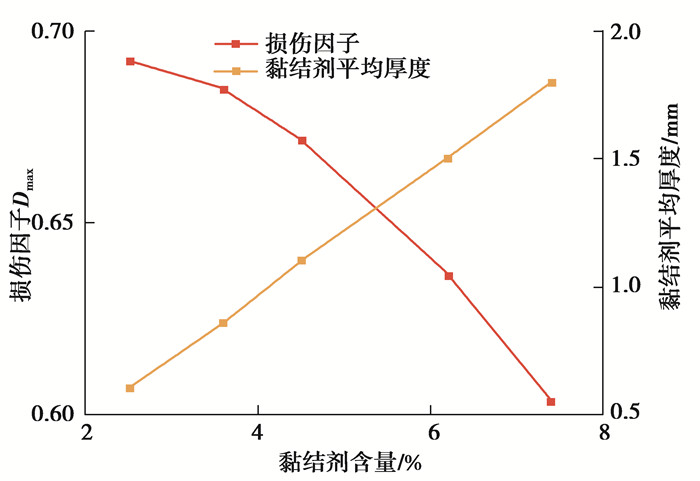
|
图 10 损伤因子与黏结剂含量的关系 Fig. 10 Relationship between damage factor and binder content |
PBX在制备时,生成的TATB含能颗粒的粒径差异较大,粒径较大的TATB颗粒可以达到300 μm以上,而通过特殊的制备工艺[27-28]可以生成粒径达到几十纳米的TATB颗粒,其粒径与分布对PBX的力学性能有重要的影响。
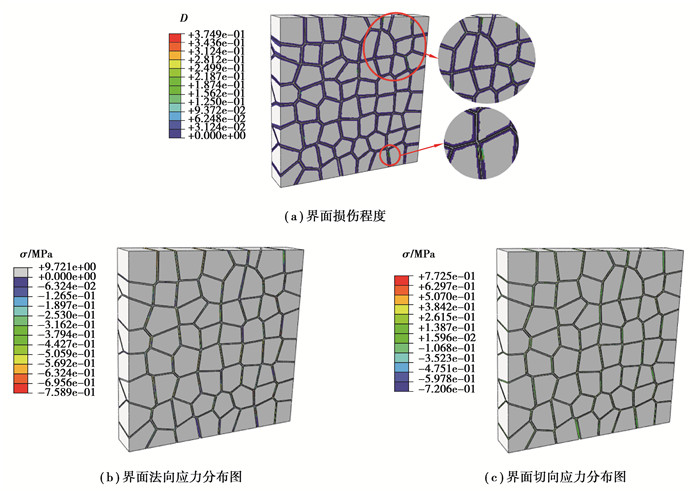
图 11中,PBX的粒径相近、颗粒分布均匀,切向应力未达到应力最大值,界面的法向应力到达了法向应力临界值,界面产生了损伤。对比图 11(a)与图 8(b),界面的损伤区域较小,损伤的程度也更低。综合以上结果,细观结构的不同对PBX的力学性能影响很大,当黏结剂含量越高、粒径越一致、颗粒分布更均匀时,界面的损伤越小。
|
图 11 各颗粒粒径相近的黏结剂含量7.4%的PBX在降温过程中的界面状态 Fig. 11 Interface state of PBX with 7.4% crystal volume fraction and similar crystal size during cooling |
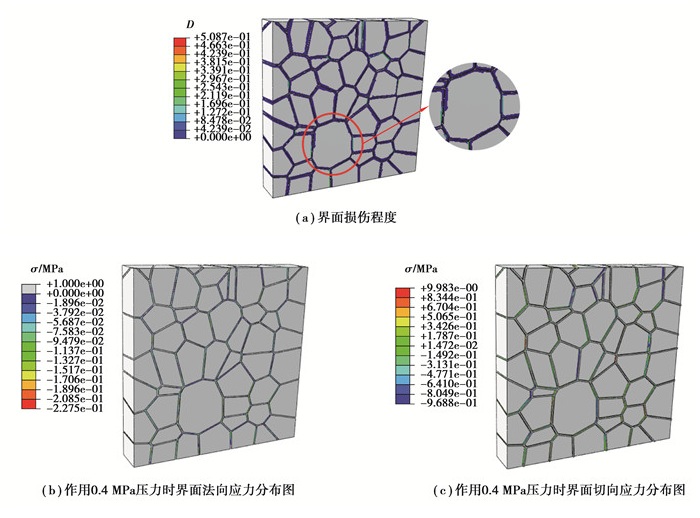
为探究低压对PBX界面损伤的影响,在降温的同时,对PBX的上边界和右边界分别作用0.2,0.3,0.4,0.6,0.8 MPa的压力。对比图 8(c)与图 12(b),作用0.4 MPa压力时,界面法向拉应力的分布范围减小,界面最大法向应力小于法向应力临界值。对比图 8(d)与图 12(c),作用0.4 MPa压力,界面的切向应力值达到了切向应力临界值,界面的损伤由切向应力引起, 但损伤程度减小。
|
图 12 降温过程施加作用力时界面应力状态 Fig. 12 Interface stress state under applied force during cooling |
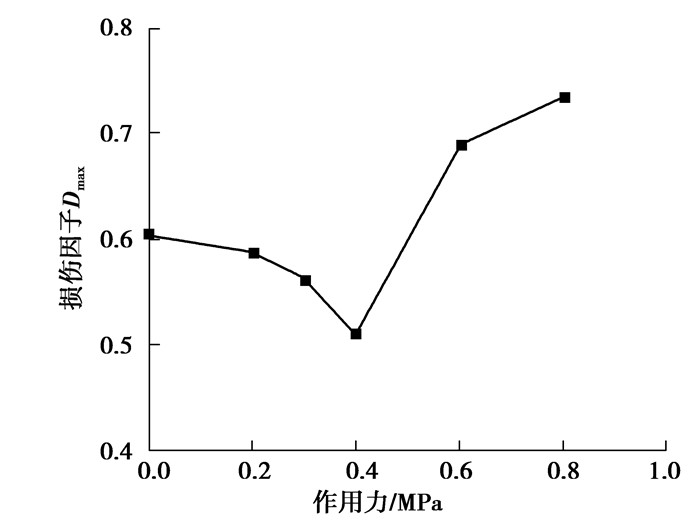
界面的损伤因子与作用力的关系如图 13所示,仅降温收缩时作用力为0 MPa,随着压力的增大,损伤因子减小,界面的损伤程度减小。作用0.4 MPa压力时,损伤因子最小,界面的损伤程度最小,继续增加压力,界面的损伤程度开始加重,作用0.6 MPa压力时损伤因子的值已经比仅降温时大。因此,作用较低压力对界面的损伤有一定的抑制作用,但压力过大会使损伤程度加重。
|
图 13 损伤因子与作用力的关系 Fig. 13 Relationship between damage factors and forces |
对TATB基PBX炸药进行升温、降温以及低压处理,模拟后得到的结果表明:
1) 升温时,由于黏结剂的热膨胀系数远小于颗粒的热膨胀系数,黏结剂对颗粒形成了包覆,使得黏结剂与颗粒受到挤压,界面主要受压应力作用,不易产生损伤。
2) 降温过程相较于升温过程,更易出现界面的损伤,损伤主要集中在大颗粒附近。界面的法向应力到达损伤临界值,切向应力接近但未达到损伤临界值,因此损伤主要是由拉应力造成。
3) 细观结构不同的PBX的力学性能差异很大,当黏结剂含量越高、粒径越一致、颗粒分布更均匀时,界面的损伤越小。
4) 降温的过程中作用低压,法向应力虽然减小到其临界值以下,但最大切应力达到其临界值。界面损伤由切应力导致,但相较于无压力作用时,损伤程度不断减小。当作用压力超过一定范围,界面的损伤程度不断增加。
| [1] |
孙华, 郭志军. PBX炸药技术特性及在水中兵器上的应用[J]. 装备指挥技术学院学报, 2009, 20(3): 108-111. Sun H, Guo Z J. Characteristics of PBX dynamite and its application in undersea weaponry[J]. Journal of the Academy of Equipment Command & Technology, 2009, 20(3): 108-111. (in Chinese) DOI:10.3783/j.issn.1673-0127.2009.03.025 |
| [2] |
肖继军, 谷成刚, 方国勇, 等. TATB基PBX结合能和力学性能的理论研究[J]. 化学学报, 2005, 63(6): 439-444. Xiao J J, Gu C G, Fang G Y, et al. Theoretical study on binding energies and mechanical properties of TATB-based PBX[J]. Acta Chimica Sinica, 2005, 63(6): 439-444, 433. (in Chinese) DOI:10.3321/j.issn:0567-7351.2005.06.001 |
| [3] |
孙国祥. 高分子混合炸药[M]. 北京: 国防工业出版社, 1985: 34. Sun G X. Polymer mixed explosives[M]. Beijing: National Defense Industry Press, 1985: 34. (in Chinese) |
| [4] |
郭虎, 罗景润. 基于微裂纹统计模型的PBX力学行为[J]. 火炸药学报, 2012, 35(5): 52-57. Guo H, Luo J R. Mechanical behavior of PBX based on SCRAM model[J]. Chinese Journal of Explosives & Propellants, 2012, 35(5): 52-57. (in Chinese) DOI:10.3969/j.issn.1007-7812.2012.05.013 |
| [5] |
Drodge D R, Williamson D M. Understanding damage in polymer-bonded explosive composites[J]. Journal of Materials Science, 2016, 51(2): 668-679. DOI:10.1007/s10853-013-7378-6 |
| [6] |
Yan G Y, Tian Q, Liu J H, et al. The microstructural evolution in HMX based plastic-bonded explosive during heating and cooling process: an in situ small-angle scattering study[J]. Central European Journal of Energetic Materials, 2016, 13(4): 916-926. DOI:10.22211/cejem/65826 |
| [7] |
顾佳伟. 撞击作用下PBX炸药响应过程的宏-细观数值模拟[D]. 北京: 北京理工大学, 2015: 50-63. Gu J W. Macro and micro simulation of PBXs' response under impact[D]. Beijing: Beijing Institute of Technology, 2015: 50-63. (in Chinese) |
| [8] |
Wang X J, Wu Y Q, Huang F L, et al. Mesoscale thermal-mechanical analysis of impacted granular and polymer-bonded explosives[J]. Mechanics of Materials, 2016, 99: 68-78. DOI:10.1016/j.mechmat.2016.05.004 |
| [9] |
Walters D J, Luscher D J, Yeager J D, et al. Cohesive finite element modeling of the delamination of HTPB binder and HMX crystals under tensile loading[J]. International Journal of Mechanical Sciences, 2018, 140: 151-162. DOI:10.1016/j.ijmecsci.2018.02.048 |
| [10] |
Rae P J, Goldrein H T, Palmer S J P, et al. Quasi-static studies of the deformation and failure of β-HMX based polymer bonded explosives[J]. Proceedings of the Royal Society of London Series A: Mathematical, Physical and Engineering Sciences, 2002, 458(2019): 743-762. DOI:10.1098/rspa.2001.0894 |
| [11] |
Palmer S J P, Field J E, Huntley J M. Deformation, strengths and strains to failure of polymer bonded explosives[J]. Proceedings of the Royal Society of London Series A: Mathematical and Physical Sciences, 1993, 440(1909): 399-419. |
| [12] |
戴开达, 刘龑龙, 陈鹏万, 等. PBX炸药有效弹性模量的有限元模拟[J]. 北京理工大学学报, 2012, 32(11): 1154-1158. Dai K D, Liu Y L, Chen P W, et al. Finite element simulation on effective elastic modulus of PBX explosives[J]. Transactions of Beijing Institute of Technology, 2012, 32(11): 1154-1158. (in Chinese) DOI:10.3969/j.issn.1001-0645.2012.11.012 |
| [13] |
Arora H, Tarleton E, Li-Mayer J, et al. Modelling the damage and deformation process in a plastic bonded explosive microstructure under tension using the finite element method[J]. Computational Materials Science, 2015, 110: 91-101. DOI:10.1016/j.commatsci.2015.08.004 |
| [14] |
郭虎, 罗景润, 史平安, 等. 静态拉伸下高聚物粘结炸药破坏行为研究[C]//第二届全国危险物质与安全应急技术研讨会论文集. 成都, 2013: 301-309. Guo H, Luo J R, Shi P A, et al. Study on the facture behavior of PBX under static tension[C]// Proceedings of the 2nd Seminar on Hazardous Materials & Safety Emergency Technology. Chengdu, 2013: 301-309. (in Chinese) |
| [15] |
Ambos A, Willot F, Jeulin D, et al. Numerical modeling of the thermal expansion of an energetic material[J]. International Journal of Solids and Structures, 2015, 60. |
| [16] |
Manner V W, Yeager J D, Patterson B M, et al. In situ imaging during compression of plastic bonded explosives for damage modeling[J]. Materials (Basel, Switzerland), 2017, 10(6). |
| [17] |
周筱雨, 杨雪梅, 韦兴文, 等. TATB基PBX界面热阻研究及导热系数预测[J]. 含能材料, 2017, 25(5): 422-427. Zhou X Y, Yang X M, Wei X W, et al. The simulation of thermal conductivity coefficien of TATB-based PBX using the interface thermal resistance model[J]. Chinese Journal of Energetic Materials, 2017, 25(5): 422-427. (in Chinese) |
| [18] |
温茂萍, 唐维, 董平, 等. 黏结剂含量对热压TATB基PBX残余应力的影响[J]. 含能材料, 2017, 25(8): 661-666. Wen M P, Tang W, Dong P, et al. Effect of binder content on residual stress of thermally compacted TATB based PBX[J]. Chinese Journal of Energetic Materials, 2017, 25(8): 661-666. (in Chinese) |
| [19] |
Sun J, Kang B, Zhang H, et al. Investigation on irreversible expansion of 1, 3, 5-triamino-2, 4, 6-trinitrobenzene cylinder[J]. Central European Journal of Energetic Materials. |
| [20] |
Dassault Systems S C. ABAQUS 6.14 Documentation[DB/CD]. Providence, Rhode Island, USA: 2014.
|
| [21] |
Tan H, Liu C, Huang Y, et al. The cohesive law for the particle/matrix interfaces in high explosives[J]. Journal of the Mechanics and Physics of Solids, 2005, 53(8): 1892-1917. DOI:10.1016/j.jmps.2005.01.009 |
| [22] |
Berezvai S, Kossa A. Characterization of a thermoplastic foam material with the two-layer viscoplastic model[J]. Materials Today: Proceedings, 2017, 4(5): 5749-5754. DOI:10.1016/j.matpr.2017.06.040 |
| [23] |
Dano M L, Gendron G, Picard A. Stress and failure analysis of mechanically fastened joints in composite laminates[J]. Composite Structures, 2000, 50(3): 287-296. DOI:10.1016/S0263-8223(00)00119-7 |
| [24] |
姚振华, 李亚智, 刘向东, 等. 复合材料层合板低速冲击后剩余压缩强度研究[J]. 西北工业大学学报, 2012, 30(4): 518-523. Yao Z H, Li Y Z, Liu X D, et al. Effectively calculating residual compressive strength of composite laminate after impact(CAI)[J]. Journal of Northwestern Polytechnical University, 2012, 30(4): 518-523. (in Chinese) DOI:10.3969/j.issn.1000-2758.2012.04.008 |
| [25] |
黄西成, 李尚昆, 魏强, 等. 基于XFEM与Cohesive模型分析PBX裂纹产生与扩展[J]. 含能材料, 2017, 25(8): 694-700. Huang X C, Li S K, Wei Q, et al. Analysis of crack initiation and growth in PBX energetic material using XFEM-based cohesive method[J]. Chinese Journal of Energetic Materials, 2017, 25(8): 694-700. (in Chinese) |
| [26] |
颜熹琳, 唐明峰, 甘海啸, 等. 拉剪复合试验测试炸药晶体/黏结剂界面力学特性[J]. 含能材料, 2016, 24(6): 587-591. Yan X L, Tang M F, Gan H X, et al. Mechanical properties of explosive crystal / binder interface based on tension-shear test[J]. Chinese Journal of Energetic Materials, 2016, 24(6): 587-591. (in Chinese) |
| [27] |
董海山, 周芬芬. 高能炸药及相关物性能[M]. 北京: 科学出版社, 1989. Dong H S, Zhou F F. Properties of high explosives and related substances[M]. Beijing: Science Press, 1989. (in Chinese) |
| [28] |
曾贵玉, 聂福德, 王建华, 等. 高速气流碰撞法制备超细TATB粒子的研究[J]. 火工品, 2003(1): 1-3. Zeng G Y, Nie F D, Wang J H, et al. Preparation of ultrafine TATB particles by high-speed gas impacting method[J]. Initiators & Pyrotechnics, 2003(1): 1-3. (in Chinese) |
 2022, Vol. 45
2022, Vol. 45




