热力耦合现象存在于众多的高新技术中，诸如航空发动机、汽车发动机和电子器件等一系列装置，特别是结构界面接触传热的研究。在实际情况中，结构部件的加工表面不可能是绝对平整光滑的，而是由许多微观的不规则的凸峰和凹谷组成的粗糙表面，而边界面的凹凸形状是直接影响耦合分析的核心因素。将热力耦合分析与计算力学相结合的数值模拟方法已经成为重要的研究方向，寻求合适的计算方法以及如何优化精确温度场和位移场分布依旧是热点问题。正因如此，结构界面接触传热的研究正逐步从简单走向复杂、从宏观走向微观、从表象走向机理、从定性走向定量，其建模方法和分析手段面临着巨大的挑战。

由材料的本构关系、热力学基本定律以及自由能表达推导的热传导方程式可以知道温度场的分布受位移场的影响^[1-8]，而位移场的分布也受温度的影响，这是典型的耦合问题，需将位移场和温度场二者耦合求解；在针对耦合热应力问题求解方面，Nowinski^[4]提出了耦合作用是将机械能转化成热能，继而耗散掉；Biot等^[9]提出将热容量作为一个新的状态变量引入虚耗散的热力学原理中，由此导出的场方程将具有积分-微分形式，避免了因考虑热源而需引入的另一变量熵；Nariboli^[10]用Laplace变换法研究了球形空腔壁温度突然有跳跃的热弹性动力学问题；Takeuti等^[11]用热弹性位势和Love位移函数求解了轴对称有限圆柱动态耦合热应力问题；Oden^[12]用有限单元法计算了各种物性系数下的半空间耦合问题并与精确解进行比较；王林翔等^[13]用微分代数的方法求解了耦合热弹性动力学问题；Gao^[14]用边界元法进行热弹性动力学问题的求解。

针对于热力耦合现象，求解的问题分为两种，一种是动态的热力耦合问题，即耦合热弹性动力学问题，另一种是准静态的热力耦合问题，即非定常拟静态的热力耦合问题。区分二者的关键在于外部机械载荷或者热载荷随时间的变化是否剧烈，也就是载荷是否具备冲击的性质，当载荷不具备冲击性质时，位移产生的加速度项影响很小可忽略，这种并非静态问题但可忽略加速度影响的计算方法，称其为准静态的计算方法，大多数的工程实践问题都属于准静态的范畴，这样一来可以极大地简化计算过程。有限元方法是求解热力耦合问题的主要方法，但计算精度受网格影响较大，在处理庞大的工程结构时，网格划分是一项巨大的任务，并且基于静态形函数的变形描述很难充分逼近弹性体在热力耦合作用下的真实位移场，因此近年来有不少学者提出了使用无网格方法解决耦合热弹性问题^[15]。无网格方法^[16-18]摆脱了网格的束缚，在计算域内使用节点分布去代替网格作用，计算点的形函数随着计算点变化而变化，即使在计算节点分布不规则时，计算精度的损失也较小；并且由于节点生成较为方便，因而自适应性能优越，将自适应技术引入无网格方法，能够合理有效地增加节点密度，继而保证计算精度，避免因为节点数量和位置的不合理造成的精度失准，在计算凹凸边界时，二者的结合能够克服凹凸边界网格难以划分问题，同时又能保证计算精度的不失准。笔者以无网格伽辽金算法(EFG)计算了二维混合边界条件下的非定常拟静态热力耦合问题，以移动最小二乘法(MLS)构建了形函数，应用后验误差公式结合采用H型自适应计算，提出了适用于非定常温度场拟静态热力耦合问题的EFG法计算模型，最后以数值算例验证了本文方法的可行性。

1 移动最小二乘法(MLS)

考虑平面域Ω的某一场变量$ u(\boldsymbol{x})(\boldsymbol{x}=((x, y))$表示在平面域Ω内的某一点的坐标)的未知标量函数，则定义在点x的MLS近似表达式为

$ {u^{\rm{h}}}(\mathit{\boldsymbol{x}}) = \sum\limits_{i = 1}^m {{p_i}} (\mathit{\boldsymbol{x}}){a_i}(\mathit{\boldsymbol{x}}) = \mathit{\boldsymbol{p}}{(\mathit{\boldsymbol{x}})^{\rm{T}}}\mathit{\boldsymbol{a}}(\mathit{\boldsymbol{x}}), $

(1)

式中(p(x))是关于二维空间坐标x=(x, y)的基函数。此基函数通常为利用Pasca三角形所决定的单项式以确保其最小完备性。m表示为基函数完备项的个数。

在二维空间中单项式基函数为：

$ \begin{array}{*{20}{c}} {线性基}&{m = 3{{(\mathit{\boldsymbol{p}}(\mathit{\boldsymbol{x}}))}^{\rm{T}}} = [1, x, y], } \end{array} $

(2)

$ \begin{array}{*{20}{c}} {二次基}&{m = 6{{(p(\mathit{\boldsymbol{x}}))}^{\rm{T}}} = \left[ {1, x, y, {x^2}, xy, {y^2}} \right], } \end{array} $

(3)

$ (\boldsymbol{a}(\boldsymbol{x}))=\left[\begin{array}{llll} a_1(\boldsymbol{x}) & a_2(\boldsymbol{x}) & \cdots & a_m(\boldsymbol{x}) \end{array}\right], $

(4)

式中a(x)为待定参数向量。

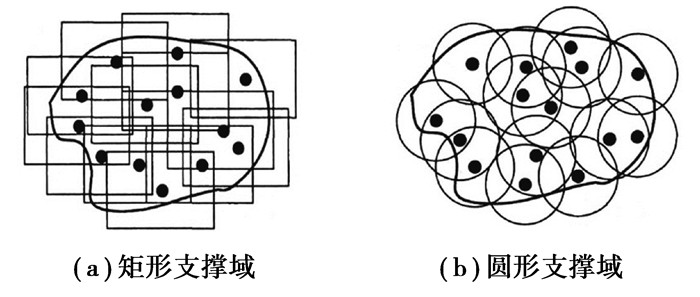
现将二维求解域Ω用N个节点进行离散，每个节点的节点值u_I已知，在每个节点x_I(I=1, 2, …, N)处定义一个权函数ω_I(x)，并且该函数是紧支的，即在支撑域Ω_I中权函数大于零，而在支撑域外面权函数等于零，支撑域形状常见有矩形和圆形，如图 1所示。

为计算方便，这里采用矩形支撑域，以及3次样条插值权函数。当支撑域为矩形时，

$ \omega_I(\boldsymbol{x})=\omega_I\left(r_x\right) \omega_I\left(r_y\right), $

(5)

$ r_x=\frac{\left|x-x_I\right|}{L} r_y=\frac{\left|y-y_I\right|}{D} 。$

(6)

式中：L，D分别为矩形支撑域的长和宽。为求a(x)，定义泛函J:

$ \mathit{\boldsymbol{J}} = \sum\limits_{I = 1}^N {{\omega _I}} (\mathit{\boldsymbol{x}}){\left[ {{u^{\rm{h}}}(\mathit{\boldsymbol{x}}) - {u_I}} \right]^2} = \sum\limits_{I = 1}^N {{\omega _I}} (\mathit{\boldsymbol{x}}){\left[ {\sum_{i = 1}^m {{p_i}} (\mathit{\boldsymbol{x}}){a_i}(\mathit{\boldsymbol{x}}) - {u_I}} \right]^2}。$

(7)

对J取最小值，即J关于a(x)取驻值$ \left(\frac{\partial J}{\partial a}=0\right)$，可得式(8)，即

$ [\boldsymbol{A}(\boldsymbol{x})]_{m \times m}(\boldsymbol{a}(\boldsymbol{x}))_{m \times 1}=[\boldsymbol{B}(\boldsymbol{x})]_{m \times N}[\boldsymbol{U}]_{N \times 1}, $

(8)

其中

$ \begin{array}{c} \mathit{\boldsymbol{A}}(\mathit{\boldsymbol{x}}) = \sum\limits_{I = 1}^N {{\omega _I}} (\mathit{\boldsymbol{x}})(p(\mathit{\boldsymbol{x}})){(p(\mathit{\boldsymbol{x}}))^{\rm{T}}}, \\ \mathit{\boldsymbol{B}}(\mathit{\boldsymbol{x}}) = \left[ {{\omega _1}(\mathit{\boldsymbol{x}})\left( {p{\mathit{\boldsymbol{x}}_1}} \right){\omega _2}(\mathit{\boldsymbol{x}})\left( {p{\mathit{\boldsymbol{x}}_2}} \right){\omega _3}(\mathit{\boldsymbol{x}})\left( {p{\mathit{\boldsymbol{x}}_3}} \right) \cdots {\omega _N}(\mathit{\boldsymbol{x}})\left( {p{\mathit{\boldsymbol{x}}_N}} \right)} \right], \end{array} $

(9)

$ \boldsymbol{U}=\left[\begin{array}{lllll} \boldsymbol{u}_1 & \boldsymbol{u}_2 & \boldsymbol{u}_3 & \cdots & \boldsymbol{u}_N \end{array}\right]^{\mathrm{T}}$是域Ω中所有节点的节点值所形成的向量。

继而可得

$ u^{\mathrm{h}}(\boldsymbol{x})=(\boldsymbol{p}(\boldsymbol{x}))^{\mathrm{T}}[\boldsymbol{A}(\boldsymbol{x})]^{-1} \boldsymbol{B}(\boldsymbol{x}) \boldsymbol{U}=\bf{N}(\boldsymbol{x}) \boldsymbol{U}, $

(10)

式中：$\boldsymbol{N}(\boldsymbol{x})=\left[\begin{array}{llll} N_1(\boldsymbol{x}) & N_2(\boldsymbol{x}) & \cdots & N_N(\boldsymbol{x}) \end{array}\right] $，类似于有限单元法中的形函数，不同之处在于无网法中的形函数是关于全求解域，而有限单元法中的形函数是关于单元区域。

2 耦合热应力问题的EFG方法 2.1 耦合热应力控制方程

设线性耦合热弹性力学的求解区域为二维平面Ω，Γ为求解平面的边界。热弹性力学中的应力应变关系为

$ {\mathit{\boldsymbol{\sigma }}_{ij}} = 2\mathit{\mu }{\mathit{\boldsymbol{\varepsilon }}_{ij}} + \lambda {\mathit{\boldsymbol{\varepsilon }}_{kk}}{\mathit{\boldsymbol{\delta }}_{ij}} - \beta \theta {\mathit{\boldsymbol{\delta }}_{ij}}, $

(11)

式中：σ_ij是应力; μ, λ代表拉梅常数; ε_ij代表应变; β代表热应力系数；θ代表物体相对于初始温度T₀的温差(θ=T-T₀)。

在小变形条件下：

$ \boldsymbol{\varepsilon}_{i j}=\left(u_{i, j}+u_{j, i}\right) / 2 \text { 。} $

(12)

在处理耦合热应力问题时，采用分区变分原理，即温度场和位移场分别采用变分离散，再并行求解，经典热弹性力学理论中温度场和位移场的控制方程及边界条件如下：

$ \boldsymbol{\sigma}_{i j, j}+\boldsymbol{b}_i=0 $

(13)

$ k \boldsymbol{T}_{, i i}-\rho c \boldsymbol{T}-\beta T_0 \dot{\boldsymbol{u}}_{i, i}+\boldsymbol{Q}=0 。$

(14)

式中：ρ为质量密度；$ \dot{\boldsymbol{u}}_{i, i}$为体积应变率；c为比热容；k为热传导系数；Q为热源；b_i为体力。在边界Γ上，边界为混合边界条件，既包含力学边界条件也包含热学边界条件：

$ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{u}}_i}(\mathit{\boldsymbol{x}}, t) = {{\mathit{\boldsymbol{\overline u}} }_i}(\mathit{\boldsymbol{x}}, t), }&{{\rm{当}}x \in {\mathit{\Gamma }_u}, } \end{array} $

(15)

$ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{T}}_i}(x, t) = {{\mathit{\boldsymbol{\overline T}} }_i}(x, t){\rm{, }}}&{{\rm{当}}x \in {\mathit{\Gamma }_T}{\rm{, }}} \end{array} $

(16)

$ \begin{array}{*{20}{c}} {k{\mathit{\boldsymbol{T}}_{, i}}{\mathit{\boldsymbol{n}}_{, i}} = \xi \left( {\mathit{\boldsymbol{T}} - {\mathit{\boldsymbol{T}}_{\rm{A}}}} \right) + \mathit{\boldsymbol{\overline q}} {\rm{, }}}&{{\rm{当}}x \in {\mathit{\Gamma }_{q \cup \xi }}。} \end{array} $

(17)

式中：$ \overline{\boldsymbol{u}}_i$为边界上给定位移；$ \overline{\boldsymbol{T}}_i$为给定边界温度；ξ为换热系数；T_A为环境温度；${\mathit{\boldsymbol{\overline q}} } $为边界上指定热流量；Γ_u, Γ_T为第一类边界，Γ_q∪ξ是二三类混合边界。

2.2 耦合热应力控制方程的弱形式及离散化

在二维求解区域内采用N个节点进行离散，在整体区域内采用加权余量法弱式，以温度T的变分δT，及位移U的变分δU作为试函数进行离散，可得式(12)的离散形式：

$ \int\limits_\mathit{\Omega } {\delta \mathit{\boldsymbol{T}}\left( {k{\mathit{\boldsymbol{T}}_{,ii}} - \rho c\mathit{\boldsymbol{\dot T}} - \beta {\mathit{\boldsymbol{T}}_0}{{\mathit{\boldsymbol{\dot u}}}_{i,i}} + \mathit{\boldsymbol{Q}}} \right){\rm{d}}\mathit{\Omega } = 0} $

(18)

运用分部积分和高斯散度定理，并施加边界条件可得：

$ \begin{array}{*{20}{c}} {\delta {\mathit{\boldsymbol{I}}^*}(\mathit{\boldsymbol{T}}) = \int\limits_\mathit{\Omega } {\left[ {k\left( {{\nabla ^{\rm{T}}}\mathit{\boldsymbol{T}}} \right)\delta \nabla \mathit{\boldsymbol{T}} - \mathit{\boldsymbol{Q}}\delta \mathit{\boldsymbol{T}} + \rho c\mathit{\boldsymbol{\dot T}}} \right]{\rm{d}}\mathit{\Omega } + \int\limits_\mathit{\Omega } {\beta {\mathit{\boldsymbol{T}}_0}\delta \mathit{\boldsymbol{T}}{\rm{d}}\mathit{\Omega }{{\mathit{\boldsymbol{\dot u}}}_{i,i}} + } } }\\ {\int\limits_{{\mathit{\Gamma }_{q \cup \xi }}} {\xi \mathit{\boldsymbol{T}}\delta \mathit{\boldsymbol{T}}{\rm{d}}\mathit{\Gamma } - } \int\limits_{{\mathit{\Gamma }_{q \cup \xi }}} {\xi {\mathit{\boldsymbol{T}}_{\rm{a}}}\delta \mathit{\boldsymbol{T}}{\rm{d}}\mathit{\Gamma } - } \int\limits_{{\mathit{\Gamma }_{q \cup \xi }}} {\mathit{\boldsymbol{\bar q}}} \delta \mathit{\boldsymbol{T}}{\rm{d}}\mathit{\Gamma } = 0。} \end{array} $

(19)

因为移动最小二乘法(MLS)构建的形函数并不满足Kronecker delta特性，因此在式(18)的基础上使用拉格朗日乘子法对求解域进行本质边界条件(第一类边界条件)施加。

$ \begin{array}{*{20}{c}} {\delta {\mathit{\boldsymbol{I}}^*}(\mathit{\boldsymbol{T}}) = \int\limits_\mathit{\Omega } {\left[ {k\left( {{\nabla ^{\rm{T}}}\mathit{\boldsymbol{T}}} \right)\delta \nabla \mathit{\boldsymbol{T}} - \mathit{\boldsymbol{Q}}\delta \mathit{\boldsymbol{T}} + \mathit{\boldsymbol{\rho }}c} \right]{\rm{d}}\mathit{\Omega }} + \int\limits_\mathit{\Omega } {\mathit{\boldsymbol{\beta }}{T_0}\delta \mathit{\boldsymbol{T}}{\rm{d}}\mathit{\Omega }{{\mathit{\boldsymbol{\dot u}}}_{i,i}}} + \int\limits_{{\mathit{\Gamma }_q}_{ \cup \xi }} h \mathit{\boldsymbol{T}}\delta \mathit{\boldsymbol{T}}{\rm{d}}\mathit{\Gamma } - }\\ {\int\limits_{{\mathit{\Gamma }_q}_{ \cup \xi }} h {\mathit{\boldsymbol{T}}_a}\delta \mathit{\boldsymbol{T}}{\rm{d}}\mathit{\Gamma } - \int\limits_{{\mathit{\Gamma }_q}_{ \cup \xi }} {\mathit{\boldsymbol{\bar q}}\delta \mathit{\boldsymbol{T}}{\rm{d}}\mathit{\Gamma }} + \int\limits_{{\mathit{\Gamma }_T}} {\lambda \delta \mathit{\boldsymbol{T}} + \delta \lambda (\mathit{\boldsymbol{T}} - \mathit{\boldsymbol{\bar T}}){\rm{d}}\mathit{\Gamma }} }。\end{array} $

(20)

式(18)中λ为拉格朗日乘子，其视为坐标的位置函数，可利用本质边界条件上的节点进行插值。

$ \boldsymbol{\varphi}=\left[\begin{array}{lllll} \varphi_1 & \varphi_2 & \cdots & \varphi_{n_\lambda-1} & \varphi_{n \lambda} \end{array}\right], $

(21)

$ \mathit{\boldsymbol{ \boldsymbol{\varLambda} }} = {\left[ {\begin{array}{*{20}{l}} {{\lambda _1}}&{{\lambda _2}}& \cdots &{{\lambda _{n\lambda }} - 1}&{{\lambda _{n\lambda }}} \end{array}} \right]^{\rm{T}}}, $

(22)

$ \lambda = \mathit{\boldsymbol{\varphi \boldsymbol{\varLambda} }}, $

(23)

式中：φ_i为拉格朗日插值函数；λ_i为本质边界条件上用于插值的节点值；n_λ为本质边界上用于拉格朗日插值的节点数目。

同理运用上述的变分过程外加在本质边界条件上施加拉格朗日乘子法，对位移场的控制方程(13)进行离散处理可得到：

$ \begin{array}{*{20}{c}} {\int\limits_\mathit{\Omega } {\left( {\mathit{\boldsymbol{L}}\delta {\mathit{\boldsymbol{u}}^{\rm{T}}}} \right)\mathit{\boldsymbol{D}}(\mathit{\boldsymbol{Lu}}){\rm{d}}\mathit{\Omega }} - \int\limits_\mathit{\Omega } {\left( {\mathit{\boldsymbol{L}}\delta {\mathit{\boldsymbol{u}}^{\rm{T}}}} \right){\mathit{\boldsymbol{D}}_n}{\rm{d}}\mathit{\Omega }T} - \int\limits_{{\mathit{\Gamma }_T}} {\lambda \delta \mathit{\boldsymbol{u}} + \delta \lambda (\mathit{\boldsymbol{u}} - \mathit{\boldsymbol{\dot u}}){\rm{d}}\mathit{\Gamma }} = }\\ {\int\limits_\mathit{\Omega } {\delta {\mathit{\boldsymbol{u}}^{\rm{T}}}\mathit{\boldsymbol{b}}{\rm{d}}\mathit{\Omega }} - \int\limits_\mathit{\Omega } {\left( {\mathit{\boldsymbol{L}}\delta {\mathit{\boldsymbol{u}}^{\rm{T}}}} \right)} {\mathit{\boldsymbol{D}}_n}{\mathit{\boldsymbol{T}}_0}{\rm{d}}\mathit{\Omega }}。\end{array} $

(24)

位移场近似函数以及温度场的近似函数分别为

$ \mathit{\boldsymbol{u}}(x, t) = \sum\limits_{I = 1}^n {{N_I}} (x){u_I}(t), $

(25)

$ \mathit{\boldsymbol{T}}(x, t) = \sum\limits_{I = 1}^n {{N_I}} (x){T_I}(x)。$

(26)

将式(25)和(26)代入式(24)和式(20)中可得到如下方程式：

$ \left\{ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{K}}_T}{\mathit{\boldsymbol{T}}_n} + \mathit{\boldsymbol{C}}\frac{{\partial {\mathit{\boldsymbol{T}}_n}}}{{\partial \mathit{\boldsymbol{t}}}} + {\mathit{\boldsymbol{G}}_u}\frac{{\partial {\mathit{\boldsymbol{u}}_n}}}{{\partial \mathit{\boldsymbol{t}}}} + {\mathit{\boldsymbol{G}}_1}{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_T} = {\mathit{\boldsymbol{F}}_T}, }\\ {\mathit{\boldsymbol{G}}_1^{\rm{T}} = {\mathit{\boldsymbol{q}}_T}, }\\ {{\mathit{\boldsymbol{K}}_u}{\mathit{\boldsymbol{u}}_n} + {\mathit{\boldsymbol{G}}_T}{\mathit{\boldsymbol{T}}_n} + {\mathit{\boldsymbol{G}}_2}{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_u} = {\mathit{\boldsymbol{F}}_u}, }\\ {\mathit{\boldsymbol{G}}_2^{\rm{T}}{\mathit{\boldsymbol{u}}_n} = {\mathit{\boldsymbol{q}}_u}。} \end{array}} \right. $

(27)

式中：

$ {\mathit{\boldsymbol{K}}_T} = \int\limits_\mathit{\Omega } {k\mathit{\boldsymbol{N}}_{, i}^{\rm{T}}\mathit{\boldsymbol{N}}_{, i}^{\rm{T}}{\rm{d}}\mathit{\Omega }} + \int\limits_{{\mathit{\Gamma }_3}} {\xi {\mathit{\boldsymbol{N}}^{\rm{T}}}\mathit{\boldsymbol{N}}{\rm{d}}\mathit{\Gamma }} , $

(28)

$ \mathit{\boldsymbol{C}} = \int\limits_\mathit{\Omega } {\rho c{\mathit{\boldsymbol{N}}^{\rm{T}}}\mathit{\boldsymbol{N}}{\rm{d}}\mathit{\Gamma }} , $

(29)

$ {\mathit{\boldsymbol{G}}_u} = \beta {\mathit{\boldsymbol{T}}_0}\int\limits_\mathit{\Omega } {{\mathit{\boldsymbol{N}}^{\rm{T}}}\left[ {\begin{array}{*{20}{l}} {\frac{\partial }{{\partial x}}}&{\frac{\partial }{{\partial y}}} \end{array}} \right]{{[\mathit{\boldsymbol{H}}]}^{\rm{T}}}{\rm{d}}\mathit{\Omega }\frac{{\partial {u_n}}}{{\partial t}}} , $

(30)

$ G_1^{Ik} = \int\limits_{{\rm{ }}{\mathit{\Gamma }_T}} {{N_I}{\varphi _k}{\rm{d}}\mathit{\Gamma }} , $

(31)

$ {\mathit{\boldsymbol{K}}_u} = \int\limits_\mathit{\Omega } {{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{DB}}{\rm{d}}\mathit{\Omega }} , $

(32)

$ {\mathit{\boldsymbol{G}}_T} = - \int\limits_\mathit{\Omega } {{\mathit{\boldsymbol{B}}^{\rm{T}}}} {\mathit{\boldsymbol{D}}_n}\mathit{\boldsymbol{N}}{\rm{d}}\mathit{\Omega }, $

(33)

$ G_2^{Ik} = \int\limits_{{\mathit{\Gamma }_u}} {{N_I}} {\varphi _k}{\rm{d}}\mathit{\Gamma }, $

(34)

$ {\mathit{\boldsymbol{F}}_T} = \int\limits_\mathit{\Omega } Q \mathit{\boldsymbol{N}}{\rm{d}}\mathit{\Omega } + \int\limits_{{\mathit{\Gamma }_2}} \mathit{\boldsymbol{q}} \mathit{\boldsymbol{N}}{\rm{d}}\mathit{\Gamma } + \int\limits_{{\mathit{\Gamma }_3}} \xi {\mathit{\boldsymbol{T}}_A}\mathit{\boldsymbol{N}}{\rm{d}}\mathit{\Gamma , } $

(35)

$ {q_T} = \int\limits_{{\mathit{\Gamma }_T}} {\bar T} {\varphi _k}{\rm{d}}\mathit{\Gamma , } $

(36)

$ {\mathit{\boldsymbol{F}}_u} = \int\limits_\mathit{\Omega } {{\mathit{\boldsymbol{N}}^{\rm{T}}}} \mathit{\boldsymbol{b}}{\rm{d}}\mathit{\Omega } - \int\limits_\mathit{\Omega } {{\mathit{\boldsymbol{B}}^{\rm{T}}}} {\mathit{\boldsymbol{D}}_n}{\mathit{\boldsymbol{T}}_0}{\rm{d}}\mathit{\Omega }, $

(37)

$ {\mathit{\boldsymbol{q}}_u} = \int\limits_{{\mathit{\Gamma }_u}} {\mathit{\boldsymbol{\overline u}} } {\varphi _k}{\rm{d}}\mathit{\Gamma }, $

(38)

$ \boldsymbol{H}=\left[\begin{array}{ccccccccc} N_1 & 0 & N_2 & 0 & N_3 & 0 & \cdots & N_n & 0 \\ 0 & N_1 & 0 & N_2 & 0 & N_3 & \cdots & 0 & N_n \end{array}\right], $

(39)

$ \boldsymbol{D}=\frac{E}{\left(1-\nu^2\right)}\left[\begin{array}{ccc} 1 & \nu & 0 \\ \nu & 1 & 0 \\ 0 & 0 & \frac{1-\nu}{2} \end{array}\right] \text {, } $

(40)

$ \beta=\frac{\alpha E}{(1-\nu)}, $

(41)

$ \boldsymbol{D}_n=\beta \cdot\left[\begin{array}{lll} 1 & 1 & 0 \end{array}\right]^{\mathrm{T}}, $

(42)

$ \boldsymbol{B}_I=\left[\begin{array}{cc} \frac{\partial N_I}{\partial x} & 0 \\ 0 & \frac{\partial N_I}{\partial y} \\ \frac{\partial N_I}{\partial y} & \frac{\partial N_I}{\partial x} \end{array}\right] \text { 。} $

(43)

式中：E, ν分别代表平面应力条件下的弹性模量和泊松比，α是热膨胀系数。

式(27)为施加边界条件以及拉格朗日乘子法后的系统一阶偏微分方程组，采用向后差分的形式对上述微分方程组进行求解可得如下方程：

$ \left\{ {\begin{array}{*{20}{c}} {\Delta t{\mathit{\boldsymbol{K}}_T}{\mathit{\boldsymbol{T}}_n} + {\mathit{\boldsymbol{G}}_u}{\mathit{\boldsymbol{u}}_n} + {\mathit{\boldsymbol{G}}_1}{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_T} = \Delta t{\mathit{\boldsymbol{F}}_T} + \mathit{\boldsymbol{C}}{\mathit{\boldsymbol{T}}_{n - 1}} + {\mathit{\boldsymbol{G}}_u}{\mathit{\boldsymbol{u}}_{n - 1}}, }\\ {\mathit{\boldsymbol{G}}_1^{\rm{T}}{\mathit{\boldsymbol{T}}_n} = {\mathit{\boldsymbol{q}}_T}, }\\ {{\mathit{\boldsymbol{K}}_u}{\mathit{\boldsymbol{u}}_n} + {\mathit{\boldsymbol{G}}_T}{\mathit{\boldsymbol{T}}_n} + {\mathit{\boldsymbol{G}}_2}{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_u} = {\mathit{\boldsymbol{F}}_u}, }\\ {\mathit{\boldsymbol{G}}_2^{\rm{T}}{\mathit{\boldsymbol{u}}_n} = {\mathit{\boldsymbol{q}}_u}。} \end{array}} \right. $

(44)

2.3 自适应

自适应分析的核心思想是根据已有的数值计算模型判断出该计算区域内的高误差分布区域，然后进行算法调整，继而改进数值计算结果精度。常用的自适应方法有R型自适应，H型自适应，以及HP型自适应。这里采用H型自适应，H型自适应在无网格方法中的本质是节点的增加和删除。它的实现主要包含以下两个方面，一方面是后验误差估计，另一方面就是节点的插入策略。通过引入局部误差计算公式(45)和全局误差计算公式(46)，利用Voronoi邻接准则去进行节点的添加，分别以设定的局部误差限ε_u和全局误差限L_u作为局部节点的添加界限和自适应过程终止界限。关于自适应详细的后验误差计算公式的推导过程，鉴于篇幅的原因，此处不再赘述，可参考文献[19-20]。有如下误差估计式。

局部误差估计式：

$ \varepsilon\left(u^{\mathrm{h}}\right)=\frac{1}{4}\left\|\left(\nabla u_2-\nabla u_1\right) \Delta \boldsymbol{x}\right\|_{F}。$

(45)

全局误差估计式：

$ L\left(u^{\mathrm{h}}\right)=\frac{\left\|\varepsilon_u\right\|_F}{\left\|u^{\mathrm{h}}\right\|_F}=\frac{\sqrt{\sum\limits_{k=1}^N \varepsilon_k^2}}{\sqrt{\sum\limits_{k=1}^N\left(u_k^{\mathrm{h}}\right)^2}} \text { 。} $

(46)

对公式中的参量做如下说明：设定$\boldsymbol{X}_1=\left(x_1, y_1\right), \boldsymbol{X}_2=\left(x_2, y_2\right) $是平面中对应的两点，u₁，u₂分别是以上2个点在求解域内对应的场函数值，$ \nabla$代表梯度，$ \Delta \boldsymbol{x}=\left(x_2-x_1, y_2-y_1\right)$表示两节点构成的向量，u^h代表利用EFG求得的场函数近似值。

3 数值算例

为了验证文中所提出计算模型的有效性，选取2类数值算例，分别是光滑平板在混合边界条件下的热力耦合问题和具有凹凸边界二维板的热力耦合问题，所选均为平面应变状态，式(40)和(41)的E, ν分别变成$ \frac{E}{1-\nu^2} \frac{\nu}{1-\nu}$，热膨胀系数α变成$ (1+\nu) \alpha$。

3.1 算例1

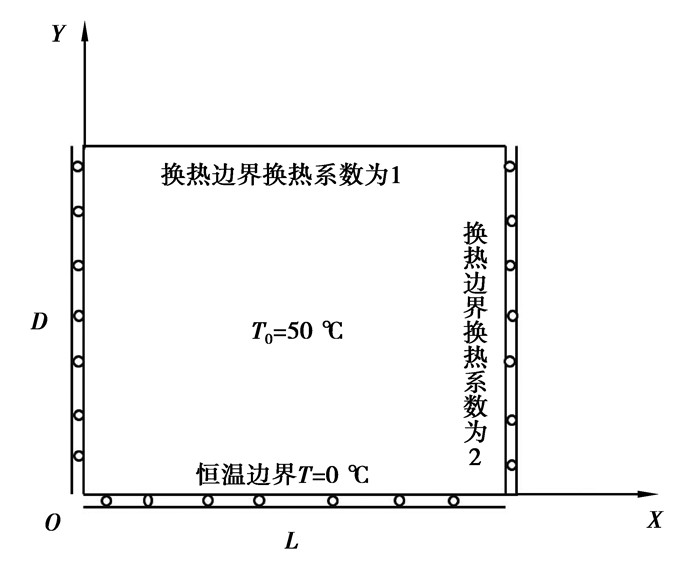
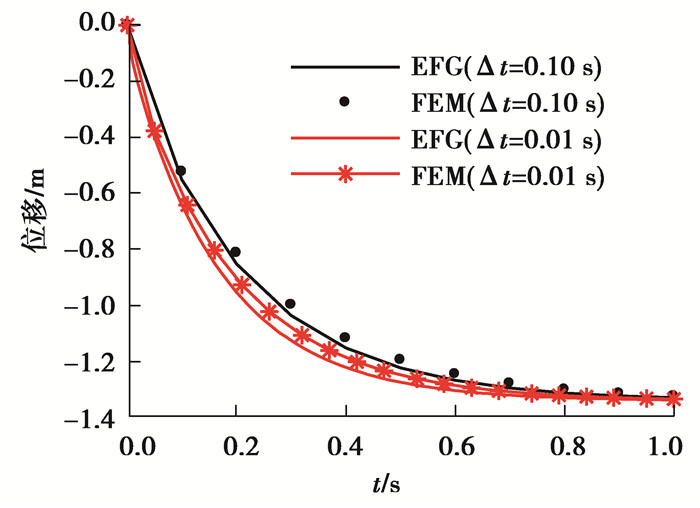
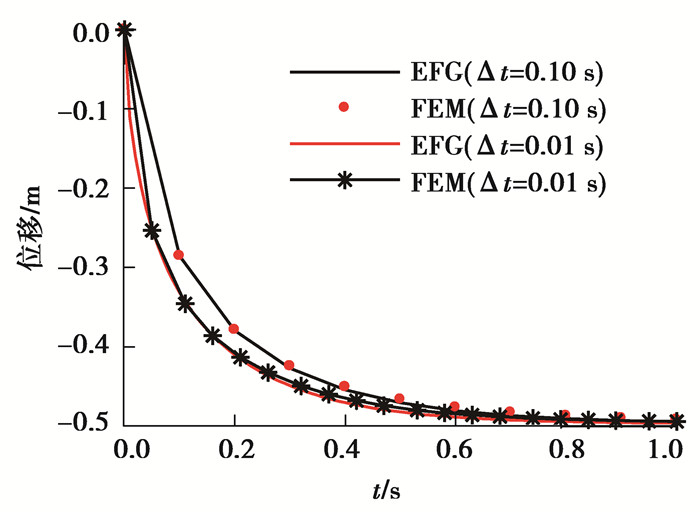
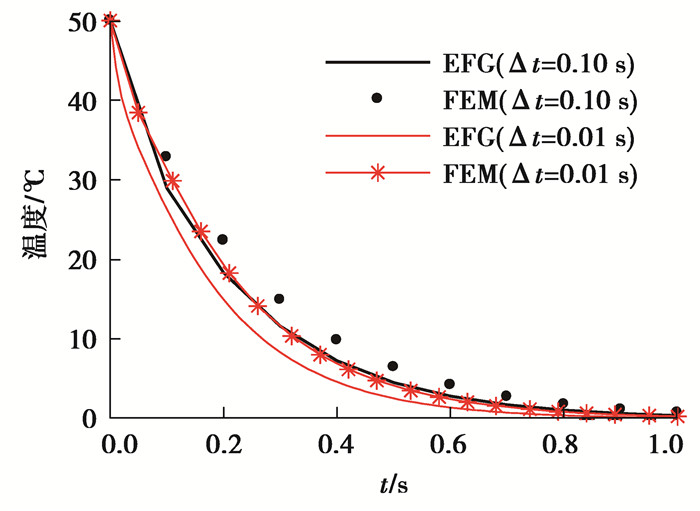
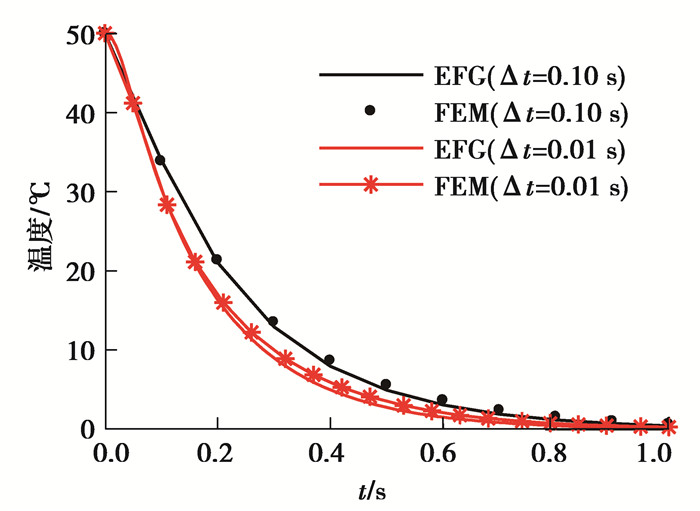
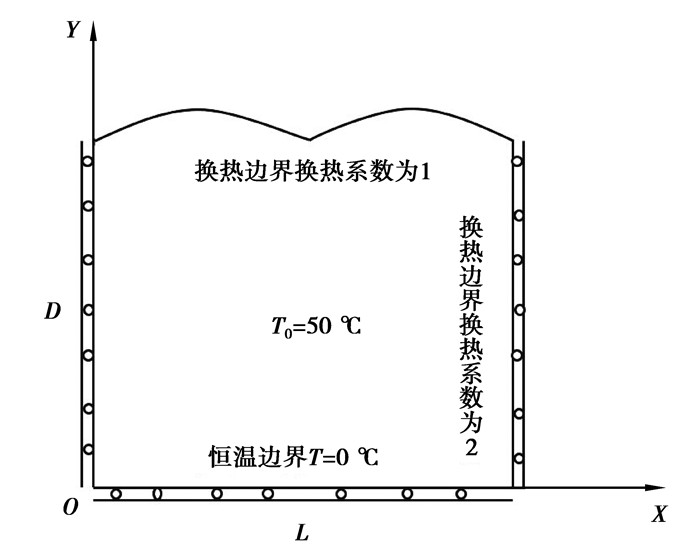
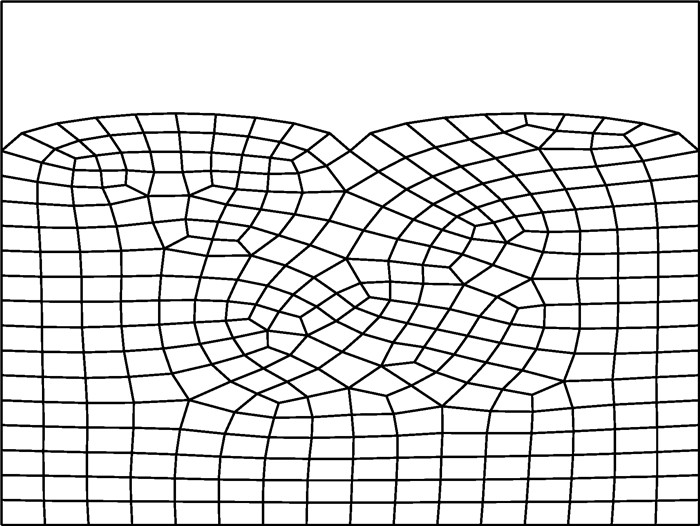
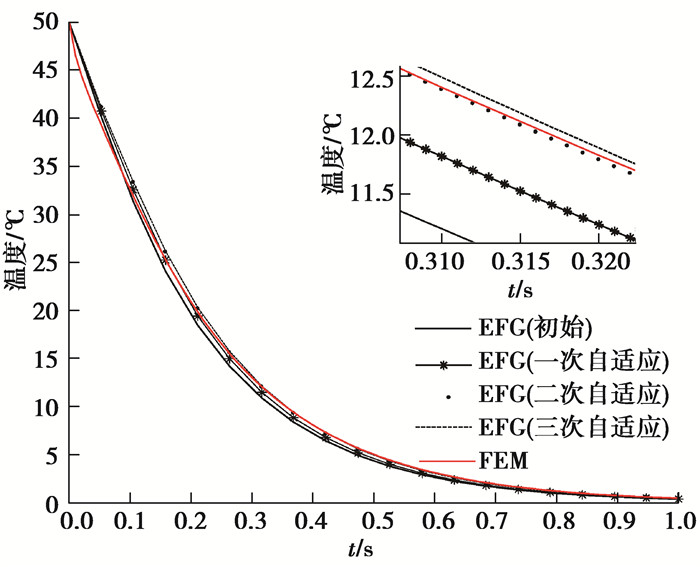
此算例是光滑平板在混合边界条件下的热力耦合计算问题，如图 2所示方板，其长度L=1 m，宽度D=1 m，厚度为1 mm，计算参数按如下公式给定，图 3、4分别表示网格示意图和布点示意图，左右两端及下端均施加位移约束，在最左端边界上是绝热边界条件，最上端和最右端存在对流热交换，对流热交换系数分别是ζ₂=1，ζ₄=2，最底部边界是第一类传热边界条件，温度恒为0 ℃，初始温度场分布是T₀=50 ℃，取分析步长度Δt₁=0.10 s，Δt₂=0.01 s，分别迭代10步和100步，为了更好地对比体现无网格伽辽金法的精度与收敛速度，采用相同网格节点(21×21)的有限单元算法在相同的时间步下进行计算，截取第231号节点(0.50，1.00)，306号节点(0.70，0.55)的温度-时间历程图及纵向位移-时间历程图，计算结果如图 5~8所示。

控制方程：

$ k \boldsymbol{T}_{, i i}=\rho c \frac{\partial T}{\partial t}, $

(47)

$ \boldsymbol{\sigma}_{i j, i}+\boldsymbol{b}_i=0 。$

(48)

边界条件：

$ \left(\frac{\partial \boldsymbol{T}}{\partial t}\right)_{x=0}=0 \quad\left(\frac{\partial \boldsymbol{T}}{\partial x}+\frac{\xi_2}{k}\left(\boldsymbol{T}-\boldsymbol{T}_{\mathrm{A}}\right)\right)_{x=L}=0, $

(49)

$ \boldsymbol{T}_{y=0}=0\left(\frac{\partial \boldsymbol{T}}{\partial y}+\frac{\xi_4}{k}\left(\boldsymbol{T}-\boldsymbol{T}_{\infty}\right)\right)_{y=D}=0, $

(50)

$ u_{x=0}=0, \quad u_{x=L}=0, \quad u_{y=L}=0, $

(51)

$ k=1, \quad \xi_2=1, \quad \xi_4=2, \quad \rho=1, \quad c=1, $

(52)

$ \boldsymbol{T}_{\mathrm{A}}=0, \quad E=1, \quad \nu=0.3, \quad \alpha=0.02 \text { 。} $

(53)

从图 5~8可以看出，无网格方法计算温度值和位移值的精度较有限元法大致相同，但在时间步为0.10 s时，EFG算法的计算结果更加靠近FEM算法下0.01 s步长时的计算结果，因而无网格方法的收敛速度较有限元收敛速度略快。

3.2 算例2

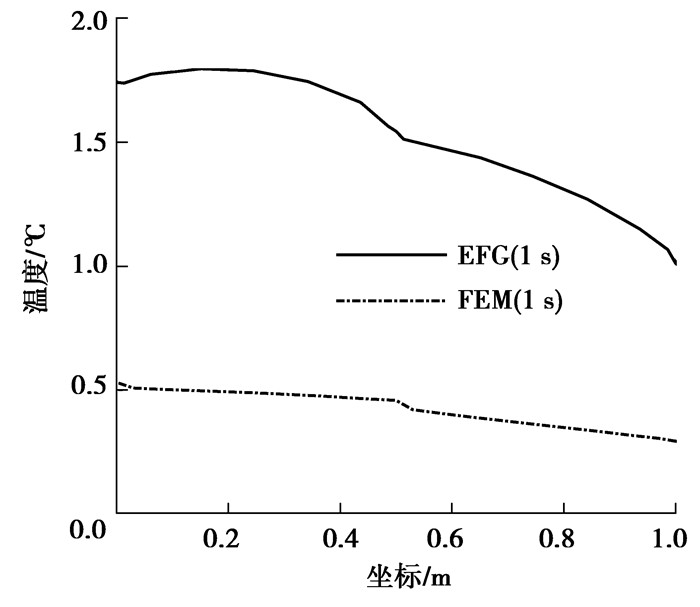
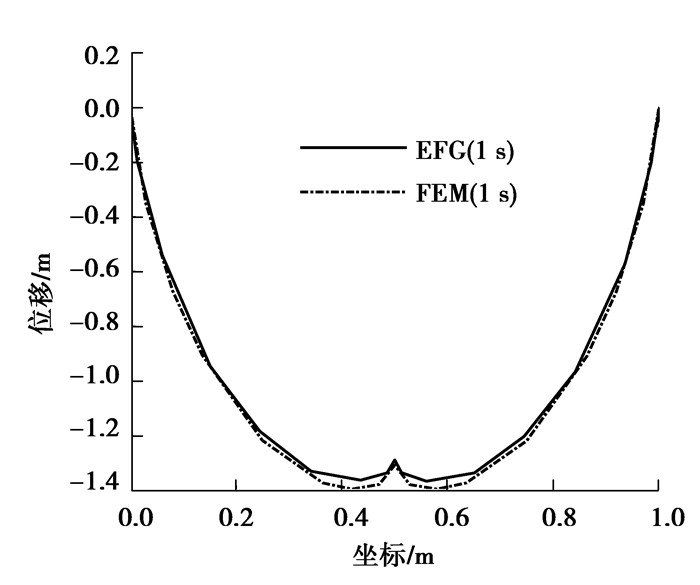
此算例是凹凸平板在混合边界条件下的热力耦合计算问题，如图 9所示，长度L=1 m，宽度D=1 m，厚度为1 mm，图 10和11为布点示意图和网格示意图。计算参数按图示给定，左右两端及下端施加位移固定约束，在最左端边界是绝热边界条件，最上端和最右端存在对流热交换，对流热交换系数分别是ζ₂=1，ζ₄=2，最底部边界是第一类传热边界条件温度恒为0 ℃，初始温度场分布是T₀=50 ℃，分析步长度Δt=0.001 s，共计迭代1 000步，为了更好地对比体现无网格伽辽金法的计算精度，采用在相同的时间步下进行计算，有限元算法采用四边形八节点二次单元计算，输出顶端凹凸边界的温度场及位移场分布，分别截取1 s的计算结果，计算结果如图 12、13所示。

控制方程：

$ k \boldsymbol{T}_{, i i}=\rho c \frac{\partial \boldsymbol{T}}{\partial t}, $

(54)

$ \boldsymbol{\sigma}_{i j, i}+\boldsymbol{b}_i=0 \text { 。} $

(55)

边界条件：

$ \left(\frac{\partial \boldsymbol{T}}{\partial t}\right)_{x=0}=0 \quad\left(\frac{\partial \boldsymbol{T}}{\partial x} n_x+\frac{\partial \boldsymbol{T}}{\partial y} n_y+\frac{\xi_2}{k}\left(\boldsymbol{T}-\boldsymbol{T}_{\mathrm{A}}\right)\right)_{y=D}=0, $

(56)

$ \boldsymbol{T}_{y=0}=0 \quad\left(\frac{\partial \boldsymbol{T}}{\partial x} n_x+\frac{\partial \boldsymbol{T}}{\partial y} n_y+\frac{\xi_4}{k}\left(\boldsymbol{T}-\boldsymbol{T}_{\mathrm{A}}\right)\right)_{x=L}=0, $

(57)

$ u_{x=0}=0, \quad u_{x=L}=0, \quad u_{y=L}=0 \text { 。} $

(58)

$ k=1, \quad \xi_2=1, \quad \xi_4=2, \quad \rho=1, \quad c=1, $

(59)

$ \boldsymbol{T}_{\mathrm{A}}=0, \quad E=1, \quad \nu=0.3, \quad \alpha=0.02 \text { 。} $

(60)

由图 12、13可看出，在t=1 s时，两种不同的算法下，温度场和位移场差异较大，使用有限元网格节点替代无网格节点并不适用，由移动最小二乘法(MLS)的推导过程，可以知道造成数据偏差较大的原因是无网格伽辽金方法的计算精度受节点密度、节点摆放位置以及权函数多重因素的影响，所以无规律地增加节点密度会影响无网格伽辽金方法计算精度，因此后续应采用自适应技术与之相结合，使用自适应技术控制节点密度合理增加。

3.3 算例3

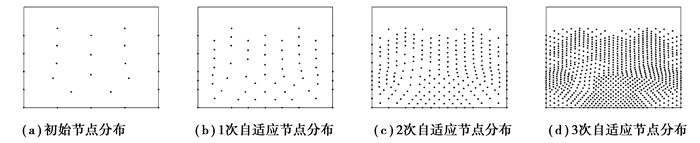
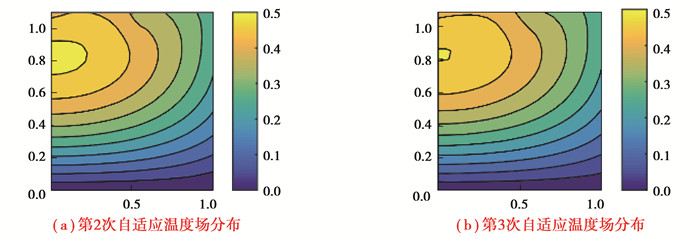
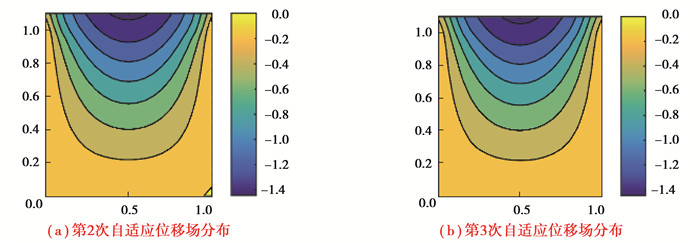
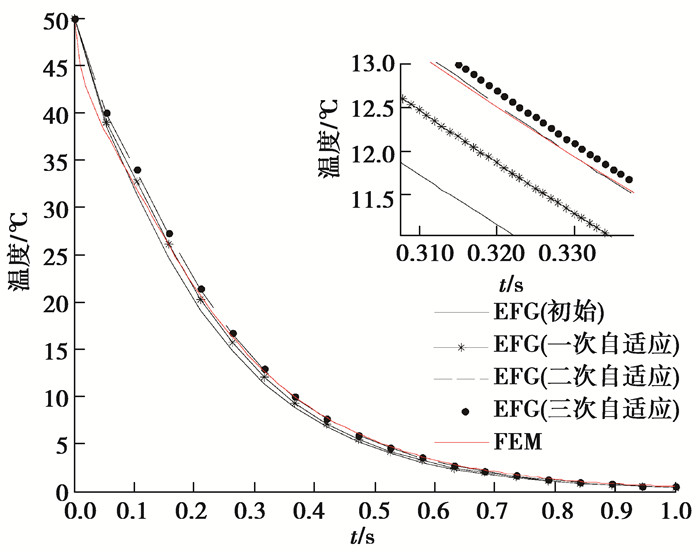
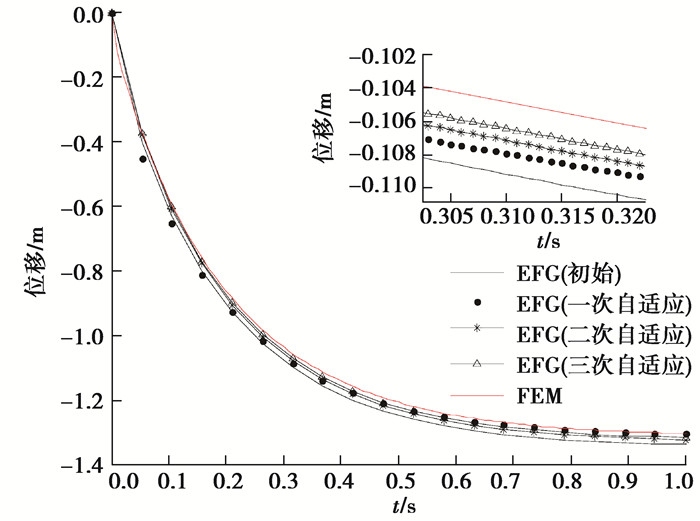
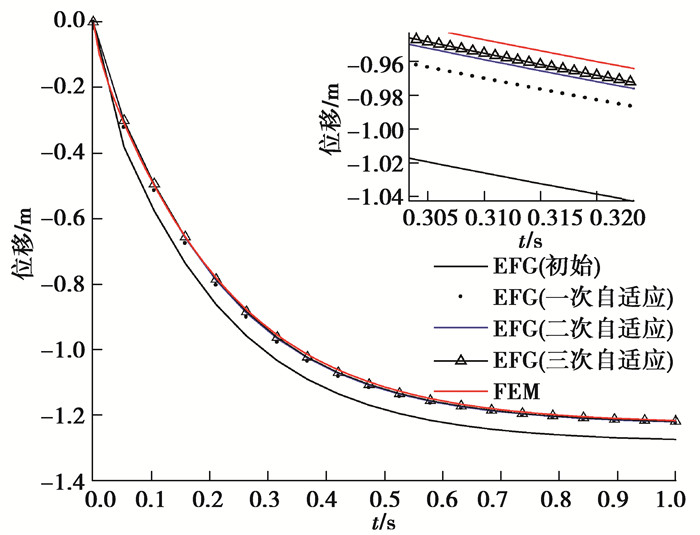
由3.2的算例数据结果分析可知，在采用有限元软件网格节点去进行EFG算法计算的过程中，虽然节点的数目变多了，但由于节点布置得不合理，导致比较大的数据误差。自适应能够通过控制节点合理增加，达到确保精度的效果。本算例同样采用图 9所示的模型和边界条件，出于对计算时间成本的考虑，在处理非定常热力耦合问题的自适应过程中，采用算例3.2相同边界条件下的定常温度场静态热力耦合问题的自适应节点布图，节点分布示意如图 14所示，初始选择简单节点布置共计26个节点，支撑域尺寸参数为3.5，设置局部误差限ε_m=0.001，以及全局误差限L(u^h)=0.020，当自适应结束后，利用得到的节点布图来计算混合边界下热力耦合问题的温度场和位移场。为了方便对比，采用算例3.2中的有限元算法下(FEM)四边形八节点单元网格分布进行对比，迭代步长为0.001 s，共计1 000步的热力耦合分析。比较t=1 s时随着自适应次数增加的温度场和位移场的分布以及11号节点(0.50，1.00)和15号节点(0.25，1.10)的时间-温度历程图和时间-位移历程图。

从图 15~20的计算结果分析，在局部放大图中，可以看到随着自适应过程的增加，对于节点11和节点15而言，不论是温度值还是位移值都随着时间的变化逐渐趋于稳定并且是收敛的，且t=1 s时整体的温度场和位移场的分布也都是稳定且收敛的。结果表明将后验误差式引入自适应调节之中，能够合理有效地控制节点的增加，继而保证计算精度，自适应技术与无网格方法相结合能够应对具有凹凸边界作用下热力耦合问题，为后续无网格方法的程序化、软件化及商业化提供了十分良好的案例。

4 结论

采用非定常温度场拟静态热力耦合问题的EFG法计算模型，分别求解了光滑平板，凹凸边界平板的热力耦合问题的位移场和温度场分布，并且采用H型自适应对实际工程中的凹凸边界热力耦合问题进行了算法优化，研究表明：

1) 在应对光滑边界的热力耦合问题时，无网格方法的精度以及收敛速度略高于有限元方法，并且由于节点施加的便捷性，可结合有限元网格剖分软件的单元节点去替代无网格节点，在实际工程中，可优先考虑使用无网格方法对结构温度场和位移场随时间的变化进行计算，能够获得十分精确的数值解。

2) 在应对结构具有凹凸边界的热力耦合问题时，将无网格方法与H型自适应技术相结合，在确保边界条件顺利施加的情况下又能够合理地增加节点密度，继而保证计算精度，考虑到计算时间成本的问题，可用相同边界条件下定常温度场静态问题的自适应节点分布图去替代计算。自适应技术与无网格算法相结合，为后续无网格算法的程序化、软件化及商业化提供了十分广阔的前景。