液滴在电场作用下发生变形及运动，这种现象广泛存在于自然界和工业应用中。例如，雨滴在雷暴中发生爆裂^[1]；在石油工业中，通过电场控制促进液滴融合，有助于实现油水分离^[2]；在微流控装置中，通过电融合可以精确、无污染地控制试剂的混合^[3]等。

相比于直流电场中的液滴研究，弱导电液滴在交变电场中的运动和变形研究还鲜有报道^[4-6]。对于单个液滴变形，Torza等^[4]通过理论和实验研究了交变电场下弱导电液滴的变形，发现交变电场频率会影响液滴的平均变形：当频率趋于0时，交变电场中液滴的平均变形收敛于等效直流电场中的漏电介质模型稳态解^[7]；当频率趋近于无穷大时，交变电场中液滴的平均变形收敛于基于理想介质模型得到的稳态解^[8]。Esmaeeli等^[9]基于漏电介质模型研究了交变电场中二维液滴的变形，结果表明对于所有的电导率比和介电常数比，液滴在交变电场中的平均变形与等效直流电场作用下的稳态变形相等。根据漏电介质模型的假设，电荷弛豫时间应当远小于流动时间，而当电场频率过高时，流动时间减小，漏电介质模型将不再适用，这就限制了Esmaeeli等的研究所采用的电场频率。为了克服漏电介质模型对电场频率的限制，López-Herrera等^[10]提出了基于电荷守恒方程的两相流模型，并被Sahu等^[11]用于交变电场中轴对称弱导电液滴的变形研究，结果表明当电导率比和介电常数比不相等时，液滴在交变电场中的平均变形与等效直流电场产生的稳态变形不相等，但他们并未对电场频率的影响进行深入研究。对于双液滴在交变电场的融合，当前研究主要关注油包水乳状液，适用于理想电介质模型，国内外学者研究了电场频率^[12-13]、电场强度^[14]、液滴半径^[15]、双液滴间距^[16-17]及油水界面张力^[18]等因素对双液滴融合的影响。此外，陈晓东等^[19]采用漏电介质模型研究了双液滴在交流电场下的相互作用变形。综上所述，当前对于交变电场中液滴变形的研究主要采用理想电介质模型和漏电介质模型，而弱导电液滴在交变电场中的变形和融合还未得到充分关注，交变电场频率对液滴变形作用的物理机理也尚不明确。

常见的界面捕捉数值方法可以分为两类：一是追踪拉格朗日界面标记点的界面追踪方法，例如front-tracking方法^[20]等；二是用一个标量标识函数(体积分数或相变量)来区分不同相态流体的界面捕捉方法，例如volume of fluid (VOF)方法^[21]、level set方法^[22]和相场方法^[23]等。采用front-tracking方法和漏电介质模型，Fernández等^[24-25]研究了直流电场和剪切流动共同作用下多个液滴的变形。Hua等^[26]采用front-tracking方法，研究了直流电场下单个液滴的变形。虽然front-tracking方法可以准确追踪相界面位置，但在处理液滴破裂和融合等复杂拓扑变化时会遇到困难，需要额外的特殊处理。界面捕捉方法通过求解关于界面识别函数的对流扩散方程来反映界面运动和变形，可以有效捕捉复杂界面拓扑变化。Mählmann等^[27]采用level set方法，研究了直流电场作用下，雷诺数对剪切流动中的液滴的影响。结合VOF方法和level set方法，Tomar等^[28]研究了直流电场中导电液滴的变形和融合。Lin等^[29]采用相场方法和漏电介质模型，研究了直流电场中双液滴的融合。考虑到漏电介质模型的局限性，López-Herrera等^[10]引入电荷守恒模型以考虑电荷的输运，发展了基于VOF方法的电场作用下两相流动模型。相比于VOF和level set方法，相场方法具有坚实的理论基础，既能保证质量、能量守恒以及满足热力学第二定律，还可以通过修正界面自由能泛函引入复杂的流体属性和物理效应，例如黏弹性多相流动^[30]、表面活性剂作用^[31]、壁面湿润性^[32-33]以及热毛细效应^[34]。此外，在数值层面上，相场方法描述相界面运动和变形无需引入额外的非物理处理。因此笔者选择相场方法捕捉界面运动和变形，采用电荷守恒模型描述电荷的输运，发展了考虑电场作用的两相流数值方法，在OpenFOAM框架下完成程序开发，研究不同频率交变电场作用下弱导电单个液滴变形和双液滴融合，系统分析了不同电物性参数条件下电场频率对液滴变形和融合时间的影响。

1 基本理论 1.1 Cahn-Hilliard相场模型

相场方法是基于自由能理论的一种扩散界面方法。对于两相不混溶流体A和B，令流体A的体积分数为C，则流体B的体积分数为1-C，体积分数C即为相变量，它随时间的演化由Cahn-Hilliard方程^[35]来控制：

$ \frac{\partial C}{\partial t}+\nabla \cdot(\boldsymbol{u}C)=\nabla \cdot(M \nabla \varphi), $

(1)

$ \varphi=\frac{1}{2} a \varepsilon^{-1} \sigma C(C-1)(2 C-1)-a \varepsilon \sigma \Delta C \text {。} $

(2)

式中：u是流动速度；M为迁移率；φ为化学势，由总自由能泛函对相分数的变分得到；ε为界面厚度；σ为表面张力系数；a为待定系数；t是时间。对于没有外界质量流入的边界，化学势φ的边界条件为

$ \boldsymbol{n}_{\mathrm{w}} \cdot \nabla \varphi=0, $

(3)

式中n_w为边界的外法向方向矢量。

van der Waals^[36]提出当相分布处于平衡状态时自由能应取极值，此时化学势φ=0，所得一维相分布为

$ C(z)=\frac{1}{2}+\frac{1}{2} \tanh \left(\frac{z}{2 \sqrt{2} \varepsilon}\right) \text { 。} $

(4)

在自由能理论中，表面张力的作用可理解为单位相界面上的自由能，对于平衡态的界面^[31]可得到

$ \sigma=\varepsilon a \sigma \int_{-\infty}^{+\infty}\left(\frac{\mathrm{d} C}{\mathrm{~d} z}\right)^2 \mathrm{d} z。$

(5)

代入方程(4)的理论解，得到$ a=6 \sqrt{2}$。定义无量纲化学势$\widehat{\varphi}=\varphi /\left(\varepsilon^{-1} \sigma a\right) $，可以得到如下基于无量纲化学势$\widehat{\varphi} $的Cahn-Hilliard方程：

$ \left\{\begin{array}{l} \frac{\partial C}{\partial t}+\nabla \cdot(\boldsymbol{u}C)=\nabla \cdot(\widehat{M} \nabla \hat{\varphi}), \\ \hat{\varphi}=\frac{1}{2} C(C-1)(2 C-1)-\varepsilon^2 \Delta C, \end{array}\right. $

(6)

式中$ \widehat{M}=M \varepsilon^{-1} \sigma a$。这里采用相场方法，表面张力为^[37-38]：

$ \boldsymbol{F}_{\mathrm{s}}=\frac{6 \sqrt{2} \sigma}{\varepsilon} \widehat{\varphi} \nabla C_{\circ} $

(7)

1.2 电场控制方程

根据电流体动力学理论，产生的动态电流很小时，可以忽略磁感应效应，因此电场强度是无旋的，即▽×E=0。对于电介质流体，由高斯定律可得

$ \nabla \cdot\left(\varepsilon_{\mathrm{E}} \boldsymbol{E}\right)=\rho^{\mathrm{E}}, $

(8)

式中：ε_E为流体的介电常数，ρ^E为体电荷密度。电荷守恒方程为：

$ \frac{\partial \rho^{\mathrm{E}}}{\partial t}+\nabla \cdot\left(\boldsymbol{u} \rho^{\mathrm{E}}\right)=-\nabla\left(\sigma_{\mathrm{E}} \boldsymbol{E}\right), $

(9)

式中σ_E为流体的电导率。

由于电场是无旋的，电场强度E和电势ϕ的关系为：

$ \boldsymbol{E}=-\nabla \phi_{\circ} $

(10)

方程(8)和(9)可写为：

$ -\nabla \cdot\left(\varepsilon_E \nabla \phi\right)=\rho^E, $

(11)

$ \frac{\partial \rho^{\mathrm{E}}}{\partial t}+\nabla \cdot\left(u \;\rho^{\mathrm{E}}\right)=\nabla\left(\sigma_{\mathrm{E}} \nabla \phi\right) 。$

(12)

电场力F_e的表达式为：

$ \boldsymbol{F}_{\mathrm{e}}=\nabla \cdot \boldsymbol{\tau}^{\mathrm{E}}=\rho^{\mathrm{E}} \boldsymbol{E}-\frac{1}{2} \boldsymbol{E} \cdot \boldsymbol{E} \nabla_{\varepsilon_\boldsymbol{E}}, $

(13)

式中：第一项为库仑力，第二项为极化应力。

1.3 流动控制方程

对于等温不可压两相流动，流体运动控制方程为不可压缩的N-S方程组：

$ \left\{\begin{array}{c} \nabla \cdot \boldsymbol{u}=0, \\ \rho\left(\frac{\partial u}{\partial t}+\boldsymbol{u} \cdot \nabla \boldsymbol{u}\right)=-\nabla p+\nabla \cdot\left(\mu\left(\nabla \boldsymbol{u}+\nabla \boldsymbol{u}^{\mathrm{T}}\right)\right)+\boldsymbol{F}_{\mathrm{s}}+\boldsymbol{F}_{\mathrm{e}}。\end{array}\right. $

(14)

式中：ρ为密度；p为压强；μ为黏性。此外，流动方程中各物性参数定义如下：

$ \begin{aligned} & \rho=\rho_1 C+\rho_2(1-C), \\ & \mu=\mu_1 C+\mu_2(1-C), \\ & \varepsilon_{\mathrm{E}}=\varepsilon_{\mathrm{E} 1} \varepsilon_{\mathrm{E} 2} /\left(\varepsilon_{\mathrm{E} 1}(1-C)+\varepsilon_{\mathrm{E} 2} C\right), \\ & \sigma_{\mathrm{E}}=\sigma_{\mathrm{E} 1} \sigma_{\mathrm{E} 2} /\left(\sigma_{\mathrm{E} 1}(1-C)+\sigma_{\mathrm{E} 2} C\right) 。\end{aligned} $

(15)

对上述控制方程系统进行无量纲处理, 选取液滴半径$R_{\mathrm{d}}$为特征长度, 特征速度$U=\sqrt{\sigma / \rho_2 R_{\mathrm{d}}}$, 外加电场强度$E_0$为特征电场强度, 相应的无量纲量分别为: 长度$x^*=x / R_{\mathrm{d}}$, 速度$\boldsymbol{u}^*=\boldsymbol{u} / U$, 时间$t^*=t \;R_{\mathrm{d}} / U$, 压力$p^*=p / \rho_2 U^2$, 电场强度$\boldsymbol{E}^*=\boldsymbol{E} / E_0$, 电导率$\sigma_{\mathrm{E}}{ }^*=\sigma_{\mathrm{E}} / \sigma_{\mathrm{E} 2}$, 介电常数$\varepsilon_{\mathrm{E}}{ }^*=\varepsilon_{\mathrm{E}} / \varepsilon_{\mathrm{E} 2}$, 密度$\rho^*=\rho / \rho_2$, 䅂度$\mu^*=$ $\mu / \mu_2$。可以得到无量纲N-S方程组为:

$ \left\{\begin{array}{c} \nabla^* \cdot \boldsymbol{u}^*=0, \\ \rho^*\left(\frac{\partial \boldsymbol{u}^*}{\partial t^*}+\boldsymbol{u}^* \cdot \nabla^* \boldsymbol{u}^*\right)=-\nabla^* p^*+\frac{1}{{Re}} \nabla^* \cdot\left(\mu^*\left(\nabla^* u^*+\nabla^* \boldsymbol{u}^{* \mathrm{T}}\right)\right)+\frac{1}{{Re} \cdot {Ca}} \boldsymbol{F}_{\mathrm{s}}^*+\frac{C a_{\mathrm{E}}}{{Re} \cdot {Ca}} \boldsymbol{F}_{\mathrm{c}}^* 。\end{array}\right. $

(16)

无量纲电场方程为：

$ \frac{\partial \rho^{\mathrm{E} *}}{\partial t^*}+\boldsymbol{u}^* \cdot \nabla^* \rho^{\mathrm{E} *}=-\frac{1}{O_{\mathrm{c}}} \nabla^* \cdot\left(\sigma_{\mathrm{E}}{ }^* \boldsymbol{E}^*\right), $

(17)

$ \nabla^* \cdot\left(\varepsilon_{\mathrm{E}}{ }^* \nabla^* \phi^*\right)=\rho^{\mathrm{E} *}。$

(18)

无量纲相场方程为：

$ \left\{\begin{array}{l} \frac{\partial C}{\partial t^*}+\nabla^* \cdot\left(\boldsymbol{u}^* C\right)=\nabla^* \cdot\left(M^* \nabla^* \hat{\varphi}\right), \\ \varphi^*=\frac{1}{2} C(C-1)(2 C-1)-C_{\mathrm{n}}^2 \Delta^* C 。\end{array}\right. $

(19)

其中涉及的无量纲参数定义为: 雷诺数$R e=\rho_2 U R_d / \mu$, 毛细数$C a=\mu_2 U / \sigma$, 电毛细数$C a_{\mathrm{E}}=\varepsilon_{\mathrm{E} 2} E_0^2 R_{\mathrm{d}} / \sigma$, $O_{\mathrm{c}}=U \varepsilon_{\mathrm{E} 2} / \sigma_{\mathrm{E} 2} R_{\mathrm{d}}, M^*=\hat{M} / R_{\mathrm{d}} U$。为了提高数值稳定性和减少数值扩散, 采用动态迁移率^[38-39], 即$M^*=$ $M_0 C(1-C), M_0$为迁移率系数, 是常数。此外, 无量纲的界面厚度参数$C_{\mathrm{n}}=\varepsilon / R_{\mathrm{d}}$, 无量纲表面张力$\boldsymbol{F}_{\mathrm{s}}^*=$ $6 \sqrt{2} \varphi^* \nabla^* C / C_{\mathrm{n}}$, 无量纲电场力$\boldsymbol{F}_{\mathrm{e}}{ }^*=\rho^{\mathrm{E}} \boldsymbol{E}^*-\boldsymbol{E}^* \cdot \boldsymbol{E}^* \nabla{ }^* \varepsilon_{\mathrm{E}}{ }^* / 2$。根据定义的无量纲速度可得韦伯数$W e=$ ${Re} \cdot {Ca}=1$。

定义密度比λ_ρ=ρ₁/ρ₂，黏性比λ_μ=μ₁/μ₂，介电常数比Q=ε_E1/ε_E2，电导率比R=σ_E1/σ_E2，由此得到的无量纲物性参数为：

$ \begin{aligned} \rho^* & =\lambda_\rho C+(1-C), \\ \mu^* & =\lambda_\mu C+(1-C), \\ \varepsilon_{\mathrm{E}}^* & =\varepsilon_{\mathrm{E} 1}^* /[Q(1-C)+C], \\ \sigma_{\mathrm{E}}^* & =\sigma_{\mathrm{E} 1}^* /[R(1-C)+C] 。\end{aligned} $

(20)

1.4 求解步骤

基于OpenFOAM开源平台自主实现上述两相流动模型，Cahn-Hilliard方程、电场方程和N-S方程组的时间离散采用交错离散的方式，即速度场u、压力场p、电荷密度ρ^E和电势ϕ离散在时间步tⁿ，体积分数C离散在时间步t^n+1/2。Cahn-Hilliard方程采用二阶Ralston方法进行时间推进，对流项采用Gauss Vanleer格式，扩散项采用Gauss linear corrected格式。电场方程和N-S方程组瞬态项采用Euler格式，速度对流项采用Gauss limited linear V格式，其余对流项采用Gauss linear格式，扩散项采用Gauss linear corrected格式，梯度项采用least squares格式。从时间步tⁿ到tⁿ⁺¹的求解步骤如下：

1) 求解对流Cahn-Hilliard方程(19)，更新相变量分布C；

2) 根据方程(20)更新物性参数ρ、μ、ε_E和σ_E；

3) 求解方程(17)(18)，更新电荷密度ρ^E和电势ϕ；

4) 计算表面张力F_s和电场力F_e；

5) 采用PISO迭代算法求解N-S方程组(16)，得到新的速度场u和压力场p。

2 模型和程序验证 2.1 Laplace定律

根据Laplace定律，在表面张力的作用下，静止的孤立液滴将会处于平衡状态，液滴的内外压差Δp_theory将由液滴半径R₀和表面张力系数σ决定，理论表达式为

$ \nabla p_{\text {theory }}=\frac{k \sigma}{R_0}, $

(21)

式中：对于二维平面问题，k=1，对于二维轴对称和三维问题，k=2。

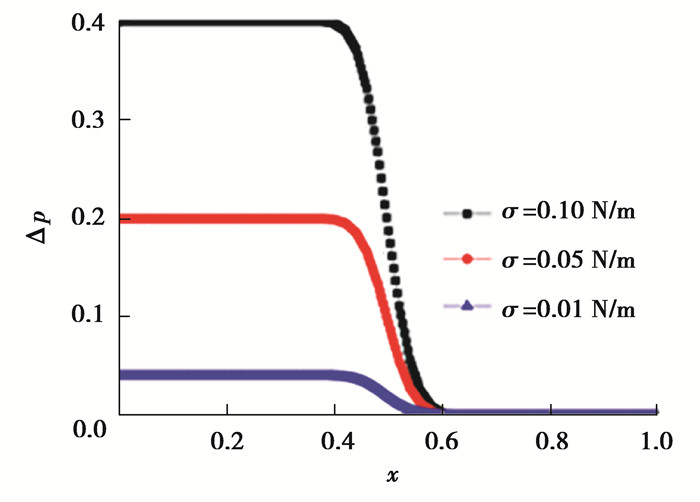
首先考虑静止轴对称液滴，计算域为长1 m，宽2 m，液滴半径为0.5 m，液滴中心位于对称轴中心点处。上下边界为无滑移固壁，左边界为轴对称边界，右边界为自由出流边界。用下标d和m分别表示液滴和环境流体，相关物性参数为ρ_d=ρ_m=1 kg/m³，μ_d=μ_m=0.1 Pa· s，表面张力分别取为σ=0.01 N/m、σ=0.05 N/m和σ=0.10 N/m，计算结果见图 1。如表 1所示，数值模拟得到的相对压差与理论压差的相对误差均在0.5%左右，与方程(21)的理论预测吻合。算例结果表明，本文中采用的相场模型以及自主开发的数值程序能够准确地描述压力场和表面张力。

2.2 剪切液滴变形

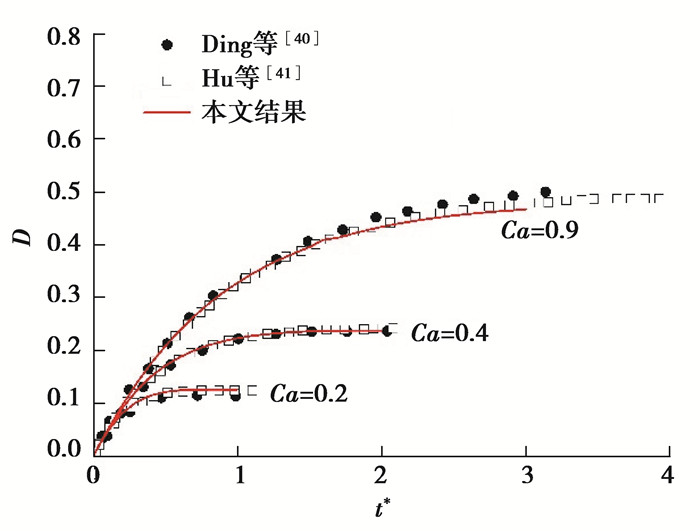
对液滴在剪切流动下的变形进行数值模拟。采用二维平面模型，计算域为边长为2的正方形，网格为200×200，液滴位于计算域中心，半径为0.5，C_n为0.01，迁移率系数M₀为0.01，液滴密度和黏性与环境流体相同。雷诺数Re为1，毛细数Ca分别取0.2、0.4和0.9。左右边界为周期边界，上下边界速度分别为(±1，0)，初始条件为库埃特流速度分布。定义变形率D=(L₁-B₁)/(L₁+B₁)，其中L₁是界面到液滴中心的最大距离，B₁是界面到液滴中心的最小距离。图 2给出了Ca分别为0.2、0.4和0.9时的计算结果，液滴随时间变化的变形率与文献结果吻合良好。Ding等^[40]和Hu等^[41]均采用相场方法描述界面运动，本文的结果和Hu等的结果更为吻合，有效验证了当前数值计算的界面变形捕捉精度。

2.3 电荷守恒模型验证

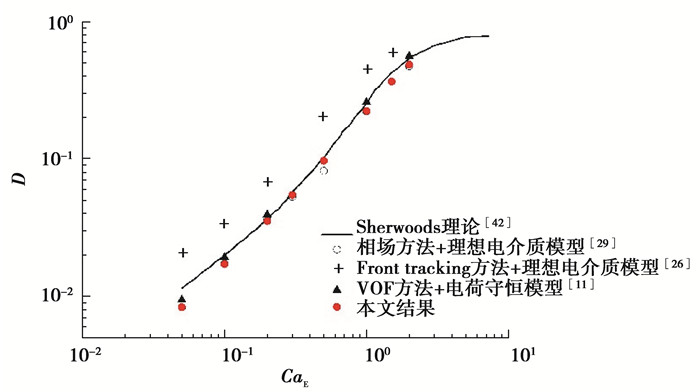
为验证电荷守恒模型，分别对直流电场作用下的理想电介质液滴和漏电介质液滴变形进行研究。对于理想电介质液滴，计算域为3×6，液滴半径为1，雷诺数Re为3.64，韦伯数We为1，介电常数比Q为5，C_n为0.02，迁移率系数M₀为0.001。图 3为直流电场中液滴变形率D随电毛细数Ca_E的变化，并与文献^{[11, 26, 29, 42]}的结果进行对比。本文的结果和Lin等^[29]采用相场方法和理想电介质模型的结果吻合较好，说明提出的模型能够准确地模拟理想电介质液滴的变形。

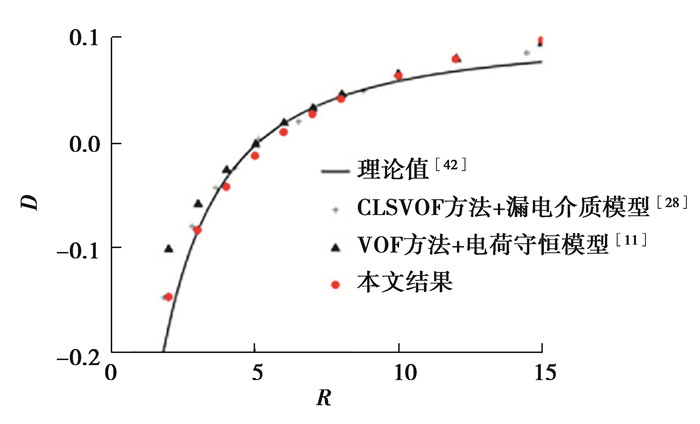
参考Sahu等^[11]对漏电介质液滴变形的研究，选择计算域为3×6(液滴半径为1)，C_n为0.02，迁移率系数M₀为0.001，雷诺数Re=1，韦伯数We=1，介电常数比Q=10，电毛细数Ca_E=0.183，O_c=2.68。图 4给出了计算得到的直流电场中液滴变形率D随电导率比R的变化，可以看出当前结果与参考结果一致，本文的数值方法能够准确描述漏电介质液滴的变形。

3 交变电场中液滴的变形和融合

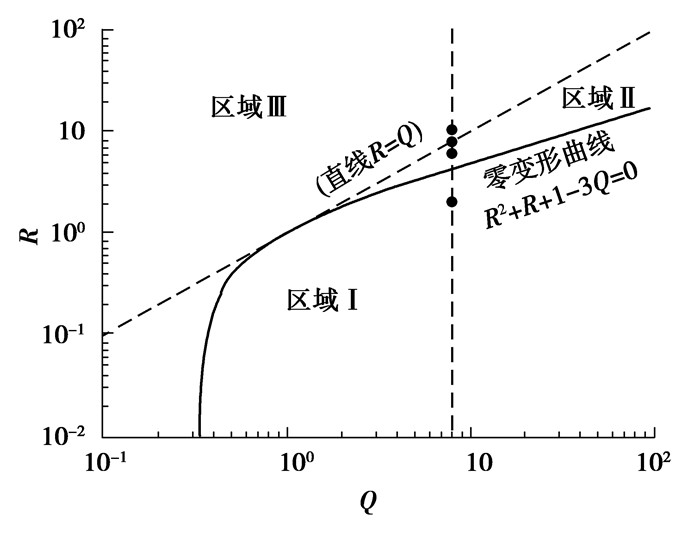
Torza等^[4]通过理论分析得到了$Q-R$坐标系下交变电场变形一流动循环图。如图 5所示, 根据零变形曲线和零流动循环线(即直线$Q=R$) 分为3个区域。变形率与变形特征函数$\mathit{\Phi}_{\mathrm{m}}=f\left(R, Q, \lambda_\mu ; \hat{\omega}\right.$) 相关, 交变电场中液滴的变形率由平均变形率$D_{\mathrm{m}}$和振荡变形率$D_{\mathrm{t}}$组成, 即$D=D_{\mathrm{m}}+D_{\mathrm{t}}$。在区域$\mathrm{I}$中, 存在无量纲临界角频率$\left.\hat{\omega}_{\mathrm{cr}}=\frac{\sqrt{3 Q-1-R-R^2}}{\left(O_{\mathrm{c}}|S-1|\right.}\right)$, 当$2 \pi f>\widehat{\omega}_{\mathrm{cr}}$时, 液滴呈扁长形(如图 6 (a)所示的液滴沿垂直方向伸长), 当$2 \pi f <\widehat{\omega}_{\mathrm{cr}}$时, 液滴呈扁圆形(如图 6(a)所示的液滴沿水平方向伸长)。随着频率增加, 平均变形率$D_{\mathrm{m}}$增大; 在区域Ⅱ中, 液滴呈扁长形, 随着频率增加, 平均变形率$D_{\mathrm{m}}$增大; 在区域Ⅲ中, 液滴呈扁长形, 随着频率增加, 平均变形率$D_{\mathrm{m}}$减小。

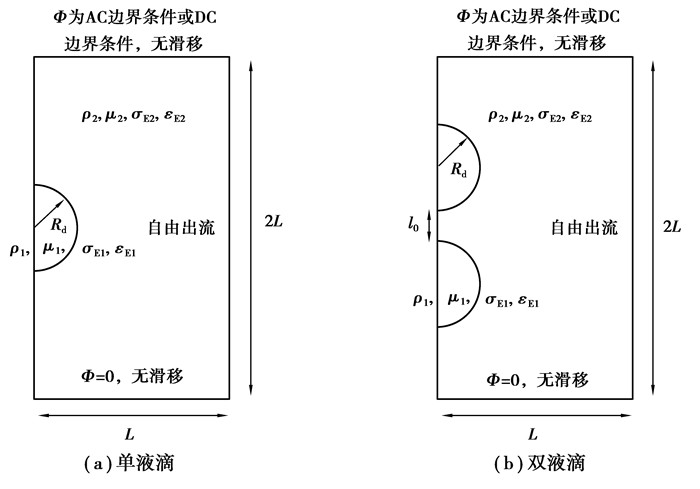
采用二维轴对称模型，分别对电场中单个液滴的变形和双液滴的融合进行研究。对于图 6(a)所示的单个液滴和图 6(b)所示的双液滴，液滴半径为R_d=1，双液滴初始界面间最短距离为l₀=0.4。计算域特征尺寸L=5，网格为320×640，C_n=0.02，迁移率系数M₀=0.001，雷诺数Re=1，毛细数Ca=1，电毛细数Ca_E=1，O_c=1。

对于等效直流电场, 上边界$\phi=5 / \sqrt{2}=3.536$, 下边界$\phi=0$; 对于交变电场, 上边界$\phi=5 \sin (2 \pi f t)$, 下边界$\phi=0$。定义变形率$D=\left(L_2-B_2\right) /\left(L_2+B_2\right)$, 其中$L_2$为液滴沿垂直方向的最大变形, $B_2$为液滴沿水平方向的最大变形。当$D>0$时, 液滴呈扁长形, 当$D <0$时, 液滴呈扁圆形。对于沿外加电场方向放置的两个液滴, 定义$l(t)$为随时间变化的两个液滴间的距离, 定义液滴融合时间为两个液滴的距离从初始间距$l_0$变化到零的时间。在等效直流电场下，单液滴的稳态变形率为D_DC，双液滴间最短界面距离为l_DC。

采用固定介电常数比Q=8，电导率比R分别取值为2、6、8和10。

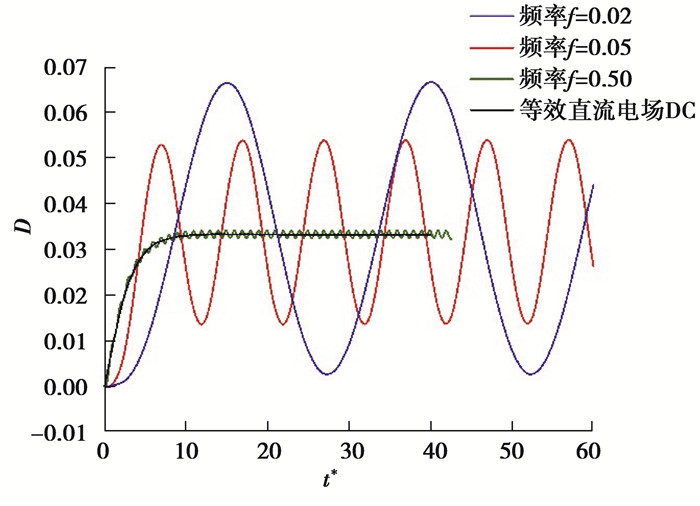
3.1 Q=R

当Q=R时，在不同频率下，液滴变形率随时间的变化率如图 7所示，双液滴之间最短距离随时间变化如图 8所示。

当Q=R时，如图 7所示，在等效直流电场和交变电场中，液滴的变形率D>0，呈扁长变形。随着频率增大，液滴变形振荡幅度减小。这是因为当交变电场频率较小时，液滴有足够的时间发生变形，产生较大的变形率。而当频率较大时，液滴还未达到变形极限，电场强度就减小，电场力随之减小，在表面张力的作用下，液滴开始回缩，变形率减小，所以振荡变形幅度减小。液滴在不同频率下的平均变形率和等效直流电场的稳态变形率相等。换言之，当Q=R时，液滴的平均变形率与频率无关。由于此时液滴的平均速度为零，界面处电荷密度为零，相当于理想电介质流体，所以仅有极化应力产生电场力作用。同时可以发现，液滴变形率的振荡频率约为交变电场频率的两倍，这与Torza等^[4]的理论分析和Esmaeeli等^[9]的数值模拟结果一致。

如图 8所示，对于双液滴融合问题，基于交变电场所得液滴界面间的最短距离l绕l_DC振荡。由于振荡变形的原因，交变电场中的双液滴会比等效直流电场中的双液滴先融合，且随着频率减小，液滴的变形振荡幅度增大，使得双液滴的融合时间缩短，有助于提高液滴融合效率。

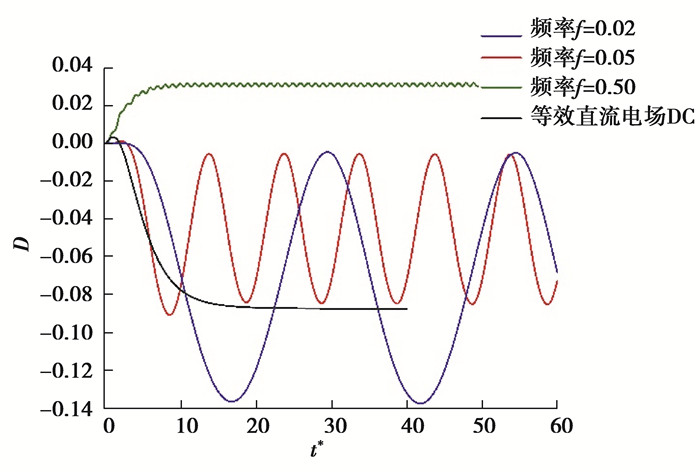
3.2 Q≠R 3.2.1 区域I

当Q=8，R=2时，位于区域I中，此时临界角频率为$ \widehat{\omega}_{\mathrm{cr}}$为0.589，对应的临界频率f_cr为0.093 7。当位于区域I时，在等效直流电场作用下，液滴呈扁圆形；在交变电场作用下，当频率小于临界频率时，液滴呈扁圆形振荡，当频率大于临界频率时，液滴呈扁长形振荡。当频率较高时，流体的电弛豫时间τ^e=ε_E/σ_E将远大于电极板间电场方向的变化时间1/ω，因此在高频交流电场作用下，液滴表现为理想电介质，平均变形呈扁长形，所以当电场由低频向高频变化时，液滴的变形模式也由扁圆形向扁长形转变，当液滴的变形率为零时，此时的频率对应为临界频率。如图 9所示，当频率f为0.02和0.05时，此时频率小于临界频率，液滴的变形率D＜0，呈扁圆形振荡。当频率f为0.50时，此时频率大于临界频率，液滴的变形率D>0，呈扁长形振荡。随着频率增大，液滴的振荡变形幅度减小，并且液滴的平均变形不断增大，逐渐大于等效直流电场的稳态变形D_DC。

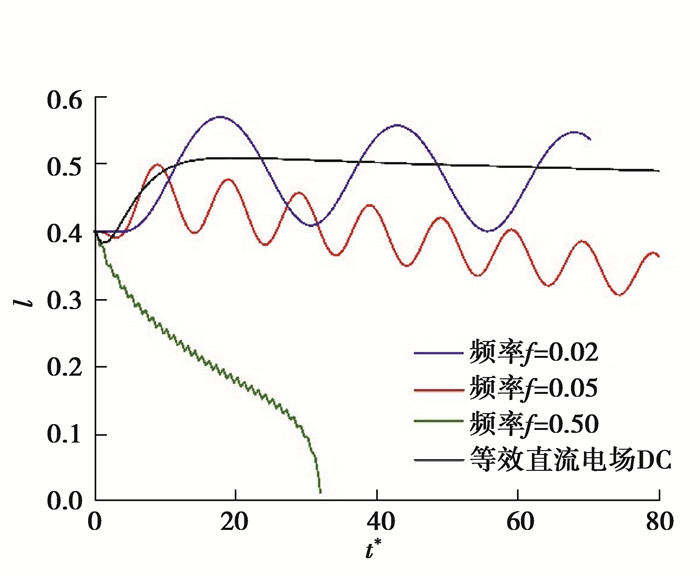
如图 10所示，随着电场频率增大，双液滴的融合时间不断减小。扁长形变形有利于液滴融合，因此当大于临界频率时，液滴的融合时间急剧减小。当小于临界频率时，液滴呈扁圆形变形，不利于液滴融合。

3.2.2 区域Ⅱ

当Q=8，R=6时，当前电物性参数取值位于区域Ⅱ。如图 11所示，在等效直流电场和交变电场中，液滴的变形率D>0，液滴呈扁长形，而且液滴的变形振荡幅度随着频率增大而减小。和位于区域I时的液滴一样，随着频率增大，液滴的平均变形率D_m不断增大，液滴的平均变形大于等效直流电场的稳态变形，即D_m>D_DC。这是因为电场力由两部分组成，如等式(13)所示，第一项为电荷产生的库仑力，第二项为极化应力产生的电场力，当Q>R时，面向电势高的电极板的界面电荷为正电荷，面向电势低的电极板的界面电荷为负电荷^[4]，电荷密度在液滴轴向两端最大，并沿着界面向径向逐渐减小，此时电荷产生的库仑力指向液滴内部。随着频率减小，界面电荷增大，电荷贡献的库仑力增大，抑制液滴向扁长变形，因此液滴的平均变形率减小。

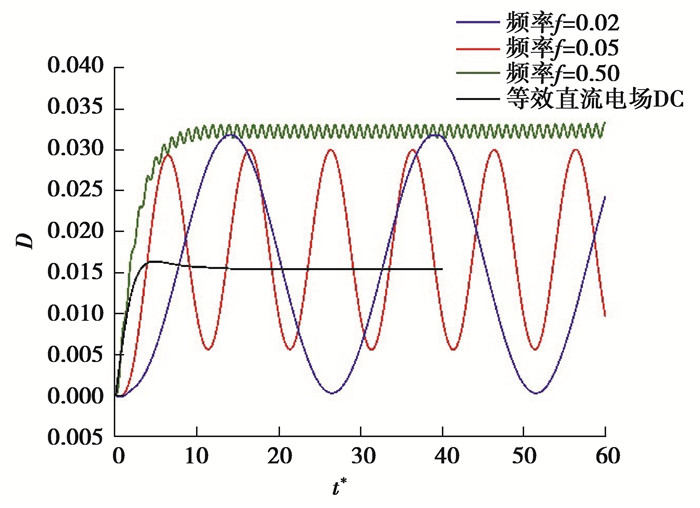
对于液滴融合，如图 12所示，由于随着频率增大，平均变形率D_m增大，使得液滴界面间的距离减小，双液滴更易于聚结。此外，还存在临界低频率值，当小于该临界频率时，虽然平均变形率D_m相对减小，但液滴的变形振荡幅度增加(如图 11所示)，双液滴间的界面间距振荡幅度也变大，易于促进液滴融合。

3.2.3 区域Ⅲ

当Q=8，R=10时，位于区域Ⅲ。如图 13所示，在等效直流电场和交变电场中，液滴的变形率D>0，液滴呈扁长形。随着频率增大，液滴的变形振荡幅度减小，且平均变形率增大。当Q＜R时，面向电势高的电极板的界面电荷为负电荷，面向电势低的电极板的界面电荷为正电荷，电荷密度在液滴轴向两端最大，并沿着界面向径向逐渐减小，此时电荷产生的库仑力指向液滴外部。随着频率减小，界面电荷增大，电荷贡献的库仑力增大，使得液滴趋向于扁长形，液滴平均变形率增大。

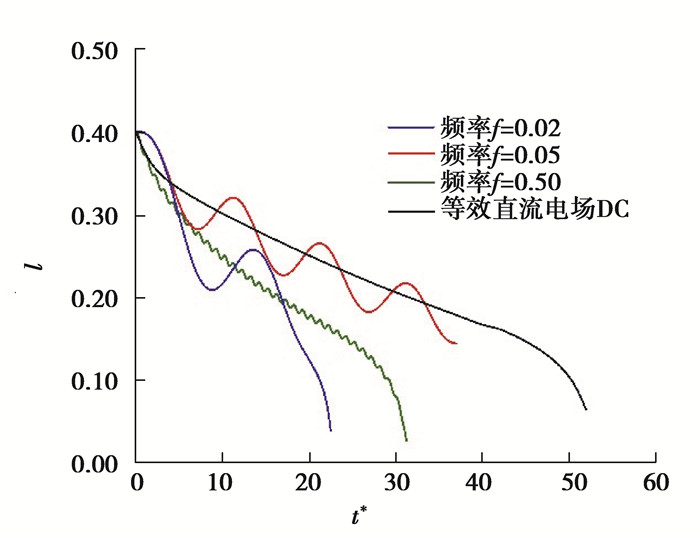
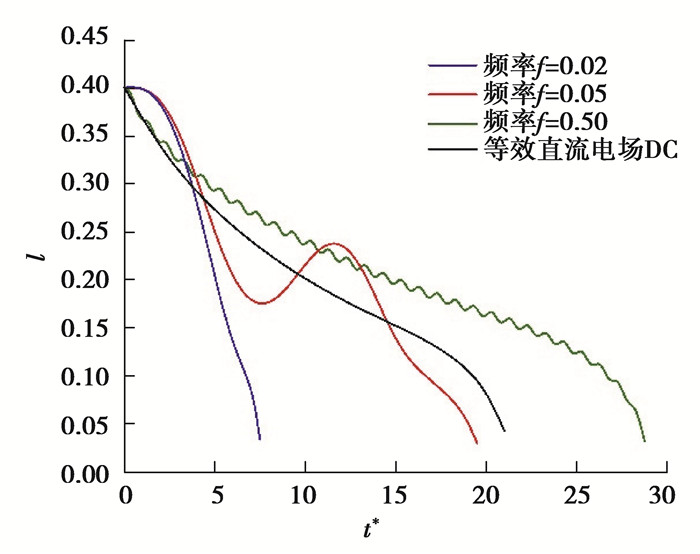
如图 14所示，随着频率减小，液滴的平均变形率和变形振荡幅度都随之增大，因此双液滴的融合时间减小。存在临界频率f_cr，当f>f_cr，液滴的平均变形小于等效直流电场的稳态变形，即D_m＜D_DC，不利于液滴融合。当f＜f_cr，液滴的平均变形大于等效直流电场的稳态变形，即D_m>D_DC，显然液滴更易聚结。

4 结论

选择相场法捕捉界面运动，采用电荷守恒模型描述电荷输运，发展了考虑电场作用的两相流动数值方法，并在OpenFOAM框架内完成程序开发，系统研究了交变电场频率对单个液滴变形和双液滴融合的影响。研究结果表明，随着频率增大，液滴的变形振荡幅度减小，变形振荡频率约为交变电场频率的2倍。当Q≥R时，相比于等效直流电场，交变电场更能够促进液滴融合。当Q=R时，液滴的平均变形率和等效直流电场的稳态变形率相等，随着频率降低，双液滴融合时间减少，此时低频能够促进液滴融合。当Q>R时，随着频率增大，液滴的平均变形率增大，双液滴的聚结时间减小，而当频率减小到一定值时，由于液滴振荡变形率增大，双液滴的聚结时间也会减少，因此高频能够促进液滴融合，同时对于当前液滴初始间距，当频率足够小，也有利于液滴融合。当Q＜R时，考虑平均变形率和振荡变形率的共同影响，低频时液滴更易融合。存在临界频率，当大于临界频率时，液滴的平均变形率小于等效直流电场的稳态变形率，随着频率增大，平均变形率减小，双液滴融合时间增加，双液滴融合时间比等效直流电场作用下液滴融合时间长；当小于临界频率时，液滴的平均变形率大于等效直流电场的稳态变形率，此时相较于等效直流电场，交变电场更能促进融合，且随着频率减小，双液滴的融合时间减小。