1b. 重庆大学 非均质材料力学重庆市重点实验室, 重庆 400044;
2. 河北工业大学 机械工程学院, 天津 300401
1b. Chongqing Key Laboratory of Heterogeneous Material Mechanics, Chongqing University, Chongqing 400044, P. R. China;
2. College of Mechanical Engineering, Hebei University of Technology, Tianjin 300401, P. R. China
随着科学技术水平的不断提高,3D打印技术已经是当前制造业最重要的研究热点之一。3D打印技术具有高精度、不受材料复杂结构限制等优点,在实际工程应用中表现出良好的适用性,因此广泛应用于生物医学、电子产品、航空航天等众多领域[1]。在材料成型过程中,不同的工艺参数对材料力学性能影响重大。目前,测量材料力学性能主要是通过静态拉伸实验、线性无损检测等手段,其中张争艳等[2]、楚蓓蓓等[3]、Guan等[4]采用拉伸实验探究了激光功率、扫描速度和扫描间距等工艺参数对材料力学性能的影响,通过实验证实了材料的力学性能与工艺参数有很大的相关性。Liu等[5]采用线性超声检测技术,研究了材料的弹性模量、波速等线性参量与3D打印钛合金孔隙率之间的关系。Song等[6]对3D打印的316L不锈钢试件进行水浸式C扫描,检测出材料内部未熔合、气孔等缺陷。但由于拉伸实验具有破坏性且受限于试样的形状,而线性测量手段难以检测微小缺陷,因此对于工艺参数众多的3D打印成型件,迫切需要一种对微观缺陷敏感有效的检测方法来评估材料的力学性能。
近年来国内外学者开展了非线性超声检测技术与材料力学性能评价的相关研究[7-11]。税国双等[12]采用非线性超声检测技术研究铝合金的早期性能退化。Mondal等[13]采用非线性超声检测技术建立了超声非线性系数与材料屈服应力的关系。Singh等[14]研究了非线性超声谐波信号与材料微观损伤和力学性能之间的联系。Kim等[15]采用非线性超声检测技术研究不锈钢的热损伤,最终建立了抗拉强度、延伸率与超声非线性系数之间的关系。徐显胜等[16]采用非线性超声检测技术研究了3D打印不锈钢材料的疲劳损伤,通过超声非线性系数预测材料的早期退化程度。可见非线性超声检测技术可用于某些材料的力学性能评价,但目前对于3D打印铝合金力学性能的检测手段研究较少,因此笔者以不同成型角度的3D打印AlSi10Mg为研究对象,利用非线性超声纵波检测技术建立超声非线性系数、宏观力学性能与微观表征之间的关系。此外,通过高周疲劳加载试验进一步探究超声非线性系数对材料早期性能退化的敏感性。
1 非线性超声基本理论由Na等[17]的研究可知谐波的产生与材料的非线性行为相关,应力σ与应变ε的非线性关系如方程(1),又被称为非线性胡克定律。
| $ \sigma=E \varepsilon(1+\beta \varepsilon+\cdots), $ | (1) |
式中:σ为应力;ε为应变;E为杨氏模量;β为超声非线性系数。在理想情况下,当单一频率的纵波信号由一端入射,在另一端被换能器接收时,假设衰减忽略不计,则一维的波动方程可以写为[18-19]
| $ \rho \frac{\partial^2 u}{\partial t^2}=\frac{\partial \sigma}{\partial x} 。$ | (2) |
式中:t为时间;ρ为材料的密度;x为传播距离;u为材料内部位于x处质点的位移,在小变形条件下,与应变ε的关系为
| $ \varepsilon=\frac{\partial u}{\partial x} 。$ | (3) |
结合方程(1)~(3),保留二阶非线性项可得
| $ \rho \frac{\partial^2 u}{\partial t^2}=E \frac{\partial^2 u}{\partial x^2}+2 E \beta \frac{\partial u}{\partial x} \frac{\partial^2 u}{\partial x^2} 。$ | (4) |
通过微扰法求解方程(4),即存在一个非线性位移,其引起的振动仅是一种微扰,不会减弱线性振动的能量,则存在通解为
| $ u=u_0+\beta u_1 \text { 。} $ | (5) |
式中u0和u1分别为线性和非线性引起的位移,将其带入到方程(4)可得
| $ \rho \frac{\partial^2}{\partial t^2}\left(u_0+\beta u_1\right)=E \frac{\partial^2}{\partial x^2}\left(u_0+\beta u_1\right)+2 E \beta \frac{\partial}{\partial x}\left(u_0+\beta u_1\right) \frac{\partial^2}{\partial x^2}\left(u_0+\beta u_1\right) 。$ | (6) |
展开并忽略β的高次项后可以得到
| $ \rho \frac{\partial^2 u_0}{\partial t^2}+\beta\left(\rho \frac{\partial^2 u_1}{\partial t^2}-E \frac{\partial^2 u_1}{\partial x^2}\right)=E \frac{\partial^2 u_0}{\partial x^2}+2 E \beta \frac{\partial u_0}{\partial x} \frac{\partial^2 u_0}{\partial x^2} 。$ | (7) |
其中不含β的线性波动方程为
| $ \rho \frac{\partial^2 u_0}{\partial t^2}=E \frac{\partial^2 u_0}{\partial x^2}, $ | (8) |
含有β项的部分为
| $ \beta\left(\rho \frac{\partial^2 u_1}{\partial t^2}-E \frac{\partial^2 u_1}{\partial x^2}\right)=2 E \beta \frac{\partial u_0}{\partial x} \frac{\partial^2 u_0}{\partial x^2} 。$ | (9) |
假设一个正弦波信号在介质中传播时的初始条件为
| $ u_0(0, t)=A_1 \sin (\omega t) 。$ | (10) |
式中:A1为基频幅值;ω为角频率。结合方程(8)~(10)并通过分离变量法求解得到[20]
| $ u=A_1 \sin (k x-\omega t)+\frac{1}{8} \beta k^2 A_1^2 x \cos 2(k x-\omega t) 。$ | (11) |
式中:k=ω/c为波数,c为纵波波速。方程(7)表明,在不考虑衰减的情况下,当单一纵波在非线性固体介质中传播时,除了频率为ω基波外,还会产生频率为2ω的谐波,则超声非线性系数可表示为
| $ \beta=\frac{8 A_2}{k^2 x A_1^2}, $ | (12) |
式中A2为二次谐波幅值。当波数k和传播距离x确定时,可以通过测量基频和倍频的幅值来计算超声非线性系数。
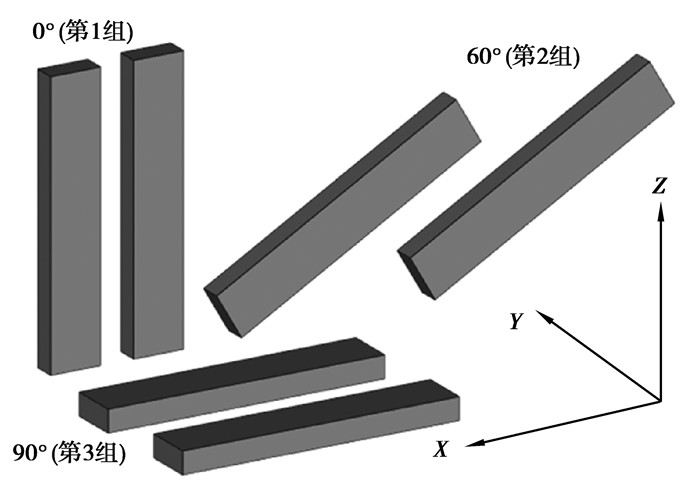
2 3D打印铝合金的材料性能研究 2.1 材料及其试样的制备采用选择性激光熔融3D打印技术制备试样,原料为粉末状的AlSi10Mg,粒度大小在15~53 μm之间,粉末的松装密度为1.33 g/cm3。文献[4]中通过实验证实了材料的力学性能与3D打印时成型角度有很大的相关性。因此,可以通过改变成型角度控制材料力学性能的差异性。设置3组成型角度分别为0°、60°、90°的试样,每组2个,共6个样件,如图 1所示。制备时3组试样仅成型角度不同,其他工艺参数例如扫描速度、扫描功率等均保持一致,所有试样均由一炉打印制成,因此同组试样中的2个样件力学性能具有一致性。
|
图 1 3D打印试样的方案 Fig. 1 Manufacturing strategy of the specimens |
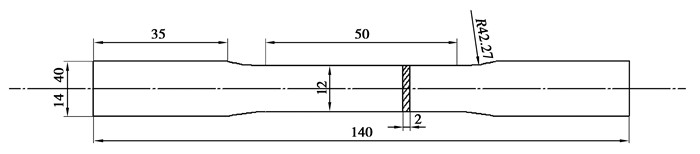
通过拉伸实验探究试样的宏观力学性能,电子万能试验机最大拉伸力可达100 kN,采用位移控制模式,加载速率2 mm/min,从3组成品试样中加工出如图 2所示的试样尺寸各1个进行拉伸试验。
|
图 2 拉伸试样示意图 Fig. 2 The diagram of the tensile specimens |
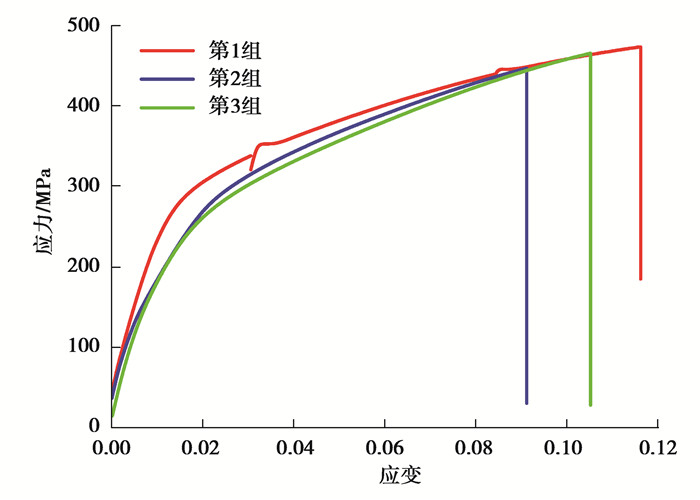
图 3为3组试样的应力应变曲线。从应力应变曲线可以看出:应力小于100 MPa时,3组试样的应力应变曲线接近平行,由此可见3组试样的弹性模量接近相等;另外,3组试样的抗拉强度与成型角度呈现出一定的规律,第1组和第3组试样的抗拉强度较大,分别为473 MPa和465MPa,第2组试样的抗拉强度较小,为446 MPa。除此之外,所有试样的延伸率均小于5%,因此断裂类型视为脆性断裂,拉伸实验所获得的力学参数见表 1。由实验结果可知,材料的抗拉强度受到成型角度的影响,随着成型角度的增大抗拉强度呈现先减小后增大的趋势,即0°和90°试样抗拉强度远大于60°试样。
|
图 3 应力应变曲线 Fig. 3 Stress and strain curve of three groups of specimens |
| 表 1 拉伸实验的结果 Table 1 Results of tensile experiment |
利用脉冲回波法测量试样的超声非线性系数,同样,3组测量试样均从3D打印成品中加工获得。试样为长方体,总长180 mm,宽14 mm,厚6.75 mm,示意图见图 4。图 5为非线性超声测量系统及实验方案,非线性超声测量系统为RIEC公司研发的RAM-5000,首先由信号激发器RAM-5000激发一个频率为6.5 MHz,8个周期的Hanning窗信号,先后通过2.25 MHz高通滤波器和双工器,最终到达换能器并垂直入射到试件,最后用同一个换能器在同一位置接收回波信号。为了保证二次谐波及其实验结果的有效性,要求换能器的有效频率必须同时包括6.5 MHz和13.0 MHz,除此之外,通过重复测量10次,进一步减小实验误差。Liu等[21]实验证实换能器和界面的耦合质量以及位置关系会影响超声非线性系数的测量精度和稳定性。因此,每次实验均要保证测量条件稳定,以提高测量的精度。

|
图 4 非线性超声实验试样示意图 Fig. 4 The diagram of nonlinear ultrasonic experiment |

|
图 5 实验方案及非线性超声测量系统 Fig. 5 Experimental setup of the nonlinear ultrasonic method |
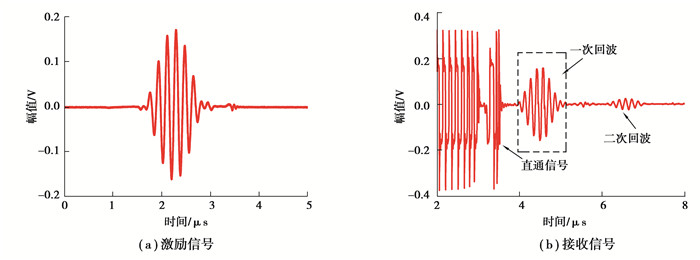
图 6为激励信号和接收信号的时域图,其中接收信号(图 6(b))2~4 μs之间为系统直通信号,虚线框为回波信号,在保证3组试样回波信号的能量均在同一水平的条件下对时域信号进行快速傅里叶变换。
|
图 6 激励信号与接收信号时域图 Fig. 6 The time domain diagram of excitation signal and receiver signal |
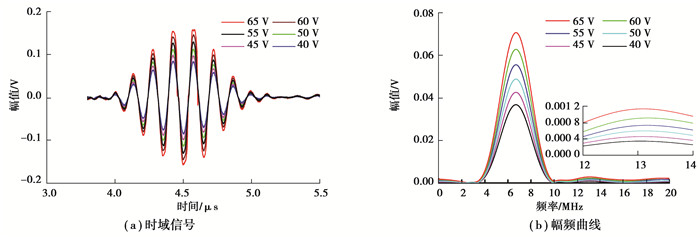
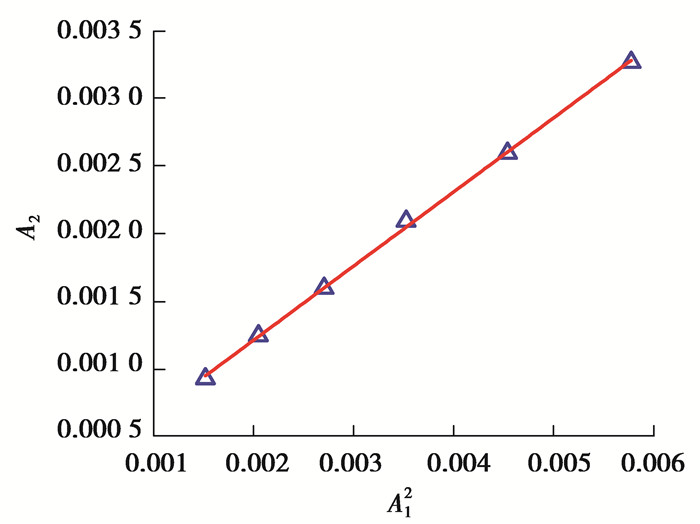
图 7(a)为不同激励电压下的时域信号,可以看出随着激励电压从40 V增大到65 V,时域信号的幅值出现相应的增大,图 7(b)幅频曲线也呈现增大的趋势。图 8为不同激励电压下的二次谐波幅值A2随基波幅值A12的变化,两者呈现明显的线性关系,由此可知超声非线性系数是来自材料本身而非测量系统或线性信号。由方程(12)可知,在传播距离和波数确定的情况下,将不同激励电压下A2/A12的平均值做为超声非线性系数的最终值,可以进一步减少测量的误差和偶然性。
|
图 7 不同激励电压下的时域信号与幅频曲线 Fig. 7 Time-domain and frequency-domain signals for varying driving voltages |
|
图 8 不同激励电压下二次谐波幅值随基波幅值平方的变化 Fig. 8 The second harmonic amplitude versus square of the fundamental amplitude for varying driving voltages |
表 2为3组试样超声非线性系数的测量结果,数据的误差棒大小均小于0.002,说明了实验系统的稳定性。表格中当成型角度从0°增大到60°时,超声非线性系数的平均值β由0.542 73增大到0.555 39;成型角度继续增大到90°时,β减小到0.550 17。以上实验结果证实了改变材料的成型角度会导致材料的非线性效应产生差异。为进一步探究超声非线性系数与材料力学性能的关系,做了以下研究。
| 表 2 超声非线性系数的测量结果 Table 2 The results of acoustic nonlinearity parameter |
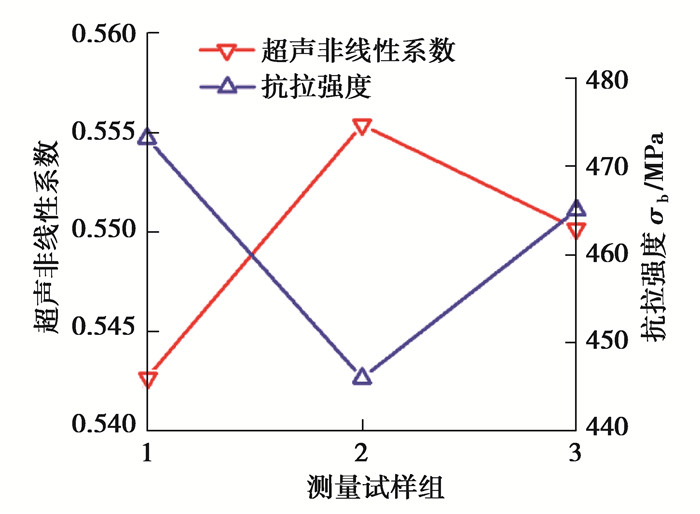
将超声非线性系数和材料的抗拉强度进行比较(图 9)可知,不同成型角度试样的超声非线性系数和抗拉强度的变化趋势相反:当抗拉强度增大时,超声非线性系数减小,当抗拉强度减小时,超声非线性系数增大。由此可见超声非线性系数可以反映材料的宏观力学性能,两者呈现相反的变化趋势。
|
图 9 超声非线性系数和抗拉强度之间的关系 Fig. 9 Acoustic nonlinearity parameter versus the tensile strength |
为解释材料的超声非线性系数与其抗拉强度的变化趋势相反这一种现象,进一步研究了材料的微观形貌。图 10为SEM扫描电镜得到的微观形貌图。为了定量地研究微观组织缺陷与超声非线性系数、力学性能的关系,引入缺陷比率,其定义为微观缺陷的面积除以总面积。从图中可以看出,图 10(a)和图 10(c)的缺陷密度相对较小,而图 10(b)缺陷密度相对较大,这与超声非线性系数和抗拉强度的变化具有很强的相关性,三者之间的关系见图 11~12。

|
图 10 不同成型角度试样的SEM照片 Fig. 10 SEM images of the different building directions |
|
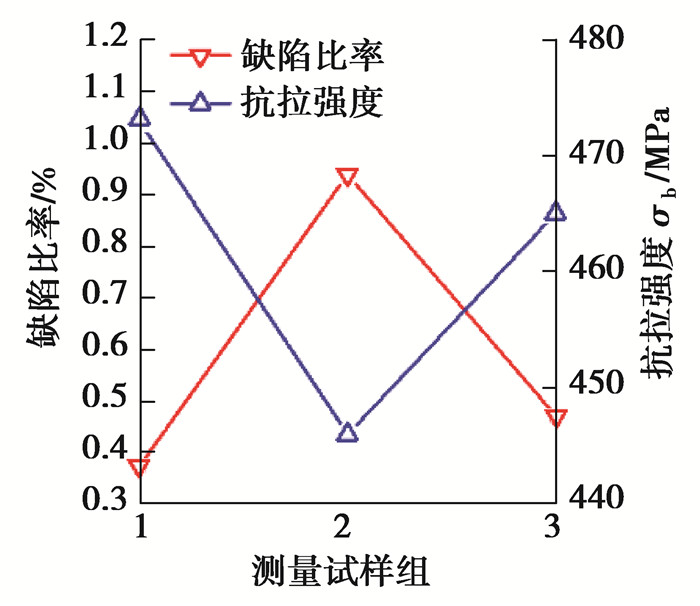
图 11 缺陷比率和抗拉强度之间的关系 Fig. 11 Defect rate versus the tensile strength |
|
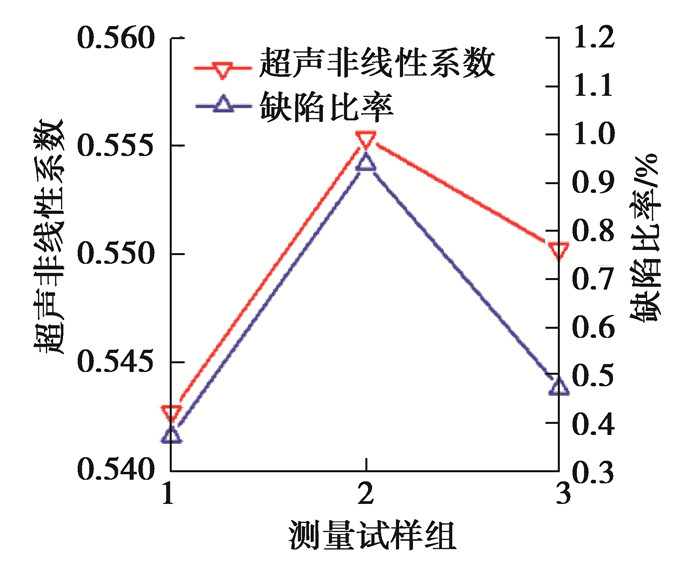
图 12 超声非线性系数和缺陷比率之间的关系 Fig. 12 Acoustic nonlinearity parameter versus defect rate |
图 11为SEM扫描电镜得到的缺陷比率与材料的抗拉强度之间的关系。缺陷比率与材料的抗拉强度呈现相反的变化趋势,当缺陷比率为最小值0.3%时,抗拉强度为最大值473 MPa;当缺陷比率为最大值0.9%时,材料的抗拉强度为最小值446 MPa。因此,通过实验结果可知缺陷比率的大小可以反映材料的力学性能,两者同样呈现相反的变化趋势。
图 12为SEM扫描电镜得到的缺陷比率与超声非线性系数之间的关系。缺陷比率与超声非线性系数的变化趋势一致,均呈现先增大后减小的变化趋势。上述结果表明,通过改变3D打印的成型角度,可以使材料的微观缺陷差异化,并且可以通过抗拉强度和超声非线性系数表征出材料的差异性,最终建立了微观缺陷、抗拉强度和超声非线性系数三者的关系,因此超声非线性系数可以用于表征材料的强度。
3 微裂纹的非线性超声检测在疲劳加载的早期阶段,疲劳损伤的主要类型为位错和微裂纹的萌生。在线性超声中,位错和微裂纹不会引起弹性模量、波速等线性参量的变化,然而非线性超声中初始的疲劳损伤类型会引起高次谐波的产生,因此可用于材料早期性能退化的检测。本研究中设计了高周疲劳试验,对3组试样进行循环加载试验以研究非线性超声检测方法对3D打印铝合金材料早期性能退化的敏感性。疲劳试验采用MTS868液压伺服疲劳试验机,采用应力控制,正弦波加载,加载应力为120 MPa,加载频率为20 Hz,应力比R=0.1。图 13为疲劳实验的现场图,整个实验在室温条件下进行,疲劳试样与拉伸试样尺寸和样品表面处理方式均一致。

|
图 13 高周疲劳试验 Fig. 13 High-cycle fatigue experiment |
通过对3组试样进行同样条件的疲劳加载引发早期性能退化,加载次数为10 000,加载完后取下试样进行非线性超声检测实验,图 14为疲劳试样和超声非线性系数测量试样示意图,为了减小微裂纹萌生的随机性,采用缺口疲劳试样。测量试样缺口处的超声非线性系数,每次测量实验重复10次以保证结果的可靠性。

|
图 14 疲劳试样和超声非线性系数测量试样示意图 Fig. 14 The diagram of acoustic nonlinearity parameter under the fatigue experiment |
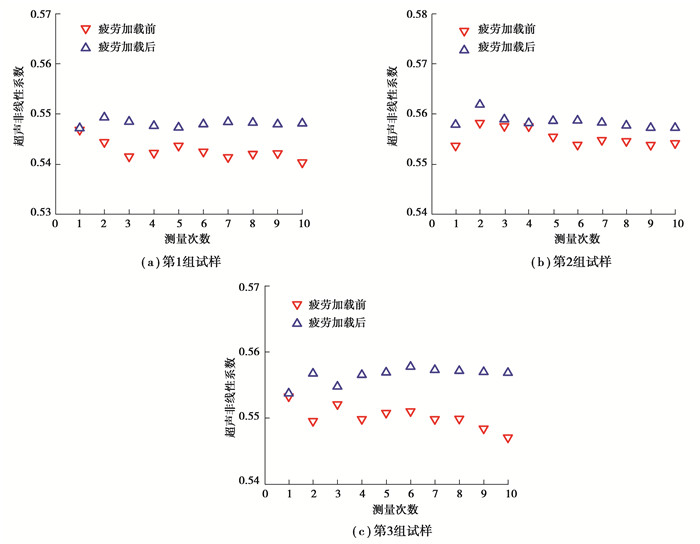
图 15为非线性超声检测实验的结果。结果表明:经过疲劳加载后,试样在测量区域的超声非线性系数均增大。为探究超声非线性系数增大的原因,采用金相显微镜观察测量区域的微观组织形貌,以第2组试样的微观形貌为例进行分析。经过疲劳加载实验后,试样内部的孔洞、空隙和未熔合等缺陷的周围由于应力集中,极易产生微裂纹,而原始缺陷本身不会随着疲劳加载而发生改变。图 16为第2组试样疲劳加载后的微观形貌图,可以发现试样出现了大量的微裂纹,大小均在100 μm下,其出现区域大部分位于原始缺陷处,而且并未出现其他缺陷类型。因此材料的早期性能退化阶段,微裂纹的萌生是主要的增长缺陷类型,也是超声非线性系数增长的主要原因。
|
图 15 疲劳实验前后的超声非线性系数 Fig. 15 Acoustic nonlinearity parameter before and after fatigue experiment |

|
图 16 疲劳后第2组试样的微观形貌 Fig. 16 Micromorphology of the second group after fatigue |
1) 不同成型角度下3D打印铝合金试样的非线性超声检测实验和力学拉伸试验表明材料的抗拉强度越小,超声非线性系数越大,反之亦然。
2) 3D打印的铝合金材料存在孔洞、未融合、夹杂等缺陷,这些缺陷是影响材料力学性能的重要因素,也是引起高次谐波的关键因素。实验结果表明,缺陷比率和超声非线性系数均呈现先增大后减小的趋势,与抗拉强度的变化趋势相反,因此非线性超声检测技术可以用于评价3D打印材料力学性能。
3) 研究了3D打印铝合金材料在循环应力载荷下超声非线性系数的变化趋势。结果表明,经过疲劳加载后,超声非线性系数均呈现增大的趋势;通过金相显微镜观察可知材料在早期性能退化阶段微裂纹萌生是引起超声非线性系数增大的主要因素。
| [1] |
帅三三, 刘伟, 王江, 等. 无损检测在增材制造技术中的应用研究进展[J]. 科技导报, 2020, 38(2): 26-34. Shuai S S, Liu W, Wang J, et al. Application of non-destructive testing in additive manufacturing technique[J]. Science & Technology Review, 2020, 38(2): 26-34. (in Chinese) |
| [2] |
张争艳, 楚蓓蓓, 王磊, 等. SLM工艺参数对316L不锈钢试件拉伸性能的影响[J]. 河北工业大学学报, 2019, 48(6): 1-5. Zhang Z Y, Chu B B, Wang L, et al. Effects of process parameters on tensile property of 316L stainless steel parts by selective laser melting[J]. Journal of Hebei University of Technology, 2019, 48(6): 1-5. (in Chinese) |
| [3] |
楚蓓蓓, 张争艳, 高铁红, 等. 激光扫描角度对316L不锈钢成型件拉伸性能和致密度的影响[J]. 河北工业大学学报, 2020, 49(2): 68-72. Chu B B, Zhang Z Y, Gao T H, et al. Effects of laser scanning angle on tensile properties and relative density of 316L stainless steel forming parts[J]. Journal of Hebei University of Technology, 2020, 49(2): 68-72. (in Chinese) |
| [4] |
Guan K, Wang Z M, Gao M, et al. Effects of processing parameters on tensile properties of selective laser melted 304 stainless steel[J]. Materials & Design, 2013, 50: 581-586. DOI:10.3969/j.issn.1001-9731.2013.04.030 |
| [5] |
Liu Y, Li X B, Chen C, et al. High throughput rapid detection for SLM manufactured elements using ultrasonic measurement[J]. Measurement, 2019, 144: 234-242. DOI:10.1016/j.measurement.2019.04.052 |
| [6] |
Song Y F, Zi X H, Fu Y D, et al. Nondestructive testing of additively manufactured material based on ultrasonic scattering measurement[J]. Measurement, 2018, 118: 105-112. DOI:10.1016/j.measurement.2018.01.020 |
| [7] |
董鹏, 陈济轮. 国外选区激光熔化成形技术在航空航天领域应用现状[J]. 航天制造技术, 2014(1): 1-5. Dong P, Chen J L. Current status of selective laser melting for aerospace applications abroad[J]. Aerospace Manufacturing Technology, 2014(1): 1-5. (in Chinese) |
| [8] |
刘瑶璐, 胡宁, 邓明晰, 等. 板壳结构中的非线性兰姆波[J]. 力学进展, 2017, 47: 503-533. Liu Y L, Hu N, Deng M X, et al. Nonlinear Lamb waves in plate/shell structures[J]. Advances in Mechanics, 2017, 47: 503-533. (in Chinese) |
| [9] |
Zeitvogel D T, Matlack K H, Kim J Y, et al. Characterization of stress corrosion cracking in carbon steel using nonlinear Rayleigh surface waves[J]. NDT & E International, 2014, 62: 144-152. |
| [10] |
阎红娟, 徐春广, 肖定国, 等. 金属材料拉伸应力非线性超声特性研究[J]. 机械工程学报, 2016, 52(6): 22-29. Yan H J, Xu C G, Xiao D G, et al. Research on nonlinear ultrasonic properties of tension stress in metal materials[J]. Journal of Mechanical Engineering, 2016, 52(6): 22-29. (in Chinese) |
| [11] |
Seo H, Jun J, Jhang K Y. Assessment of thermal aging of aluminum alloy by acoustic nonlinearity measurement of surface acoustic waves[J]. Research in Nondestructive Evaluation, 2017, 28(1): 3-17. |
| [12] |
税国双, 汪越胜, 曲建民. 材料力学性能退化的超声无损检测与评价[J]. 力学进展, 2005, 35(1): 52-68. Shui G S, Wang Y S, Qu J M. Advances in nondestructive test and evaluation of material degradation using nonlinear ultrasound[J]. Advances in Mechanics, 2005, 35(1): 52-68. (in Chinese) |
| [13] |
Mondal C, Mukhopadhyay A, Sarkar R. A study on precipitation characteristics induced strength variation by nonlinear ultrasonic parameter[J]. Journal of Applied Physics, 2010, 108(12): 124910. |
| [14] |
Singh A K, Chen B Y, Tan V B C, et al. Finite element modeling of nonlinear acoustics/ultrasonics for the detection of closed delaminations in composites[J]. Ultrasonics, 2017, 74: 89-98. |
| [15] |
Kim J, Kim J G, Kong B, et al. Applicability of nonlinear ultrasonic technique to evaluation of thermally aged CF8M cast stainless steel[J]. Nuclear Engineering and Technology, 2020, 52(3): 621-625. |
| [16] |
徐显胜, 闫晓玲. 选区激光熔化316L不锈钢疲劳损伤非线性超声检测研究[J]. 制造技术与机床, 2021(6): 34-38. Xu X S, Yan X L. Nonlinear ultrasonic detection for fatigue damage in 316L stainless steel melted by selective laser technology[J]. Manufacturing Technology & Machine Tool, 2021(6): 34-38. (in Chinese) |
| [17] |
Na J K, Cantrell J H, Yost W T. Linear and nonlinear ultrasonic properties of fatigued 410Cb stainless steel[M]. Springer US, 1996.
|
| [18] |
张海澜. 理论声学[M]. 北京: 高等教育出版社, 2007. Zhang H L. Theoretical acoustics[M]. Beijing: Higher Education Press, 2007. (in Chinese) |
| [19] |
Rose J L, Nagy P B. Ultrasonic waves in solid media[M]. Cambridge: Cambridge University Press, 1999.
|
| [20] |
Breazeale M A, Philip J. Determination of third-order elastic constants from ultrasonic harmonic generation measurements[J]. Physical Acoustics, 1984, 17: 1-60. |
| [21] |
Liu S M, Croxford A J, Neild S A, et al. Effects of experimental variables on the nonlinear harmonic generation technique[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2011, 58(7): 1442-1451. |
 2022, Vol. 45
2022, Vol. 45


