b. 重庆大学 非均质材料力学重庆市重点实验室, 重庆 400044
b. Chongqing Key Laboratory of Heterogeneous Material Mechanics, Chongqing University, Chongqing 400044, P. R. China
由于信息技术的快速发展,半导体材料被广泛应用于制造集成电路、智能传感器等电子元器件。以GaAs、GaN和AlN等为代表的半导体材料因具有突出的光、电、磁等性质而受到越来越多的关注和研究[1-4]。均质半导体材料的性能有时难以满足实际应用的需求,因此异质结构设计的半导体材料成了更好的选择。然而具有不同性质的嵌入对象被埋入基体材料形成异质结构时,往往会因为晶格失配或与基体之间的热膨胀差而产生本征应变。Eshelby[5-6]的弹性夹杂理论为解决这一类非均质体弹性场问题提供了思路。该理论被广泛用于解决各领域与夹杂相关的问题,如材料等效性能预测[7-8]、压电材料力电耦合场[9-11]、热应力[12-13]以及材料的缺陷损伤[14]等问题。
不同形状的夹杂体会在局部和整体干扰材料的弹性场,从而极大地影响其机械和物理性能。而椭球形状的夹杂可以近似模拟很多形状。Xiao等[15]研究了嵌在无限大各向同性基体中的硬币形裂纹和球状非均质体,得到了内部应力场。Kim等[16]利用椭圆积分导出了椭圆形圆柱体夹杂外场的封闭解。Wu等[17-18]得到了圆柱体夹杂内外第一类、第二类和第三类椭圆积分形式的解析解。另一方面,对于更复杂形状的夹杂体,Chiu[19]采用基于格林函数的等效夹杂法求解出了半空间长方体夹杂物弹性场。Onaka等[20-21]则使用格林函数求解了环形和超球形夹杂物的弹性场。
除了夹杂体的形状以外,材料的各向异性对弹性场的影响也不可忽视。早期的研究多对介质进行各向同性假设以便简化计算,并且更容易得到解析解。Downs等[22]研究了各向同性介质中的量子阱应变松弛对电子的影响。Rodin[23]推导了多边形和多面体夹杂的Eshelby问题的封闭解。Pan等[24-25]通过格林函数法得到各向同性介质中的力电全耦合场。然而对于各向异性介质,一般很难得到解析解,大多数解决方案都是半解析的。比如Andreev等[26]提出了各向异性格林函数的傅里叶变换的一般分析方法,计算了任意形状半导体量子点结构三维应变分布,该方法适用于量子点与基体材料的弹性常数相等的情况。Franciosi等[27]通过Radon变换为各向异性无限大介质中的一般夹杂问题提供了另一种解决方案。Faux等[28]采用实空间的二阶多项式级数格林张量得到立方晶体中的应力和应变。但是这些研究结果仅给出了均质材料的弹性场结果,忽略了材料的非均匀性的影响。考虑到实际半导体材料多为非均质结构,非均匀性是影响材料机械和物理性能的重要因素,因此针对非均质材料的解答更具有现实意义。
由此可见,现有研究对含夹杂体材料的弹性场求解多采用各向同性材料性质加以简化,且大多局限于使用夹杂体内弹性场的结果(即Eshelby张量)进行材料等效性能预测等相关研究。然而,考虑到实际半导体材料的各向异性和非均质性,并且半导体器件设计一般需要同时提供夹杂体内外的弹性场信息,即含夹杂体的异质结构全空间弹性场分布情况,笔者基于格林函数法,通过等效夹杂理论建立异质结构椭球夹杂模型,使用傅里叶变换和逆变换,推导各向异性条件下的格林函数及其导数,获得该模型全空间的弹性场的一般解析表达式,具有一定的通用性。经过与文献和有限元方法进行对比,验证公式的正确性。最后重点研究非均质体形状和材料的弹性常数对非均质体和基体应变场的影响,以期为半导体材料的设计提供一定的理论依据和指导。
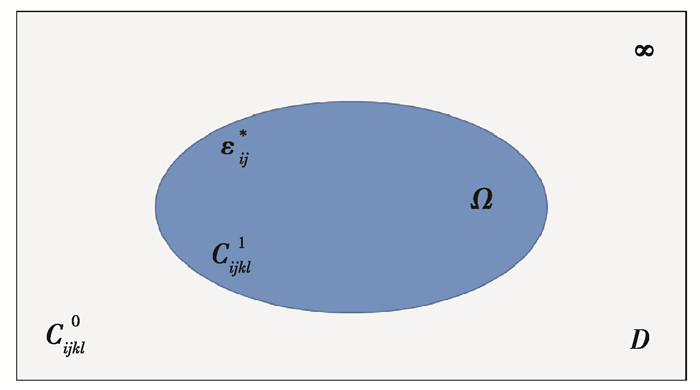
1 理论模型 1.1 异质结构椭球夹杂模型如图 1所示,建立无限大弹性体异质结构椭球夹杂模型。非均质体Ω内承受着热膨胀或晶格失配引起的本征应变εij*,弹性材料常数为Cijkl1。无限大基体D的弹性材料常数为Cijkl0。为方便起见,本文的张量同时采用直接记法(粗斜体)和下标记法,下标i、j、k、l等符号取值1~3,对应该张量的每一个分量,并默认重复下标遵守爱因斯坦求和约定。
|
图 1 异质结构椭球夹杂模型 Fig. 1 Ellipsoidal inhomogeneity model of heterogeneous structures |
若非均质体与基体具有相同的材料常数Cijkl,即得到经典的Eshelby夹杂问题,该问题可用点力格林函数的积分方程形式描述。由本征应变εij*产生的位移ui(x)用积分方程表示为[29-30]
| ui(x)=∫DGim(x,y)(−Cmjklε∗kl),,j dV(y)+∫∂D[Gim(x,y)σmj(y)nj(y)−um(y)CmjklGik,l(x,y)nj(y)]dS(y), | (1) |
式中:Gim(x, y)为格林函数,表示作用于点y处m方向的点力在点x处i方向产生的位移;nj(y)为边界∂D外法线向量;Cmjkl为材料弹性常数;εkl*为本征应变;σmj(y)为应力;um(y)为位移;Gik, l(x, y)为格林函数的偏导数,用逗号表示。因为本征应变εij*只作用于夹杂Ω内,且格林函数在边界∂D上为零,故上式可转换为
| ui(x)=∫ΩGim(x,y)(−Cmjklε∗kl),jdV(y) 。 | (2) |
在夹杂Ω内,本征应变为常量,通过高斯公式,式(2)可进一步转换为
| ui(x)=Cmjklε∗kl∫∂ΩGim(x,y)nj(y)dS(y)。 | (3) |
该式即表示夹杂与基体内任意一点的位移,对该式取微分,即得到总的应变场
| εin(x)=12Cmjklε∗kl∫∂Ω[Gim,n(x,y)+Gnm,i(x,y)]nj(y)dS(y)。 | (4) |
式中:Gim, n(x, y)和Gnm, i(x, y)为格林函数的偏导数。
为方便起见,上述夹杂问题的应变场ε和应力场σ采用直接记法可简要地表示为如下形式:
| ε=Sε∗ | (5) |
| σ={C(ε−ε∗)inΩ,Cε in D−Ω, | (6) |
式中:ε*为本征应变张量;C为弹性张量;S在夹杂内为Eshelby张量[5],在基体中仅表示该张量的积分形式
| Sijkl(x)=12Cklmn∫∂ΩGim,n(x,y)nj(y)+Gim,n(x,y)ni(y)]dS(y)。 | (7) |
式中Cklmn为弹性张量。
当夹杂的材料与基体不一致时,可通过等效夹杂法在夹杂内引入另一本征应变εp以消除材料不同的影响,即[30]
| C0(ε−ε∗−εp)=C1(ε−ε∗) 。 | (8) |
式中: C0为基体弹性张量;C1为夹杂体弹性张量。
该方程即为等效夹杂方程,令等效本征应变ε** =ε*+εp,再将式(5)代入式(8)可得
| C0(Sε∗∗−ε∗∗)=C1(Sε∗∗−ε∗)。 | (9) |
通过上式可解得等效特征应变
| ε∗∗=S−1(H+C1)−1C1ε∗, | (10) |
式中H=C0S-1-C0为Hill张量。将等效本征应变代入式(5)和式(6),得到非均质体内外的应变和应力
| ε=Sε∗∗=(H+C1)−1C1ε∗; | (11) |
| σ={C0(ε−ε∗∗) in Ω,C0ε in D−Ω. | (12) |
求解式(11)和(12)的关键在于求解格林函数及其导数的积分,然而格林函数在各向异性的情况下无法得到封闭解析表达式,因此只能通过数值积分的方法求得数值解。
1.2 各向异性格林函数数值解假设在连续介质域内y点处存在一个点力,且介质为各向异性线弹性材料,那么在另一点x处的位移和平衡方程可以表示为[29]
| CijklGmi,jk(x−y)+δlmδ(x−y)=0, | (13) |
式中: δ(x-y)为狄拉克函数,δlm为克罗内克符号,Gmi, jk为格林函数的二阶导数。通过对格林函数和狄拉克函数进行傅里叶变换和逆变换可以将方程(13)转换到傅里叶空间中进行求解,得到格林函数的积分表达式如下
| Gij(x)=1(2π)3∫∞−∞(zz)−1ijw2exp(iw⋅x)dw, | (14) |
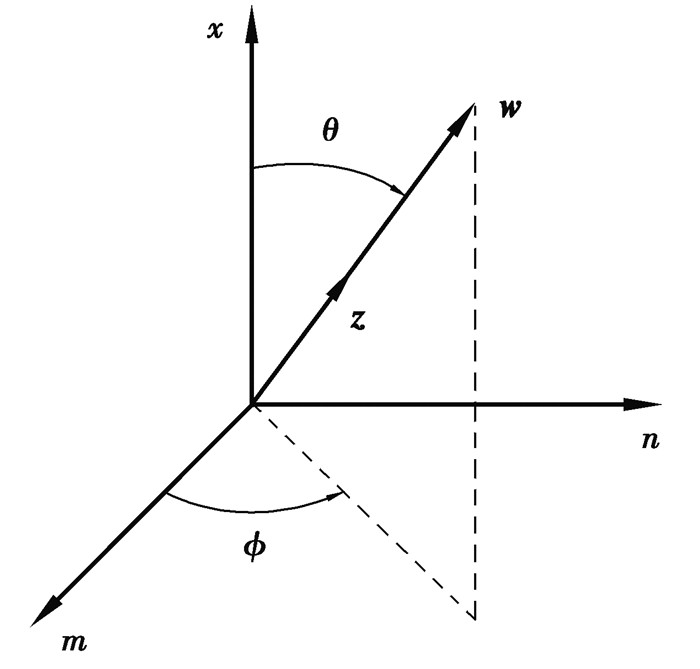
式中:w为傅里叶变换空间矢量, w是其模量:
|
图 2 矢量w在傅里叶空间的示意图 Fig. 2 Vector w in Fourier space |
| Gij(x)=18π2x∫2π0(zz)−1ij dθ|x,z=0。 | (15) |
式(15)即为各向异性格林函数的积分表达式,积分最后可以在单位圆上进行。
1.3 各向异性格林函数导数的数值解由式(14)可知,格林函数Gij(x)的积分是在傅里叶空间进行的,结果包含实部和虚部,但格林函数Gij(x) 本身却是在实空间,故可只在实部进行积分[31],即
| Gij(x)=1(2π)3∫∞−∞(zz)−1ijw2cos(wz⋅x)dw。 | (16) |
自然地,格林函数的一阶导数可表示为
| Gij,k(x)=−1(2π)3∫∞−∞zk(zz)−1ijwsin(wz⋅x)dw。 | (17) |
令x=xt,即t为x的单位向量;定义变换关系
| Gij,k(x)=−1(2π)3x2∫∞−∞zk(zz)−1ijssin(sz⋅t)ds 。 | (18) |
又因为
| ∫∞0ssin(scosθ)ds=πsinθ∂∂θδ(cosθ) 。 | (19) |
将式(19)的结果代入式(18)得
| Gij,k(x)=18π2x2∫2π0dϕ∫π0zk(zz)−1ij∂∂θδ(cosθ)dθ。 | (20) |
由分部积分,式(20)可简化为
| Gij,k(x)=18π2x2∫2π0∂∂θ(zk(zz)−1ij)|θ=π2 dϕ。 | (21) |
令
| Gij,k(x)=18π2x2∫2π0(−tk(zz)−1ij+zkFij)dϕ。 | (22) |
式(22)即为各向异性格林函数一阶导数的积分形式,积分最后同样是在单位圆上进行。
2 结果将前文得到的格林函数及其导数与(4)式结合,通过数值积分获得异质结构椭球夹杂模型全空间的弹性场。将数值积分得到的弹性场结果分别与文献中的均匀夹杂体条件下的结果以及由有限元方法得到的非均质体条件下的结果进行对比,以验证上述积分公式的正确性。
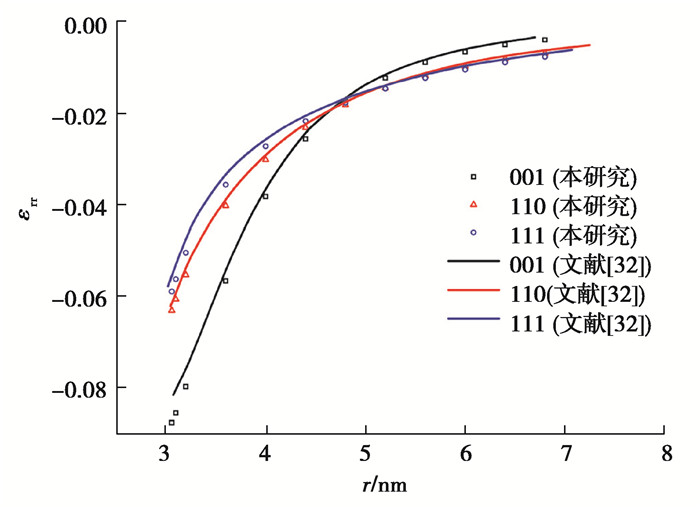
2.1 均质夹杂体将数值积分的结果与Andreev等[32]的研究结果进行对比。Andreev研究的对象为InAs/GaAs系统,即半径为3 nm的球形夹杂材料InAs和无限大基体材料GaAs。由晶格失配在夹杂体内产生的本征应变为ε*=0.067。但在实际计算过程中,却假设夹杂体与基体材料相同,均为GaAs立方晶体材料。因此,实际上这是一种均匀介质的情况。
立方晶体GaAs的材料常数为C11=122.1 GPa,C12=56.6 GPa,C44=60.0 GPa。由于球状夹杂体内部为均匀分布的常应变,故只取基体中的应变进行对比,结果如图 3所示。
|
图 3 均质材料下基体中本文的应变场结果与Andreev的结果[32]对比 Fig. 3 Comparison of strain field in the matrix between results of this study and Andreev's results in homogeneous materials |
图 3中εrr为径向应变,r为路径上的点到原点的距离,实线分别为Andreev结果中沿[001]、[110]和[111]3个方向路径上的应变εrr的分布曲线,散点为本文的数值积分结果。从图 3中可以看出,数值积分结果与Andreev的结果几近相同,验证了本文积分公式的正确性。另一方面,由图 3可知,εrr在3个方向上的分布并不相同,且存在较大差距。在[001]与[111]方向界面附近的应变差距最大,接近30%。这正是由于材料的各向异性而产生的结果,说明对材料的各向同性假设在某些条件下并不适用。
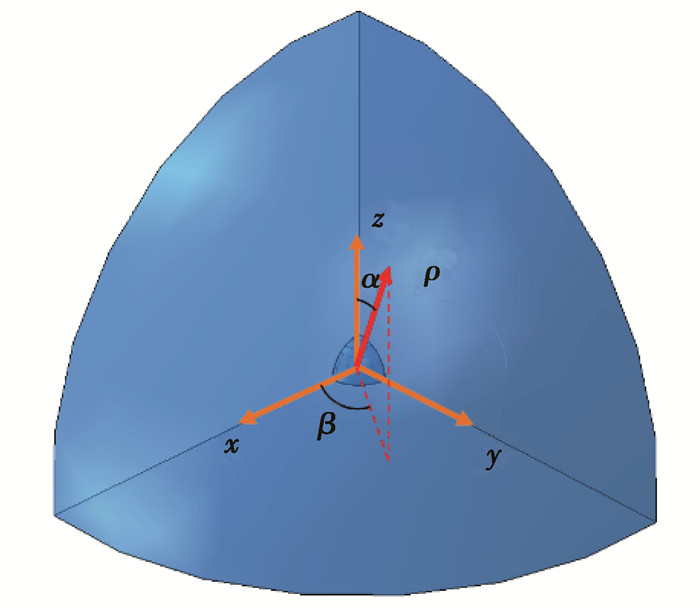
2.2 非均质体为了进一步验证积分公式的正确性,以球形非均质体模型为例,将上述积分公式的数值计算结果与有限元方法得到结果进行对比分析。在有限元软件ABAQUS中建立模型如图 4所示,取八分之一球体结构,ρ为极径,α和β分别表示极角和方位角。其中球形非均质体材料为InAs,半径取1 nm,基体材料为GaAs。材料的具体弹性常数如表 1所示。
|
图 4 非均质结构有限元模型 Fig. 4 FEM model of heterogeneous structures |
| 表 1 材料参数[1] Table 1 Material parameters |
假设非均质体中由热膨胀引起的本征应变为ε* =0.067。图 5所示为球坐标下模型[111]方向路径上的正应变分布曲线。由于模型为球状对称结构,切向应变εαα与周向应变εββ数值上相等,因此只取径向应变εrr与切向应变εαα数值进行对比分析。其中实线为有限元计算结果,散点部分为积分公式的数值计算结果。由图 5可知,在球状非均质体内部,应变均匀分布,这与经典夹杂理论解的结果一致。而在基体中,应变均呈指数级衰减,在夹杂体外2~3倍夹杂体半径处接近于0。不同的是εαα呈连续分布状态,而εrr在界面处由拉应变突变为压应变,为非连续分布。从图 5中实线与散点的对比结果可知,数值积分的结果与有限元计算的结果完全一致,进一步证明了本文数值积分公式的正确性,并且该公式适用于非均质体,在实际工程问题中更具普遍性。
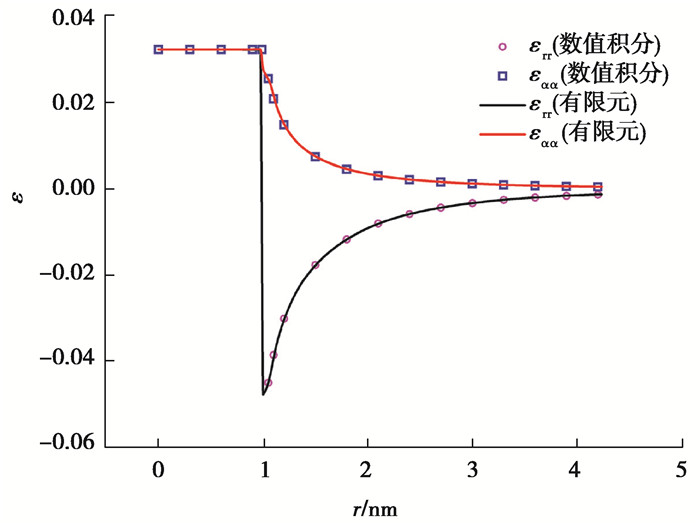
|
图 5 非均质材料中应变场数值积分结果与有限元结果对比 Fig. 5 Comparison of strain field between numerical integration results and FEM results in heterogeneous materials |
半导体材料在实际应用中为了性能方面的需要,夹杂物可以呈现各种形状,如立方体形、方锥形、截断金字塔形、透镜形、半球形、圆柱体形等。不同形状的夹杂物对其体内和周围基体的弹性场状态有很大影响。除此以外,由于半导体材料中非均质结构的存在,材料弹性常数的差异是影响弹性场的另一个重要因素。因此本文中分别从非均质体的形状和材料参数两个方面讨论其对应变场分布变化的影响。
3.1 形状参数的影响椭球非均质体的形状可用如下公式表示:
| x2a2+y2b2+z2c2≤1。 | (23) |
如图 6所示,通过改变椭球的轴长a、b和c可以近似模拟各种形状。

|
图 6 各种椭球类形状夹杂 Fig. 6 Various ellipsoid shape inclusions |
在本研究中使a = b = 1 nm保持恒定,只改变c的大小来模拟各种形状的非均质体,以探究形状因素对应变分布的影响。由于模型关于z轴对称,因此沿x轴和y轴的应变分布相同,故只研究沿x轴和z轴的应变。由于非均质体中的应变分布是均匀的,因此将非均质体和基体中的应变分开进行讨论。图 7所示为非均质体内部的正应变随形状改变的变化曲线。从图中可以看出,随着横坐标log(c/a)增大,即非均质体形状由扁平的硬币状逐渐向细长的圆柱状变化过程中,εxx从极小值(约0)逐渐增大到极大值(约0.054),εzz从极大值(约0.14)逐渐减小到极小值(约0),受力状态近似于从平面应力状态逐渐转变为平面应变状态。
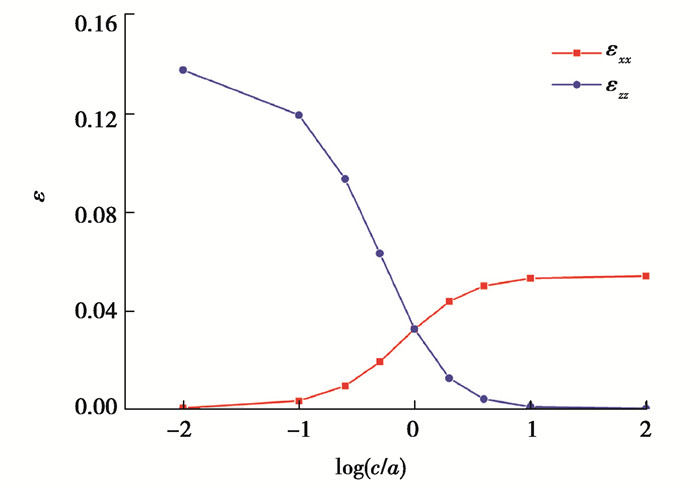
|
图 7 非均质体形状对其内部应变的影响 Fig. 7 Effect of inhomogeneity shape on the strain inside the inhomogeneity |
图 8(a)和图 8(b)为各种非均质体形状下,基体中εxx沿x轴的分布变化曲线。从图 8(a)可以明显看出,当c/a < 1且逐渐减小,即非均质体越趋于扁平状时,应变εxx越小,衰减越快,而且应变场大小在靠近界面附近有明显区别。与之相反,从图 8(b)可以明显看出,当c/a>1且逐渐增大,即非均质体越趋于细长状时,应变εxx随非均质体形状变化并不明显,说明细长状非均质体形状的改变对基体中的应变εxx影响不大。图 9则显示出基体中x轴上的应变εyy随着c/a增大而增大,且随着x增大应变衰减趋势一致,呈现层次分明的状态。
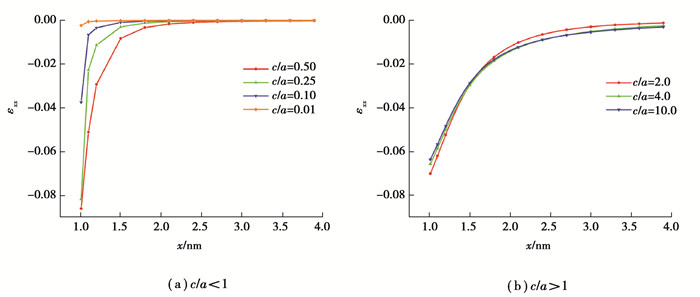
|
图 8 非均质体形状对基体中应变εxx沿x轴分布的影响 Fig. 8 Effect of inhomogeneity shape on the strain εxx distribution along x axis in matrix |
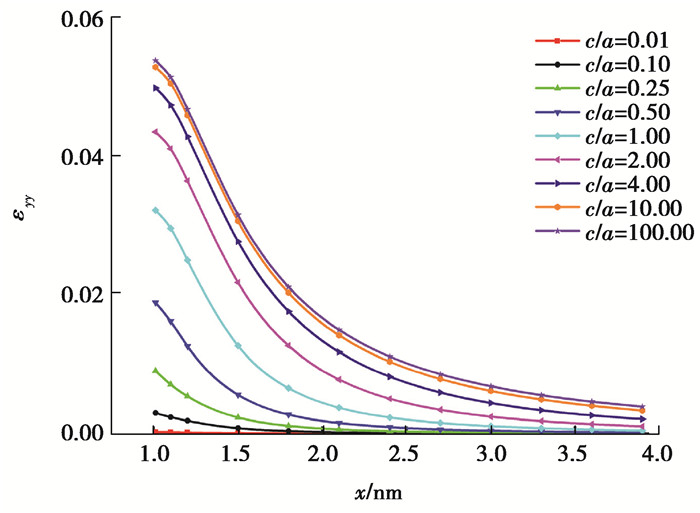
|
图 9 非均质体形状对基体中应变εyy沿x轴分布的影响 Fig. 9 Effect of inhomogeneity shape on the strain εyy distribution along x axis in matrix |
图 10(a)和(b)为基体中εzz沿x轴的分布情况。与εxx的不同,当c/a < 1时,随着c/a的递增,界面附近的应变εzz呈现出先增大后减小的趋势,在c/a=0.25达到峰值。当c/a>1时,基体中的应变εzz随着c/a的递增而减小,当c/a>10时,应变小到可以忽略。
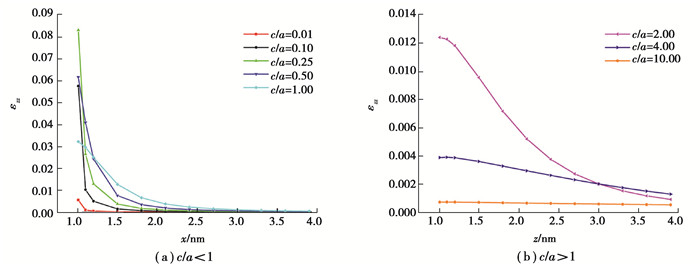
|
图 10 非均质体形状对基体中应变εzz沿x轴分布的影响 Fig. 10 Effect of inhomogeneity shape on the strain εzz distribution along x axis in matrix |
图 11(a)和(b)分别为基体中εxx和εzz沿z轴的分布曲线,可以看出应变都随着c/a递增而增大,另一个显著的特点是c/a越大,应变在界面附近衰减得越剧烈,在基体距离界面极近处已接近为0。εxx的分布曲线还表明当c/a < 1时,εxx的最大值并不在界面处,而是在界面附近的基体中。
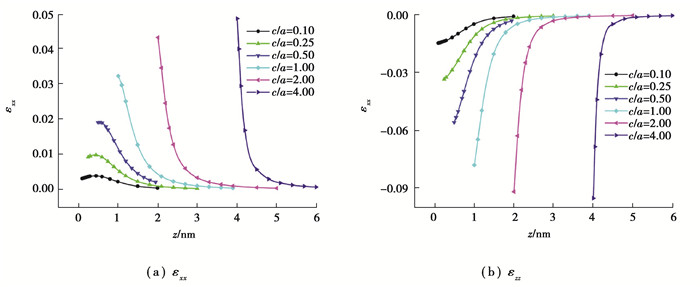
|
图 11 非均质体形状对基体中应变εxx和εzz沿z轴分布的影响 Fig. 11 Effect of inhomogeneity shape on the strain εxx and εzz distribution along z axis in matrix |
实际半导体材料多为非均质结构,非均匀性是影响材料机械和物理性能的重要因素。以常见的立方晶体半导体材料为例(如GaAs, InAs等),立方晶体具有3个独立的弹性常数C11、C12和C44,前两个与材料的拉伸性能相关,最后一个与材料的剪切性能相关。其弹性常数对比情况见表 2。
| 表 2 常见半导体材料参数 Table 2 Material parameters of common semiconductors |
通过表 2可以看出,不同半导体材料的弹性常数差异明显,对于异质结构,这是影响弹性场的重要因素。本文中所建立的各向异性异质结构椭球夹杂模型可以设置不同夹杂体材料的弹性常数来研究其对弹性场分布情况的影响。有趣的是,当采用固定立方晶体的拉伸弹性常数C11和C12而使用不同的剪切弹性常数C44时,数值积分结果与有限元结果均显示最终弹性场分布情况未发生任何改变,即结果与夹杂体剪切弹性常数C44无关。这看起来似乎有悖直觉,但借助于本文中所建立的各向异性异质结构椭球夹杂模型可以解释如下。由式(11)可知,最终弹性场由Hill张量H、夹杂体弹性张量C1和本征应变ε*决定。其中,Hill张量H只跟基体弹性张量C0有关,所以只需要考虑夹杂体弹性张量C1和本征应变ε*的共同作用对最终弹性场的影响。虽然夹杂体弹性张量C1确实包含剪切弹性常数C44,但该弹性常数需要和本征应变ε*的剪切分量相乘时才会对最终弹性场产生影响。然而异质结构中的本征应变往往是由晶格失配或热膨胀差而产生,该本征应变仅包含正应变分量而无剪应变分量。因此由式(11)可知,剪切弹性常数C44不影响最终应变场的分布情况。事实上,这一结论可以推广到具有正交或更高对称性晶体结构的半导体材料中(如常见的纤锌矿晶体结构的GaN、AlN等),即本征应变仅包含正应变分量时,弹性场分布情况与夹杂体剪切弹性常数无关,而只和拉伸弹性常数有关。
基于上述原因,为了考虑各向异性夹杂体材料参数对弹性场的影响,本文中采用固定立方晶体的弹性常数C12和C44而使用不同的拉伸弹性常数C11的方式探究其对应变状态的影响。以下计算中,选取非均质体的弹性常数C11作为变量,其余弹性常数与2.2节一致,结果如图 12(a)和(b)所示。从中可以明显看出非均质体和基体中的应变εxx和εzz都随着非均质体拉伸弹性常数C11增大而增大,但其影响主要集中在内部和界面附近,在距离界面较远处的基体中几乎没有影响。
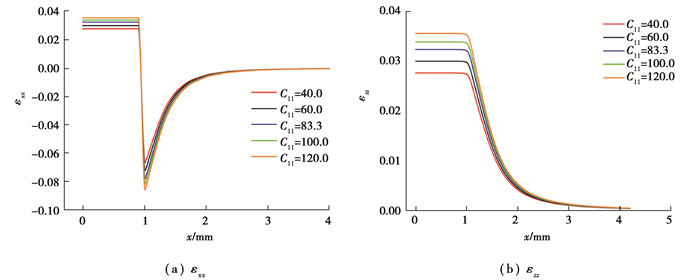
|
图 12 非均质体弹性常数C11对应变εxx和εzz沿x轴分布的影响 Fig. 12 Effect of inhomogeneity elastic constant C11 on strain εxx and εzz distribution along x axis |
建立了各向异性异质结构椭球夹杂模型,采用格林函数法和等效夹杂理论,获得了全空间弹性场的解析解。与文献和有限元结果的对比证明了理论公式的正确性。以InAs/GaAs系统为例分析了非均质体的形状和弹性常数对应变的影响,得出以下结论:
1) 非均质体形状由扁平状变化到细长状时,非均质体内的应变状态由平面应力状态过渡到平面应变状态;
2) 扁平状非均质体形状的改变对基体中的应变εxx沿x轴分布情况影响明显,但细长状非均质体形状的改变对基体中的应变εxx沿x轴分布情况影响不大;
3) 本征应变仅包含正应变分量时,最终弹性场分布情况与具有正交或更高对称性晶体结构的夹杂体的剪切弹性常数无关;
4) 应变场整体变化趋势与夹杂体的拉压弹性常数变化趋势一致。
| [1] |
Vurgaftman I, Meyer J R, Ram-Mohan L R. Band parameters for Ⅲ-V compound semiconductors and their alloys[J]. Journal of Applied Physics, 2001, 89(11): 5815-5875. DOI:10.1063/1.1368156 |
| [2] |
陈良惠, 杨国文, 刘育衔. 半导体激光器研究进展[J]. 中国激光, 2020, 47(5): 0500001. Chen L H, Yang G W, Liu Y X. Development of semiconductor lasers[J]. Chinese Journal of Lasers, 2020, 47(5): 0500001. (in Chinese) |
| [3] |
Wang Z H, Chen Y, Zheng K W, et al. Review on property regulation of semiconducting materials in flexible electronics[J]. Acta Physica Sinica, 2021, 70(16): 164203. DOI:10.7498/aps.70.20210095 |
| [4] |
孙天宇, 夏明俊, 乔雷. 半导体激光器失效机理与检测分析研究进展[J]. 激光与光电子学进展, 2021, 58(19): 1900003. Sun T Y, Xia M J, Qiao L. Failure mechanism and detection analysis of semiconductor laser[J]. Laser & Optoelectronics Progress, 2021, 58(19): 1900003. (in Chinese) |
| [5] |
Eshelby J D. The determination of the elastic field of an ellipsoidal inclusion, and related problems[J]. Proceedings of the Royal Society of London Series A Mathematical and Physical Sciences, 1957, 241(1226): 376-396. |
| [6] |
Eshelby J D. The elastic field outside an ellipsoidal inclusion[J]. Proceedings of the Royal Society of London Series A Mathematical and Physical Sciences, 1959, 252(1271): 561-569. |
| [7] |
黄敏杰, 马利锋, 尚福林. 基于等效特征应变原理的复合材料有效模量细观力学分析[J/OL]. 固体力学学报(2021-12-16)[2022-03-10]. https://kns.cnki.net/kcms/detail/detail.aspx?dbcode=CAPJ&dbname=CAPJLAST&filename=GTLX20211214002&uniplatform=NZKPT&v=aZL1Gjo5o466dioVAH8UTwusQcoC8z--MBjr2OPrln4dJmgJxHgaNqfJN-WH0JCw. DOI: 10.19636/j.cnki.cjsm42-1250/o3.2021.062. Huang M J, Ma L F, Shang F L. Micro-mechanical analysis of effective moduli of composite materials based on the principle of equivalent eigenst rain[J/OL]. Chinese Journal of Solid Mechanics, (2021-12-16)[2022-03-10]. https://kns.cnki.net/kcms/detail/detail.aspx?dbcode=CAPJ&dbname=CAPJLAST&filename=GTLX20211214002&uniplatform=NZKPT&v=aZL1Gjo5o466dioVAH8UTwusQcoC8z--MBjr2OPrln4dJmgJxHgaNqfJN-WH0JCw. DOI: 10.19636/j.cnki.cjsm42-1250/o3.2021.062.(inChinese)). |
| [8] |
李涛, 邹文楠. 平面任意形状等剪切模量异质夹杂问题的解析解[J]. 固体力学学报, 2021, 42(5): 552-566. Li T, Zou W N. Analytical solution for the eshelby problem of an arbitrarily shaped inhomogeneous inclusion with the same shear modulus as the matrix in an infinite plane[J]. Chinese Journal of Solid Mechanics, 2021, 42(5): 552-566. (in Chinese) DOI:10.19636/j.cnki.cjsm42-1250/o3.2021.037 |
| [9] |
Arefi M. Size-dependent electro-elastic analysis of a three-layered piezoelectric doubly curved nano shell[J]. Mechanics of Advanced Materials and Structures, 2020, 27(23): 1945-1965. DOI:10.1080/15376494.2018.1533605 |
| [10] |
Chen Q, Wang G N. Computationally-efficient homogenization and localization of unidirectional piezoelectric composites with partially cracked interface[J]. Composite Structures, 2020, 232: 111452. DOI:10.1016/j.compstruct.2019.111452 |
| [11] |
Wang X, Schiavone P. Electroelastic field for a blunt crack in an anisotropic piezoelectric material[J]. Continuum Mechanics and Thermodynamics, 2021, 33(6): 2509-2514. DOI:10.1007/s00161-021-01035-x |
| [12] |
Zhang J, Huang Y H, Liu W D, et al. Micromechanical investigation of thermal stresses of a finite plane containing multiple elliptical inclusions based on the equivalent inclusion method and distributed dislocation method[J]. Journal of Mechanical Science and Technology, 2021, 35(1): 247-256. DOI:10.1007/s12206-020-1224-y |
| [13] |
Bai X Y, Dong Q B, Zheng H, et al. Modelling of non-Newtonian starved thermal-elastohydrodynamic lubrication of heterogeneous materials in impact motion[J]. Acta Mechanica Solida Sinica, 2021, 34(6): 954-976. DOI:10.1007/s10338-021-00284-2 |
| [14] |
付云伟, 倪新华, 刘协权, 等. 颗粒缺陷相互作用下复合材料的细观损伤模型[J]. 力学学报, 2016, 48(6): 1334-1342. Fu Y W, Ni X H, Liu X Q, et al. Micro-damage model of composite materials with particle and defect interaction[J]. Chinese Journal of Theoretical and Applied Mechanics, 2016, 48(6): 1334-1342. (in Chinese) |
| [15] |
Xiao Z M, Pae K D. The interaction between a penny-shaped crack and a spherical inhomogeneity in an infinite solid under uniaxial tension[J]. Acta Mechanica, 1991, 90(1/2/3/4): 91-104. |
| [16] |
Kim B R, Lee H K. Closed form solution of the exterior-point eshelby tensor for an elliptic cylindrical inclusion[J]. Journal of Applied Mechanics, 2010, 77(2): 024503. DOI:10.1115/1.3197236 |
| [17] |
Wu L Z, Du S Y. The elastic field caused by a circular cylindrical inclusion-Ⅰ: inside the region |
| [18] |
Wu L Z, Du S Y. The elastic field caused by a circular cylindrical inclusion-Ⅱ: inside the region |
| [19] |
Chiu Y P. On the stress field and surface deformation in a half space with a cuboidal zone in which initial strains are uniform[J]. Journal of Applied Mechanics, 1978, 45(2): 302-306. DOI:10.1115/1.3424292 |
| [20] |
Onaka S. Strain fields caused by doughnut-like and tubular inclusions with uniform eigenstrains[J]. Mechanics Research Communications, 2005, 32(3): 316-322. DOI:10.1016/j.mechrescom.2004.05.009 |
| [21] |
Onaka S, Sato H, Kato M. Elastic states of doughnut-like inclusions with uniform eigenstrains treated by averaged Eshelby tensors[J]. Philosophical Magazine Letters, 2002, 82(1): 1-7. DOI:10.1080/01418610208239992 |
| [22] |
Downes J R, Faux D A, O'Reilly E P. Influence of strain relaxation on the electronic properties of buried quantum wells and wires[J]. Materials Science and Engineering: B, 1995, 35(1/2/3): 357-363. |
| [23] |
Rodin G J. Eshelby's inclusion problem for polygons and polyhedra[J]. Journal of the Mechanics and Physics of Solids, 1996, 44(12): 1977-1995. DOI:10.1016/S0022-5096(96)00066-X |
| [24] |
Pan E. Elastic and piezoelectric fields around a quantum dot: fully coupled or semicoupled model?[J]. Journal of Applied Physics, 2002, 91(6): 3785-3796. DOI:10.1063/1.1448869 |
| [25] |
Pan E N, Tonon F. Three-dimensional Green's functions in anisotropic piezoelectric solids[J]. International Journal of Solids and Structures, 2000, 37(6): 943-958. DOI:10.1016/S0020-7683(99)00073-6 |
| [26] |
Andreev A D, O'Reilly E P. Theory of the electronic structure of GaN/AlN hexagonal quantum dots[J]. Physical Review B, 2000, 62(23): 15851-15870. DOI:10.1103/PhysRevB.62.15851 |
| [27] |
Franciosi P, Lormand G. Using the radon transform to solve inclusion problems in elasticity[J]. International Journal of Solids and Structures, 2004, 41(3/4): 585-606. |
| [28] |
Faux D A, Christmas U M E. Real-space Green's tensors for stress and strain in crystals with cubic anisotropy[J]. Journal of Applied Physics, 2005, 98(3): 033534. DOI:10.1063/1.1990266 |
| [29] |
Mura T. Micromechanics of defects in solids[M]. 2nd ed. Dordrecht, the Netherlands: Martinus Nijhoff, 1987.
|
| [30] |
Qu J M, Cherkaoui M. Fundamentals of micromechanics of solids[M]. Hoboken, NJ, USA: John Wiley & Sons, Inc., 2006.
|
| [31] |
Barnett D M. The precise evaluation of derivatives of the anisotropic elastic Green's functions[J]. Physica Status Solidi (B), 1972, 49(2): 741-748. |
| [32] |
Andreev A D, Downes J R, Faux D A, et al. Strain distributions in quantum dots of arbitrary shape[J]. Journal of Applied Physics, 1999, 86(1): 297-305. DOI:10.1063/1.370728 |
 2022, Vol. 45
2022, Vol. 45



