2. 重庆大学 航空航天学院, 重庆 400044
2. College of Aerospace Engineering, Chongqing University, Chongqing 400044, P. R. China
蒙西地区工业园区或其他走廊紧张的输电线路常采用同塔四回路输电杆塔,相较于单回路和双回路杆塔,该类杆塔塔型高、结构复杂。蒙西地区地势开阔,输电线路受风荷载作用时间长,容易发生杆塔破坏事故。研究杆塔在随机风荷载作用下的强度和疲劳寿命具有十分重要的意义。
输电线路设计规程中的杆塔设计[1],将风荷载转换为拟静载荷进行分析,通过风振系数来考虑风荷载的风振响应。郭勇等[2]针对多回路输电塔研究发现,现有规范求解风振系数偏于危险,存在不足。近年,采用数值模拟方法研究输电塔线体系在风荷载作用下的动力响应的工作时有报道。窦汉岭等[3]建立了大跨越转角塔的两塔三档模型,进行风荷载时程响应分析,研究输电塔的受力规律以及动力响应,但并未考虑螺栓等连接细节的影响。原迁等[4]建立输电杆塔的精细化三维有限元模型,对单塔及塔线体系模型的风振时程进行分析,但研究仍局限于对杆梁模型的分析。刘孟龙[5]通过CFD模拟近地面三维风场,进而模拟了复杂地形中塔线体系的结构动力特征,同样未考虑杆塔连接细节对模型的影响。Kitipornchai等[6]提出了2种模拟螺栓滑移的模型,研究了螺栓滑移对结构极限强度的影响。齐立忠等[7]研究了螺栓滑移对杆塔变形和承载能力的影响,但其以空间杆梁模型为基础,在杆件连接处通过引入连接单元来模拟螺栓的滑移,没有考虑螺栓连接的细节。沈康[8]针对输电塔线体系在风载荷作用下的破坏区域,建立节点精细化有限元模型,研究螺栓承载性能的变化,但节点精细化模型相较于实体模型仍存在不足。Ju等[9]研究了输电塔安全销的极限承载力,并通过Miner线性损伤累积理论计算了安全销的疲劳寿命。Xie等[10]利用试验方法对500 kV输电杆塔2个子结构在模拟冰荷载作用下的破坏机理进行了研究。Zhou等[11]研究了风雨载荷诱发的输电杆塔振动,并提出配件与塔架可能发生金属疲劳。严波等[12]研究了针对同塔双回四分裂线路,考虑螺栓连接区域细节,模拟研究在脱冰和断线情况下杆塔的强度,并分析了螺栓预紧力的影响。另一方面,陆兴华等[13]通过对复合横担建立局部有限元模型,模拟研究了其在舞动、微风振时的疲劳评估。Prasad Rao等[14]实验研究了塔腿、支撑杆和冗余杆件破坏、细节设计和连接结构破坏、材料缺陷和制造误差等的影响,并利用梁单元模拟螺栓,对杆塔进行了大变形弹塑性分析及失效分析。孙中浩[15]研究了输电塔在风振响应下的疲劳性能,并对典型焊点接头进行疲劳寿命研究。但都没有考虑杆塔危险区域的结构细节和螺栓预紧力对杆塔疲劳寿命的影响。
笔者以蒙西地区220 kV同塔四回路典型线路段为研究对象,建立实际线路段的塔线体系有限元模型,模拟塔线体系在最大设计基本风速和年平均风速随机风场中的动力响应,确定杆塔的危险区域,进而建立杆塔危险区域精细有限元模型,研究风荷载和螺栓预紧力对杆塔强度和疲劳寿命的影响。
1 随机风场中塔线体系动力响应 1.1 塔线耦合体系有限元模型以蒙西地区220 kV同塔四回路典型线路段为对象。如图 1所示,该线路段考虑直线杆塔大水平大垂直档距组合、大水平小垂直档距组合、大水平档距大高差组合等条件,包括四塔五档,档距分别为300,445,310,445,300 m,基础高差分别为0,-1,2.5,7.5,0 m。杆塔为SSZ1直线塔,杆塔I和IV的呼高为30 m,塔Ⅱ和Ⅲ的呼高为21 m。杆塔构件采用了Q235、Q345、Q420三种材料,其杨氏模量均为210 GPa,泊松比均为0.3。同塔四回线路总共包括12相导线,每一相导线均为二分裂导线,型号为JL/G1A-400/35。地线为JLB20A-150。导线初始张力为57.9 MPa,地线初始张力为286.4 MPa,导地线的物理参数如表 1所示。该线路段中的杆塔均为直线塔,导线通过I型悬垂绝缘子串悬挂在杆塔上,型号为XWP-100,质量为311.92 kg,串长3.33 m。该线路段中没有耐张杆塔,所以不考虑耐张绝缘子串。
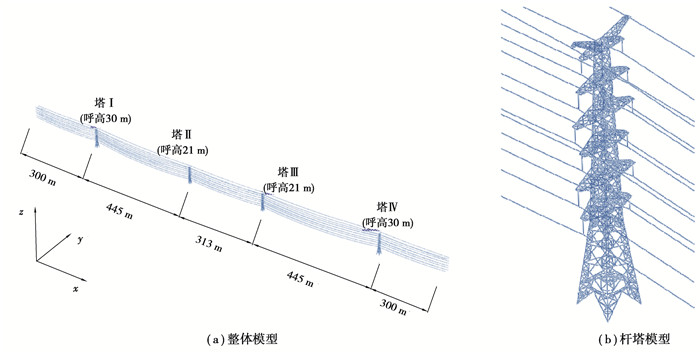
|
图 1 塔线耦合体系有限元模型 Fig. 1 Finite element model of tower line system |
| 表 1 导线和地线的物理参数 Table 1 The parameters of conductor and ground wire |
杆塔有限元模型采用空间杆梁混合模型,根据构件之间的连接关系将斜撑简化为轴力杆,其余构件为梁,分别用桁架单元和空间梁单元离散。将双分裂导线等效为单导线,采用空间梁单元进行离散[16-17]。悬垂绝缘子串简化为圆形截面的梁,其质量与原型相等。悬垂绝缘子串与导线的连接关系设置为Beam关系,与杆塔的连接关系设为Join+Rotation。所有杆塔塔腿根部为固定约束,线路段两端的导线和地线端点均设置为固定约束。建立的塔线体系有限元模型如图 1所示。该塔线体系模型共划分51 644个单元B31单元,1 592个T3D2单元。对该塔线体系有限元模型进行了单元收敛性检查,其网格划分满足单元收敛性要求。
1.2 随机风场中塔线体系风载荷自然风速可视为平均风速V(z)与脉动风速v(x, z, t)两部分之和,
| $ V(x, z, t)=\bar{V}(z)+v(x, z, t) 。$ | (1) |
平均风速与高度有关,其与10 m高的基本风速V10存在如下关系[17],
| $ \frac{\bar{V}(z)}{\bar{V}_{10}}=\left(\frac{z}{10}\right)^a, $ | (2) |
式中:a为地面粗糙度系数,与地貌有关,z为离地面的高度。
各国学者提出了多种脉动风速功率谱,工程中常采用考虑随高度变化的Kaimal谱[17],
| $ S(z, f)=\frac{200 f_* V_*^2}{f\left(1+50 f_*\right)^{\frac{5}{3}}}, V_*=0.35 \frac{\bar{V}(z)}{\ln \left(z / z_0\right)}, f_*=\frac{f_z}{\bar{V}(z)}, $ | (3) |
式中:V*为剪切速度;z0为地面粗糙长度,f为频率。
考虑风的空间相关性,脉动风速互相干谱可写成,
| $ S_{k l}(r, f)=\sqrt{S_{k k}\left(z_k, f\right) S_{l l}\left(z_l, f\right)} \cdot \operatorname{Coh}(r, f) e^{i \theta}, k \neq l, $ | (4) |
式中,Skk(zk, f)和Sll(zl, f)为相距r的空间两点的自功率谱,由式(3)确定;θ f为互谱相位角;Coh(r, f) 为相干函数,根据Davenport建议采用竖向和横向相干函数,
| $ \operatorname{Coh}(r, f)=\exp \left(\frac{-2 f \sqrt{C_y^2\left(y_k-y_l\right)^2+C_z^2\left(z_k-z_l\right)^2}}{\bar{V}\left(z_k\right)+\bar{V}\left(z_l\right)}\right), $ | (5) |
式中:yk,yl和zk,zl分别表示空间两点的横向坐标和竖向坐标,两点的连线与平均风速的方向垂直,V (zk)和V (zl)分别为高度为zk和zl和处的平均风速。Cy和Cz和分别为横向和竖向相关的指数衰减系数,其取值可以由试验确定,它与平均风速、离地面高度和地表面粗糙长度等有关,一般可取Cy=8,Cz=7。
根据Shinozuka理论,结合FFT算法,可以快速有效地模拟得到脉动风速时程样本[18],再利用式(1)即可计算得到模拟点的风速时程曲线。
根据气象统计数据,蒙西地区10 m高度处的年平均风速约为10 m/s,线路的设计基本风速为27 m/s。在此分别选择该2种基本风速模拟生成随机风场。根据蒙西地区地形条件,选择B类地貌,其地面粗糙系数a取0.16,地面粗糙长度z0取0.03,并根据当地10 m高度下的湍流强度为0.126对地面粗糙系数进行修正。导线和地线水平方向每隔10 m生成一个风速时程点。杆塔沿高度方向分成5段,每段生成一个风速时程点。模拟时程总长T=600 s,时间步长Δt=0.5 s,频率的截取范围取0.00~6.28 rad/s,频率范围等分数N=3 000,即Δω=0.002 09 rad/s。模拟的风速V10分别取27 m/s和10 m/s。生成的典型风速点的风速时程及其对应的功率谱密度如图 2所示。
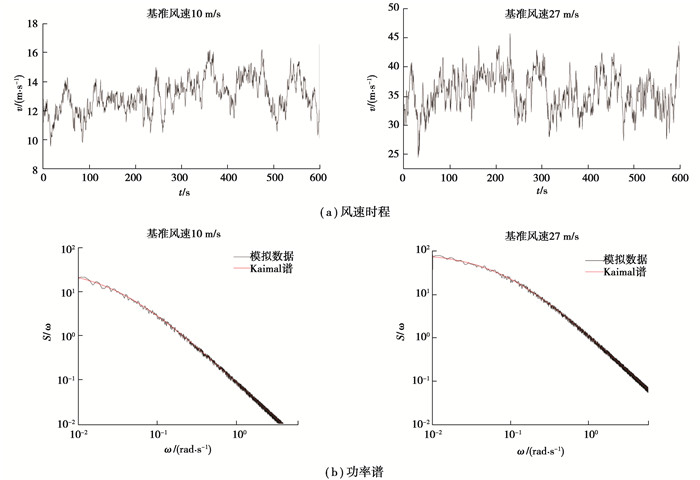
|
图 2 不同基本风速下典型点风速时程及功率谱 Fig. 2 Wind speed time history and power spectrum at typical points under different basic wind speeds |
根据我国架空输电线路载荷规范[1],作用于导地线上的风载荷按式(6)计算。
| $ W_x=\beta_{\mathrm{C}} \cdot \alpha_{\mathrm{L}} \cdot W_0 \cdot \mu_{\mathrm{z}} \cdot \mu_{\mathrm{SC}} \cdot d \cdot L_{\mathrm{P}} \cdot B_1 \cdot \sin ^2 \theta, $ | (6) |
式中:βC为导地线阵风系数;αL为档距折减系数;W0为基准风压,kN/m2;μz为风压高度变化系数,μSC为导线或地线的体型系数,d为导线或地线的外径或覆冰时的计算外径,LP为杆塔的水平档距,B1为导地线覆冰风荷载增大系数。基本风压为:
| $ W_0=V_0^2 / 1600, $ | (7) |
式中V0为基本风速。
由于模拟随机风场时考虑了风的空间相关性和随高度的变化,风荷载以风压的方式直接施加在模拟导线的梁单元上,故无需考虑系数βC、αL、μz、LP,即这些系数都取1.0。在本文中不考虑覆冰,故B1也取1.0。根据规范,导线或地线的体型系数μSC,线径≥17 mm时取1.0,线径<17 mm时取1.1。参见表 1,由导线和地线的直径可知,导线μSC取1.0,地线的取1.1。
作用于绝缘子串的风荷载为
| $ W_I=W_0 \cdot \mu_\text{z} \cdot B \cdot A_I, $ | (8) |
式中:B为覆冰时风载荷增大系数,这里取1.0;AI为绝缘子串的受风面积,m2。
作用于杆塔的风载荷为
| $ W_{\mathrm{s}}=W_0 \cdot \mu_{\mathrm{z}} \cdot \mu_{\mathrm{s}} \cdot \beta_{\mathrm{z}} \cdot B \cdot A_{\mathrm{s}}, $ | (9) |
式中:μs为构件风载体型系数,根据杆件形状取值;βz为高度z处的风振系数,反映载荷的动力效应,在进行动力响应时程分析时取1.0;覆冰时风载荷增大系数B取1.0;As为构件承受风压面积计算值。
值得一提的是,在利用式(6)~(9)计算作用于导地线、绝缘子串和杆塔的风载荷时,采用的风速为载荷计算点的风速,即随机风场模拟得到的该计算点的风速时程。
1.3 塔线体系动力响应数值模拟利用ABAQUS软件对塔线体系在基本风速为27 m/s和年平均风速10 m/s随机风作用下的动力响应进行模拟,得到塔线体系的变形和应力时程。图 3所示为最大设计基本风速随机风场作用下塔线体系在最大应力时刻的应力分布和杆塔危险区域。图 3(a)所示为塔线体系的Mises应力分布,结果表明,最大应力出现在地线上,为362.9 MPa;导线上的最大应力为95.7 MPa,均未超过它们的最大拉断应力。所有4个杆塔中,塔Ⅱ上的应力最大,该杆塔的Mises应力分布如同3(b)所示。其最大Mises应力为274.2 MPa,出现在Q420杆件上,该应力远小于材料的强度极限。此外,Q345杆件的最大Mises应力为259.0 MPa,相对于出现最大应力的Q420杆件而言,该杆件更为危险。由于杆塔有限元模型没有考虑杆件连接区域的细节,没有考虑连接板上螺栓的连接和预紧力等,计算得到的应力可能远小于实际结构的应力。将最危险杆件的相邻区域视为危险区域,用于建立考虑螺栓连接细节的局部三维实体模型。
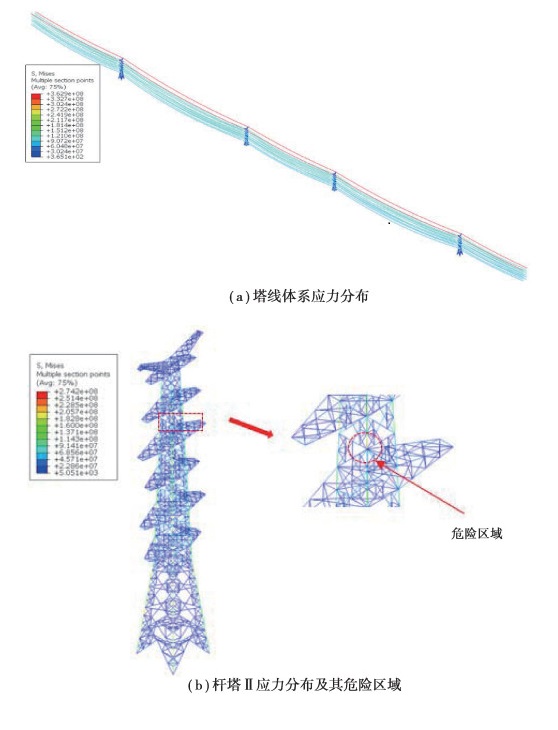
|
图 3 随机风作用下塔线体系最大应力时刻的应力分布及杆塔的危险区域(基本风速27 m/s) Fig. 3 Stress distribution at the time of maximum stress to tower line system under random wind and dangerous area of tower (basic wind speed 27 m/s) |
在年平均风速10 m/s随机风作用下塔线体系的应力水平远小于最大设计基本风速随机风作用下的应力,但杆塔的应力分布类似,出现最大应力的危险区域基本一致。
2 杆塔危险区域精细化分析 2.1 杆塔实体与杆梁混合模型根据1.3节塔线体系在随机风场作于下的动力响应,在最大设计基本风速27 m/s情况下,危险区域的最大应力值达到其材料Q345屈服极限的75.07%。由于计算模型没有考虑杆件连接区域的细节,没有考虑连接板上螺栓的连接和预紧力等,计算得到的应力可能远小于实际结构的应力,有必要对危险区域建立三维精细化实体有限元模型进行分析,获得准确的应力。
利用ABAQUS/CAE建立杆塔危险区域三维实体与杆梁混合模型,如图 4所示。确定的危险区域共包含152颗6.8级M20螺栓,8根主材L型杆件,64根副材L型杆件,两种不同型号的连接板各8块。连接关系包括杆件与螺母的表面接触、杆件与螺栓的内部接触、杆件与杆件之间接触和Tie约束。螺栓与L型杆件的接触摩擦系数设为0.3。根据施工规范[19],6.8级M20螺栓应施加25 000 N预紧力。局部区域实体模型采用六面体单元进行离散,该段实体模型一共划分343 752个六面体八结点等参单元。局部三维实体模型与其他部分的杆梁模型的连接方法采用耦合约束,在三维实体模型与杆梁模型连接的截面上选定一个连接面,选择对应的杆梁上的连接点作为控制点,并设置为“连续分布”,参见图 4(b)。
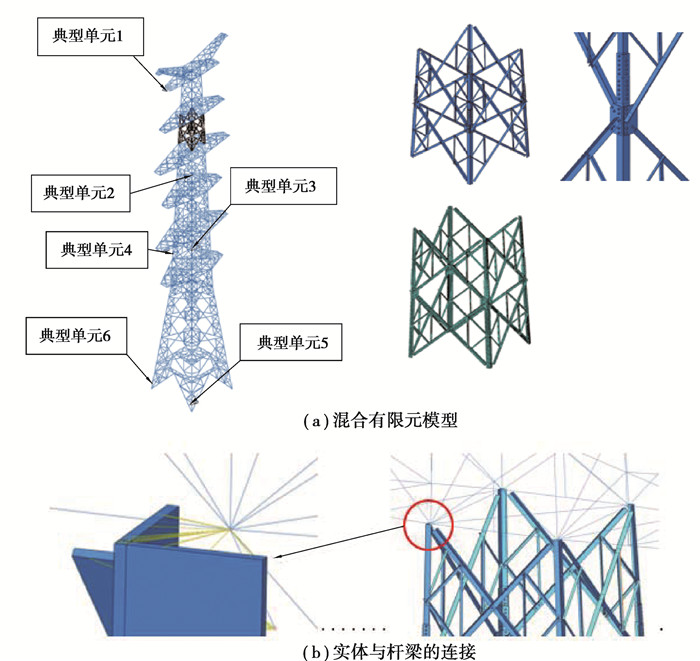
|
图 4 杆塔实体与杆梁混合有限元模型 Fig. 4 Finite element model of hybrid tower |
利用塔线体系随机风场作用下的动力响应模拟结果,提取杆塔Ⅱ导线和地线挂点载荷在整体坐标系下3个分量的时程,施加在实体与杆梁混合模型的对应挂点处,并在杆塔上施加塔线上的随机风荷载时程。杆塔4个塔腿根基处采用固定约束。
2.2 杆塔混合有限元模型动力响应利用建立的实体与杆梁混合模型计算最大设计基本风速27 m/s下的动力响应。图 5所示为杆塔混合有限元模型和1.3节塔线体系中杆塔Ⅱ在相同时刻变形和位移分布的比较,可见两种模型的最大位移分别为58.25 cm和57.17 cm。混合模型中局部区域采用三维实体模型,特别是连接板处的三维结构会增大结构的刚度,因而其位移小于杆梁简化模型,但两种差别不大。此外,表 2给出了该两个模型同一时刻图 4(a)中所示典型单元的最大Mises应力,这些单元均为杆或梁单元。可见,除了单元1外,两个模型的计算结果差别非常小,单元1差别较大可能是该单元在导线挂点附近出现应力集中所致。由此,建立的混合有限元模型是合理的。

|
图 5 两种杆塔模型同一时刻的变形和位移分布(基本风速27 m/s) Fig. 5 Deformation and displacement distribution of two tower models at the same time (basic wind speed 27 m/s) |
| 表 2 两种模型典型单元最大Mises应力(基本风速27 m/s) Table 2 Maximum Mises stress of typical elements of two models (basic wind speed 27 m/s) |
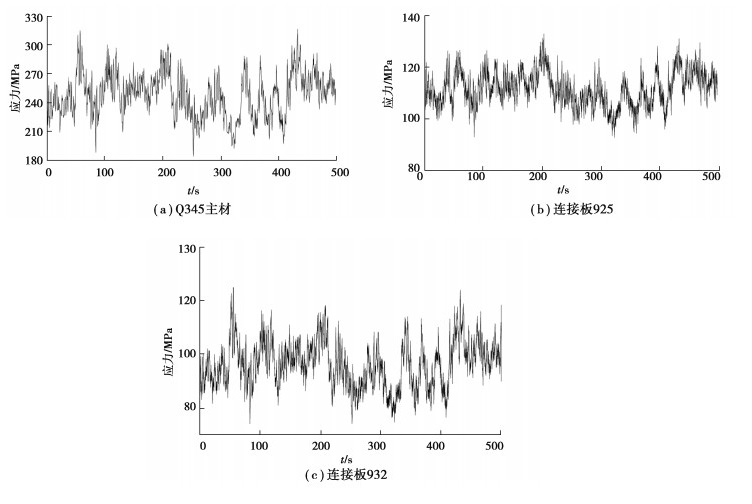
图 6所示为杆塔最大应力时刻整体和典型构件的Mises应力分布,这些构件上都出现了应力集中。由图 6(a)和图 6(b)可知,最大应力为314.1 MPa,出现在Q345杆件上,其明显大于塔线体系得到的最大应力259.0 MPa。图 7所示为实体与杆梁混合模型危险区域典型构件最大应力点的应力Mises应力时程,应力时程可用于构件的疲劳寿命估算。

|
图 6 杆塔危险区域最大应力时刻应力分布图(基本风速27 m/s) Fig. 6 Stress distribution at the time of maximum stress in tower dangerous area (basic wind speed 27 m/s) |
|
图 7 危险区域典型构件最大应力点Mises应力时程(基本风速27 m/s) Fig. 7 Mises stress time history of maximum stress point of typical components in dangerous area (basic wind speed 27 m/s) |
输电杆塔实际运行中发生的倒塌事故分析表明,很多情况下破坏都发生在螺栓连接区域。一方面,在杆塔安装施工过程中,由于人工操作不到位,可能导致螺栓预紧力不够;另一方面,杆塔长期运行后螺栓可能发生松弛,预紧力下降。螺栓预紧力的降低可能导致局部应力增大,严重时可能导致杆塔的破坏。
如前所述,该杆塔连接螺栓为6.8级M20螺栓,应施加25 000 N预紧力。本节分别计算预紧力为规定值80%和50%两种情况下,杆塔在随机风作用下的动力响应。图 8给出了基本风速27 m/s时实体与杆梁混合模型在50%螺栓预紧力情况下危险区域典型构件应力最大时刻的Mises应力分布。相较于2.2节中100%预紧力作用时,除螺栓外的构件应力最大值均明显增大,个别构件的应力水平接近了其材料的屈服极限。图 9为螺栓预紧力50%时危险区域典型构件最大应力点Mises应力时程曲线,可见其明显大于如图 7所示的100%预紧力的情况。

|
图 8 螺栓预紧力50%时危险区域最大应力时刻Mises应力分布(基本风速27 m/s) Fig. 8 Mises stress distribution at the time of maximum stress in the dangerous area when the bolt preload is 50% (basic wind speed 27 m/s) |

|
图 9 螺栓预紧力50%时危险区域典型构件最大应力点Mises应力时程(基本风速27 m/s) Fig. 9 Mises stress time history of the maximum stress point of typical components in dangerous area when the bolt preload is 50% (basic wind speed 27 m/s) |
表 3列出了危险区域典型构件在不同预紧力作用下的最大Mises应力,可以看出,随着预紧力的减小,各构件的应力水平逐渐增大。
| 表 3 不同螺栓预紧力情况下杆塔典型构件最大Mises应力(基本风速27 m/s) Table 3 Maximum Mises stress of typical tower components under different bolt preloads (basic wind speed 27 m/s) |
由2.2与2.3节的计算结果可知,危险区域构件的最大应力均出现在Q345杆件的螺栓连接位置附近。在最大设计基本风速情况下3种预紧力作用下其应力水平均较大。其余杆件、连接板和螺栓等构件的最大应力均远小于屈服极限。
此外,螺栓预紧力对构件应力水平的影响不可忽略,随着预紧力的减小,构件的最大应力值逐渐增大,当预紧力小于50%时,可能引起危险区域的Q345杆件发生屈服变形,导致杆塔倒塌事故的发生,应当引起注意。
3.2 疲劳寿命估计前面计算得到了杆塔在特征时间段内的应力时程,根据Miner线性损伤理论,该时间段内产生的损伤因子为
| $ D=\sum \frac{r_i}{N_{\text{f} i}}, $ | (10) |
式中:ri为第i级应力幅值作用下的循环数,Nfi为该级应力幅值作用下的疲劳寿命,其可由材料的S-N曲线得到。当累计损伤因子D达到1.0时结构发生疲劳破坏。假设该特征时间段重复n次后D达到1.0,则
| $ n=\frac{1}{D}=1 /\left(\sum \frac{r_i}{N_{\text{f} i}}\right) \text {, } $ | (11) |
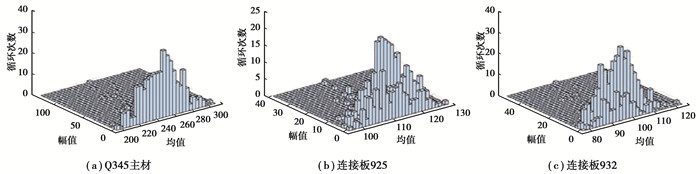
选择杆塔典型构件的最大应力时程,采用雨流计数法得到不同水平应力幅值的次数。如图 10所示为最大设计基本风速,螺栓预紧力100%时杆塔典型构件最大应力时程雨流计数结果,其中考虑了平均应力的影响。
|
图 10 杆塔典型构件应力时程雨流计数结果(基本风速27 m/s,螺栓预紧力100%) Fig. 10 Rain flow counting results of stress time history of typical tower components (basic wind speed 27m/s, 100% bolt preload) |
该3种构件均为Q345材料,根据文献[20],Q345钢的等效应力幅与疲劳寿命的关系式为
| $ \sigma_{\mathrm{ar}}=\frac{\sigma_{\mathrm{a}}}{1-\left(\sigma_{\mathrm{m}} / 445.216\right)^{1.190\;35}}=541.299\;4\left(2 N_{\mathrm{f}}\right)^{-0.055\;56}, $ | (12) |
式中:σar为等效应力幅,σa为应力幅,σm为应力均值,Nf为疲劳寿命。将应力时程中不同的应力幅值σai和平均应力σmi代入式(12)可得对应的疲劳寿命Nfi,再将由雨流计数法统计得到的循环次数ri代入式(11),即可得到发生疲劳破坏时该特征段载荷时间的次数n。
计算了最大设计基本风速27 m/s和年平均风速10 m/s随机风场中杆塔的动力响应,并考虑了螺栓预紧力100%、80%和50%的情况,进而根据杆塔危险区域典型构件最大应力的时程,计算了杆塔的疲劳寿命。结果表明,若以年平均风速10 m/s进行计算,杆塔的应力水平和应力幅值均较小,各构件均不会发生疲劳破坏。若按最大设计基本风速27 m/s计算,在螺栓预紧力100%的情况下,连接板925与连接板932应力水平和应力幅值较小,均不会发生疲劳破坏。而出现最大应力的Q345杆件的疲劳寿命为2.36 a。在不同螺栓预紧力情况下,杆塔疲劳寿命如表 4中所列。值得一提的是,表中给出的疲劳寿命是在最大设计基本风速27 m/s随机风持续作用下的寿命,杆塔发生疲劳破坏前的实际使用年限取决于蒙西地区每年出现这种风速的时间。另外,螺栓松动对疲劳寿命的影响很大,当螺栓预紧力降低到80%时,其疲劳寿命几乎降低了10倍;当螺栓预紧力降低为一半时,在基本风速27 m/s的情况下,其疲劳寿命不到2 d时间。
| 表 4 杆塔的Q345杆件疲劳寿命估计(基本风速27 m/s) Table 4 Fatigue life estimation of Q345 member of tower (basic wind speed 27 m/s) |
以蒙西地区220 kV同塔四回直线塔SSZ1为研究对象,采用有限元方法分析杆塔的强度和疲劳寿命,主要结论如下:
1) 建立了同塔四回杆塔的有限元模型和典型四塔伍档塔线体系有限元模型,模拟研究了在最大设计基本风速27 m/s和年平均风速10 m/s随机风场作用下塔线体系的动力响应,确定了杆塔危险区域。最大应力出现在杆塔Ⅱ上,最大设计基本风速情况下应力水平最危险的区域出现在杆塔Ⅱ的Q345杆件上,应力值为259.0 MPa。
2) 建立了杆塔危险区域三维实体有限元模型,进而得到杆塔的实体和杆梁的混合有限元模型。计算了该混合模型在不同基本风速下的动力响应。结果表明,考虑危险区域结构细节后杆塔的最大应力明显大于杆梁模型,最大设计基本风速情况下最大应力为314.1 MPa,出现在相同的Q345杆件上。
3) 模拟研究了螺栓预紧力降低到80%和50%时杆塔的应力,结果表明,螺栓预紧力对杆塔最大应力影响明显;随着螺栓预紧力的降低,杆塔最大应力逐渐增大,但所有情况下杆塔构件的应力均小于其屈服应力,结构静强度满足要求。
4) 采用雨流计数法对不同基本风速和不同螺栓预紧力情况下杆塔典型位置应力时程进行了统计分析,进而利用Miner损伤准则估计了杆塔的疲劳寿命。结果表明,若以年平均风速10 m/s进行计算,杆塔各构件均不会发生疲劳破坏。若按最大设计基本风速27 m/s计算,在螺栓预紧力100%的情况下,杆塔的疲劳寿命为2.36 a;当螺栓预紧力降低到80%时,其疲劳寿命几乎降低了10倍;当螺栓预紧力较小一半时,其疲劳寿命不到2 d时间。可见螺栓预紧力对杆塔的疲劳寿命影响非常明显,必须引起高度重视。在线路施工时应按规范要求施加螺栓预紧力,在线路运行中应对杆塔的连接螺栓进行定期检查,发现螺栓松动要及时拧紧,避免发生杆塔破坏事故。
| [1] |
国家能源局. 架空输电线路载荷规范DL/T 5551—2018[S]. 北京: 中国计划出版社, 2018. National Energy Administration. Load code for the design of overhead transmission line DL/T 5551—2018[S]. Beijing: China Planning Press, 2018. (in Chinese) |
| [2] |
郭勇, 叶尹, 应建国. 多回路输电塔风振系数研究[J]. 建筑结构, 2011, 41(3): 110-113. Guo Y, Ye Y, Ying J G. Wind vibration coefficient of the multi-loop transmission towers[J]. Building Structure, 2011, 41(3): 110-113. (in Chinese) |
| [3] |
窦汉岭. 220kV大跨越转角输电线塔的力学分析[D]. 合肥: 合肥工业大学, 2019. Dou H L. Mechanics analysis of 220 k V long-span turning-angle transmission tower[D]. Hefei: Hefei University of Technology, 2019. (in Chinese) |
| [4] |
原迁, 张德凯. 大跨越输电塔线体系风振响应及风振系数分析[J]. 山西建筑, 2021, 47(6): 34-38. Yuan Q, Zhang D K. Analysis of wind-induced response and vibration coefficient of long-span transmission line tower[J]. Shanxi Architecture, 2021, 47(6): 34-38. (in Chinese) DOI:10.3969/j.issn.1009-6825.2021.06.012 |
| [5] |
刘孟龙. 复杂地形条件下输电塔线体系风致响应数值模拟[D]. 杭州: 浙江大学, 2020. Liu M L. Wind-induced response simulation of transmission tower-line system under complex terrain condition[D]. Hangzhou: Zhejiang University, 2020. (in Chinese) |
| [6] |
Kitipornchai S, Al-Bermani F G A, Peyrot A H. Effect of bolt slippage on ultimate behavior of lattice structures[J]. Journal of Structural Engineering, 1994, 120(8): 2281-2287. DOI:10.1061/(ASCE)0733-9445(1994)120:8(2281) |
| [7] |
齐立忠, 江文强, 陈大斌. 螺栓连接滑移对输电铁塔力学性能的影响研究[J]. 电力科学与工程, 2013, 29(3): 12-17. Qi L Z, Jiang W Q, Chen D B. Influences of bolted joint slippage on the mechanical behavior of transmission tower[J]. Electric Power Science and Engineering, 2013, 29(3): 12-17. (in Chinese) |
| [8] |
沈康. 风荷载作用下输电杆塔连接节点承载性能研究[D]. 武汉: 湖北工业大学, 2019. Shen K. Study on joint force-bearing capacity of transmission tower subjected to wind loads[D]. Wuhan: Hubei University of Technology, 2019. (in Chinese) |
| [9] |
Ju Y Z, Zhang J L, Jiang F. Theoretical calculation of ultimate bearing capacity and fatigue of safety pin of transmission tower[J]. Energy Procedia, 2012, 17: 1057-1063. DOI:10.1016/j.egypro.2012.02.207 |
| [10] |
Xie Q, Sun L. Failure mechanism and retrofitting strategy of transmission tower structures under ice load[J]. Journal of Constructional Steel Research, 2012, 74: 26-36. DOI:10.1016/j.jcsr.2012.02.003 |
| [11] |
Zhou C, Liu Y B. Analytical model of rain-wind induced vibration of high-voltage transmission line[J]. Advances in Mechanical Engineering, 2014, 6: 638653. DOI:10.1155/2014/638653 |
| [12] |
严波, 刘力宇, 毕承财, 等. 螺栓预紧力对输电杆塔强度的影响[J]. 重庆大学学报, 2015, 39(5): 17-25. Yan B, Liu L Y, Bi C C, et al. Effect of bolt pre-tightening force on the strength of transmission line tower[J]. Journal of Chongqing University, 2015, 39(5): 17-25. (in Chinese) |
| [13] |
陆兴华, 刘建军, 张廼龙, 等. 考虑舞动和微风振动的复合横担疲劳评估[J]. 力学季刊, 2020, 41(4): 704-717. Lu X H, Liu J J, Zhang N L, et al. Fatigue assessment of composite cross arm considering galloping and aeolian vibration[J]. Chinese Quarterly of Mechanics, 2020, 41(4): 704-717, 41. (in Chinese) |
| [14] |
Prasad Rao N, Samuel Knight G M, Mohan S J, et al. Studies on failure of transmission line towers in testing[J]. Engineering Structures, 2012, 35: 55-70. DOI:10.1016/j.engstruct.2011.10.017 |
| [15] |
孙中浩. 特高压输电铁塔风振疲劳性能及典型焊接接头疲劳寿命研究[D]. 杭州: 浙江大学, 2015. Sun Z H. Research on UHV transmission tower wind vibration fatigue performance and typical welded joint fatigue life[D]. Hangzhou: Zhejiang University, 2015. (in Chinese) |
| [16] |
胡位勇, 严波, 程皓月, 等. 输电塔线体系断线动力响应及杆塔破坏模拟研究[J]. 应用力学学报, 2012, 29(4): 431-436, 487. Hu W Y, Yan B, Cheng H Y, et al. Numerical investigation on dynamic response and failure of transmission line and tower after wire breaking[J]. Chinese Journal of Applied Mechanics, 2012, 29(4): 431-436, 487. (in Chinese) |
| [17] |
Simiu E, Scanlan R H. Wind effects on structures: an introduction to wind engineering[M]. 2rd edition. New York: John Wiley & Sons, 1986.
|
| [18] |
Yan B, Lin X S, Luo W, et al. Numerical study on dynamic swing of suspension insulator string in overhead transmission line under wind load[J]. IEEE Transactions on Power Delivery, 2010, 25(1): 248-259. |
| [19] |
中华人民共和国建设部, 中华人民共和国质量监督检验检疫总局. 110~500 kV架空送电线路施工及验收规范GB 50233—2005[S]. 北京: 中国计划出版社, 2005. Ministry of Construction of P. R. China, General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China. Code for construction and acceptance of 110~500 kV overhead transmission line. GB 50233—2005[S]. Beijing: China Planning Press, 2005. (in Chinese) |
| [20] |
刘曦程, 刘光连, 聂振超, 等. 应力控制下的Q345钢疲劳寿命预测研究[J]. 塑性工程学报, 2018, 25(3): 212-216. Liu X C, Liu G L, Nie Z C, et al. Study on fatigue life prediction of Q345 steel under stress control[J]. Journal of Plasticity Engineering, 2018, 25(3): 212-216. (in Chinese) |
 2022, Vol. 45
2022, Vol. 45

