2. 中国建筑西南设计研究院有限公司, 成都 610041;
3. 重庆大学 土木工程学院, 重庆 400044
2. China Southwest Architectural Design and Research Institute, Chengdu 610041, P. R. China;
3. School of Civil Engineering, Chongqing University, Chongqing 400044, P. R. China
近年来,由于风雪运动所导致的自然灾害不断发生,造成了大量的经济损失,并构成生命威胁。对雪灾所导致的工程事故进行研究[1-3]后发现,雪荷载对建筑物造成的影响为:1)在静风条件下持续大量的降雪,造成积雪大量堆积,积雪所产生的重力超过了结构设计时所采用的雪荷载值,从而会造成房屋建筑整体的垮塌;2)在风雪天气条件下,雪粒会发生复杂的漂移运动,导致建筑的屋面发生风致雪漂移现象,造成积雪在屋面不均匀堆积,导致背风屋面局部的实际雪荷载值超过设计雪荷载值。
风致雪漂移研究方法分别有现场实测、试验方法、数值模拟等。3种方法各有不同的适用范围和优缺点,往往需要配合使用。周暄毅等[4]对几种方法的研究现状进行了总结,同时阐述了几种方法的优缺点:现场实测可获得真实情况下积雪分布,获得的资料可用来验证后两种方法结果的正确性,由于在真实的自然环境中进行实地测量,所获得数据是最贴近真实情况的,在所有数据当中也最具说服力。但是现场实测也有不足之处: 其一,实测对人力物力要求较高;其二,实地测量无法避免环境的突发性和随机性。试验方法包括水槽试验和风洞试验,两类试验都需在满足流动形态相似、堆积相似、运动相似等条件下,采用其他介质来代替雪颗粒尽可能地模拟真实情况。试验方法存在成本高、耗时长、难以满足所有相似性等缺点。而数值模拟方法具有如下优势:周期短、成本低;多工况、全尺度[5];可严格控制各种外界因素;可较为便利控制单一变量,研究各影响因素的变化规律,易于对风雪运动的机理进行研究。因此,数值模拟方法被广泛应用,并逐渐成为风致雪漂移研究的主要方法。但其结果需要通过实地观测和试验方法进行验证。
雪荷载数值模拟研究主要采用基于两相流的理论方法,即欧拉-拉格朗日和欧拉-欧拉2种主流方法,二者的不同主要体现在对于雪相和空气相状态的处理上。前者将空气视为连续,将雪相视为离散相,由牛顿运动定律计算雪颗粒运动轨迹,从而得出积雪情况。而两欧拉方法在处理雪相和空气相时,则统一采用连续相处理,计算时在空气相控制方程的基础上引入雪相方程。Liston等[6]在分析一个起伏地形上积雪分布规律时引入了其开发的SnowTran-3D模型。Beyers等[7]模拟一个边长2 m的立方体周围的雪漂,其结果与实测结果吻合得较好。何连华等[8]基于VOF(volume of fluid)多相流模型对雪荷载进行数值模拟,将其转化为建筑结构屋面积雪分布系数,并指出高低屋面处的屋面积雪分布系数大于规范所规定的值。莫华美[9]在单向耦合假定的基础上,采用二维数值模拟研究了单跨双坡屋面、双跨双坡屋面和高低屋面的积雪分布形式,表明屋面坡度、跨度和女儿墙高度都是影响积雪重分布的显著因素。洪财滨[10]进行了二维和三维风致雪漂移数值模拟并指出数值模拟结果与实测值存在一定的差别,如近壁面的模拟结果较接近实测值,而远离壁面区域则误差较大。莫华美等[11]以黑龙江省各气象台站1981—2010年气象资料为基础,以当地基本风速的0.45倍作为积雪漂移风洞试验与数值模拟中的输入风速,采用新的双向耦合欧拉-欧拉CFD(computational fluid dynamics)公式来代替平衡经验公式,使用了一种允许计算雪相动量方程中的粘性应力张量的粘性模型来模拟雪颗粒漂移,最后得到了较为理想的雪通量、湍流等结果,证明该模型在模拟风雪耦合作用时的有效性。罗熙越[12]采用几何相似、风剖面相似、无量纲风速相似以及颗粒沉积体积相似对高度屋面两种典型坡屋面的雪荷载进行了数值模拟,发现将颗粒的速度云图等效变换为堆积无量纲曲线方法时,将初始铺设厚度定为20 mm更为合适;坡屋面产生风致雪漂移时,屋面中后部位置的积雪厚度更大,即雪荷载更大,是设计时需要重点考虑的部位。刘博雅等[13]采用多相流模型Mixture对高低屋面积雪分布进行数值模拟,分析了不同屋面跨度、高低跨高差等因素对积雪分布的影响,提出了减少雪堆积的防护措施。Boutanios等[14]采用新的双向耦合欧拉-欧拉CFD公式来代替平衡经验公式,使用了一种允许计算雪相动量方程中的粘性应力张量的粘性模型来模拟雪颗粒漂移,得到了较为理想的雪通量、湍流等结果,证明该模型在模拟风雪耦合作用时的有效性。Kang等[15]综合了各种因素对CFD模拟结果的影响,如网格大小、雪下降时的速度、施密特数、临界摩擦速度等,提出雪下降时的速度和施密特数与雪浓度具有高度相关性,实测过程要充分体现区域雪浓度或雪通量、沉降速度和摩擦速度等关键信息,为以后模型研究提供足够的依据。
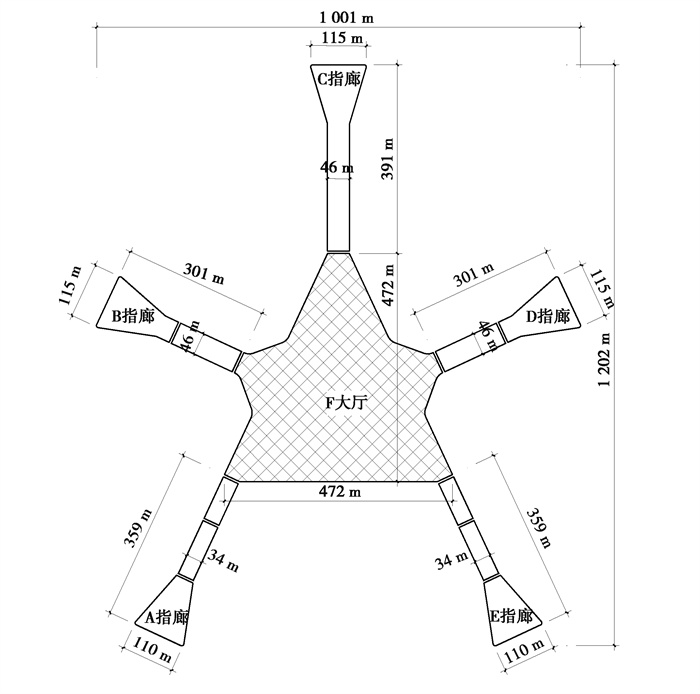
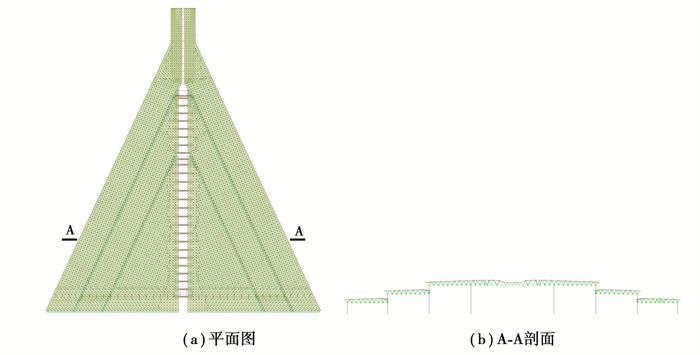
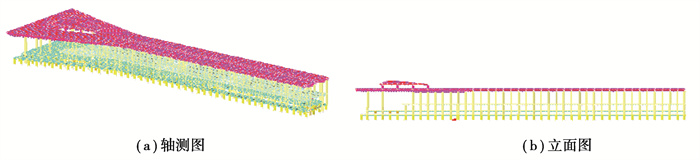
1 工程背景文中以长沙机场T3航站楼为背景,对大型机场航站楼屋面雪荷载的不均匀分布进行研究,采用数值模拟技术分析雪荷载受风荷载作用产生的不均匀分布,结合建筑结构荷载设计规范的内容,对航站楼屋面雪荷载设计取值进行研究。长沙机场T3航站楼位于长沙市,为超大型大跨屋盖结构,其平面纵向长约1 200 m,指廊间的最大间距约1 000 m。该航站楼钢结构屋盖主要包括大厅和指廊两部分(见图 1),其中,大厅为三阶错标高屋面,平面轮廓及错标高边界均为三角形(见图 2);指廊为长条状,大部分为平屋面,在端部扩大头处有凸起天窗(见图 3),航站楼大跨屋盖造型复杂。文中采用CFD数值模拟方法对其屋盖积雪分布进行数值模拟,并对设计取值进行分析。
|
图 1 长沙机场T3航站楼分区示意图 Fig. 1 Schematic diagram of the zoning of the Changsha Airport terminal 3 |
|
图 2 长沙机场T3航站楼大厅屋盖钢网架示意图 Fig. 2 Schematic diagram of the steel grid structure of the hall roof of the Changsha Airport terminal 3 |
|
图 3 长沙机场T3航站楼C区指廊屋盖钢结构示意图 Fig. 3 Schematic diagram of the steel structure of the corridor roof in area C of the Changsha Airport terminal 3 |
根据中国《建筑结构荷载规范》(GB 50009—2012)(下面简称“荷载规范”),雪荷载标准值的取值规定为当地基本雪压与屋面积雪分布系数的乘积。其中,屋面积雪分布系数的含义为地面基本雪压转换为屋面雪荷载的系数,其值取为雪荷载在屋面水平投影面积上与基本雪压的比值。
| $ s_k=\mu_{\mathrm{r}} s_0, $ | (1) |
式中:s0表示当地基本雪压,kN/m2;μr表示屋面积雪分布系数。
屋面积雪分布形式受到不同因素的影响,如风速大小、来流方向、屋面形式等。在中国规范中只给出了若干基本形式结构物的积雪分布系数;在实际情况中,由于风的搬运作用造成雪颗粒漂移,不同屋面形式具有复杂的屋面积雪分布形式。在三维空间中,积雪分布受建筑物三维形态影响更复杂,而现行规范未对三维空间中积雪分布进行明确规定。因此,采用CFD数值模拟是相对灵活经济的技术手段。文中在模拟长沙机场T3航站楼试验工况时,利用计算流体力学软件Fluent,采用风雪两相流模型VOF法模拟风致雪颗粒漂移,通过求解各相的控制方程得到相关物理量。
风致雪漂移数值模拟的主要意图是研究屋盖已有均匀积雪在一定风速作用后发生的不均匀重分布,从而提取供设计使用的最不利雪压荷载状态。风致雪漂移数值模拟分为2步:第1步,在计算域中模拟降雪,得到建筑物表面的均匀积雪分布;第2步,待积雪稳定后施加空气风速,模拟积雪在流动空气作用下的重分布。计算完成后,得到空气流动前后的屋面压强差值和屋面积雪的不均匀压强,其与平均雪压值之比,即为屋面雪压分布系数。
VOF模型的原理主要是通过设定各相的体积分数(在单位体积内总和为1)模拟各相的分布,各相体积分数经过加权处理可得到单位体积内材料特性,它们之间的界面主要通过计算连续方程得到。
对第q相,VOF模型的体积分数连续性方程可表示为
| $ \frac{1}{\rho_2}\left[\frac{\partial}{\partial t}\left(\alpha_2 \rho_2\right)+\nabla \cdot\left(\alpha_2 \rho_2 \boldsymbol{v}_2\right)\right]=s_{\alpha 2}+\left(\dot{m}_{12}-\dot{m}_{21}\right), $ | (2) |
式中:ρ2为第2相流体的密度;α2为第2相的体积分数;v2为第2相流体的速度矢量;ṁ12为第1相到第2相的质量输运;ṁ21为第2相到第1相的质量输运;sα2源相一般为零。体积分数一般不为主相求解,主相的体积分数由各相体积分数之和为1得到。
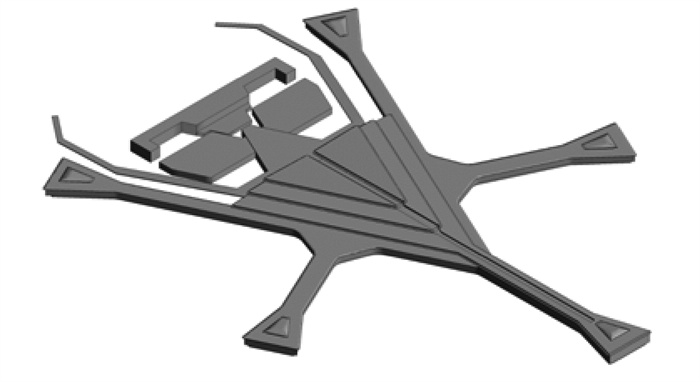
2.2 数值建模长沙机场T3航站楼CFD数值模拟的结构几何模型如图 4所示,包含大厅主体结构、5处指廊结构及邻近附属建筑物。几何模型由建模软件Rhino建立,导入ANSYS中进行计算流域建立和网格划分。
|
图 4 长沙新机场航站楼CFD几何模型 Fig. 4 CFD geometry of Changsha new airport terminal |
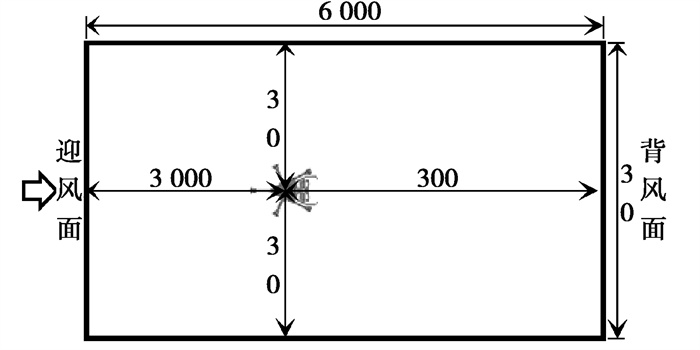
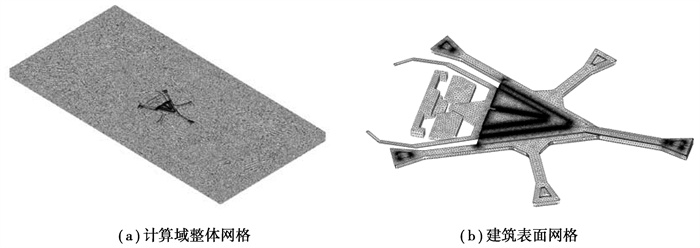
该屋盖在进行数值模拟时应注意2点:1)来流属于不同尺度涡旋叠加而成的湍流流动;2)结构在空间上也具有不同的尺寸。在划分网格时应结合上述2点来考虑。计算域在x、y、z上分别取为6 000,3 000,2 000 m,如图 5所示。采用非结构化网格,在航站楼附近区域进行加密处理,同时在航站楼表面设置薄壁面层网格(采用三角形网格处理)。体网格采用Robust方法生成四面体网格。结构周围整体网格以及附近局部网格,如图 6所示。在网格划分中,考虑积雪在屋面的风致重分布,对大厅主体结构三阶屋面区域进行局部加密,而指廊及裙房等屋面的网格较稀疏。其中,计算域整体的基本单元长度为0.5 m,多阶屋面加密部位单元长度为20 m。计算域总体单元量约为2 100万个。
|
图 5 长沙新机场CFD数值模拟计算流域(单位:m) Fig. 5 Changsha new airport CFD numerical simulation calculation basin (in meters) |
|
图 6 长沙新机场航站楼CFD计算网格示意图 Fig. 6 A grid diagram of CFD calculations in Changsha's new airport terminal |
流场含2组入口边界条件,包括空气流入射边界条件与雪相入射边界条件。空气流入射边界条件设置在计算域一侧入口处,雪相入射边界条件设置在航站楼建筑物表面。风速对于积雪分布的影响较为显著,结合实际情况,结构发生破坏时多为暴风强降雪天气,故风速选为与雪压相同重现期的风压换算得到。流场的空气入口处采用速度来流边界条件(velocity-inlet),平均风剖面采用指数律表示:
| $ U(z)=U_{10}\left(\frac{z}{10}\right)^\alpha, $ | (3) |
式中:U10为10 m高度处来流平均风速,根据当地基本风压计算得出;α为地面粗糙度指数,按长沙市区近郊场地类型,根据荷载规范,取B类风场α=0.15。入流面湍动能和耗散率分别采用式(4)(5)表达:
| $ k(z)=\frac{3}{2}\left[U(z) \cdot I_u(z)\right]^2, $ | (4) |
| $ \varepsilon(z)=C_\mu^{3 / 4} \cdot \frac{k^{2 / 3}(z)}{k \cdot z}。$ | (5) |
式中:Cμ为模型常数,值为0.09;k为卡门常数,值为0.42;Iu(z)为高度z处来流紊流度,采用荷载规范建议表达式:
| $ I_u(z)=I_{10} \cdot\left(\frac{z}{10}\right)^\alpha, $ | (6) |
式中,在B类风场中,I10取为0.14。出口边界条件采用压力出流边界条件(pressure-outlet),上空面及侧面的边界条件采用对称边界条件(symmetry),建筑物表面及地面采用无滑移壁面边界条件(wall)。
对于雪相入口边界,计算过程中前期为雪相速度入口,速度一般设置为较低值,此时雪的体积分数为1;经过一段时间,降雪过程完成,速度改为0,固壁处理。待雪相无速度运动后允许空气相进入流程计算域。文中数值模拟的雪材料参数为:雪材料密度取150 kg/m3,运动黏度取10 kg/(m·s-1),雪颗粒平均粒径取0.15 mm。
2.3 计算工况针对雪荷载迁移数值模拟的湍流模型选用两方程模型经常用到的k-ε模型,该模型可满足精度要求。湍流模型各参数取Fluent中加载的自定义函数中对应值。采用时程计算对整个时间段进行数值模拟,单个时间步为0.1 s,共900步,每个时间步迭代步数取100步,计算精度采用二阶精度计算,计算收敛准则取残差值为5×10-4。雪荷载数值模拟共分析90 s。分别提取第50 s前一时间步的建筑物表面压强数值和计算终止时刻的建筑物表面压强数值,两者之差即为积雪不均匀分布差值,经计算后得到航站楼屋面积雪分布系数。
根据航站楼几何外观的特点,多级屋盖的积雪在气流作用下可能发生迁移,在背风面形成高低角落堆积的现象,从而造成雪荷载的不均匀分布。
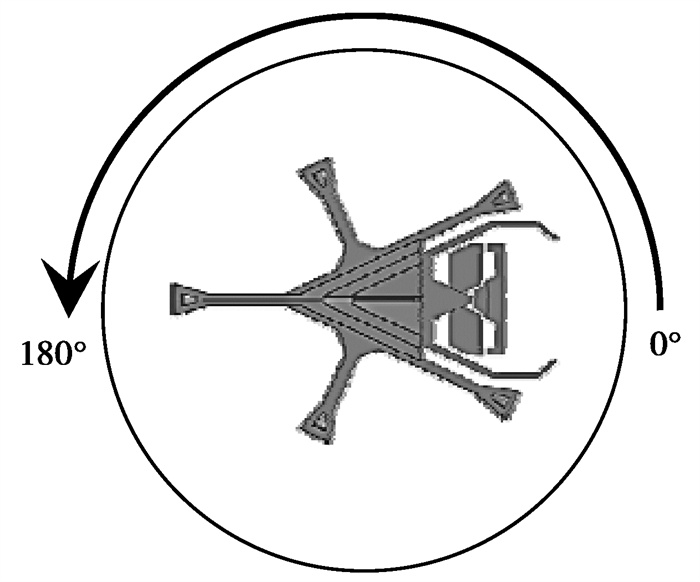
考虑结构的对称特点,针对长沙机场T3航站楼工程分别进行了0°~180°范围内,共13个风向角下的数值模拟计算,风向角间隔为15°,通过在固定计算域中旋转航站楼模型实现不同风向角的计算。CFD数值模拟计算中风向角定义如图 7所示。
|
图 7 CFD数值模拟风向角定义 Fig. 7 The CFD numerical simulation wind angle definition |
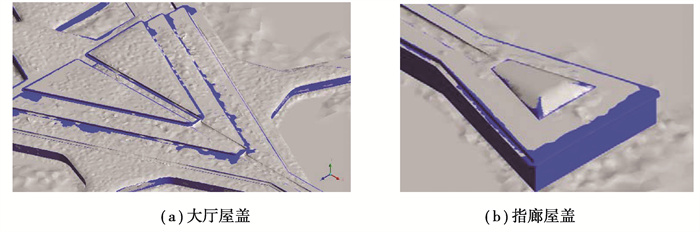
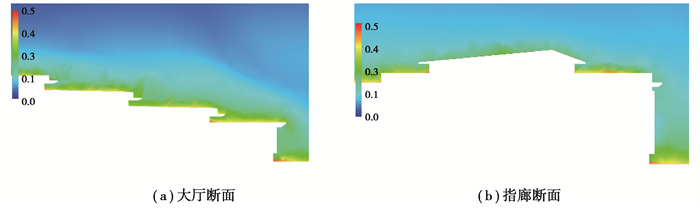
通过CFD数值模拟得到计算域中雪相体积分数分布,通过雪相的等参面绘图可得到航站楼大厅及指廊屋盖表面积雪效果图。因篇幅所限,文中给出典型180°风偏角下大厅和指廊位置的表面积雪分布(见图 8),同时给出大厅和指廊位置的雪相体积分数分布断面图(见图 9)。由体积分数分布图可见,对于航站楼大厅,多级屋面对积雪分布产生显著影响。在迎风面前缘位置,积雪发生了迁移现象,造成明显积雪分布不均匀,导致雪荷载分布不均匀;在多级屋面的内凹处,积雪发生了一定程度的聚集,这是由于来流在各级屋盖前缘已发生流动分离,内凹处风速下降,积雪迁移量下降,且处于前缘后方,受迁入雪量增减而出现积雪聚集。
|
图 8 航站楼屋盖表面积雪效果图(180°风偏角) Fig. 8 Image of snow effect on terminal building roof surface (180° wind angle) |
|
图 9 计算域雪相体积分数分布(180°风偏角) Fig. 9 Calculate the distribution of domain snow phase volume fractions |
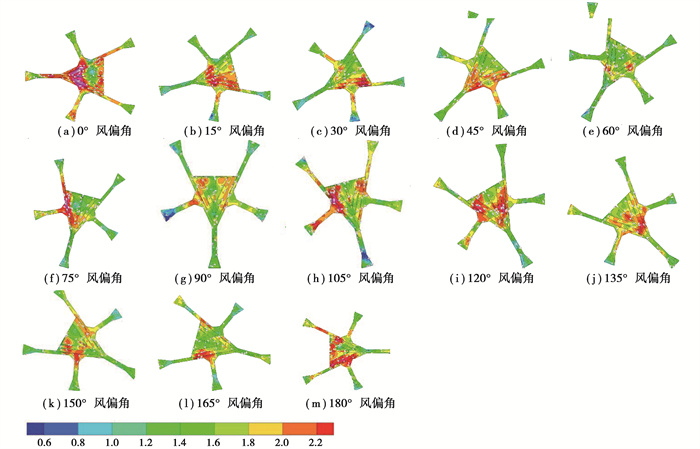
对于指廊部分,来流在指廊主体结构及顶层屋盖的前缘发生流动分离,雪相向后聚集到二层墙面附近,二层屋盖表面相对平缓,发生显著的积雪迁移,在二层屋盖后方形成一定程度的积雪聚集,造成显著的雪荷载分布不均匀。按式(1)可计算得到航站楼屋面积雪分布系数,绘制得到各风偏角下的等值线图(见图 10)。
|
图 10 航站楼屋面积雪分布系数等值线图 Fig. 10 Contour map of snow distribution coefficient on terminal roof |
根据荷载规范表7.2.1对积雪分布系数的要求,大厅及指廊端部天窗区域屋盖积雪分布系数可按第8项高低屋面取值,指廊平屋面区域可按第2项单跨双坡屋面取值。根据航站楼设计尺寸,取h=7.5 m, b1=b2=40 m,计算得到积雪分布系数:
| $ \mu_{r, m}=\frac{b_1+b_2}{2 h}=\frac{40+40}{2 \times 7.5}=5.3>40 \text { 。} $ | (7) |
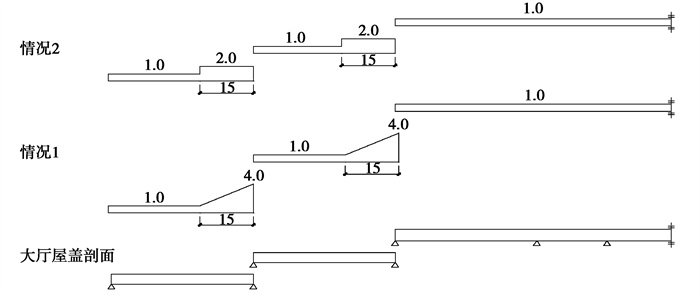
式中:b1为高跨屋面跨度;b2为低跨屋面跨度;h为高低跨高差。故取μr, m=4.0。覆盖宽度a=15 m,据此计算得到大厅区域的情况1和情况2雪荷载分布系数,如图 11所示。
|
图 11 按规范计算的局部屋面积雪分布系数分布 Fig. 11 Local roof snow distribution coefficient distribution calculated according to the code |
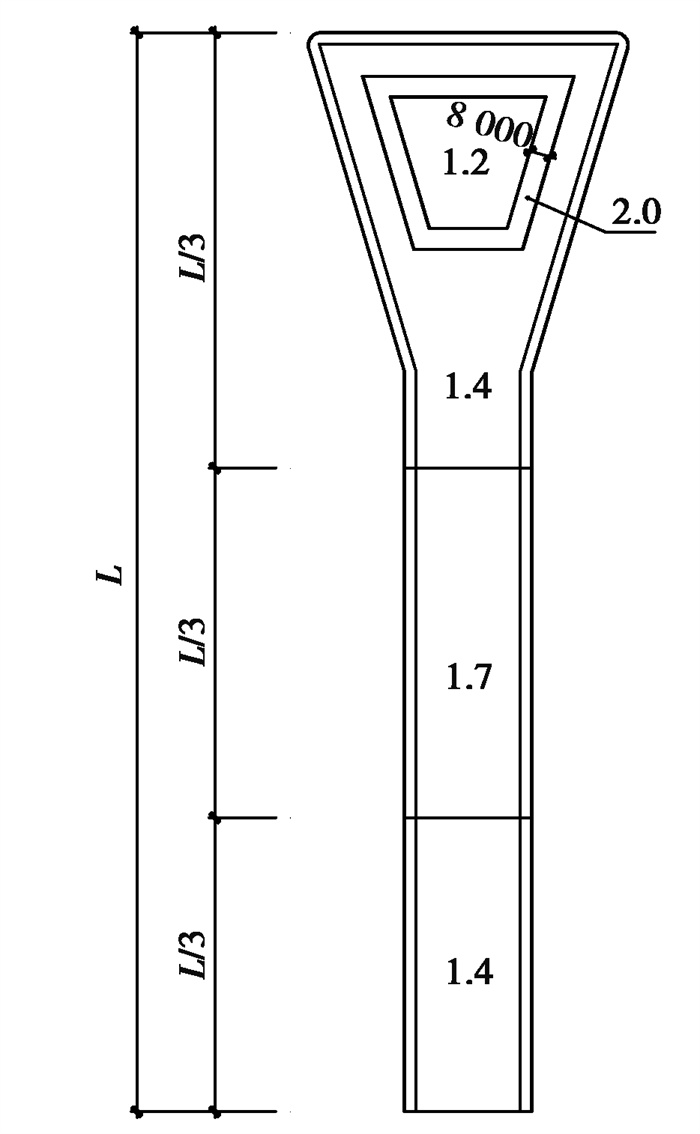
根据CFD数值模拟结果,整个屋盖的积雪分布系数的分布规律呈显著不均匀,较低两阶屋面在部分风向角下出现大面积较重积雪的情况。为保证结构安全,雪荷载设计值取荷载规范与数值模拟结果的包络,较低两阶屋面的雪荷载分布系数整体取2.2,最高阶整体取1.6。同理,对于指廊钢结构,端部天窗区域根据规范要求计算分布,平屋面区域根据风致雪飘移模拟结果分3个区域,取值为1.4、1.7、1.4(见图 12)。针对类似多阶屋面的处理,应充分考虑低阶屋面可能出现积雪重分布导致的分布系数增大。根据数值模拟结合和荷载规范的包络,建议低阶屋面考虑2以上的分布系数,考虑较不利的荷载工况。
|
图 12 指廊平屋面区域屋面积雪分布系数分布 Fig. 12 Refers to the distribution of roof snow cover distribution coefficient in the corridor flat roof area |
文中基于ANSYS Fluent对长沙机场T3航站楼的积雪分布形式进行数值模拟,经过对VOF模型法中雪相体积分数的分析处理得到航站楼结构的屋面积雪分布系数。
1) 采用VOF法对长沙机场T3航站楼进行雪荷载数值模拟,得到了计算域中雪相体积分数的空间分布情况;将数值模拟得到的结果,按照屋积雪分布系数的定义做转换,给出简化的形式以便于工程设计使用。
2) 根据数值模拟结果,长沙机场T3航站楼屋盖的积雪分布系数呈现显著不均匀性分布,局部区域雪压分布系数较大。在各个风向角下,高层屋盖的积雪分布系数整体较高,且出现局部集中较大值现象;指廊与主体连接部位的积雪分布系数整体较高,出现局部集中较大值现象。上述现象表明,空气流动导致屋面原有积雪发生重分布,产生不均匀的积雪分布系数。航站楼屋面积雪分布系数的整体数值分布区间在0.6~2.2范围内,呈现一定的不均匀分布特征,该结果范围与荷载规范规定的数值范围较接近。
3) 屋面积雪分布不局限于主体结构,仍受其周边区域地面或邻近建筑物的积雪重分布的影响,在风作用下,主体结构屋盖积雪分布受来流方向变化而发生相应方向的重分布。
| [1] |
陈氏凤. 浅析雪灾中轻钢结构的受损原因与设计建议[J]. 浙江建筑, 2010, 27(7): 34-36, 55. Chen S F. Brief analysis of the cause of damage to light weight steel structure in snow disaster and the design proposals[J]. Zhejiang Construction, 2010, 27(7): 34-36, 55. (in Chinese) |
| [2] |
袁杨, 陈忠范. 雪荷载下加油站單棚倒塌事故分析及若干建议[J]. 江苏建筑, 2009(1): 34-36. Yuan Y, Chen Z F. Analysis of gas station sheds collapse under snow load and relevant recommendations[J]. Jiangsu Construction, 2009(1): 34-36. (in Chinese) |
| [3] |
张延年. 大跨度钢结构屋面风雪荷载[M]. 北京: 科学出版社, 2013. Zhang Y N. Wind and snow load on large-span steel structure roof[M]. Beijing: Science Press, 2013. (in Chinese) |
| [4] |
周眶毅, 顾明. 风致积雪漂移堆积效应的研究进展[J]. 工程力学, 2008, 25(7): 5-10, 17. Zhou X Y, Gu M. Simulation of the wind-induced snowdrift: state of the art[J]. Engineering Mechanics, 2008, 25(7): 5-10, 17. (in Chinese) |
| [5] |
Okaze T, Takano Y, Mochida A, et al. Development of a new k-e model to reproduce the aerodynamic effects of snow particles on a flow field[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2015, 144: 118-124. DOI:10.1016/j.jweia.2015.04.016 |
| [6] |
Liston G E, Sturm M. A snow-transport model for complex trrin[J]. Journal of Glaciology, 1998, 44(148): 498-516. DOI:10.1017/S0022143000002021 |
| [7] |
BeyersJ H M, Sundsbo P A, Harms T M. Numerical simulation of three-dimensional, transient snow drifting around a cube[J]. Journal of W ind Engineering and Indutrial Aerodynamics, 2004, 92(9): 725-747. DOI:10.1016/j.jweia.2004.03.011 |
| [8] |
何连华, 陈凯, 符龙彪. 基于VOF方法的雪荷载数值模拟及工程应用[J]. 建筑结构, 2011, 41(11): 141-144. He L H, Chen K, Fu L B. Application and numerical simulation of snow loads based on the VOF method[J]. Building Structure, 2011, 41(11): 141-144. (in Chinese) |
| [9] |
莫华美. 典型屋面积雪分布的数值模拟与实测研究[D]. 哈尔滨: 哈尔滨工业大学, 2011. Mo H M. Numerical simulation and experimental study of snow distribution on typical roofs[D]. Harbin: Harbin Institute of Technology, 2011. (in Chinese) |
| [10] |
洪财滨. 典型形式大跨度屋盖风致雪漂移的数值模拟研究[D]. 哈尔滨: 哈尔滨工业大学, 2012. Hong C B. Numerical simulation of snow drifting on typical form of long-span roofs[D]. Harbin: Harbin Institute of Technology, 2012. (in Chinese) |
| [11] |
莫华美, 范峰, 洪汉平. 积雪漂移风洞试验与数值模拟研究中输入风速的估算[J]. 建筑结构学报, 2015, 36(7): 75-80, 90. Mo H M, Fan F, Hong H P. Evaluation of input wind speed used in wind tunnel test and numerical simulation to estimate drifting snow profile[J]. Journal of Building Structures, 2015, 36(7): 75-80, 90. (in Chinese) |
| [12] |
罗熙越. 基于试验相似理论的风致雪漂移数值模拟[D]. 重庆: 重庆大学, 2020. . Luo X Y. Numerical simulation of wind-induced snow drift based on experimental similarity theory[D]. Chongqing: Chongqing University, 2020. (in Chinese) |
| [13] |
刘博雅, 张清文, 刘盟盟, 等. 高跨为双坡屋面的高低屋面低跨平屋面积雪分布研究[J]. 建筑结构学报, 2019, 40(6): 48-55. Liu B Y, Zhang Q W, Liu M M, et al. Research of snow distribution on lower roof of step roofs with gable-roof on high par[J]. Journal of Building Structures, 2019, 40(6): 48-55. (in Chinese) |
| [14] |
Boutanios Z, Jasak H. Improvements of the viscous treatment of the snow phase in two-way coupled Eulerian-Eulerian simulations of drifting snow[C]//Proceedings of the 8th International Conference on Snow Engineering, Nantes, F rance. 2016: 20-25.
|
| [15] |
Kang L Y, Zhou X Y, van Hooff T, et al. CFD simulation of snow transport over flat, uniformly rough. open trrain: impact of physical and computational parameters[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2018, 177: 213-226. |
 2022, Vol. 45
2022, Vol. 45


