微纳输流管道系统在现阶段多领域有着极大的应用前景,尤其在生物医药领域,微纳管道以其特有的小尺度性在生物传感器、药物输送等方面有着不可替代的作用,其中碳纳米管因其具有1~40 nm的平均直径以及完美的空心管道结构已被认为是输送基因药品、抗癌药物等的最佳输流管道之一[1-4]。在微纳管道输送药物的具体应用中,常通过施加外加磁场来增强系统的稳定性,使流体能更为精准地送至靶向目标,基于此大量相关研究随之出现[5-8],而在众多研究中,纳米流固耦合系统的振动机理是现阶段亟待了解与掌握的热点研究之一[9-13]。大量研究表明这类系统的振动与管内流体流速及系统的边界条件有关,即:管内流体流速增加,输流管道会产生失稳现象,但边界条件不同失稳类型又不尽相同。过去的十几年中纳米输流管道系统另一个研究热点是如何反映纳米管道的小尺度效应,由此基于小尺度效应的许多高阶连续介质理论得以应用于纳米输流管道的振动以及失稳特性[14-16]的研究中。Ghane等[17]应用非局部连续介质理论,以Euler-Bernoulli梁模型研究了纵向磁场中输流碳纳米管的振动及颤振失稳。Bahaadini等[18]则应用非局部应变梯度理论采用Timoshenko梁模型研究了小尺度效应、稀薄效应对碳纳米输流管道振动以及失稳特性的影响。在纳米流体储存、运输以及纳米复合材料等纳米技术领域,碳纳米管常嵌于某一基体中,而研究纳米管动力学特性所涉及的基体大都等效为Winkler弾性模型、Pasternak弾性模型以及其他一些粘弹性模型等[19-21].
目前文献中对作用于输流碳纳米管道系统各参数间相互影响的研究鲜少提及。笔者依据非局部Euler-Bernoulli梁模型,弹性基体采用Pasternak弾性模型,针对纵向磁场作用下嵌入弹性基体中的简支输流单层碳纳米管(SWCNT)系统,研究各项参数耦合作用时该系统的振动及稳定性问题,并着重对各参数间的相互影响做进一步地分析,以期为纳米管在各领域中的应用提供一定的理论依据。
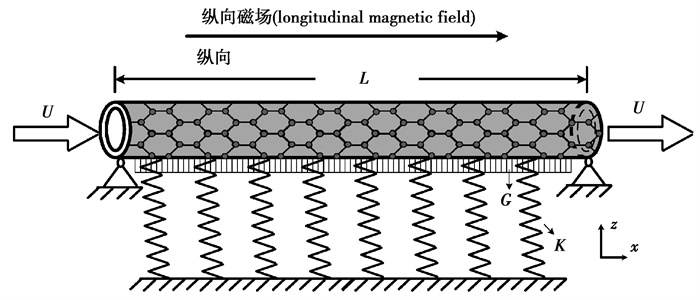
1 振动控制方程图 1为弹性基体中简支输流碳纳米管在纵向磁场中的示意图。
|
图 1 纵向磁场中嵌入Pasternak弹性基体简支输流单层碳纳米管 Fig. 1 A fluid-conveyed SWCNT embedded in Pasternak elastic matrix subjected to a longitudinal magnetic field |
如图所示建立坐标系,X为纳米管的轴向坐标,碳纳米管长度记为L,外径为D,弯曲刚度记为EI。该系统仅发生面内横向小幅振动,不计重力及管道外部拉、压力的影响,管内流体流动为理想流体的定常流动,不计流动阻力,流速不变记为U。
小变形情况下,Euler-Bernoulli梁应变-位移关系为
| $ \varepsilon_{X X}=-Z \frac{\partial^2 W}{\partial X^2}, $ | (1) |
式中:W(X, t)为z向位移,t为时间,eXX为x方向的应变。
由非局部弹性理论[22],SWCNT应力-应变关系可表示为:
| $ \sigma_{X X}-\left(e_0 a\right)^2 \frac{\partial^2 \sigma_{X X}}{\partial X^2}=E \varepsilon_{X X}, $ | (2) |
式中:σXX为x方向的应力,E为纳米管弹性模量,e0为材料常数,a为材料内部特征长度,对于碳纳米管而言C—C键长一般为0.142 nm[23]。
碳纳米管内部流体作用于纳米管的力可表示为[24]
| $ F_{\mathrm{f}}=m_{\mathrm{f}}\left(\frac{\partial^2 W}{\partial t^2}+2 U \frac{\partial^2 W}{\partial X \partial t}+U^2 \frac{\partial^2 W}{\partial X^2}\right) \text {, } $ | (3) |
式中,mf为每单位长度上纳米管内部流体的质量。
纵向磁场中,由磁场引起的作用于纳米管z方向上单位长度的磁场力为[6]
| $ F_Z=f_Z A=\eta A H_X^2 \frac{\partial^2 W}{\partial X^2}, $ | (4) |
式中:A为管道横截面积,fZ为z方向上的洛伦兹力,其大小表示为
Pasternak弾性基体由弹性参数K与剪切参数G来描述,其对纳米管作用力表示为[25]
| $ F=K W-G \frac{\partial^2 W}{\partial X^2}。$ | (5) |
基于上述各式,由弹性基体、磁场以及管内流体共同作用于碳纳米管的功为:
| $ W_{\mathrm{Ext}}=\frac{1}{2} \int_0^L-\left(K W-G \frac{\partial^2 W}{\partial X^2}+F_Z+F_{\mathrm{f}}\right) W \mathrm{~d} X。$ | (6) |
管道系统的总动能为
| $ T=\frac{1}{2}\left(m_{\mathrm{c}}+m_{\mathrm{f}}\right) \int_0^L\left(\frac{\partial W}{\partial t}\right)^2 \mathrm{~d} X, $ | (7) |
式中,mc为每单位长度上纳米管的质量。
管道系统的应变能为
| $ U=\frac{1}{2} \int_0^L \int_A \varepsilon_{X X} \sigma_{X X} \mathrm{~d} A \mathrm{~d} X。$ | (8) |
考虑到弯矩M与应力σXX的关系式:
| $ M=\iint \sigma_{X X} Z \mathrm{~d} A, $ | (9) |
应用哈密顿原理:
| $ {\int {{t_2}} _{t1}}\delta \left( {U - T - {W_{Ext}}} \right){\rm{d}}t = 0, $ | (10) |
可以得到输流简支碳纳米管的运动方程为:
| $ \begin{gathered} E I \frac{\partial^4 W}{\partial X^4}+\left(m_{\mathrm{f}} U^2-\eta A H_X^2-G\right) \frac{\partial^2 W}{\partial X^2}+2 m_{\mathrm{f}} \frac{\partial^2 W}{\partial X \partial t}+K W+\left(m_{\mathrm{c}}+m_{\mathrm{f}}\right) \frac{\partial^2 W}{\partial t^2}- \\ \left(e_0 a\right)^2\left[\left(m_{\mathrm{f}} U^2-\eta A H_X^2-G\right) \frac{\partial^4 W}{\partial X^4}+2 m_{\mathrm{f}} \frac{\partial^4 W}{\partial X^3 \partial t}+K \frac{\partial^2 W}{\partial X^2}+\left(m_{\mathrm{c}}+m_{\mathrm{f}}\right) \frac{\partial^4 W}{\partial X^2 \partial t^2}\right]=0, \end{gathered} $ | (11) |
边界条件为:
| $ X=0, L: W=\frac{\partial^2 W}{\partial X^2}=0 \text { 。} $ | (12) |
为便于后续的理论分析,引入下列无量纲化的变量及参数:
则上述横向振动方程(11)及边界条件(12)可分别转化为下述的无量纲方程
| $ \begin{gathered} \frac{\partial^4 w}{\partial x^4}+\left(u^2-\psi-g\right) \frac{\partial^2 w}{\partial x^2}+2 u \sqrt{\beta} \frac{\partial^2 w}{\partial x \partial \tau}+k w+\frac{\partial^2 w}{\partial \tau^2}- \\ \mu\left[\left(u^2-\psi-g\right) \frac{\partial^4 w}{\partial x^4}+2 u \sqrt{\beta} \frac{\partial^4 w}{\partial x^3 \partial \tau}+k \frac{\partial^2 w}{\partial x^2}+\frac{\partial^4 w}{\partial x^2 \partial \tau^2}\right]=0 。\end{gathered} $ | (13) |
无量纲边界条件
| $ x=0, 1: w=\frac{\partial^2 w}{\partial x^2}=0。$ | (14) |
设方程(13)的解为w=φ(x)eΩ τ,代入方程(13)有
| $ \begin{gathered} \frac{\mathrm{d}^4 \varphi}{\mathrm{d} x^4}+\left(u^2-\psi-g\right) \frac{\mathrm{d}^2 \varphi}{\mathrm{d} x^2}+2 u \sqrt{\beta} \varOmega \frac{\mathrm{d} \varphi}{\mathrm{d} x}+\left(\varOmega^2+k\right) \varphi- \\ \mu\left[\left(u^2-\psi-g\right) \frac{\mathrm{d}^4 \varphi}{\mathrm{d} x^4}+2 u \sqrt{\beta} \varOmega \frac{\mathrm{d}^3 \varphi}{\mathrm{d} x^3}+\left(\varOmega^2+k\right) \frac{\mathrm{d}^2 \varphi}{\mathrm{d} x^2}\right]=0 。\end{gathered} $ | (15) |
采用微分变换法(DTM)求解上述高阶微分方程,DTM算法是将待求解的微分方程转换成相应的代数方程组,进而通过求解该代数方程组来获得原微分方程闭合级数解的一种半解析算法。DTM法应用于纳米级别输流管道系统振动稳定性分析已在文献[4]得到证实。
基于DTM运算法则[26],可得到方程(15)的微分变换形式:
| $ \begin{array}{r} {\left[1-\mu\left(u^2-\psi-g\right)\right](n+4) ! \varPhi(n+4)-2 \mu u \sqrt{\beta} \varOmega(n+3) ! \varPhi(n+3)+2 u \sqrt{\beta} \varOmega(n+1) ! \varPhi(n+1)+} \\ {\left[\left(u^2-\psi-g\right)-\mu\left(\varOmega^2+k\right)\right](n+2) ! \varPhi(n+2)+\left(\varOmega^2+k\right) n ! \varPhi(n)=0 。} \end{array} $ | (16) |
其中Φ (n)为φ (x) 变换函数。
边界条件的微分变换形式:
| $ \varPhi(0)=\varPhi(2)=0 $ | (17) |
| $ \sum\limits_{n=0}^{\infty} \varPhi(n)=0, \sum\limits_{n=0}^{\infty} n(n-1) \varPhi(n)=0 \text { 。} $ | (18) |
令Φ (1) = C1, Φ(3) = C2,进而与式(17)一起代入式(16),迭代求得Φ(n),n = 4, 5, …, N。然后将Φ(n),n = 0, 1, 2, …, N代入式(18),可得到以下2个方程:
| $ \left[\begin{array}{ll} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array}\right]\left\{\begin{array}{l} C_1 \\ C_2 \end{array}\right\}=0。$ | (19) |
令上式系数矩阵行列式为零即可获得输流碳纳米管系统无量纲复频率Ω,其中虚部Im(Ω)是系统的无量纲频率,研究表明[27],在Im(Ω) = 0时,简支管道系统出现屈曲失稳,此时流速称为系统发散失稳的临界流速,记为ucr。
3 数值算例分析采用的纳米管几何与材料参数分别为[6]:管内流体的密度rf = 1 000 kg/m3, 碳纳米管密度rc = 2 300 kg/m3,外层半径R0 = 3 nm,壁厚td = 0.1 nm,弹性模量E = 3.4 TPa,泊松比n =0.3。振动中为不计纳米管剪切变形与转动惯量,长径比取L/2R0 = 40,磁导率h = 4π×10-7,质量比β = 0.5,其余参数选择在算例中将给与说明,选取DTM算法收敛截取数60以确保各项数值解足够精确[6]。
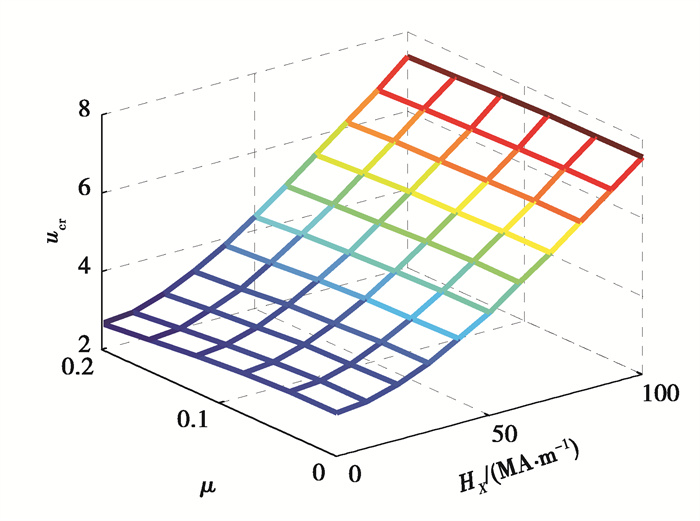
图 2为不考虑弹性基体时,简支输流SWCNT系统无量纲临界流速在小尺度系数μ及磁场强度HX耦合作用下的变化规律。由图 2可以看出随着小尺度系数的增加系统临界流速降低,系统更易出现失稳现象;而随着磁场强度的增强系统临界流速增大、稳定性提高。进一步分析图 2可以发现,小尺度系数越大,磁场的增强对临界流速的提高越明显,例如:磁场强度由0提高到1×108 A/m,在m = 0时,临界流速提升量Δucr = 4.42;在μ = 0.2时,Δucr = 4.714. 而磁场强度越大,改变小尺度效应对临界流速的影响越不明显,例如:小尺度参数μ由0增加到0.2,当磁场强度HX = 0 A/m时,临界流速降低值Δucr = 0.481;当磁场强度HX =1×108 A/m时,Δucr= 0.187.
|
图 2 输流SWCNT无量纲临界流速随磁场强度与小尺度系数变化规律(k = g = 0) Fig. 2 Critical flow velocities for the fluid-conveyed SWCNT with the change of both nonlocal parameter and magnetic field(k = g = 0) |
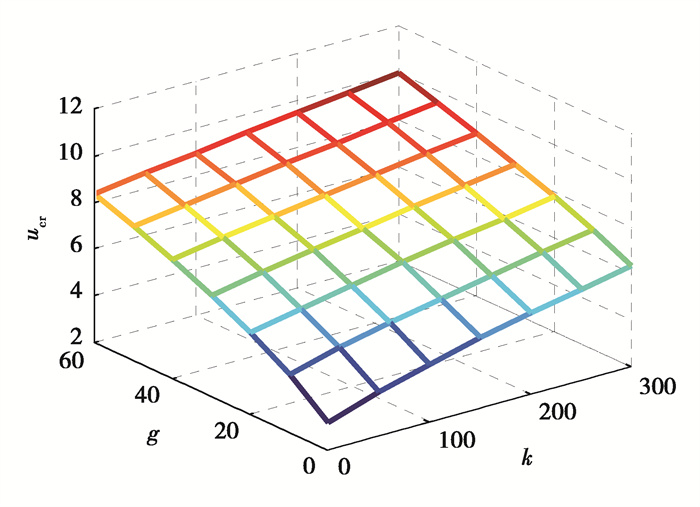
图 3为不计小尺度效应及磁场作用时,弹性基体无量纲弹性参数k及剪切参数g对系统无量纲临界流速u的影响。由图 3可以看到,随着弹性基体双参数的增加系统临界流速均提高,说明弹性基体增强了系统的刚度。比较双参数耦合作用的影响可以发现,剪切参数g对系统稳定性的影响优于弹性参数k。
|
图 3 输流SWCNT无量纲临界流速随弹性基体双参数变化规律(μ = 0, HX = 0 A/m) Fig. 3 Critical flow velocities for the fluid-conveyed SWCNT with the change of Pasternak matrix parameters (μ = 0, HX = 0 A/m) |
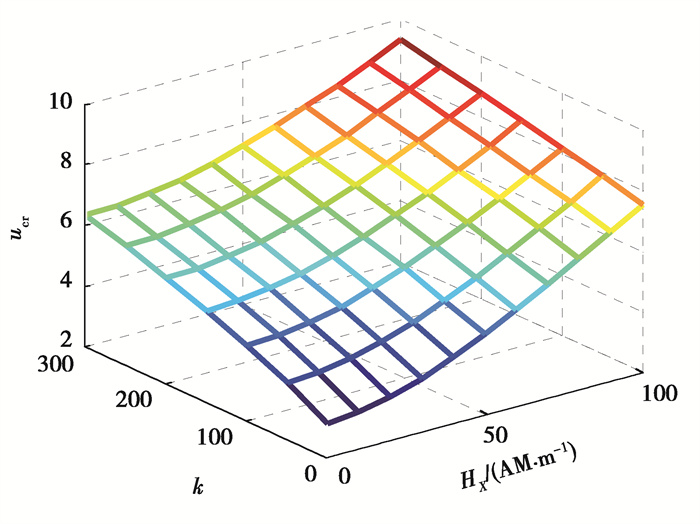
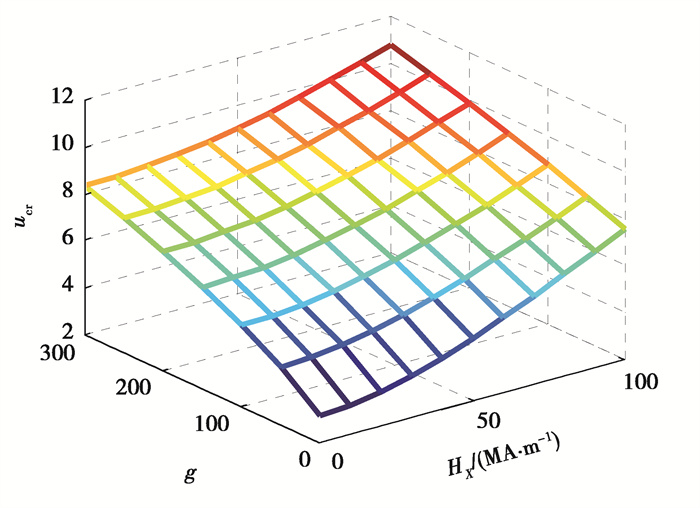
图 4和图 5为不计小尺度效应时,弹性基体与磁场共同作用下输流SWCNT系统无量纲临界流速的变化规律,其中图 4剪切参数g = 0、图 5弹性参数k = 0。由图 4、5可以看到增强外加磁场及弹性基体均可提高系统的临界流速,说明弹性基体与纵向磁场均能增强系统的刚度。进一步比较各参数间的相互影响可以发现:在较强磁场中,弹性基体的改变对系统临界流速的影响程度降低,例如:无量纲弹性参数k由0增至300(图 4),磁场强度为0 A/m时,临界流速提升量Δucr = 3.024;磁场强度为1×108 A/m时,Δucr = 1.797。而在较强弹性基体下,磁场的增强对系统临界流速的提升程度也相应降低,如:外加磁场时由0增至1×108 A/m,在弹性参数k = 0时,Δucr = 4.42;在k = 300时,Δucr = 3.013。分析图 5数据也可得到类似结论,这里不再赘述。这意味着在对系统刚度的提升作用中,纵向磁场与弹性基体并没有“遇强更强”,而是出现了“此长彼消”的变化情况。
|
图 4 输流SWCNT无量纲临界流速随磁场与弹性参数k变化规律(μ = g = 0) Fig. 4 Critical flow velocities for the fluid-conveyed SWCNT with the change of both magnetic field and elastic parameter k (μ = g = 0) |
|
图 5 输流SWCNT无量纲临界流速随磁场与剪切参数g变化规律(μ = k = 0) Fig. 5 Critical flow velocities for the fluid-conveyed SWCNT with the change of both magnetic field and shear parameter g (μ = k = 0) |
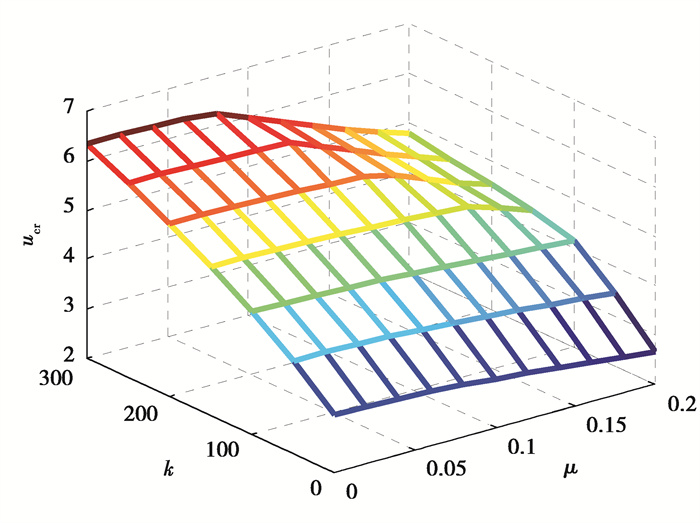
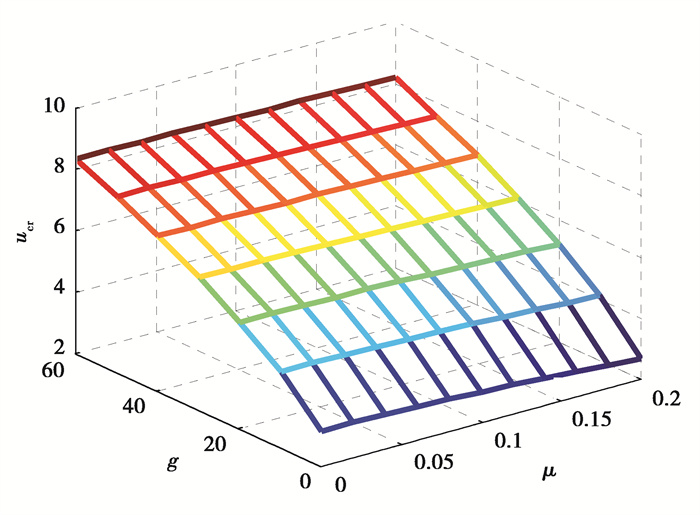
图 6和图 7为不计磁场作用时,弹性基体与小尺度效应共同作用时输流SWCNT系统无量纲临界流速的变化规律,其中图 6剪切参数g = 0、图 7弹性参数k = 0。由图 6、7可以看到有无弹性基体,小尺度系数μ的增加都会降低系统的临界流速,而增强弹性基体可以提高系统临界流速。进一步比较各参数间的相互影响可以发现:小尺度效应与弹性基体间的相互影响作用表现得较为复杂。小尺度效应越强,弹性参数k的变化对系统临界流速的影响越弱,但剪切参数g对临界流速的影响越强,如:弹性参数k由0增至300,在小尺度系数为0时,临界流速提升值Δucr = 3.204,小尺度系数为0.2时,Δucr = 2.123(图 6);剪切参数g由0增至60,在小尺度系数为0时,Δucr = 5.217,小尺度系数为0.2时,Δucr = 5.53(图 7)。反观弹性基体,在较大弹性参数k与较小剪切参数g时,小尺度效应的改变对临界流速的影响越明显,如:μ由0增加到0.2,在k= 0时,临界流速降低值Δucr = 0.481,k = 300时,Δucr =1.562(图 6);同样的μ由0增加到0.2,在g = 0时,临界流速降低值Δucr = 0.481,g = 60时,Δucr = 0.168(图 7)。
|
图 6 输流SWCNT无量纲临界流速随小尺度系数与弹性参数k变化规律(g = 0, HX = 0 A/m) Fig. 6 Critical flow velocities for the fluid-conveyed SWCNT with the change of both nonlocal parameter and elastic parameter k (g = 0, HX = 0 A/m) |
|
图 7 输流SWCNT无量纲临界流速随小尺度系数与剪切参数g变化规律(k = 0, HX = 0 A/m) Fig. 7 Critical flow velocities for the fluid-conveyed SWCNT with the change of both nonlocal parameter and shear parameter g (k = 0, HX = 0 A/m) |
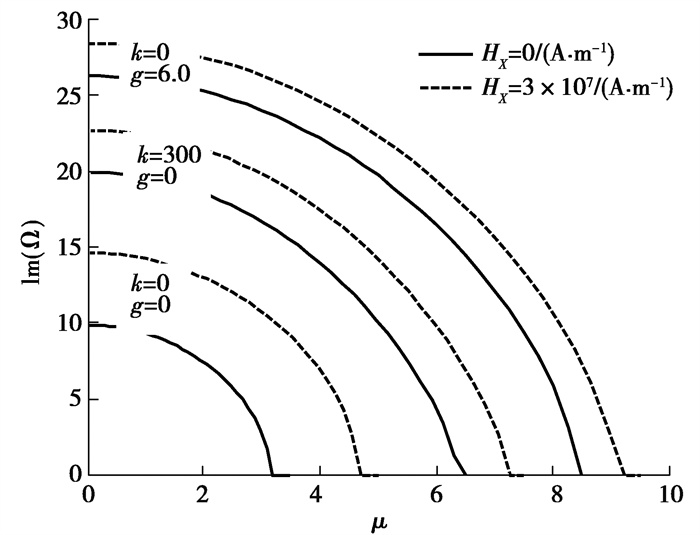
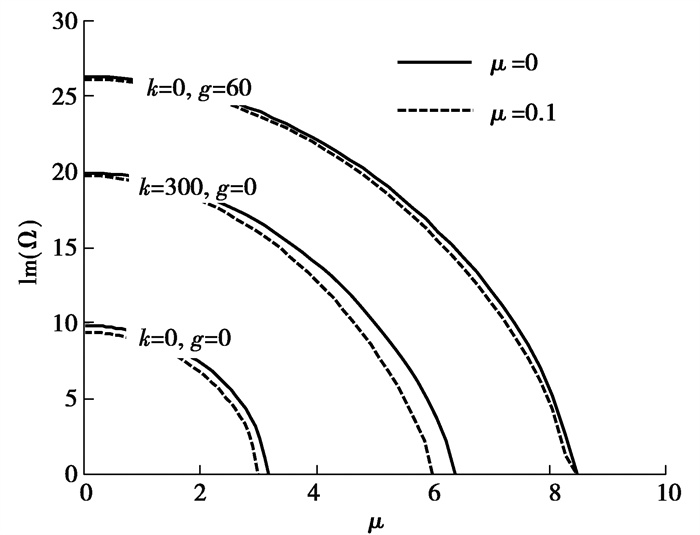
图 8和图 9分别给出了外加纵向磁场与小尺度效应对弹性基体中输流管道系统振动频率的影响,其中图 8小尺度系数m = 0,图 9磁场强度HX = 0 A/m。由图 8、9可以发现,不同参数情形下,管道系统振动频率均随管内流体流速增加而降低,且当流速达到相应的某一临界流速时,管道系统均产生了发散失稳。由图 8、9还可以看出,外加纵向磁场与弹性基体可提高系统的振动频率,而小尺度效应降低系统振动频率。进一步分析可以发现,磁场在没有弹性基体时对频率的提高程度优于有弹性基体时的情况;而对于小尺度效应,由图 9可以看到,在较大弹性参数与较小剪切参数的弹性基体中,小尺度系数的变化对系统频率的影响程度较强。
|
图 8 不同纵向磁场与弹性基体系统无量纲流速与频率的关系(m = 0) Fig. 8 The dimensionless complex frequency as a function of u for different elastic matrixes and magnetic fields(m = 0) |
|
图 9 不同小尺度系数与弹性基体系统无量纲流速与频率的关系(HX = 0 A/m) Fig. 9 The dimensionless complex frequency as a function of u for different elastic matrixes and nonlocal parameters(HX = 0 A/m) |
基于非局部连续介质理论,以Euler-Bernoulli梁模型,弹性基体采用Pasternak弾性模型,研究了纵向磁场作用下嵌入弹性基体中的输流SWCNT管道系统在小尺度系数、磁场强度及弹性基体共同作用下的发散失稳问题,并着重研究了上述耦合作用的各参数相互之间的影响情况,得到如下结论:
1) 弹性基体、纵向磁场均能提升系统刚度,从而提高系统稳定性;而小尺度效应则降低了系统的刚度,使纳米管道系统更易出现失稳现象。
2) 弹性基体在对系统刚度的提升中,其剪切参数的作用优于弹性参数的作用。
3) 弹性基体与外加纵向磁场在共同提升系统稳定性的过程中,出现了“此长彼消”这一现象,即较强的弹性基体将降低外加磁场对系统稳定性的提升效率,反之亦然。
4) 弹性基体与小尺度效应的相互作用显得较为复杂,具体表现为:弹性基体的弹性参数越大、剪切参数越小,小尺度效应对输流管道系统的影响越强;而小尺度效应越明显,弹性基体中弹性参数对系统的影响越弱、剪切参数对系统的影响越强。
上述结论意味着,在实际应用中,为了增强纳米输流管道的稳定性,可通过外加磁场或弹性基体的方式来实现,但二者耦合作用时一味增大二者强度并不是一个较为经济的做法。另外,可适当增强磁场强度或选择弹性参数小、剪切参数大的弹性基体来降低小尺度效应对系统的影响。
| [1] |
Lyu Z, Yang Y W, Liu H. High-accuracy hull iteration method for uncertainty propagation in fluid-conveying carbon nanotube system under multi-physical fields[J]. Applied Mathematical Modelling, 2020, 79: 362-380. DOI:10.1016/j.apm.2019.10.040 |
| [2] |
Gao M, Bian L C. Thermal environment and strain energy related micromechanics analysis for properties of carbon nanotubes[J]. Journal of Applied Mathematics and Mechanics, 2019, 99(3): e201800169-1-e201800169-16. |
| [3] |
黄小林, 钟德月, 刘思奇, 等. 轴向运动碳纳米管增强复合材料板的自由振动研究[J]. 河南理工大学学报(自然科学版), 2022, 41(1): 153-158. Huang X L, Zhong D Y, Liu S Q, et al. Study on free vibration of axially moving carbon nanotube-reinforced composite plate[J]. Journal of Henan Polytechnic University (Natural Science), 2022, 41(1): 153-158. (in Chinese) DOI:10.16186/j.cnki.1673-9787.2020040104 |
| [4] |
Arani A H, Aghdam M M, Saeedian M J. Wave propagation analysis of CNT reinforced composite micro-tube conveying viscose fluid in visco-Pasternak foundation under 2D multi-physical fields[J]. Journal of Solid Mechanics, 2018, 10(2): 232-248. |
| [5] |
Liu H, Lv Z. Vibration and instability analysis of flow-conveying carbon nanotubes in the presence of material uncertainties[J]. Physica A: Statistical Mechanics and Its Applications, 2018, 511: 85-103. DOI:10.1016/j.physa.2018.07.043 |
| [6] |
李明, 吕刘飞, 郑华升, 等. 磁场对不同温度场中输流悬臂碳纳米管颤振稳定性的影响[J]. 固体力学学报, 2021, 42(1): 87-93. Li M, Lyu L F, Zheng H S, et al. Magnetic field effect on flutter stability of a fluid-conveying cantilevered carbon nanotube under different temperature fields[J]. Chinese Journal of Solid Mechanics, 2021, 42(1): 87-93. (in Chinese) DOI:10.19636/j.cnki.cjsm42-1250/o3.2020.027 |
| [7] |
Sadeghi-Goughari M, Jeon S, Kwon H J. Fluid structure interaction of cantilever micro and nanotubes conveying magnetic fluid with small size effects under a transverse magnetic field[J]. Journal of Fluids and Structures, 2020, 94: 102951. DOI:10.1016/j.jfluidstructs.2020.102951 |
| [8] |
Dini A L, Zandi-Baghche-Maryam A, Shariati M. Effects of van der Waals forces on hygro-thermal vibration and stability of fluid-conveying curved double-walled carbon nanotubes subjected to external magnetic field[J]. Physica E: Low-Dimensional Systems and Nanostructures, 2019, 106: 156-169. DOI:10.1016/j.physe.2018.10.005 |
| [9] |
Wang Y, Bian L, Gao M. A non-local modeling for the influence of fluid forces on vibration characteristics of carbon nanotubes[J]. Materials Science and Engineering: B, 2021, 272: 115348. DOI:10.1016/j.mseb.2021.115348 |
| [10] |
Bahaadini R, Hosseini M. Flow-induced and mechanical stability of cantilever carbon nanotubes subjected to an axial compressive load[J]. Applied Mathematical Modelling, 2018, 59: 597-613. DOI:10.1016/j.apm.2018.02.015 |
| [11] |
Amiri A, Vesal R, Talebitooti R. Flexoelectric and surface effects on size-dependent flow-induced vibration and instability analysis of fluid-conveying nanotubes based on flexoelectricity beam model[J]. International Journal of Mechanical Sciences, 2019, 156: 474-485. DOI:10.1016/j.ijmecsci.2019.04.018 |
| [12] |
Azarboni H R. Magneto-thermal primary frequency response analysis of carbon nanotube considering surface effect under different boundary conditions[J]. Composites Part B: Engineering, 2019, 165: 435-441. DOI:10.1016/j.compositesb.2019.01.093 |
| [13] |
Liu H C, Li B H, Liu Y S. The inconsistency of nonlocal effect on carbon nanotube conveying fluid and a proposed solution based on local/nonlocal model[J]. European Journal of Mechanics - A/Solids, 2019, 78: 103837. DOI:10.1016/j.euromechsol.2019.103837 |
| [14] |
王腾飞, 黄坤, 郭荣鑫. 考虑非线性本构和小初始变形的单壁碳纳米管的Bernoulli-Euler梁模型[J]. 科学技术与工程, 2021, 21(16): 6575-6581. Wang T F, Huang K, Guo R X. Bernoulli-Euler beam model of single-walled carbon nanotubes with small initial deformation and nonlinear constitutive model[J]. Science Technology and Engineering, 2021, 21(16): 6575-6581. (in Chinese) DOI:10.3969/j.issn.1671-1815.2021.16.005 |
| [15] |
Liu H, Lv Z, Wu H. Nonlinear free vibration of geometrically imperfect functionally graded sandwich nanobeams based on nonlocal strain gradient theory[J]. Composite Structures, 2019, 214: 47-61. DOI:10.1016/j.compstruct.2019.01.090 |
| [16] |
Ghorbanpour Arani A, Jalilvand A, Haghparast E. Theoretical investigation on wave propagation in embedded DWBNNT conveying ferrofluid via stress and strain-inertia gradient elasticity[J]. Proceedings of the Institution of Mechanical Engineers, Part L: Journal of Materials: Design and Applications, 2018, 232(9): 719-732. DOI:10.1177/1464420716644761 |
| [17] |
Ghane M, Saidi A R, Bahaadini R. Vibration of fluid-conveying nanotubes subjected to magnetic field based on the thin-walled Timoshenko beam theory[J]. Applied Mathematical Modelling, 2020, 80: 65-83. DOI:10.1016/j.apm.2019.11.034 |
| [18] |
Bahaadini R, Saidi A R, Hosseini M. Flow-induced vibration and stability analysis of carbon nanotubes based on the nonlocal strain gradient Timoshenko beam theory[J]. Journal of Vibration and Control, 2019, 25(1): 203-218. DOI:10.1177/1077546318774242 |
| [19] |
Sadeghi-Goughari M, Jeon S, Kwon H J. Flutter instability of cantilevered carbon nanotubes caused by magnetic fluid flow subjected to a longitudinal magnetic field[J]. Physica E: Low-Dimensional Systems and Nanostructures, 2018, 98: 184-190. DOI:10.1016/j.physe.2018.01.004 |
| [20] |
Zhu B, Chen X C, Dong Y H, et al. Stability analysis of cantilever carbon nanotubes subjected to partially distributed tangential force and viscoelastic foundation[J]. Applied Mathematical Modelling, 2019, 73: 190-209. DOI:10.1016/j.apm.2019.04.018 |
| [21] |
Malikan M, Dimitri R, Tornabene F. Transient response of oscillated carbon nanotubes with an internal and external damping[J]. Composites Part B: Engineering, 2019, 158: 198-205. DOI:10.1016/j.compositesb.2018.09.092 |
| [22] |
Eringen A C. Nonlocal polar elastic continua[J]. International Journal of Engineering Science, 1972, 10(1): 1-16. DOI:10.1016/0020-7225(72)90070-5 |
| [23] |
Eringen A C. On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves[J]. Journal of Applied Physics, 1983, 54(9): 4703-4710. DOI:10.1063/1.332803 |
| [24] |
Wang L, Ni Q. A reappraisal of the computational modelling of carbon nanotubes conveying viscous fluid[J]. Mechanics Research Communications, 2009, 36(7): 833-837. DOI:10.1016/j.mechrescom.2009.05.003 |
| [25] |
Ghavanloo E, Daneshmand F, Rafiei M. Vibration and instability analysis of carbon nanotubes conveying fluid and resting on a linear viscoelastic Winkler foundation[J]. Physica E: Low-Dimensional Systems and Nanostructures, 2010, 42(9): 2218-2224. DOI:10.1016/j.physe.2010.04.024 |
| [26] |
Chen C K, Ho S H. Transverse vibration of a rotating twisted Timoshenko beams under axial loading using differential transform[J]. International Journal of Mechanical Sciences, 1999, 41(11): 1339-1356. |
| [27] |
Dini A L, Zandi-Baghche-Maryam A, Shariati M. Effects of van der Waals forces on hygro-thermal vibration and stability of fluid-conveying curved double-walled carbon nanotubes subjected to external magnetic field[J]. Physica E: Low-Dimensional Systems and Nanostructures, 2019, 106: 156-169. |
 2022, Vol. 45
2022, Vol. 45

