与传统的渐开线齿廓相比,摆线齿廓具有滑动率低、强度高、重合度大等突出优点,然而摆线齿廓由于啮合角变化大、传递效率低等问题,应用范围受到了很大的限制,主要应用在钟表齿轮、摆线针轮传动、转子泵等特殊领域[1-4]。近年来,越来越多的专家学者开始研究新型摆线类齿廓。
Pollitt等[5]探讨了几种摆线的生成方法,对摆线的实际应用进行了探索。Lai等[6]以坐标变换、包络理论和共轭曲面理论为基础,推导出了摆线行星齿轮的啮合方程,还开发了求解网格和共轭曲面方程的程序,得到了外摆线剖面。Zhu等[7]综合定轴齿轮传动、摆线针轮传动和摆线齿轮传动的优点后,提出了一种新型摆线针轮传动。贵新成等[8]提出了一种具有高重合度的新型内啮合复合摆线齿轮副,并分析了影响重合度的相关因素。Han等[9]基于传统摆线的成形原理,提出了一种新的复合摆线,能够比传统摆线更加方便地控制齿廓形状。石万凯等[10]利用几何形状可调性强的四阶复合摆线作为内齿廓,建立复合摆线齿轮少齿差行星传动啮合理论,分析其传动特性。刘昶等[11]提出了一种基于渐开线插齿刀具运动控制的复合摆线齿轮加工方法,解决了新型复合摆线齿轮的加工问题。黄思雨[12]等提出了一种少齿差金属橡胶复合摆线齿轮副,减少了振动和冲击,提高了传动精度。
与传统摆线相比,复合摆线齿形的几何可控性强,具有很大的应用潜力,但是相关文献[9~12]没有考虑齿廓参数对复合摆线少齿差行星齿轮副应力影响的问题。基于此,笔者采用几何特性可调性强的四阶复合摆线作为内齿廓,设计了复合摆线少齿差行星传动的共轭齿廓,并针对加工制造误差进行了修形。最后建立实体模型进行有限元分析,分析各齿廓参数以及不同工作条件对复合摆线齿轮副应力的影响规律,以期降低齿轮副应力并提高齿轮寿命。
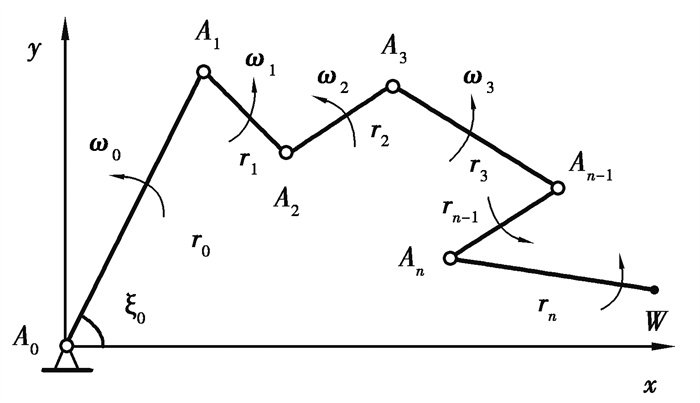
1 复合摆线行星传动共轭齿廓设计 1.1 复合摆线齿廓成型原理如图 1所示,A0、A1、A2、A3…An表示连杆转动中心,r0、r1、r2、r3…rn表示连杆的长度。在开始运动时,An-1依次位于An的左端,各连杆运动的方向均为逆时针,转动角速度分别为ω0、ω1、ω2、ω3…ωn。转动时间t后,各连杆的转角分别为ξ0、ξ1、ξ2、ξ3…ξn,把n+1连杆末端W的运动轨迹定义为广义的n阶摆线。
|
图 1 复合摆线原理 Fig. 1 Composite cycloid principle |
文献[9]详细地讨论了各阶复合摆线的优缺点。复合摆线的阶数过高,齿廓曲线的敏感性下降,不能够保证加工的精度;反之,阶数过小,齿廓的可调性差。综合考虑,四阶复合摆线几何可调性强并且加工的精度较高。所以本研究中选择四阶复合摆线作为齿廓曲线,建立复合摆线内啮合共轭传动理论,并对齿轮副的力学性能进行研究。
当n=4,r1=r2=e1,r3=r4=e2,此时摆线的轨迹为四阶复合摆线[9],四阶摆线齿廓的轨迹方程]如下所示:
| {x=r0cosξ0−2e1cos(zξ0)cosξ0−2e2sin(2zξ0)sinξ0;y=r0sinξ0−2e1cos(zξ0)sinξ0+2e2sin(2zξ0)cosξ0。 | (1) |
式中:ξ0为连杆r0转角,这里为了简化方程,减少参数,将各连杆的转角进行统一,都为ξ0; z为摆线齿轮的齿数。
1.2 复合摆线行星传动共轭理论将四阶复合摆线齿廓方程作为内齿轮(齿轮2)齿廓的方程,再根据齿轮啮合定理求出与其共轭的外齿轮(齿轮1)的齿廓方程。
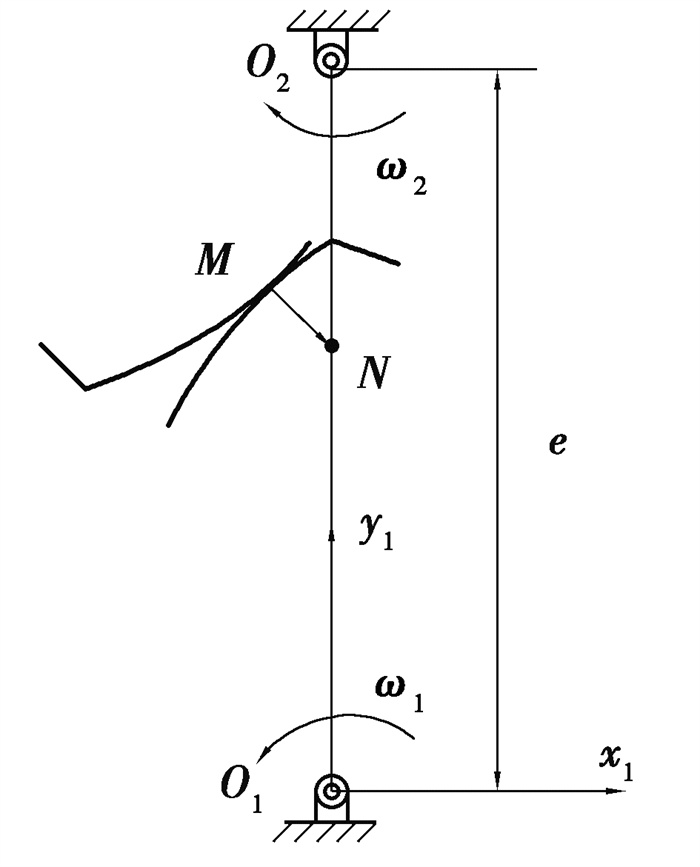
如图 2所示,根据Lewis定理,共轭齿形在啮合点M处的公法线与回转中心线O1O2相交于瞬时回转中心点N,点N将回转中心线O1O2分为两段O1N和O2N,两线段的关系如下:
|
图 2 Lewis齿轮啮合定理 Fig. 2 Lewis gear meshing theorem |
| O2NO1N=ω1ω2=i 。 | (2) |
基于Lewis定理的啮合方程为:
| XN−x2Nx2=YN−y2Ny2。 | (3) |
式中:x2与y2为齿轮副啮合点的坐标,XN和YN为瞬时回转中心N在齿轮2的坐标系中的坐标。Nx2=x′2,Ny2=-y′2;其中y′2为y2对ξ0的偏导,x′2为x2对ξ0的偏导。
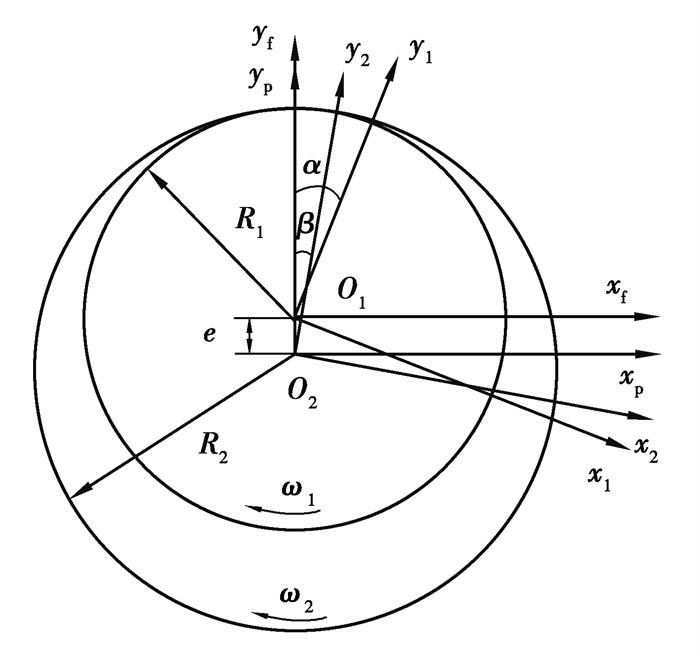
内啮合齿轮副同样符合Lewis定理。如图 3所示:O2为已知齿廓的内齿轮的中心,O1为待求的外齿轮的中心,两齿轮中心到公共瞬时回转中心N的差值O1O2为齿轮1与齿轮2之间的偏心距e; xfO1yf为齿轮1的固定坐标系,x1O1y1为其动坐标系;xpO2yp为齿轮2的固定坐标系,x2O2y2为其动坐标系;齿轮1以角速度ω1绕圆心O1旋转,转过的角度为α;齿轮2以角速度ω2绕圆心O2旋转,转过的角度为β。
|
图 3 内啮合齿轮副运动包络坐标系 Fig. 3 Internal enveloping gear pair motion envelope coordinate system |
由图 3可知,瞬时回转中心N在坐标系x2O2y2中的坐标为:
| (XN=−r2sinβ,YN=r2cosβ∘ | (4) |
根据式(3)和(4)可求出ξ0和β之间的关系:
| f(ξ0,β)=(XN−x2)Ny2−(YN−y2)Nx2=0 。 | (5) |
根据各坐标系之间的关系将啮合点在坐标系x2O2y2的坐标(x2, y2)转换得到在坐标系x1O1y1的坐标(x1, y1),运动坐标系x2O2y2到x1O1y1的坐标变换矩阵为:
| M12=[cos(α−β)−sin(α−β)esinαsin(α−β)cos(α−β)−ecosα001]。 | (6) |
经过坐标转换得到共轭齿廓的坐标向量:
| [x1y11]=M12[x2y21]。 | (7) |
共轭齿廓方程即:
| {x1=x2cos(α−β)−y2sin(α−β)+esinα,y1=y2cos(α−β)+x2sin(α−β)−ecosα,α/β=z2/z1,f(ξ0,β)=(XN−x2)Ny2−(YN−y2)Nx2=0。 | (8) |
式中:z1为外齿轮齿数,z2为内齿轮齿数。
2 复合摆线齿廓修形由于加工装配误差以及工作时产生的振动和变形等原因,会使齿轮副啮合时产生干涉,因此理论齿廓不能直接使用,需要对摆线齿廓进行修形。齿廓修形的目的是改善轮齿啮合载荷的分布,可以尽可能地使齿轮在受载变形后齿面压力分布均匀,同时还起到提高传动精度、增加齿轮强度、减小振动和噪声的作用。
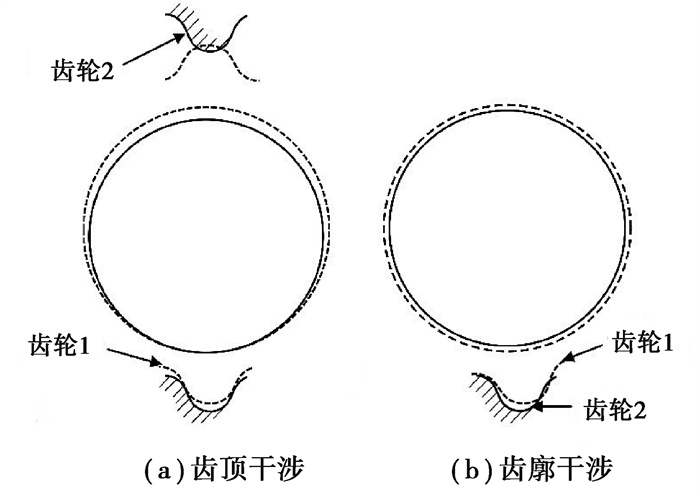
如图 4所示,摆线齿廓可能产生的干涉主要有两种:(a)齿顶干涉,若齿轮因加工误差或运行时产生的振动等原因使齿轮1整体上移,这时在啮合点处的齿就有可能产生干涉;(b)啮合齿廓干涉,若齿轮2因加工误差导致齿厚增加,就会使齿轮副产生齿廓干涉。
|
图 4 齿轮干涉示意图 Fig. 4 Schematic diagram of gear interference |
对复合摆线齿廓的修形可以参考摆线针轮传动中摆线轮的修形[13]。根据《现代机械设计手册》中所述,摆线轮合理的修形应当满足:1)能够形成合理的啮合侧隙和径向间隙来补偿实际的加工和安装误差,并且保证有足够的齿同时啮合;2)齿廓的主要啮合区域应最大限度逼近共轭齿形,使传动平稳;3)工艺简单。摆线齿轮的修形主要有移距修形法、等距修形法、转角修形法。考虑到上文分析的复合摆线齿廓可能发生的干涉情况,在这里采用“负移距+转角”的修形方法,减小齿高和齿厚以增加径向间隙和侧隙,避免干涉产生。选取的复合摆线齿轮副的参数如表 1所示。
| 表 1 复合摆线齿轮副的基本参数 Table 1 Basic parameters of compound cycloidal gear pair |
摆线轮单个齿距偏差Δfpt是指的两个轮齿间在接近齿高中部的一个与摆线轮轴线同轴心的圆上,实际弧长尺寸与公称弧长尺寸的偏差,而径向跳动Δfrt则指的是摆线轮回转表面在同一横剖面内实际表面上各点到基准轴线间距离的最大变动量。根据两者定义,转角修形量以单个齿距偏差为参考,而移距修形量则以径向跳动为参考。根据《JB 10419—2016-T摆线针轮行星传动摆线齿轮和针轮精度》[14]提到的不同精度以及不同齿数的相关偏差数值进行选取,取齿数按照5级精度在标准中查到的Δfpt和Δfrt如表 2所示。
| 表 2 摆线齿轮偏差数值 Table 2 Cycloid gear deviation |
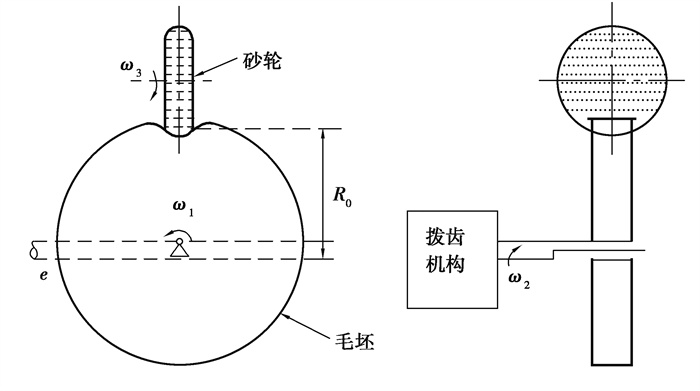
摆线齿廓的具体修形方法如下。首先进行移距修形,在摆线齿轮最后进行精加工时采用砂轮磨削的方法磨削摆线轮齿廓,这时将砂轮向摆线齿轮方向或者向远离摆线齿轮方向移动特定的距离Δ1。如图 5所示,若将摆线齿轮2作为砂轮,齿轮1作为移距修形的齿轮,对齿轮1进行负移距修形就是把齿轮1和齿轮2的中心距增加Δ1。根据复合摆线齿廓方程,经过移距修形后的坐标转换矩阵为:
| M12=[cos(α−β)−sin(α−β)(e+Δ1)sinα1sin(α−β)cos(α−β)−(e+Δ1)cosα001]。 | (9) |
|
图 5 磨削加工原理 Fig. 5 Schematic diagram of grinding process |
齿轮1经过移距修形后的齿廓方程为:
| {x1=x2cos(α−β)−y2sin(α−β)+(e+Δ1)sinα,y1=y2cos(α−β)+x2sin(α−β)−(e+Δ1)cosα,α/β=z2/z1。 | (10) |
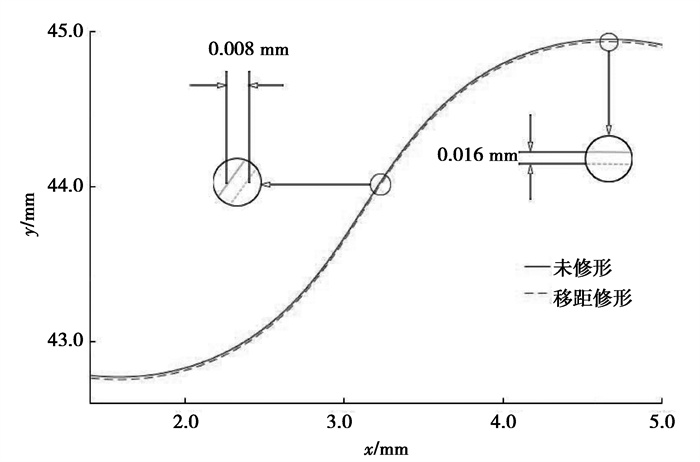
取移距修形量Δ1=Δfrt=0.016 mm,修形后的齿廓如图 6所示。
|
图 6 摆线齿廓移距修形 Fig. 6 Cycloid tooth profile displacement modification |
移距修形可以准确控制齿顶高的修形量,但同时也产生了一定的齿侧间隙,在进行转角修形时要考虑到这一部分的值。转角修形主要是对砂轮在磨削摆线齿轮时偏转了的微小角度δ进行修形。复合摆线的修形与针齿摆线的修形区别较大,通过改变复合摆线的齿形调控参数进行控制,可以达到针齿摆线转角修形的效果。如图 6所示,单边侧隙量达到了0.008 mm,而标准中查取的单个齿距偏差Δfpt为0.008 mm,转化为单边侧隙量0.004 mm,因此转角修形需要将齿厚增大以减小摆线齿轮的侧隙。转角修形的齿廓方程如下:
| {x2=r0cosξ0−(e1−Δ2)cos(z2−1)ξ0−(e1+Δ2)cos(z2+1)ξ0−e2cos(2z2−1)ξ0+e2cos(2z2+1)ξ0,y2=r0sinξ0+(e1−Δ2)sin(z2−1)ξ0−(e1+Δ2)sin(z2+1)ξ0+e2sin(2z2−1)ξ0+e2sin(2z2+1)ξ0; | (11) |
| {x1=x2cos(α−β)−y2sin(α−β)+esinα,y1=y2cos(α−β)+x2sin(α−β)−ecosα,α/β=z2/z1。 | (12) |
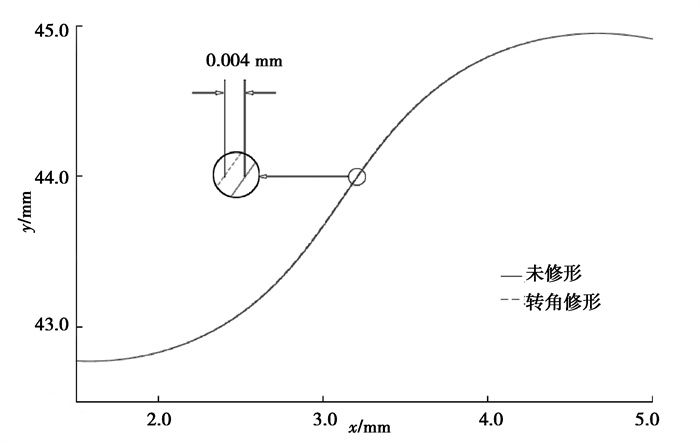
将式(11)中的x2和y2代入式(12),得到转角修形后的摆线齿廓。经过多次尝试,转角修形齿廓侧隙变量和转角修形量Δ2之间存在2倍关系,当转角修形量Δ2取0.002 mm时,齿廓侧隙变量为0.004 mm。修形后的齿廓曲线如下图 7所示。
|
图 7 摆线齿廓转角修形 Fig. 7 Cycloid tooth profile corner modification |
如图 7所示,通过改变齿形调控参数对摆线齿轮进行转角修形,摆线齿廓单边侧隙量增加了0.004 mm,实现了精准的摆线齿廓侧隙调控。
综合以上两种修形方法,得到最终的齿廓方程为:
| {x2=r0cosξ0−(e1−Δ2)cos(z2−1)ξ0−(e1+Δ2)cos(z2+1)ξ0−e2cos(2z2−1)ξ0+e2cos(2z2+1)ξ0,y2=r0sinξ0+(e1−Δ2)sin(z2−1)ξ0−(e1+Δ2)sin(z2+1)ξ0+e2sin(2z2−1)ξ0+e2sin(2z2+1)ξ0; | (13) |
| {x1=x2cos(α−β)−y2sin(α−β)+(e+Δ1)sinα,y1=y2cos(α−β)+x2sin(α−β)−(e+Δ1)cosα,α/β=z2/z1。 | (14) |
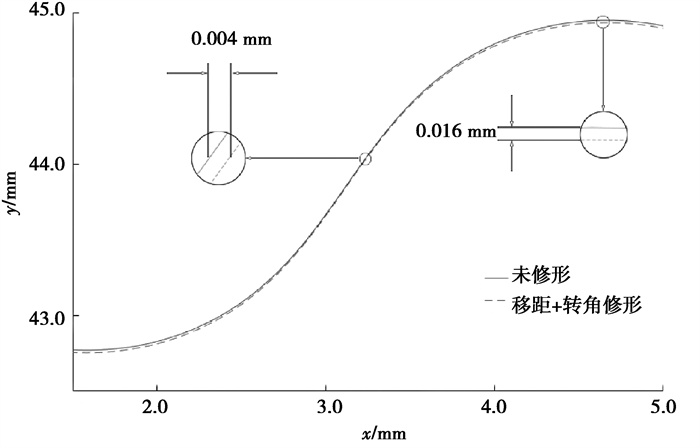
经过“转角+移距”修形后的齿廓曲线如图 8所示。
|
图 8 摆线齿廓转角+移距修形 Fig. 8 Modification of rotation angle and displacement of cycloid tooth profile |
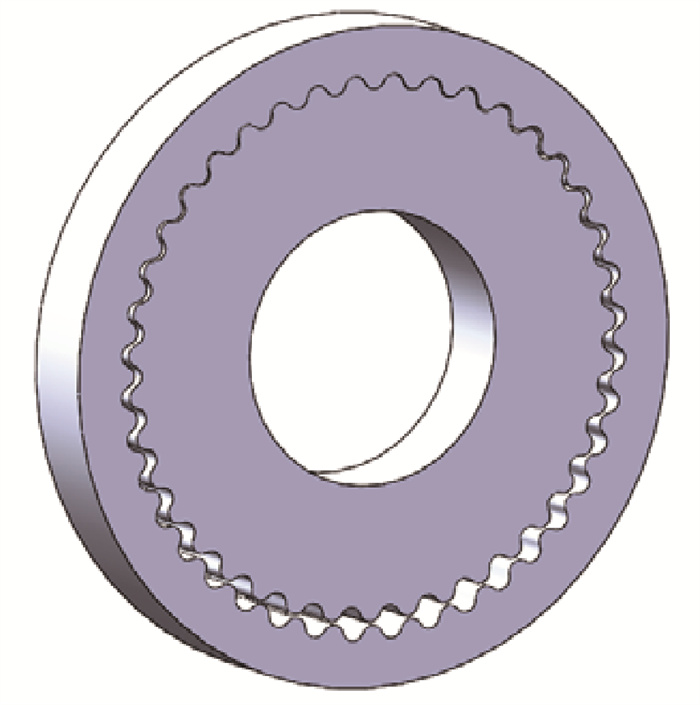
将上文得到的齿廓数据导入到三维建模软件SolidWorks中进行实体建模,齿宽设置为5 mm,建立的复合摆线齿轮副如图 9所示。
|
图 9 复合摆线齿轮副示意图 Fig. 9 Schematic diagram of composite cycloid gear pair |
为了减少网格的数量以提高计算效率,需要对实体模型进行简化。如图 10所示,截取了啮合处附近的轮齿,将网格划分为四面体单元,全局网格尺寸为1 mm,齿面网格尺寸为0.1 mm。内齿轮和外齿轮的材料均设置为40CrMo,材料属性如表 3所示。

|
图 10 简化后的齿轮副有限元模型 Fig. 10 Simplified finite element model of gear pair |
| 表 3 齿轮材料属性 Table 3 Gear material properties |
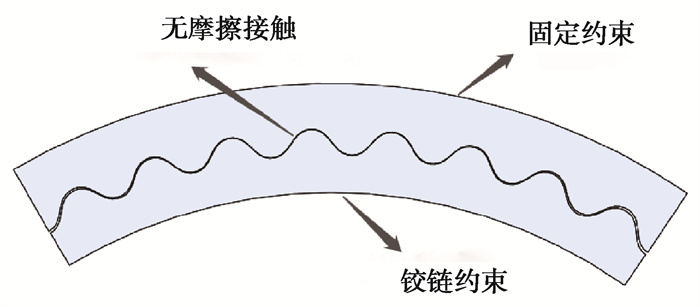
如图 11所示,考虑到行星传动的特点[15],将内齿轮的外圈固定,外齿轮的内圈施加铰链约束并添加扭矩,扭矩大小为200 N·m;两齿面之间设置为无摩擦接触。
|
图 11 边界条件的设定 Fig. 11 Setting of boundary conditions |
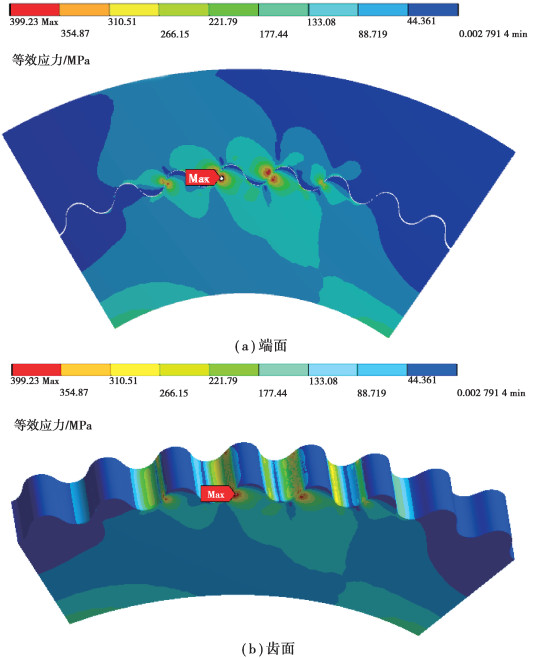
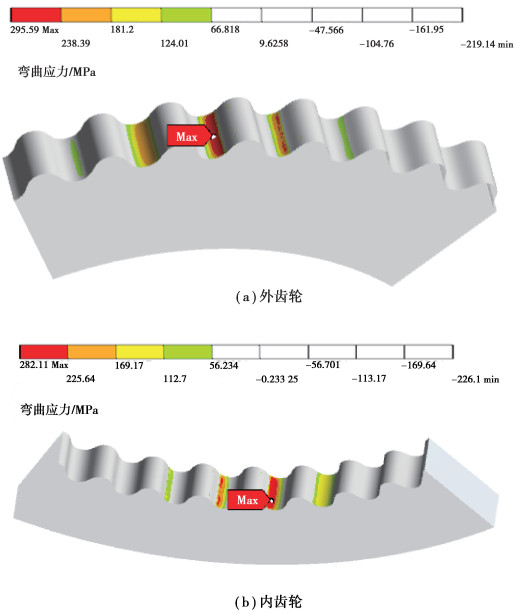
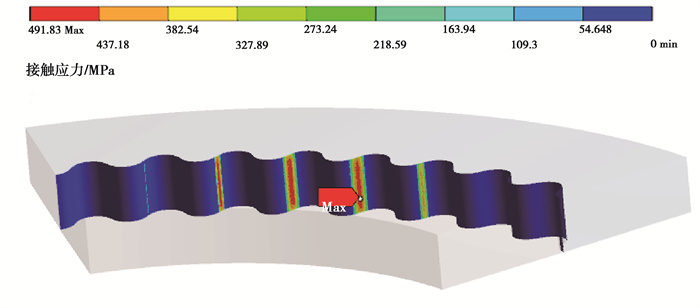
图 12为齿轮副的等效应力云图,可见复合摆线行星齿轮传动为多齿啮合传动,在啮合接触位置应力值最大,为399.2 MPa,且在啮合接触位置呈现典型的赫兹接触的应力分布特征,应力分布呈环形不断扩散;在齿根处有轻微的应力集中区域,而齿顶部分应力很小。图 13为齿轮副受拉侧的齿根弯曲应力云图,由于轮齿的疲劳折断通常发生在受拉侧,所以将受拉侧的弯曲应力作为齿轮的齿根弯曲应力。从云图中可以看出,内、外齿轮的齿根弯曲应力分别为282.1 MPa和295.6 MPa,内齿轮的齿根弯曲应力比外齿轮的略小。图 14为齿轮副的接触应力云图,最大接触应力为491.8 MPa。
|
图 12 摆线齿轮副等效应力云图 Fig. 12 Equivalent stress nephogram of cycloid gear pair |
|
图 13 摆线齿轮副齿根弯曲应力云图 Fig. 13 Tooth root bending stress nephogram of cycloidal gear pair |
|
图 14 摆线齿轮副接触应力云图 Fig. 14 Contact stress nephogram of cycloidal gear pair |
根据式(1)~(8)可知,影响复合摆线齿轮齿廓的参数有半径r0、齿数z1和z2、连杆长度e1、e2。为了使参数不失一般性,这里引入模数m,令:
| {r0=mz,e1=mh1,e2=f1e1。 | (15) |
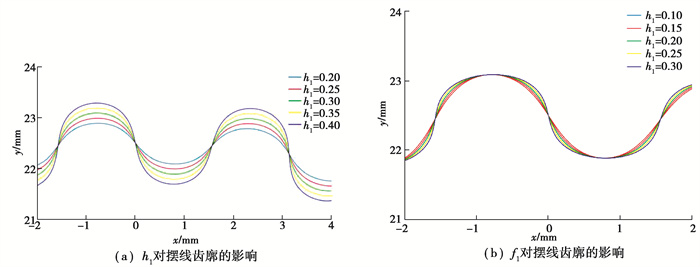
如图 15(a)所示,f1的取值为0.2,h1的取值分别是0.20,0.25,0.30,0.35,0.40,随着h1增大,摆线齿廓逐渐增高,定义h1为摆线齿廓的齿高调节系数。同时,随着齿高调控系数增大,分度圆和齿顶圆之间的齿厚增加,而分度圆与齿根圆之间的齿厚减小;如图 15(b)所示,h1的取值为0.30,f1的取值分别是0.10,0.15,0.20,0.25,0.30,随着f1增加,摆线齿廓的齿形发生变化,分度圆和齿顶圆之间的齿厚增加,而分度圆与齿根圆之间的齿厚减小,定义f1为齿形调节系数。
|
图 15 齿廓参数对复合摆线齿形的影响 Fig. 15 Influence of tooth profile parameters on the profile of composite cycloid |
由于齿数由减速比决定,所以应选取模数m,齿高调节系数h1以及齿形调节系数f1作为变量去优化复合摆线齿廓的力学性能。
4.1 模数对齿轮副应力的影响规律分析为了研究模数对齿轮副应力的影响,取模数m分别为1.0, 1.5, 2.0, 2.5 mm,齿轮副的其他结构参数和作用载荷见表 4。
| 表 4 齿轮参数和作用载荷 Table 4 Gear parameters and load |
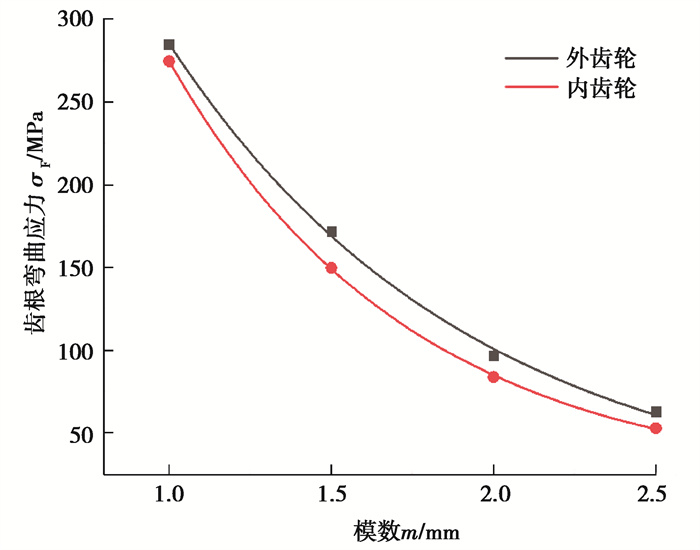
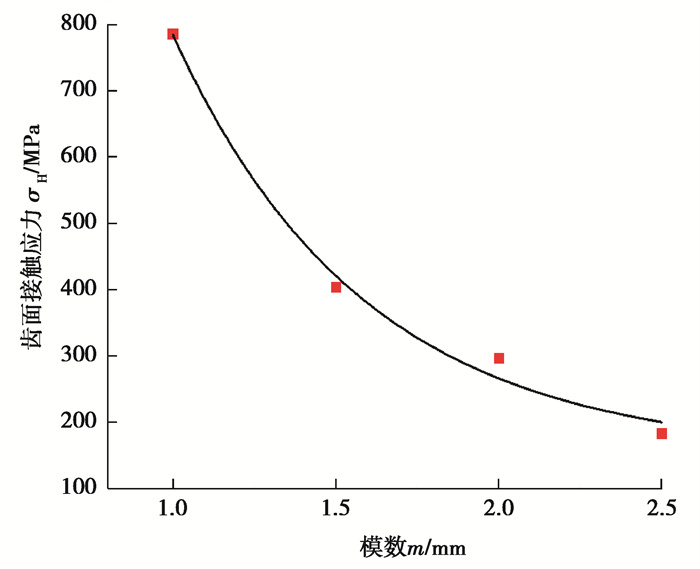
经仿真计算,得到不同模数下齿轮副的应力变化曲线如图 16~17所示。
|
图 16 不同模数齿轮的齿根弯曲应力 Fig. 16 Tooth root bending stress of gears with different modules |
|
图 17 不同模数齿轮副的接触应力 Fig. 17 Contact stress of gear pairs with different modules |
可见,随着模数增大,两齿轮齿根弯曲应力以及齿面接触应力显著减小,因此,在可能的情况下,可以取较大的模数以提高齿轮副的承载能力;当模数为1.0 mm时,根据表 3数据可知,此时齿轮副的接触应力已经超过许用接触应力,而齿根弯曲应力只达到许用弯曲应力的一半,所以,齿轮副的承载能力主要受限于齿面接触疲劳强度。
4.2 齿高调节系数对齿轮副应力的影响规律分析为了研究齿高调节系数对齿轮副应力的影响,取齿高调节系数h1分别为0.20、0.25、0.30、0.35、0.40,齿轮副的其他结构参数和作用载荷见表 5。
| 表 5 不同齿高调节系数的齿轮参数和作用载荷 Table 5 Gear parameters and load of different tooth height adjustment coefficients |
经仿真计算,得到不同齿高调节系数下齿轮副的应力变化曲线如图 18、19所示。
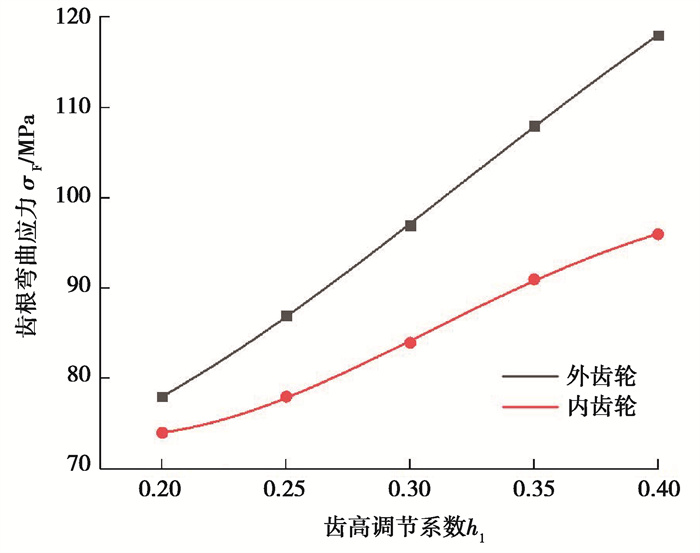
|
图 18 不同齿高调节系数下齿轮的齿根弯曲应力 Fig. 18 Tooth root bending stress of gears with different tooth height adjustment coefficients |

|
图 19 不同齿高调节系数下齿轮副的接触应力 Fig. 19 Contact stress of gear pairs with different tooth height adjustment coefficients |
可见,随着齿高调节系数增大,两齿轮齿根弯曲应力增大,齿面接触应力减小。对承载能力起决定性作用的是齿面接触强度,因此在其他条件满足时,选择较大的齿高调节系数可以提高齿轮副的承载能力。
4.3 齿形调节系数对齿轮副应力的影响规律分析为了研究齿形调节系数对齿轮副应力的影响,取齿形调节系数f1分别为0.100、0.125、0.150、0.175、0.200,齿轮副的其他结构参数和作用载荷见表 6。
| 表 6 不同齿形调节系数的齿轮参数和作用载荷 Table 6 Gear parameters and load of different tooth profile adjustment coefficients |
经仿真计算,得到不同齿形调节系数下齿轮副的应力变化曲线如图 20、21所示。
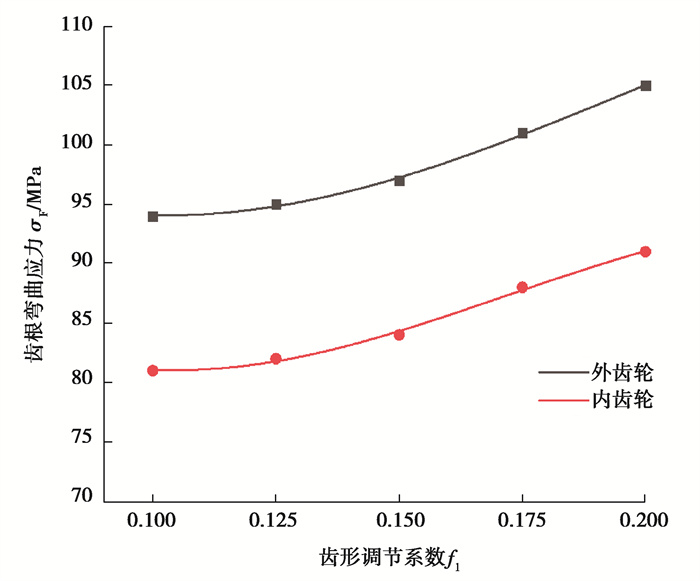
|
图 20 不同齿形调节系数下齿轮的齿根弯曲应力 Fig. 20 Tooth root bending stress of gears with different tooth profile adjustment coefficients |
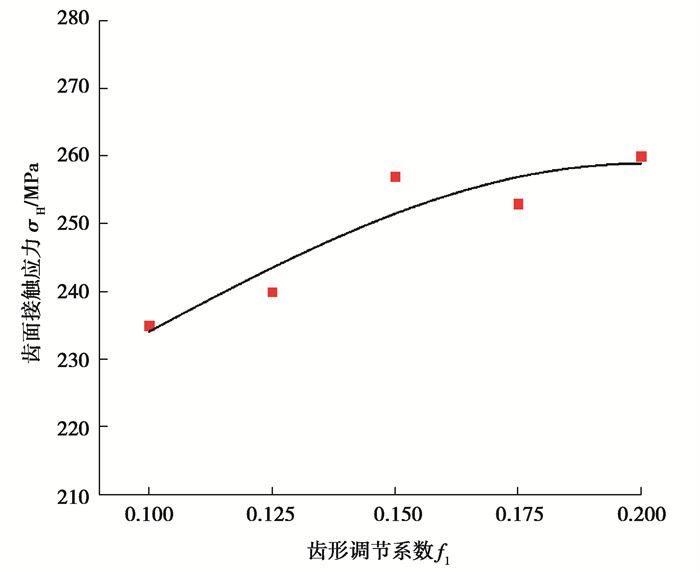
|
图 21 不同齿形调节系数下齿轮副的接触应力 Fig. 21 Contact stress of gear pairs with different tooth profile adjustment coefficients |
可见,随着齿形调节系数的增大,齿轮齿根弯曲应力和齿面接触应力都有所增大,不过,这种影响很小,即减小齿形调节系数对齿轮副承载能力的提高作用有限。
5 结语1) 复合摆线行星齿轮传动为多齿啮合传动,在啮合接触的位置应力最大,且呈现典型的赫兹接触的应力分布特征,应力分布呈环形不断扩散,在齿根有轻微的应力集中区域,且内齿轮的齿根弯曲应力比外齿轮的略小。
2) 移距修形可以准确控制齿顶高的修形量,但同时也产生了一定的齿侧间隙,而转角修形的齿廓侧隙的值和转角修形量Δ2之间存在2倍关系,通过转角修形可以精确地调整侧隙。因此,通过移距修形和转角的组合修形方法能够得到期望的顶隙和侧隙,且修形后的齿廓主要啮合区域比较接近共轭齿形。
3) 影响复合摆线齿轮齿廓的参数有模数m、齿数z1和z2、齿高调节系数h1和齿形调节系数f1。由于齿数是由传动比决定的,因此在摆线齿廓设计时,应重点关注模数m、齿高调节系数h1、齿形调节系数f1。
4) 摆线齿轮副的承载能力主要受限于齿面接触疲劳强度,且受模数影响最大,受齿高调节系数影响次之,而受齿形调节系数影响最小。在可能的情况下,应选取较大的模数、较大的齿高调节系数和较小的齿形调节系数,以提高齿轮副的承载能力。
| [1] |
张也, 李朝阳, 黄多. 多因素综合作用的摆线针轮传动误差分析[J]. 重庆大学学报, 2020, 43(12): 1-12. Zhang Y, Li C Y, Huang D. Transmission error analysis of cycloidal pinwheel based on multi-factor comprehensive effect[J]. Journal of Chongqing University, 2020, 43(12): 1-12. (in Chinese) |
| [2] |
Wang Y L, Qian Q J, Chen G D, et al. Multi-objective optimization design of cycloid pin gear planetary reducer[J]. Advances in Mechanical Engineering, 2017, 9(9): 168781401772005. DOI:10.1177/1687814017720053 |
| [3] |
Xu L X. A method for modelling contact between circular and non-circular shapes with variable radii of curvature and its application in planar mechanical systems[J]. Multibody System Dynamics, 2017, 39(3): 153-174. DOI:10.1007/s11044-016-9549-0 |
| [4] |
韩振华, 石万凯, 肖洋轶, 等. 新型复合摆线外啮合圆柱齿轮副的传动特性分析[J]. 西安交通大学学报, 2016, 50(9): 10-19, 131. Han Z H, Shi W K, Xiao Y Y, et al. Analysis on transmission characteristics of novel composite cycloid cylindrical gears for external driving[J]. Journal of Xi'an Jiaotong University, 2016, 50(9): 10-19, 131. (in Chinese) |
| [5] |
Pollitt E P. Some applications of the cycloid in machine design[J]. Journal of Engineering for Industry, 1960, 82(4): 407-414. DOI:10.1115/1.3664265 |
| [6] |
Lai T S. Design and machining of the epicycloid planet gear of cycloid drives[J]. The International Journal of Advanced Manufacturing Technology, 2006, 28(7/8): 665-670. |
| [7] |
Zhu C C, Liu M Y, Du X S, et al. Analysis on transmission characteristics of new axis-fixed cycloid gear[J]. Advanced Materials Research, 2010, 97/98/99/100/101: 60-63. |
| [8] |
贵新成, 詹隽青, 叶鹏, 等. 高重合度内啮合复合摆线齿轮传动设计与分析[J]. 机械工程学报, 2017, 53(1): 55-64. Gui X C, Zhan J Q, Ye P, et al. Design and analysis of internal compound cycloid gear transmission with high contact ratio[J]. Journal of Mechanical Engineering, 2017, 53(1): 55-64. (in Chinese) |
| [9] |
Han Z H, Shi W K, Liu C, et al. Geometry generation principle and meshing properties of a new gear drive[J]. Journal of Advanced Mechanical Design, Systems, and Manufacturing, 2018, 12(1): JAMDSM0012. DOI:10.1299/jamdsm.2018jamdsm0012 |
| [10] |
石万凯, 徐浪, 韩振华, 等. 复合摆线少齿差行星传动的啮合性能分析[J]. 华南理工大学学报(自然科学版), 2017, 45(2): 66-74. Shi W K, Xu L, Han Z H, et al. Analysis of meshing properties of composite cycloid planetary driving with small teeth difference[J]. Journal of South China University of Technology (Natural Science Edition), 2017, 45(2): 66-74. (in Chinese) |
| [11] |
刘昶, 石万凯, 韩振华, 等. 基于插齿刀具运动控制的复合摆线齿轮加工方法[J]. 华南理工大学学报(自然科学版), 2018, 46(2): 31-37. Liu C, Shi W K, Han Z H, et al. Machining method of composite cycloid gear based on the kinematic control of shaping cutter[J]. Journal of South China University of Technology (Natural Science Edition), 2018, 46(2): 31-37. (in Chinese) |
| [12] |
黄思语, 王博, 曾星宇, 李俊阳. 少齿差金属橡胶复合摆线齿轮副动态特性分析[J/OL]. 重庆大学学报: 1-15[2021-05-01]. http://kns.cnki.net/kcms/detail/50.1044.N.20210202.1424.002.html. Huang S Y, Wang B, Zeng X Y, et al. Dynamic characteristic analysis of metal rubber compound cycloid gear pair with small tooth difference[J/OL]. Journal of Chongqing University: 1-15[2021-05-01]. http://kns.cnki.net/kcms/detail/50.1044.N.20210202.1424.002.html. (in Chinese) |
| [13] |
秦大同, 谢里阳. 现代机械设计手册[M]. 北京: 化学工业出版社, 2019. Qin D T, Xie L Y. Modern machinery design manual[M]. Beijing: Chemical Industry Press, 2019. (in Chinese) |
| [14] |
中华人民共和国国家发展和改革委员会. 中华人民共和国机械行业推荐性行业标准: 摆线针轮行星传动摆线齿轮和针轮精度JB/T 10419—2005[S]. 北京: 机械工业出版社. National Development and Reform Commission of the People's Republic of China. Machinery Standard of the People's Republic of China: Accuracy of cycloidcl gear and pin wheel for cycloidcl drives. JB/T 10419—2005[S]. Beijing: China Machine Press. (in Chinese) |
| [15] |
Feng S, Chang L H, He Z X. A hybrid finite element and analytical model for determining the mesh stiffness of internal gear pairs[J]. Journal of Mechanical Science and Technology, 2020, 34(6): 2477-2485. |
 2022, Vol. 45
2022, Vol. 45



