b. 成都工业学院 大数据与人工智能学院, 成都 611730
b. School of Big Data and Artificial Intelligence, Chengdu Technological University, Chengdu 611730, P. R. China
地质勘查能够给社会带来重要的能源资源。然而,在野外地质勘查中,各种不可预知的因素给采集到的地震数据带来随机噪声干扰,使地震剖面分辨率不高,不利于地震数据解释,因而需要对地震数据的随机噪声进行消除[1]。为了去除随机噪声,学者们根据随机噪声与有效信号的差异,提出了一些随机噪声消除方法,如K-L变换、傅里叶变换、倾斜叠加法等。这些降噪方法需要数据的一些先验条件,但实际上地震数据受到的人为影响、机器影响、地质环境影响等干扰是无法预知的。因此,这些算法降噪效果不佳[2]。近年来,盲源分离[3]中的ICA算法[4]、FASTICA算法[5]、JADE算法[6]等也广泛应用于地震数据降噪,但是盲源分离方法要求各个信号是相互独立而且高斯信号最多为一个,彼此之间的混合不复杂[2]。地震数据埋藏较深,受到干扰影响严重,各种数据信息并非线性混合,利用盲源分离进行地震数据降噪存在缺陷。在随机噪声降噪中,小波降噪具有一定的处理优势,因为小波变换不仅具有良好的时频局部变换特征,还具有“时间频率”窗口自适应特征,号称信号降噪的“显微镜”[7]。小波变换降噪主要通过小波分解把地震数据分解到低频和高频不同尺度空间上,通过选取合理阈值方法对各尺度上的小波系数进行噪声压制,然后利用小波重构变换恢复原始信号[8]。在阈值处理中,应用最广泛的是Donoho软硬阈值降噪算法[9],然而该类阈值算法由于算法特性使降噪具有一定的缺陷性。软阈值降噪算法通过恒定的方式压缩小波系数,会丢失某些有效的高频信号;硬阈值降噪算法处理后的小波系数在阈值处不连续,给重构信号带来振荡,降噪后的信号不光滑。因此直接利用软硬阈值降噪效果不理想[10]。但是软阈值法处理后的小波系数具有连续性,硬阈值能够避免软阈值法以恒定的方式压缩小波系数的影响[10]。因此,笔者在软硬阈值降噪原理基础上,结合其降噪的优点,设计了一种改进的软硬阈值降噪方法,以弥补软硬阈值降噪的不足,提高地震数据降噪效果。
1 新阈值降噪算法 1.1 算法基础对于一组观测信号:
| $ f(t)=s(t)+n(t), $ | (1) |
式中:f(t)是含有噪声的观测信号,s(t)是有效信号,n(t)是随机干扰信号。
如果有N个采样点,对观察信号f(t)的一维小波变化[11]如下:
| $ W_{j, k}=2^{\frac{j}{2}} \sum\limits_{n=0}^{N} f(n) \psi\left(2^{-j} n-k\right), $ | (2) |
式中:Wj, k为小波系数,ψ(t)为一个母小波。一维离散小波重构变换、二维小波分解和重构变换见文献[1]。对分解的小波系数利用软、硬阈值函数进行去噪。
软、硬阈值降噪原理为[12]:
| $\hat{W}_{j, k}= \begin{cases}\operatorname{sgn}\left(W_{j, k}\right)\left(\left|W_{j, k}\right|-\lambda\right), & \left|W_{j, k}\right| \geqslant \lambda ; \\ 0, & \left|W_{j, k}\right| <\lambda_{0}\end{cases} $ | (3) |
| $\hat{W}_{j, k}= \begin{cases}W_{j, k}, & \left|W_{j, k}\right| \geqslant \lambda ; \\ 0, & \left|W_{j, k}\right| <\lambda。\end{cases} $ | (4) |
式中:sgn(·)为符号函数;λ为阈值,
经过软阈值降噪处理后的小波系数整体上具有连续性,然而对大于阈值的信号进行恒定方式压缩,会去除一些高频信号,因此经过小波重构的信号不能代表真实信息。硬阈值降噪能够避免软阈值降噪恒定偏差的影响,但是处理后的小波系数在阈值处不具有连续性,很有可能给重构数据带来振荡影响,使原信息光滑度变差。因此在软、硬阈值降噪原理基础上提出了一种改进的新阈值降噪算法,以弥补软、硬阈值降噪的缺陷。
1.2 新阈值降噪算法在软、硬阈值基础上设计的新的阈值降噪函数如下:
| $ \hat{W}_{j, k}=\left\{\begin{array}{l} (1-\nu) W_{j, k}+\sqrt{\nu(2-\nu)} \operatorname{sgn}\left(W_{j, k}\right)\left(\left|W_{j, k}\right|-\lambda\right), \quad\left|W_{j, k}\right| \geqslant \lambda ;\\ 0, \quad\left|W_{j, k}\right| <\lambda。\end{array}\right. $ | (5) |
式中:
1) 当β→0时,
2) 当Wj, k→λ,ν→1时,
3) 当Wj, k→∞,ν→0时,
可见,新阈值降噪函数同时具备软、硬阈值函数降噪功能。其优点是不仅避免了软阈值函数在恒定偏差上的影响,还克服了硬阈值函数在阈值处的不连续性影响。因此新阈值降噪更具有优势。
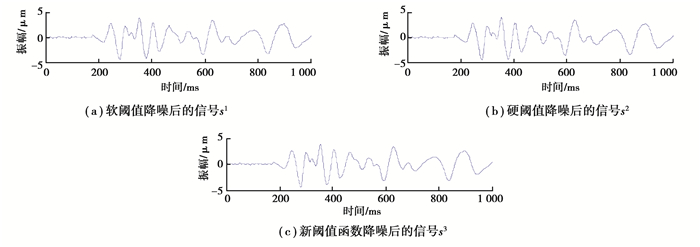
2 仿真实验为了确定新阈值降噪算法的有效性,选取采样间隔1 ms,采样点为1 000的有效信号s(图 1(a)),给s添加随机噪声获得观测信号o(图 1(b)),选取三层小波分解[2, 13],利用软、硬阈值函数,新阈值函数分别对观测信号进行噪声压制,再通过小波重构信号得到降噪后的有效信号(图 2)。由图 2知,经过新阈值降噪,信号的峰值毛刺干扰被消除,几乎无信号损失和失真,对噪声进行了有效消除,降噪效果优于软、硬阈值降噪。

|
图 1 原始信号 Fig. 1 The original signal |
|
图 2 降噪处理 Fig. 2 The data denoising |
用信噪比(SNR)和均方根误差(RMSE)对软、硬阈值函数和新阈值函数的降噪效果进行评价[14]。
| $ \mathrm{SNR}=10 \times \lg \left\{\frac{\sum\limits_{k=1}^{n} x^{2}(k)}{\sum\limits_{k=1}^{n}\left[x(k)-x^{\prime}(k)\right]^{2}}\right\}; $ | (6) |
| $\mathrm{RMSE}=\sqrt{\frac{1}{n} \sum\limits_{k=1}^{n}\left[x(k)-x^{\prime}(k)\right]^{2}} 。$ | (7) |
式中:x(k)为原始观测信号;x′(k)为降噪后的信号;SNR值越大,降噪效果越好;RMSE值越小,降噪效果越好。
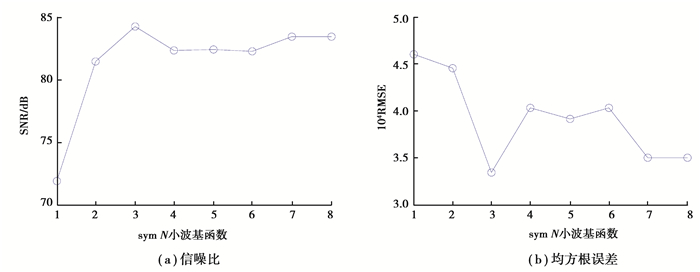
经计算,软、硬阈值函数和新阈值函数降噪后的SNR和RMSE如表 1所示。由表 1知,新阈值降噪的SNR最大,RMSE最小,从而进一步说明新阈值降噪较软、硬阈值函数降噪更合理。目前在小波变换中常用的小波基有sym N系列、db N系列等,而地震数据降噪常选取sym N系列[15]。因此选取不同的sym N,利用式(6)和(7),得出不同sym N下新阈值函数降噪后的信号SNR和RMSE(图 3)。由图 3知,sym 3的SNR最大,RMSE最小。因此新阈值函数选取sym 3,降噪效果最佳。
| 表 1 不同阈值函数信噪比和均方根误差 Table 1 The SNR and RMSE with different threshold functions |
|
图 3 不同sym N小波基的信噪比和均方根误差 Fig. 3 The SNR and RMSE with different values of sym N |
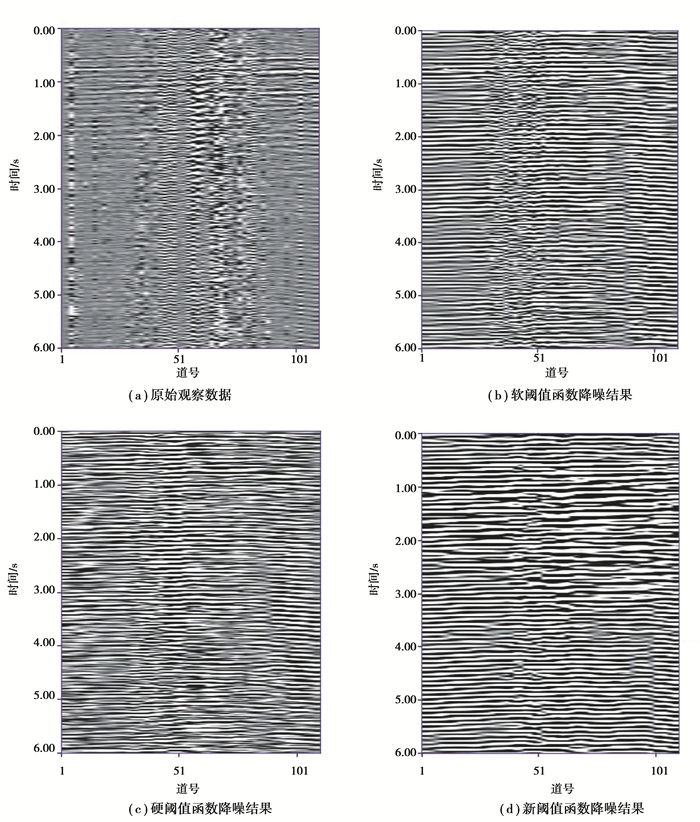
将提出的新阈值函数用于实际地震数据降噪处理,数据来自中国地质调查局计划项目(1212010916040),数据样本采样间隔道号为1,采样点数为6 000,采样间隔为1 ms。为了便于显示,截取其中的1~111道地震信号数据进行降噪处理(图 4(a))。由图 4(a)知,原始地震数据剖面被随机噪声干扰严重,分辨率低,看不出地震数据形态,不利后期地质解释。因此,选取小波基为sym 3,3层小波分解。利用小波变换中的软、硬阈值函数对原始地震数据进行降噪,降噪后的信号分别如图 4(b)(c)所示。由图 4(b)(c)知,软、硬阈值函数能够去除地震数据大部分干扰噪声,地震分辨率有所改善,然而降噪效果不理想,仍然存在大量噪声影响地震剖面,分辨不高。利用所提出的新阈值函数对原始地震数据进行降噪处理,降噪后的信号结果如图 4(d)所示。由图 4(d)知,整个降噪后的地震剖面数据双曲线特征明显,纹理清晰,分辨率高,几乎所有干扰噪声均被移除,表明新阈值函数降噪效果比软、硬阈值函数降噪效果更理想。
|
图 4 地震数据降噪 Fig. 4 The seismic data denoising |
在软、硬阈值函数降噪基础上提出了一种新阈值降噪函数,结论如下:
1) 新的阈值降噪函数同时具备软、硬阈值降噪函数功能,其优点是避免了软阈值函数在恒定偏差上的影响,也避免了硬阈值函数在阈值处的不连续性影响;
2) 通过仿真实验确定了新阈值函数的小波基为sym 3,信噪比(SNR)和均方根误差(RMSE)结果表明新阈值函数降噪效果更好;
3) 在实际数据降噪处理中,新阈值函数能够去除地震数据的各类干扰噪声,降噪后的地震剖面分辨率高,对比软、硬阈值函数结果表明新阈值函数降噪更有效。
| [1] |
秦飞龙. 二维盲小波算法及其在金属地震数据降噪处理中的研究[D]. 成都: 成都理工大学, 2013. Qin F L. 2D blind-wavelet algorithm and its application in the processing of de-noising on metal seismic data[D]. Chengdu: Chengdu University of Technology, 2013. (in Chinese) |
| [2] |
Qin F L, Liu J, Yan W Y. The improved ICA algorithm and its application in the seismic data denoising[J]. Journal of Chongqing University English Edition, 2018, 17(4): 162-170. |
| [3] |
刁瑞, 吴国忱, 尚新民, 等. 地面阵列式微地震数据盲源分离去噪方法[J]. 物探与化探, 2017, 41(3): 521-526. Diao R, Wu G C, Shang X M, et al. The blind separation denoising method for surface array micro-seismic data[J]. Geophysical and Geochemical Exploration, 2017, 41(3): 521-526. (in Chinese) |
| [4] |
Safont G, Salazar A, Vergara L, et al. Nonlinear estimators from ICA mixture models[J]. Signal Processing, 2019, 155: 281-286. DOI:10.1016/j.sigpro.2018.10.003 |
| [5] |
Jiang S C, Lin P, Chen Y M, et al. Mixed-signal extraction and recognition of wind turbine blade multiple-area damage based on improved Fast-ICA[J]. Optik, 2019, 179: 1152-1159. DOI:10.1016/j.ijleo.2018.10.137 |
| [6] |
Piotrowski A P, Napiorkowski J J. Step-by-step improvement of JADE and SHADE-based algorithms: success or failure?[J]. Swarm and Evolutionary Computation, 2018, 43: 88-108. DOI:10.1016/j.swevo.2018.03.007 |
| [7] |
程鲁, 秦飞龙, 张津, 等. 改进的Mallat算法在金属地震数据降噪处理中的应用[J]. 桂林理工大学学报, 2017, 37(4): 602-607. Cheng L, Qin F L, Zhang J, et al. Application of improved Mallat algorithm in noise reduction processing of metal seismic data[J]. Journal of Guilin University of Technology, 2017, 37(4): 602-607. (in Chinese) DOI:10.3969/j.issn.1674-9057.2017.04.007 |
| [8] |
宋立业, 周乐, 刘昕明. 基于邻域相关性多阈值新函数寻优法的小波降噪分析[J]. 信息与控制, 2019, 48(1): 57-64. Song L Y, Zhou L, Liu X M. Wavelet denoising analysis based on an optimization method of multi-threshold new function with neighborhood correlation[J]. Information and Control, 2019, 48(1): 57-64. (in Chinese) |
| [9] |
Donoho D L, Johnstone I M. Ideal spatial adaptation by wavelet shrinkage[J]. Biometrika, 1994, 81(3): 425-455. DOI:10.1093/biomet/81.3.425 |
| [10] |
刘书俊, 李生林, 蒋明, 等. 一种基于加权平均的改进型小波阈值降噪算法[J]. 化工自动化及仪表, 2017, 44(3): 239-242, 318. Liu S J, Li S L, Jiang M, et al. An improved wavelet threshold de-noising algorithm based on weighted average method[J]. Control and Instruments in Chemical Industry, 2017, 44(3): 239-242, 318. (in Chinese) |
| [11] |
Wang G X, Chen L, Guo S, et al. Application of a new wavelet threshold method in unconventional oil and gas reservoir seismic data denoising[J]. Mathematical Problems in Engineering, 2015, 2015: 1-7. |
| [12] |
Bayer F M, Kozakevicius A J, Cintra R J. An iterative wavelet threshold for signal denoising[J]. Signal Processing, 2019, 162: 10-20. DOI:10.1016/j.sigpro.2019.04.005 |
| [13] |
Cotronei M, Rossini M, Sauer T, et al. Filters for anisotropic wavelet decompositions[J]. Journal of Computational and Applied Mathematics, 2019, 349: 316-330. DOI:10.1016/j.cam.2018.09.015 |
| [14] |
成枢, 马卫骄, 牛英杰, 等. 融合加权平均的改进小波阈值函数的测量数据处理[J]. 中国科技论文, 2018, 13(15): 1811-1816. Cheng S, Ma W J, Niu Y J, et al. Measurement data processing of improved wavelet threshold function with weighted average[J]. China Sciencepaper, 2018, 13(15): 1811-1816. (in Chinese) DOI:10.3969/j.issn.2095-2783.2018.15.020 |
| [15] |
周仲礼, 秦飞龙, 夏欢欢, 等. 盲小波算法在金属矿床地震资料去噪处理中的应用[J]. 成都理工大学学报(自然科学版), 2013, 40(2): 120-124. Zhou Z L, Qin F L, Xia H H, et al. Application of blind wavelet algorithm to de-noising of the metallic ore deposit seismic data[J]. Journal of Chengdu University of Technology(Science & Technology Edition), 2013, 40(2): 120-124. (in Chinese) |
 2022, Vol. 45
2022, Vol. 45


